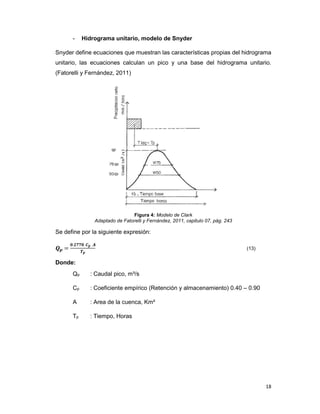
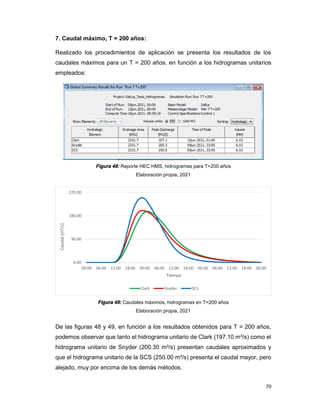
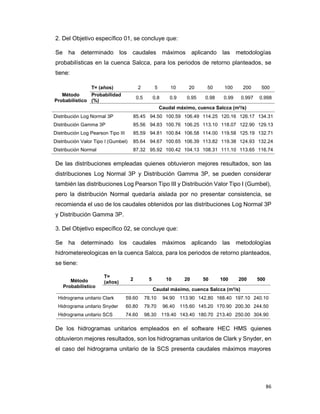
Este documento presenta la tesis de grado de Iván Fritz Zela Galiano para obtener el título de Ingeniero Civil. La tesis determina los caudales máximos en el río Salcca en Cusco, Perú aplicando metodologías probabilísticas e hidrometereológicas. El estudio analiza series históricas de datos de caudales y precipitaciones, y utiliza métodos como SCS y análisis de frecuencias para calcular caudales máximos de retornos de 2, 5, 10, 20, 50, 100, 200 y 500 años. El objet