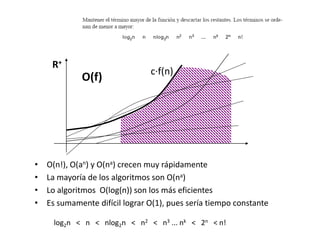
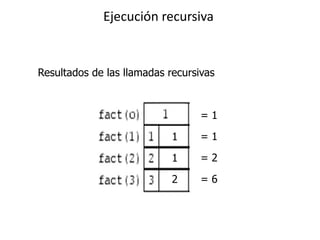
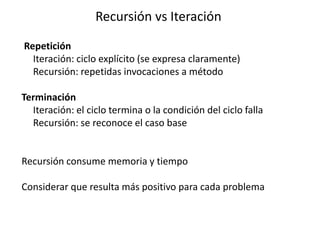
El documento describe conceptos clave sobre recursividad y eficiencia de algoritmos. Explica que la recursividad implica que un método se llame a sí mismo, y debe contener un caso base y uno recursivo. También cubre temas como bucles, notación asintótica, y ejemplos como factoriales y búsqueda binaria que ilustran el enfoque "dividir para vencer".

1. Estructuras de Datos
Miguel Realpe
mrealpe@fiec.espol.edu.ec

2. La eficiencia de un algoritmo es la propiedad mediante la cual un
algoritmo debe alcanzar la solución al problema en el tiempo más corto
posible o utilizando la cantidad más pequeña posible de recursos físicos y
que sea compatible con su exactitud o corrección
Se puede expresar mediante una función:
f (n) = eficiencia
Es decir, la eficiencia del algoritmo se examina como una función del
número de elementos que tienen que ser procesados.
Eficiencia de un programa

3. En los bucles se repiten las sentencias del cuerpo del bucle un número
determinado de veces
f(n) = n
f(n) = n / 2
Bucles lineales

4. Bucle en el que su variable de control se multiplica o divide dentro de
dicho bucle.
f(n) = [log2 n]
Bucles algorítmicos

5. El total de iteraciones es el producto del número de iteraciones del bucle
interno y el número de iteraciones del bucle externo.
Para i de 1 a n
Para j de 1 a n
escribir i+j
fpara
fpara
n n*n -> n2
Bucles anidados

6. • f(n)
Nos indica el tiempo de ejecución
• Un algoritmo A es “mejor” que otro B si
Al aumentar el tamaño del datos aumenta su tiempo de ejecución en
un grado menor al de B
• Lo que nos interesa es la velocidad del crecimiento de f(n)
Y se conoce como Notación Asintótica (‘O grande’)
Comparando la eficiencia

7. O(f(n))
• O(n!), O(an) y O(na) crecen muy rápidamente
• La mayoría de los algoritmos son O(na)
• Lo algoritmos O(log(n)) son los más eficientes
• Es sumamente difícil lograr O(1), pues sería tiempo constante
R+
c·f(n)
O(f)
log2n < n < nlog2n < n2 < n3 ... nk < 2n < n!

8. Propiedad que posee un método por la cual puede llamarse a sí mismo.
Usualmente es menos eficiente en términos de tiempo y uso de recursos de
computadora que una solución iterativa
metodo1(...)
{
...
metodo1();
...
}
Recursividad

9. Los métodos recursivos se componen de:
– Caso base o condición de parada: una solución simple para un caso
particular (puede haber más de un caso base).
– Caso recursivo: una solución que involucra volver a utilizar la función
original con parámetros que se acercan más al caso base.
Ni el paso base ni el paso recursivo son necesariamente únicos.
Recursividad

10. Los pasos que sigue el caso recursivo son los siguientes:
1. El procedimiento se llama a sí mismo
2. El problema se resuelve tratando el mismo problema pero de
tamaño menor
3. La manera en la cual el tamaño del problema disminuye
asegura que el caso base eventualmente se alcanzará
Para que funcione la recursión el progreso de las llamadas debe tender
a la condición de parada.
Recursividad

11. Escribir un programa que calcule el factorial (!) de un entero no negativo.
Por ejemplo:
0! = 1  1
1! = 1  1
2! = 2  2 * 1
3! = 6  3 * 2 * 1
4! = 24  4 * 3 * 2 * 1
5! = 120  5 * 4 * 3 * 2 * 1
n! 
= 1 * 0!
= 2 * 1!
= 3 * 2!
= 4 * 3!
= 5 * 4!
= n * (n – 1)!
= 1
Ejemplo: Factorial

12. 1 si n = 0 (base)
n ! =
n * (n – 1) ! si n > 0 (recursión)
Ejemplo: Factorial

13. public int factorial (int n) {
if (n = = 0)
return 1;
else
return n * factorial (n-1);
}
Es importante determinar un
caso base, es decir un punto en
el cual existe una condición que
no requiera volver a llamar a la
misma función.
Ejemplo: Factorial (recursivo)

14. Llamadas recursivas
Ejecución recursiva

15. Resultados de las llamadas recursivas
= 1
= 11
= 21
2 = 6
Ejecución recursiva

16. Ejecución recursiva

17. ¿Qué pasa si se hace una llamada recursiva que no termina?
• Cada llamada recursiva almacena los parámetros que se
pasaron al procedimiento, y otras variables necesarias para el
correcto funcionamiento del programa.
• Por lo tanto si se produce una llamada recursiva infinita, llega
un momento en que no quedará memoria para almacenar más
datos, y en ese momento se abortará la ejecución del programa
Recursividad

18. public int factorial (int n) {
int fact = n;
for (int i = n-1; i > 0; i--)
fact = fact* i;
return fact;
}
Ejemplo: Factorial (iterativo)

19. Repetición
Iteración: ciclo explícito (se expresa claramente)
Recursión: repetidas invocaciones a método
Terminación
Iteración: el ciclo termina o la condición del ciclo falla
Recursión: se reconoce el caso base
Recursión consume memoria y tiempo
Considerar que resulta más positivo para cada problema
Recursión vs Iteración

20. Permite especificar soluciones naturales, sencillas, que serían, en caso
contrario, difíciles de resolver.
Existen ciertas estructuras cuya definición es recursiva, tales como los árboles, y
los algoritmos que utilizan árboles suelen ser en general recursivos.
• LA RECURSIVIDAD SE DEBE USAR CUANDO SEA REALMENTE NECESARIA, ES
DECIR, CUANDO NO EXISTA UNA SOLUCIÓN ITERATIVA SIMPLE.
Por qué recursividad ?

21. Diversas técnicas algorítmicas utilizan la recursión, como los algoritmos de
Backtracking y los algoritmos divide y vence.
Para eliminar la recursión se puede almacenar en una estructura los valores de
las variables locales que haya para un procedimiento en cada llamada recursiva
Recursividad

22. Backtracking  Retroceso o Vuelta Atrás
• Realiza una búsqueda exhaustiva de una posible solución
– Consiste en seguir un camino buscando una solución
– Si por ese camino no se llega a la solución, se retrocede por el camino
seguido hasta que se encuentre otro camino
– O hasta que se llegue al inicio, lo cual indica que ya no hay solución
• Como se implementa
– Con Recursividad o
– Con Pilas Dinámicas
Backtracking

23. public void pintarCuadro(Punto p, int color) {
if( p.pintado() )
System.out.println(“Ya pintado”)
else{
p.pintar (color);
pintarCuadro (p.getArr , color);
pintarCuadro (p.getAbj , color);
pintarCuadro (p.getIzq, color);
pintarCuadro (p.getDer , color);
}
}
Pintar cuadro y todos los adyacentes blancos de un color
public void pintarCuadro(Punto p, int color)
Ejemplo: relleno de color

24. pintarCuadro(new Punto (10, 1) , ‘negro’)
public void pintarCuadro(Punto p, int color) {
if( p.pintado() )
System.out.println(“Ya pintado”)
else{
p.pintar (color);
pintarCuadro (p.getArr , color);
pintarCuadro (p.getAbj , color);
pintarCuadro (p.getIzq, color);
pintarCuadro (p.getDer , color);
}
}
Ejemplo: relleno de color
Pintar cuadro y todos los adyacentes blancos de un color

25. • Dividir el problema complejo en sub-problemas simples
• Conquistar (resolver) los problemas simples
• Vencer (resolver) el problema original a partir de las
soluciones de los problemas simples
Dividir para Vencer

26. Programación, UH 2013-2014 26
Algoritmo RECURSIVO
IF (Problema Simple)
Resolverlo directamente
ELSE
Dividir en subproblemas P1, P2, ..., Pn
Resolver(P1); Resolver(P2); ... Resolver(Pn)
Combinar las soluciones de cada subproblema
Dividir
Conquistar
Vencer
Dividir para Vencer

27. Búsqueda binaria
Buscar un valor en un arreglo ordenado.
Compara el valor con el elemento en el medio del arreglo
• Si no son iguales, la mitad en la cual el valor no puede estar es
eliminada
• La búsqueda continúa en la mitad restante hasta que el valor se
encuentre.
Dividir para Vencer (ejemplo)

28. Búsqueda binaria
Dividir para Vencer (ejemplo)

29. Central si a[central] == clave (base)
No encontrado si inferior > superior (base)
buscar en (inferior, central-1) si clave < a[central]
buscar en (central+1, superior) si clave > a[central]
Búsqueda binaria
Dividir para Vencer (ejemplo)

30. Valores: 0, 1, 1, 2, 3, 5, 8...
Cada término de la serie suma los 2 anteriores. Fórmula recursiva
fib(n) = fib (n - 1) + fib (n - 2)
Caso recursivo: fib (i) = fib (i -1) + fib(i -2)
Caso base: fib (0)=0; fib (1)=1
Serie de Fibonacci

31. Traza del cálculo recursivo
Fib(1)return
Fib(3)
Fib(2) +
return 1Fib(0)return Fib(1) +
return 1 return 0
Serie de Fibonacci

32. Implemente un método iterativo que evalúe si una cadena es palíndromo.
public static boolean palindromoIter(String palabra){
for(int i=0, f=palabra.length()-1; i<f; i++,f--)
if (palabra.charAt(i) != palabra.charAt(f))
return false;
return true;
}
Ejercicio

33. Implemente un método recursivo que evalúe si una cadena es palíndromo.
public static boolean palindromo(String palabra){
return palindromo(palabra,0,palabra.length()-1);
}
private static boolean palindromo(String palabra,int i, int f){
if (i>f)
return true;
if (palabra.charAt(i) != palabra.charAt(f))
return false;
return palindromo(palabra,i+1,f-1);
}
Ejercicio

34. Implemente un método recursivo que evalúe si una cadena es palíndromo.
Ejercicio
public static boolean palindromo(String palabra){
if (palabra.length()<=1)
return true;
if (palabra.charAt(0) != palabra.charAt(palabra.length()-1))
return false;
return palindromo(palabra.substring(1,palabra.length()-1));
}

35. • Recursividad es la propiedad que posee un método por la cual puede
llamarse a sí mismo.
• Contiene:
– Caso base o condición de parada
– Caso recursivo
• El progreso de las llamadas recursivas debe tender a la condición de
parada.
• Consume memoria y tiempo
• SE DEBE USAR CUANDO SEA REALMENTE NECESARIA, ES DECIR, CUANDO
NO EXISTA UNA SOLUCIÓN ITERATIVA SIMPLE.
Resumen