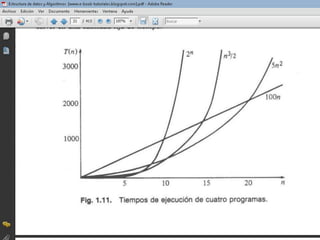
El documento habla sobre el análisis de algoritmos y la complejidad de tiempo. Explica conceptos como la notación O para describir el orden de complejidad asintótico de un algoritmo, así como reglas para calcular la complejidad de estructuras como secuencias, decisiones if/else, bucles anidados y llamadas a procedimientos. También incluye ejemplos de código y sus respectivos órdenes de complejidad como O(n3).

1. U1.- Análisis de Algoritmos.

2. 1.1.- Concepto de complejidad de un algoritmo.Fácil de entender, codificar y depurar.AlgoritmoUso efectivo de los recursos del computador + menor tiempo de ejecuciónCuando se resuelve un problema

3. Tiempo de ejecución de un programa.Datos de entradaCalidad del código generado para crear el código objeto.Tiempo de ejecuciónNaturaleza y rapidez de las instrucciones maquinaComplejidad de tiempo del algoritmo

4. Tiempo de ejecución de un programa.T(n). Tiempo de ejecución de un programa con una entrada de tamaño n.T(n) como tiempo de ejecución del “peor caso”. Máximo valor del tiempo de ejecución para entradas de tamaño n.No es posible expresar T(n) en unidades de tiempo. ¿Por qué?.

5. AsíntotasComportamiento asintótico de un algoritmo es cuando el tamaño de las entradas N tiende a infinito.A un conjunto de funciones que comparten un mismo comportamiento asintótico le denominaremos un orden de complejidad

6. Ordenes de complejidad

8. 1.2 Aritmética de la notación O.La notación O conocida también como notación asintótica, se utiliza para hacer referencia a la velocidad de crecimiento de los valores de una función.Ejemplo: T(n) = O(n2). Se lee “o de n al cuadrado”.Significa que existen constantes enteras c y n0 tales que para n mayor o igual que n0, se tiene que T(n) ≤ cn2.

9. 1.2 Aritmética de la notación O.Regla de la suma: T1(n) + T2(n) = O(max(f(n),g(n))). Calcula el tiempo de ejecución de una secuencia de pasos de programa, donde cada paso de programa puede contener ciclos y ramificaciones.Ejemplo: Se tienen O(n2), O(n3), O(nlogn) => O(max(n2,n3) ) es O(n3); y O(max(n3, nlogn)) es O(n3). Por lo tanto la suma de los tres es igual a O(n3).

10. 1.2 Aritmética de la notación O.Regla del producto: T1(n)T2(n) = O(f(n)f(g)).Según esta regla O(cf(n)) es lo mismo que O(f(n)).Ejemplo: O(n2/2) = O(n2).

11. Reglas prácticas para el cálculo de la complejidad de un algoritmo.Los algoritmos bien estructurados combinan las sentencias de alguna de las formas siguientessentencias sencillassecuencia (;)decisión (if)buclesllamadas a procedimientos, que en nuestro caso pudiera ser llamadas a métodos de alguna clase.

12. Reglas prácticas para el cálculo de la complejidad de un algoritmo.Sentencias sencillas => O(1).Estructura IF/ELSE => O(1).Bucles o ciclos. Cuando existe un número limitado de veces que se repite un grupo de sentencias, su complejidad es O(1). Pero si N forma parte del límite de iteraciones, entonces es O(n).Cuando tenemos dos bucles anidados es O(n2).Bucles multiplicativos donde la variable de control no es lineal es O(log n).O(nlogn) es un bucle interno multiplicativo anidado a otro que es normal.Las llamadas a procedimientos o métodos generan una orden de complejidad según el análisis de sentencias de cada uno de ellos.

14. EjemplosO(n3)

15. EjemplosO(n3)

16. Ejemplos

17. Ejemplos intcont = 0; for (int i = 2; i <= 1000; i++){ for (int j = 1; j <= i; j++){ if (i % j == 0){ cont = cont + 1; } } if (cont < 3){ Console.Write(i+", "); } cont = 0; } Console.ReadKey();

18. EjemplosFor(int j = 0; j < n; j++){For(int i = n; i > 0; i /2){Console.WriteLine(i);}}