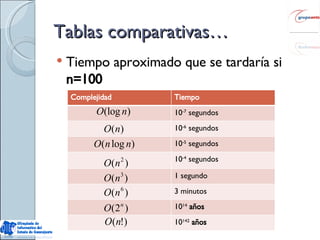
El documento introduce los conceptos básicos del análisis de complejidad algorítmica. Explica que es importante medir el tiempo de ejecución de los algoritmos y cómo se mide a través del número de operaciones en función del tamaño de la entrada. Luego, presenta dos algoritmos clásicos de ordenación, Burbuja y Búsqueda Binaria, y analiza su complejidad computacional.

1. Introducción a los Algoritmos Complejidad Computacional Joemmanuel Ponce G.

2. ¿Análisis de complejidad? Una de las cosas más importantes a tomar en cuenta al momento de seleccionar un algoritmo es el tiempo que va a tardar en arrojar una salida.

4. ¿Por qué es importante? A pesar de que las computadoras de hoy en día son capaces de realizar millones de operaciones en un segundo, es muy fácil encontrar ejemplos de problemas y soluciones que tardarán años en terminar…

5. ¿Cómo se mide? Las computadoras de hoy en día tienen diferentes capacidades en cuanto a velocidad de procesamiento. Saber con exactitud el tiempo que va a tardar un programa en dar una salida se vuelve una tarea muy difícil hoy en día.

6. ¿Cómo se mide? En vez de calcular el tiempo exacto que va a tardar nuestro algoritmo… se calcula la cantidad de operaciones en función del tamaño de la entrada (n).

7. ¿Cómo se mide? Por lo general para estimar el tiempo de ejecución, esta función de crecimiento se multiplica por una constante c que representa una estimación del tiempo que la computadora se tarda en realizar una operación.

8. ¿Cómo se mide? Tamaño de la entrada Tiempo de 1 operación

9. Nota En estos tiempos (2007) podemos asumir que una PC de escritorio puede realizar aproximadamente 10 9 operaciones por segundo. Sin embargo, este indicador no es absoluto dado que unas operaciones son más lentas que otras.

10. Otra Nota El tiempo exacto de ejecución de un algoritmo también depende mucho de los detalles de implementación .

11. EL PROBLEMA DE LA ORDENACIÓN Un ejemplo clásico

12. El problema de la ordenación de números Dado un conjunto de n números: Un algoritmo de ordenación debe encontrar una permutación del conjunto A tal que para cualquier (en otras palabras, ordenar del más chico al más grande)

13. Algoritmos de ordenación La ordenación de datos es quizás el problema más común dentro de las Ciencias Computacionales. Es por eso que existen bastantes algoritmos para resolver este problema. ¿Cuál es la diferencia entre ellos? Aparte del nombre

14. Algoritmos de ordenación La complejidad No de escribirlos, sino su función de crecimiento.

15. Análisis de complejidad de Algoritmos de Ordenación Para ejemplificar la función de crecimiento vamos a estudiar uno de los algoritmos más famosos de ordenación (y lento…): Ordenación por Burbuja (BubbleSort)

16. Ordenación por Burbuja La idea de la ordenación por burbuja es tomar el elemento de mayor valor de un arreglo de datos y llevarlo al final; y esto repetirlo a todos los elementos. (se llama burbuja por que alguien se imagino que el número que se va recorriendo es como si una burbuja subiera desde el fondo del agua).

17. Ordenación por Burbuja Para evitar el proceso de encontrar el máximo cada iteración, la mejor estrategia es recorrer el arreglo desde la posición 0 con un índice i. En cada paso preguntamos si el elemento en la posición i+1 es menor al elemento i. En este caso, intercambiamos los valores. Si seguimos este proceso observamos que el elemento mayor quedará hasta el fondo.

18. Ordenación por Burbuja Supongamos el siguiente arreglo de elementos: [1,2,15,5,7,6]

19. Ordenación por Burbuja [ 1 ,2,15,5,7,6] 1>2?

20. Ordenación por Burbuja [1, 2 ,15,5,7,6] 2>15?

21. Ordenación por Burbuja [1,2, 15 ,5,7,6] 15>5?

22. Ordenación por Burbuja [1,2,5, 15 ,7,6] Intercambiamos (nota que el índice sigue avanzando, una vez intercambiado los valores, el índice quedará posicionado en el número 15 otra vez).

23. Ordenación por Burbuja [1,2,5, 15 ,7,6] 15>7?

24. Ordenación por Burbuja [1,2,5,7, 15 ,6] Intercambiamos (y avanzamos el índice)

25. Ordenación por Burbuja [1,2,5,7, 15 ,6] 15>6?

26. Ordenación por Burbuja [1,2,5,7,6,15] Intercambiamos… Podemos observar que el elemento de mayor tamaño ha quedado al fondo del arreglo. La operación se repite hasta que se hayan “recorrido” todos los elementos.

27. Ejercicio Escriba el código (o pseudocódigo) del BubbleSort

28. Solución for (i=0;i<a.size()-1;i++) for (j=i+1;j<a.size();j++) if(a[i]>a[j]){ int temp=a[i]; a[i]=a[j]; a[j]=temp; }

29. Análisis del algoritmo Normalmente se habla de dos tipos de análisis: Análisis del peor caso Análisis del caso promedio

30. Análisis del peor caso El análisis del peor caso es, como su nombre lo dice, es calcular su función de crecimiento dándole la peor de todas las entradas posibles.

31. Análisis del caso promedio El análisis del caso promedio es, como su nombre lo dice, el promedio de cuánto tardaría nuestro algoritmo de cada una de las entradas posibles.

32. ¿Cuál es mejor? De los dos análisis, el del peor caso es el más fácil de razonar y es el más usado para pruebas de benchmark. A partir de que es casi imposible probar todas las entradas posibles, los análisis de complejidad se pueden volver algo truculentos.

33. Análisis del algoritmo Para analizar el costo computacional de un algoritmo, básicamente se siguen tres pasos: Suponer el peor de los casos (en el que se ejecutan más líneas y el más grande) A veces encontrar el peor caso no es sencillo… Asignar un costo a cada operación o línea de código Ver cuantas veces va a ser ejecutada cada línea de código .

34. Ejercicio En el Algoritmo de Burbuja (supón un tamaño del arreglo de n) : ¿Cuál es el peor caso? ¿Cuántas veces es ejecutada cada línea?

35. Solución: Análisis del Peor Caso Código Costo Veces que se ejecuta for (i=0;i<n-1;i++) C1 N for (j=i+1;j<n;j++) C2 if (a[i]>a[j]){ C3 int temp=a[i]; C4 a[i]=a[j]; C5 a[j]=temp; C6 }

36. Por lo tanto… La estimación del tiempo total de ejecución sería la suma del tiempo de cada una de las líneas multiplicado por su factor de costo de operación.

37. Por lo tanto: Código Costo Veces que se ejecuta for (i=0;i<n-1;i++) C1 N for (j=i+1;j<n;j++) C2 if (a[i]>a[j]){ C3 int temp=a[i]; C4 a[i]=a[j]; C5 a[j]=temp; C6 }

38. Sabemos que… Entonces:

39. Concluyendo… Para simplificar el análisis, supongamos que todas las constantes son iguales

40. Concluyendo Cuando se analizan algoritmos, sólo importa el término de la función que crece más rápido y se eliminan las constantes.

41. Concluyendo En nuestro caso, el término de mayor crecimiento es la n cuadrada. Por lo que decimos que la Ordenación por Burbuja tiene una complejidad de

42. A recordar… El cálculo de la complejidad tan sólo nos da una aproximación del tiempo. Los detalles de implementación son un factor importante… aunque la complejidad sea la misma.

43. Calcula la complejidad… Código Costo Veces que se ejecuta for (i=0;i<n-1;i++) C1 N for (j=0;j<n;j++) C2 N 2 if (a[i]>a[j]){ C3 N 2 int temp=a[i]; C4 N 2 a[i]=a[j]; C5 N 2 a[j]=temp; C6 N 2 }

44. Calcula la complejidad… Código Costo Veces que se ejecuta for (i=0;i<n-1;i++) C1 N for (j=0;j<n;j++) C2 N 2 if (a[i]>a[j]){ C3 N 2 int temp=a[i]; C4 N 2 a[i]=a[j]; C5 N 2 a[j]=temp; C6 N 2 }

45. Ejercicio Compara los dos algoritmos… ¿Tardarán exactamente el mismo tiempo en ejecutarse?

46. Ejercicio Prueba el BubbleSort con diferentes tamaños de entrada y toma el tiempo ¿Hasta que tamaño de entrada se puede ejecutar en 1 sec?

47. BÚSQUEDA BINARIA Un ejemplo más retador

48. ¿Qué es la búsqueda binaria? La búsqueda binaria es uno de los algoritmos más importantes dentro de las ciencias computacionales. Básicamente nos permite encontrar un elemento dentro de una secuencia (o un arreglo), mientras sus elementos estén ordenados.

49. ¿Qué es la búsqueda binaria? Por claridad, llamaremos al número que deseemos encontrar como objetivo . Llamaremos espacio de búsqueda a la secuencia (o subsecuencia, en este caso contigua) donde seguramente se encuentra el objetivo.

50. ¿Cuál es la idea? Inicialmente nuestro espacio de búsqueda es la secuencia completa. La idea es ir reduciendo la cantidad de lugares donde nuestro objetivo pueda estar, es decir, ir reduciendo nuestro espacio de búsqueda.

51. ¿Cuál es la idea? En cada paso, el algoritmo compara el valor de en medio (mediana) del espacio de búsqueda con el objetivo. Basado en la comparación y utilizando la propiedad de que los elementos están ordenados, se puede eliminar la mitad del espacio de búsqueda.

52. ¿Cuál es la idea? Si continuamos reduciendo de mitad en mitad, eventualmente llegaremos a un espacio de búsqueda de tamaño 1. ¿Qué quiere decir esto? Hemos encontrado nuestro número

53. Por ejemplo Supongamos que tenemos la siguiente secuencia: Y buscamos el 43 -1 2 10 43 44 55 60 71 82 0 1 2 3 4 5 6 7 8

54. Por ejemplo Ahora escogemos el valor de en medio del arreglo, que es el valor en el índice 4 (el punto medio entre 0 y 8 ) en este caso el 44. Comparamos esta mediana con nuestro valor objetivo ( 43 )

55. Por ejemplo… Utilizando la propiedad de ordenación del arreglo, podemos concluir que el 43 sólo puede estar en la parte izquierda de la secuencia . (43<44) Por lo que descartamos la mitad del espacio de búsqueda que no nos sirve. (Nos quedamos con los elementos 0 a 3 ). (Nota: Solo llevamos una operación) 43 -1 2 10 43 44 55 60 71 82 0 1 2 3 4 5 6 7 8

56. Por ejemplo 43 El proceso se repite. 43>10 por lo tanto tomamos la mitad de la derecha (elemento en la posición 3). -1 2 10 43 0 1 2 3

57. Por ejemplo En 3 operaciones encontramos un elemento en un arreglo ordenado de tamaño 8 . 43

58. Ejercicio… ¿Cuál es el peor caso de una Búsqueda Binaria? Cuándo el elemento a buscar no se encuentra en el arreglo hace la mayor cantidad de preguntas.

59. Ejercicio… Implementa una Búsqueda Binaria sobre un arreglo de enteros que regrese el índice de la posición donde se encuentra el objetivo. Si el elemento no está en el arreglo, regresar -1. Analiza: ¿Cuál es la condición de paro del ciclo?

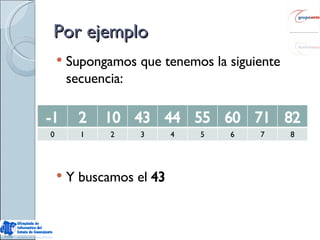
60. Ejercicio int binSearch(int[] a, int x){ int i=0; int j=a.length-1; int m; while(i<=j){ m=(i+j)/2; if(a[m]==x) return m; else if(x<a[m]) j=m-1; else i=m+1; } return -1; }

61. ¿CUÁL ES LA COMPLEJIDAD DE LA BÚSQUEDA BINARIA? Análisis de Complejidad

62. Complejidad de la búsqueda binaria La complejidad de la búsqueda binaria no es tan intuitiva como las revisadas anteriormente. Antes de responder debemos analizar detenidamente el algoritmo ¿Qué sucede con el tamaño del espacio de búsqueda en cada paso?

63. Ejemplo… Si n=10 esto es lo que sucede:

64. Complejidad de la búsqueda binaria Es dividido a la mitad… Entonces la pregunta clave es: ¿Cuántas veces puedo dividir por la mitad a N ?

65. Ejemplo… Si viéramos al revés el proceso:

66. Ejemplo… Podemos decir que el problema se trata de encontrar una x tal que: (Observa que x se convierte en el número de pasos realizados).

67. Conclusión La búsqueda binaria tiene una complejidad de: Recuerda que lo que nos interesa es la función de crecimiento, por lo que la base del logaritmo se omite.

68. Observaciones El logaritmo es una función creciente muy lenta . Para encontrar en un dato en una lista de un millón de datos ordenados se ocupan a lo más 21 comparaciones.

69. Observaciones Si pudieras tener una lista con información de todas las personas del mundo tardarías a lo más 35 pasos .

70. Tablas comparativas… Tiempo aproximado que se tardaría si n=100 Complejidad Tiempo 10 -7 segundos 10 -6 segundos 10 -5 segundos 10 -4 segundos 1 segundo 3 minutos 10 14 años 10 142 años

71. Problema Tercias (OMI 2007) Descripción : Se dice que 3 números a , b , y c están en sucesión aritmética si, a < b < c , y c - b = b - a. Por ejemplo los números 1, 2 y 3 están en sucesión aritmética, los números 2, 20 y 38 también lo están. Pero los números 2, 3 y 20 no lo están. Determinar si 3 números están en sucesión aritmética es una tarea simple, pero dado un conjunto de números determinar cuántos de ellos están en sucesión aritmética es algo un poco más difícil.

72. Problema Tercias (OMI 2007) Problema: Debes escribir un programa que lea un conjunto de números distintos e imprima en pantalla cuantas tercias de esos números están en sucesión aritmética. Tu programa deberá leer del teclado de la PC los siguientes datos: En la primera línea el número 0 < N ≤ 7,000 que representa la cantidad de números en el conjunto. Cada una de las siguientes N líneas contendrá un número del conjunto el cuál será un entero mayor a 0 y menor o igual a 1,000,000,000, además, estos números estarán ordenados de manera creciente.

73. Problema Tercias (OMI 2007) Ejemplo: Entrada Salida 5 1 2 3 20 38 2

74. Problema Tercias (OMI 2007) Explicación: En el ejemplo anterior se tiene un conjunto con 5 números, con estos 5 números se pueden formar las siguientes tercias: (1,2,3) (1,2,20) (1,2,38) (1,3,20) (1,3,38) (1,20,38) (2,3,20) (2,3,38) (2,20,38) (3,20,38) De las tercias anteriores sólo las tercias (1,2,3) y (2,20,38) están en sucesión aritmética, por lo tanto la respuesta es 2.

75. Problema Tercias (OMI 2007) Requerimientos de ejecución: Obtendrás 10 puntos por cada caso resuelto. Para obtener puntos en este problema, además de entregar la solución correcta tu programa deberá ejecutarse en un tiempo menor a 1 segundo.

76. Fuentes: http://www.topcoder.com http://www.olimpiadadeinformatica.org.mx http://www.cimat.mx/oieg