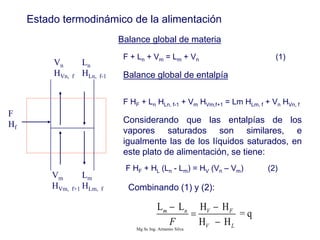
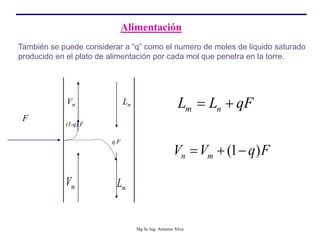
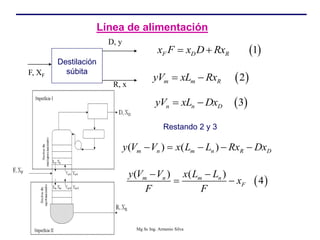
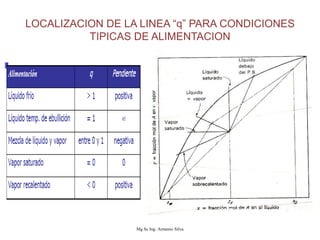
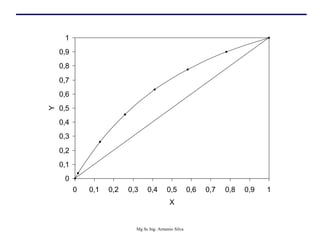
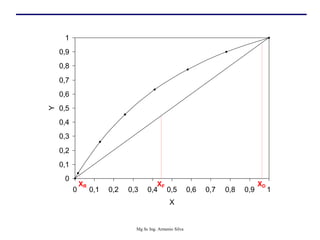
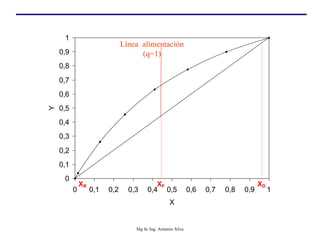
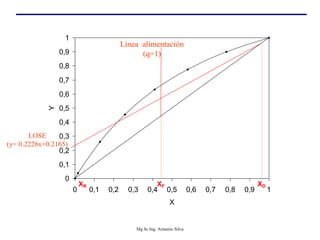
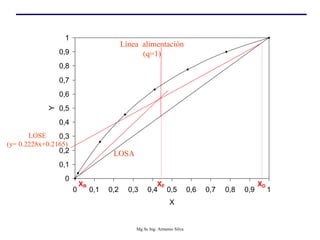
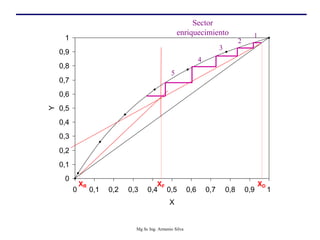
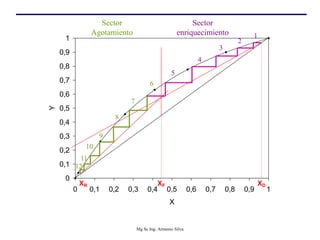
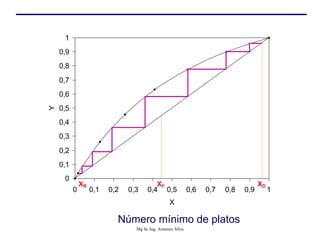
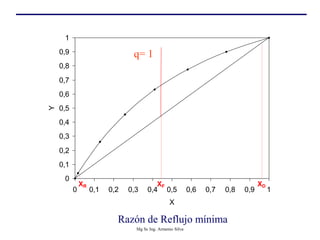
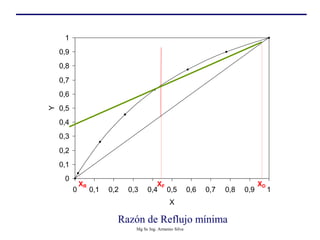
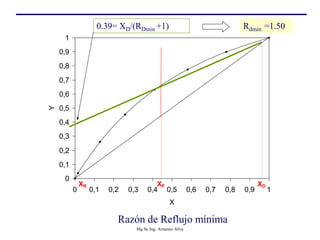
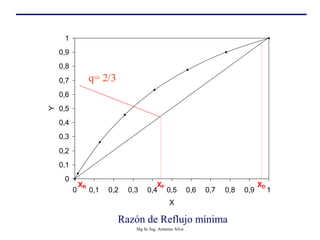
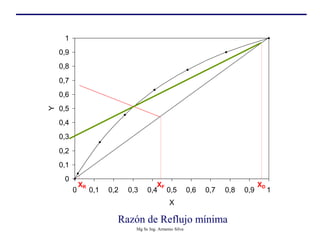
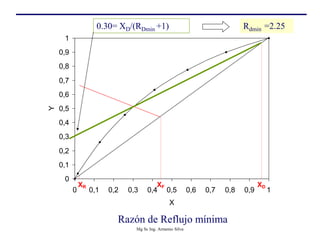
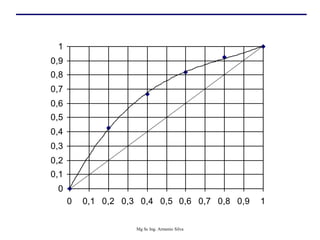
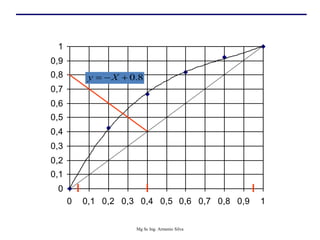
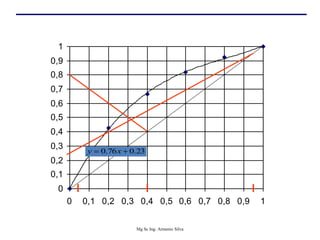
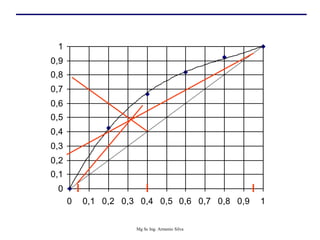
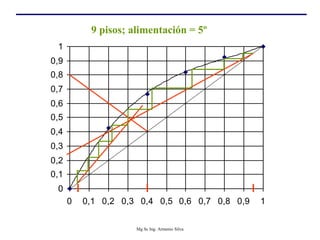
Este documento presenta información sobre la destilación fraccionada. Explica cómo las condiciones de la corriente de alimentación afectan las relaciones entre los vapores y líquidos en las secciones de empobrecimiento y enriquecimiento. También describe los balances de materia y entalpía que se aplican en el plato de alimentación y la determinación de la línea "q".

1. OPERACIONES UNITARIA III
PRQ-603
DESTILACIÓN FRACCIONADA
Docente: Mg Sc Ing. Armenio Silva Manzaneda

2. EFECTO DE LAS CONDICIONES OPERACION
• Las condiciones de la corriente de alimentación “F” que entra a la
torre determina la relación entre el vapor Vm en la sección de
empobrecimiento y Vn sección de enriquecimiento y entre Lm y Ln.
Mg Sc Ing. Armenio Silva
1 lim
lim
Calor necesario para vaporizar mol dea entacionencondiconesdeentrada
q
Calorlatentemolar devaporizaciondela a entacion

V F
V L
H H
q
H H



HV =Entalpia de la alimentación al punto de roció
HL= Entalpia de la alimentación al punto de burbuja
HF= Entalpia de la alimentación en condiciones de entrada

3. Estado termodinámico de la alimentación
Ln
HLn, f-1
Vn
HVn, f
Lm
HLm, f
Vm
HVm, f+1
F
Hf
Balance global de materia
Balance global de entalpía
Considerando que las entalpías de los
vapores saturados son similares, e
igualmente las de los líquidos saturados, en
este plato de alimentación, se tiene:
F HF + HL (Ln - Lm) = HV (Vn – Vm) (2)
L L H H
= q
H H
m n V F
V L
F
 


F + Ln + Vm = Lm + Vn (1)
F HF + Ln HLn, f-1 + Vm HVm,f+1 = Lm HLm, f + Vn HVn, f
Combinando (1) y (2):
Mg Sc Ing. Armenio Silva

4. Vn Ln
m
L
m
V
F
q F
(1-q) F
Alimentación
m n
L L qF
 
(1 )
n m
V V q F
  
También se puede considerar a “q” como el numero de moles de liquido saturado
producido en el plato de alimentación por cada mol que penetra en la torre.
Mg Sc Ing. Armenio Silva

5. Línea de alimentación
Destilación
súbita
F, XF
D, y
R, x
 
1
F D R
x F x D Rx
 
 
2
m m R
yV xL Rx
 
 
3
n n D
yV xL Dx
 
Restando 2 y 3
( ) ( )
m n m n R D
y V V x L L Rx Dx
    
 
( ) ( )
4
m n m n
F
y V V x L L
x
F F
 
 
Mg Sc Ing. Armenio Silva

6. Línea de alimentación
( 1) 1
F
X
q
y x
q q
 
 
Balance global de materia
Vm - Vn = Lm - Ln- F
( ) ( )
1
m n m n
V V L L
F F
 
 
( )
1
m n
V V
q
F

 
Reemplazando en (4)
F + Ln + Vm = Lm + Vn
Mg Sc Ing. Armenio Silva

7. LOCALIZACION DE LA LINEA “q” PARA CONDICIONES
TIPICAS DE ALIMENTACION
Mg Sc Ing. Armenio Silva

8. Se desea diseñar una columna de para separar 10.000kg/h de una mezcla que contiene 40% de
benceno y 60% de tolueno, con el fin de obtener un producto de cabeza (destilado) con 92% de
benceno y un producto de cola (residuo) con 98% de tolueno. Todos estos porcentajes están en
peso. Se utilizará una relación de reflujo externa de 3,5.
a) Calcular los caudales de destilado y residuo producidos.
b) Determinar el número de platos ideales y la ubicación del plato de alimentación en los
siguientes casos:
i) la alimentación entra como líquido a su temperatura de ebullición
ii) la alimentación consiste en una mezcla de dos tercios de vapor y un tercio de líquido.
Datos de equilibrio del sistema Benceno-Tolueno a 260 mmHg
X 0 0,0169 0,1292 0,2529 0,4113 0,5810 0,2801 1
Y 0 0,0389 0,2613 0,4561 0,6320 0,2262 0,9002 1
PROBLEMA 2.1
Mg Sc Ing. Armenio Silva

9. 4402
0
92
60
78
40
78
40
,
X F 


9744
0
92
3
78
97
78
97
,
X D 


0235
0
92
98
78
2
78
2
,
X B 


h
/
kmol
.
.
.
F 5
116
92
6
0
78
4
0
10000 








Mg Sc Ing. Armenio Silva

10. Calculo de caudales de destilado y residuo
F D R
 
kmol/h
05
.
51

D
65.45kmol/h
R 
116,5 /
D R kmol h
 
F D R
FX DX RX
 
)
0235
.
0
(
)
9744
.
0
(
)
4402
.
0
)(
5
,
116
(
B
D 

Mg Sc Ing. Armenio Silva

11. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
Mg Sc Ing. Armenio Silva

12. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Mg Sc Ing. Armenio Silva

13. 1 1
F
x
q
y x recta de pendiente
q q
   
 
Línea de alimentación (q=1)
Mg Sc Ing. Armenio Silva

14. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Línea alimentación
(q=1)
Mg Sc Ing. Armenio Silva

15. 2165
0
7778
0
5
4
9744
0
5
4
5
3
1
1
.
x
.
.
.
x
.
.
R
x
x
R
R
y
D
D
D
D 







Línea operativa del sector de enriquecimiento LOSE
Mg Sc Ing. Armenio Silva

16. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Línea alimentación
(q=1)
LOSE
(y= 0.2228x+0.2165)
Mg Sc Ing. Armenio Silva

17. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Línea alimentación
(q=1)
LOSE
(y= 0.2228x+0.2165)
LOSA
Mg Sc Ing. Armenio Silva

18. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Sector
enriquecimiento 1
2
3
4
5
Mg Sc Ing. Armenio Silva

19. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Sector
enriquecimiento 1
2
3
4
5
Sector
Agotamiento
6
7
8
9
10
11
12
Mg Sc Ing. Armenio Silva

20. Cálculo de caudales
kmol/h
.
.
.
D
L
V 725
229
05
51
675
178 




kmol/h
178.675
L
.
L
.
D
L
RD 




05
51
5
3
Mg Sc Ing. Armenio Silva

21. Calcular la razón de reflujo mínima y el número mínimo de
platos para cada uno de los casos de alimentación del
problema anterior.
PROBLEMA 2.2
Mg Sc Ing. Armenio Silva

22. Número mínimo de platos
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Mg Sc Ing. Armenio Silva

23. Razón de Reflujo mínima
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
q= 1
Mg Sc Ing. Armenio Silva

24. Razón de Reflujo mínima
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Mg Sc Ing. Armenio Silva

25. Razón de Reflujo mínima
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
0.39= XD/(RDmin +1) Rdmin =1.50
Mg Sc Ing. Armenio Silva

26. Razón de Reflujo mínima
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
q= 2/3
Mg Sc Ing. Armenio Silva

27. Razón de Reflujo mínima
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
Mg Sc Ing. Armenio Silva

28. Razón de Reflujo mínima
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
X
Y
XF
XR XD
0.30= XD/(RDmin +1) Rdmin =2.25
Mg Sc Ing. Armenio Silva

29. Se desea rectificar una mezcla ideal de dos componentes A y B, siendo el
valor de la presión de vapor del componente más volátil (A) tres veces mayor
que la del otro componente (B) a la misma temperatura. El alimento, con un
caudal de 5 kmol/h, entra en la columna mitad vapor y mitad líquido, con un
40% en moles del componente A. El destilado debe tener una concentración
molar de A del 95% y el residuo del 4% en el mismo componente.
Si en el condensador de cabeza de columna se eliminan 82000 kcal/h,.
Calcular:
a) Caudal de destilado obtenido
b) Ecuaciones de las dos rectas de operación
c) Número de pisos teóricos de la columna
d) Piso teórico en que debe introducirse el alimento
e) Número de pisos reales si la eficacia de plato es de 0,8
Datos: El calor latente de vaporización de cualquier mezcla de ambos
componentes vale =10000 kcal/kmol, independientemente de la temperatura.
PROBLEMA 2.3
Mg Sc Ing. Armenio Silva

30. a) Caudales de destilado y residuo
5 /
F D R kmol h
  
F D R
FX DX RX
 
)
.
(
B
)
.
(
D
)
.
)(
( 04
0
95
0
4
0
5 

kmol/h
.
D 98
1

3.02 kmol/h
R 
Mg Sc Ing. Armenio Silva

31. b) Condensador
h
kcal
V /
82000


kmol/h
.
.
.
D
V
L
D
L
V 22
6
98
1
20
8 







14
3
98
1
22
6
.
.
.
D
L
RD 


23
.
0
76
.
0
14
.
4
95
.
0
14
.
4
14
.
3
1
1







 x
x
R
x
x
R
R
y
D
D
D
D
h
kmol
V
V /
20
.
8
)
10000
(
82000 


Mg Sc Ing. Armenio Silva

32. c) Calculo del número de platos
0.5
q 
0.5 0.4
0.8
1 1 0.5 1 0.5 1
F
x
q
y x x X
q q
      
   
Mg Sc Ing. Armenio Silva

33. Datos de equilibrio
)
x
(
)
y
(
x
y
B
B
A
A
AB
x
y
x
y




1
1

P
x
P
y
P
x
P
y B
B
B
A
A
A
0
0
; 

3
/
/
0
0
0
0




B
A
B
A
B
B
A
A
AB
P
P
P
P
P
P
x
y
x
y

Mg Sc Ing. Armenio Silva

34. Datos de equilibrio
x
x
y
)
x
(
)
y
(
x
y
AB
2
1
3
3
1
1 







x 0 0,2 0,4 0,6 0,8 1
y 0 0,429 0,667 0,818 0,923 1
Mg Sc Ing. Armenio Silva

35. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Mg Sc Ing. Armenio Silva

36. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
8
.
0


 X
y
Mg Sc Ing. Armenio Silva

37. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
23
.
0
76
.
0 
 x
y
Mg Sc Ing. Armenio Silva

38. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Mg Sc Ing. Armenio Silva

39. 0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
9 pisos; alimentación = 5º
Mg Sc Ing. Armenio Silva

40. 10
8
0
8



,
eficacia
teóricos
pisos
nº
reales
pisos
º
n
Mg Sc Ing. Armenio Silva