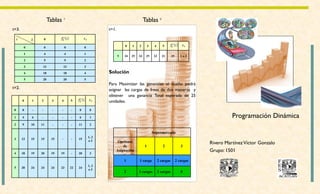
Un propietario de supermercados quiere asignar 5 cargas de fresas entre sus 3 tiendas para maximizar las ganancias esperadas, basadas en las distribuciones de probabilidad de ventas de cada tienda. La programación dinámica puede usar para determinar la asignación óptima de cargas que maximice la ganancia total, dividiendo el problema en etapas correspondientes a cada tienda, estados como el número de cargas disponibles, y usando una función recursiva para encontrar la política óptima.

1. Ejemplo Prototipo.
¿Qué Es La Un propietario de una cadena de 3 supermercados compro 5 cargas
de fresas frescas. La distribución de probabilidad estimada para las
Programación Dinámica? ventas potenciales de fresas antes de que se echen a perder difieren
en los tres supermercados. El propietario quiere saber como asignar
Como la técnica de Dividir y Conquistar, La Programación Di-
las 5 cargas en las tiendas para maximizar la ganancia esperada. Por
námica es una técnica para resolver problemas, a partir de la
solución de subproblemas y la combinación de esas soluciones. razones administrativas no quiere dividir las cargas entre las tiendas,
sin embargo esta de acuerdo en asignar cero cargas a cualquiera de
las tiendas. ¿ Cuantas cargas deben asignarse para determinar la ga-
nancia total?
¿Cuáles Son Sus Características?
Supermercado
1. El problema se puede dividir en etapas que requieren # de cargas 1 2 3
0 0 0 0
una política de decisión en cada una de ellas. 1 5 6 4
2. Cada etapa tiene un cierto numero de estados asocia- 2 4 11 9
dos a ella. 3 14 15 13
3. El efecto de la política de decisión en cada etapa es 4
5
17
21
19
22
18
20
transformar el estado actual en un estado asociado con
la siguiente etapa .
4. El procedimiento de solución esta diseñado para en- Solución
contrar una política optima para el problema completo.
5. El procedimiento de Solución se inicia al encontrar la Este problema requiere que se tomen tres decisiones interrelacio-
política optima para la ultima etapa. nadas, a saber cuantas cargas debe asignar a cada uno de los tres su-
6. Se Dispone de una relación recursiva que identifica la permercados. Ahora definiremos las Etapas, Estados, Decisiones y
política optima para la etapa n, dada la política optima
Función Recursiva.
para la etapa (n+1).
Etapas.Xn=(1,2,3). Serian el numero de cargas asignadas a la
etapa (supermercado) n.
¿Cuáles Son Sus Ventajas?
1. A diferencia de la técnica de dividir y Conquistar, La Estados.# de cargas disponibles para el supermercado t
Programación Dinámica es aplicable cuando los subpro- donde t=(1,2,3).
blemas no son independientes.
2. El Algoritmo resuelve el SubProblema una sola vez, lo Decisiones: # Cargas asignadas a la Tienda t.
guarda en una tabla y así evitamos volver a resolverlo.
Función Recursiva.

2. Tablas 1 Tablas 2
t=3. t=1.
i j 0
0 0 0 0 0 1 2 3 4 5
1 4 4 1
5 24 25 24 25 23 21 25 1o3
2 9 9 2
3 13 13 3
4 18 18 4 Solución
5 20 20 5
Para Maximizar las ganancias el dueño podrá
t=2. asignar las cargas de fresa de dos maneras y
obtener una ganancia Total esperada de 25
0 1 2 3 4 5 unidades.
0 0 - - - - - 0 0
1 4 6 - - - - 6 1 Programación Dinámica
2 9 10 11 - - - 11 2
Supermercado
1, 2
3 13 15 15 15 - - 15
o3 Opciones Rivero Martínez Víctor Gonzalo
de 1 2 3
4 18 19 20 19 19 - 20 2
Asignación Grupo: 1501
1 1 carga 2 cargas 2 cargas
1, 2
5 20 24 24 24 23 22 24
o3
2 3 cargas 2 cargas 0