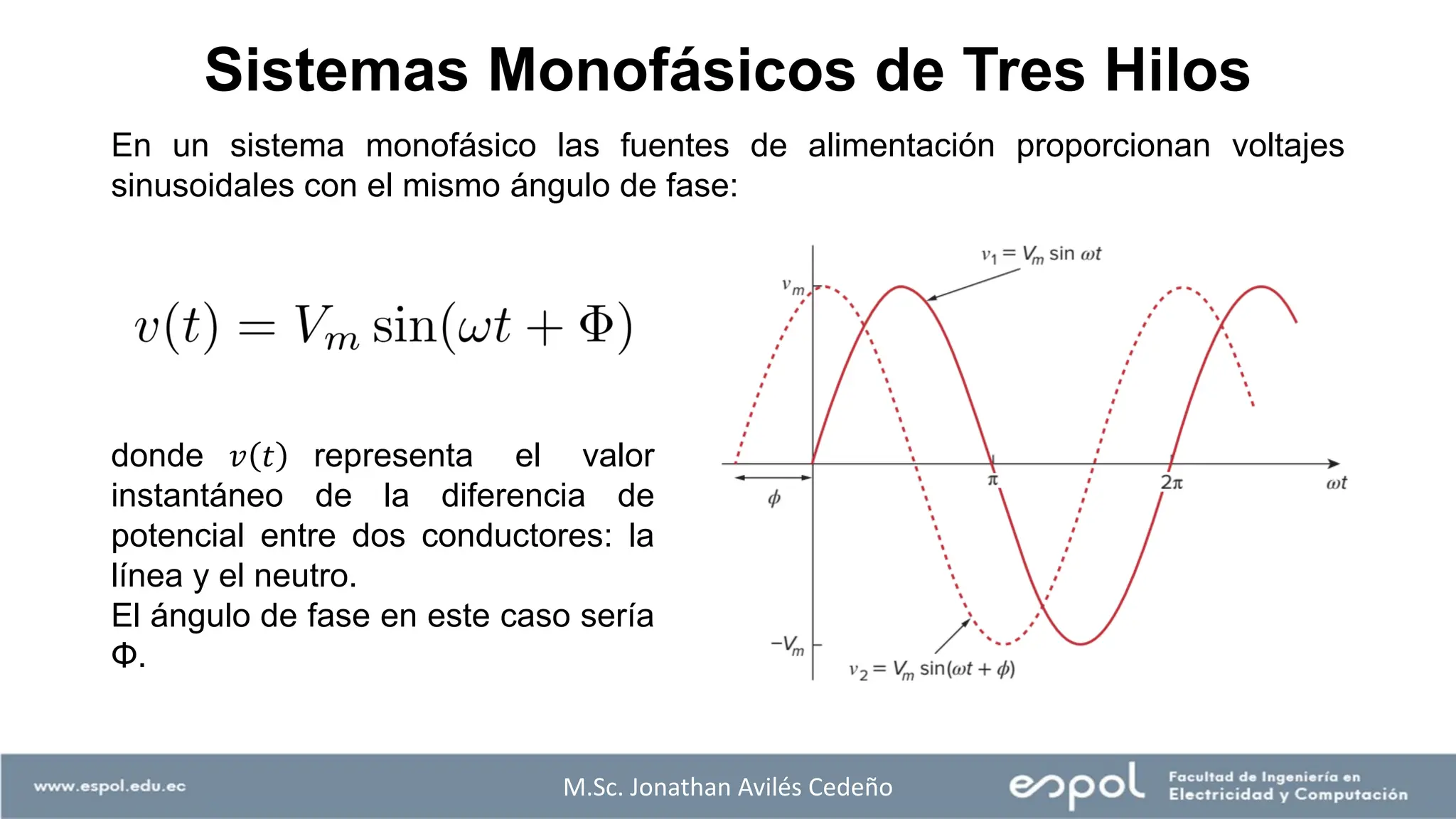
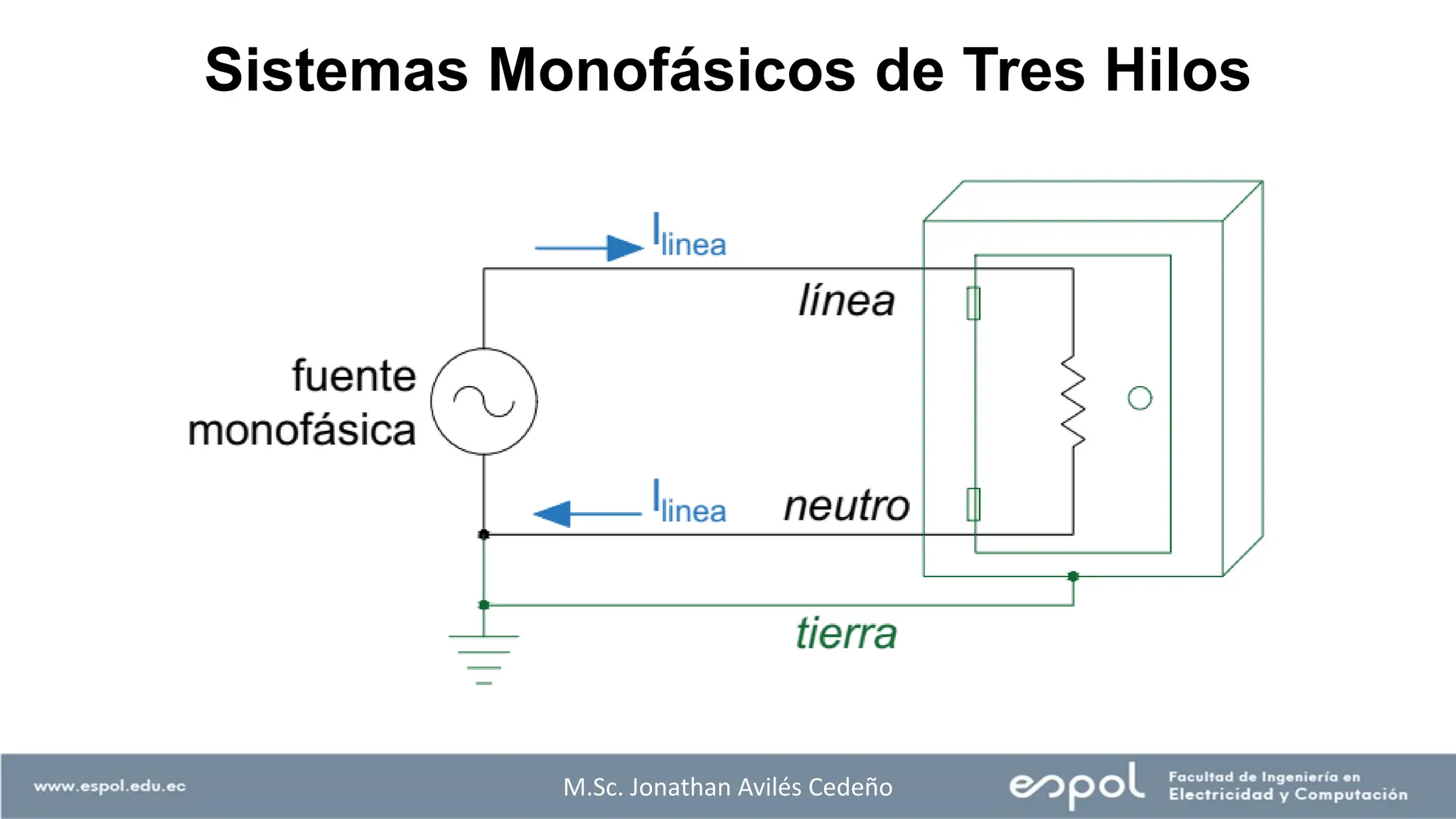
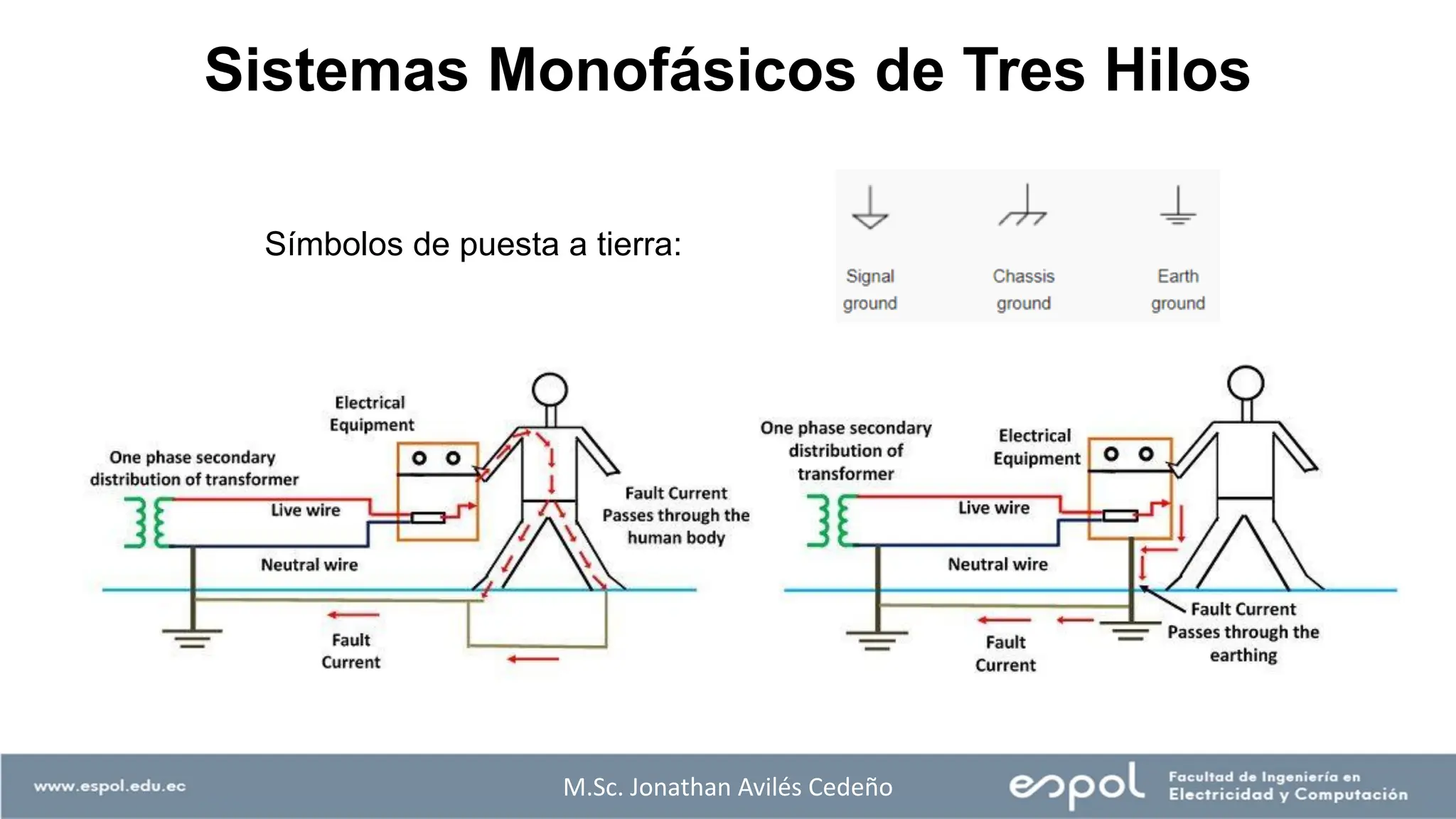
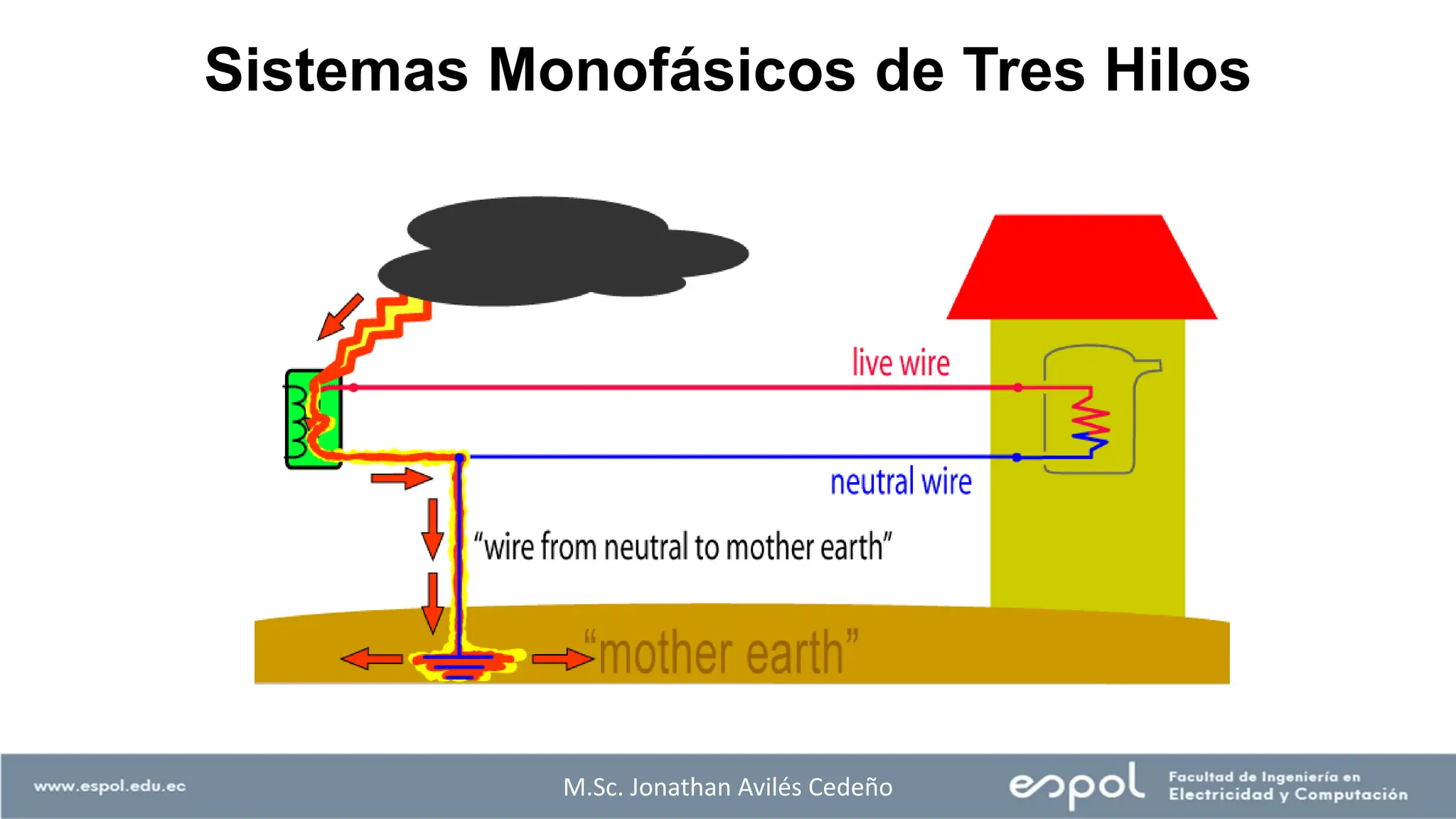
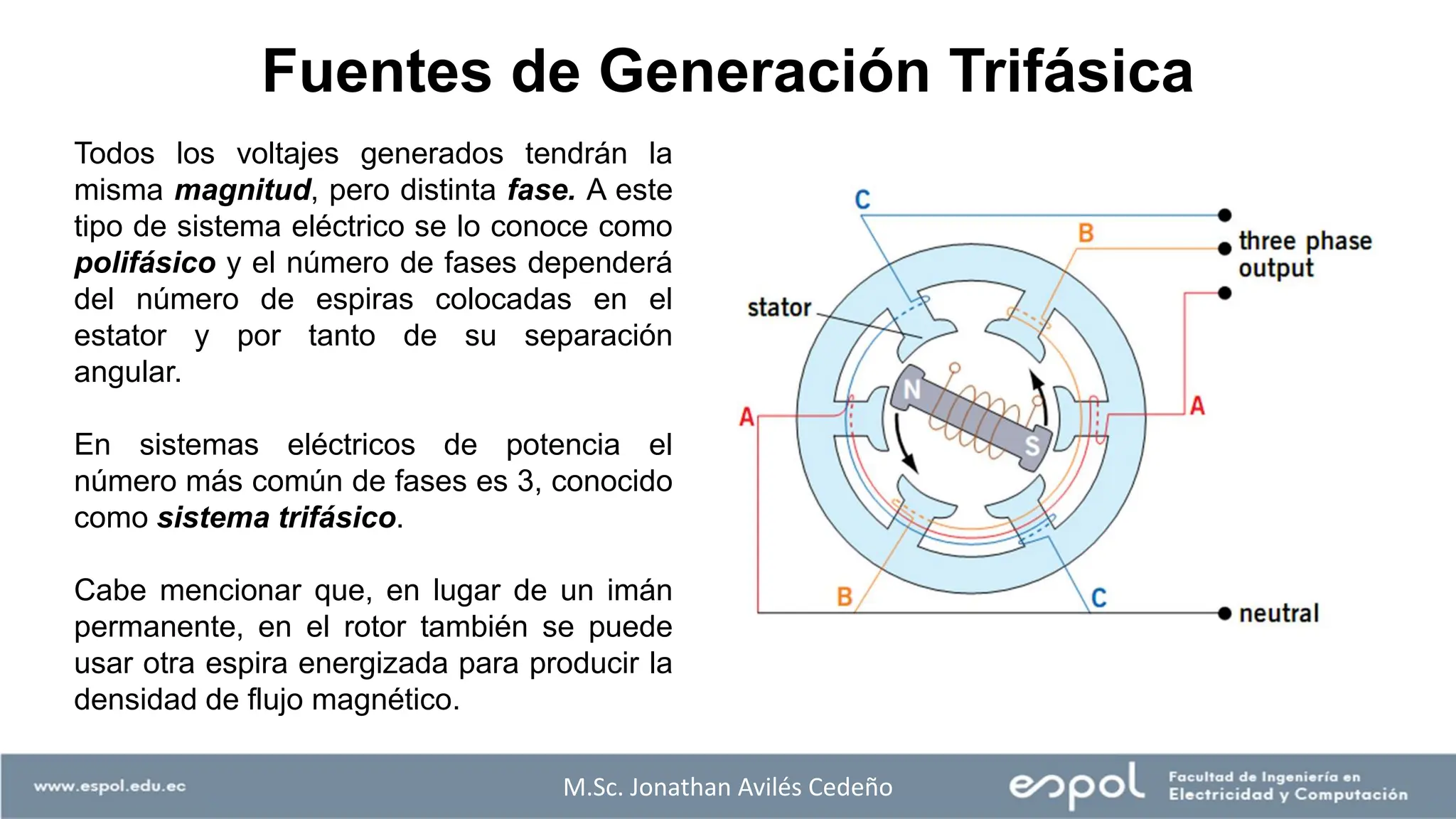
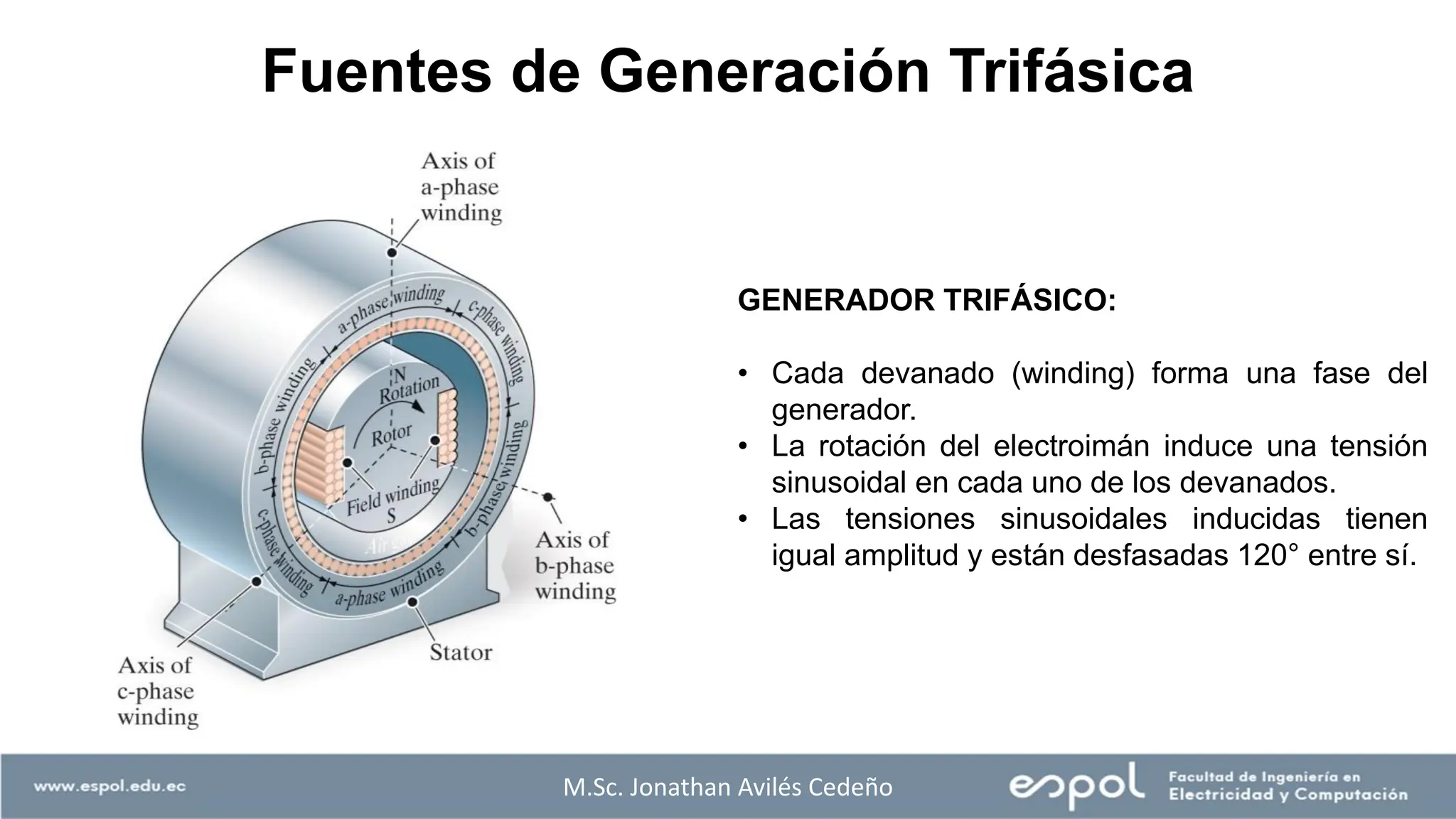
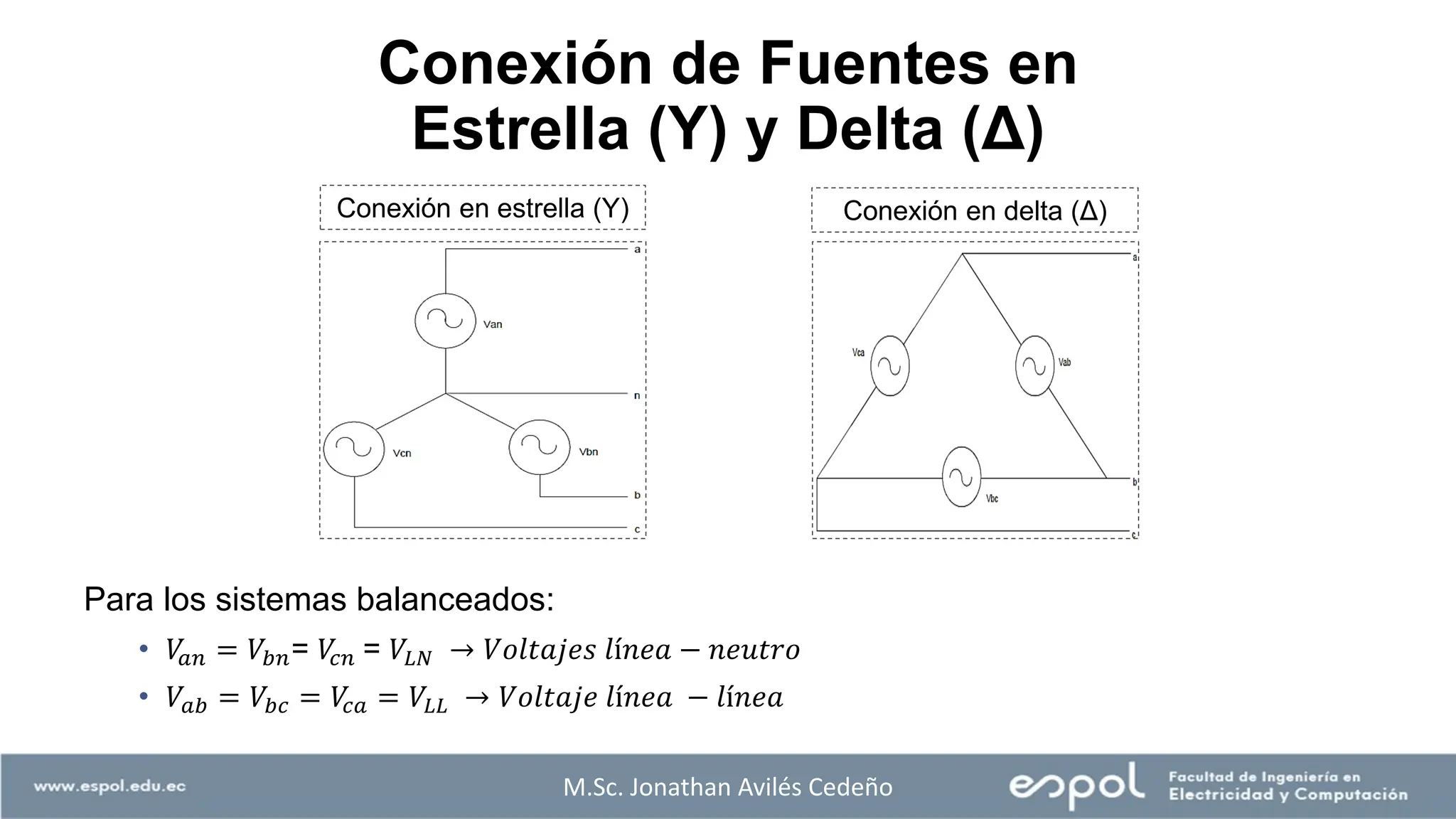
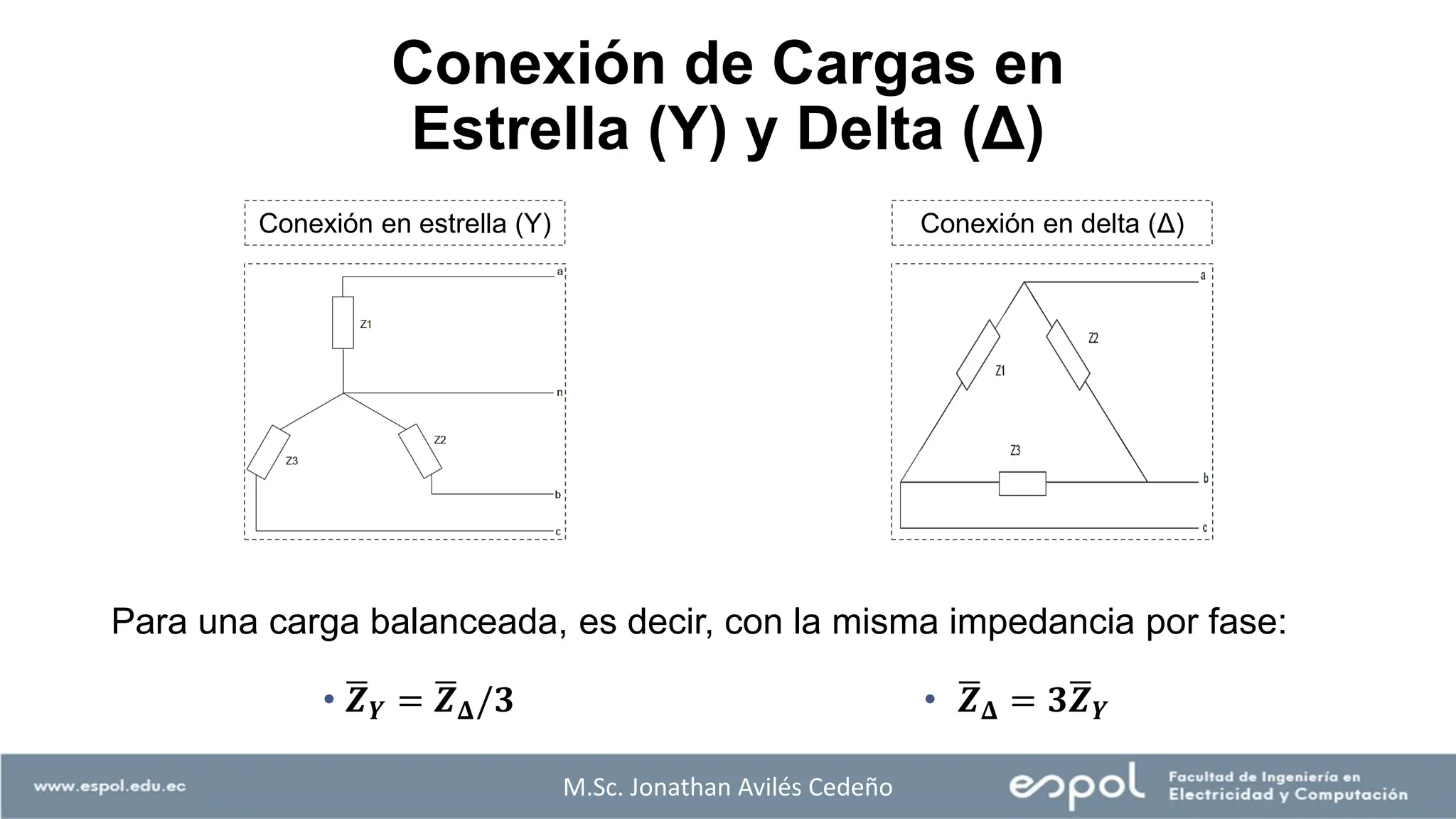
El documento aborda el análisis de sistemas eléctricos, enfocándose en los circuitos monofásicos y trifásicos, y la distribución de cargas en conductores metálicos. Se discuten principios de generación de voltajes, el funcionamiento de generadores eléctricos, y la importancia de conectar estructuras metálicas a tierra para prevenir riesgos eléctricos. Además, se explican conexiones trifásicas, el cálculo de potencias en sistemas balanceados y ejemplos prácticos para ilustrar conceptos clave.




![Vamos a unir ambas esferas con un
conductor ideal (puenteamos las esferas):
➢ 𝑄𝑎
′
y 𝑄𝑏
′
serán la nueva distribución de
carga en los conductores.
➢ 𝑄𝑎
′
+ 𝑄𝑏
′
= 𝑄𝑎 + 𝑄𝑏 por conservación de
carga
➢ Después de puentear las esferas,
tendrán el mismo potencial V
൞
𝑉 =
𝑄𝑎
′
4𝜋𝜀0𝑎
=
𝑄𝑏
′
4𝜋𝜀0𝑏
𝑄𝑎
′ + 𝑄𝑏′ = 𝑄𝑎 + 𝑄𝑏
Finalmente:
𝑉 =
𝑄𝑎 + 𝑄𝑏
4𝜋𝜀0 𝑎 + 𝑏
[V]
𝑄𝑎′ = 𝑄𝑎 + 𝑄𝑏
𝑎
𝑎 + 𝑏
[𝐶]
𝑄𝑏′ = 𝑄𝑎 + 𝑄𝑏
𝑏
𝑎 + 𝑏
[𝐶]
Distribución de Cargas en Cuerpos Metálicos
M.Sc. Jonathan Avilés Cedeño](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-6-2048.jpg)
![Distribución de Cargas en Cuerpos Metálicos
Si consideramos que el radio a es mucho mayor que el radio b, mediante el uso de
límites (𝑎 → ∞) obtendremos lo siguiente:
Es decir, si tenemos un conductor lo suficientemente grande, toda la carga
eléctrica de otros conductores pasaría a este conductor “infinito” al momento de
interconectarlos y debido al tamaño del conductor, el campo eléctrico efectivo
producido por cualquier cantidad de carga es despreciable y su voltaje estático
puede ser considerado igual cero.
Este conductor existe y lo llamamos tierra.
𝑉(𝑎 ≫ 𝑏) = 0 [V]
𝑄𝑎′(𝑎 ≫ 𝑏) = 𝑄𝑎 + 𝑄𝑏 [𝐶]
𝑄𝑏′(𝑎 ≫ 𝑏) = 0[𝐶]
M.Sc. Jonathan Avilés Cedeño](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-7-2048.jpg)









![M.Sc. Jonathan Avilés Cedeño
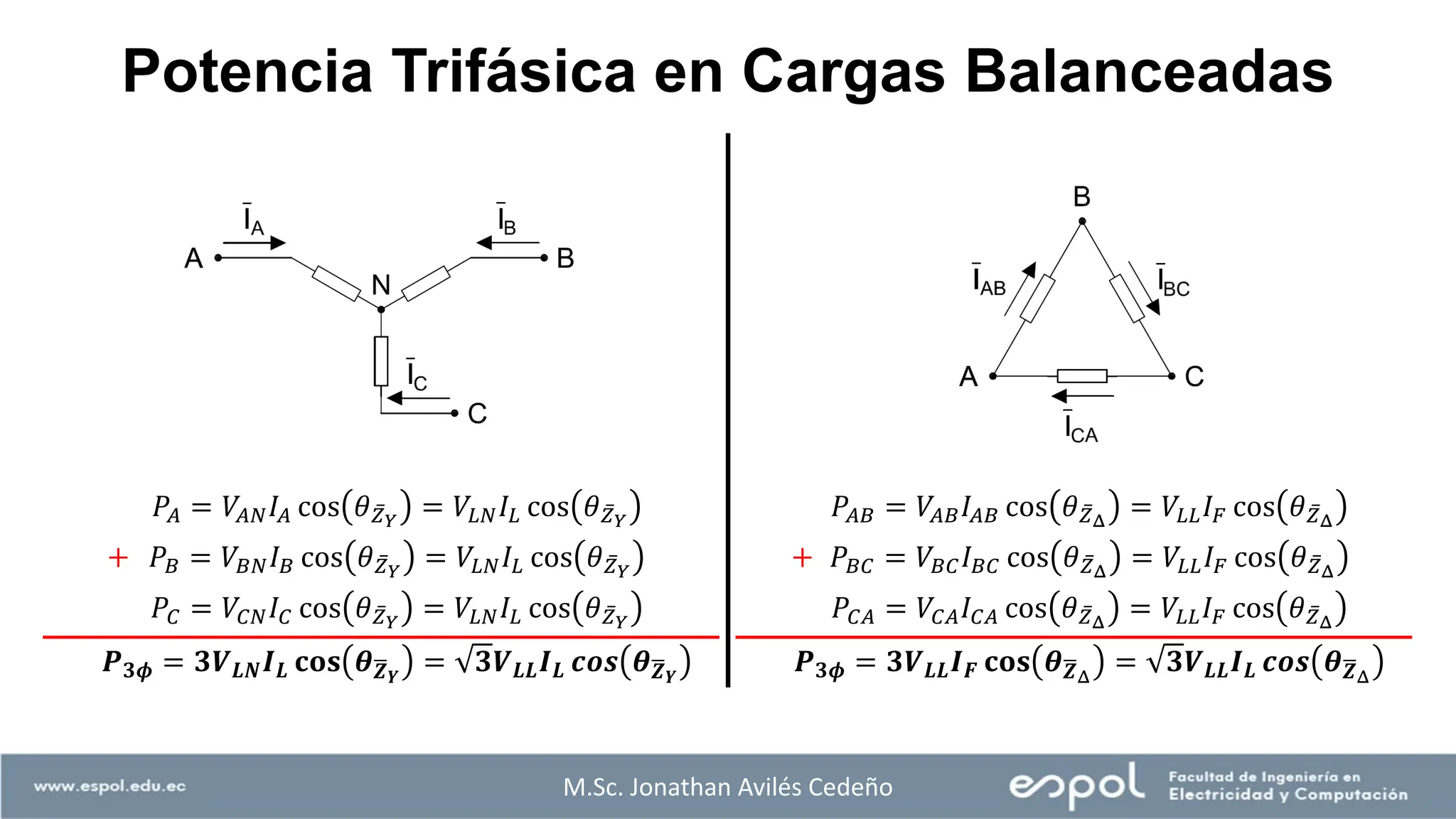
Potencia Trifásica en Cargas Balanceadas
Dado que ҧ
𝑍𝛥 = 3 ҧ
𝑍𝑌 en cargas balanceadas:
𝜃 ҧ
𝑧𝑌
= 𝜃 ҧ
𝑧𝛥
= 𝜃 = 𝜃 ҧ
𝑆3𝛷
Y por tanto, podemos generalizar las fórmulas para potencia en ambos tipo de
conexión trifásica:
Potencia Activa Trifásica [W]: P3𝜙 = 3VLLIL cos θ
Potencia Reactiva Trifásica [VAR]: Q3ϕ = 3VLLIL sin θ
Potencia Aparente Trifásica [VA]: 𝑆3ϕ = 3VLLIL
Potencia Compleja Trifásica [VA]: ҧ
𝑆3ϕ = 3VLLIL∡θ](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-36-2048.jpg)
![Ejemplo 1 de Potencia Trifásica
Datos:
• Carga 3𝜙 balanceada, abc, referencia ത
𝑉
𝑎𝑛.
• 𝑃3𝜙 = 480 [𝑘𝑊]
• 𝑓𝑝 = 0.8 𝑒𝑛 𝑎𝑡𝑟𝑎𝑠𝑜
• ҧ
𝑍𝐿 = 0.005 + 𝑗0.0025 [𝛺]
• 𝑉𝐿𝐿 = 600 𝑉 → 𝐴𝑝𝑙𝑖𝑐𝑎𝑑𝑜 𝑎 𝑙𝑎 𝑐𝑎𝑟𝑔𝑎
Determine:
a) Circuito monofásico
b) ത
𝑰𝑨
c) ഥ
𝑽𝑨𝑩 → 𝐷𝑒 𝑙𝑎 𝑓𝑢𝑒𝑛𝑡𝑒
d) 𝒇𝒑 → 𝐷𝑒 𝑙𝑎 𝑓𝑢𝑒𝑛𝑡𝑒
M.Sc. Jonathan Avilés Cedeño
Potencia Trifásica en Cargas Balanceadas](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-37-2048.jpg)
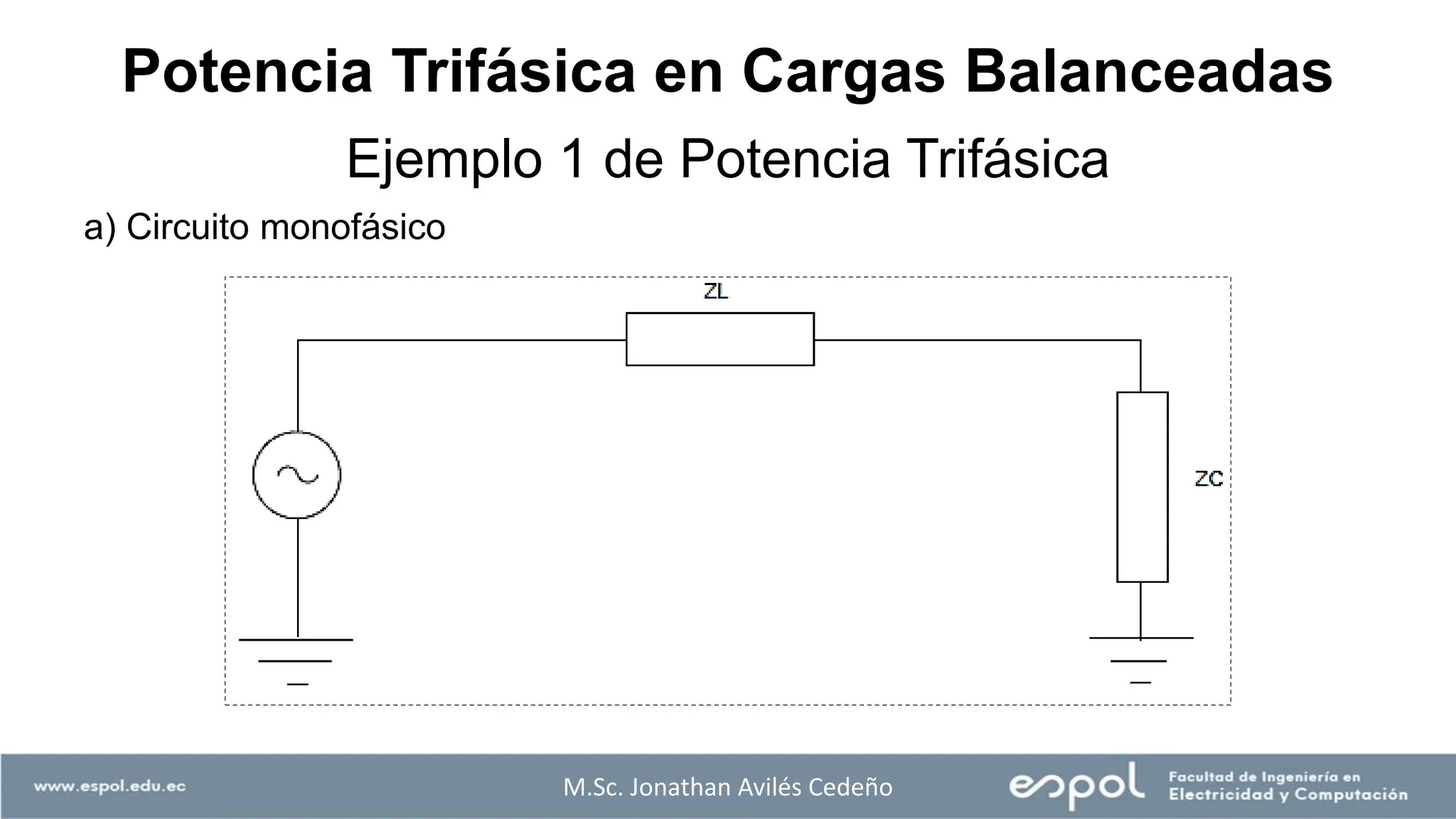
![M.Sc. Jonathan Avilés Cedeño
Ejemplo 1 de Potencia Trifásica
Potencia Trifásica en Cargas Balanceadas
b) ത
𝑰𝑨
ҧ
𝑍𝑌 = ҧ
𝑍𝐿 + ҧ
𝑍𝐶
ത
𝑉
𝑎𝑛 =
600
3
∡0°[V]
𝑍𝐶 =
𝑉𝐿𝐿
2
𝑆3𝜑
=
600 2
480000
0.8
= 0.6 [Ω]
𝜃 = cos−1
0.8 = 36.87°
ҧ
𝑍𝐶 = ҧ
𝑍𝐶𝑎𝑟𝑔𝑎 = 0.6∡36.87° [𝛺]](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-39-2048.jpg)
![M.Sc. Jonathan Avilés Cedeño
Ejemplo 1 de Potencia Trifásica
Potencia Trifásica en Cargas Balanceadas
b) ത
𝑰𝑨
ҧ
𝐼𝐴 =
ത
𝑉𝐴𝑁
ҧ
𝑍𝐶
=
600/ 3∡0°
0.6∡36.87°
= 577.35∡ − 36.87° 𝐴
c) ഥ
𝑽𝑨𝑩 → 𝐷𝑒 𝑙𝑎 𝑓𝑢𝑒𝑛𝑡𝑒
ത
𝑉𝐴𝑁 = ത
𝑉
𝑎𝑛 + ҧ
𝐼𝐴
ҧ
𝑍𝐿 = 600∡0° + 577∡ − 36.87° 0.005 + 𝑗0.025 = 357.51∡1.57° [𝑉]
ത
𝑉𝐴𝐵 = ത
𝑉𝐴𝑁 ∙ 3∡30° = 619.23∡31.57°[𝑉]](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-40-2048.jpg)

![Datos:
• 𝑃𝐴 = 2 𝑀𝑊 , 𝑓𝑝 = 0.8 𝑒𝑛 𝑎𝑡𝑟𝑎𝑠𝑜
• 𝑃𝐵 = 3 𝑀𝑊 , 𝑓𝑝 = 0.8 𝑒𝑛 𝑎𝑡𝑟𝑎𝑠𝑜
• 𝑃𝐶 = 4 𝑀𝑊 , 𝑓𝑝 = 0.8 𝑒𝑛 𝑎𝑡𝑟𝑎𝑠𝑜
• 𝑅𝐴𝐵 = 100 Ω 𝐿𝐴𝐵 = 80 [𝑚𝐻]
• 𝑅𝐵𝐶 = 50 Ω 𝐿𝐵𝐶 = 50 [𝑚𝐻]
• 𝑅𝐶𝐴 = 25 Ω 𝐿𝐶𝐴 = 25 [𝑚𝐻]
• 𝑉𝐿𝐿 = 4160 𝑉 𝑒𝑛 sec(+)
M.Sc. Jonathan Avilés Cedeño
Ejemplo 1 de Trifásico Desbalanceado
Circuitos Trifásicos Desbalanceadas](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-43-2048.jpg)

![M.Sc. Jonathan Avilés Cedeño
a) Hallar ത
𝑰𝑳𝑳𝟏, ത
𝑰𝑳𝟏 de la carga delta.
ത
𝑰𝑨𝑩𝟏 =
ഥ
𝑽𝑨𝑩
ഥ
𝒁𝑨𝑩
=
4160∡0°
100 + 𝑗 2𝜋 (60) 0.08
= 39.8281∡ − 16.7829°[𝐴]
ത
𝑰𝑩𝑪𝟏 =
ഥ
𝑽𝑩𝑪
ഥ
𝒁𝑩𝑪
=
4160∡ − 120°
50 + 𝑗 2𝜋 (60) 0.05
= 77.8515∡ − 140.6560° 𝐴
ത
𝑰𝑪𝑨𝟏 =
ഥ
𝑽𝑪𝑨
ഥ
𝒁𝑪𝑨
=
4160∡120°
25 + 𝑗 2𝜋 (60) 0.025
= 155.7030∡99.3440°[𝐴]
ത
𝑰𝑨𝟏 = ത
𝑰𝑨𝑩𝟏 − ത
𝑰𝑪𝑨𝟏 = 176.8937∡ − 68.9935°[𝐴]
ത
𝑰𝑩𝟏 = ത
𝑰𝑩𝑪𝟏 − ത
𝑰𝑨𝑩𝟏 = 105.3731∡ − 158.9456°[𝐴]
ത
𝑰𝑪𝟏 = ത
𝑰𝑪𝑨𝟏 − ത
𝑰𝑩𝑪𝟏 = 205.9757∡80.2374°[𝐴]
Ejemplo 1 de Trifásico Desbalanceado
Circuitos Trifásicos Desbalanceadas](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-45-2048.jpg)
![M.Sc. Jonathan Avilés Cedeño
b) Hallar ഥ
𝑺𝟑𝝓_𝜟 de la carga delta.
ഥ
𝑺𝟑𝜱_𝜟 = ഥ
𝑽𝑨𝑩
ത
𝑰𝑨𝑩𝟏
∗
+ ഥ
𝑽𝑩𝑪
ത
𝑰𝑩𝑪𝟏
∗
+ ഥ
𝑽𝑪𝑨
ത
𝑰𝑪𝑨𝟏
∗
= 1.0678 + 𝑗0.3906 [𝑀𝑉𝐴]
c) Hallar ത
𝑰𝑳𝟐 de la carga estrella.
ത
𝑰𝑨𝟐 =
𝑃𝐴
𝑉𝐴𝑁𝑓𝑝
∡(𝜃ഥ
𝑽𝐴𝑁
−𝜃ഥ
𝒁𝑌
) =
2000000
4160
3
0.8
∡( − 30° − cos−1
0.8) = 1040.8959∡ − 66.87°[𝐴]
ത
𝑰𝑩𝟐 =
𝑃𝐵
𝑉𝐵𝑁𝑓𝑝
∡(𝜃ഥ
𝑽𝐵𝑁
− 𝜃ഥ
𝒁𝑌
) = 1561.3439∡173.13°[𝐴]
ത
𝑰𝑪𝟐 =
𝑃𝐶
𝑉𝐶𝑁𝑓𝑝
∡(𝜃ഥ
𝑽𝐵𝑁
− 𝜃ഥ
𝒁𝑌
) = 2081.7918∡53.13°[𝐴]
Ejemplo 1 de Trifásico Desbalanceado
Circuitos Trifásicos Desbalanceadas](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-46-2048.jpg)
![M.Sc. Jonathan Avilés Cedeño
d) Hallar 𝑸𝒀 total.
𝑄𝑌_𝑡𝑜𝑡𝑎𝑙 =
𝑃𝑌_𝑡𝑜𝑡𝑎𝑙
𝑓𝑝
sin cos−1 0.8 = 6.75[𝑀𝑉𝐴𝑅]
e) Hallar ത
𝑰𝑳 de la fuente.
ത
𝑰𝑨 = 176.8937∡ − 68.9935° 𝐴 + 1040.8159∡ − 66.86° 𝐴 = 1217.6858∡ − 67.1783°[𝐴]
ത
𝑰𝑩 = 105.3731∡ − 158.9456° 𝐴 + 1561.3439∡173.13° 𝐴 = 1655.1838∡174.8385°[A]
ത
𝑰𝑪 = 205.9757∡80.2374° 𝐴 + 2081.7918∡53.13° 𝐴 = 2267.0857∡55.5028°[A]
Ejemplo 1 de Trifásico Desbalanceado
Circuitos Trifásicos Desbalanceadas](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-47-2048.jpg)
![M.Sc. Jonathan Avilés Cedeño
f) Hallar ഥ
𝑺𝟑𝝓 total.
ഥ
𝑺𝟑𝝓 = ഥ
𝑺𝟑𝝓_𝚫+ ഥ
𝑺𝟑𝝓_𝒀
ഥ
𝑺𝟑𝝓 = 1.0678 + 𝑗0.3906 + 9 + 𝑗6.75 = 10.068 + 𝑗7.1406 [𝑀𝑉𝐴]
Ejemplo 1 de Trifásico Desbalanceado
Circuitos Trifásicos Desbalanceadas](https://image.slidesharecdn.com/chapter1threephasecircuitspart13-241027223823-b0f3dc13/75/Chapter1_ThreePhase_Circuits_part1-3-pdf-48-2048.jpg)