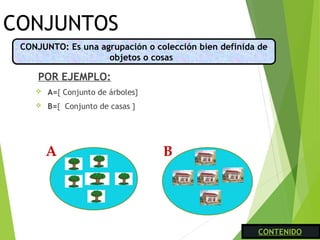
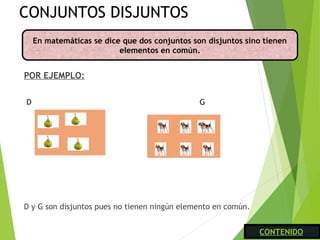
El documento describe conceptos básicos sobre conjuntos, incluyendo ejemplos de conjuntos, la definición formal de conjunto, formas de determinar un conjunto (extensión y comprensión), operaciones entre conjuntos como unión, intersección, diferencia y diferencia simétrica, y clasificaciones de conjuntos como finitos, infinitos, vacíos y universales. También cubre subconjuntos, diagramas de Venn y relaciones entre conjuntos como inclusión, disyunción e igualdad.

1. CONJUNTOS
POR EJEMPLO:
 A={ Conjunto de árboles}
 B={ Conjunto de casas }
CONJUNTO: Es una agrupación o colección bien definida de
objetos o cosas
A B
CONTENIDOCONTENIDO

2.  Para establecer si un objeto pertenece
o no a un conjunto, debe verificarse
 que posea la característica o
propiedad declarada por el conjunto.
De aquí
 que es importante que esta
característica no sea ambigua.
 Los conjuntos usualmente se denotan
con letras mayúsculas del alfabeto
español.

3.  Algunas agrupaciones que representan
conjuntos son:
 • Los números enteros.
 • Los habitantes de la Luna.
 • Los animales en extinción.
 • Los números primos.

4. Todas estas agrupaciones poseen una característica
que puede ser verificable con precisión.
Para decir que x es un elemento del conjunto A,
escribiremos x A. Para decir que∈ x no está en A,
escribiremos x A.∉

6. 6
Determinación de un conjunto :
Un conjunto se puede determinar:
por extensión y por comprensión
Por extensión :
Nombrando uno a uno los elementos del conjunto
Ejemplo: A = {m , n , p , q}
Por Comprensión :
Enunciando una propiedad o característica común a los
elementos del conjunto.
Ejemplo: A = {x / x es un número par }
X Forma general del elemento
/ Tal que
Características del Elemento
Llamado forma abreviada o sintética de llamar a un elemento

7. LOS DIAGRAMAS DE VENN
EJEMPLO 1: EJEMPLO 2 :
A= a,b,c,d
Los diagramas de Venn nos sirven para encontrar relaciones entre
conjuntos de manera gráfica mediante dibujos o diagramas.
1 2
3 4
5 a c
d e f
b
CONTENIDO
}
B= {}
c }
d }
a b
c
B
C
{
{
{
{
a, b a,b,c,d,e,f
A=
}
{1,2,3,4,5}
A B
d
D
A
D=
B=
C=

8. Tarea
.Realizar 5 ejemplos de conjuntos y
expresarlo por comprensión y
extensión, representar mediante
diagrama de ven.
. A los ejercicios anteriores aplicarles
ejemplos de pertenece y no
pertenece.

9. CLASIFICACIÓN DE
CONJUNTOS

10. CONJUNTO FINITO
En este tipo de conjunto podemos contar sus elementos ,
es decir tienen un principio y un fin
POR EJEMPLO:
M= { } 4 Manzanas
F= { } 6 Sillas
CONTENIDOCONTENIDO

11. CONJUNTO INFINITO
POR EJEMPLO:
 B={Números pares}
 J={Múltiplos de 5 }
Es el que tiene un número ilimitado de elementos, es
decir tiene un principio pero no tiene un fin
2 4 6
8 10 12
14 16
18 20….
5 10 15
20 25
30 35
40…
B J
CONTENIDOCONTENIDO

12. CONJUNTO VACIO
POR EJEMPLO:

D = {Números pares entre 6 y 8}

F = { Meses del año que tienen mas de 31 días }
Es un conjunto que carece de elementos. Se lo representa
con el símbolo Ø o también { }
Ø
CONTENIDOCONTENIDO

13. CONJUNTO UNIVERSAL.
POR EJEMPLO:
Sean los conjuntos
 C= { conejos}
 D= { monos }
Existe otro conjunto que incluye a los conjuntos C y D y es conjunto
de todos los animales
U= { animales }
Es el conjunto que contiene a todos los elementos,
que normalmente se lo denota por la letra U
conejos
monos
U
CONTENIDO

14. CONJUNTO POTENCIA
Es la familia de todos los subconjuntos de un conjunto N se llama
Conjunto Potencia de N. Se le denota como 2
EJEMPLO 1:
CONTENIDOCONTENIDO
M = { 1, 2 } El conjunto M tiene 2 elementos
2M
= { {1}, {2}, {1, 2}, ø} entonces 22
= 4 elementos
EJEMPLO 2:
M = { 1, 2, 3 } El conjunto M tiene 3 elementos
2M
= { {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, ø} entonces 23
= 8 elementos

15. IGUALDAD DE CONJUNTOS
Son los conjuntos que tienen los mismos elementos sin importar
su orden o repetición
EJEMPLO 1:
H= { }
P= { }
N= { 2,4,6,8,10,12 }
M= { 4,8,2,12,4,10 }
EJEMPLO 2:
CONTENIDOCONTENIDO

16. RELACIONES
ENTRE CONJUNTO

17. Inclusión

19. CONJUNTOS DISJUNTOS
POR EJEMPLO:
D G
D y G son disjuntos pues no tienen ningún elemento en común.
En matemáticas se dice que dos conjuntos son disjuntos sino tienen
elementos en común.
CONTENIDO

20. CONJUNTOS DE CONJUNTOS.
POR EJEMPLO:
A={4,8 }
B={ 4}
C={ A,B}
C={ {4,8} , {4} }
CONTENIDOCONTENIDO
Se llama así al conjunto formado por todos los subconjuntos posibles
de un conjunto dado.

21. SUBCONJUNTOS
POR EJEMPLO:
Representación:
 A={ Letras del alfabeto}
 B= { Letras del alfabeto, vocales}
 C= { Letras del alfabeto, consonantes}
Interpretación:
Dentro del conjunto A podemos seleccionar algunos elementos con
características aun más especiales tales como el conjunto B y C , se
dice entonces que tanto como el conjunto B y el conjunto C son
subconjuntos del conjunto A
CONTENIDOCONTENIDO
Es un conjunto de elementos que pertenecen a otro conjunto, es decir
podemos escoger ciertas características de algunos elementos del
conjunto original.

22. OPERACIONES
ENTRE CONJUNTOS

23. 7
6
55
6
A B
El conjunto “A unión B” que se representa asi
es el conjunto formado por todos los elementos que
pertenecen a A,a B o a ambos conjuntos.
∪A B
}{∪ = ∈ ∨ ∈A B x / x A x B
Ejemplo:
9
87
3
1
4
2
A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9}
A U B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

24. 7
6
55
6
A B
El conjunto “A intersección B” que se representa
es el conjunto formado por todos los elementos que
pertenecen a A y pertenecen a B.
∩A B
}{A B x / x A x B∩ = ∈ ∧ ∈
Ejemplo:
9
87
3
1
4
2
A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9}
A B = { 5, 6, 7}

25. 7
6
55
6
A B
El conjunto “A menos B” que se representa
es el conjunto formado por todos los elementos que
pertenecen a A y no pertenecen a B.
A B−
}{A B x / x A x B− = ∈ ∧ ∉
Ejemplo:
9
87
3
1
4
2
A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9}
A – B = {1, 2, 3, 4}

26. 7
6
55
6
A B
El conjunto “B menos A” que se representa
es el conjunto formado por todos los elementos que
pertenecen a B y no pertenecen a A.
B A−
}{B A x / x B x A− = ∈ ∧ ∉
Ejemplo:
9
87
3
1
4
2
A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9}
B – A = {8, 9}

27. 7
6
55
6
A B
El conjunto “A diferencia simétrica B ” que se
representa es el conjunto formado por todos los
elementos que pertenecen a (A-B) o(B-A).
A B∆
}{A B x / x (A B) x (B A)∆ = ∈ − ∨ ∈ −
Ejemplo:
9
87
3
1
4
2
A = {1, 2, 3, 4, 5, 6, 7} y B = {5, 6, 7, 8, 9}
A B = {1, 2, 3, 4} U {8, 9}

28. También es correcto afirmar que:
A B (A B) (B A)∆ = − ∪ −
A B (A B) (A B)∆ = ∪ − ∩
A B
A-B B-A
A B

29. Dado un conjunto universal U y un conjunto
A,se llama complemento de A al conjunto
formado por todos los elementos del
universo que no pertenecen al conjunto A.
Notación: A’ o AC
Ejemplo:
U ={1,2,3,4,5,6,7,8,9} A ={1,3, 5, 7, 9}y
Simbólicamente: }{A ' x / x U x A= ∈ ∧ ∉
A’ = U - A

30. 1
2 3
4
5
6
7
8
9
U
AA
A’={2,4,6,8}

32. Dados los conjuntos:
A = { 4, 7, 10, ... ,34}
B = { 2, 4, 6,...,26}
C = { 7,11,15,...,31}
a) Expresar B y C por extensión
b) Calcular: A B , C – A

33. a) A = {4,7,10,13,16,19,22,25,28,31,34}
B = {2,4,6,8,10,12,14,16,18,20,22,24,26}
C = {7,11,15,19,23,27,31}
A B = { 4,10,16,22 }
C – A = { 11,15,23,27 }
Sabemos que A B esta formado por los
elementos comunes de A y B, entonces:
Sabemos que C - A esta formado por los
elementos de C que no pertenecen a A,
entonces:
b) Calcular: A B , C – A

34. Resolver:
 A = {x / x es un número mayor que 4 y menor que 8}
B = {x / x es un número positivo menor que 7}
 Calcular la unión entre A y B
 Calcular la intersección entre A y B
 Representar mediante diagrama de ven, y pintar las
parte afectadas por las operaciones.

35. Dados los conjuntos:
P = {x Z / 2x2
+5x-3=0 }
M = { x/4 N / 4≤ x < 21 }
T = { x R / (x2
- 9)(x - 4)=0 }
a) Calcular: M - ( T – P )
b) Calcular: (M T )
c) Calcular: (M U T) – P
∈
∈
∈

37. P = { x Z / 2x2
+5x-3=0 }
Analicemos cada conjunto:
2x2
+ 5x – 3 = 0
2x – 1
+ 3x


(2x-1)(x+3)=0
2x-1=0 ⇒ x = 1/2
x+3=0 ⇒ x = -3
Observa que x Z ,
entonces: P = { -3 }
M = { x/4 N / 4≤ x < 21 }
Como x/4 N entonces los valores de x son :
4 ; 8 ; 12 ; 16 ; 20 pero los elementos de M se
obtienen dividiendo x entre 4,por lo tanto :
M = {1, 2, 3, 4, 5 }
∈
∈
∈
∈

38. T = { x R / (x2
- 9)(x - 4)=0 }
Cada factor lo igualamos a cero y calculamos
los valores de x
x – 4 = 0 x = 4
x2
– 9 = 0 x2
= 9 x = 3 o x =-3
Por lo tanto: T = { -3,3,4 }
a) Calcular: M - ( T – P )
T – P = { -3,3,4 } - { -3 } T – P = {3, 4 }
M - (T –P)= {1, 2, 3, 4, 5 } - {3, 4 }
M - (T –P)= {1, 2, 5 }
∈

39. M T = {3, 4}
b) Calcular: ( M T )
M T = {1, 2, 3, 4, 5 } { -3,3,4 }
c) Calcular: (M U T) – P
M U T = {1, 2, 3, 4, 5 } U { -3, 3, 4 }
M U T = { -3, 1, 2, 3, 4, 5 }
(M U T) – P = { -3, 1, 2, 3, 4, 5 } - { -3 }
(M U T) – P = {1, 2, 3, 4, 5 }

40. Operaciones con
Mas de tres
conjuntos.

41. Expresar la región sombreada en
términos de operaciones entre los
conjuntos A,B y C.
A B
C
A
B
C

42. A B
C
A B
C
A
B
C
A
B
C
[(A B) – C]
[(B C) – A]
[(A C) – B]
U U

43. A B
A
B
C
Observa como se
obtiene la región
sombreada
Toda la zona de amarillo es
AUB
La zona de verde es A B
Entonces restando se obtiene la zona
que se ve en la figura : (A U B) - (A B)
C
Finalmente le agregamos C y se obtiene:
[ (A U B) - (A B) ] U C ( A B ) U C=