#include <conio.h> #include <stdio.h> void main() { int matriz[10][10], factor, limite, i, j; printf("Ingrese el factor: "); scanf("%d", &factor); printf("Ingrese el limite: "); scanf("%d", &limite); for(i=1; i<=limite; i++) { for(j=1; j<=limite; j++) { matriz[i][j] = i * factor; printf("%d ", matriz[i][j]); } printf("\n"); } getch(); } Este programa genera una

1. 1

2.  Portada……………………………………...pag1
 Índice …………………………..................pag2
 Historia matriz ……………………………pag3
 Concepto matriz……………………………pag4
 Librerías a utilizar………………………….pag5
 Declarar una matriz……………………….pag6
 Ejemplos: declaración matriz……………pag7
 Propiedades……………………................pag8
 Tipos de matrices………………………….pag9
 Definir tipos…………………………………pag10
 Ingresar datos………………………………pag11
 Imprimir datos………………………………pag12
2

3. definición vector……………………………..pag13
Grafico………………………………………....pag14
Tipos de datos………………………………..pag15
Inicialización datos…………………………..pag16
Características…………………………….....pag17
Tipos vectores………………………….........pag18
Definición tipos……………………………….pag19
Ingreso de datos…………………………......pag20
Impresión datos………………………………pag21
Diferencia vector - matriz………………pag22
Ejercicios resueltos …………………….pag26-62
3

4.  El origen de las matrices es muy antiguo. Uncuadrado mágico, 3 por 3, se registra en la literatura
china hacia el 650 a. C.2
 Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un importante texto
matemático chino que proviene del año 300 a. C. a200 a. C., Nueve capítulos sobre el Arte de las
matemáticas (Jiu Zhang Suan Shu), es el primer ejemplo conocido de uso del método de matrices
para resolver un sistema de ecuaciones simultáneas.3 En el capítulo séptimo, "Ni mucho ni poco", el
concepto de determinante apareció por primera vez, dos mil años antes de su publicación por el
matemático japonés Seki Kōwa en 1683 y el matemático alemán Gottfried Leibniz en 1693.
 Los "cuadrados mágicos" eran conocidos por los matemáticos árabes, posiblemente desde
comienzos del siglo VII, quienes a su vez pudieron tomarlos de los matemáticos y astrónomos de
la India, junto con otros aspectos de las matemáticas combinatorias. Todo esto sugiere que la idea
provino de China. Los primeros "cuadrados mágicos" de orden 5 y 6 aparecieron en Bagdad en
el 983, en laEnciclopedia de la Hermandad de Pureza (Rasa'il Ihkwan al-Safa).2
 Después del desarrollo de la teoría de determinantes por Seki Kowa y Leibniz, a finales del siglo
XVII, Cramer presentó en 1750 la ahora denominada regla de Cramer. Carl Friedrich Gauss y Wilhelm
Jordan desarrollaron la eliminación de Gauss-Jordan en el siglo XIX.
 El término "matriz" fue acuñado en 1848, por J. J. Sylvester. En 1853, Hamilton hizo algunos aportes a la
teoría de matrices. Cayleyintrodujo en 1858 la notación matricial, como forma abreviada de escribir
un sistema de m ecuaciones lineales
4

5.  Una matriz (array ) es una zona de almacenamiento
contiguo, que contiene una serie de elementos del
mismo tipo, los elementos de la matriz [1]. Desde el
punto de vista lógico podemos considerarlas como un
conjunto de elementos ordenados en fila. Así pues, en
principio todas las matrices son de una dimensión, la
dimensión principal, pero veremos que los elementos
de esta fila pueden ser a su vez matrices.
 En general, una matriz es un conjunto ordenado en
una estructura de filas y columnas. Los elementos de
este conjunto pueden ser objetos matemáticos de muy
variados tipos.
5

6.  include<conio.h>
 include<stdio.h>
 Int
 Char
include<math.h>
 Scanf
 Printf
 Void main
6

7. Sintaxis
La declaración de matrices sigue la siguiente sintaxis:
tipoX etiqueta [<expr-const>]
tipoX es el tipo de los elementos que serán
almacenados en la matriz. Puede ser cualquier type-id
( 2.2) válido a excepción de void y de funciones (no
pueden existir matrices de funciones, pero sí de
punteros-a-función).
etiqueta es el identificador
<expr-const>: una expresión cuyo resultado debe ser
una constante entera positiva n distinta de cero, que
es el número de elementos de la matriz. Los
elementos están numerados desde 0 hasta n-1.
7

8.  int a[10]; // declara una matriz de 10
elementos enteros
 char ch[10] // ídem de 10 elementos
char
 char* p[10] // ídem de 10 elementos
puntero-a-carácter.
 struct St mst[10] // ídem de 10 elementos
estructuras tipo St
8

9.  Una matriz puede
ser unidimensional, multidimensional o escalonada.
 El valor predeterminado de los elementos numéricos de
matriz se establece en cero y el de los elementos de
referencia se establece en null.
 Una matriz escalonada es una matriz de matrices y por
consiguiente sus elementos son tipos de referencia y se
inicializan en null.
 Las matrices se indizan basadas en cero: una matriz
con n elementos se indiza desde 0 hasta n-1.
 Los elementos de una matriz pueden ser de cualquier
tipo, incluido el tipo matriz.
 Los tipos de matriz son tipos de referencia derivados del
tipo base abstracto Array. Puesto que este tipo
implementa IEnumerable e IEnumerable(Of T), puede
utilizar la iteración foreach en todas las matrices de C#.
9

10.  Multidimensionales.
 Unidimensionales.
 Escalonadas.
 Cuadrada.
 Traspuesta.
 Simétrica.
10

11.  Matriz cuadrada: Es aquella que tiene el mismo número de filas que de
columnas, es decir m = n. En
 estos casos se dice que la matriz cuadrada es de orden n, y no n × n.
Los elementos aij
 con i = j, o sea aii
 forman la llamada diagonal principal de la matriz cuadrada, y los
 elementos aij
 con i + j = n +1 la diagonal secundaria.
 Matriz traspuesta: Dada una matriz A, se llama traspuesta de A, y se
representa por A
 t
 , a la matriz que se
 obtiene cambiando filas por columnas. La primera fila de A es la
primera fila de A
 t
 , la segunda fila de A es
 la segunda columna de A
11

12.  Para ingresar datos se necesita la
siguiente sentencia;
SCANF: Nos permite ingresar datos de tipo
entero.
 EJEMPLO:
scanf(“%d”,&matriz[i ] [j ]);
12

13.  Para imprimir datos en una matriz se
necesita la siguiente sentencia:
 PRINTF: Provee una descripción de la salida,
con placeholders marcados por caracteres
de escape "%", para especificar la
localización relativa y el tipo de salida que
la función debe producir.
EJEMPLO:
 printf(“%d”,matriz [i ] [j ]);
13

14.  Una zona de almacenamiento continuo, que
contiene una serie de elementos del mismo tipo, los
elementos de la matriz. Desde el punto de vista
lógico una matriz se puede ver como un conjunto de
elementos ordenados en fila (o filas y columnas si
tuviera dos dimensiones).
En principio, se puede considerar que todas las
matrices son de una dimensión, la dimensión
principal, pero los elementos de dicha fila pueden
ser a su vez matrices (un proceso que puede
ser recursivo), lo que nos permite hablar de la
existencia de matrices multidimensionales, aunque
las más fáciles de imaginar son los de una, dos y tres
dimensiones.
14

15. 15

16.  ENTEROS
 FLOTANTES
 CARACTERES
 OBJETOS
16

17.  float R[10] = {2, 32, 4.6, 2, 1, 0.5, 3, 8, 0,
12};
 float S[] = {2, 32, 4.6, 2, 1, 0.5, 3, 8, 0, 12};
 int N[] = {1, 2, 3, 6};
 int M[][3] = { 213, 32, 32, 32, 43, 32, 3, 43,
21};
 char Mensaje[] = "Error de lectura";
 char Saludo[] = {'H', 'o', 'l', 'a', 0};
17

18.  Almacenar los elementos del array en posiciones
de memoria contínua.
 - Tener un único nombre de variable que representa a
todos los elementos, y éstos a su vez se diferencian por un
índice o subíndice.
 - Acceso directo o aleatorio a los elementos individuales
del array.
 todos los arrays son de tamaño variable, tanto si se
especifica como no un tamaño al ser declarados
 Para ver el contenido de los arrays según van siendo
ejecutadas las líneas de código que los declaran,
utilizaremos la ventana Locales del depurador, que
muestra las variables de ámbito local
al procedimiento que estamos ejecutando actualmente
18

19.  UNIDIMENSIONALES
 BIDIMENSIONALES
 MULTIDIMENSIONALES
19

20.  Un array de una dimensión (unidimensional), también
llamado vector o fila, es un tipo
de datos estructurado compuesto de un número
determinado de elementos, de tamaño fijo y
elementos homogéneos (del mismo tipo). La
característica de tamaño fijo se refiere a que el
tamaño del array debe ser conocido en tiempo de
compilación.
Por ejemplo, si deseamos conservar las puntuaciones
de los 50 estudiantes de un examen de informática,
se necesita reservar cincuenta posiciones de
memoria, dar un nombre al arreglo y a cada uno de
los 50 estudiantes asignarles una posición o índice del
arreglo.
20

21.  Un array bidimensional (también llamado tabla
o matriz) es un array con dos índices. Al igual que
los vectores deben ser ordinales. Se declaran de
igual manera que los arrays de una dimensión.
Un array bidimensional recoge valores de una tabla
de doble entrada. Cada uno de los elementos se
identifica y se asigna mediante una variable
($nombre) seguida de dos ([]) que contienen
los índices del array.
Los índices puede ser escalares -equivaldrían al
número de fila y columna que la celda ocuparía en
la tabla, o puede ser asociativo que equivaldría en
alguna medida a usar como índices los nombres de
la fila y de la columna.
21

22.  Para ingresar datos en un vector
necesitamos la siguiente sintaxis:
 Scanf.-Nos permite ingresar datos a un
vector.
 scanf(“%d”,&vector[i]);
22

23.  Para imprimir datos en un vector
necesitamos la siguiente sintaxis:
 PRINTF.-Permite imprimir datos de tipo
entero en un vector.
 printf(“%d”, vector[i]);
23

24.  Bueno, la principal diferencia es que el
vector es así como una sola línea de „n‟
datos, comparado con el vector que son
„m‟ líneas de „n‟ datos, la idea es
imaginarse el vector como una de esas
cajitas de huevos que tienen una sola línea,
donde en cada espacio va un huevo…
 En cambio las matrices son así como un
vector metido dentro de otro vector, me
explico: Es como si cada espacio de una
de las cajas de huevos, tuviera otra línea
de cajas de huevo metida dentro…
24

25.  ENUNCIADO;
 Diseñe un programa que me permita
ingresar n elementos en una matriz
cuadrática.
25

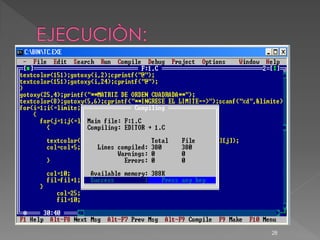
26.  #include <conio.h>
 #include <stdio.h>
void main()
{
int matriz[10][10];
int op,i,j,limite,col=10,fil=10;
do{
clrscr();
gotoxy(19,4);printf("**MATRIZ DE ORDEN CUADRADA**");
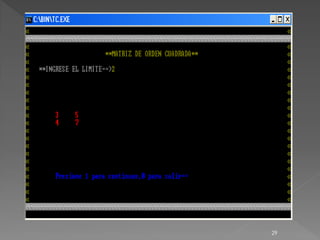
gotoxy(19,5);printf("**INGRESE EL LIMITE**");scanf("%d",&limite);
for(i=1;i<=limite;i++)
{
for(j=1;j<=limite++)
{
26

27. for(i=1;i<=limite;i++)
{
for(j=1;j<=limite++)
{
gotoxy(col ,fil);scanf("%d", &matriz[i][j]);
col=col+5;
}
col=10;
fil=fil+1;
}
col=25;
fil=10;
gotoxy(10,20);printf("Presione 1 para continuar,0 para salir");scanf("%d",&op);
}
while(op==1);
getch();
}
27

28. 28

29. 29

30.  ENUNCIADO;
 Diseñe un programa que me permita
ingresar e imprimir n elementos en una
matriz cuadrática.
30

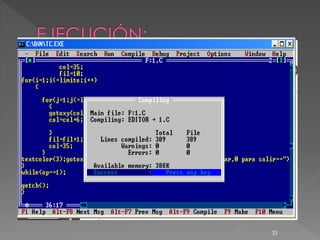
31. #include <conio.h>
#include <stdio.h>
void main()
{
int matriz[10][10];
int op,i,j,limite,col=10,fil=10;
do{
clrscr();
gotoxy(19,4);printf("**MATRIZ DE ORDEN CUADRADA**");
gotoxy(19,5);printf("**INGRESE EL LIMITE**");scanf("%d",&limite);
for(i=1;i<=limite;i++)
{
for(j=1;j<=limite++)
{
gotoxy(col,fil);scanf("%d",&matriz[i][j]);
col=col+5;
}
col=10;
fil=fil+1;
}
col=25;
fil=10;
31

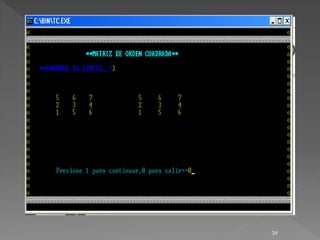
32. for(i=1;i<=limite;i++)
{
for(j=1;j<=limite;j++)
{
gotoxy(col,fil);printf("%d",matriz[i][j]);
col=col+5;
}
fil=fil+1;
col=25;
}
gotoxy(10,20);printf("Presione 1 para continuar,0 para
salir");scanf("%d",&op);
}
while(op==1);
getch();
}
32

33. 33

34. 34

35. ENUNCIADO;
Diseñe un programa que me permita
generar n múltiplos de cualquier factor
ingresado desde teclado que se
encuentre dicho factor entre 2 y 9, la
matriz es
de orden cuadrática se visualiza la
entrada y la salida.
35

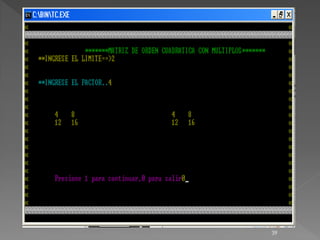
36.  #include <conio.h>
 #include <stdio.h>
 void main()
 {
int matriz1[10][10],matriz2[10][10];
int fact , mul , op , i, j, limite , x=1,col=10,fil=10;
do{
clrscr();
gotoxy(19,4);printf("**MATRIZ DE ORDEN CUADRATICA CON MULTIPLOS**");
gotoxy(19,5);printf("**INGRESE EL LIMITE**");scanf("%d",&limite);
do{
gotoxy(36,10);printf(" ");
gotoxy(19,7);printf("**INGRESE EL FACTOR**");scanf("%d",&fact);
}
while(fact<=2 || fact>=9);
for(i=1;i<=limite;i++)
{
for(j=1;j<=limite++)
{
matriz1[i][j]=fact*x;
gotoxy(col , fil);printf("%d",matriz1[i][j]);
36

37. x=x+1;
col=col+5;
}
col=10;
fil=fil+1;
}
col=35;
fil=10;
for(i=1;i<=limite;i++)
{
for(j=1;j<=limite;j++)
{
gotoxy(col,fil);printf("%d",matriz1[i][j]);
col=col+5;
}
fil=fil+1;
col=35;
}
gotoxy(10,20);printf("Presione 1 para continuar,0 para salir");scanf("%d",&op);
}
while(op==1);
getch();
}
37

38. 38

39. 39

40.  ENUNCIADO;
 Realice un programa que me permita
obtener el producto de una matriz.
40

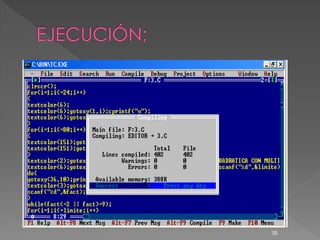
41.  #include<stdio.h>
#include<conio.h>
int lim,c,c1,c2,f,f1,f2,k,i,j,op1;
int matriz1[10][10],matriz2[10][10],matriz3[10][10];
void borde()
{
for(i=1;i<=24;i++)
{
textcolor(6);
textcolor(6);gotoxy(1,i);cprintf("®");
textcolor(6);gotoxy(80,i);cprintf("®");
}
for(i=1;i<=80;i++)
{
textcolor(151);gotoxy(i,2);cprintf("@");
textcolor(151);gotoxy(i,24);cprintf("@");
}
}
void ingreso() {
for(i=1;i<=lim;i++)
{
for(j=1;j<=lim;j++)
{
gotoxy(c,f);scanf("%d",&matriz1[i][j]);
c=c+5;
}
c=5;
f=f+1;
}
41

42. for(i=1;i<=lim;i++)
{
for(j=1;j<=lim;j++)
{
gotoxy(c1,f1);scanf("%d",&matriz2[i][j]);
c1=c1+5;
}
c1=25;
f1=f1+1;
}
}
void productom()
{
for(i=0;i<=lim;i++)
{
for(j=0;j<=lim;j++)
{
matriz3[i][j]=0;
for(k=0;k<=lim;k++)
{
matriz3[i][j]=matriz3[i][j]+matriz1[i][k]*matriz2[k][j];
}
} }
for(i=1;i<=lim;i++)
{
for(k=1;k<=lim;k++)
{
textcolor(8);
gotoxy(c2,f2);cprintf("%d",matriz3[i][k]);
c2=c2+4;
}
c2=42;
f2=f2+1;
}
 }
42

43. void main()
{
do
{
clrscr();
borde();
c=5;
c1=25;
c2=42;
f=10;
f1=10;
f2=10;
textcolor(2);(9);gotoxy(19,3);cprintf("PRODUCTO ALGEBRAICO DE UNA MATRIZ");
textcolor(5);gotoxy(35,4);cprintf("NOMBRE : CRISTINA GANAN.");
gotoxy(10,5);printf("INGRESE UN LIMITE===> ");scanf("%d",&lim);
gotoxy(6,7);printf("MATRIZ N-1");
gotoxy(27,7);printf("MATRIZ N-2");
textcolor(8);gotoxy(45,7);cprintf("MATRIZ - RESULTANTE");
ingreso();
productom();
gotoxy(8,22);printf("presione 1 para continuar y 0 para salir ");scanf("%d",&op1);
}
while(op1==1);
getch();
}
43

44. 44

45. 45

46. ENUNCIADO;
 Realice un programa que me permita
encontrar la diagonal principal y
secundaria de una matriz.
46

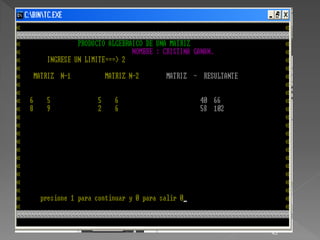
47.  #include<stdio.h>
 #include<conio.h>
 void main()
 {
 int i,j,fila,col,p,l,acumul,col1,fila2;
 int matriz[10][10];
 do
 {
 clrscr();
 textcolor(12);
 for(i=1;i<=80;i++)
 {
 textcolor(3);gotoxy(i,2);cprintf("¯");
 textcolor(3);gotoxy(i,80);cprintf("¯");
 }
 for(i=1;i<=23;i++)
 {
 gotoxy(1,i);cprintf("²");
 gotoxy(80,i);cprintf("²");
 }
 col=5;
 fila=15;
47

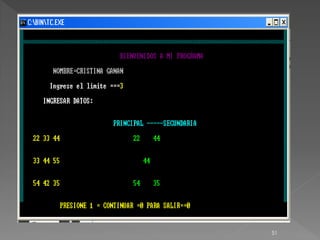
48.  textcolor(11);gotoxy(28,13);cprintf(" PRINCIPAL -----
SECUNDARIA");
 for(i=1;i<l+1;i++)
 {
 for(j=1;j<l+1;j++)
 {
 if(i==j)
 {
 textcolor(10);gotoxy(col,fila);cprintf("%d",matriz[i][j]);
 col=col+3;
 fila=fila+3;
 }
 }
 }
 col1=col-3;
 fila2=15;
 acumul=l;
 for(i=1;i<l+1;i++)
 {
48

49.  textcolor(10);gotoxy(col1,fila2);cprintf("%d",mat
riz[i][acumul]);
 acumul=acumul-1;
 fila2=fila2+3;
 col1=col1-3;
 }
 textcolor(14);gotoxy(13,24);cprintf("PRESIONE 1
= CONTINUAR =0 PARA
SALIR==");scanf("%d",&p);
 }
 while(p==1);
 getch();
 }
49

50. 50

51. 51

52. ENUNCIADO:
Realice un programa que me permita realizar
un menú de opciones el cual me pida lo
siguiente:
Números primos
Serie de fibonaci
Guardar las posiciones pares e impares en un
vector en forma ordenada.
Ordenar los datos de una matriz en forma
ascendente.
52

53. #include<stdio.h>
#include<conio.h>
#include<stdlib.h>
#include<math.h>
int opcion,op,r,N, vec1[10], mat[10][10],vecPares[100], vecImpares[100], mat[10][10],aux,p=0,
ip=0,m1[5][5],m[10][10],k,j,f,fil,a=0, lim, b=0,c,n,op,g,res,nc,c1,c2,x,y,i,col=1,fila=1,n;
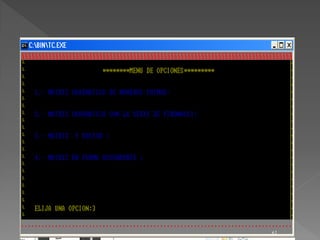
void main() {
Do {
col=1,fila=1;
clrscr();
gotoxy(25,5);printf("********MENU DE OPCIONES*********");
textcolor(1);
gotoxy(5,8);cprintf("1.- MATRIZ CUADRATICA DE NUMEROS PRIMOS: ");
gotoxy(5,11);cprintf("2.- MATRIZ CUADRATICA CON LA SERIE DE FIBONACCI: ");
gotoxy(5,14);cprintf("3.- MATRIZ Y VECTOR : ");
gotoxy(5,17);cprintf("4.- MATRIZ EN FORMA ASCENDENTE : ");
fila=2,col=0;
for(i=1;i<=25;i++)
{
gotoxy(1,i);printf("®");
gotoxy(80,i);printf("®");
}
for(i=1;i<=80;i++)
{
gotoxy(i,2);printf("¯");
gotoxy(i,25);printf("¯");
}
53

54. textcolor(22);gotoxy(5,22);cprintf("ELIJA UNA OPCION:");scanf("%d",&opcion);
switch (opcion)
{
{
case 1:
clrscr();
flushall();
gotoxy(2,4);printf("NUMERO - PRIMO");
gotoxy(5,3);printf("ingrese el limite: ");scanf("%d",&n);
x=10;
y=15;
for(c=1;c<=n;c++)
{
for(c2=1;c2<=c;c2++)
{
res=c%c2;
if(res==0)
{
nc=nc+1;
}}
if(nc==2)
{
gotoxy(x,y);printf("%d",c);
x=x+3;
}
nc=0;
}
f=f+2;
break;
}
{
54

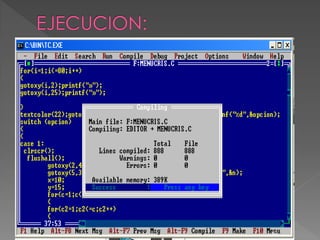
55. case 2:
clrscr();
a=-1;
c=0;
b=1;
clrscr();
gotoxy(2,2);cprintf("Ingrese la matriz: "); scanf("%d",&N);
//mat[0][0] = c;
// Ingreso de datos a la matriz
for(i=0; i<N; i++)
{
k = 0;
for(j=0; j<N; j++, k+=4)
{
c = a+b;
a = b;
b = c;
mat[i][j] = c;
gotoxy(5+k, 4+i); printf("%d", mat[i][j]);
}
}
}
break;
{
55

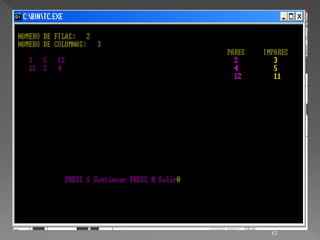
56. case 3:
clrscr();
gotoxy(2,2);cprintf("NUMERO DE FILAS: "); scanf("%d",&fil); gotoxy(2,3);cprintf("NUMERO DE COLUMNAS: ");
scanf("%d",&col);
for(i=0; i<fil; i++)
k = 0;
for(j=0; j<col; j++, k+=4) {
do{
gotoxy(5+k, 5+i); printf(" ");
gotoxy(5+k, 5+i); scanf("%d", &mat[i][j]);
}while(mat[i][j]<1 || mat[i][j]>32);
}
}
for(i=0; i<fil; i++)
{
for(j=0; j<col; j++)
{
if(mat[i][j]%2 == 0)
{
vecPares[p] = mat[i][j];
p++;
}
else
{
vecImpares[ip] = mat[i][j];
ip++;
}
}
}
56

57. gotoxy(60,4); printf("PARES");
for(i=0; i<p; i++)
{
gotoxy(62, 5+i); printf("%d", vecPares[i]);
 }
gotoxy(70,4); printf("IMPARES");
for(i=0; i<p; i++)
{
gotoxy(73, 5+i); printf("%d", vecImpares[i]);
}
break;
{
case 4:
clrscr();
gotoxy(32,5);printf("MATRIZ ASCENDENTE ");
gotoxy(15,7);printf("Ingrese el L¡mite ");scanf("%d",&lim);
a=1;b=0;c=1;col=7;fila=12;
gotoxy(8,9);printf("MATRIZ");
for(i=1;i<=lim;i++)
{
for(j=1;j<=lim;j++)
{
57

58. gotoxy(col,fila);scanf("%d",&m1[i][j]);
col=col+5;
}
fila=fila+3;col=7;
}
gotoxy(44,9);printf("ASCENDENTE");
a=1;col=45;fila=12;
for(i=1;i<=lim;i++)
{
for(j=1;j<=lim;j++)
{
for(a=1;a<=lim;a++)
{
for(b=1;b<=lim;b++)
{
if(m1[i][j]<m1[a][b])
{
c=m1[i][j];
m1[i][j]=m1[a][b];
m1[a][b]=c;
}
}
}
}
}
for(i=1;i<=lim;i++)
{
for(j=1;j<=lim;j++)
{
58

59. gotoxy(col,fila);printf("%d",m1[i][j]);
col=col+5;
}
fila=fila+3;
col=45;
}
}
break;
}
}
textcolor(5);gotoxy(15,20);cprintf("PRESS 1 Continuar PRESS 0
Salir");scanf("%d",&oper);
}
while(oper==1);
getch();
}
59

60. 60

61. 61

62. 62

63. http://es.wikipedia.org/wiki/Printf
http://www.zator.com/Cpp/E4_3_7.htm
//www.itescam.edu.mx/principal/sylabus/fpdb/recursos/r416
06.PDF
http://es.wikipedia.org/wiki/Vector_(inform%C3%A1tica)
http://ronnyml.wordpress.com/2009/07/04/vectores-matrices-
y-punteros-en-c/
http://c.conclase.net/curso/?cap=010
http://www.monografias.com/trabajos71/clasificacion-
arrays/clasificacion-arrays.shtml#caracteria
http://www.sc.ehu.es/sbweb/fisica/cursoJava/numerico/mat
rics/matriz/matriz.htm
http://www.uhu.es/04004/material/Practica6_Curso0809.pdf
http://www.forosdelweb.com/f13/diferencia-entre-vector-
matriz-420381/
63

64.  http://elrafita.wordpress.com/2007/05/26
/ingresando-datos-en-un-vector-o-
matriz/
 http://palillo.usach.cl/Pamela/historia.ht
m
 http://es.wikipedia.org/wiki/Matriz_(mate
m%C3%A1tica).
64