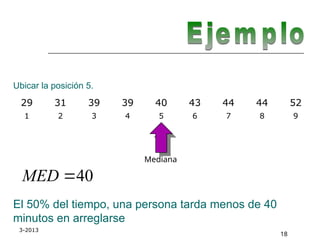
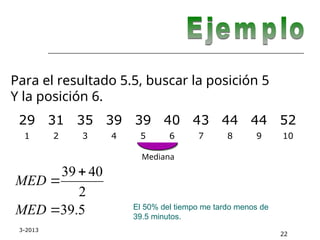
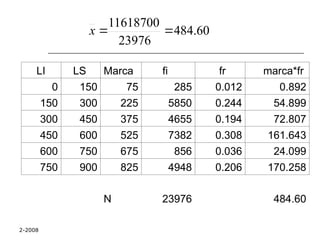
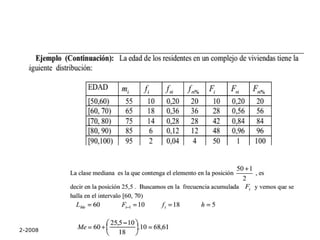
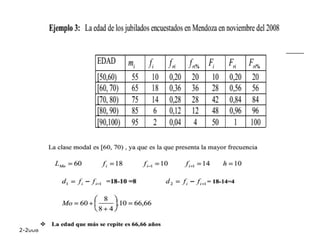
El documento aborda las medidas de tendencia central en estadística, incluyendo la media aritmética, mediana y moda, explicando sus definiciones y métodos de cálculo. Se ilustra cómo calcular la media y mediana a partir de conjuntos de datos y se discuten las características y aplicaciones de cada medida. Además, se menciona la importancia de los cuantiles, cuartiles, deciles y percentiles en la descripción de conjuntos de datos.

1. 3-2013 1
Medidas de tendencia
central
Estadística
Capítulo 3

2. 3-2013
2
Medidas
 Medidas de
Tendencia Central

3. 3-2013
3
Medidas de Tendencia Central
La mayoría de los levantamientos de
encuestas mantienen una tendencia bien
definida a agruparse o aglomerarse
alrededor de cierto punto central.
Siempre se puede obtener un valor típico
que representa o describe a todos los
demás datos de la muestra.

4. 3-2013
4
Medidas de Tendencia Central
 Media Aritmética
 Mediana
 Moda

5. 3-2013 5
Media Aritmética

6. 3-2013
6
Media Aritmética
Es la medida de tendencia central más
utilizada, también se le conoce con el
nombre de Promedio.
Para calcular la media aritmética, se
suman todos los datos de la muestra y el
resultado se divide entre el total de datos.

7. 3-2013
7
El símbolo que representa a la media aritmética
es una letra X con una barra sobre ella.
La letra x significa uno de los datos de la muestra y la i es el
conteo de los datos específicos
Media Aritmética
n
x
X
n
i

 1

8. 3-2013
8
La fórmula en su esquema de desarrollo
se presenta de la siguiente manera:
n
x
x
x
x
x
X n
2 





...
4
3
1
Media Aritmética

9. 3-2013
9
Se define en minutos el tiempo que le lleva
arreglarse, desde que se levanta hasta que sale
de casa. A lo largo de 10 días hábiles
consecutivos, Usted recaba los tiempos
(redondeados a minutos) que se muestra a
continuación
39 29 43 52 39
44 40 31 44 35

10. 3-2013
10
39 29 43 52 39
44 40 31 44 35
DATOS
min
6
.
39
10
396
10
35
44
31
40
44
39
52
43
29
39
10
10
1















X
X
X
x
X i
i
El tiempo que tarda
para arreglarse es
aproximadamente 40
minutos cada día

11. 3-2013 11
Mediana
X
~ MED

12. 3-2013
12
Mediana
Es el valor medio de un arreglo ordenado de
datos numérico, si no hay empates, la primera
mitad de las observaciones será menor que la
mediana y la segunda mitad será mayor.
Si un valor extremo se presenta en una
secuencia de datos, es mejor utilizar la
mediana.

13. 3-2013
13
Mediana
La mediana es el valor tal que el 50% de los
datos son menores y el otro 50% son mayores
Ojo: se muestra una pequeña diferencia cuando el total de
datos de la muestra es par o impar
)
2
1
(


n
ión
ValorPosic
MED

14. 3-2013
14
Mediana
Regla 1
Si el número de datos es impar, la mediana es el
dato que queda exactamente en el medio del
arreglo ordenado
Datos Menores , , Datos Mayores

15. 3-2013
15
Calcular la mediana de una muestra de
tiempos que se tarda una persona en
arreglarse durante 9 días.
39 29 43 52 39
44 40 31 44

16. 3-2013
16
Datos de la muestra ordenados
)
2
1
(


n
ión
ValorPosic
MED
Tamaño de la muestra
N = 9
Formulación
29 31 39 39 40 43 44 44 52

17. 3-2013
17
)
5
(
)
2
10
(
)
2
1
9
(
ión
ValorPosic
MED
ión
ValorPosic
MED
ión
ValorPosic
MED





18. 3-2013
18
29 31 39 39 40 43 44 44 52
1 2 3 4 5 6 7 8 9
Ubicar la posición 5.
40

MED
El 50% del tiempo, una persona tarda menos de 40
minutos en arreglarse
Mediana

19. 3-2013
19
Mediana
Regla 2
Si el número de datos es par, la mediana es el
promedio de los dos datos medios del arreglo
ordenado
Datos Menores , a , b , Datos Mayores
)
2
(
b
a
MED



20. 3-2013
20
Se define en minutos el tiempo que le lleva
arreglarse, desde que se levanta hasta que sale
de casa. A lo largo de 10 días hábiles
consecutivos, Usted recaba los tiempos
(redondeados a minutos) que se muestras a
continuación
39 29 43 52 39
44 40 31 44 35

21. 3-2013
21
Se ordenan los datos
29 31 35 39 39 40 43 44 44 52
Ubicar la posición del valor de la mediana
)
5
.
5
(
)
2
11
(
)
2
1
10
(
ión
valorposic
MED
ión
valorposic
MED
ión
valorposic
MED




Posición
impar

22. 3-2013
El 50% del tiempo me tardo menos de
39.5 minutos.
22
Para el resultado 5.5, buscar la posición 5
Y la posición 6.
5
.
39
2
40
39



MED
MED
29 31 35 39 39 40 43 44 44 52
1 2 3 4 5 6 7 8 9 10
Mediana

23. 3-2013 23
Moda
MO

24. 3-2013
24
Moda
Es el valor que aparece con mayor
frecuencia en un conjunto de datos.
La ocurrencia de un dato extremo no afecta
el resultado de la moda. De igual manera
puede darse lo siguiente:

25. 3-2013
25
Moda
 La moda esté en los extremos
 Exista más de una moda
 La moda no existe
Recordar siempre que la moda es el dato
que más veces se repite en una muestra

26. 3-2013
26
Moda
 Es útil sólo como descripción general
 Se utiliza con el arreglo ordenado
Observaciones

27. 3-2013
27
Se define en minutos el tiempo que le lleva
arreglarse, desde que se levanta hasta que sale
de casa. A lo largo de 10 días hábiles
consecutivos, Usted recaba los tiempos
(redondeados a minutos) que se muestras a
continuación
39 29 43 52 39
44 40 31 44 35

28. 3-2013
28
 Los datos de ordenan de menor a mayor
 Buscar el número que más se repite
 De 39 minutos hay 2 días
 De 44 minutos hay 2 días
29 31 35 39 39 40 43 44 44 52
1 2 3 4 5 6 7 8 9 10

29. 3-2013
 La mayoría del tiempo se tarda 39 ó 44 minutos en
arreglarse.
29
29 31 35 39 39 40 43 44 44 52
1 2 3 4 5 6 7 8 9 10

30. Medidas de tendencia central
para datos agrupados
2-2008

31. 2-2008
Medidas de tendencia central para
datos agrupados: La Media
Media aritmética para datos agrupados:
Cuando se cuenta con datos agrupados en
una distribución de frecuencia, todos los
valores que caen dentro de un intervalo de
clase dado se consideran igual a la marca
de clase, o punto medio del intervalo.

32. 2-2008
n
X
f
X
n
i
i
i


 1

33. 2-2008

34. 2-2008
Ejemplo:
A partir de la
siguiente tabla de
distribución de
frecuencia,
encuentre la media.
LI LS Marca fi fr
0 150 75 285 0.012
150 300 225 5850 0.244
300 450 375 4655 0.194
450 600 525 7382 0.308
600 750 675 856 0.036
750 900 825 4948 0.206
N 23976

35. 2-2008
Se puede hacer de dos maneras. Ambas
provienen de la definición de promedio
ponderado.
La primera suma las frecuencias
multiplicadas por su marca y se divide por
N.
La segunda simplemente suma la
multiplicación de las marcas por las
frecuencias relativas.

36. 2-2008
LI - LS
Marca
de clase fi fr M*fi
0 150 75 285 0.012 21375
150 300 225 5850 0.244 1316250
300 450 375 4655 0.194 1745625
450 600 525 7382 0.308 3875550
600 750 675 856 0.036 577800
750 900 825 4948 0.206 4082100
N 23976 11618700

37. 2-2008
60
.
484
23976
11618700


x
LI LS Marca fi fr marca*fr
0 150 75 285 0.012 0.892
150 300 225 5850 0.244 54.899
300 450 375 4655 0.194 72.807
450 600 525 7382 0.308 161.643
600 750 675 856 0.036 24.099
750 900 825 4948 0.206 170.258
N 23976 484.60

38. 2-2008

39. 2-2008
Medidas de tendencia central para
datos agrupados: La Mediana
 La mediana se obtiene por interpolación y
está dada por:
mediana
clase
la
de
Ancho
A
mediana
clase
la
de
Frecuencia
mediana
la
a
inferiores
clases
las
de
s
frecuencia
las
de
Suma
total)
a
(frecuenci
datos
de
Número
mediana)
la
a
contiene
que
(la
mediana
clase
la
de
inferior
Frontera
2
1
1
1
1
1























fi
f
N
L
A
f
f
n
L
Mediana
i
i
i

40. 2-2008

41. 2-2008

42. 2-2008

43. 2-2008
43
Cuantiles
 Cuartiles
 Deciles
 Percentiles
Los cuantiles son medidas de posición “no
central” que se utilizan con mayor frecuencia y se
emplean sobre todo para resumir o describir las
propiedades de conjuntos grandes de datos
numéricos.

44. 2-2008
44
Cuartiles
De la misma manera que la mediana divide un
conjunto de datos en dos grupos iguales, los
cuartiles lo dividen en cuatro grupos iguales.
Cada grupo está formado por 25% de los datos de la
muestra y se denotan por Q1, Q2 y Q3 respectivamente
25% 25% 25% 25%
Q1 Q2 Q3

45. 2-2008
45
Cuartiles
)
4
)
1
(
3
(
)
4
)
1
(
2
(
)
4
1
(
3
2
1






n
ión
ValorPosic
Q
n
ión
ValorPosic
Q
n
ión
ValorPosic
Q
La obtención de los cuartiles depende del número de datos
de la muestra; se utilizan los mismo conceptos del cálculo
de la mediana. Las fórmulas para cada los cuartiles 1 y al
vienen a ser:

46. 2-2008
46
Se define en minutos el tiempo que le lleva arreglarse, desde que se
levanta hasta que sale de casa. A lo largo de 10 días hábiles
consecutivos, Usted recaba los tiempos (redondeados a minutos) que
se muestras a continuación
39 29 43 52 39
44 40 31 44 35

47. 2-2008
47
Tamaño de la muestra N=10
35
)
3
(
)
75
.
2
(
)
4
1
10
(
)
4
1
(
1
1
1
1
1







Q
VP
Q
VP
Q
VP
Q
n
VP
Q
29
31
35
39
39
40
43
44
44
52
Cuartil 1
3

48. 2-2008
48
Tamaño de la muestra N=10
5
.
39
2
40
39
)
5
.
5
(
)
4
)
1
10
(
2
(
)
4
1
(
2
2
2
2
1








Q
Q
VP
Q
VP
Q
n
VP
Q
29
31
35
39
39
40
43
44
44
52
Cuartil 2
5.5

49. 2-2008
49
Tamaño de la muestra N=10
44
)
8
(
)
25
.
8
(
)
4
)
1
10
(
3
(
)
4
1
(
3
3
3
3
1







Q
VP
Q
VP
Q
VP
Q
n
VP
Q
29
31
35
39
39
40
43
44
44
52
Cuartil 3
8

50. 2-2008
50
Deciles
Los deciles dividen una muestra en 10 grupos
iguales y cada decil acumula el 10% de los
datos.
Se trabajan igual que los cuartiles
10% 10% 10% 10% 10% 10% 10% 10% 10% 10%

51. 3-2013
51
Percentiles
Los percentiles dividen una muestra en 100
grupos iguales y cada percentil acumula el 1% de
los datos.
Se trabajan igual que los cuartiles y deciles
1% 1% 1% 1% 1% 1% 1%

52. 3-2013 52
Fin