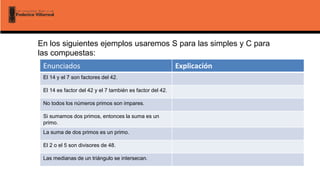
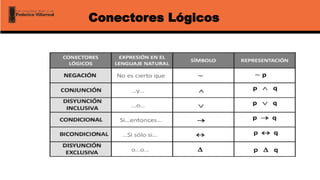
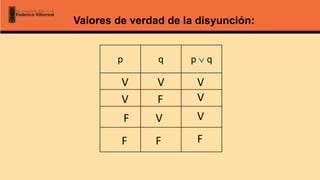
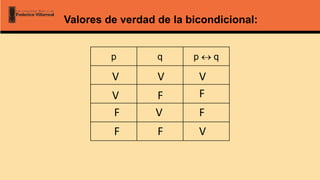
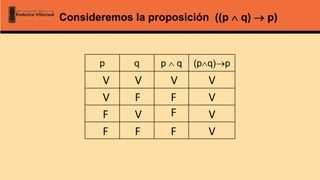
El documento aborda la lógica matemática, centrándose en las proposiciones y los conectores lógicos, que son fundamentales para una interpretación precisa del razonamiento matemático. Se describen los tipos de proposiciones, como las simples y compuestas, así como los conectores lógicos como la negación, conjunción, disyunción y condicional. Además, se analizan los valores de verdad asociados a estas proposiciones y se introducen conceptos como tautologías, contingencias y contradicciones.

1. Tema: Lógica matemática
(proposiciones, conectivos lógicos)
Docente: Anabel Rojas Espinoza
ASIGNATURA: MATEMATICA

2. LENGUAJE MATEMATICO
El lenguaje matemático está formado por una
parte del lenguaje natural, al cuál se le
agregan variables y símbolos lógicos que
permiten una interpretación precisa de cada
frase o enunciado.

3. Lógica Proposicional
En un intento por sistematizar el razonamiento
matemático, surge el concepto de Lógica Proposicional.
Como su nombre lo explícita, se trabaja con
proposiciones lógicas; las cuales poseen un valor de
verdad (verdadero o falso). Por convención, se denotan
con letras minúsculas. Por ejemplo:
p, q, r, s

4. Proposiciones
Llamaremos proposiciones a aquellas frases
del lenguaje natural, las cuales podamos
afirmar que son verdaderas o falsas.
Ejemplos de proposiciones:
• Dos es par
• Tres es mayor que diez
• Tres más cuatro es nueve
( )
( )
( )

5. Son ejemplo de proposiciones lógicas:
p: El gato es café.
q: 3 es un número primo.
r: 18 es múltiplo de 3 y múltiplo de 6.
s: π < e
Estas proposiciones tienen un valor de verdad. En
particular, p, q, r, s son ……….. mientras que s es ………...
Proposiciones

6. 1) Proposición simple o atómica: cuando expresa un contenido de
manera sencilla y carecen de conectores o negaciones entre
oraciones. Ejemplos:
• “El hombre es alto”
• “Dos es un número par".
• "Tres es mayor que cuatro".
• "Tres más cinco es mayor que cuatro".
• “Alberto es alto y guapo”
Tipos de Proposiciones

7. Tipos de Proposiciones
2) Proposiciones compuestas: están constituidas por más de
una proposición simple, relacionadas entre sí por medio
de conectores lógicos, como negaciones, conjunciones,
disyunciones, condicionales, entre otras. Ejemplos:
• Belén estudia abogacía y Pablo, biología.
• Puerto Montt es una ciudad de Chile y Montevideo es una ciudad de
Uruguay.
• El valor de “e” es 2,7182 y “π” vale 3,1415

8. En los siguientes ejemplos usaremos S para las simples y C para
las compuestas:
Enunciados Explicación
El 14 y el 7 son factores del 42.
El 14 es factor del 42 y el 7 también es factor del 42.
No todos los números primos son impares.
Si sumamos dos primos, entonces la suma es un
primo.
La suma de dos primos es un primo.
El 2 o el 5 son divisores de 48.
Las medianas de un triángulo se intersecan.

9. Conectores Lógicos

10. Conectivos
Negación: Es aquel conectivo que niega la proposición, y
normalmente se utiliza anteponiendo “no”, o anteponiendo
la frase es falso que.
Simbólicamente la negación se puede representar en
lenguaje matemático, de tres formas diferentes:
I.- Anteponiendo el símbolo “” . “ p” significa “no
p”.
II.- Sobreponiéndole una barra “ p “
III.- Anteponiendo el símbolo “” . “ p” significa “no p”.

11. Conjunción: Es aquel conectivo que une dos
proposiciones, incluyéndolas obligatoriamente a ambas.
Se utiliza “y” como conectivo de conjunción.
"dos es par y tres es impar
Simbólicamente la conjunción “y” se representa en
lenguaje matemático con el símbolo 
y  

12. Disyunción: Es aquel conectivo que une dos proposiciones ofreciendo una
alternativa entre una proposición o la otra, así como también ofrece la
posibilidad que sean ambas.
"dos es mayor que siete o siete es mayor que dos".
La proposición está compuesta por las proposiciones simples
"dos es mayor que siete"
junto con
" siete es mayor que dos",
conectadas por la palabra "o“, que constituye el conectivo de
disyunción, y su símbolo es “”

13. Disyunción excluyente: Es la disyunción pero que su valor de verdad
acepta una sola proposición como verdadera. No pueden ocurrir las dos
proposiciones al mismo tiempo.
Ejemplo:
• Me caso con Rosita o con Doris
• Hoy a las 3 voy al Parque Arauco o al Alto Las Condes.
Su notación es:

p q


14. Implicación o condicional: Es aquél conectivo en el que
se establece una condición para que se cumpla la otra
proposición.
Normalmente se establece como:
“Si se cumple p, entonces se cumple q”
p  q

15. Bicondicional o doble implicancia.
Es aquel conectivo de la forma:
“se cumple p si y solamente si se cumple q”.
Esto significa que también se cumple la
situación inversa,
es decir que como se cumple q, también se
cumple p
p  q”.

16. p p
Valores de verdad de la negación:
V
F
V F

17. p q p  q
Valores de verdad de la conjunción:
V
F
V
F
F
V
F
V
V
F
F
F

18. p q p  q
Valores de verdad de la disyunción:
V
F
V
V
F
F F
V
V
V
V
F

19. p q p q
Valores de verdad
Disyunción excluyente
V
F
V
V
F
F F
V
F
V
V
F


20. p q p  q
Valores de verdad de la implicancia:
F
V
V
V
F V
F F
V
F
V
V

21. p q p  q
Valores de verdad de la bicondicional:
F
V V
V
F V
F F
V
F
F
V

22. Verdad lógica o Tautología
Son aquellas proposiciones que siempre son
verdad, sin importar los valores de verdad de
las proposiciones que la componen.

23. p q p  q (pq)p
Consideremos la proposición ((p  q)  p)
F
V V
V
F V
F F
V
F
F
F
V
V
V
V

24. Contingencia
Son aquellas proposiciones que pueden
ser verdad o falso, dependiendo de los
valores de verdad de las proposiciones
que le componen.

25. Contradiccione
s
Son aquellas proposiciones que
siempre son falsas, sin importar los valores
de verdad de las proposiciones que la
componen.

26. Álgebra de
proposiciones
q
p
q
p 


p q q
V V V F V V
V F F F F F
F V V V V V
F F V V F V
q
p  p q
p 

27. ((p  q)  p)  q
((p  q)  (q  r))  (p  r)
((p  q)  (q  r))  (p  r)
(p  q)  (  q)
(p  q)  (p  q)  (q  p)
((p  q)  (q  r)  (r  p))  ((p  q)  (q  r))
((p  q)  (  q))  q
((p  q)  (r  q))  ((p  q)  q)
((p  (q  r))  ((p  q)  (p  r))
((p  (q  r))  ((p  q)  (p  r))
((p  r)  q))  (p  (r  q))
p
p
Proposiciones lógicas x resolver

28. ¡TODOS JUNTOS RUMBO LA LICENCIAMIENTO
INSTITUCIONAL
Gracias por su atención
Comisión Responsable
Licenciamiento Institucional