Este documento describe los principales métodos de raíces cerrados y abiertos. Entre los métodos cerrados se encuentran el método de bisección y falsa posición. Los métodos abiertos incluyen el método de la secante, punto fijo y Newton-Raphson. Para cada método se provee una explicación general del procedimiento, así como ejemplos numéricos para ilustrar los pasos.

1. METODOS DE RAICESCYNDY ARGOTE SIERRAUNIVERSIDAD INDUSTRIAL DE SANTANDER

2. METODOS CERRADOS BISECCIÓN

3. FALSA POSICIÓNMETODO BISECCIONEn este método se recomienda:Graficar la función que se nos proporciona lo cual me permite hallar el intervalo a evaluar (Xa,Xb).Hallar XmCompletar la siguiente tabla:

4. EJEMPLOEmpleando el método de Bisección calcule la raíz de:SOLUCIÓNGraficar la función que se nos proporciona lo cual me permite hallar el intervalo a evaluar (Xa,Xb).Observando de esta manera que la raíz se encuentra entre 0 y 0,5 siendo este nuestro intervalo inicial.

5. Hallar XmProcedemos a completar la tablaVemos que en la iteración 6 el Ea es menor de 1% encontrando que el valor de la raíz es 0,42578125

6. METODO DE FALSA POSICIÓN En este método se siguen algunos de los pasos llevados a cabo en el método de bisección. En esté se recomienda:Graficar la función que se nos proporciona lo cual me permite hallar el intervalo a evaluar (Xa,Xb).Hallar Xm:Completar la siguiente tabla:

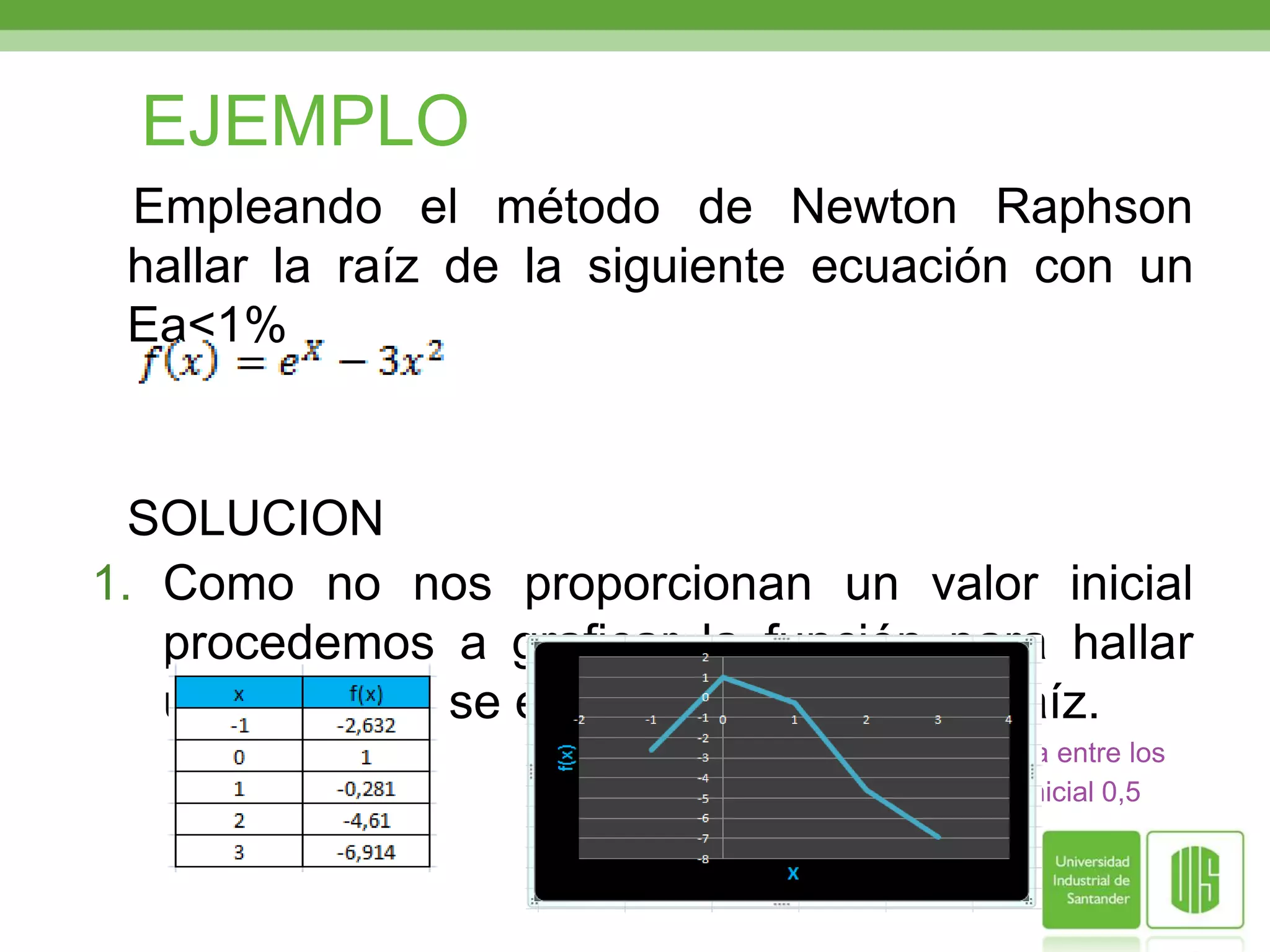
7. EJEMPLOComenzando en el intervalo [1,2] y con un Ea menor que o,o1Use el método de Falsa posición para aproximar la raíz de:SOLUCIONEn este caso no es necesario graficar puesto que nos proporcionan los valores de a y b, por tanto procedemos a hallar Xm

8. Para hallar este valor necesitamos tanto la imagen de Xa como Xb procedemos a hallarlas: Donde

9. Procedemos a completar la tabla para hallar el valor de la raíz. Vemos que en la iteración 2 el Ea es menor de 1% encontrando que el valor de la raíz es 1,31126956. También cabe notar que mediante este método se obtiene la convergencia en un número menor de iteraciones.

10. METODOSABIERTOSSECANTE

11. PUNTO FIJO

12. NEWTON RAPHSONMETODO DE LA SECANTE En este método se recomienda:Para este método el problema nos debe proporcionar dos valores iniciales(Xi,Xi-1), que nos permita hallar Xi+1.Hallar Xi+1Completar la siguiente tabla:

13. EJEMPLO Usar el método de la secante para aproximar la raíz de Comenzando con Xo=O y X1=1, hasta que Ea<1% SOLUCIONTeniendo en cuenta que tenemos los valores de Xi y Xi-1, procedemos a hallar Xi+1.

14. Para hallar Xi+1 requiero hallar la imagen de Xi y Xi-1. Hallo Xi+1

15. Completando la tabla tenemos que:En este método la raíz que buscamos es el valor que toma X en la iteración actual, es decir, en este caso Xm= -0,85313041

16. MÉTODO DE PUNTO FIJOPara este método el problema nos debe proporcionar un valor inicial (Xi), que nos permita hallar g(x).Hallar g(x) o Completar la siguiente tabla:

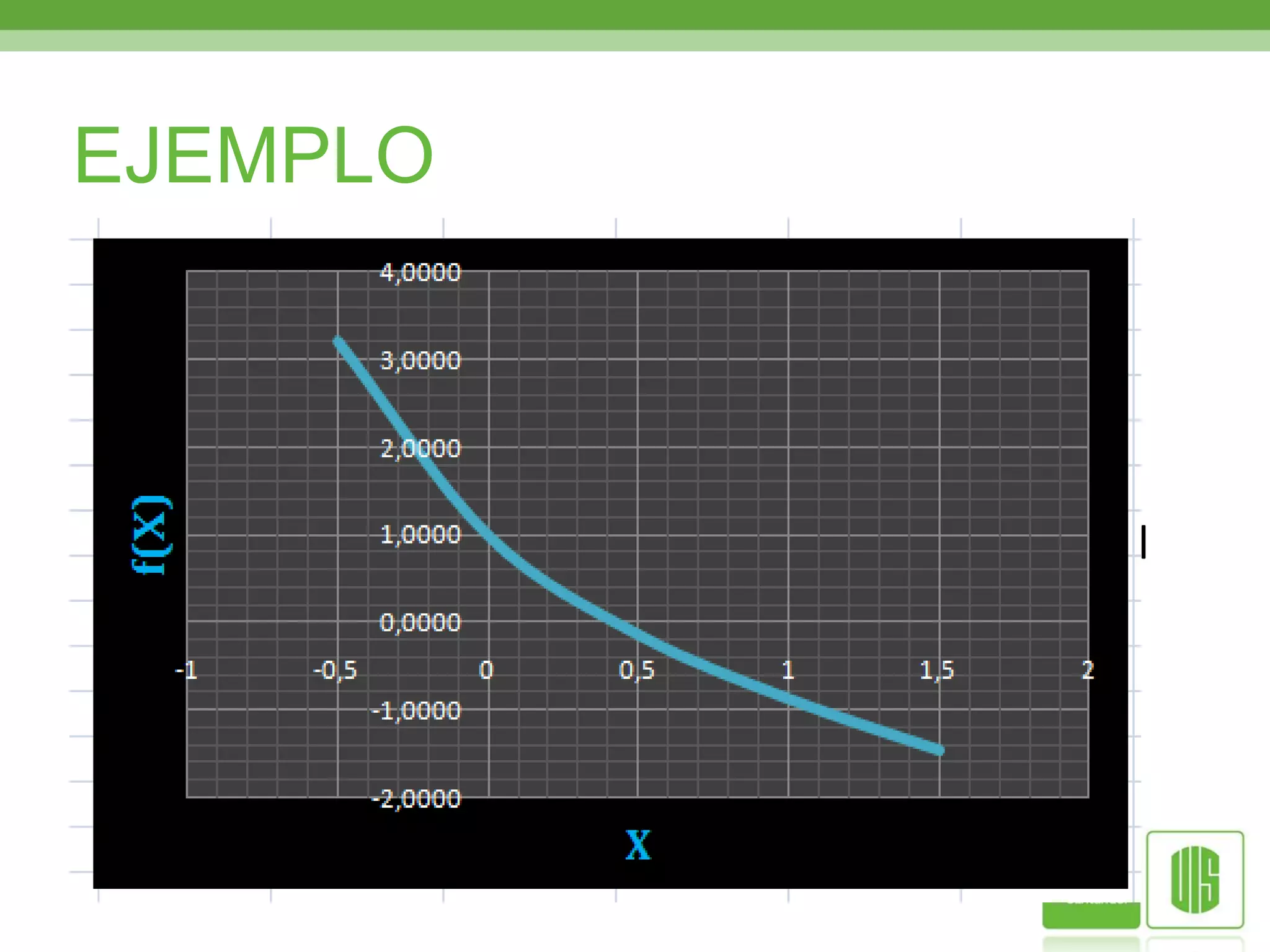
17. EJEMPLO Usando el método de punto fijo vamos a aproximar la solución de la ecuación con un valor inicial igual a dos [2]SOLUCION Como sabemos que procedemos a despejar x de la función. luego Finalmente

18. Con el valor inicial y teniendo g(x) procedemos ha hallar la raíz completando la tabla. En este caso se alcanzo la raíz en la 3 iteración, obteniendo la raíz con un valor de 1,36538433, esto se puede comprobar reemplazando esté valor en la función original.

19. Método de Newton RaphsonEn este método se nos proporciona un valor inicial para hallar Xi+1.Procedemos a hallar Xi+1Hallar la derivada de la función y proceder a completar la siguiente tabla

20. EJEMPLO Empleando el método de Newton Raphson hallar la raíz de la siguiente ecuación con un Ea<1% SOLUCIONComo no nos proporcionan un valor inicial procedemos a graficar la función para hallar un valor que se encuentre cerca de la raíz.podemos notar que la raíz se encuentra entre los valores 0 y 1, tomaremos como valor inicial 0,5

21. Procedemos a hallar la derivada de la función hallamos el valor de la imagen y la derivada de la función para determinar el valor de Xi+1Teniendo estos valores procedemos a hallar Xi+1

22. Finalmente completamos la tablaObteniendo que el valor de la raíz es 0,91000766 en la cuarta iteración.

23. BIBLIOGRAFIAEjercicios resueltos, datos tabulados y graficados Argote.Cyndy