Este documento describe tres métodos iterativos para resolver sistemas de ecuaciones lineales: el método de Jacobi, el método de Gauss-Seidel y el método de Gauss-Seidel con relajación. Explica los pasos para implementar cada método y provee un ejemplo numérico para ilustrar cómo se aplican. Concluye que el método de Gauss-Seidel converge más rápido que el método de Jacobi y que el método de Gauss-Seidel con relajación puede acelerar aún más la convergencia.

1. MÉTODOS ITERATIVOS CYNDY ARGOTE SIERRAESCUELA DE INGENIERIA DE PETRÓLEOS MÉTODOS NUMERICOS

2. MÉTODO DE JACOBI Este método junto con el de gauss Seidel comprenden los métodos iterativos para la solución de sistemas de ecuaciones lineales. El método parte de un sistema de ecuaciones al cual se le aplicaran unos arreglos si es necesario para poder implementar este método. Cuando se tiene el sistema de ecuaciones definido se debe hacer lo posible para que la matriz tenga la forma de diagonalmente dominante. Es decir:

3. PASOS A SEGUIR…Para emplear este método se nos debe proporcionar un vector inicial.Este método se basa en el despeje de cada incógnita de un sistema de ecuaciones como el siguiente.a11X1 + a12X2 +… + a1nXn = b1 a21X1 + a22X2 +… +a2nXn = b1 . . . . . . an1X1+ an2X2 + … + annXn = bnDespejamos las incógnitas (variable x) de estas ecuaciones y empleamos el valor inicial para la primera iteración.Realizamos una serie de iteraciones hasta lograr que el Ea sea menor de la tolerancia dada.

4. EJEMPLOCon un vector inicial X1 = 0 X2 = 0 X3 = 0 Resolver por el método de Jacobi, el siguiente sistema de ecuaciones. 6x1 + 2x2 + x3 = 22 -x1 + 8x2 + 2x3 =30 x1 - x2 + 6x3 =23

5. SOLUCIÓN Despejamos la variable x de cada una de las ecuaciones como sigue: x1 = (22-2x2-x3)/6 x2 = (30+x1-2x3)/8 x3 = (23-x1+x2)/6Para un vector inicial (0 ; 0 ; 0) hallo los valores de x1, x2, x3.x1 = [22-2(0)-(0)]/6 x2 = [30+(0)-2(0)]/8 x3 = [23-(0)+(0)]/6Teniendo para nuestra primera iteración los siguientes valores: X1= 3,66 X2= 3,75 X3= 3,83

6. Reemplazamos en las ecuaciones despejadas inicialmente los valores obtenidos anteriormente e iteramos hasta que Ea<1%Observamos que en la 6 Iteración se alcanza la convergencia.

7. GAUSS SEIDELEl método de Gauss Seidel es casi idéntico al método de Jacobi. Este ultimo encuentra valores para cada incógnita del sistema de ecuaciones lineales y en la siguiente iteración sustituye estos valores en el sistema. La única diferencia entre estos dos métodos esta en que, en el método de Gauss Seidel una vez que se ha calculado el valor de Xi, este valor se sustituye inmediatamente en la misma iteración.

8. EJEMPLOResuelva el siguiente sistema de ecuaciones lineales por medio del método de Gauss Seidel, con una tolerancia de 0,1% 6x1 + 2x2 + x3 = 22 -x1 + 8x2 + 2x3 =30 x1 - x2 + 6x3 =23 Con un Vector inicial X1=0 X2=0 X3=0

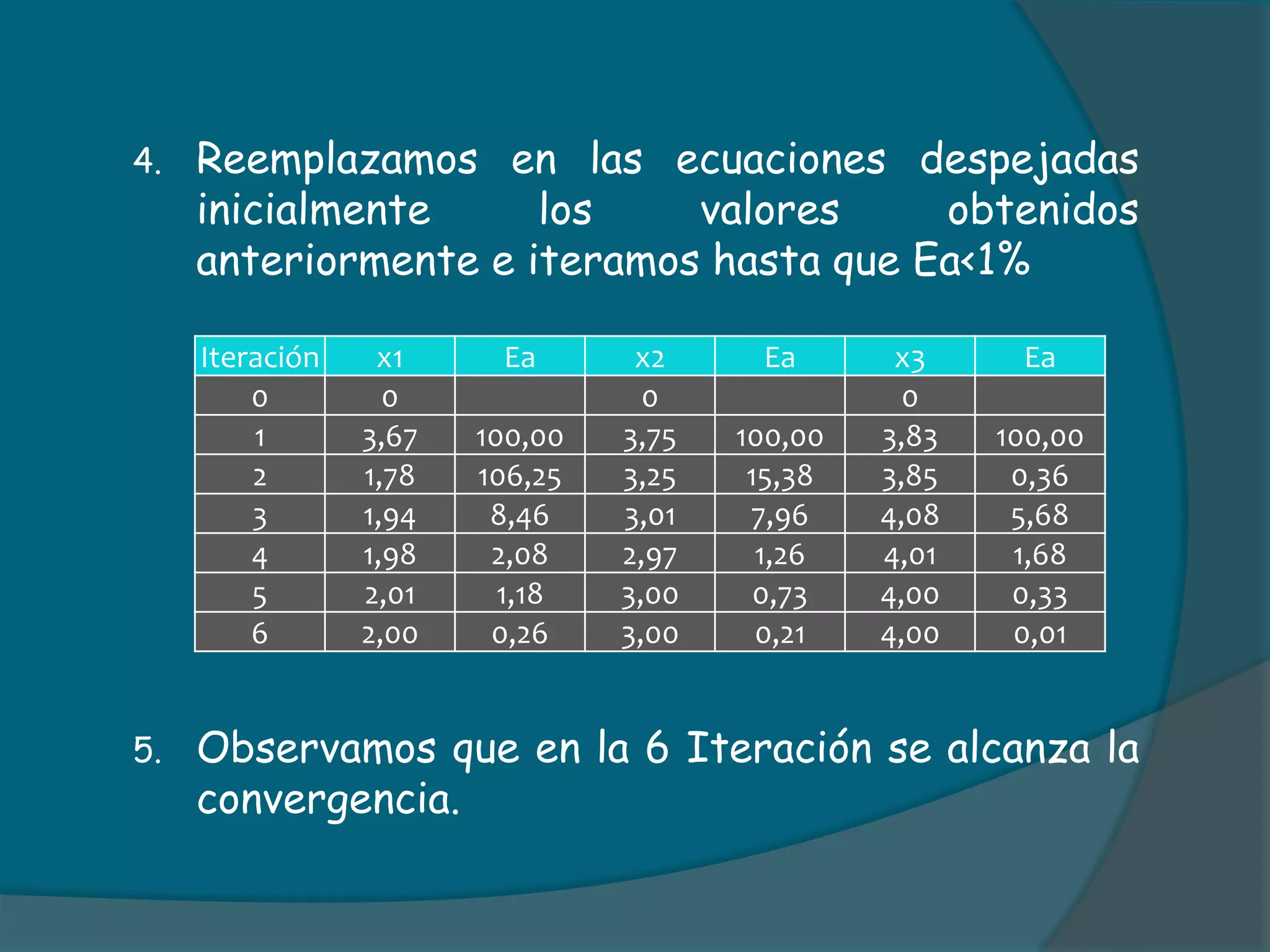
9. SOLUCIÓNAl igual que en el método de Jacobi despejo en cada ecuación cada una de las incógnitas respectivamente. x1 = (22-2x2-x3)/6 x2 = (30+x1-2x3)/8 x3 = (23-x1+x2)/6Empleando el vector inicial, hallo el valor de la primera incógnita. x1 = (22-2x2-x3)/6 x1=[(22-2(0)-(0)]/6 x1=3,66

10. Hallo la segunda incógnita (X2) empleando el valor hallado anteriormente. x2 = (30+x1-2x3)/8 x2 = [30+(3,66)-2(0)]/8 x2= 4,21De igual manera hallamos el valor de X3 empleando los valores de X1 y x2 hallados anteriormente. x3 = (23-x1+x2)/6 x3 = [23-(3,66)+(4,21)]/6 x3= 3,925Con estos valores empiezo a iterar hasta alcanzar un Ea<0,1%.

11. Realizamos la tabla de iteraciones en Excel como se muestra a continuación:Observamos de esta manera que aunque toma mas iteraciones que el método de Jacobi esté es mucho mas preciso.

12. GAUSS SEIDEL CON RELAJACIÓN Después de calcular un nuevo valor de x por la ecuación de Gauss Seidel, ese valor se modifica por un promedio ponderado de los resultados de las iteraciones hechas con Gauss-Seidel, esto se conoce como técnica SOR o de relajación. El esquema es el siguiente:

13. Pasos a seguir…Para hallar los valores de X en el sistema de ecuaciones empleo la ecuación fundamental:Xi=W*Xi + (1-W)*XiReemplazo el W dado inicialmente, y obtengo un nuevo sistema de ecuaciones.Reemplazo los valores iniciales, y empiezo a iterar hasta alcanzar un Ea menor a la tolerancia dada.

14. EJEMPLOResuelva el siguiente sistema de ecuaciones empleando el método de Gauss Seidel Relajado (SOR). 6x1 + 2x2 + x3 = 22 -x1 + 8x2 + 2x3 =30 x1 - x2 + 6x3 =23Con un vector inicial (0 ; 0 ; 0), y con factor de relajación de W=1,25

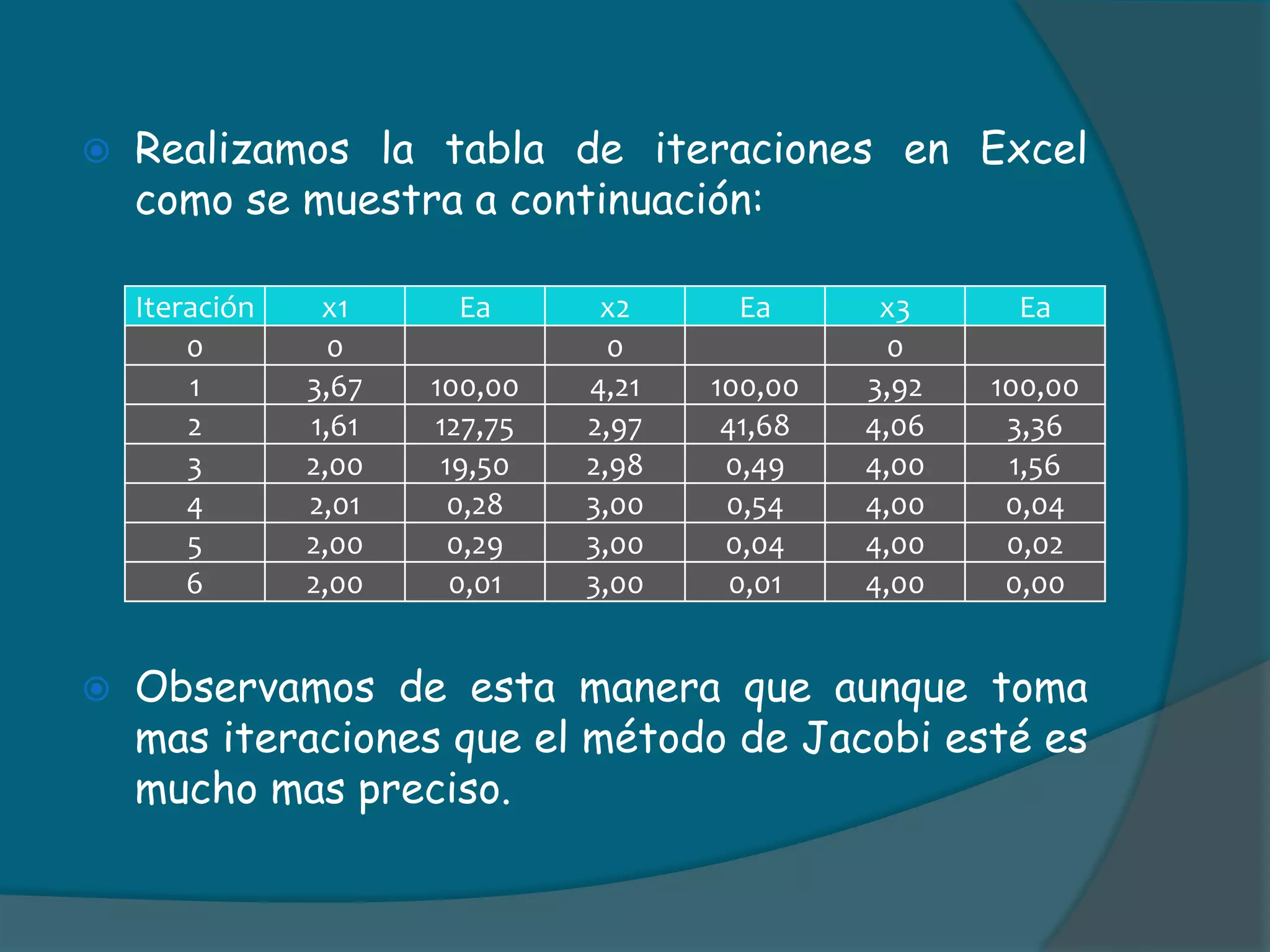
15. SOLUCIÓNPlanteo el sistema de ecuaciones de la siguiente forma:X1= [22*W-2X2*W-X3*W+6X1*(1-W)]/6 X2=[30*W-2X3*W+X1*W+8X2*(1-W)]/8 X3=[23*W-X1*W+X2*W+6X3*(1-W)]/6Reemplazo el valor del W dado y obtengo el nuevo sistema de ecuaciones.X1= [22*(1,25)-2X2*(1,25)-X3*(1,25)+6X1*(1-1,25)]/6 X2=[30*(1,25)-2X3*(1,25)+X1*(1,25)+8X2*(1-1,25)]/8 X3=[23*(1,25)-X1*(1,25)+X2*(1,25)+6X3*(1-1,25)]/6

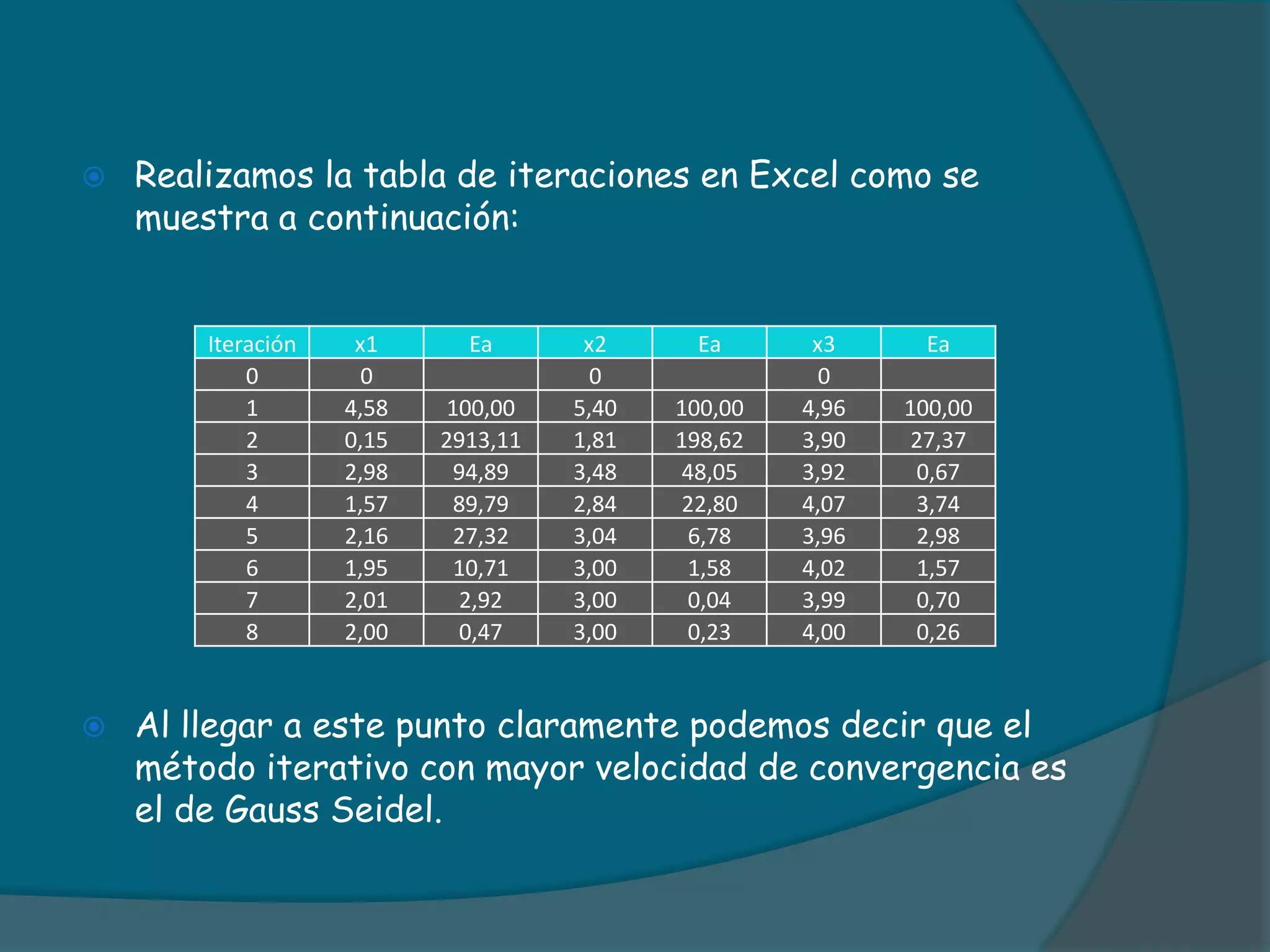
16. Llevando a cabo la operación anterior se tiene que: X1= [27,5 - 2,5X2 - 1,25X3 - 1,5X1]/6 X2=[37,5 – 2,5X3 + 1,25X1 - 2X2]/8 X3=[28,75 – 1,25X1 + 1,25X2 – 1,5X3]/6Empleo los valores iniciales para la primera iteración, teniendo en cuenta que este método trabaja de igual forma que Gauss Seidel. X1= [27,5 - 2,5X2 - 1,25X3 - 1,5X1]/6 X1= [27,5 - 2,5(0) - 1,25(0) - 1,5(0)]/6 X1= 4,58

17. Realizo el mismo procedimiento para X2 y X3X2=[37,5 – 2,5X3 + 1,25X1 - 2X2]/8 X2=[37,5 – 2,5(0) + 1,25(4,58) – 2(0)]/8 X2= 5,40 X3=[28,75 – 1,25X1 + 1,25X2 – 1,5X3]/6 X3=[28,75 – 1,25(4,58) + 1,25(5,40) – 1,5(0)]/6 X3= 4,962Empiezo a iterar hasta alcanzar un Ea < a la tolerancia dada.

18. Realizamos la tabla de iteraciones en Excel como se muestra a continuación:Al llegar a este punto claramente podemos decir que el método iterativo con mayor velocidad de convergencia es el de Gauss Seidel.