Este documento presenta la tesis doctoral de Marta Prades Tena sobre materiales ferroeléctricos basados en BaTiO3 y Ba2(Nd,Sm)Ti2Nb3O15. La tesis estudia la caracterización eléctrica de estas cerámicas mediante espectroscopia de impedancia. La tesis fue dirigida por Anthony R. West, Eloisa Cordoncillo Cordoncillo y Héctor Beltrán Mir en la Universitat Jaume I.












![vii
ARTÍCULOS RELACIONADOS CON ESTA TESIS
Publicación Capítulo
“Field enhanced bulk conductivity of BaTiO3:Mg ceramics” M. Prades, N. Masó,
H. Beltrán, E. Cordoncillo y A. R. West, J. Mater. Chem. 20, 5335-5344 (2010)
7
“Voltage-Dependent Low-Field Bulk Resistivity in BaTiO3:Zn Ceramics”,
H. Beltrán, M. Prades, N. Masó, E. Cordoncillo y A.R. West, J. Am. Ceram. Soc. 93
[2], 500-505 (2010)
8
“Field enhanced bulk conductivity of acceptor-doped BaTi1-xCaxO3-x ceramics”,
N. Masó, M. Prades, H. Beltrán, E. Cordoncillo, D. C. Sinclair y A. R. West, Appl.
Phys. Lett. 97, 062907 (2010)
9
“Enhanced Conductivity and Non-Linear Voltage-Current Characteristics of Non-
stoichiometric BaTiO3 Ceramics”, aceptado para su publicación en la revista
Journal of American Ceramic Society
10
“Polymorphism of BaTiO3 Acceptor Doped with Mn3+
, Fe3+
and Ti3+
”, M. Prades,
N. Masó, H. Beltrán, E. Cordoncillo y A. R. West, J. Am. Ceram. Soc. 91 [7], 2364-
2366 (2008)
11
“Non-Ohmic Phenomena in Mn.doped BaTiO3” M. Prades, H. Beltran,
E. Cordoncillo, N. Masó y A. R. West, enviado para su publicación en la revista
Nature Materials
11
“Phase transition hysteresis and anomalous Curie-Weiss behavior of ferroelectric
tetragonal tungsten bronzes Ba2RETi2Nb3O15: RE=Nd, Sm”, M. Prades, H. Beltrán,
N. Masó, E. Cordoncillo y A.R. West, J. Appl. Phys. 104, 104118 (2008)
13, 14](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-13-320.jpg)

![Índice de tablas
ix
INDICE DE TABLAS
Tabla III.1. Grupos puntuales para los siete sistemas cristalinos. 16
Tabla III.2. Diferentes aplicaciones de algunas cerámicas ferroeléctricas. 21
Tabla V.1. Clasificación de los CCM según las especificaciones de la Electrical
Industry Alliance (EIA). Tabla adaptada de la referencia [66].
54
Tabla VI.1. Relaciones molares de reactivos por mol de acetato de bario de los
diferentes ensayos.
62
Tabla VI.2. Estudio de los procesos de hidrólisis/condensación del isopropóxido
de titanio y características de los geles obtenidos.
65
Tabla VII.1. Composiciones preparadas en la disolución sólida BaTi1-xMgxO3-x. 74
Tabla VII.2. Temperatura de transición (TC) y temperatura de Curie (T0) para las
composiciones estudiadas en la disolución sólida BaTi1-xMgxO3-x
sinterizadas a 1400 ºC.
82
Tabla VIII.1. Composiciones preparadas en la disolución sólida BaTi1-xZnxO3-x. 107
Tabla VIII.2. Parámetros de celda para las composiciones x = 0 y x = 0.01. 108
Tabla IX.1. Composiciones preparadas en las disoluciones sólidas Ba1-yCayTiO3 y
BaTi1-xCaxO3-x
129
Tabla IX.2. Parámetros de celda de las disoluciones sólida cúbico/tetragonal para
los sistemas BaTi1-xCaxO3-x y Ba1-yCayTiO3, y densidades relativas.
131
Tabla X.1. Composiciones preparadas en las disoluciones sólidas BaTi1-xO3-2x y
Ba1-yTiO3-y.
145
Tabla X.2. Densidad de todas las composiciones sinterizadas a 1400 ºC. 146
Tabla X.3. Valores de TC y T0 para todas las composiciones estudiadas. 149
Tabla X.4. Valores de conductividad obtenidos a 400 ºC por
interpolación/extrapolación, y energías de activación para R1 y R2 para
todas las muestras estudiadas.
161
Tabla XI.1. Composiciones preparadas en la disolución sólida BaTi1-xMnxO3-δ. 172
Tabla XI.2. Valores de capacidad obtenidos a partir del pico de Z” para el
elemento de baja frecuencia.
188
Tabla XI.3. Conductividad de la muestra x = 0.005 a 456 ºC. 193
Tabla XII.1. Algunos compuestos con estructura tipo “tetragonal de bronce de
tungsteno”. Tabla adaptada de la referencia [173].
204
Tabla XIII.1. Estudio de solubilidad del isopropóxido de Sm en función de la
cantidad de acetilacetona.
211
Tabla XIII.2. Estudio de solubilidad del isopropóxido de Sm en función de la
cantidad de metanol.
212](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-15-320.jpg)

![Índice de figuras
xi
INDICE DE FIGURAS
Figura 3.1. Esquema del intervalo de propiedades y aplicaciones asociadas al
desplazamiento iónico en los sólidos. Figura adaptada de la
referencia [6].
17
Figura 4.1. Respuesta I-V característica de un varistor cerámico basado en ZnO.
Diferentes regiones de la curva definen los parámetros funcionales
del dispositivo protector (el recuadro en línea discontinua marca la
región de corriente de fuga). Figura adaptada de la referencia [10].
27
Figura 4.2. Esquema de la estructura real (a) e idealizada según el modelo de
ladrillos (brickwork model) (b) del varistor de ZnO. Figura adaptada
de la referencia [17].
28
Figura 4.3. Esquema de la barrera Schottky de potencial en un borde de grano
en varistores basados en ZnO y las regiones del aislante: (a,b) sin y
(c) con voltaje aplicado. Figura adaptada de la referencia [10].
29
Figura 4.4. Los cuatro elementos fundamentales de un circuito eléctrico:
resistor, capacitor, inductor y memristor. Figura adaptada de la
referencia [21].
31
Figura 4.5. Curvas voltaje-intensidad: (a) hipotética propuesta por Chua y (b)
experimental obtenida por Strukov. Figura adaptada de las
referencias [19] y [20].
32
Figura 4.6. (a) Circuito eléctrico laminar; (b) esquema de una unión
nanométrica memristiva y (c) esquema del memristor TiO2/TiO2-x
actuando como unión. Figuras (a) y (b) adaptadas de la referencia
[26]; figura (c) adaptada de la referencia [22].
33
Figura 4.7. Influencia del material del cátodo en la conductividad del BaTiO3.
Área de electrodo 0.07cm2
; temperatura de medida 153 ºC. Figura
adaptada de la referencia [35].
35
Figura 4.8. Conductividad en función del tiempo tras la aplicación de
~ 4 kVcm-1
en muestras de BaTiO3 con diferentes electrodos. Figura
adaptada de la referencia [34].
36
Figura 5.1. Diagrama de fases del sistema BaO-TiO2 según Lee y col. [42]. 41
Figura 5.2. Representación esquemática de la estructura de la perovsquita
BaTiO3.
42
Figura 5.3. (a) Transición de fase de cúbica a tetragonal en la pervosquita
BaTiO3 y (b) octaedro de TiO6 distorsionado por el desplazamiento
del Ti de su posición de equilibrio.
43
Figura 5.4. Representación de las transiciones de fase de la perovsquita BaTiO3
y la variación de la permitividad en función de la temperatura.
44
Figura 5.5. (a) Polarización espontánea, (b) permitividad relativa y (c) espaciado
en función de la tempertura para un monocristal de BaTiO3. Figura
45](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-17-320.jpg)
![Índice de figuras
xii
adaptada de las referencias [44] y [45].
Figura 5.6. Diagrama de fases polimórficas para el BaTiO3 puro en función del
tamaño cristalino y de la temperatura. Figura adaptada de la
referencia [50].
47
Figura 5.7. Representación esquemática de log σ frente a log PO2 para una
cerámica de BaTiO3 sin dopar a diferentes temperaturas. Figura
adaptada de la referencia [53].
48
Figura 5.8. Comportamiento de las transiciones en función de la composición
para diversas disoluciones sólidas BaTiO3:ABO3. Figura adaptada de
la referencia [8].
50
Figura 5.9. Condensador cerámico multicapa (CCM). 52
Figura 5.10. Evolución de la producción mundial de CCM. Figura adaptada de la
referencia [66].
53
Figura 5.11. Perfil de la resistencia-temperatura de una cerámica PTCR. 55
Figura 6.1. Evolución estructural durante la hidrólisis de Ti(OPri
)3acac. 64
Figura 6.2. Esquema experimental de síntesis del BaTiO3. 66
Figura 6.3. Análisis termogravimétrico y térmico diferencial de la muestra de
BaTiO3.
67
Figura 6.4. Ciclos de calcinación del polvo crudo (a) y sinterización de las
pastillas (b) para las muestras de BaTiO3.
68
Figura 7.1. Diagrama de fases parcial para la disolución sólida del sistema
BaTi1-xMgxO3-x: ○ polimorfo tetragonal/cúbico, ● mezcla de
polimorfos tetragonal/cúbico y hexagonal, y Δ polimorfo hexagonal.
75
Figura 7.2. Difractograma de rayos X de las muestras: (a) x = 0.01 a 1200 ºC y
(b) x = 0.06 a 1400 ºC.
76
Figura 7.3. Parámetros de celda de la disolución sólida cúbico/tetragonal del
sistema BaTi1-xMgxO3-x.
77
Figura 7.4. Imagen de la superficie de las pastilla de la muestra x = 0.01
sinterizada a 1400 ºC, utilizando el detector de electrones
retrodispersados.
78
Figura 7.5. Calorimetría diferencial de barrido de la muestra x = 0.01 sinterizada
a 1400 ºC.
79
Figura 7.6. Datos de permitividad en función de la temperatura a 100kHz para la
muestra x = 0.01 sinterizada a 1300 ºC y 1400 ºC.
80
Figura 7.7. (a) Datos de permitividad a 100 kHz en función de la temperatura y
(b) temperatura de transición de la disolución sólida del sistema
BaTi1-xMgxO3-x, a la temperatura de sinterización de 1400 ºC.
81
Figura 7.8. Gráficas de Curie-Weiss a 100 kHz para la muestra x = 0.01
sinterizada a 1400 ºC.
81](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-18-320.jpg)
![Índice de figuras
xiii
Figura 7.9. (a,b) Plano complejo de la impedancia, Z*, a dos temperaturas de
medida para la muestra x = 0.01 sinterizada a 1400 ºC. Los círculos
negros en (a) y (b) representan la frecuencia de 3 kHz.
83
Figura 7.10. Gráfica espectroscópica de Z”/M” a 442 ºC para la muestra x = 0.01
sinterizada a 1400 ºC (mismos datos que figura 7.9).
84
Figura 7.11. (a,b) Gráficas espectroscópicas de capacidad a diferentes
temperaturas de medida para la muestra x = 0.01 sinterizada a 1400
ºC y (c) circuito equivalente.
*Las capacidades de alta y baja frecuencia corresponden con C1 y C2
respectivamente, asumiendo que C1<<C2 y que R1<<R2.
85
Figura 7.12. Gráfica espectroscópica de M” frente log f para x = 0.005 sinterizada
a 1400 ºC.
86
Figura 7.13. Datos de impedancia a 603 ºC para la muestra x = 0.003 medida
usando diferentes atmósferas. El círculo blanco representa la
frecuencia de 32 kHz.
87
Figura 7.14. Gráficas de Arrhenius de R1 y R2 para la muestra x = 0.01
sinterizada a 1400 ºC.
87
Figura 7.15. Gráficas de Arrhenius de R1 (a) y R2 (b) para el intervalo de
composiciones sinterizada a 1400 ºC.
88
Figura 7.16. (a) Plano complejo de la impedancia, Z*, a 242 ºC para la muestra
x = 0.01 antes y después de aplicar 10V [166.67 Vcm-1
] a diferentes
tiempos; (b) gráfica espectroscópica de M” (mismos datos que en
(a)); (c) gráfica espectroscópica de M” para la muestra en el estado
excitado (10V) y a dos tiempos, t1 y t2, después de eliminar el voltaje
dc bias.
89
Figura 7.17. (a) Plano complejo de la impedancia, Z*, y (b) gráfica
espectroscópica de M” a 472 ºC para la muestra con x = 0 antes y
después de aplicar 10V [67 Vcm-1
] durante 8 horas.
91
Figura 7.18. (a) Conductividad del bulk (σ1) en función del tiempo después de
aplicar voltajes de 0.3, 0.7 y 1.2 V [5.3, 12.3 y 21.1 Vcm-1
] a 374 ºC
y (b) conductividad estacionaria del bulk en función del voltaje dc
bias aplicado a 374 ºC para la muestra x = 0.01.
92
Figura 7.19. Gráficas de Arrhenius de σ1 para las muestras x = 0.01 (a) y
x = 0.003 (b) medidas sin voltaje aplicado y con un voltaje dc de
10V [175.4 y 107.5 Vcm-1
, respectivamente] después de alcanzarse
el estado estacionario.
92
Figura 7.20. Datos de impedancia a 605 ºC para la muestra x = 0.01 medida
usando diferentes atmósferas tras la aplicación de un voltaje dc de
10V.
93
Figura 7.21. Conductividad del bulk (σ1) para la muestra x = 0.01 en función del
tiempo después de aplicar un voltaje dc de 10V y al eliminar el
voltaje, a 274 ºC, en vacío (a) y en aire (b).
94](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-19-320.jpg)
![Índice de figuras
xiv
Figura 7.22. Gráfica espectroscópica de M”, a 231 ºC, para la muestra x = 0.003
preparada por el método cerámico y sinterizada a 1400 ºC, antes y
después de aplicar 10V a diferentes tiempos.
95
Figura 7.23. Estructura defectuosa del BaTiO3 dopado con Mg con vacantes de
oxígeno.
96
Figura 8.1. Difractograma de rayos X de la muestra x = 0.01 sinterizada a
1400 ºC.
108
Figura 8.2. Datos de permitividad a 100kHz en función de la temperatura para la
muestra x = 0.01 sinterizada a 1300 ºC y 1400 ºC.
109
Figura 8.3. Datos de permitividad a 100 kHz en función de la temperatura y
temperatura de transición de la disolución sólida del sistema
BaTi1-xZnxO3-x, a la temperatura de sinterización de 1400 ºC (margen
superior izquierdo de la figura)
110
Figura 8.4. (a,b) Plano complejo de la impedancia, Z*, a dos temperaturas de
medida para la muestra x = 0.01. El círculo negro en (a) representa
la frecuencia de 60kHz.
110
Figura 8.5. (a) Gráfica espectroscópica de Z”/M” a 427 ºC (mismos datos que
figura 8.4.a); (b) gráficas espectroscópicas de capacidad a diferentes
temperaturas de medida para la muestra x = 0.01 y (c) circuito
equivalente.
*Las capacidades de alta y baja frecuencia corresponden con C1 y C2
respectivamente, asumiendo que C1<<C2 y que R1<<R2.
111
Figura 8.6. Gráficas de Arrhenius de R1 y R2 para la muestra x = 0.01. 112
Figura 8.7. Gráficas de Arrhenius de R1 (a) y R2 (b) para un intervalo de
composiciones del sistema BaTi1-xZnxO3-x.
113
Figura 8.8. (a) Plano complejo de la impedancia, Z*, a 282 ºC para la muestra
x = 0.01 antes y después de aplicar 10V [139 Vcm-1
] a diferentes
tiempos; (b) gráfica espectroscópica de M” (mismos datos que en
(a)) y (c) gráfica espectroscópica de M” para la muestra en el estado
excitado (10V) y a diferentes tiempos, después de eliminar el voltaje
dc bias.
114
Figura 8.9. Resistencia R1 a diferentes tiempos después de eliminar el voltaje dc
bias para la composición x = 0.01.
115
Figura 8.10. Valores límite de la conductividad del bulk en función del voltaje dc
bias aplicado a 322 ºC para la muestra x = 0.01.
115
Figura 8.11. Gráficas de Arrhenius de R1 y R2 para la muestra x = 0.01, medida
sin voltaje aplicado y con un voltaje dc de 10V [138.9 Vcm-1
]
después de alcanzar un estado estacionario.
116
Figura 8.12. Gráficas de Arrhenius de (a) σ1 y (b) σ2 para dos muestras con
x = 0.01 con diferentes espesores [0.72 y 2.21 mm] medidas sin
voltaje aplicado y con un voltaje dc de 4V [55 y 18 V/cm,
respectivamente] después de alcanzar un estado estacionario.
117](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-20-320.jpg)
![Índice de figuras
xv
Figura 8.13. Gráficas de Arrhenius de (a) σ1 y (b) σ2 para muestras con diferente
composición medidas sin voltaje aplicado y con un voltaje dc de
10V. Espesores de las muestras: 0.56 mm para x = 0.00003,
0.70 mm para x = 0.0003 y 0.69 mm para x = 0.003.
118
Figura 8.14. Estructura defectuosa del BaTiO3 dopado con Zn con vacantes de
oxígeno.
119
Figura 9.1. Diagrama de fases para el sistema BaTiO3-CaTiO3. Figura adaptada
de la referencia [123].
124
Figura 9.2. Temperaturas de transición de Ba1-yCayTiO3 en función del
contenido de Ca. (Las zonas sombreadas representan el error en la
determinación de la temperatura). Figura adaptada de la referencia
[57].
125
Figura 9.3. TC vs % molar de Ca para las disoluciones sólidas: Ba1-yCayTiO3
(BCT) y BaTi1-xCaxO3-x (BTC).Figura adaptada de la referencia
[137].
127
Figura 9.4. Diagrama de fases parcial para el sistema BaO-TiO2-CaO. 129
Figura 9.5. Ciclos de calcinación del polvo crudo (a) y sinterización de las
pastillas (b) para las muestras BCT y BTC, respectivamente.
130
Figura 9.6. Datos de permitividad en función de la temperatura a 100kHz para la
muestra BCT3 sinterizada a 1400 ºC y 1500 ºC.
132
Figura 9.7. (a) Datos de permitividad en función de la temperatura a 100kHz
para las muestras BT, BCT3 y BTC3 y (b) punto de Curie en
función de la composición. Los símbolos negros están extraídos de
la referencia [124].
132
Figura 9.8. (a,b) Plano complejo de la impedancia, Z*, (b,c) gráfica
espectroscópica de Z”/M” y (e,f) gráfica espectroscópica de la
capacidad para las muestras BCT1 y BTC1, respectivamente.
134
Figura 9.9. Gráficas de Arrhenius de σ1 (▲, Δ) y σ2 (●, ○) para las muestras
BCT1 (a), BTC1 (b), BCT3 (c) y BTC3 (d), medidas sin voltaje
aplicado (símbolos negros) y con un voltaje dc de 10V (símbolos
blancos) después de alcanzarse el estado estacionario.
136
Figura 9.10. σ1 a 600 ºC para la muestra BTC1 después de aplicar y eliminar un
voltaje de 10V [84 Vcm-1
] a diferentes tiempos, en atmósfera de
nitrógeno, aire y oxígeno.
137
Figura 10.1. Difractograma de rayos X de las muestras B099T, BT y BT099
preparadas por sol-gel.
146
Figura 10.2. Imagen de la superficie de las pastillas sinterizadas a 1400º C y
preparadas por sol-gel (a, c, e) y por el método cerámico tradicional
(b, d, f).
147
Figura 10.3. Datos de permitividad a 100 kHz en función de la temperatura para
las muestras BT099 (ο), BT (▲) y B099T (Δ), preparadas por sol-
148](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-21-320.jpg)
![Índice de figuras
xvi
gel (a) y por el método cerámico (b).
Figura 10.4. Gráficas de Curie-Weiss (la inversa de la permitividad en función de
la temperatura) a 100 kHz en función de la temperatura para las
muestras BT099 (■), BT (▲) y B099T (○), preparadas por sol-gel
(a) y por el método cerámico (b).
149
Figura 10.5. Plano complejo de la impedancia, Z*, gráficas espectroscópicas de
Z”/M” y gráficas espectroscópicas de la capacidad a 472 ºC para la
muestra BT preparada por sol-gel (a, b, c) (mismos datos mostrados
en la figura 7.17) y por cerámico (d, e, f) antes y después de aplicar
un voltaje dc de 10V [6.7 y 7.1Vcm-1
], respectivamente.
151
Figura 10.6. Gráficas de Arrhenius de (a) σ1 y (b) σ2 para las muestras BTSG y
BTC medidas sin voltaje y con un voltaje dc de 10V [6.7 y
7.1 V/cm-1
, respectivamente] después de alcanzar el estado
estacionario. Se indican las energías de activación en eV, con errores
en el intervalo de 0.002 - 0.005 eV.
152
Figura 10.7. Plano complejo de la impedancia, Z*, gráficas espectroscópicas de
Z”/M” y gráficas espectroscópicas de la capacidad a 485 ºC para la
muestra BT099 preparada por sol-gel (a, b, c) y por cerámico
(d, e, f) antes y después de aplicar un voltaje dc de 10V [15.1 y
9.52Vcm-1
], respectivamente.
154
Figura 10.8. Plano complejo de la impedancia, Z*, gráficas espectroscópicas de
Z”/M” y gráficas espectroscópicas de la capacidad a 469 ºC para la
muestra B099T preparada por sol-gel (a, b, c) y por cerámico
(d, e, f) antes y después de aplicar un voltaje dc de 10V [13.7 y
8.7Vcm-1
], respectivamente.
155
Figura 10.9. Conductividad del bulk, σ1, a diferentes temperaturas después de
aplicar un voltaje dc de 10V para la muestra BT099SG [15.1 Vcm-1
]
(a) y para B099TSG [13.7 Vcm-1
] (b).
156
Figura 10.10. Conductividad del bulk, σ1 tras la aplicación de diferentes voltajes a
temperatura constante para la muestra BT099SG (a) y para B099TSG
(b).
157
Figura 10.11. Conductividad del bulk, σ1, a diferentes tiempos de medida tras
eliminar el voltaje dc para la muestra BT099SG (a) y B099TSG (b) a
diferentes temperaturas de medida. Las líneas indican el estado
estacionario para cada temperatura.
158
Figura 10.12. Conductividad límite del bulk en función del voltaje dc para las
muestras BT099SG y B099TSG medidas a 335 ºC y 306 ºC,
respectivamente.
159
Figura 10.13. Gráficas de Arrhenius de σ1 (a,c) y σ2 (b,d) sin voltaje y con un
voltaje dc de 10V para las muestras B099TSG [13.7 Vcm-1
], B099TC
[8.7 Vcm-1
], BT099SG [15.1 Vcm-1
]y BT099C [9.52 V/cm-1
].
160
Figura 10.14. Datos de impedancia para la muestra BT099 (a) y B099T (b) medida
usando diferentes atmósferas.
162](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-22-320.jpg)
![Índice de figuras
xvii
Figura 10.15. Estructura defectuosa del BaTiO3 no estequiométrico con vacantes
de titanio y de oxígeno. Las vacantes de oxígeno se sitúan en
disposición cis, pero pueden también estar en trans.
163
Figura 11.1. Conductividad eléctrica (σ) de una muestra de BaTiO3 dopada con
1 % molar en Mn vs. la presión parcial de oxígeno a diferentes
temperaturas. Figura adaptada de la ref. [167].
171
Figura 11.2. Diagrama de fases parcial para la disolución sólida del sistema
BaTi1-xMnxO3-δ: ○ polimorfo tetragonal/cúbico, ● mezcla de
polimorfos tetragonal/cúbico y hexagonal, y ◊ polimorfo hexagonal.
174
Figura 11.3. Difractograma de rayos X de las muestras: (a) x = 0.005 a 1200 ºC y
x = 0.04 a 1400 ºC (b) y 1200 ºC (c).
176
Figura 11.4. Diagrama de fases genérico del BaTiO3 conteniendo dopantes
aceptores.
177
Figura 11.5. Diagrama ternario del sistema BaTiO3-BaTiO2.5-BaMO2.5. 179
Figura 11.6. Parámetros de celda de la disolución sólida tetragonal del sistema
BaTi1-xMnxO3-δ.
180
Figura 11.7. Imagen de la superficie de la pastilla de la muestra x = 0.003
sinterizada a 1300 ºC utilizando el detector de electrones
retrodispersados y % molar de las fases presentes. *Inferior al límite
de detección.
181
Figura 11.8. (a) Datos de permitividad a frecuencia fija a 100 kHz en función de
la temperatura y (b) temperatura de transición de la disolución sólida
del sistema BaTi1-xMnxO3-δ.
182
Figura 11.9. Datos de permitividad a frecuencia fija a 1, 10 y 100 kHz en función
de la temperatura para la muestra x = 0.005 sinterizada a 1400 ºC.
182
Figura 11.10. Permitividad frente a la frecuencia a 80, 100, 121, 131 y 141 ºC para
la muestra x = 0.003 sinterizada a 1300 ºC.
183
Figura 11.11. Gráficas de Curie-Weiss (a), de Smolenskii (b) y de Uchino (c) para
x = 0.003 sinterizada a 1300 ºC.
185
Figura 11.12. (a,b) Plano complejo de la impedancia, (c,d) gráfica espectroscópica
de Z’’/M’’ y (e,f) datos de capacidad para x = 0.003 sinterizada a
1100 ºC (○) y 1300 ºC (●). Los círculos marcados representan la
frecuencia de 100 kHz.
186
Figura 11.13. (a) Plano complejo de la impedancia y (b) gráfica espectroscópica de
Z’’/M’’ para la muestra x = 0.005 sinterizada a 1400 ºC.
187
Figura 11.14. Representación espectroscópica de M’’ frente log f para (a)
x = 0.003 y (b) x = 0.01 sinterizadas a 1300 ºC.
188
Figura 11.15. Plano complejo de la impedancia, Z*, con los datos obtenidos a 555
ºC para la muestra x = 0.003 medida usando diferentes atmósferas.
189
Figura 11.16. (a) Plano complejo de la impedancia y (b) gráfica espectroscópica de
Z’’/M’’ para la muestra x = 0.005 sinterizada a 1400 ºC, antes y
190](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-23-320.jpg)
![Índice de figuras
xviii
después de aplicar un voltaje de 10V [160Vcm-1
] durante 68h.
Figura 11.17. Datos de permitividad a la frecuencia fija de 100 kHz en función de
la temperatura para la muestra x = 0.005 sinterizada a 1400 ºC y
enfriada rápidamente.
191
Figura 11.18. (a) Plano complejo de la impedancia y (b) gráfica espectroscópica
M’’ para la muestra x = 0.005, sinterizada a 1400 ºC y enfriada
rápidamente sobre nitrógeno líquido, antes y después de aplicar un
voltaje de 10V [160Vcm-1
], a diferentes tiempos a 485 ºC. Las
medidas eléctricas se realizaron en atmósfera de nitrógeno.
192
Figura 11.19. (a) Plano complejo de la impedancia y (b) gráfica espectroscópica
M’’ para la muestra x = 0.005, sinterizada a 1400 ºC y enfriada
rápidamente sobre nitrógeno líquido, antes y después de aplicar un
voltaje de 10V [160Vcm-1
] durante 3h a 379 ºC. Las medidas
eléctricas se realizaron en atmósfera reductora (5% H2 / 95% N2).
193
Figura 11.20. Gráficas de Arrhenius de la conductividad total para la muestra x =
0.005 sinterizada a 1400 ºC y enfriada lentamente, y enfriada
rápidamente sobre nitrógeno líquido y medida en atmósfera de N2 ó
H2/N2.
194
Figura 11.21. (a) Gráficas de Arrhenius para la conductividad total para la muestra
x = 0.005 sinterizada a 1400 ºC y enfriada lentamente, y enfriada
rápidamente sobre nitrógeno líquido y medida en atmósfera de N2 o
H2/N2, (mismos datos mostrados en la figura 11.20) y para R1 y R2
después de aplicar un voltaje dc de 10V [160Vcm-1
]; volumen
relativo de los componentes en función del tiempo tras la aplicación
de un voltaje dc de 10V, medida en atmósfera de nitrógeno y a la
temperatura de 485 ºC(b) y medida en atmósfera de hidrógeno y a
la temperatura de 379 ºC (c).
Nota: los valores de R1 y R2 en la figura 11.21.a están corregidos por
el volumen relativo de los dos componentes.
195
Figura 12.1. Proyecciones de las estructuras de los bronces de tungsteno: (a)
estructura de perovsquita de los bronces cúbicos, (b) la misma
mostrando solamente los iones alcalinos (círculos sombreados) y los
átomos W (círculos pequeños), (c) y (d) armazones de W y de los
iones alcalinos de los bronces tetragonal y hexagonal. Figura
adaptada de la referencia [172].
203
Figura 12.2. Representación esquemática de la estructura del bronce de
tungsteno. Se muestran dos celdas unidad; los octaedros (B1,B2)O6
a la izquierda y los enlaces (B1,B2)-O a la derecha.
206
Figura 13.1. Esquema de la síntesis sol-gel y solvotermal. 213
Figura 13.2. Difractogramas de rayos X de la muestra Ba2SmTi2Nb3O15
preparada por metodología solvotermal.
214
Figura 13.3. Imágenes de METAR de la muestra Ba2SmTi2Nb3O15 cruda (170 ºC)
(a,c) y de la muestra calcinada a 900 ºC (b,d).
215](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-24-320.jpg)
![Índice de figuras
xix
Figura 13.4. (a) Patrón de difracción para la muestra Ba2SmTi2Nb3O15 calcinada
a 900 ºC y (b) patrón de difracción a lo largo del eje de zona [2 3 7]
para el grupo espacial P4mm.
216
Figura 14.1. Representación esquemática de la estructura del bronce de tungsteno
a lo largo del eje c. Se indican las posiciones B1/B2, las posiciones
pentagonales (A1), cuadradas (A2) y triangular (C).
222
Figura 14.2. Análisis termogravimétrico y térmico diferencial de las muestras
BSTN sinterizada por (a) sol-gel y (b) solvotermal.
225
Figura 14.3. Análisis termogravimétrico y térmico diferencial de la muestra
BNTN sinterizada por solvotermal.
225
Figura 14.4. Difractogramas de rayos X de las muestras BSTN (a) y BNTN (b)
preparadas por el método solvotermal y enfriadas rápidamente a
varias temperaturas durante la medida del ATD/TG.
226
Figura 14.5. Difractogramas de rayos X de la muestra BSTN preparadas por el
método solvotermal y enfriada rápidamente a varias temperaturas
durante la medida del ATD/TG.
227
Figura 14.6. Ciclos de calcinación del polvo crudo (a,b) y sinterización de las
pastillas (c,d) para las muestras preparadas por sol-gel y solvotermal.
228
Figura 14.7. Difractogramas de rayos X de la muestra BSTN preparada por
metodología sol-gel (a) y solvotermal (b) y sinterizada a varias
temperaturas.
230
Figura 14.8. Difractogramas de rayos X de la muestra BSTN sinterizada a
1400 ºC preparada por ambos métodos.
231
Figura 14.9. Micrografías usando el detector de electrones retrodispersados y
análisis semicuantitativos de las superficies de las pastillas BSTN
sinterizada a 1400 ºC preparada por método solvotermal.
232
Figura 14.10. Difractogramas de rayos X de la muestra BNTN preparada por el
método solvotermal y sinterizada a varias temperaturas.
233
Figura 14.11. Micrografías usando el detector de electrones retrodispersados y
análisis semicuantitativos de las superficies de las pastillas BNTN
sinterizada a 1300 ºC.
233
Figura 14.12. (a,b) Plano complejo de la impedancia, (c,d) gráficas
espectroscópicas de Z”/M” y (e,f) datos de capacidad para la
muestra BNTN sinterizada a (●) 1100 ºC y (○) 1300 ºC. Los círculos
marcados representan la frecuencia de 100 kHz.
236
Figura 14.13. (a,b) Plano complejo de la impedancia, (c,d) gráficas
espectroscópicas de Z”/M” y (e,f) datos de capacidad para la
muestra BSTN sinterizada a (Δ) 1100 ºC y (▲) 1400 ºC.
237
Figura 14.14. Gráfica espectroscópica de M” frente log f para (a) la muestra
BNTN sinterizada a 1300 ºC y (b) la muestra BSTN sinterizada a
1400 ºC.
238](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-25-320.jpg)




![Capítulo 1
- 6 -
- Cerámicas superconductoras: las cerámicas superconductoras de alta
temperatura (HTSC), se descubrieron a mediados de los años 80, con temperaturas de
transición inferiores a los -173 ºC, como YBa2Cu3O7-δ. Estos sistemas pueden aplicarse
en cables de transmisión de energía de alto voltaje (p. ej. 1 GVA) o en equipos de
almacenaje de energía magnética (1-100 MWh).
La mayoría de los materiales y componentes cerámicos se producían típicamente
por el método convencional de prensado de polvos, tape casting o técnicas de impresión
en pantalla, seguidos por los procesos de sinterización. A finales de los años 80, estas
técnicas fueron complementadas por técnicas alternativas de deposición del material en
forma de lámina delgada, como sputtering, deposición de láser pulsado, deposición
química en disolución y deposición química de vapor. El creciente interés en las
cerámicas en forma de lámina delgada fue motivado por dos hechos. Por una parte, el
reciente descubrimiento de las cerámicas superconductoras de alta temperatura, sugería
que la preparación de estos materiales en forma de lámina delgada podría aumentar
considerablemente la densidad de corriente. En segundo lugar, los avances realizados en
la tecnología de los semiconductores de Si, permitieron el estudio de las memorias
ferroeléctricas semiconductoras, idea originada a finales de 1960. Estos hechos
condujeron a un gran desarrollo en esta nueva área de preparación de materiales,
combinando las numerosas aplicaciones ofrecidas por estos materiales electrocerámicos
en forma de lámina delgada, con los circuitos integrados estándar. Por ejemplo,
materiales ferroeléctricos en forma de lámina delgada se utilizan como memorias
ferroeléctricas no-volátiles RAM2
, accionadores piezoeléctricos, bombas y
micromotores, y dispositivos electro-ópticos3
.
Obviamente, los óxidos cerámicos proporcionan una amplia área de
funcionalidades. Casi ningún otro tipo de materiales (semiconductores, metales,
polímeros) ofrece tal variedad de propiedades que pueden ser explotadas para
aplicaciones electrónicas. Es probable todavía que aparezcan nuevos materiales, como
lo hicieron los HTSC, y que alguno de ellos sirva para la industrialización; sin embargo,
según la tendencia en el área de los materiales electrocerámicos y áreas adyacentes
durante esta última década, los esfuerzos en investigación y desarrollo han estado
centrados en la tecnología y en los dispositivos. En general, la tendencia actual se puede
clasificar en tres grupos diferentes. En primer lugar, los materiales integrados, que han
tenido una importante función en la integración de cerámicas electrónicas en los chips
semiconductores convencionales, así como la evolución de componentes y sistemas
multifuncionales. En segundo lugar, en el proceso de producción industrial, donde está
ocurriendo una transición desde los estudios empíricos y demostraciones físicas, al
diseño y ensayo virtual, y en tercer lugar, la creciente miniaturización de los
dispositivos electrónicos ha provocado la expansión de la nanotecnología frente a la
microtecnología.
2
C. A. P. Araujo, N. Solyappan, L. D. McMillan, T. Otsuki, y K. Arita, J. Electroceram. 3 [2], 134-42
(1999)
3
C. Buchal, D. Fluck y P. Günter, J. Electroceram. 3 [2], 179-93 (1999)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-30-320.jpg)




![Materiales cerámicos ferroeléctricos
- 15 -
3. MATERIALES CERÁMICOS FERROELÉCTRICOS
3.1. INTRODUCCIÓN
Desde el descubrimiento de la ferroelectricidad4,5
en monocristales de la sal de Rochelle
(NaKC4H4O6·4H2O) en el año 1921, y la posterior comprobación en materiales
policristalinos (BaTiO3) durante la primera mitad de los años 40, ha habido una
continua sucesión de materiales nuevos y desarrollo tecnológico que ha dado origen a
un importante número de aplicaciones industriales y comerciales, que pueden atribuirse
a este fenómeno inusual.
La ferroelectricidad se origina por la presencia de un momento eléctrico
espontáneo (alineación espontánea de dipolos eléctricos o polarización espontánea) en
un cristal, el cual puede orientarse según dos o más direcciones cristalográficas distintas
por aplicación de un campo eléctrico externo. Algunos de los conceptos físicos
necesarios para entender los fenómenos eléctricos asociados a este tipo de materiales,
como por ejemplo capacidad, resistencia dieléctrica, factor de pérdida, polarización o
relajación dieléctrica, se detallan en el Apéndice 1.
Para que se manifieste el fenómeno de la ferroelectricidad, los materiales
cristalinos deben tener unos requisitos de simetría. Los grupos puntuales centro-
simétricos no muestran polaridad, mientras que los sistemas que no tienen centro de
simetría poseen cristalográficamente uno o más ejes direccionales únicos y, por tanto,
presentan efectos piezoeléctricos a lo largo de los ejes direccionales.
Existen 32 grupos puntuales diferentes que pueden dividirse en los siete sistemas
cristalinos. De estos 32 grupos puntuales, 21 son no centrosimétricos y 11 son
centrosimétricos (tabla III.1), y de los 21 no centrosimétricos, 20 son piezoeléctricos.
Los materiales piezoeléctricos se caracterizan porque se polarizan eléctricamente como
resultado de una presión mecánica. Cabe señalar que el grupo puntual (432), que no
posee centro de simetría, no es piezoeléctrico debido a la combinación de otros
elementos de simetría.
4
G.H. Haertling, J. Am. Ceram. Soc. 82 [4], 797-818 (1999)
5
J.Ravez “Ferroelectricity in solid state chemistry”, C.R. Acad. Sci. París, Série Iic, Chimie/Chemistry 3,
267-283 (2000)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-35-320.jpg)

![Materiales cerámicos ferroeléctricos
- 17 -
Figura 3.1. Esquema del intervalo de propiedades y aplicaciones asociadas al desplazamiento iónico en
los sólidos. Figura adaptada de la referencia [6].
Como puede verse, al aumentar el grado del desplazamiento iónico las
propiedades varían, desde dieléctricos de baja permitividad a dieléctricos de elevada
permitividad, a continuación ferroeléctricos y finalmente, los conductores iónicos y
electrónicos. Las propiedades que hacen a los materiales cerámicos ferroeléctricos útiles
en una gran variedad de aplicaciones son:
- Aparición de histéresis eléctrica al actuar sobre el material un campo eléctrico
alterno, dando lugar a una curva de histéresis típica: Polarización - Intensidad de
campo (P-E) ó Carga - Voltaje (Q-V).
- Constante dieléctrica elevada debido a la polarización espontánea.
- Pérdidas dieléctricas bajas.
- Resistencia eléctrica elevada.
- Constantes piezoeléctricas altas.
- Dependencia con la temperatura de todos los parámetros dieléctricos.
Todas estas propiedades hacen que el estudio de materiales ferroeléctricos sea
abordado por gran cantidad de investigadores y sea tan utilizado por numerosas
empresas del sector de la electrónica.
Incremento del desplazamiento atómico (iónico)/ Å
0 Å ~0.1 Å 5 Å
DIELÉCTRICOS
Baja permitividad ε’
Ej. Al2O3
DIELÉCTRICOS
Alta permitividad ε’
Ej. BaNd2Ti4O12
COMUNICACIONES
MÓVILES
FERROELÉCTRICOS
Alta permitividad ε’
Ej. BaTiO3
CONDENSADORES
CONDUCTORES
IÓNICOS
Baja resistencia
R=101
-104
Ωcm-1
Ej. β alúmina de sodio
SÓLIDOS
ELECTROLÍTICOS:
BATERIAS Y
SENSORES
CONDUCTORES
IÓNICOS
CONDUCTORES
ELECTRÓNICOS
Ej. LixCoO2
ELECTRODOS
AISLANTES](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-37-320.jpg)
![Capítulo 3
- 18 -
3.2. PUNTO DE CURIE Y TRANSICIÓN DE FASE
Las propiedades ferroeléctricas se presentan sólo en determinados intervalos de
temperatura, y existe una temperatura límite a la cual ocurren los cambios de
polarización. Generalmente el comportamiento ferroeléctrico viene marcado por esta
temperatura límite o de transición que se conoce como punto de Curie, TC. La transición
ferroeléctrica-paraeléctrica se asigna a la rotura, por la agitación térmica, de una
determinada orientación de los dipolos moleculares generados por desplazamientos
precisos de las subredes de cationes respecto a las subredes de aniones que originan la
polarización espontánea. Los materiales ferroeléctricos poseen valores de permitividad
(ε’) máximos a dicha temperatura, mientras que si se supera (T TC) el material pierde
las propiedades ferroeléctricas y pasa a ser un material paraeléctrico; volviendo a
adquirir el carácter ferroeléctrico en una posterior reducción de la temperatura.
En general, por encima de la TC, la relación entre la permitividad y la
temperatura, viene dada por la Ley de Curie-Weiss:
0
'
T
T
Cw
−
=
ε [3.1]
siendo Cw (K-1
) la constante de Curie, cuyo valor generalmente es del orden de 103
-105
K-1
, y T0 la temperatura de Curie-Weiss. La temperatura de transición o punto de Curie
(TC) es diferente a la temperatura de Curie-Weiss (T0). La temperatura de Curie-Weiss
se obtiene por extrapolación, mientras que el punto de Curie es la temperatura real a la
tiene lugar la inversión de la estructura. En un ferroeléctrico que presenta una transición
de fase de segundo orden, en que las propiedades y constantes físicas cambian con la
temperatura pero de forma discontinua, la temperatura de Curie-Weiss y el punto de
Curie pueden ser idénticos (T0 = TC). Por el contrario, en el caso de transiciones de
primer orden, donde las propiedades cambian de manera discontinua, la temperatura de
Curie-Weiss puede ser ~ 10 ºC inferior al punto de Curie (T0 TC).
3.3. TIPOS DE MATERIALES FERROELÉCTRICOS
Los materiales ferroeléctricos suelen agruparse en cuatro grandes grupos de acuerdo con
la estructura que presentan:
o Compuestos formados por estructuras que contienen octaedros de oxígeno
BO6 que se unen por compartición de vértices, como el BaTiO3.
o Compuestos que contienen radicales hidrógeno enlazados, como la sal de
Rochelle (KNaC4H4O6.4H2O).
o Polímeros orgánicos, como el polifluoruro de vinilideno, PVDF [(CH2-CF2)n]
y copolímeros de PVDF con trifluoroetileno [P(VDF-TrFE)] que tienen
aplicaciones como materiales piezoeléctricos y piroeléctricos.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-38-320.jpg)




![Materiales con resistencia óhmica variable
- 25 -
4. MATERIALES CON RESISTENCIA ÓHMICA
VARIABLE
La mayoría de los dispositivos y equipos electrónicos que se utilizan en la actualidad,
requieren sistemas de protección de sus componentes. Generalmente, la principal
característica de los materiales que se utilizan para este fin, es que su resistencia varía
de forma no lineal cuando se modifica la temperatura o cuando se aplica un voltaje, no
cumpliendo, por tanto, estos últimos, una de las leyes básicas de la electricidad: la Ley
de Ohm.
4.1. LEY DE OHM
La Ley de Ohm establece que la intensidad de corriente eléctrica (I) que circula por un
conductor eléctrico es directamente proporcional a la diferencia de potencial aplicada
(V) e inversamente proporcional a la resistencia del mismo (R), y se expresa
matemáticamente según la siguiente ecuación:
R
V
I = [4.1]
Esta ley, formulada por el físico alemán Georg Simon Ohm (1789-1854), la
cumplen con sorprendente precisión muchos conductores en un amplio intervalo de
valores de potencial V, de intensidad I y de temperatura. En la ecuación anterior, R se
expresa en volt/amperio ó m2
kgs-1
C-2
. Esta unidad se define como ohm (símbolo, Ω).
Así pues, un ohm es la resistencia de un material por el cual pasa una corriente de un
amperio cuando se establece entre sus extremos una diferencia de potencial igual a un
voltio.
Esta ley no se cumple, por ejemplo, cuando la resistencia del conductor varía
con la temperatura, y la temperatura del conductor depende de la intensidad de corriente
y el tiempo que esté circulando. Por tanto, se cumplirá la Ley de Ohm si al representar
V frente a I, el ajuste es lineal, es decir, si la resistencia es independiente de V y de I.
Los materiales cerámicos obedecen normalmente la ley de Ohm, especialmente
para voltajes pequeños, ya que el gradiente de potencial a través de una muestra
homogénea es demasiado pequeño para causar cambios estructurales que puedan afectar
a la conducción iónica o causar cambios electrónicos, como la promoción a niveles de
energía mayor. Los materiales que conducen electrónicamente por un mecanismo por
saltos, iónico o electrónico, el salto es un proceso arbitrario que puede ser ajustado
efectivamente usando la random walk theory9
. Un pequeño voltaje simplemente da un
leve dc bias al movimiento por saltos, dando lugar a un flujo neto en una dirección
9
R. A. Huggins, en Difusión in Solids, Recent Development, editado por A. S. Nowich y J. J. Burton,
Academic Press, 145 (1975)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-43-320.jpg)
![Capítulo 4
- 26 -
particular. Por tanto, se considera que la conducción por saltos de electrones (o iones)
no está influenciada por la aplicación de un pequeño voltaje dc.
Sin embargo, hasta el momento, únicamente hay dos excepciones que presentan
una dependencia no lineal con el voltaje, es decir, que no cumplen la ley de Ohm:
materiales aislantes sometidos a alto voltaje, donde ocurre una rotura dieléctrica, y
materiales cuya resistencia está controlada por efectos interfaciales o de contacto.
Los fenómenos dependientes del voltaje, donde la variación de la resistencia no
es lineal, están asociados generalmente con efectos interfaciales como las barreras de
Schottky. La dimensión de esta barrera es un fenómeno carga-espacio controlado entre
dos materiales que pueden tener diferente energía de Fermi (EF) o en los cuales hay un
cúmulo de carga en un lado de la interfase que induce a la polarización en el otro lado.
En estos casos, la dimensión de esta barrera y por tanto, la conducción a través de la
interfase, se pueden reducir por la aplicación de un voltaje (dc) provocando que la
resistencia dependa ahora del voltaje. Ese efecto es crítico para el funcionamiento de los
varistores debido a que la reducción de la barrera hace que el material sea reversible
cuando cesa el voltaje.
Recientemente, se ha desarrollado un dispositivo que presenta una dependencia
no lineal de la resistencia con el voltaje y tiene características de memristor. Aunque a
continuación se detallarán sus características, el memristor es un dispositivo que
“recuerda” su resistencia, y es considerado como el cuarto elemento de un circuito
eléctrico.
Un tercer caso de materiales que no cumplen la ley de Ohm, son los materiales
aislantes sometidos a voltajes altos, en los que tiene lugar una cesión de carga de los
electrodos a la banda de conducción del material, lo cual puede conducir a la rotura
dieléctrica.
A continuación, se van a describir las propiedades de estos materiales que no
cumplen la ley de Ohm, es decir, los materiales cuyas propiedades, en particular su
resistencia, varían con el voltaje, concretamente los varistores, los memristores y los
materiales aislantes que sufren una rotura dieléctrica tras la aplicación de voltajes
elevados.
4.2. VARISTOR
Esencialmente un varistor (variable resistor) es una resistencia de impedancia variable
que presenta un comportamiento no lineal intensidad-voltaje10
. Este hecho los convierte
en materiales adecuados para la protección de sistemas frente a sobretensiones
transitorias, entendiendo como tal, un aumento no permanente del potencial eléctrico
por encima del umbral de tolerancia de la tensión nominal de trabajo en un determinado
sistema. Estos altos voltajes pueden dañar los transistores y los circuitos integrados, y
por ello habitualmente, se coloca un varistor en paralelo al circuito a proteger,
10
D. R. Clarke, J. Am. Ceram. Soc. 82 [3], 485-502 (1999)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-44-320.jpg)
![Materiales con resistencia óhmica variable
- 27 -
absorbiendo todos los picos mayores de su tensión nominal. El varistor sólo suprime
picos transitorios; si lo sometemos a una tensión elevada constante, deja de funcionar.
Los varistores originales fueron desarrollados en los años 30 para reemplazar los
rectificadores de selenio en la protección de los sistemas telefónicos11,12
. Estos
materiales consistían en partículas de SiC parcialmente sinterizadas. Generalmente los
varistores cerámicos están basados en ZnO, y habitualmente también contienen
pequeñas cantidades de Bi2O3 y otros óxidos (manganeso, cobalto o antimonio).
El comportamiento intensidad-voltaje del varistor presenta una forma
característica que recibe el nombre de curva I-V del varistor13
(figura 4.1). Como se
puede observar, pequeñas variaciones en el campo aplicado producen enormes cambios
en el valor de la densidad de corriente que fluye a través del material. En la curva I-V se
pueden distinguir tres zonas diferenciadas: la región de pre-encendido (I), en la cual la
intensidad de corriente que circula a través del material o corriente de fuga, es función
de la temperatura y el comportamiento es óhmico; la región de conmutación (II),
altamente no lineal e independiente prácticamente de la temperatura; y la región de altas
corrientes (III), donde el varistor vuelve a tener un comportamiento lineal, es decir,
óhmico. La transición entre el estado altamente resistivo y el estado conductor, tiene
lugar para un determinado valor de voltaje que se denomina voltaje de corte. El valor de
este parámetro definirá el campo de aplicación del dispositivo varistor protector.
Figura 4.1. Respuesta I-V característica de un varistor cerámico basado en ZnO. Diferentes regiones de
la curva definen los parámetros funcionales del dispositivo protector (el recuadro en línea
discontinua marca la región de corriente de fuga). Figura adaptada de la referencia [10].
11
C. F. Frosch, Bell Lab. Rec. 32, 336-40 (1954)
12
H. F. Dienel, Bell Lab. Rec. 34, 407-11 (1956)
13
M. Peiteado, Bol. Soc. Esp. Ceram. V. 44 [2], 77-87 (2005)
Intensidad de corriente (A/cm2
)
10-6
10-5
10-4
10-3
10-2
10-1
100
101
102
103
104
105
C
a
m
p
o
(
V
/c
m
)
101
102
103
104
105
Región I
Pre-encendido
Región II
No lineal
Región III
Altas corrientes
ρ ~ 1010
-1012
Ωcm I∝Vα
, α ~ 35-80 ρ ~ 0.1-10 Ωcm
Voltaje
de corte
α = dln(I) / dln(V)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-45-320.jpg)
![Capítulo 4
- 28 -
En el régimen de no linealidad, la relación entre la intensidad corriente y el
voltaje se expresa normalmente en términos de la siguiente ley de potencia:
I = k Vα
[4.2]
donde k es una constante y α es el coeficiente de no linealidad del varistor y presenta
valores entre 35 y 80. En una situación ideal, la anchura de la región I se reducirá
totalmente a cero, de tal manera que hasta no alcanzar un determinado valor de voltaje,
el varistor se comporta como un aislante perfecto. En la región II, la línea horizontal
(α = ∞) corresponde a un varistor “perfecto”, donde el valor del voltaje es
independiente de la intensidad de corriente. Aunque α es casi constante en un intervalo
limitado de corriente, un varistor dado no se caracteriza por un único valor. En la
práctica, α es un número finito, y lo que se pretende es alcanzar un valor lo más elevado
posible en dicho coeficiente de no linealidad. Actualmente existen varistores que
pueden proteger circuitos en un amplio intervalo de voltaje, en los que el cambio de
aislante a conductor tiene lugar en nanosegundos.
El comportamiento del varistor está estrechamente relacionado con la
microestructura14-16
. En la figura 4.2 se esquematiza la microestructura que caracteriza a
un varistor17
.
Figura 4.2. Esquema de la estructura real (a) e idealizada según el modelo de ladrillos (brickwork model)
(b) del varistor de ZnO. Figura adaptada de la referencia [17].
Como puede verse en la figura, estas cerámicas están formadas por granos
semiconductores de ZnO (tipo n) y fronteras de grano aislantes, responsables de las
propiedades eléctricas inusuales que presentan los varistores. Cada una de estas regiones
se caracteriza por una estructura electrónica específica que interactúa con la de las otras
contribuyendo a la estructura electrónica global y es responsable de las propiedades
físicas que presenta el material. La frontera de grano está formada por el mismo
material semiconductor, pero contiene defectos y dopantes. Como resultado, su nivel de
Fermi es diferente al de los granos (figura 4.3.a). Para mantener el equilibrio
14 L. M. Levinson y H. R. Philipp, J. Appl. Phys. 46 [3], 1332-41 (1975)
15 J. Wong, J. Appl. Phys. 46 [4], 1653-9 (1975)
16 W. G. Morris, J. Vac. Sci. Technol. 13 [4], 926-31 (1976)
17 P. R. Emtage, J. Appl. Phys. 48 [10], 4372-84 (1977)
Granos
de ZnO
Material
intergranular
Electrodo
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-46-320.jpg)
![Materiales con resistencia óhmica variable
- 29 -
termodinámico, los electrones fluyen a la frontera de grano y quedan atrapados por los
defectos y dopantes para aumentar su nivel de Fermi hasta que es el mismo en todo el
material. Como consecuencia, los electrones atrapados forman una capa de carga
negativa en el borde de grano que es neutralizada por una capa de sitios dadores
cargados positivamente a ambos lados del borde de grano, dando lugar a la mencionada
región de carga espacial o región de agotamiento (depletion layer). De esta forma se
genera un campo electrostático en la zona que provoca la curvatura de las bandas de
energía y ello origina la formación de una doble barrera Schottky de potencial en el
borde de grano (figura 4.3.b), de altura Φ y de anchura d.
Figura 4.3. Esquema de la barrera Schottky de potencial en un borde de grano en varistores basados en
ZnO y las regiones del aislante: (a,b) sin y (c) con voltaje aplicado. Figura adaptada de la
referencia [10].
Frontera de
grano
Dopantes,
impurezas
+ defectos
(a)
- - - - -
+ + + + +
EF
- - - - -
+ + + + +
EF
Aislante ZnO
ZnO
Φ0 Φ0
-
-
-
-
-
-
Electrones
atrapados
d dA d
EF
Φ1
V
d1
d2
P
o
t
e
n
c
i
a
l
0
(c)
Φ2](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-47-320.jpg)
![Capítulo 4
- 30 -
El transporte de electrones a través del borde de grano cargado depende del
voltaje aplicado a través del mismo, o lo que es lo mismo, los electrones solo tendrán
energía suficiente para atravesar las barreras cuando se alcance un determinado valor
del potencial entre los electrodos del material, el voltaje de corte del varistor. En la
figura se representa la barrera de Schottky al aplicar un voltaje dc suficientemente alto
(figura 4.3.c). En este caso, la barrera es asimétrica debido al movimiento de los
electrones. En este proceso, los electrones quedan atrapados en la derecha, es decir, en
la dirección del campo. Como consecuencia, la altura de esta barrera aumenta y la altura
de la barrera de la izquierda disminuye lentamente con el voltaje hasta que todos los
electrones están atrapados en la zona aislante. Además, la anchura de la barrera aumenta
en la dirección inversa al campo, mientras que disminuye en la dirección del campo.
Este punto es el indicado en la gráfica como voltaje de corte. A mayores voltajes la
altura de la barrera disminuye rápidamente con el aumento del voltaje. Este modelo
implica que en la rotura, la transición de bajo voltaje a intermedio, ocurra en las
regiones donde el aislante es más delgado. Estas regiones son aproximadamente 400 Å
de espesor.
4.3. MEMRISTOR
Existen cuatro variables fundamentales de los circuitos eléctricos: la corriente eléctrica
(I), el voltaje (V), la carga (Q) y el flujo magnético (ϕ), y seis expresiones matemáticas
diferentes que relacionan estas cuatro variables. Estas variables describen el
comportamiento de los diferentes elementos básicos usados en la construcción de
circuitos eléctricos, y son: el condensador (descubierto en 1745), la resistencia
(descubierto en 1827) y la bobina (descubierto en 1831).
La resistencia (o resistor) es el componente electrónico diseñado para introducir
una resistencia eléctrica determinada entre dos partes de un circuito. Los resistores se
utilizan en los circuitos para limitar el valor de la corriente o para fijar el valor de la
tensión. El resistor presenta una relación entre la intensidad de corriente (I) y el voltaje
(V). El condensador (o capacitor) es un dispositivo que almacena energía eléctrica, es
un componente pasivo. La carga almacenada en una de las placas es proporcional a la
diferencia de potencial entre esta placa y la otra, siendo la constante de proporcionalidad
la capacidad o capacitancia. El capacitor proporciona una relación entre la carga (Q) y
el voltaje (V). La bobina (o inductor) es un componente pasivo que, debido al
fenómeno de la autoinducción, almacena energía en forma de campo magnético. El
inductor relaciona la corriente eléctrica (I) con el flujo magnético (ϕ).
En 1971, L. Chua y col.
18
sugirieron de forma teórica y por primera vez que
debería existir un cuarto elemento que relacionase la carga (Q) y el flujo magnético (ϕ).
A este hipotético elemento lo denominaron “memristor”. Este elemento no podía ser
sustituido por ningún otro circuito usando sólo los otros tres elementos conocidos, y por
ello, el memristor se consideró fundamental. El término memristor es la abreviatura de
18 L. O. Chua, IEEE Trans. Circuit Theory, 18 [5], 507-519 (1971)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-48-320.jpg)
![Materiales con resistencia óhmica variable
- 31 -
“resistencia con memoria”, porque su función es propiamente ésta: recordar su historia.
Su comportamiento puede describirse por la ecuación:
V = R(Q)·I [4.3]
donde R es la resistencia.
En la figura 4.4, se ilustra un esquema con las cuatro variables fundamentales y
los cuatro elementos básicos de los circuitos, así como las relaciones que rigen su
comportamiento:
Figura 4.4. Los cuatro elementos fundamentales de un circuito eléctrico: resistor, capacitor, inductor y
memristor. Figura adaptada de la referencia [21].
La relación que caracteriza al memristor es dϕ = Mdq, donde M es la
memristencia. En el caso de elementos lineales, M es una constante, y por tanto, la
memristencia es igual a la resistencia. Sin embargo, para el caso del memristor, M es
función de la carga, no es una constante, generando un elemento de circuito no lineal, y
ésta es la característica interesante de este elemento.
Básicamente, un memristor puede definirse como un dispositivo de dos
terminales que almacena información ya que su resistencia depende de la magnitud y
polaridad del voltaje aplicado, así como del tiempo de aplicación del voltaje. Cuando
cesa la aplicación del voltaje, el memristor recuerda su resistencia más reciente hasta
que se vuelve a aplicar un voltaje, ya sea un día o un año después.
Después de 35 años desde que Chua había teorizado el memristor, Strukov y
col.19
presentaron por primera vez un modelo físico de un dispositivo eléctrico que se
comportaba como un memristor perfecto. Este material supuso el primer ejemplo físico
de memristor. Según los autores, el sistema estaba basado en láminas delgadas de
TiO2/TiO2-x, con x = 0.05, sobre un sustrato de Pt. Al aplicar un voltaje positivo sobre la
lámina, éste repele las vacantes de oxígeno, y se desplazan hacia la zona aislante de
TiO2. Esto genera una interfase que separa la capa del TiO2 y del TiO2-x. Cuanto mayor
19 D. B. Strukov, G. S. Snider, D. R. Stewart y R. S. Williams, Nature, 453, 80-83 (2008)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-49-320.jpg)
![Capítulo 4
- 32 -
es el voltaje positivo aplicado, más conductor resulta el sistema. Al aplicar un voltaje
negativo tiene lugar el proceso contrario, en el que las vacantes de oxígeno se mueven
en la misma dirección del campo, desplazando la interfase entre TiO2/TiO2-x. Cuanto
más negativo sea el voltaje aplicado, menos conductor resulta el sistema. Por tanto, se
trata del transporte electrónico e iónico acoplado bajo la acción de un voltaje dc.
La particularidad de este material es que cuando cesa el voltaje, las vacantes de
oxígeno permanecen inmóviles, es decir, la interfase entre TiO2/TiO2-x se mantiene
constante. Así, la propiedad que caracteriza al memristor es la capacidad de recordar el
voltaje que se ha sometido previamente a través de él, siendo la clave de este proceso la
existencia de dos láminas con dos composiciones diferentes de TiO2.
Tal y como predijo Chua20
, el memristor se caracteriza por presentar una curva
voltaje-intensidad de corriente característica, que consiste en un ciclo de histéresis
estrecho. En la figura 4.5 se ilustra la curva que dedujo Chua20
, siendo ω la frecuencia
de excitación, y la curva experimental obtenida para el primer ejemplo de memristor
obtenido por Strukov19
. En esta gráfica puede observarse que el voltaje aumenta desde
cero hasta alcanzar un valor constante y luego disminuye hasta un valor mínimo
negativo, para finalmente recuperar el valor de cero. Además, Strukov y col.
19
demostraron que el cambio en la resistencia depende del tiempo de aplicación del
voltaje, indicando que a mayor tiempo de aplicación del voltaje positivo, menor es la
resistencia que se alcanza. A mayor voltaje negativo que se aplica, se alcanza un valor
de la resistencia mayor hasta un valor límite. Al cesar la aplicación del voltaje, se
mantiene la resistencia del dispositivo hasta que se vuelva a aplicar un voltaje.
Figura 4.5. Curvas voltaje-intensidad: (a) hipotética propuesta por Chua y (b) experimental obtenida por
Strukov. Figura adaptada de las referencias [19] y [20].
Las propiedades que presenta el memristor hacen que éste pueda utilizarse como
memoria no volátil, reemplazando los discos duros o las memorias DRAM, y utilizarse
por ejemplo, en los ordenadores portátiles ya que estos dispositivos tienen la capacidad
de almacenar datos indefinidamente. Además, los memristores pueden ser
extremadamente pequeños por lo que pueden funcionar como dispositivos de unión.
Utilizando estos memristores será posible construir circuitos electrónicos que puedan
ajustarse a unas dimensiones específicas. A medida que se construyan dispositivos más
20 L. O. Chua y S. M. Kang, Proceedings of the IEEE, 64 [2], 209-223 (1976)
V
I
ω1 ω2
ω1
ω2
ω∞
(a) (b)
V
I](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-50-320.jpg)
![Materiales con resistencia óhmica variable
- 33 -
y más pequeños, la memristencia será más perceptible y en algunos casos dominante.
En la figura 4.6 se presenta un esquema que simplifica el funcionamiento de un
memristor, donde éste actúa como dispositivo de unión entre los dos hilos de platino en
un circuito eléctrico.
Figura 4.6. (a) Circuito eléctrico laminar; (b) esquema de una unión nanométrica memristiva y (c)
esquema del memristor TiO2/TiO2-x actuando como unión. Figuras (a) y (b) adaptadas de la
referencia [26]; figura (c) adaptada de la referencia [22].
Después de la publicación de dicho artículo en la revista “Nature” en el año
2008, han aparecido más de 150 trabajos relacionados con el memristor21-26
. En este
sentido, Driscoll y col.
27
han presentado otro ejemplo de material con propiedades de
memristor, basado en láminas delgadas de VO2. Chen y col.
28
desarrollaron un
dispositivo con propiedades de memoria en el sistema Pt/Mg0.2Zn0.8O/Pt, y Tulina y
col.
29
obtuvieron propiedades semejantes para el sistema basado en Bi2Sr2CaCu2P8+y.
Posteriormente, Gergel-Hackett y col.
30
presentaron un dispositivo memristor flexible.
Este dispositivo presenta flexibilidad física, está fabricado mediante procesos
competitivos económicamente, puede someterse a voltajes de aplicación menores de
10V, presenta un potencial de memoria no volátil de 1.2·106
s y es posible utilizarlo
después de ser doblado 4000 veces. Por todas estas propiedades es un excelente
candidato para usarse en dispositivos electrónicos portátiles, de bajo peso y económicos,
como por ejemplo, en sensores desechables.
21 J. M. Tour y T. He, Electronics Nature, 453, 42-43 (2008)
22 R. Stanley Williams, IEEE Spectrum, 29-35 (2008)
23 N. D. Mathur, Nature 455, E13 (2008)
24 J. J. Yang, M. D. Pickett, X. Li, D. A. A. Ohlberg, D. R. Stewart y R. S. Williams, Nature
Nanotechnology 3 [7], 429-433 (2008)
25 Y. V. Pershin y M. D. Ventra, Phys. Review B 78, 113309-1-4 (2008)
26 G. S. Snider, IEEE/ACM International Symposium on Nanoscale Architecture, 85-92 (2008)
27 T. Driscoll. H. T. Kim, B. G. Chae, M. D. Ventra y D. N. Basov, Appl. Phys. Lett. 95, 043503-1-3
(2009)
28 X. Chen, G. Wu y D. Bao, Appl. Phys. Lett. 93, 093501-1-3 (2008)
29 N. A. Tulina, I. Y. Borisenko y V. V. Sirotkin, Phys. Lett. A. 372, 6681-6686 (2008)
30 N. G. Hackett, B. Hamadani, B. Dunlap, J. Suehle, C. Richter, C. Hacker y D. Gundlach, IEEE
Electron Device Lett. (2009)
(a)
Hilo de Pt
(40-50 nm x 2-3 nm)
Hilo de Pt
(40-50 nm x 2-3 nm)
Interfase
(3-30 nm de espesor)
TiO2
TiO2-x
(c)
Alambre
nanométrico
Alambre
nanométrico
Unión memristiva
(b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-51-320.jpg)
![Capítulo 4
- 34 -
Parece ser que el descubrimiento del memristor ha sido un logro muy importante
para el desarrollo de la nanotecnología, y que provocará un cambio en el diseño de los
circuitos electrónicos en el siglo XXI tan radicalmente como lo hizo el transistor en el
siglo XX.
4.4. MATERIALES QUE PRESENTAN ROTURA DIELÉCTRICA
La rotura dieléctrica es un proceso universal que tiene lugar en una gran variedad de
fenómenos naturales, como la descarga eléctrica que tiene lugar en las tormentas en
forma de relámpagos.
En materiales aislantes, la rotura dieléctrica supone la variación no lineal de la
conductividad con el voltaje aplicado. De forma general, la rotura dieléctrica está
relacionada con la formación de regiones eléctricamente conductoras en un material
aislante expuesto a un campo eléctrico elevado31
. Aunque ha sido objeto de estudio
durante muchos años, no existe todavía un modelo que explique la rotura dieléctrica en
cristales iónicos.
Cox y col.
32
estudiaron el comportamiento eléctrico de monocristales de BaTiO3
observando un comportamiento no-óhmico a altos voltajes, ≥ 1000 Vcm-1
, y que la
rotura dieléctrica dependía del material del electrodo. En particular, estudiaron
diferentes tipos de materiales como cátodo (Al, Au y Ni) y como ánodo (Au). Según
estos autores, el comportamiento no-óhmico se asocia a la cesión de carga de los
electrodos a la banda de conducción del material, concretamente a la cesión de
electrones al cátodo y de huecos al ánodo. Los mismos autores, realizaron estudios
semejantes en monocristales de SrTiO3, concluyendo que el aumento en la intensidad de
corriente que se producía al utilizar ánodos de Au y Ag podía deberse a la formación de
una superficie anódica en la interfase ánodo-muestra33
. Por otra parte, indicaron que
existía un campo crítico mínimo (por ejemplo ∼500 Vcm-1
para Au), a partir del cual la
intensidad de corriente aumentaba con el voltaje aplicado.
Branwood y col.
34,35
estudiaron la conductividad eléctrica en monocristales de
BaTiO3, en función de la temperatura, campo eléctrico aplicado, material del electrodo,
espesor de la muestra y tiempo. A campos eléctricos bajos, el comportamiento fue
óhmico, pero a campos elevados el comportamiento fue no-óhmico. Como
anteriormente, en la región no-óhmica, la conductividad depende del material del
electrodo. Estos autores, estudiaron el comportamiento utilizando diferentes electrodos.
En la figura 4.7, se muestra este comportamiento para diferentes electrodos utilizados
como cátodos y ánodos.
31 X. Li, C. H. Tung y K. L. Pey, Appl. Phys. Lett. 93, 072903-1-3 (2008)
32 G. A. Cox y R. H. Tredgold, Phys. Letters, 4 [3], 199-200 (1963)
33 G. A. Cox y R. H. Tredgold, Brit. J. Appl. Phys. 16, 427-430 (1965)
34 A. Branwood y R. H. Tredgold, Proc. Phys. Soc. 76, 93-8 (1960)
35 A. Branwood, O. H. Hughes, J. D. Hurd y R. H. Tredgold, Proc. Phys. Soc. 79, 1161-5 (1962)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-52-320.jpg)
![Materiales con resistencia óhmica variable
- 35 -
Figura 4.7. Influencia del material del cátodo en la conductividad del BaTiO3. Área de electrodo
0.07cm2; temperatura de medida 153 ºC. Figura adaptada de la referencia [35].
Además, observaron que la conductividad, a un determinado voltaje, era
dependiente del tiempo para algunos electrodos. En la figura 4.8 se muestra la
conductividad en función del tiempo tras la aplicación de 4 kVcm-1
a la temperatura de
medida de 102 ºC, y como puede verse, el incremento de la conductividad es diferente
en función del electrodo utilizado.
I
n
t
e
n
s
i
d
a
d
d
e
c
o
r
r
i
e
n
t
e
(
A
·1
0
-
9
)
Voltaje (kVcm-1
)
○ Al (cátodo y ánodo)
Au (cátodo y ánodo)
● Al (cátodo) / Au (ánodo)
Au (cátodo) / Al (ánodo)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-53-320.jpg)
![Capítulo 4
- 36 -
Figura 4.8. Conductividad en función del tiempo tras la aplicación de ~ 4 kVcm-1
en muestras de BaTiO3
con diferentes electrodos. Figura adaptada de la referencia [34].
En los cristales con ánodo de Au, encontraron que la conductividad aumentaba
un orden de magnitud después de la aplicación de 4 kVcm-1
durante dos semanas, y que
éste tiempo disminuía al aumentar el voltaje aplicado. El aumento de la conductividad
se relacionó con la cesión de huecos al ánodo de Au.
tiempo/ días
0 5 10 15
C
o
n
d
u
c
t
i
v
i
d
a
d
/
S
c
m
-
1
x
1
0
1
0
0
1
2
3
4
5
6
Au
Au/Cr
Cr](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-54-320.jpg)
![Antecedentes del BaTiO3
- 41 -
5. ANTECEDENTES DEL BaTiO3
5.1. ASPECTOS GENERALES
Los compuestos existentes en el sistema BaO-TiO2 han sido estudiados en gran medida
por las interesantes propiedades que poseen, que les lleva a formar parte de muchos
dispositivos electrónicos. Especialmente el BaTiO3 ha sido el compuesto más estudiado.
Además de éste, existen otros compuestos interesantes en dicho sistema; compuestos
ricos en TiO2, como BaTi4O9 y el Ba2Ti9O20 ya que presentan una baja pérdida
dieléctrica y elevada constante dieléctrica en la región de microondas del espectro
electromagnético, y la nueva fase ferroeléctrica de composición BaTi2O5.36,37
El
diagrama de fases para este sistema se ha estudiado por diferentes autores
modificándolo a lo largo de los años38-42
. En la figura 5.1 se muestra la última
modificación del diagrama completo, propuesto por Lee y col.42
para el sistema BaO-
TiO2, aunque existe una modificación del diagrama más reciente en el intervalo de
existencia del BaTi2O5.43
Figura 5.1. Diagrama de fases del sistema BaO-TiO2 según Lee y col. [42].
36
Y. Akishige, K. Fukano y H. Shigematsu, Jpn. J. Appl. Phys. 42, L946-48 (2003)
37
H. Beltrán, B. Gómez, N. Masó, E. Cordoncillo, P. Escribano y A. R. West, J. Appl. Phys. 97, 084104-
1-6 (2005)
38
D. E. Rase y R. Roy, J. Am. Ceram. Soc. 38 [3], 102-13 (1955)
39
T. Negas, R. S. Roth, H. S. Parker y D. Minor, J. Solid State Chem. 9, 297-307 (1974)
40
J. J. Ritter, R. S. Roth y J. E. Blendell, J. Am. Ceram. Soc. 65 [2], 155-62 (1986)
41
K. W. Kirby y B. A. Weschsler, J. Am. Ceram. Soc. 74 [8], 1841-47 (1991)
42
S. Lee, C. A. Randall y Z. K. Liu, J. Am. Ceram. Soc. 90 [8], 2589-94 (2007)
43
N. Zhu y A. R. West, J. Am. Ceram. Soc. 93 [1], 295-300 (2010)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-55-320.jpg)

![Antecedentes del BaTiO3
- 43 -
misma dirección, originando dominios que se alinean paralelamente provocando una
polarización espontánea. Este desplazamiento es el responsable de la ferroelectricidad
en el BaTiO3.6
Figura 5.3. (a) Transición de fase de cúbica a tetragonal en la pervosquita BaTiO3 y (b) octaedro de TiO6
distorsionado por el desplazamiento del Ti de su posición de equilibrio.
A temperatura ambiente, es bastante difícil cambiar la orientación de los
dominios porque esto supondría que los átomos de Ti en octaedros TiO6 adyacentes
sufrieran un desplazamiento colectivo hacia uno de los otros seis oxígenos. Este proceso
es bastante difícil y como consecuencia la permitividad relativa, ε’, del BT a
temperatura ambiente es del orden de 103
. Esta permitividad es, sin embargo, bastante
elevada en comparación con los materiales dieléctricos comunes en los que se asocia al
desplazamiento de los átomos de Ti a las fronteras de dominio.
La dependencia de la permitividad con la temperatura del BT, pasa a través de
un máximo a la temperatura de transición o punto de Curie, ~ 130 ºC. A esta
temperatura, la estructura de dominios característica de la fase tetragonal desaparece y
por tanto, los octaedros TiO6 individuales pueden responder independientemente al
campo eléctrico aplicado, originando una elevada permitividad. A temperaturas
superiores de la TC, en la región paraeléctrica, aunque no existen dominios permanentes,
los octaedros TiO6 probablemente están distorsionados y los dipolos individuales dan
lugar a la respuesta clásica de Curie-Weiss, cumpliendo:
ε’ = Cw / (T-T0) [3.1]
donde Cw es la constante de Curie y T0 es la temperatura de Curie Weiss.
Una segunda transición tiene lugar en el BaTiO3 tetragonal alrededor de 0 ºC
(± 5 ºC), en que el cristal mantiene su ferroelectricidad pero la estructura pasa a ser
ortorrómbica. Por debajo de -90 ºC, tiene lugar una tercera transición de fase en la que
el BaTiO3 adopta una simetría romboédrica. En la figura 5.4 se resumen las tres
Ti ~0.1 Å
Ti ~0.1 Å
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-57-320.jpg)
![Capítulo 5
- 44 -
transiciones de fase, así como la variación de la permitividad en función de la
temperatura, asociada con cada una de las transiciones de fase.
Figura 5.4. Representación de las transiciones de fase de la perovsquita BaTiO3 y la variación de la
permitividad en función de la temperatura.
Como consecuencia del cambio de polarización espontánea al enfriar desde altas
temperaturas, se producen cambios en los parámetros de la celda unidad44
y en la
constante dieléctrica45
. En la figura 5.5 se puede observar la relación entre el cambio de
polarización espontánea, los parámetros de la celda unidad y la constante dieléctrica.
44
R. Clarke, J. Appl. Cryst. 9, 335-38 (1976)
45
W. J. Merz, Phys. Rev. 76 [8], 1221-25 (1949)
Temperatura/ ºC
-150 -125 -100 -75 -50 -25 0 25 50 75 100 125 150 175
ε'
0
1000
2000
3000
4000
5000
6000
7000
Cúbico
Tetragonal
Romboédrico 130 ºC
0 ºC
-90 ºC](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-58-320.jpg)
![Antecedentes del BaTiO3
- 45 -
-160 -120 -80 -40 0 40 80 100
0
2
4
6
8
10
P
e
r
m
i
t
i
v
i
d
a
d
r
e
l
a
t
i
v
a
·1
0
3
Temperatura (ºC)
ejes a
ejes c
-140 -120 -100 -80 -60 -40 -20 0 20 40 60 80 100
Tc
0,25
0,20
0,15
0,10
0,05
P
s
(
C
m
-
2
)
Temperatura (ºC)
404
400
402
398
-100 -50 0 50 100 150
a=c
a=b
b
c
a
a
E
s
p
a
c
i
a
d
o
s
(
p
m
)
Temperatura (ºC)
(a)
(b)
(c)
120
Figura 5.5. (a) Polarización espontánea, (b) permitividad relativa y (c) espaciado en función de la
temperatura para un monocristal de BaTiO3. Figura adaptada de las referencias [44] y [45].
Cuando la temperatura desciende justo por debajo del punto de Curie, se
alcanzan niveles máximos para la polarizabilidad lo que produce que la constante](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-59-320.jpg)
![Capítulo 5
- 46 -
dieléctrica pueda superar valores de 10000. Al disminuir la temperatura unos pocos
grados centígrados por debajo del punto de Curie, la constante dieléctrica disminuye
hasta un nivel mínimo en la dirección polar, ~150. La polarizabilidad en la dirección
perpendicular de desplazamiento del ión Ti(IV) también disminuye al disminuir la
temperatura pero la constante dieléctrica permanece un orden de magnitud mayor que la
correspondiente en la dirección polar. Tal y como ocurre en la transición de Curie, la
polarizabilidad iónica se incrementa en la segunda y en la tercera transición por lo que
se obtienen picos en las gráficas de permitividad frente a la temperatura. En cuanto a los
desplazamientos iónicos, a temperaturas inferiores a la segunda transición, los iones Ti
se desplazan hacia el centro de una de las aristas, y a temperaturas inferiores a la tercera,
estos se desplazan hacia el centro de una de las caras del octaedro. Como consecuencia
de los desplazamientos iónicos se produce un cambio en los parámetros de la celda
unidad. La celda se expande en la dirección que se desplazan los iones Ti(IV) y se
contrae en la dirección perpendicular.
o Influencia del tamaño de grano
Las propiedades eléctricas y microestructurales del BaTiO3, dependen de una serie de
factores como el tamaño de grano, la densidad, las impurezas y los defectos debidos a
las distintas condiciones de síntesis del material. Varios autores muestran como el
tamaño de grano46-50
ó la densidad afecta al valor de la permitividad eléctrica del
material y a la temperatura de transición de fase. En la figura 5.6 se ilustra el diagrama
de fases polimórficas para el BaTiO3 puro (sin dopar) en función del tamaño de grano y
de la temperatura.
46
K. Kinoshita y A. Yamaji, J.Appl. Phys. 47 [1], 371-73 (1976)
47
W. R. Buessem, L. E. Cross y A. K. Goswami, J. Am. Ceram. Soc. 49 [1], 33-36 (1966)
48
G. Arlt, D. Hennings y G. With, J. Apply. Phys. 58 [4], 1619-25 (1985)
49
V. Tura, L. Mitoseriu, C. Papusoi, T. Osaka y M. Okuyama, J. Electroceram. 2 [3], 163-69 (1998)
50
C. A. Randall, R. E. Newnham y L. E. Cross, “History of the First Ferroelectric Óxide: BaTiO3”,
Comunicación Privada](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-60-320.jpg)
![Antecedentes del BaTiO3
- 47 -
Figura 5.6. Diagrama de fases polimórficas para el BaTiO3 puro en función del tamaño cristalino y de la
temperatura. Figura adaptada de la referencia [50].
Mientras que la temperatura de transición tetragonal-cúbica disminuye al
disminuir el tamaño de grano, la temperatura de las otras dos transiciones aumenta. A
temperatura ambiente, el BT adopta la estructura cúbica cuando el tamaño de partícula
es del orden de 25 a 200 nm. Sin embargo, este tamaño crítico depende
considerablemente del método de síntesis utilizado.
5.2. MODELO DE CONDUCCIÓN
El BaTiO3 es un ejemplo de material aislante ya que su conductividad a temperatura
ambiente es del orden de 10-10
Scm-1
y su intervalo de energía prohibido (band gap) es
de 3.0-3.4 eV 51,52
. Según la estructura de bandas del BaTiO3, al aumentar la
temperatura se produce un aumento de energía térmica disponible para la excitación de
electrones y, por tanto, se origina un aumento de la conductividad. Según esto, cabría
esperar que el mecanismo de conducción del BaTiO3 “puro” (sin dopar) fuera
intrínseco.
Parece ser que el BaTiO3 es capaz de perder cierta cantidad de oxígeno cuando
se somete a elevadas temperaturas. Por ello, el defecto químico generado en el BT sin
dopar se ha investigado por medidas de la conductividad eléctrica, σ, en función la
presión parcial de oxígeno, 2
O
P , a temperaturas superiores a 750 ºC.53,54
La gráfica de
log σ frente a log 2
O
P para cerámicas de BT no dopado a temperaturas por debajo de
1000 ºC se ilustran en la figura 5.7. La conductividad es tipo p en el intervalo
51
R. C. Casella y S. P. Keller; Phys. Rev. 116 [6], 1469-73 (1959)
52
M. DiDomenico y S. H. Wemple, Phys. Rev. 166 [2], 565-76 (1968)
53
N.-H. Chan, R. K. Sharma y D. M. Smyth, J. Am. Ceram. Soc. 64 [9], 556-62 (1981)
54
I. J. Clark, F. B. Marques y D. C. Sinclair, J. Eur. Ceram. Soc. 22, 579-83 (2002)
Temperatura/ ºC
T
a
m
a
ñ
o
d
e
g
r
a
n
o
/
μ
m
fase
cúbica
fase
tetragonal
fase
ortorrómbica
fase
romboédrica](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-61-320.jpg)
![Capítulo 5
- 48 -
~10-1
-105
Pa y tipo n por debajo de ~10-1
Pa. La conductividad mínima a 0
2
O
P , que
separa las regiones tipo p y n, se desplaza a mayores valores de PO2 al aumentar la
temperatura y corresponde con la conductividad intrínseca asociada con la ionización
directa de portadores de carga a través del band gap.
Figura 5.7. Representación esquemática de log σ frente a log PO2 para una cerámica de BaTiO3 sin dopar
a diferentes temperaturas. Figura adaptada de la referencia [53].
Muchos autores han asociado el comportamiento tipo p a la presencia de
impurezas en el BaTiO3. Chan y col.
55
han descrito la conductividad de las cerámicas de
BT sin dopar en términos del llamado modelo “extrínseco”, donde el inesperado
comportamiento tipo p por debajo de ~1000 ºC y PO2 10-1
Pa se atribuye a la presencia
de las inevitables impurezas aliovalentes como Fe y Al en las posiciones del Ti. Estas
impurezas aliovalentes, presentes en niveles bajos en reactivos de elevada pureza,
producen vacantes de oxígeno en el retículo del BT y proporcionan un mecanismo fácil
para explicar el comportamiento tipo p observado. Este mecanismo puede escribirse
según la notación de Kröger-Vink (apéndice 4) como:
•
•
O
V + ½ O2
x
O
O + 2h·
[5.1]
donde •
•
O
V , x
O
O y 2h·
representan vacantes de oxígeno, iones de oxígeno y huecos de
electrones, respectivamente.
Basándose en este modelo, las gráficas de log σ frente a log PO2 deberían tener
una pendiente de 1/m (donde m es el exponente) de +1/4 en la región tipo p. Sin
embargo, se detectan un amplio intervalo de valores de m desde +3.45 a +9.09 para
temperaturas entre 700 y 1200 ºC.55
55
N.-H. Chan, R. K. Sharma y D. M. Smyth, J. Am. Ceram. Soc. 65, 167-70 (1981)
l
o
g
σ
/
S
m
-
1
log PO2/ MPa
tipo-n tipo-p
0
2
O
P](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-62-320.jpg)
![Antecedentes del BaTiO3
- 49 -
5.3. MODIFICACIONES COMPOSICIONALES
Se ha establecido que la estabilidad de la estructura perovsquita depende de dos
factores: la diferencia de los radios iónicos de la subred y de la naturaleza del enlace
entre los cationes y aniones, que debe ser fundamentalmente iónica.
En relación con el primer factor, los óxidos ABO3 se consideran como cristales
puramente iónicos. De la geometría de la estructura, se deduce que para la estructura
“ideal” existe la siguiente relación entre los radios de los iones A, B y O2-
:
)
(
2 O
B
O
A r
r
r
r +
=
+ [5.2]
En la práctica, las estructuras perovsquita o sus variantes ligeramente
distorsionadas se encuentran para iones que no siguen exactamente esta relación, de ahí
que se introduzca lo que se denomina factor de tolerancia (t):
)
(
2 O
B
O
A r
r
t
r
r +
=
+ [5.3]
Todos los compuestos con estructura de perovsquita presentan un valor de t
entre 0.88 y 1.09 aproximadamente. Si el valor de t es menor, la estructura sería de
ilmenita. Las distorsiones se pueden explicar teniendo en cuenta la razón de radios de
los iones constituyentes, ya que si dicha razón se encuentra en el límite, se puede dar el
fenómeno conocido como polimorfismo, distorsiones en la estructura o desplazamientos
de los cationes alrededor de sus posiciones de coordinación. Es el caso del BaTiO3, en
el que el catión Ti(IV) se encuentra en un entorno de aniones algo grande en relación a
su tamaño, y por ello, puede moverse o sufrir pequeños desplazamientos dentro del
poliedro como se ha visto anteriormente.
Relacionado con el segundo factor, se establece que a mayor electronegatividad
de los cationes y aniones, mayor ionicidad del enlace, y como consecuencia, mayor
estabilidad de la estructura de la perovsquita.
Debido a que el BaTiO3 es uno de los compuestos más utilizados en la
fabricación de condensadores cerámicos multicapa56
, y con el objetivo de entender el
comportamiento de cada uno de las impurezas que presenta el BaTiO3 comercial, se han
realizado numerosos estudios de posibles disoluciones sólidas con diferentes iones
sustituyentes. Los resultados muestran que es posible modificar/mejorar las propiedades
del BaTiO3, tal como aumentar su permitividad, disminuir las pérdidas y moderar su
dependencia con la temperatura. Sin embargo, el entendimiento de muchas de las
propiedades que aparecen es todavía incierto.
En el retículo del BaTiO3 (ABO3) pueden albergarse un amplio intervalo de
dopantes tanto en la posición del Ba como del Ti. Generalmente, los iones con menor
valencia y mayor radio sustituyen al Ba2+
(sitio A) mientras que los iones con mayor
valencia y menor tamaño tienen afinidad para sustituir al Ti(IV) (sitio B).
Algunos dopantes se utilizan para modificar la temperatura de las transiciones
del BaTiO3. Entre los dopantes isovalentes más utilizados se encuentran el Pb(II), el
56
R. E. Newnham, “Electroceramics”, Rep. Prog. Phys. 52 [2], 123-156 (1989)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-63-320.jpg)
![Capítulo 5
- 50 -
Sr(II), el Ca(II), el Sn(IV), el Hf(IV) y el Zr(IV). Los iones divalentes ocupan las
posiciones A, mientras que los tetravalentes se incorporan en la posición del Ti(IV). En
la figura 5.8 se muestra el efecto producido por estos iones en las distintas temperaturas
de transición del BaTiO3.
Figura 5.8. Comportamiento de las transiciones de fase en función de la composición para diversas
disoluciones sólidas BaTiO3:ABO3. Figura adaptada de la referencia [8].
En general, pequeñas cantidades de estos dopantes modifican el valor de la TC,
produciendo un incremento para el caso del Pb(II) y una disminución para el resto de
iones, a excepción del Ca que no modifica sustancialmente el valor de la TC pero se ha
observado que existe un máximo en la TC para un porcentaje atómico de Ca del 8%.57
Por otra parte, existe una gran variedad de iones aliovalentes que pueden
acomodarse en la red huésped del BaTiO3. En general, forman disoluciones sólidas
parciales y provocan una disminución en la temperatura de Curie y en el valor máximo
de la permitividad. El Y(III), Bi(III) y Cu(III) incrementan el valor de la TC, y el La(III)
disminuye la TC, pero aumenta el valor máximo de la permitividad58
. Otros iones que
disminuyen el valor de la TC, afectan a la anchura del pico de permitividad
ensanchándolo o incluso haciéndolo desaparecer. La sustitución parcial del Ti por Sn,
Zr ó Hf da lugar a la reducción del valor de TC y a la disminución en el valor máximo de
la permitividad al aumentar el contenido de dopante. Por tanto, es posible modular el
57
T. Mitsui y W. B. Westphal, Phys. Rev. 124 [5], 1354-59 (1961)
58
F. D. Morrison, D. C. Sinclair, J. M. S. Shakle y A. R. West, J. Am. Ceram. Soc. 81 [7], 1957-1960
(1998)
% atómico
T
e
m
p
e
r
a
t
u
r
a
/
º
C](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-64-320.jpg)
![Antecedentes del BaTiO3
- 51 -
valor de la TC, ε’max, así como la naturaleza de la transición mediante un dopaje
adecuado.
Las propiedades eléctricas del BT varían considerablemente en función del
dopante. Los dopantes dadores, definidos como aquellos que tienen un carga mayor que
el ión al que sustituyen, por ejemplo, iones lantánidos (La(III), Sm(III), etc.) en la
posición del Ba2+
o pentavalentes (Nb(V), Ta(V), etc.) en la posición del Ti(IV), pueden
dar lugar al comportamiento semiconductor o aislante en función del contenido del
dopante, siendo semiconductor a temperatura ambiente, con contenidos bajos, y aislante
con altos contenidos59,60
. Para el Nb(V), esta transición tiene lugar a ~0.5 % molar. El
Nb ocupa las posiciones del Ti, y como tiene una carga superior a éste, se comporta
como dador. Por cada dos átomos de Nb que se incorporan, hay un átomo de oxígeno en
exceso. Para bajas concentraciones de Nb, este oxígeno se elimina, dejando dos
electrones responsables de la semiconductividad en el BT. Sin embargo, al aumentar el
contenido de Nb, las cerámicas son aislantes y por tanto, este oxígeno queda retenido en
el retículo. En este caso, se proponen varios mecanismos para mantener la
electroneutralidad: (a) creación de vacantes de Ba, (b) creación de vacantes de Ti, (c)
creación del mismo número de vacantes de Ba y de Ti, u (d) oxígenos intersticiales. El
mecanismo de compensación de carga es electrónico para composiciones con x 0.5
sinterizadas en atmósferas reductoras, mientras que el mecanismo más probable para las
muestras con x 0.5 sinterizadas en atmósferas oxidantes, es la creación de vacantes de
titanio61,62
.
Los dopantes aceptores, definidos como aquellos que tienen una carga inferior al
ión que sustituyen, por ejemplo Fe(III) en lugar de Ti(IV), generalmente mantienen la
carga mediante la creación de vacantes de oxígeno, y los materiales resultantes son
electrónicamente aislantes a temperatura ambiente63
. La excepción es el Ti(III); puesto
que el único electrón 3d del Ti(III) entra en la banda de conducción de los átomos de Ti
y el BT resultante es semiconductor.
Las condiciones de procesado son críticas para controlar la microestructura
eléctrica de cerámicas del BT puro y dopado. Las cerámicas de BT de elevada pureza
sinterizadas a 1100 ºC son aislantes, mientras que pierden una pequeña cantidad de
oxígeno a altas temperaturas (T ≥ 1200 ºC) originando un aumento en la
conductividad64
. La reoxidación parcial o completa en el subsiguiente enfriamiento, a
menores temperaturas o mediante enfriamiento lento en aire, puede originar gradientes
en el contenido de oxígeno, y por tanto en el contenido de Ti(III). Por tanto, en
principio, es posible obtener cerámicas totalmente semiconductoras, totalmente aislantes
59
O. Saburi, J. Phys. Soc. Jpn. 14, 1159-74 (1959)
60
M. T. Buscaglia, V. Buscaglia, M. Viviani, P. Nanni y M. Hanuskovs, J. Eur. Ceram. Soc. 20, 1997-
2007 (2000)
61
H. M. Chan, M. P. Harmer y D. M. Smyth, J. Am. Ceram. Soc. 69 [6], 507-10 (1986)
62
N. Masó, H. Beltrán, E. Cordoncillo, A. Arenas Flores, P. Escribano, D. C. Sinclair y A. R. West, J.
Mater. Chem. 16, 3114-19 (2006)
63
N. Masó, H. Beltrán, E. Cordoncillo, P. Escribano y A. R. West, J. Mater. Chem. 16, 1626-33 (2006)
64
H. Beltrán, E. Cordoncillo, P. Escribano, D. C. Sinclair y A. R. West, J. Appl. Phys. 98, 094102-1-7
(2005)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-65-320.jpg)

![Antecedentes del BaTiO3
- 53 -
la producción de condensadores cerámicos multicapa creció anualmente un 15 %,
debido al rápido incremento de la producción de dispositivos electrónicos.
Figura 5.10. Evolución de la producción mundial de CCM. Figura adaptada de la referencia [66].
Las cuestiones más importantes en la fabricación de condensadores, son la
reducción del tamaño de los condensadores cerámicos multicapa (CCM) y el aumento
del valor de la capacidad.
Existen cuatro métodos mediante los cuales la permitividad de un material
cerámico ferroeléctrico se puede maximizar en el intervalo de temperaturas para su uso
como condensador:
Control del punto de Curie mediante la alteración de la composición.
Ensanchamiento del perfil de permitividad mediante el mezclado de una serie
de composiciones las cuales posean puntos de Curie a diferentes temperaturas,
generalmente basados en disoluciones sólidas binarias tal como BaTiO3, SrTiO3,
CaZrO3 y MgTiO3.
Ensalzar la permitividad por debajo del punto de Curie sin alterar el perfil
permitividad-temperatura del pico, mediante la introducción de una fase intergranular,
como por ejemplo composiciones no estequiométricas con una relación BaO/TiO2
diferente a la unidad, y/o mediante el control del tamaño de partícula.
Eliminar el punto de Curie mediante la adición de pequeñas cantidades de
compuestos, como óxido de hierro, debido a la inhibición del crecimiento de grano.
Año
U
n
i
d
a
d
e
s
/
b
i
l
l
ó
n
CCM
Teléfonos móviles
Ordenadores](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-67-320.jpg)
![Capítulo 5
- 54 -
La elevada constante dieléctrica de las cerámicas dieléctricas basadas en el
BaTiO3, hace este material muy atractivo para la fabricación de pequeños
condensadores cerámicos multicapa (CCM) en el intervalo de 1 a 100 nF. Para cumplir
con las especificaciones de los CCM, la dependencia de la constante dieléctrica con la
temperatura debe estar bien controlada, ya que los CCM no pueden mostrar degradación
dieléctrica en el intervalo de temperatura de aplicación. Para reunir estos requisitos, se
añaden habitualmente dopantes como iones lantánidos para controlar la microestructura
y el tamaño de grano, ya que estos pueden reducir la fuerte dependencia de la constante
dieléctrica con la temperatura cerca del punto de Curie67
. En la tabla V.1 se muestran las
características de varios dispositivos CCM, como la constante dieléctrica, el coeficiente
de temperatura de la capacidad y el contenido relativo de BaTiO3 para las diferentes
aplicaciones basadas en las especificaciones de la Electrical Industry Alliance (EIA)68
.
Tabla V.1. Clasificación de los CCM según las especificaciones de la Electrical Industry Alliance (EIA).
Tabla adaptada de la referencia [66].
Designación Intervalo de
temperatura/ ºC
Constante
dieléctrica
Coeficiente de
temperatura/ %
Contenido de
BaTiO3 (% en masa)
NPO -55 ~ 125 ~ 100 ± 30 (ppm) 10 ~ 50
X5R -55 ~ 85 ~ 4000 ± 15 90 ~ 98
X7R -55 ~ 125 ~ 4000 ± 15 90 ~ 98
Z5U -10 ~ 85 ~ 14000 ± 22, -56 80 ~ 90
Y5V -30 ~ 85 ~ 18000 ± 22, -82 80 ~ 90
Habitualmente, el BaTiO3 contenía dopantes dadores y además se requería que
la sinterización se realizara bajo elevada presión de oxígeno. Como consecuencia, las
cerámicas tendían a ser semiconductoras debido a que los dopantes dadores generaban
electrones móviles. Esta fue una cuestión importante ya la sinterización debe hacerse en
contacto con los electrodos metálicos. Por este motivo, hasta 1995 se utilizaron como
electrodos metales nobles de elevada temperatura de fusión, como el Pd, lo que
provocaba un encarecimiento en la fabricación de estos dispositivos. Se estudiaron
diversas posibilidades para reemplazar el Pd por otros electrodos más económicos. Una
de ellas fue utilizar Ni como electrodo69
, utilizando una atmósfera suficientemente
reductora (PO2 10-9
Pa) para evitar la oxidación del Ni, como pueden ser mezclas de
H2 y H2O ó CO y CO2. La sustitución de los electrodos de Pd por Ni supuso una
disminución en el coste de fabricación de los CCM del 50 - 80 %. Para asegurar que las
cerámicas fueran altamente aislantes tras la sinterización, se utilizaron dopantes
67
D. H. Yoon, J. Ceram. Proc. Res. 7 [4], 343-54 (2006)
68
Electrical Industry Alliance (EIA), World Capacitor Trade Statistics (WCTA) (2004)
69
D. F. K. Hennings, J. Eur. Ceram. Soc. 21, 1637-42 (2001)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-68-320.jpg)

![Capítulo 5
- 56 -
resistencia es máxima, Tmax, ya que ésta controla la velocidad en que la resistencia
supera la TC.71
La adición de pequeñas cantidades de elementos de transición como Mn, Cr y
Cu mejora el efecto PTCR. En particular, el Mn ha sido utilizado como uno de los
elementos más efectivos. De hecho, la adición de Mn en los materiales PTCR se
considera habitual para su comercialización.
5.4.3. Dispositivos microondas
Los materiales ferroeléctricos pueden utilizarse en la fabricación de dispositivos
sintonizadores de alta-frecuencia (tunable high-frequency devices). Su principal interés
radica en la posibilidad de miniaturizar los dispositivos y los sistemas de microondas y
su integración en circuitos microelectrónicos mediante la conformación en lámina
delgada.
Los requerimientos de estos materiales son: una elevada capacidad de
modulación (tunability) y bajas pérdidas dieléctricas72
. La modulación es la diferencia
entre la permitividad dieléctrica bajo un campo eléctrico nulo y bajo un campo eléctrico
no nulo. Los materiales más interesantes en estas aplicaciones son las fases
paraeléctricas de los ferroeléctricos, como la disolución BaxSr1-xTiO3, ya que presentan
elevados valores de la permitividad dieléctrica, incluso más allá del punto de Curie. Este
hecho también reduce la sensibilidad de la permitividad a los cambios de temperatura.
Por otra parte, la ausencia de dominios ferroeléctricos ayuda a mantener el bajo nivel de
pérdidas.
5.4.4. Aplicaciones piezoeléctricas
La piezoelectricidad, descubierta por Jacques y Pierre Curie4
en 1880, puede definirse
como la generación de electricidad como resultado de una presión mecánica. Las
cerámicas piezoeléctricas se utilizan en limpiadores de ultrasonidos, timbres eléctricos,
cabezales de impresión por chorro de tinta, controles táctiles, transformadores
piezoeléctricos, etc.
Los materiales policristalinos usualmente no muestran un efecto piezoeléctrico
macroscópico debido a que los ejes piezoeléctricos de los cristales están aleatoriamente
distribuidos y microscópicamente promediados. Esto no es siempre cierto en los
ferroeléctricos. La ferroelectricidad es una propiedad de muchos cristales
piezoeléctricos: la orientación de los ejes ferroeléctricos pueden ser reorientados
mediante la aplicación de un campo eléctrico. En el estado previo a la calcinación de la
cerámica ferroeléctrica, los ejes piezoeléctricos están también orientados al azar. Con la
aplicación de un campo eléctrico intenso, preferiblemente a elevada temperatura, los
71
M. Martínez Gallego y A. R. West, J. Appl. Phys. 90 [1], 394-403 (2001)
72
A. K. Tagantsev, V. O. Sherman, K. F. Astafiev, J. Venkatesh y N. Setter, J. Electroceram. 11, 5-66
(2003)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-70-320.jpg)


![Procedimiento experimental de la síntesis del BaTiO3
- 61 -
6. PROCEDIMIENTO EXPERIMENTAL DE LA
SÍNTESIS DEL BaTiO3
6.1. ESTUDIO PREVIO
La síntesis de las cerámicas de BaTiO3 se realizó mediante el método sol-gel a partir del
acetato de bario y el isopropóxido de titanio (IV). Se eligió el acetato de bario porque es
más barato que los alcóxidos de bario y, además, debido a su baja sensibilidad a la
humedad, no presenta dificultad en su manipulación en atmósfera de aire, a diferencia
de lo que ocurre con los alcóxidos de bario, que necesitan manipularse en atmósfera de
nitrógeno. Por otra parte, como precursor de Ti se utilizó el isopropóxido de titanio
(IV).
A pesar de que existen diferentes rutas sintéticas descritas en la bibliografía73-78
para la síntesis de BaTiO3 a partir del acetato de bario y del alcóxido de titanio (IV), en
la mayoría de los casos, no se especifica la homogeneidad de los geles obtenidos,
aspecto importante a la hora de estudiar las propiedades del producto obtenido. Otra
desventaja añadida es que los procesos requieren muchos pasos. Por ello, nuestro grupo
de investigación buscó una ruta alternativa intentando realizar el proceso a temperatura
ambiente79,80
. A continuación, se detallarán de manera resumida los principales estudios
realizados y la ruta de síntesis que se diseñó para este material cerámico.
En primer lugar, se estudiaron diversas relaciones de agua: ácido acético:
metanol para disolver el acetato de bario, analizándose posteriormente el resultado de la
adición de éstas en los procesos de hidrólisis/condensación del isopropóxido de
titanio (IV) [Ti(OPri
)4].
El acetato de bario se disolvió en agua utilizándose una relación inicial
ligeramente superior a la de su solubilidad en agua a 25 ºC [0.75 g Ba(CH3COO)2 / mL
H2O; relación molar Ba:H2O = 1:20]. Posteriormente, se añadió el metanol apareciendo
un precipitado de acetato de bario debido a la disminución de la solubilidad de éste en la
mezcla agua/metanol. Por último, se redisolvió el precipitado con ácido acético glaciar.
En la tabla VI.1 se muestran los resultados, en moles de reactivo por mol de acetato de
bario, de los diferentes ensayos realizados.
73
P. P. Phule y S. H. Risbud, Mater. Sci. Engg. B3 [3], 241-247 (1989)
74
P. P. Phule y S. H. Risbud, J. Mater. Sci. 25 [2], 1169-83 (1990)
75
U.Y. Hwang, H.S. Park y K.K. Koo, Ind. Eng. Chem. Res. 43, 728-34 (2004)
76
A. Mosset, I. Gautier-Luneau, J. Galy, P. Strehlow y H. Schmidt, J. Non-Cryst. Solids, 100 [1-3], 339-
44 (1988)
77
H. B. Sharma, R. P. Tandon, A. Mansingh y R. Rup, J. Mater. Sci. Lett. 12, 1795-96 (1993)
78
O. A. Harizanov, Mater. Lett. 34, 345-50 (1998)
79
Nahum Masó i Carcasés, Tesis Doctoral (2006)
80
H. Beltrán, E. Cordoncillo y P. Escribano, J. Am. Ceram. Soc. 87 [11], 2132-2134 (2004)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-73-320.jpg)

![Procedimiento experimental de la síntesis del BaTiO3
- 63 -
pico, lo que excluye una coordinación octaédrica en el Ti. La intensidad de estos picos
muestra que la acac se coordina al Ti, que incrementa su coordinación a 5. Los datos de
EXAFS (Extended X-ray Absorption Fine Structure) mostraban la no existencia de
enlaces Ti-Ti. Además, se observaban dos distancias Ti-O con una relación de
intensidad 3:2 correspondientes a los ligandos OPri
y acac enlazados al Ti, respectiva-
mente. Por tanto, la reacción que se produce conduce a la formación de un precursor
quelato Ti(OPri
)3acac de la siguiente manera:
[6.1]
Una mezcla 2:1 de Ti(OPri
)3:acacH conduce a la formación de un precursor
diquelato con una coordinación octaédrica:
[6.2]
La adición de agua al precursor Ti(OPri
)3acac conduce a la formación de
ligandos OPri
hidrolizados. Tal y como se comprueba por IR82
cuando el número de
moléculas de agua es mayor de 3, las bandas correspondientes a los enlaces Ti—O—Pri
desaparecen completamente, apareciendo otras asociadas a la presencia de acac libre.
Las bandas correspondientes a los enlaces dobles acac-Ti siguen apareciendo, incluso
Ti(OPr
i)4 + acac Pr
i-O-Ti-O- Pr
i
O O
C C
C
HCH HCH
H
OPr
i
+ Pr
iOH
H
H
H
Ti(OPr
i)
4 + 2acac Pr
i-O-Ti-O- Pr
i
O O
C C
C
HCH HCH
H
+ 2Pr
iOH
O
O
C
C
C HCH
HCH H
H
H
H
H
H](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-75-320.jpg)

![Procedimiento experimental de la síntesis del BaTiO3
- 65 -
Tabla VI.2. Estudio de los procesos de hidrólisis/condensación del isopropóxido de titanio y
características de los geles obtenidos.
Ref. H2O : CH3OH : CH3COOH Ti(OPr
i
)4 : acacH Características
2a 0 : 40 : 105 1 : 0 * Precipitado
2b 21 : 40: 7.5 1 : 1/8 Gel transparente a las 48h
2c 21 : 20 : 4.5 1 : 1/8 Precipitan especies oxo/hidroxo de Ti
2d 42 : 40 : 2.7 1 : 1/8 Precipitan especies oxo/hidroxo de Ti
* La hidrólisis se lleva a cabo mediante un exceso de agua.
En las condiciones experimentales de Ti(OPri
)4 : acacH fijadas, la única mezcla a
partir de la cual se obtuvo un gel homogéneo es aquella en que la relación agua/metanol
es ~0.5 (disolución referenciada como 2b). En las otras mezclas ensayadas, relación
agua: metanol ~1, la cantidad de 2, 4-pentanodiona añadida no fue suficiente para evitar
la precipitación de especies oxo/hidroxo de titanio. Considerando que se obtuvo un gel
transparente mediante la relación referenciada como 2b, ésta se eligió como punto de
partida para la síntesis de los diversos materiales objeto de estudio.
6.2. PROCEDIMIENTO EXPERIMENTAL
Las muestras de BaTiO3 se prepararon siguiendo el procedimiento experimental
mostrado en la figura 6.2, utilizando como reactivos: acetato de bario [Ba(CH3COO)2
99%, Strem Chemicals], isopropóxido de titanio [Ti(OPri
)4 98% (2% isopropanol)
Strem Chemicals], metanol [CH3OH 99%, Probus], ácido acético glaciar [CH3COOH
99-100%, J. B. Baker] y 2, 4-pentanodiona [CH3COCH2COCH3, acacH, 99.5%,
Panreac] y siendo las relaciones molares Ba : H2O : CH3OH y Ti : acacH de 1:21:40 y
1:8 respectivamente. En primer lugar, se disolvió el acetato de bario utilizando las
relaciones molares Ba:H2O:CH3OH:CH3COOH indicadas anteriormente.
Posteriormente, esta disolución se añadió a la del Ti(OPri
)4 con acacH, formándose una
disolución transparente (sol) de color amarillento.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-77-320.jpg)



![BaTiO3 dopado con Mg
- 71 -
7. BaTiO3 DOPADO Mg
7.1. INTRODUCCIÓN
Como se ha comentado con anterioridad, las propiedades eléctricas del BaTiO3 pueden
ser modificadas por la adición de diferentes dopantes, dando lugar a una gran variedad
de aplicaciones. De entre estos dopantes, aquellos con menor carga que el Ti(IV)
(dopantes aceptores) como Mg(II), Zn(II), Mn(III), sustituyen al Ti(IV) en el retículo
del BaTiO3 siendo el mecanismo de compensación de carga más usual, la creación de
una cantidad estequiométrica de vacantes de oxígeno.
El óxido de magnesio ha sido ampliamente utilizado como aditivo en los
condensadores cerámicos multicapa (CCM). Particularmente, el MgO junto con óxidos
de iones lantánidos mejora la estabilidad térmica de estos condensadores. El óxido de
magnesio se usa generalmente para conseguir las características del condensador X7R
(X7R: variación del valor de la constante dieléctrica a 25 ºC inferior al 15% en el
intervalo de temperatura de -55 a 155 ºC) con una estructura en capas (core-shell),
proporcionar cerámicas donde las condiciones reductoras no modifiquen las
propiedades y evitar el crecimiento de grano.83-86
Atendiendo a los radios iónicos en coordinación octaédrica, el Mg2+
(86 pm)87
puede sustituir al Ti4+
(74.5 pm), generando vacantes de oxígeno cargadas positivamente
para mantener la electroneutralidad; utilizando la notación de Kröger-Vink (apéndice 4),
tendríamos:
BaO + MgO BaBa + Mg’’
Ti + 2OO + V··
O [7.1]
Varios autores determinaron que, según la variación en la temperatura de Curie y
las medidas de conductividad eléctrica, el límite de la disolución sólida
BaTi1-xMgxO3-x es ~1 % molar de Mg a 1320 ºC 88
. Según otros autores89,90
, el límite de
solubilidad se encontraría entre el 1-2 % molar, siendo la variación en la temperatura de
Curie del BaTiO3 de ~ 50 ºC para un contenido en Mg del 2 % molar, indicando que la
tetragonalidad del BaTiO3 disminuye al aumentar el contenido de Mg.
Estudios estructurales mostraron que el Mg actúa como un inhibidor del
crecimiento de grano en el BT, favoreciendo un tamaño de partícula pequeño y una alta
densidad 85,91
. Según Li y col.92
la densidad aparente de las cerámicas sinterizadas en N2
83
Y. Sakabe, Am. Ceram Soc.Bull. 66, 1338-41 (1987)
84
H. Saito, H. Chazono, H. Kishi y N. Yamaoka, Jpn. J. Appl. Phys. 30, 2307-2310 (1991)
85
H. Kishi, N. Kohzu, J. Sugino, H. Ohsato, Y. Iguchi y T. Okuda, J. Eur. Ceram. Soc. 19, 1043-6 (1999)
86
J. H. Hwang, S. K. Choi y Y. Han, Jpn. J. Appl. Phys. 40, 4952-5 (2001)
87
R. D. Shannon, Acta Crystallogr. A32, 751-67 (1976)
88
J. Jeong y Y. H. Han, Phys. Chem. Chem. Phys. 5, 2264-7 (2003)
89
Los resultados de S. Waku (1962) se citan en la referencia: K Okazaki, Ceramic Engineering for
Dielectrics, 4th ed.; p. 281. Gakken-sha Publishing Co., Ltd., Tokio, Japan, 1992.
90
T. Nagai, K. Iijima, H. J. Hwang, M. Sando, T. Sekino y K. Niihara, J. Am. Ceram. Soc. 83 [1], 107-12
(2000)
91
H. Miao, M. Dong, G. Tan y Y. Pu, J. Electroceram. 16, 297-300 (2006)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-81-320.jpg)

![BaTiO3 dopado con Mg
- 73 -
Además, determinaron que la energía de activación (Ea) a bajas temperaturas
(~ 0.5 eV) es la requerida para el movimiento de las vacantes de oxígeno sin la
disociación del complejo y la Ea a altas temperaturas es mayor (~ 1.1 eV),
correspondiendo a la energía necesaria para la migración de las vacantes de oxígeno a
largo alcance y a la disociación de los complejos. La diferencia en las energía de
activación se atribuye a la energía extra requerida para la disociación del complejo
MgTi
’’
-VO
··
ó MnTi
’
-VO
··
. Posteriormente, Hahn y col.98
estudiaron la evolución de la
capacitancia con el tiempo tras la aplicación de un voltaje dc en BT dopado con Mn y
Mg. La capacitancia disminuye inmediatamente en un corto periodo de tiempo, y en una
segunda etapa, decrece continuamente con el tiempo. Según los autores, la disminución
de la capacitancia en la primera etapa es dependiente del tamaño de grano, mientras que
el cambio en la capacitancia en la segunda etapa está afectado principalmente por la
concentración de los complejos (MgTi
’’
-VO
··
) que eliminan el movimiento de las barreras
de dominio.
Jeong y col.88
, determinaron que la conductividad eléctrica del BaTiO3 dopado
con Mg en función de la P(O2) a diferentes temperaturas de sinterización presenta dos
zonas diferenciadas: la región de conducción tipo n a bajas P(O2), donde la
conductividad aumenta al disminuir la P(O2), y la región de conducción tipo p a altas
P(O2), donde la conductividad aumenta al aumentar la P(O2). Para las muestras dopadas
con Mg, determinaron que la conductividad en la región n disminuye al aumentar el
contenido de Mg, mientras que aumenta en la región de conducción p. Parece ser que
las vacantes del oxígeno extrínsecas, retardan la reacción de reducción a bajas P(O2),
mientras que facilitan la oxidación a altas P(O2).
Yoon y col.99-102
estudiaron las propiedades eléctricas del BT dopado con Mg,
mostrando que las muestras sinterizadas en aire eran aislantes, mientras que las
sinterizadas en atmósfera reductora eran semiconductoras a temperatura ambiente. La
espectroscopia de impedancia del BT dopado con Mg, muestra dos componentes
eléctricos: interior de grano (bulk) y frontera. Según las gráficas de Arrhenius mostradas
la conductividad del bulk aumenta sistemáticamente con el aumento del contenido de
Mg, mientras el cambio no es tan acusado para la frontera de grano. Según los autores,
la electromigración de las vacantes cargadas tras la aplicación de un voltaje dc es la
responsable de la degradación eléctrica en estas cerámicas.
Teniendo en cuenta que estos últimos trabajos publicados son bastante
recientes 102-106
, que hay bastantes discrepancias entre ellos, y que este trabajo se inició
con anterioridad, el objetivo que nos planteamos fue estudiar el efecto del dopado con
pequeñas cantidades de magnesio en los diferentes polimorfos del BaTiO3 y la
construcción del diagrama de fases parcial para este sistema, así como analizar la
respuesta eléctrica de las disoluciones sólidas formadas que presentaban el polimorfo
98
D. W. Hahn, J. O. Hong y Y. H. Han, Jpn. J. Appl. Phys. 47 [7], 5526-9 (2008)
99
S. Yoon, M. Hong, J. Hong, Y. Kim y K. Hur, J. Appl. Phys. 102, 054105-11-8 (2007)
100
S. Yoon, C. A. Randall y K. Hur, J. Am. Ceram. Soc. 92 [8], 1758-65 (2009)
101
S. Yoon, C. A. Randall y K. Hur, J. Am. Ceram. Soc. 92 [8], 1766-72 (2009)
102
S. Yoon, C. A. Randall y K. Hur, J. Am. Ceram. Soc. 92 [12], 2944-52 (2009)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-83-320.jpg)
![Capítulo 7
- 74 -
tetragonal/cúbico únicamente. Con ese propósito se procedió a la síntesis mediante
metodología sol-gel de composiciones en el sistema BaTi1-xMgxO3-x donde
0.00003 ≤ x ≤ 0.1.
7.2. PROCEDIMIENTO EXPERIMENTAL
Se prepararon diferentes composiciones de la disolución sólida BaTi1-xMgxO3-x
realizando una pequeña modificación en la metodología sol-gel desarrollada en el
apartado 6.2.
Para preparar las muestras de BaTi1-xMgxO3-x, se utilizó el acetato de magnesio
[Mg(CH3COO)2 100%, Strem Chemicals] como precursor de Mg. Éste se añadió a la
disolución del acetato de bario en agua, obteniéndose una disolución transparente. A
continuación se añadió el MeOH y posteriormente, para redisolver el acetato se añadió
el ácido acético, siendo las relaciones molares de Ba:H2O:CH3OH:CH3COOH las
indicadas anteriormente. Para las composiciones más diluidas, se preparó una
disolución de acetato de magnesio 0.0183 mg/mL en metanol y se añadieron alícuotas
de ésta sobre la disolución del acetato de bario en agua.
Finalmente la disolución del acetato de bario y acetato de magnesio, se añadió
gota a gota a la disolución del isopropóxido de titanio, la cual se preparó previamente
utilizando las relaciones Ti(OPri
)4:acacH establecidas. La disolución transparente
resultante (sol) fue de color amarillento. Las composiciones preparadas se resumen en la
tabla VII.1.
Tabla VII.1. Composiciones preparadas en la disolución sólida BaTi1-xMgxO3-x.
x Composición
0 BaTiO3
0.00003 BaTi0.99997Mg0.00003O2.99997
0.0003 BaTi0.9997Mg0.0003O2.9997
0.003 BaTi0.997Mg0.003O2.997
0.005 BaTi0.995Mg0.005O2.995
0.01 BaTi0.99Mg0.01O2.99
0.015 BaTi0.985Mg0.015O2.985
0.02 BaTi0.98Mg0.02O2.98
0.03 BaTi0.97Mg0.03O2.97
0.04 BaTi0.96Mg0.04O2.96
0.06 BaTi0.94Mg0.06O2.94
0.1 BaTi0.9Mg0.1O2.9](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-84-320.jpg)

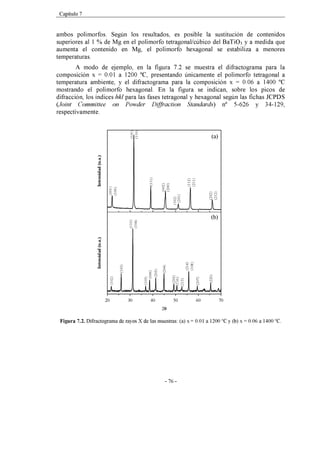
![BaTiO3 dopado con Mg
- 77 -
x en BaTi
1-x
Mg
x
O
3-x
0.000 0.002 0.004 0.006 0.008 0.010
p
a
r
á
m
e
t
r
o
s
d
e
c
e
l
d
a
/
3.99
4.00
4.01
4.02
4.03
4.04
x en BaTi
1-x
Mg
x
O
3-x
0.000 0.002 0.004 0.006 0.008 0.010
V
/
Å
3
64.15
64.20
64.25
64.30
64.35
64.40
7.3.2. Estudio de las composiciones 0 ≤ x ≤ 0.01 en el sistema
BaTi1-xMgxO3-x
Todas las composiciones fueron caracterizadas estructural y microestructuralmente,
estudiando las propiedades eléctricas de aquellas composiciones sinterizadas a 1300 ºC
y 1400 ºC que presentaron polimorfo tetragonal/cúbico, concretamente 0 ≤ x ≤ 0.01.
7.3.2.1. Difracción de rayos X y microscopía electrónica de barrido
Todas las muestras sinterizadas a 1300 ºC y 1400 ºC y enfriadas lentamente en el horno,
fueron fase única BaTiO3 por DRX. A partir de los difractogramas, y mediante una
rutina de minimización por mínimos cuadrados, se obtuvieron los parámetros de celda
que se muestran en la figura 7.3. Como puede observarse, el parámetro a aumenta y el
parámetro c disminuye ligeramente, al igual que el volumen de la celda, es decir, la
tetragonalidad disminuye al aumentar x.
Figura 7.3. Parámetros de celda de la disolución sólida cúbico/tetragonal del sistema BaTi1-xMgxO3-x.
Debido a que el valor de la densidad puede influir en las propiedades finales del
material, se calculó la densidad relativa de las pastillas a partir de la geometría de ésta y
de la densidad teórica, utilizando las ecuaciones [A3.1]-[A3.3] (ver apéndice 3). Las
densidades fueron ~ 65 y ~ 90 % a las temperaturas de sinterización de 1300 y 1400 ºC
para todas las muestras, respectivamente.
Por otra parte, se llevó a cabo un estudio microestructural mediante microscopía
electrónica de barrido (MEB) con el fin de observar si existen heterogeneidades
composicionales no detectadas a partir de los difractogramas de rayos X. Se analizaron
las muestras con 0.003 ≤ x ≤ 0.01 sinterizadas a 1400 ºC y enfriadas lentamente en el
horno. La micrografía para la composición x = 0.01 se muestra en la figura 7.4.
a
c
Å](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-87-320.jpg)






![Capítulo 7
- 84 -
Figura 7.10. Gráfica espectroscópica de Z”/M” a 442 ºC para la muestra x = 0.01 sinterizada a 1400 ºC
(mismos datos que figura 7.9)
Algunos datos se presentan en forma de gráficas espectroscópicas en escala
logarítmica de la capacidad, C’, figura 7.11. Estos demuestran claramente la presencia
de una meseta independiente de la frecuencia a altas frecuencias y T ≤ 393 ºC, atribuido
al bulk de la muestra, C1, que es dependiente de la temperatura y presenta datos de
capacidad consistentes con los de la figura 7.7.a. A bajas frecuencias y temperaturas
101 ºC, aparece otra meseta con capacidades de ~ (3-5) x 10-9
F. Tal valor de
capacidad, a menudo seria considerado como demasiado alto para una frontera de grano,
pero dado que la permitividad para estos materiales es mayor que la de los dieléctricos
normales, esta segunda capacidad, C2, puede atribuirse a una frontera de grano
convencional. A mayores temperaturas y menores frecuencias, figura 7.11.b, la
capacidad alcanza valores de 10-6
-10-7
F y se asocia a la presencia de una superficie
delgada en la muestra o, más probablemente, a una interfase muestra-electrodo103
. Esta
capacidad corresponde con el efecto adicional de baja frecuencia observado en la figura
7.9.b, y tiene una resistencia asociada relativamente pequeña. El circuito equivalente
usado, idealmente, para ajustar los datos de impedancia se muestra en la figura 7.11.c.
Todas las composiciones tuvieron una respuesta eléctrica semejante.
103
D. C. Sinclair y A. R. West, J. Appl. Phys. 66 [8], 3850-6 (1989)
f / Hz
102 103 104 105 106 107
Z
'
'
/
k
Ω
c
m
-40
-30
-20
-10
0
1
0
-
1
0
M
e0
-
1
/
F
-
1
c
m
0.0
0.5
1.0
1.5
2.0
f / Hz
10
5
10
6
10
7
Z
'
'
/
Ω
c
m
-350
-300
-250
-200
-150
f / Hz
10
2
10
3
10
4
10
5
1
0
-
8
M
e0
-
1
/
F
-
1
c
m
0.0
0.5
1.0
1.5
2.0](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-94-320.jpg)




![BaTiO3 dopado con Mg
- 89 -
dc bias aplicado. En la figura 7.16.a se muestra el elemento de alta frecuencia, R1, en la
representación del plano complejo de la impedancia para la muestra x = 0.01 sin voltaje
aplicado y tras la aplicación de un voltaje dc de 10V a distintos periodos de tiempo. Los
resultados muestran que el valor de R1 disminuye gradualmente antes de alcanzar un
estado estacionario después de varias horas tras la aplicación del voltaje. A mayores
temperaturas de medida, como 343 ºC, R1 alcanza el estado estacionario en tan solo
unos minutos.
Figura 7.16. (a) Plano complejo de la impedancia, Z*, a 242 ºC para la muestra x = 0.01 antes y después
de aplicar 10V [166.67 Vcm-1
] a diferentes tiempos; (b) gráfica espectroscópica de M”
(mismos datos que en (a)); (c) gráfica espectroscópica de M” para la muestra en el estado
excitado (10V) y a dos tiempos, t1 y t2, después de eliminar el voltaje dc bias*
.
*
En las figuras se expresan los datos en forma de Vcm-1
ya que el grosor de las cerámicas es una variable
importante a tener en cuenta.
f / Hz
101
102
103
104
105
106
107
1
0
-
9
M
e0
-
1
/
F
-
1
c
m
0.0
2.5
5.0
7.5
0V
10V 30min
10V 100min
10V 205min
Z' / kΩcm
0 20 40 60
Z
'
'
/
k
Ω
c
m
-60
-40
-20
0
(a)
R1
(b)
f / Hz
10
2 10
3 10
4 10
5 10
6 10
7
1
0
-
9
M
e0
-
1
/
F
-
1
c
m
0.0
2.5
5.0
7.5
(c)
166.67
V/cm
0 V/cm
t1
0 V/cm
t2
1
0
V
3
0
m
in
1
0
V
1
0
0
m
in
1
0
V
2
0
5
m
in
0
V](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-99-320.jpg)

![BaTiO3 dopado con Mg
- 91 -
verse, R1 y R2 no disminuyen tras la aplicación de 10 V durante varias horas, resultado
muy diferente al observado anteriormente (un estudio más detallado se presenta en el
capítulo 10). Por lo tanto, el dopaje con magnesio parece ser la clave del aumento de la
conductividad del bulk al aplicar un voltaje.
Figura 7.17. (a) Plano complejo de la impedancia, Z*, y (b) gráfica espectroscópica de M” a 472 ºC para
la muestra con x = 0 antes y después de aplicar 10V [67 Vcm-1
] durante 8 horas.
Para profundizar en el fenómeno del aumento de la conductividad con el voltaje,
se realizaron varios experimentos. Se realizó inicialmente un estudio cinético del
proceso, midiendo la conductividad del bulk, σ1, en función del tiempo tras la aplicación
de diferentes voltajes para la muestra x = 0.01. En cada caso, σ1 aumenta con el tiempo
hasta un valor aproximadamente constante, siendo el estado final más conductor al
aumentar el voltaje aplicado, figura 7.18.a. Estos valores de conductividad estacionarios
se representan en función del voltaje dc en la figura 7.18.b. Entre 0 y ~ 40 Vcm-1
, σ1
aumenta un factor de ~ 40, llegando a saturarse y aumentando ligeramente por encima
de 50 Vcm-1
.
f / Hz
102 103 104 105 106 107
1
0
-
1
0
M
e0
-
1
/
F
-
1
c
m
0.0
0.5
1.0
1.5
0 V
10 V
Z
'
'
/
k
Ω
c
m
-150
-100
-50
0
Z' / kΩcm
0 100 200 300 400
Z
'
'
/
k
Ω
c
m
-400
-300
-200
-100
0
0 V
10 V
Z' / kΩcm
0 5 10
Z
''/k
Ω
c
m
-10
-5
0
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-101-320.jpg)
![Capítulo 7
- 92 -
Figura 7.18. (a) Conductividad del bulk (σ1) en función del tiempo después de aplicar voltajes de 0.3, 0.7
y 1.2 V [5.3, 12.3 y 21.1 Vcm-1
] a 374 ºC y (b) conductividad estacionaria del bulk en
función del voltaje dc bias aplicado a 374 ºC para la muestra x = 0.01.
Para determinar el aumento de la conductividad en función de la temperatura, se
representaron los datos en forma de gráficas de Arrhenius para la conductividad del bulk
en ausencia de dc bias (0V) y bajo un voltaje dc bias de 10V, tras la estabilización del
valor de la conductividad, figura 7.19. El efecto del voltaje fue el aumento de la
conductividad 1 ó 2 órdenes de magnitud en un amplio intervalo de temperaturas, ~140
a 440 ºC. Todas las muestras de composiciones 0.00003 ≤ x ≤ 0.01 mostraron un
aumento similar en σ1 tras la aplicación del dc bias. Como ejemplo, se muestran los
datos de conductividad en forma de gráficas de Arrhenius para las muestras con
x = 0.01 y x = 0.003.
Figura 7.19. Gráficas de Arrhenius de σ1 para las muestras x = 0.01 (a) y x = 0.003 (b) medidas sin
voltaje aplicado y con un voltaje dc de 10V [175.4 y 107.5 Vcm-1
, respectivamente] después
de alcanzarse el estado estacionario.
1000 K/T
1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8
l
o
g
σ
1
/
S
c
m
-
1
-7
-6
-5
-4
-3
-2
1000 K/T
1.2 1.6 2.0 2.4 2.8
l
o
g
σ
1
/
S
c
m
-
1
-6
-5
-4
-3
-2
-1
(a) x = 0.01 x = 0.003 (b)
10V
0V
10V
0V](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-102-320.jpg)




![BaTiO3 dopado con Mg
- 97 -
oxígeno97
. Sin embargo, como este proceso es ac o es un proceso local por saltos, no
puede ser atribuido a la conducción de largo alcance observada y representada por R1.
Finalmente se concluye que la conductividad está dominada por el movimiento
de especies electrónicas. Si la disociación/reorientación dipolar ocurre, no contribuye de
forma importante en la conductividad. Si la conducción de iones óxido tuviese lugar,
sería un proceso de conducción minoritario y no el responsable de las conductividades
medidas.
Los resultados de impedancia con diferentes atmósferas durante la medida,
muestran para ambos estados, el excitado y el fundamental, un mecanismo de
conducción tipo p. Los resultados mostrados en este capítulo muestran una dependencia
cualitativa de la conductividad con la atmósfera, a relativamente bajas temperaturas,
bajo condiciones que no representan el equilibrio con la atmósfera, pero sin embargo,
indican la naturaleza del portador de carga en estas muestras.
Existen en la bibliografía numerosos trabajos en los que se determina el
mecanismo responsable de la conductividad en el BT estequiométrico, siendo, al igual
que en nuestro caso, tipo p. En estos se concluye que la presencia inevitable de dopantes
aceptores como Fe(III) son los responsables de la conductividad tipo p
104
. Por el
contrario, está bien establecido que, bajo condiciones reductoras que conducen a la
pérdida de oxígeno, la conducción del BT es tipo n, y a partir de medidas de
conductividad en función de la presión parcial de oxígeno, la transición de tipo p a tipo
n tiene lugar al aumentar la reducción.
Los resultados obtenidos muestran un aumento sistemático en la conductividad
tipo p al aumentar x, que descarta la posibilidad de que las impurezas de Fe asociadas a
los reactivos sean las responsables. Se necesita una explicación alternativa para el
comportamiento tipo p. Ninguno de los componentes de estas muestras puede ser
oxidado originando huecos. La única fuente de huecos es el ión O2-
. El ión O2-
resultante
se estabiliza en el estado sólido sólo como consecuencia de la energía reticular extra
asociada con los iones óxido doblemente cargados; el ión óxido es termodinámicamente
inestable en fase gas como resultado de la segunda afinidad electrónica para la reacción
O-
+ e-
O2-
, que es positiva. Es interesante considerar bajo qué condiciones un ión O2-
puede desestabilizarse en el retículo cristalino y como consecuencia se ionice fácilmente
para dar el ión O-
.
En las muestras de BaTiO3 dopadas con Mg, los iones Mg(II) están rodeados por
cinco iones O2-
(asumiendo cargas iónicas ideales) y una vacante de oxígeno, figura
7.23. Los cinco iones óxidos adyacentes (O2) están débilmente enlazados como
consecuencia de la carga del Mg2+
, dos veces menor que el Ti(IV); bajo condiciones
adecuadas, estos iones O2-
pueden ionizarse según:
O2-
O-
+ e [7.2]
Los iones O-
resultantes constituyen la fuente de portadores de carga tipo p
(huecos) y los electrones liberados probablemente ocupen los orbitales 3d del Ti.
104
D. M. Smyth, en The Defect Chemistry of Metal Oxides, Oxford University Press, Ic. New Cork, 2000](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-107-320.jpg)

![BaTiO3 dopado con Mg
- 99 -
Es interesante considerar la relación entre el aumento de la conductividad del
bulk observada en este estudio y los fenómenos de degradación, típicamente observados
a voltajes elevados 105-107
. En nuestros resultados, las conductividades aumentan hasta
un estado estacionario al aumentar el voltaje y no son una respuesta previa a la ruptura
dieléctrica, ya que, estos ocurren a voltajes mayores. Además, la ruptura dieléctrica se
asocia normalmente a la movilidad de las vacantes de oxígeno 105,107
. En este caso, el
proceso tiene lugar a voltajes bajos, y las especies conductoras son electrónicas. No se
excluye la posibilidad de la conducción de vacantes de oxígeno, pero éstas no son los
principales portadores de carga en nuestras condiciones experimentales. La conducción
del ión óxido parece ser significativa a bajas presiones parciales de oxígeno en la región
del mínimo de la conductividad cuanto el mecanismo de conducción cambia de tipo p a
tipo n
106
. En BT puro y dopado con cationes aceptores53,55,108
, este cambio suele ocurrir
en la región de 10-5
a 10-10
atm de O2, que es varios órdenes de magnitud menor que las
medidas en aire presentadas en este trabajo. Se anticipa que, al aumentar la reducción, la
conductividad de las muestras puede que se reduzca a un mínimo, en cuyo punto la
conducción de los iones óxido puede llegar a ser significativa; en mayor reducción,
asociada con la pérdida de oxígeno, la conductividad puede que aumente otra vez
debido a la conducción tipo n.
Una cuestión importante a considerar es porqué este efecto no se ha visto
previamente, en otros materiales, ya que es común estudiar la dependencia con el dc
bias de las propiedades eléctricas con el fin de identificar fenómenos interfaciales como
barreras de Schottky. Claramente, el material necesita un defecto en la estructura que
permita un estado excitado accesible, altamente conductor y estable, además del estado
fundamental. Como hemos visto, el efecto no se observa en BaTiO3 puro, mientras que
si que se observa en el BT dopado con Mg, como consecuencia de la estructura
defectuosa, altamente polarizada, que se genera. O simplemente que las medidas bajo
un dc bias no se hayan realizado a temperaturas lo suficientemente altas como para
apreciar el efecto. Teniendo en cuenta que no hay efecto en el BaTiO3 puro, la
estructura defectuosa en el BT dopado con Mg parece ser la causa principal del efecto
no lineal y en particular, se requiere que la electroneutralidad local conduzca a una
transferencia de carga interna. Estas consideraciones sugieren que el nuevo fenómeno
de la variación no lineal de la resistencia, puede observarse en BaTiO3 conteniendo
otros dopantes aceptores (menor valencia). Puede predecirse también que la diferencia
de la conductividad entre el estado fundamental y el excitado en muestras gruesas
(~ 1mm) puede aumentarse significativamente en lámina delgada originando tiempos de
excitación-desexcitación enormemente menores y como consecuencia, la posible
aplicación en dispositivos de memoria.
Se prevén que efectos similares asociados con el aumento de la conducción tipo
p pueden ser observados en otros materiales dopados con cationes aceptores. El dopaje
aceptor no es un mecanismo que se considera normalmente como un medio de aumento
105
R. Waser, T. Baiatu y K. H. Härdtl, J. Am. Ceram. Soc.73 [6], 1645-53 (1990)
106
R. Waser, T. Baiatu y K. H. Härdtl, J. Am. Ceram. Soc. 73 [6], 1654-62 (1990)
107
T. Baiatu, R. Waser y K. H. Härdtl, J. Am. Ceram. Soc. 73 [6], 1663-73 (1990)
108
N. H. Chan y D. M. Smyth, J. Electrochem. Soc. 123, 1584-5 (1976)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-109-320.jpg)
![Capítulo 7
- 100 -
de la conductividad; es más, dopantes aceptores como el Mg(II) se usan habitualmente
para aumentar la degradación de la resistencia y la estabilidad a altos voltajes100-102
. Sin
embargo, el mecanismo de conducción más considerado es el tipo n y se asocia con
dopantes dadores.
Si comparamos los resultados obtenidos aquí con los esperables para efectos
varistores y memristores, observamos, en primer lugar, que la variación no lineal de la
resistencia se asocia a la frontera de grano y, muy importante, al bulk. Es un efecto de
todo el material y no es un fenómeno interfacial. Además, el cambio en la conductividad
al aplicar y eliminar el voltaje indica que pueden ocurrir cambios significantes en la
estructura electrónica, con una barrera de activación para la aplicación de un dc bias y la
consecuente eliminación. Las características son totalmente diferentes a los cambios
rápidos interfaciales que ocurren, por ejemplo, en los varistores basados en ZnO.
Consecuentemente, no es un efecto varistor. Es independiente del material del
electrodo: se obtuvieron resultados similares con electrodos de Au que los mostrados
aquí con electrodos de Pt. Es también independiente de la atmósfera, ya que se obtienen
resultados semejantes en atmósfera de aire, N2 y O2.
El primer ejemplo práctico de memristor19
se basa en el transporte electrónico y
iónico a través de las interfases de nanoestructuras heterogéneas de TiO2. Se trata de un
efecto de lámina delgada ya que el proceso de transporte ocurre en una escala de tiempo
razonable y puede requerir una reacción electroquímica entre Ti(IV) y Ti(III).109
El
cambio de conductividad que resulta es reversible al invertir el voltaje. Cuando el
voltaje cesa, el memristor tiene la capacidad de recordar su resistencia previa hasta que
nuevamente se aplica un voltaje, por lo que en teoría puede ser usado como un
dispositivo de almacenaje. Aunque tiene algunas semejanzas, el mecanismo propuesto
para explicar el fenómeno presentado en este capítulo es diferente al propuesto en el
caso de los memristores.
Existen varios trabajos en la literatura, publicados muy recientemente, basados
en cerámicas de BT dopadas con Mg99-102
, que muestran que la resistencia del BT
dopado con Mg disminuye con el tiempo tras la aplicación de un voltaje dc y que dicha
disminución es mayor al aumentar el contenido en Mg Aunque existen algunas
similitudes con nuestros resultados, hay diferencias en las técnicas experimentales así
como en la interpretación de los resultados. Utilizan un método de síntesis diferente y
sinterizan las muestras bajo condiciones reductoras, con lo cual, no está claro si existe
una distribución homogénea de Mg y/o si existen gradientes de oxígeno en las muestras.
Por otra parte, en estos trabajos se aplican voltajes en el intervalo 1.2 a 12kVcm-1
,
mucho mayores que los utilizados en el presente estudio. La impedancia presentada en
estos trabajos muestran conducción electrónica e iónica, mostrando niveles
considerables de conducción del ión óxido, probablemente debidos a las condiciones
reductoras, conduciendo a las muestras a la región en la que se produce el cambio de
conducción tipo p a tipo n, mientras que en nuestro caso, las muestras fueron
sinterizadas en aire, y su comportamiento fue tipo p. Por lo tanto, aunque existan
109
J. Wu y R. L. McCreery, J. Electrochem. Soc. 156 [1], P29-P37 (2009)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-110-320.jpg)


![BaTiO3 dopado con Zn
- 105 -
8. BaTiO3 DOPADO Zn
8.1. INTRODUCCIÓN
En relación a la variación de la conductividad con el voltaje presentada en el capítulo
anterior para las cerámicas de BaTiO3 dopadas con Mg, se plantea la posibilidad de
utilizar otros dopantes aceptores para ver si presentan el mismo efecto. Por ello, se
eligió el dopante divalente Zn(II), debido a que presenta un estado de oxidación fijo y
unas características químicas semejantes al Mg(II). En el presente capítulo, se presentan
los resultados obtenidos de este estudio.
El ZnO es un compuesto semiconductor del grupo II-VI que presenta la
estructura cristalina de wurtzita, y unas propiedades ópticas, electrónicas y
piezoeléctricas excelentes. Tradicionalmente, en la fabricación de dispositivos
microondas se usan óxidos mixtos de bario y titanio, concretamente BaTi4O9 y
Ba2Ti9O20, como componentes mayoritarios en estas cerámicas de elevada frecuencia
dieléctrica. Además, se utiliza el ZnO como aditivo para contrarrestar el efecto del
coeficiente de temperatura negativo en la constante dieléctrica.
Hay relativamente pocos trabajos en los que se utiliza el Zn como dopante en el
BT, y además existe cierta controversia en la bibliografía acerca de la posición que
ocupa el Zn(II) en el retículo del BaTiO3, así como el límite de disolución sólida. En
principio, el Zn(II) puede actuar como dopante isovalente110
y como aceptor111
. Ciertos
autores111
determinaron que el límite de la disolución sólida de Zn(II) en la posición del
Ti(IV) era 0.7 % en peso. Roth y col.
112
determinaron el diagrama de fases ternario
BaO-ZnO-TiO2, indicando que el BaTiO3 acepta menos del 2 % molar de ZnO y éste se
sitúa en las posiciones del Ba. Caballero y col.113-115
estudiaron la microestructura y las
propiedades eléctricas del BaTiO3 dopado con Zn. Observaron que la adición de ZnO
conducía a la formación de microestructuras homogéneas con tamaños de grano
pequeño, y como consecuencia, se obtenían cerámicas de elevada densidad (97-99%).
Estos materiales presentaron unas características excelentes como dieléctricos para
condensadores de elevada calidad, ya que presentaban valores elevados de constante
dieléctrica (2000-3000) y pérdidas dieléctricas inferiores al 1 %. Por tanto, la adición de
ZnO en las cerámicas de BT disminuía el valor de la pérdida dieléctrica y aumentaba la
densidad de las cerámicas. Según estos autores, el Zn(II) se incorpora en el retículo del
BT en la posición del Ba(II) y el límite de la disolución sólida es inferior al 0.5 % en
peso. Según estos autores, parece ser que el Zn se segrega hacia las fronteras de grano
como consecuencia de la diferencia en tamaños, lo que origina el control en el
110
P. Baxer, N. J. Hellicar y B. Lewis, J. Am. Ceram. Soc. 42[10], 465-470 (1959)
111
Jaffe, W. R. Cook, H. Jaffe, Piezoelectric Ceramics, Academic Press, London-New York (1971)
112
R. S. Roth, C. J. Rawn, C. G. Lindsay y W. Won-Ng, J. Solid State Chem. 104, 99-118 (1993)
113
A. C. Caballero, J. F. Fernández, C. Moure y P. Durán, J. Eur. Ceram. Soc. 17, 513-523 (1997)
114
A. C. Caballero, J. F. Fernández, C. Moure, P. Durán y J. L. G. Fierro, J. Eur. Ceram. Soc. 17, 1223-
1230 (1997)
115
A. C. Caballero, J. F. Fernández, C. Moure, P. Durán y Y-M. Chiang, J. Am. Ceram. Soc. 81 [4], 939-
44 (1998)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-113-320.jpg)
![Capítulo 8
- 106 -
crecimiento de grano. Por otra parte, estudiaron el codopado con otros iones como Si y
P, observando también una inhibición en el crecimiento de grano para contenidos de Zn
inferiores al 1 % en peso.
Yoon y col.116
determinaron las propiedades dieléctricas del BT dopado con
Sb2O3 (sustituyendo al Ba) y ZnO (sustituyendo al Ti), ya que el Sb2O3 activa el
crecimiento de grano y el ZnO lo inhibe, y dichas propiedades dependen de estos
efectos. Observaron que la constante dieléctrica aumenta considerablemente en
composiciones superiores a 0.15 % molar de Sb2O3 y ZnO, según los autores, debido a
la formación de vacantes de oxígeno y bario. Según éstos, la constante dieléctrica
depende de los defectos cristalinos y de la polarización de carga de los dopantes en el
intervalo de baja frecuencia. Dong y col.117
estudiaron la adición de ZnO en el
compuesto Ba0.3Sr0.7TiO3 observando un aumento de la densidad de las cerámicas y de
la capacidad, que fue máxima al dopar con un contenido de Zn del 1.6 % en peso.
En cuanto a las propiedades ópticas, Fasasi y col.
118
estudiaron el BT en forma
de lámina delgada, dopado con Zn y determinaron las propiedades en función del
contenido en Zn y del espesor de la lámina. Mbenkum y col.119
determinaron las
propiedades dieléctricas y ópticas de láminas delgadas de BT de alta calidad depositadas
sobre sustratos de ZnO. Parece ser que las capas de ZnO actúan como electrodos
conductores transparentes.
Aunque según la bibliografía parece ser que el Zn puede entrar en la posición A
y B del retículo del BT, en este estudio nos planteamos la sustitución del Zn en la
posición del Ti (ión aceptor) según la estequiometría BaTi1-xZnxO3-x.
8.2. PROCEDIMIENTO EXPERIMENTAL
Las muestras de BaTiO3 dopadas con Zn, BaTi1-xZnxO3-x, se prepararon siguiendo la
metodología sol-gel desarrollada en el apartado 6.2. Se utilizó el acetato de cinc (II)
[Zn(CH3COO)2·2H2O 99.99%, Strem Chemicals] como precursor de Zn, el cual se
añadió a la disolución del acetato de bario en agua, obteniéndose una disolución
transparente. Las relaciones molares de Ba:H2O:CH3OH:CH3COOH fueron las
indicadas anteriormente. Por otra parte, en las muestras con menores contenidos de cinc,
se preparó previamente una disolución de acetato de cinc 0.0235 mg/mL en metanol.
Para obtener la estequiometría deseada, se añadieron alícuotas de esta disolución sobre
la disolución del acetato de bario en agua. Finalmente, se añadió la disolución de los dos
acetatos, de bario y cinc, sobre la disolución del isopropóxido de titanio con
acetilacetona (acacH), obteniéndose finalmente un sol de color amarillento.
116
K. Y. Yoon, J. W. Kim y K. H. Jo, J. Mater. Science. Lett. 8, 153-6 (1989)
117
G. Dong, S. Ma, J. Du y J. Cui, Ceram. Internacional 35, 2069-75 (2009)
118
A. Y. Fasasi, M. Maaza, E. G. Rohwer, D. Knoessen, Ch. Theron, A. Leitch y U. Buttner; Thin Solid
Films 516, 6226-32 (2008)
119
B. N. Mbenkum, N. Ashkenov, M. Schubert, M. Lorez, H. Hochmuth, D. Michel, M. Grundmann y G.
Wagner; Appl. Phys. Lett. 86, 091904-1-3 (2005)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-114-320.jpg)







![Capítulo 8
- 114 -
crecimiento, en que la fracción de volumen de la región de la muestra en el estado
excitado aumenta gradualmente con el tiempo mientras que la muestra en el estado
fundamental disminuye con el tiempo.
Figura 8.8. (a) Plano complejo de la impedancia, Z*, a 282 ºC para la muestra x = 0.01 antes y después
de aplicar 10V [139 Vcm-1
] a diferentes tiempos; (b) gráfica espectroscópica de M” (mismos
datos que en (a)) y (c) gráfica espectroscópica de M” para la muestra en el estado excitado
(10V) y a diferentes tiempos, después de eliminar el voltaje dc bias.
Para comprobar la reversibilidad en la respuesta eléctrica, se realizaron medidas
de impedancia en función del tiempo tras la supresión del voltaje. Estos resultados se
presentan en forma de gráfica espectroscópica de M” en la figura 8.8.c. Al eliminar el
voltaje, el pico de M” gradualmente se desplaza a menores frecuencias y alcanza su
estado original después de ~ 268 h. Durante este proceso, el pico de M” retiene su forma
sin evidencia del ensanchamiento del pico y tiene aproximadamente la misma altura. La
interpretación de estos datos es que la resistencia del bulk de la muestra decae
gradualmente desde el estado excitado al estado fundamental mediante un proceso
cooperativo.
Z' / kΩcm
0 50 100 150
Z
'
'
/
k
Ω
c
m
-150
-100
-50
0
0 5 10 15
Z
''/k
Ω
c
m
-15
-10
-5
0
Z' / kΩcm
(a)
0V
10V
0min
10V
12min
10V
1290min
f / Hz
10
2 10
3 10
4 10
5 10
6 10
7
1
0
-
9
M
e0
-
1
/
F
-
1
c
m
0.0
2.5
5.0
7.5
10.0
(b)
0V
10V
0min
10V
12min 10V
1290min
f / Hz
10
2 10
3 10
4 10
5 10
6 10
7
1
0
-
9
M
e0
-
1
/
F
-
1
c
m
0.0
2.5
5.0
7.5
10.0
0V
10V 1290min
0V 25h
0V 96h
0V 147h
0V 268h
(c)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-122-320.jpg)

![Capítulo 8
- 116 -
Para determinar la magnitud del aumento en la conductividad del bulk y de la
frontera de grano con la temperatura después de la aplicación de un voltaje de 10V, se
representan los valores de R1 y R2 en forma de gráficas de Arrhenius para la
composición x = 0.01 (figura 8.11). En el estado excitado, tanto R1 como R2 presentan
una respuesta lineal con energía de activación similar, ~ 0.76 eV; la conductividad tanto
del bulk como de la frontera de grano aumenta aproximadamente un orden de magnitud
en el estado excitado.
Figura 8.11. Gráficas de Arrhenius de R1 y R2 para la muestra x = 0.01, medida sin voltaje aplicado y con
un voltaje dc de 10V [138.9 Vcm-1
] después de alcanzar un estado estacionario.
Los valores de voltaje habitualmente se corrigen por el espesor de la pastilla, ya
que el gradiente de potencial a través de la muestra depende del espesor de ésta. Para
estudiar el aumento de la conductividad en función del gradiente de potencial, se realizó
un experimento en el que se midieron dos pastillas de la misma composición con
diferente espesor, 0.72 y 2.21 mm respectivamente, tras la aplicación de 4V; los
resultados obtenidos se muestran en la figura 8.12 en forma de gráfica de Arrhenius
para el bulk y la frontera de grano.
1000 K / T
0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4
l
o
g
σ
/
S
c
m
-
1
-7
-6
-5
-4
-3
-2
-1
R1
R2
0V
10V](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-124-320.jpg)
![BaTiO3 dopado con Zn
- 117 -
Figura 8.12. Gráficas de Arrhenius de (a) σ1 y (b) σ2 para dos muestras con x = 0.01 con diferentes
espesores [0.72 y 2.21 mm] medidas sin voltaje aplicado y con un voltaje dc de 4V [55 y
18 V/cm, respectivamente] después de alcanzar un estado estacionario.
El aumento de la conductividad tanto para R1 como para R2 fue mayor para la
pastilla más delgada, ya que estuvo sometida a un gradiente mayor,
~ 55 Vcm-1
. Según la figura 8.10, bajo un voltaje de 55 Vcm-1
, se alcanza el valor
máximo de la conductividad. Sin embargo, el gradiente de potencial a través de la
muestra más gruesa fue solo de 18 Vcm-1
y por tanto el valor de conductividad
estacionario alcanzado no era el máximo. Como era de esperar, el aumento en la
conductividad de la muestra más delgada fue mayor que en la más gruesa, ya que ésta
estuvo sometida a un gradiente de potencial mayor.
Según los resultados presentados, las cerámicas de BT dopadas con Zn también
responden al fenómeno descrito, y parece ser, que el mecanismo y las características de
este efecto son semejantes a las analizadas para el caso del dopado con Mg. Aunque los
resultados que se han presentado son para la composición x = 0.01, se ha comprobado
esta dependencia en el resto de composiciones estudiadas, observando respuestas
semejantes. En la figura 8.13, se representan gráficas de Arrhenius para R1 y R2, antes y
después de aplicar el voltaje, para un intervalo de composiciones. Como puede verse,
los valores de conductividad para las regiones del bulk y de la frontera de grano
aumentan con x y al mismo tiempo, las energías de activación disminuyen. Estos
resultados que dependen de la composición, nos sugieren que existe un contenido de Zn
mayor en el bulk que en la frontera de grano. Por otra parte, se observa para todas las
composiciones un aumento de ~1-2 órdenes de magnitud en el valor de la
conductividad.
1000 K / T
0.8 1.0 1.2 1.4 1.6 1.8 2.0
l
o
g
σ
2
/
S
c
m
-
1
-5.5
-5.0
-4.5
-4.0
-3.5
-3.0
-2.5
-2.0
-1.5
l = 2.21 mm
l = 0.72 mm
1000 K / T
1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6
l
o
g
σ
1
/
S
c
m
-
1
-6.5
-6.0
-5.5
-5.0
-4.5
-4.0
-3.5
-3.0
-2.5
l = 2.21 mm
l = 0.72 mm
0V
4V
(a) (b)
0V 4V](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-125-320.jpg)



![BaTiO3 dopado con Ca
- 123 -
9. BaTiO3 DOPADO CON Ca
9.1. INTRODUCCIÓN
Considerando los resultados obtenidos para otros sistemas en los que se han utilizado
iones aceptores, como Mg y Zn, en cuanto a la dependencia de la conductividad del bulk
con el voltaje se refiere, nos planteamos estudiar un ión que pueda ocupar ambas
posiciones, A y B, del retículo del BaTiO3. Como veremos a continuación, el Ca(II),
puede sustituir al Ba(II) en la posición A, y también al Ti(IV) en la posición B. Por ello,
se eligió este ión para comprobar dicha dependencia con el voltaje.
En los capítulos anteriores, se ha visto que las propiedades eléctricas del BaTiO3
(BT) son muy sensibles a la presencia de dopantes, y en particular a su naturaleza, si son
aceptores (menor valencia que el ión al que sustituyen) ó dadores (mayor valencia). Los
materiales con dopantes aceptores, como el Ca(II) en la posición del Ti(IV), son menos
sensibles a la reducción120,121
. Parece ser que las vacantes de oxígeno, generadas para
mantener la electroneutralidad, son las responsables de este comportamiento, ya que
éstas evitan la perdida de oxígeno a alta temperatura. Este es un aspecto importante a
tener en cuenta en el procesado de los condensadores cerámicos multicapa (CCM), los
cuales se fabrican bajo condiciones reductoras con electrodos metálicos (BME) como
Ni.
El Ca es un dopante inusual en el BT, como es el caso también de ciertos iones
lantánidos, puesto que puede sustituir tanto al Ba, en la posición A, como al Ti, en la
posición B, y las propiedades eléctricas resultantes son muy diferentes. De acuerdo con
el estudio bibliográfico del BaTiO3, la relación molar A/B influye considerablemente en
la posición que ocupan estos dopantes. Cuando la relación A/B 1, el dopante tiende a
ocupar la posición B, es decir, cuando hay un exceso de BaO, cierto número de iones
Ca(II) se mueven desde la posición A a la posición B.122
Sustitución en la posición A
Los datos bibliográficos indican que el BaTiO3 puede formar disolución sólida con la
perovsquita ferroeléctrica CaTiO3, mediante la sustitución parcial de Ba por Ca,
actuando éste como dopante isovalente. La sustitución de Ca (rIC=12 = 148pm) por Ba en
la posición A (rIC=12 = 175pm), puede escribirse según la estequiometría Ba1-yCayTiO3.
El intervalo de esta disolución sólida es 0 ≤ y ≤ 0.25.123
El diagrama de fases para el
sistema BaTiO3-CaTiO3 fue estudiado por Devries y col.123
y se ilustra en la figura 9.1.
Para contenidos superiores al ~ 25 % de Ca aparece una región de insolubilidad, que se
extiende hasta un 90 % de CaTiO3, lo que parece ser debido a una distribución
inhomogénea de Ca en la disolución sólida (Ba,Ca)TiO3. Por encima del 90 % en Ca,
120
Y. H. Han, J. B. Appleby y D. M. Smyth, J. Am. Ceram. Soc. 70, 96-100 (1987)
121
T. T. Fang y J. T. Shuei, J. Mater. Res. 14 [5], 1910-5 (1999)
122
N. H. Chan, M. P. Harmer, M. Lal y D. M. Smyth, Mater. Res. Soc. Symp.Proc. 31, 345-50 (1984)
123
R. C. Devries y R. Roy, J. Am. Ceram. Soc. 38 [4], 142-6 (1955)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-129-320.jpg)
![Capítulo 9
- 124 -
vuelve a incorporarse formando una disolución sólida, que como ilustra el diagrama es
CaTiO3 ss.
Figura 9.1. Diagrama de fases para el sistema BaTiO3-CaTiO3. Figura adaptada de la referencia [123].
Generalmente, el Ca se añade al BT para controlar la conductividad eléctrica y el
tamaño de grano en la producción de condensadores cerámicos y cerámicas PTCR. La
sustitución parcial de Ba por Ca reduce el tamaño medio del grano en las cerámicas
PTCR, debido probablemente a la tensión que tiene lugar en el retículo cristalino como
consecuencia del diferente tamaño. Otra aplicación que presentan las cerámicas de BT
dopadas con Ca es como moduladores electro-ópticos y dispositivos de memoria.
La sustitución parcial de Ba por Ca en el retículo del BT no provoca un cambio
aparente en la temperatura de transición. El punto de Curie para el BT puro es de 130 ºC
y cuando el Ca sustituye al Ba se alcanza un valor máximo de 137 ºC para y = 0.08 y
posteriormente disminuye hasta 118 ºC para el límite de la disolución sólida, que es
para y ≈ 0.24 (~ 1 ºC/at)57,124
. Aunque este comportamiento puede explicarse como un
efecto del tamaño del ión sustituyente, el origen del aumento del TC para y 0.08 no se
entiende completamente; sin embargo, puede asociarse con un efecto de tensión
asociado con la variación de los cationes en la posición A.
En la figura 9.2 se muestran las temperaturas de transición de Ba1-yCayTiO3 en
función del contenido de Ca. Como se ha comentado, la primera transición cúbico-
tetragonal (punto de Curie) no se ve afectada prácticamente, mientras que las
temperaturas de las transiciones tetragonal-ortorrómbico y ortorrómbico-romboédrico
disminuyen considerablemente con el contenido de Ca.57
124
D. C. Sinclair y J. P. Attfield, Chem. Commun. 1497-98 (1999)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-130-320.jpg)
![BaTiO3 dopado con Ca
- 125 -
Figura 9.2. Temperaturas de transición de Ba1-yCayTiO3 en función del contenido de Ca. (Las zonas
sombreadas representan el error en la determinación de la temperatura). Figura adaptada de
la referencia [57].
Se han realizado numerosos estudios sobre la microestructura y las propiedades
eléctricas de cerámicas de BT dopadas con Ca en la posición A125-127
. Lin y col.125
indicaron que la microestructura, las propiedades dieléctricas y la resistividad eléctrica
dependen del contenido de Ca. Según estos autores, la relación (Ba+Ca)/Ti es el factor
que determina si las cerámicas de BT se ven afectadas por la atmósfera reductora a alta
temperatura o no, es decir, cuando esta relación es superior a la unidad, su resistencia no
varía con la atmósfera presente en la sinterización de la muestra. Wada y col.126
estudiaron la función de las fronteras de grano en cerámicas de BT dopadas con Ca.
Según estos autores, el Ca se concentra en las fronteras de grano. Parece ser que las
fronteras de grano en estas cerámicas, sin estructura en capas, tienen una función
importante en las propiedades dieléctricas de estas cerámicas, ya que presentan una
dependencia de la constante dieléctrica con la temperatura estable.
Yasukawa y col.128
estudiaron la estructura local del Ca en cerámicas
Ba1-yCayTiO3 para la composición con y = 0.125, mediante cálculos teóricos y medidas
de EXAFS, determinando que el Ca se sitúa a 0.3 Å de la posición de equilibrio de Ba a
lo largo de la dirección [001].
Existen en la bibliografía numerosos trabajos en los que se estudia el efecto del
dopado de Ca junto con el codopado de otros elementos. Cerámicas de BT dopadas con
Ca y codopadas con iones lantánidos, como Ho, Eu o La, presentan interesantes
125
T. F. Lin, C. T. Hu y I. N. Lin, J. Appl. Phys. 67 [2], 1042-7 (1990)
126
N. Wada, T. Hiramatsu, T. Tamura y Y. Sakabe, Ceram. Inter. 34, 933-7 (2008)
127
X. Wang, H. Yamada y C-N. Xu, Appl. Phys. Let. 86, 022905-1-3 (2005)
128
K. Yasukawa, M. Tanaka y Y. Azuma, IEEE Sym. Appl. Ferroelectrics, 1, 4693885 (2008)
% molar CaTiO3 en (Ca.Ba)TiO3
T
e
m
p
e
r
a
t
u
r
a
d
e
t
r
a
n
s
i
c
i
ó
n
/
º
C](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-131-320.jpg)
![Capítulo 9
- 126 -
propiedades129-131
. Para el caso del La, composiciones en el intervalo de
1.005 ≤ (Ba+Ca+La)/Ti ≤ 1.01, exhiben características PTCR notables131
. Las
cerámicas de BT semiconductoras con (Ba+Ca+La)/Ti =1.005 y dopadas con un 20 %
molar de Ca, presentan unas características PTCR interesantes con un salto de la
resistividad de dos órdenes de magnitud cuando son reoxidados a 800 ºC después de la
sinterización en atmósfera reductora. Cheng y col.132
estudiaron cerámicas de BT
dopadas con Ca y codopadas con Sr, mostrando un aumento importante en la
polarización como consecuencia del aumento en la relación de los parámetros
reticulares c/a debido a las distorsiones en el retículo y a las tensiones desarrolladas
como consecuencia del dopado con Sr. Yoon y col.133
mostraron que, la temperatura de
transición y la constante dieléctrica de cerámicas de BT dopadas con Ca en la posición
A y con Zr en la posición B, disminuyen al aumentar la concentración de estos iones
Sustitución en la posición B
En cuanto a la sustitución del Ca en la posición del Ti, cabe señalar que el radio iónico
del Ca2+
en coordinación octaédrica es de 114pm, es decir, 150 veces mayor que el
tamaño del Ti4+
(74.5pm). Sin embargo, parece ser que el Ca puede albergarse en la
posición B del retículo del BT.120,134-136
La incorporación del Ca en la posición de Ti
puede escribirse según la notación de Kröger y Vink (apéndice 4) como:
BaO + CaO BaBa + '
'
Ti
Ca + 2OO + •
•
O
V [9.1]
Como consecuencia de esta sustitución, se generan defectos cargados
negativamente (Ca’’
Ti) y el correspondiente número de vacantes de oxígeno para
mantener la electroneutralidad. El intervalo de disolución sólida BaTi1-xCaxO3-x es de
0 ≤ x ≤ 0.05,134-136
mucho más limitada que en el caso anterior debido a la diferencia de
tamaños entre el Ca y el Ti. La sustitución de Ti por Ca genera cambios importantes,
tanto en la temperatura de transición como en las propiedades eléctricas. Además, la
incorporación del Ca(II) en la posición del Ti(IV) en el retículo del BT provoca una
reducción importante en el punto de Curie, TC, de aproximadamente 12.5 ºC por mol
para contenidos inferiores al 2 % molar 135, 137-140.
En la figura 9.3 se compara la
129
W. K. Jo y Y. H. Han, Aplications of Ferroelectrics, 2008. ISAF 2008. 17th
IEEE International
Symposium
130
Q. Yang, L. Fang, F. Zheng y M. Shen, Mater. Chem and Phys. 118, 484-9 (2009)
131
H. Niimi, K. Mihara y Y. Sakabe, J. Am. Ceram. Soc. 90 [6], 1817-21 (2007)
132
X. Cheng y M. Shen, Solid State Commun. 141, 587-590 (2007)
133
M. S. Yoon y S. C. Ur, Ceram. Inter. 34, 1941-8 (2008)
134
Z. Q. Zhuang, M. P. Harmer, D. M. Smyth y R. E. Newnham, Mater. Res. Bull. 22, 1329-35 (1987)
135
D. F. K. Hennings y H. Schreinemacher, J. Eur. Ceram. Soc. 15, 795-800 (1995)
136
X. W. Zhang, Y. H. Han, M. Lal y D. M. Smyths, J. Am. Ceram. Soc. 70, 100-3 (1987)
137
L. Zhang, O. P. Thakur, A. Feteira, G. M. Keith, A. G. Mould, D. C. Sinclair y A. R. West, Appl.
Phys. Let. 90, 142914-1-3 (2007)
138
Y. Li, X. Yao y L. Zhang, Ceram. Inter. 30, 1283-1287 (2004)
139
Z. Zhuang y R. E. Newnham, Ferroelectrics Lett. 6, 155-64 (1987)
140
S. J. Lee, I. J. Park y Y. H. Han, Mater. Chem. Phys. 121, 161-4 (2010)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-132-320.jpg)
![BaTiO3 dopado con Ca
- 127 -
temperatura de transición tetragonal-cúbica para las dos sustituciones, en la posición A
(BCT) y en la posición B (BTC).
Figura 9.3. TC vs % molar de Ca para las disoluciones sólidas: Ba1-yCayTiO3 (BCT) y BaTi1-xCaxO3-x
(BTC). Figura adaptada de la referencia [137].
La microestructura141
y las propiedades dieléctricas de las cerámicas de BT
dopadas en la posición B han sido ampliamente estudiadas. Han y col.120
realizaron
estudios de la conductividad en función de la presión parcial de oxígeno a altas
temperaturas (700 ºC) para los sistemas Ba1-yCayTiO3 y BaTi1-xCaxO3-x, mostrando que
cuando el Ca actúa como isovalente sólo se detecta un pequeño cambio, mientras que
cuando actúa como aceptor presenta un equilibrio de conductividad típico para un
comportamiento aceptor. Por otra parte, cuando el Ca actúa como ión aceptor, se
observa un aumento en la conductividad del bulk con el contenido de éste, sobretodo en
muestras sinterizadas en atmósferas reductoras a altas temperaturas, así como un
aumento en la perdida dieléctrica sobre el TC.137
Lee y col.140
estudiaron las propiedades eléctricas y mostraron que al aumentar
el contenido de Ca, aumenta el número de complejos defectuosos (Ca’’
Ti-VO
··
). Según
estos autores, existe un cambio en la energía de activación a alta y baja temperatura.
Entre 200-300 ºC la energía de activación es ~ 0.38-0.65 eV y se asocia al movimiento
de las vacantes alrededor de los centros defectuosos, mientras que a 350-500 ºC, la
energía de activación es de 0.72 - 1.04 eV. Esta mayor energía de activación se asocia
con la energía extra requerida para el movimiento de las vacantes de oxígeno a largo
alcance.
Cerámicas de fórmula BaTi0.98Ca0.02O2.98 muestran envejecimiento
ferroeléctrico, conmutación reversible de los dominios ferroeléctricos, con una
polarización remanente de Pr ~ 0 μC/cm2
, y una tensión de deformación eléctrica
(electrostrain) no lineal recuperable de ~ 0.04 % a ~ 11 kV/cm a temperatura ambiente.
141
M. R. Panigrahi y S. Panigrahi, Physica B 404, 4267-72 (2009)
BCT
BTC
% molar Ca
T
c
/
º
C](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-133-320.jpg)
![Capítulo 9
- 128 -
Este comportamiento se atribuye a la movilidad de las vacantes del ión óxido, creadas
por el mecanismo de compensación de carga del dopaje aceptor, y una tendencia de los
defectos a alinearse con la simetría cristalina.142
Chang y col.
143
realizaron estudios de Raman en cerámicas cristalinas para
ambas disoluciones sólidas: Ba1-yCayTiO3 (BCT) y BaTi1-xCaxO3-x (BTC), demostrando
que la incorporación de Ca en la posición del Ti induce una mayor disminución en la
tetragonalidad. Chang y col.
144
realizaron estudios de los estados electrónicos para
cerámicas cristalinas en estos sistemas mediante medidas de XPS, observando un pico
adicional para el O1s en las muestras BTC debido a la diferencia en la carga formal
entre el Ca y el Ti.
Considerando que el Ca puede actuar como ión isovalente sustituyendo al Ba o
como ión aceptor sustituyendo al Ti, en este capítulo nos planteamos estudiar el dopado
con Ca, en las dos posiciones, haciendo especial hincapié en la respuesta de la
conductividad con el voltaje aplicado.
9.2. PROCEDIMIENTO EXPERIMENTAL
La síntesis de estas composiciones se llevó a cabo siguiendo el procedimiento
experimental descrito en el apartado 6.2, utilizando el acetato de calcio
[Ca(CH3COO)2·H2O 99%, Sigma-Aldrich] como precursor de Ca. Se prepararon
diferentes composiciones según las estequiometrías tanto sustituyendo al Ba como al Ti:
Ba1-yCayTiO3 (0 ≤ y ≤ 0.03) y BaTi1-xCaxO3-x (0 ≤ x ≤ 0.03).
El acetato de calcio se añadió a la disolución de bario en agua, obteniendo una
disolución transparente. A continuación, se adicionó el MeOH de forma habitual
formándose un precipitado, que se redisolvió añadiendo ácido acético. Finalmente, esta
disolución se añadió lentamente sobre la disolución del isopropóxido de Ti en
acetilacetona, obteniendo una disolución transparente de color amarillento. En todos los
casos, los soles obtenidos se mantuvieron en agitación durante 48h. Posteriormente, se
introdujeron en un desecador con el fin de evaporar el disolvente y, al cabo de dos días
aproximadamente, se obtuvieron geles homogéneos y transparentes. Estos geles se
secaron bajo lámparas de Infrarrojo.
En la tabla IX.1 se indican las composiciones preparadas en las dos disoluciones
sólidas.
142
L. Zhang. L. Ben, O. P. Thakur, A. Feteira, A. G. Mould, D. C. Sinclair y A. R. West, J. Am. Ceram.
Soc. 91 [9], 3101-3104 (2008)
143
M. C. Chang y S. C. Yu, J. Mater. Sci. Lett. 19, 1323-25 (2000)
144
M. C. Chang y S. Sugihara, J. Mater. Scien. Lett. 20, 237-239 (2001)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-134-320.jpg)



![Capítulo 9
- 132 -
Temperatura/ ºC
50 100 150 200 250
ε'
0
2000
4000
6000
8000
10000
12000
BT
BCT3
BTC3
x en BaTi
1-x
Ca
x
O
3-x
0.00 0.01 0.02 0.03 0.04 0.05
y en Ba
1-y
Ca
y
TiO
3
0.00 0.01 0.02 0.03 0.04 0.05
T
c
/
º
C
40
60
80
100
120
140
(a) (b)
Temperatura/ ºC
50 100 150 200
ε'
0
1000
2000
3000
4000
5000
6000
7000
1400 ºC
1500 ºC
Figura 9.6. Datos de permitividad en función de la temperatura a 100 kHz para la muestra BCT3
sinterizada a 1400 ºC y 1500 ºC.
Con el fin de estudiar como afecta la sustitución de Ca por Ba ó por Ti, en la
figura 9.7.a se muestran los perfiles de permitividad para las muestras BT, BTC3
(sinterizadas a 1400 ºC) y BCT3 (sinterizada a 1500 ºC). En todos los casos se detectó
un único pico correspondiente a la transición ferroeléctrica. El perfil de permitividad
para la muestra BCT3 no varía su posición con respecto al BT puro, mientras que
decrece considerablemente para la muestra BTC3.
Figura 9.7. (a) Datos de permitividad en función de la temperatura a 100 kHz para las muestras BT,
BCT3 y BTC3 y (b) punto de Curie en función de la composición. Los símbolos negros
están extraídos de la referencia [124].](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-138-320.jpg)

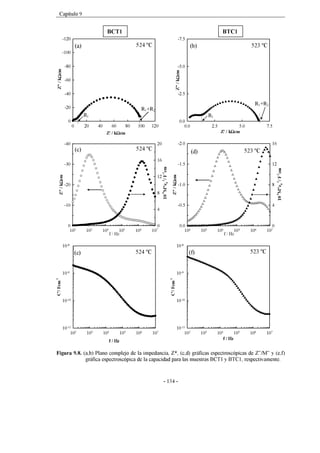


![BaTiO3 dopado con Ca
- 137 -
t/ minutos
σ
1
/
S
c
m
-
1
10-4
10-3
10-2
10 V 0 V
10 V
1
0 V
10 V 0 V
10 10
2
1 10 10
2
1 10 10
2
1 10 10
2
1 10 10
2
1 10 10
2
10
3
nitrógeno
aire oxígeno
Por otra parte, se analizó el efecto de la atmósfera durante la medida, realizando
medidas de impedancia con atmósfera de nitrógeno, aire y oxígeno. La conductividad
fue mayor en atmósfera de oxígeno, en donde adsorción de oxígeno se produce en la
superficie de la muestra. La reacción de adsorción puede escribirse como:
O2 + 4e 2O2-
[9.2]
Según estos resultados, el mecanismo de conducción es principalmente tipo p.
Posteriormente se aplicó un voltaje de 10V, en atmósfera de nitrógeno, y se midió la
conductividad en función del tiempo. La conductividad del bulk aumentó hasta alcanzar
un valor constante tras varias horas de aplicación. A continuación, se eliminó el voltaje
dc y se comprobó que la conductividad recuperaba gradualmente su estado original.
Este experimento se repitió en atmósfera de aire y de oxígeno, obteniéndose resultados
semejantes (figura 9.10). Finalmente, se cambió la atmósfera a nitrógeno y se recuperó
el valor inicial de la conductividad. Estos experimentos permitieron demostrar que el
mecanismo de conducción es principalmente electrónico más que iónico, y que el
mecanismo de conducción es tipo p, es decir, el portador de carga es el hueco. Además
demostraron que el aumento de la conductividad del bulk, R1, no depende de la
atmósfera.
Figura 9.10. σ1 a 600 ºC para la muestra BTC1 después de aplicar y eliminar un voltaje de 10V
[84 Vcm-1
] a diferentes tiempos, en atmósfera de nitrógeno, aire y oxígeno.
Se realizó un experimento semejante, pero manteniendo el dispositivo de medida
a vacío, observándose un comportamiento semejante a las presentadas en la figura 9.10.
Este experimento permitió demostrar que no tiene lugar un intercambio de oxígeno
entre la muestra y la atmósfera responsable de los cambios en la conductividad
observados tras aplicar el voltaje dc.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-143-320.jpg)
![Capítulo 9
- 138 -
9.4. DISCUSIÓN
Los resultados obtenidos para este sistema concuerdan con los obtenidos anteriormente
para los otros sistemas estudiados. Aquellos sistemas de BT dopados con iones
aceptores, muestran una dependencia no lineal de la conductividad con el voltaje,
mientras que el BT estequiométrico no muestra variación de la conductividad con el
voltaje dc. Otra muestra de ello ha sido el BT dopado con Ca en la posición del Ba, que
muestra una ligera variación de la conductividad con el voltaje dc. Por tanto, todos estos
resultados parecen demostrar y corroborar el modelo propuesto, en el que los dopantes
aceptores, que generan vacantes de oxígeno para mantener la electroneutralidad,
provocan que los iones óxidos de su alrededor estén más débilmente unidos, y como
consecuencia, que puedan ionizarse más fácilmente al aplicar un voltaje dc. Como
resultado de esta ionización, tiene lugar un aumento acusado de la conductividad,
debido a los portadores de carga positivos (h) asociados con los iones O-
.
La dependencia de la conductividad con el voltaje se observa tanto en el bulk
como en la frontera de grano, y no depende de la naturaleza del electrodo, ya que se
sustituyó el electrodo de platino por uno de oro, obteniéndose resultados idénticos. Este
efecto no se asocia tampoco con la descomposición electroquímica de las muestras, ni
con la creación de gradientes de composición asociados con migración iónica. Tampoco
se asocia con el intercambio de oxígeno entre la muestra y la atmósfera, ni con la cesión
de carga desde el electrodo a la banda de conducción del material. A pesar de que está
muy bien establecido que las vacantes de oxígeno generadas en el BT dopado con
aceptores son móviles, en este caso las especies conductoras son electrónicas y no
iónicas. Además, los datos representan conducción a largo alcance y no hay evidencia
del bloqueo en el electrodo relacionado con la conducción iónica. Consecuentemente,
las conductividades no representan movimiento de iones o reorientación de los dipolos
como Ca”
Ti-V··
O.
Tal y como se predijo en los capítulos anteriores, el modelo propuesto para
explicar el comportamiento observado, comienza con la creación de vacantes de
oxígeno asociadas con el dopante aceptor, en este caso con Ca”
Ti. En segundo lugar,
tiene lugar la ionización de los iones óxidos alrededor del centro defectuoso. Un ión
óxido adyacente al dopante aceptor no tiene el mismo grado de estabilización que un ión
óxido en un retículo cristalino no defectuoso, y como consecuencia, se ioniza fácilmente
bajo un potencial relativamente bajo, y con ello provoca un incremento neto en la
conductividad. Considerando que el mecanismo de conducción es tipo p, los huecos
positivos asociados con los iones O-
, parecen ser los principales portadores de carga, y
los electrones, probablemente queden atrapados en los orbitales 3d del Ti.
Según los resultados presentados en la figura 9.10 la conductividad tipo p puede
aumentarse dos órdenes de magnitud mediante la aplicación de un dc bias o aumentando
la presión parcial de oxígeno. La adsorción de oxígeno, principalmente en la superficie
de la pastilla, puede expresarse como:
•
•
O
V + ½ O2 + x
O
O 2 •
O
O [9.3]](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-144-320.jpg)


![BaTiO3 no estequiométrico
- 143 -
10. BaTiO3 NO ESTEQUIOMÉTRICO
10.1. INTRODUCCIÓN
En los capítulos anteriores se han presentado tres ejemplos de cerámicas de
composición BaTiO3 dopadas con dopantes aceptores, Mg(II), Zn(II) y Ca(II), en los
que la conductividad del bulk y de la frontera de grano, aumentaban 1 ó 2 órdenes de
magnitud al aplicar un voltaje dc. Este novedoso fenómeno se ha asociado a la
ionización de los iones óxidos favorecida por la estructura cristalina defectuosa que se
genera. Este fenómeno no se había visto con anterioridad en muestras de BaTiO3, por lo
que fue importante determinar bajo qué condiciones ocurría tal efecto. Con el objetivo
de comprobar si únicamente la estructura defectuosa que se genera provoca esta
respuesta, y si el dopante influye o no en el fenómeno, nos planteamos la posibilidad de
preparar muestras de BaTiO3 deficientes en BaO y en TiO2 respectivamente, las cuales
presentarían de igual forma vacantes de oxígeno, y en las que no existirá la influencia
del ión dopante.
Como ya se ha comentado en el capítulo 5, la existencia de la no estequiometría
en el BaTiO3 ha sido estudiada por diversos autores, ya que parece ser que el BaTiO3
puede existir con una relación Ba/Ti variable. Entre los muchos trabajos relacionados,
Rase y Roy38
estudiaron el diagrama de fases para el sistema BaO-TiO2, identificando
la existencia de una zona alrededor del BaTiO3 rica en TiO2. Posteriormente, varios
autores39,41
han determinado que el BaTiO3 puede incorporar cierta cantidad de Ti
formando disolución sólida. Se estima que el límite de la disolución sólida en la fase
hexagonal y tetragonal es 2 % molar en TiO2 a 1600 ºC, mientras que la fase cúbica
puede disolver ∼ 1 % molar de TiO2 a 1400 ºC.38
Eror y col.
145
propusieron que la
formación de vacantes de Ba y O, que en base al tamaño y a la carga son defectos
favorables, favorece la formación de composiciones ricas en TiO2.
Varios autores han estudiado la solubilidad de BaO en el BaTiO3. Entre estos,
Chan y col.
53
y Hu y col.
146
estudiaron la solubilidad de BaO en BaTiO3 mediante
medidas de conductividad eléctrica y difracción de rayos X. Estos autores establecieron
que el límite de esta disolución era 100 ppm de BaO en BT, pero indicaron que se
trataba de una fase metaestable.
Tal y como indicaron Salje y col.147
y, Strukov y col.148
, los defectos pueden
modificar las transiciones en los materiales ferroeléctricos y ferroelásticos. Para el caso
del BaTiO3, la variación de la temperatura de transición cúbico/tetragonal en función de
la concentración de defectos, permite la determinación del límite de solubilidad y la
relación Ba/Ti (g*) para una temperatura de sinterización dada. Lee y col.
42
estudiaron
el comportamiento de la transición de fase ferroeléctrica del BaTiO3 en función de la
temperatura y el tiempo de sinterización y de la relación Ba/Ti, utilizando la técnica de
145
N. G. Eror y D. M. Smyth, J. Solid State Chem. 24 [3-4], 235-44 (1978)
146
Y. H. Hu, M. P. Harmer y D. M. Smyth, J. Am. Ceram. Soc. 68 [7], 372-6 (1985)
147
E. Salje, U. Bismayer, B. Wruck y J. Hensler, Phase Transitions, 35 [2], 61-74 (1991)
148
B. A. Strukov y A. P. Levanyuk, “Ferroelectrics Phenomena in crystals”, Springer, New York, 1998](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-147-320.jpg)
![Capítulo 10
- 144 -
calorimetría diferencial de barrido. Para las composiciones con una relación Ba/Ti
cercana a 1, existe una variación sistemática de la temperatura de transición al aumentar
o disminuir la relación Ba/Ti. Estos autores establecieron que la región de disolución
sólida en la zona rica en TiO2 es mucho mayor que la rica en BaO y determinaron los
límites para estas disoluciones en función de la temperatura de sinterización que fueron
de: 0.9834 ≤ g* ≤ 1.0051 para 1200 ºC, 0.9665 ≤ g* ≤ 1.0097 para 1320 ºC y
0.9817 ≤ g* ≤ 1.0108 para 1400 ºC. A 1320 ºC se obtiene una mayor disolución sólida
en la zona rica en TiO2, mostrando el efecto de la reacción eutéctica que tiene lugar a
1320 ºC. Además el límite de solubilidad de BaO en BT es mucho mayor que el
determinado por medidas eléctricas (100 ppm)146
.
Como conclusión, parece ser que el BaTiO3 no es un compuesto con una
composición fija, sino que puede presentar una relación Ba/Ti variable. Pero, aunque
existen algunos trabajos acerca de la no estequiometría en el BaTiO3, continúa
existiendo gran controversia acerca de los límites de solubilidad de BaO y TiO2 en el
BaTiO3.
Cabe destacar que, aunque como se ha visto anteriormente, en la bibliografía se
hace referencia a muestras de BaTiO3 con excesos de TiO2 ó de BaO, hemos
considerado más adecuado referirnos a muestras de BaTiO3 defectuosas en Ba o en Ti
respectivamente. Dichas sustituciones pueden expresarse según la notación de Kröger-
Vinker (apéndice 4), en las que puede observarse la creación de defectos de Ti o de Ba
según el caso:
BaO BaBa
x
+ OO
x
+ VTi
’’’
+ 2VO
··
[10.1]
TiO2 TiTi
x
+ 2OO
x
+ VBa
’’
+ VO
··
[10.2]
Considerando que pueden existir composiciones de BaTiO3 deficientes en BaO y
TiO2, y que por tanto, presenten estructuras defectuosas con vacantes de oxígeno, en
este trabajo nos planteamos estudiar el comportamiento eléctrico de dichas muestras y
comprobar el efecto observado con el voltaje en estas cerámicas de BT no
estequiométrico.
10.2. PROCEDIMIENTO EXPERIMENTAL
Siguiendo la metodología experimental descrita detalladamente en el apartado 6.2, se
prepararon cerámicas de BaTiO3 deficientes en BaO y en TiO2, según las disoluciones
sólidas: BaTi1-xO3-2x y Ba1-yTiO3-y. Las composiciones preparadas se indican en la tabla
X.1.
BaTiO3
BaTiO3](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-148-320.jpg)






![BaTiO3 no estequiométrico
- 151 -
Figura 10.5. Plano complejo de la impedancia, Z*, gráficas espectroscópicas de Z”/M” y gráfica
espectroscópica de la capacidad a 472 ºC para la muestra BT preparada por sol-gel
(a, b, c) (mismos datos mostrados en la figura 7.17) y por cerámico (d, e, f) antes y después
de aplicar un voltaje dc de 10V [6.7 y 7.1 Vcm-1
], respectivamente.
Z' / kΩcm
0 100 200 300 400
Z
''/k
Ω
c
m
-400
-300
-200
-100
0
0V
10V
f / Hz
102
103
104
105
106
107
10
-10
Me
0
-1
/F
-1
cm
0.0
0.5
1.0
1.5
0 V
10 V
Z
''/k
Ω
c
m
-150
-100
-50
0
f/ Hz
102
103
104
105
106
107
C
'/F
c
m
-
1
10-11
10-10
10-9
10-8
Z' / kWcm
0 100 200 300 400 500
Z
''/k
Ω
c
m
-500
-400
-300
-200
-100
0
R1+R2
0V
10V
f / Hz
102 103 104 105 106 107
10
-10
Me
0
-1
/F
-1
cm
0.0
0.5
1.0
1.5
Z
''/k
Ω
c
m
-125
-100
-75
-50
-25
0
0V
10V
f/ Hz
102 103 104 105 106 107
C
'/F
c
m
-
1
10-11
10-10
10-9
(f)
0 V
10 V
Z' / kΩcm
0 5 10
Z
'
'
/
k
Ω
c
m
-10
-5
0
(a)
(b)
(c)
(d)
(e)
(f)
0V
10V
0V
10V
0V
10V
0V
10V](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-155-320.jpg)
![Capítulo 10
- 152 -
1000 K / T
0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2
l
o
g
σ
1
/
S
c
m
-
1
-8
-7
-6
-5
-4
-3
-2
1000 K / T
0.9 1.0 1.1 1.2 1.3 1.4
l
o
g
σ
2
/
S
c
m
-
1
-6.0
-5.5
-5.0
-4.5
-4.0
-3.5
-3.0
-2.5
El efecto del voltaje aplicado se observa también en la figura 10.5. Como puede
verse, la conductividad del bulk y de la frontera de grano para el BTSG, muestran una
ligera variación con el voltaje dc. Para el BTC, R1 y R2 muestran una ligera disminución
con el voltaje dc, pero C1 no cambia y C2 muestra un ligero aumento con el voltaje
aplicado.
En la figura 10.6 se muestran gráficas de Arrhenius obtenidas a partir de los
datos de impedancia para la conductividad del bulk (σ1) y de la frontera de grano (σ2)
para el BT antes y después de aplicar un voltaje dc. Como se ha indicado anteriormente,
la conductividad tanto el bulk como la frontera de grano, presentan únicamente una
ligera variación con el voltaje aplicado. Puede notarse además, una variación en la
conductividad de las muestras preparadas por ambas rutas.
Figura 10.6. Gráficas de Arrhenius de (a) σ1 y (b) σ2 para las muestras BTSG y BTC medidas sin voltaje y
con un voltaje dc de 10V [6.7 y 7.1 V/cm-1
, respectivamente] después de alcanzar el estado
estacionario. Se indican las energías de activación en eV, con errores en el intervalo de
0.002 - 0.005 eV.
Estudio de las muestras BT099 y B099T
Una vez analizada la respuesta eléctrica de las muestras BTSG y BTC, se procedió al
análisis de la conductividad de muestras no estequiométricas, tanto sin voltaje como con
voltaje aplicado, y para los dos métodos de síntesis, con el objetivo de comprobar, por
una parte, que la estructura defectuosa origina la dependencia de la conductividad con el
voltaje, y por otra, que la porosidad de las cerámicas no influye en dicho resultado.
Para las muestras no estequiométricas, los datos de impedancia fueron muy
diferentes sin y con voltaje dc aplicado (figuras 10.7 y 10.8). La respuesta eléctrica de
las muestras BT099SG, B099TSG y B099TC pueden asociarse al bulk y a frontera de
(a) (b)
0.71
1.15 1.05
1.25
1.42
1.24
1.49
0V 10V
• ο método cerámico
▲ Δ método sol-gel](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-156-320.jpg)

![Capítulo 10
- 154 -
Z' /KΩcm
0 50 100 150 200 250 300
Z
/K
Ω
c
m
-300
-250
-200
-150
-100
-50
0
0V
10V
R1+R2
Z' /KΩcm
0 5 10 15 20
Z
/
K
Ω
c
m
-20
-15
-10
-5
0
R1
R1
R1+R2
f /Hz
102
103
104
105
106
107
Z
/K
Ω
c
m
-120
-100
-80
-60
-40
-20
0
0V
10V
1
0-
1
0
M
e
0
-
1
/F-
1
c
m
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
f /Hz
102
103
104
105
106
107
C
'/F
c
m
-
1
10-11
10-10
10-9
10-8
0V
10V
Z' /KΩcm
0 5 10 15 20 25 30
Z
/K
Ω
c
m
-30
-25
-20
-15
-10
-5
0
0V
10V
R1
f /Hz
102
103
104
105
106
107
Z
/K
Ω
c
m
-12
-10
-8
-6
-4
-2
0
0V
10V
1
0-
1
0
M
e
0
-
1
/
F-
1
c
m
0.0
0.4
0.8
1.2
1.6
f /Hz
102
103
104
105
106
107
C
'/F
c
m
-
1
10-11
10-10
10-9
0V
10V
Figura 10.7. Plano complejo de la impedancia, Z*, gráficas espectroscópicas de Z”/M” y gráfica
espectroscópica de la capacidad a 485 ºC para la muestra BT099 preparada por sol-gel
(a, b, c) y por cerámico (d, e, f) antes y después de aplicar un voltaje dc de 10V
[15.1 y 9.52 Vcm-1
], respectivamente.
(a)
(b)
(c)
(d)
(e)
(f)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-158-320.jpg)
![BaTiO3 no estequiométrico
- 155 -
Figura 10.8. Plano complejo de la impedancia, Z*, gráficas espectroscópicas de Z”/M” y gráfica
espectroscópica de la capacidad a 469 ºC para la muestra B099T preparada por sol-gel
(a, b, c) y por cerámico (d, e, f) antes y después de aplicar un voltaje dc de 10V
[13.7 y 8.7 Vcm-1
], respectivamente.
Z' /KΩcm
0 20 40 60 80 100 120
Z
/K
Ω
c
m
-120
-100
-80
-60
-40
-20
0
0V
10V
R1+R2
Z' /KΩcm
0 2 4 6 8 10
Z
/
K
Ω
c
m
-10
-8
-6
-4
-2
0
R1
R1+R2
f /Hz
102
103
104
105
106
107
Z
/K
Ω
c
m
-35
-30
-25
-20
-15
-10
-5
0
0V
10V
1
0-
1
0
M
e
0
-
1
/F-
1
c
m
0.0
0.5
1.0
1.5
2.0
2.5
f /Hz
102
103
104
105
106
107
C
'/F
c
m
-
1
10-11
10-10
10-9
10-8
10-7
0V
10V
R1
Z' /KΩcm
0 30 60 90 120 150 180
Z
/K
Ω
c
m
-180
-150
-120
-90
-60
-30
0
0V
10V
R1+R2
Z' /KWcm
0 5 10 15 20
Z
/
K
W
c
m
-20
-15
-10
-5
0
R1
R1+R2
f /Hz
102 103 104 105 106 107
Z
/K
Ω
c
m
-50
-40
-30
-20
-10
0
0V
10V
1
0-
1
0
M
e
0
-
1
/F-
1
c
m
0.0
0.6
1.2
1.8
f /Hz
10
2
10
3
10
4
10
5
10
6
10
7
C
'/F
c
m
-
1
10
-11
10
-10
10
-9
10
-8
10
-7
0V
10V
R1
(a)
(b)
(c)
(d)
(e)
(f)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-159-320.jpg)
![Capítulo 10
- 156 -
De forma semejante a como se hizo en los sistemas previos, se realizaron
diferentes experimentos para caracterizar la dependencia de la conductividad con el
voltaje. En primer lugar, se realizaron medidas de impedancia en función del tiempo a
tres temperaturas de medida, figura 10.9, tras la aplicación de un voltaje de 10V. Las
conductividades aumentaron rápidamente al principio, pero gradualmente se
estabilizaron lo suficiente a tiempos largos. La diferencia entre la conductividad inicial
y final fue aproximadamente de dos órdenes de magnitud a bajas temperaturas de
medida pero esta diferencia fue mayor al aumentar la temperatura. Por otra parte, al
aumentar la temperatura, el tiempo necesario para alcanzar el valor final disminuyó.
Figura 10.9. Conductividad del bulk, σ1, a diferentes temperaturas después de aplicar un voltaje dc de
10V para la muestra BT099SG [15.1 Vcm-1
] (a) y para B099TSG [13.7 Vcm-1
] (b).
En segundo lugar, se realizaron medidas de impedancia a una temperatura dada,
aplicando diferentes voltajes entre 0.5 y 2 V. La conductividad en función del tiempo
para diferentes voltajes dc aplicados se muestra en la figura 10.10. Se obtuvieron
respuestas semejantes, y el valor de la conductividad límite fue mayor para voltajes dc
mayores.
tiempo/min
0 400 800 1200 1600
σ
1
/
S
c
m
-
1
10-7
10-6
10-5
10-4
10-3
431ºC
386ºC
335ºC
tiempo /min
0 20 40 60 80 100
σ
1
/
S
c
m
-
1
10-7
10-6
10-5
10-4
10-3
tiempo/ min
0 200 400 600 800 1000 1200 1400
σ
1
/
S
c
m
-
1
10-7
10-6
10-5
10-4
10-3
432 ºC
385 ºC
301 ºC
tiempo/min
0 20 40 60 80
σ
1
/
S
c
m
-
1
10-6
10-5
10-4
10-3
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-160-320.jpg)



![Capítulo 10
- 160 -
Figura 10.13. Gráficas de Arrhenius de σ1 (a,c) y σ2 (b,d) sin voltaje y con un voltaje dc de 10V para las
muestras B099TSG [13.7 Vcm-1
], B099TC [8.7 Vcm-1
], BT099SG [15.1 Vcm-1
] y BT099C
[9.52 V/cm-1
].
Como resumen, en la tabla X.4 se indican los valores de las energías de
activación, junto con las conductividades (R1
-1
y R2
-1
), a una temperatura determinada
para las muestras BT, BT099 y B099T, sol-gel y cerámicas, sinterizadas a 1400 ºC.
1000 K / T
0.8 1.2 1.6 2.0 2.4
l
o
g
σ
2
/
S
c
m
-
1
-7
-6
-5
-4
-3
-2
l
o
g
σ
1
/
S
c
m
-
1
-7
-6
-5
-4
-3
-2
1.08
0.76
0.80
1.30
1.30
0.73
10V
0V
solid state
sol-gel
1000 K / T
0.8 1.2 1.6 2.0 2.4
l
o
g
σ
2
/
S
c
m
-
1
-7
-6
-5
-4
-3
-2
l
o
g
σ
1
/
S
c
m
-
1
-7
-6
-5
-4
-3
-2
1.35
1.24
0.82
1.18
1.30
0.77
10V
0V
solid state
sol-gel
1.11
1.59
(a)
(b)
(c)
(d)
BT099
BT099
B099T
B099T
0.72
1.28](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-164-320.jpg)
![BaTiO3 no estequiométrico
- 161 -
Tabla X.4. Valores de conductividad obtenidos a 400 ºC por interpolación/extrapolación y energías de
activación para R1 y R2 para todas las muestras estudiadas.
BaTi0.99O2.98 Ba0.99TiO2.99 BaTiO3
0V 1.30(4) 1.34(5) 0.71(1)
Ea /eV
10V 0.80(1) 0.82(1) -
0V 4.22x10-6
7.09x10-6
6.39x10-5
R1
σ /Scm-1
10V 6.03x10-4
5.39x10-4
-
0V 1.28(3) 1.30(2) 1.49(2)
Ea /eV
10V 0.72(1) 0.77(1) -
0V 5.21x10-7
1.62x10-6
2.38x10-7
Sol-gel
R2
σ /Scm-1
10V 3.31x10-5
4.97x10-5
-
0V 1.08(4) 1.18(3) 1.15(4)
Ea /eV
10V 0.76(3) 1.24(6) 1.05(4)
0V 5.89x10-6
2.61x10-6
1.36x10-6
R1
σ /Scm-1
10V 4.08x10-5
3.74x10-5
2.51x10-6
0V - 1.59(5) 1.24(4)
Ea /eV
10V - 1.11(3) 1.25(4)
0V - 7.79x10-7
6.10x10-7
Solid state
R2
σ /Scm-1
10V - 1.10x10-5
7.34x10-7
Finalmente, para conocer el mecanismo de conducción en estas muestras, se
realizaron medidas de impedancia variando la atmósfera durante la medida (nitrógeno,
aire y oxígeno). Los resultados confirmaron que la conducción es predominantemente
tipo p, tal y como se había concluido en los sistemas anteriores. En la figura 10.14
puede verse que para ambas muestras, BT099 y B099T, la conductividad disminuye al
disminuir la presión parcial de oxígeno, ya que se produce una inyección de electrones a
la muestra como consecuencia de la adsorción de oxígeno en la superficie demostrando
un mecanismo tipo p.
2O2-
O2 + 4e [10.3]](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-165-320.jpg)

![BaTiO3 no estequiométrico
- 163 -
asociado exclusivamente a los cambios estructurales locales, como reorientación de
dipolos, en los complejos defectuosos; los datos de impedancia muestran que afecta a
un amplio intervalo de conductividad de la muestra.
Previamente, se ha observado la dependencia de la conductividad con el voltaje
en cerámicas de BT dopado con Mg(II), Zn(II) y Ca(II) (actuando éste como ión
aceptor) en los que la compensación de carga tiene lugar mediante la creación de un
número igual de vacantes de oxígeno de acuerdo con:
BaO + MO x
Ba
Ba + MTi
’’
+ •
•
O
V + 2 x
O
O [10.4]
M2+
= Ca2+
, Mg2+
ó Zn2+
Para los casos anteriores, podemos considerar que los dopantes aceptores
generan la no estequiometría, al contrario de lo que ocurre en el BT no estequiométrico
en el que los dopantes aceptores son vacantes catiónicas cero-valentes, por ejemplo:
TiO2
'
'
'
'
Ti
V + 2 •
•
O
V + x
Ti
Ti +2 x
O
O [10.5]
BaO '
'
Ba
V + •
•
O
V + x
Ba
Ba + x
O
O [10.6]
La estructura local defectuosa, tanto del BT dopado con iones aceptores como en
el BT no estequiométrico, indica grandes desviaciones de la electroneutralidad local. La
estructura defectuosa del BT deficiente en TiO2 se muestra esquemáticamente en la
figura 10.15. Esta contiene una vacante de Ti con dos vacantes de oxígeno adyacentes, y
por tanto se asocia un gran exceso de carga negativa (nominalmente 4-) en la vacante de
Ti y un gran exceso de carga positiva (nominalmente 2+) en las vacantes de oxígeno
adyacentes, en disposición trans o cis.
Figura 10.15. Estructura defectuosa del BaTiO3 no estequiométrico con vacantes de titanio y de oxígeno.
Las vacantes de oxígeno se sitúan en disposición cis, pero pueden también estar en trans.
Ti1 Ti1
Ti1
x
y
Ti2
Ti1
2(+)
O2
O2
O1
O1
4(-)
2(+)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-167-320.jpg)



![BaTiO3 dopado con Mn
- 169 -
11. BaTiO3 DOPADO CON Mn
11.1. INTRODUCCIÓN
Como ya se ha comentado anteriormente, los dopantes aceptores (Mg(II), Ca(II),
Zn(II)), tienen una influencia considerable en las propiedades eléctricas y,
consecuentemente, en las aplicaciones de los materiales electrocerámicos basados en
BaTiO3. Una vez estudiados estos dopantes aceptores, cuyo estado de oxidación no
varía, nos planteamos estudiar el efecto en las propiedades eléctricas del BT de un ión
cuyo estado de oxidación puede ser variable, como el Mn, y que a su vez es utilizado
como aditivo en una de las aplicaciones más importantes del BT como material PTCR.
Desde el descubrimiento del efecto PTCR (resistencia con un coeficiente de
temperatura positivo) en BaTiO3, se han realizado muchas investigaciones con el
objetivo de desarrollar nuevas composiciones mejorando sus propiedades y sus
características de procesado.
Se ha estudiado el efecto de la adición de metales de transición, como Mn(II),
Cr(II) y Cu(II), en el efecto PTCR del BaTiO3 y se observó que la adición de pequeñas
cantidades de estos elementos mejoran considerablemente el efecto PTCR149
. En
particular, el Mn es uno de los elementos más eficaces150
, utilizándose en los materiales
PTCR comerciales. La segregación de impurezas de metales de transición a las fronteras
de grano, parece ser la causa de esta mejora en el efecto PTCR al utilizar estos dopantes
aceptores151
. Chiang y col.152
observaron la segregación de Mn en la frontera de grano
por MET en muestras de BaTiO3 codopadas con Mn y Nb. Lee y col.153
estudiaron el
efecto PTCR en muestras de BaTiO3 codopadas con Mn y La, comprobando que el
manganeso actúa como aceptor y que la segregación de éste a la frontera de grano es la
responsable de la mejora en dicho efecto.
El uso de manganeso como dopante aceptor es también importante en los
condensadores basados en BaTiO3 porque mejora la resistencia de las cerámicas en
atmósferas reductoras y en particular, éstas pueden ser calcinadas con electrodos
metálicos, como Ni, sin interaccionar éstos con la muestra. Otras propiedades
interesantes de este dopado son que el manganeso inhibe la reducción del BaTiO3 y, a
diferencia de otros elementos de transición como Fe, Zn y Ni, no provoca una
disminución del punto de Curie.
El estado de oxidación del Mn puede variar de divalente (Mn(II)) a trivalente
(Mn(III)) ó tetravalente (Mn(IV)). Atendiendo a los radios iónicos en coordinación
octaédrica87
, el Mn(III) (72 pm) puede ser introducido en las posiciones del Ti(IV)
(74.5 pm) en el BT. La incorporación puede escribirse, según la notación de Kröger-
Vink (apéndice 4), como:
149
H. Ueoka, Ferrelectrics 7 [1-4], 351-53 (1974)
150
T. R. N. Kutty y P. Murugaraj, Materials Letters 3 [5-6], 195-9 (1985)
151
W. Heywang, J. Mater. Sci. 6 [9], 1214-26 (1971)
152
Y. M. Chiang y T. Takagi, J. Am. Ceram. Soc. 73 [11], 3278-85 (1990)
153
J.H.Lee, S.H. Kim y S.H.Cho, J. Am. Ceram. Soc. 78 [10], 2845-48 (1995)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-171-320.jpg)
![Capítulo 11
- 170 -
2BaO + Mn2O3 2 x
Ba
Ba + 2 '
Ti
Mn + 5 x
O
O + •
•
O
V [11.1]
El límite de solubilidad del Mn en el polimorfo tetragonal/cúbico de la
disolución sólida BaTi1-xMnxO3-δ es ≤ 1.0 mol%154,155
. Al aumentar el contenido de Mn,
se incrementa el número de vacantes de oxígeno. La concentración de vacantes de
oxígeno depende del estado de oxidación del manganeso, disminuyendo al cambiar de
Mn(II) a Mn(III)ó Mn(IV).
El estado de oxidación del manganeso varía en función de la atmósfera y de las
condiciones de sinterización156
. Algunos autores157,158
mostraron que si el enfriamiento
es lento y en atmósfera de oxígeno, el estado de oxidación para el manganeso es +4,
mientras que, si el enfriamiento es rápido y la atmósfera de sinterización es H2, es +2. El
estado de oxidación el Mn muestra una gran dependencia con la 2
O
P durante la
sinterización, determinando éste por medidas de susceptibilidad magnética, y
concluyendo, de la misma forma, que el estado de oxidación es +4 si la atmósfera de
sinterización es O2, una mezcla de +3 y +4 en aire y +2 en H2 a 1400 ºC. Al disminuir el
estado de oxidación se observan pérdidas de peso en los compuestos, correspondientes a
la creación de vacantes de oxígeno. Wang y col.
159
demostraron que durante la
sinterización del BaTiO3 se produce una pérdida de oxígeno, pero los iones
Mn(III)/Mn(IV) atrapan electrones originando una disminución en la conductividad.
La temperatura de transición del BT y los parámetros reticulares muestran una
gran dependencia con la atmósfera de sinterización. Albersten y col.
160
mostraron que la
temperatura de transición dependía de la 2
O
P y consecuentemente, del estado de
oxidación del Mn. Estos autores indicaron que bajo una 2
O
P = 2.1·10-5
Pa, el estado de
oxidación del Mn era principalmente 2+ y la variación en la temperatura de transición
era de ~ 19.5 ºC/ at. % Mn, mientras que bajo una 2
O
P = 5 Pa, el estado de oxidación
era Mn(III) y como consecuencia la variación en la temperatura de Curie era de
~ 5.7 ºC/ at. % Mn.
En cuanto al polimorfismo del BaTiO3, se ha encontrado que la adición de una
pequeña cantidad de Mn estabiliza la fase hexagonal del BT,161,162
que sólo es estable a
temperaturas superiores a 1460 ºC en BT puro38,41
. Resultados de DRX en muestras de
BaTi1-xMnxO3-δ calcinadas a 1350 ºC durante 2h en aire, indican que la fase es
tetragonal en el intervalo 0 ≤ x ≤ 0.002, hexagonal en el intervalo 0.03 ≤ x ≤ 0.04 y que
en 0.005 ≤ x ≤ 0.02 hay mezcla de las fases tetragonal y hexagonal, mientras que las
154
J. Jeong y Y. H. Han, J. Electroceram. 13, 549-53 (2004)
155
H. Ihrig, J. Phys. C: Solid State Phys. 11, 819-27 (1978)
156
D. K. Lee, H. I. Yoo y K. D. Becker, Solid State Ionics 154-155, 189-93 (2002)
157
H-J Hagemann y H Ihrig, Phys Rev B, 20 [9], 3871-8 (1979)
158
H-J.Hagemann y D- Henning,s J. Am. Ceram. Soc. 64 [10] 590-594 (1981)
159
X. Wang, M. Gu, B. Yang, S. Zhu y W. Cao, Microelectronic Engineering 66, 855-9 (2003)
160
K. Albertsen, D. Hennings y O. Steigelmann, J Electroceram. 2 [3], 193-8 (1998)
161
R. M. Glaister y H. F. Kay, Proc. Phys. Soc. London, 76, 763-71 (1960)
162
H. T. Langhammer, T. Müller, A. Polity, K. H. Felgner y H. P. Abicht, Materials Letters 26, 205-10
(1996)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-172-320.jpg)
![BaTiO3 dopado con Mn
- 171 -
muestras calcinadas en hidrógeno presentan fase tetragonal en todo el intervalo de
composiciones163
. Langhammer y col.
164
encontraron en muestras sinterizadas a 1400 ºC
en aire un cambio en la estructura de tetragonal a hexagonal entre 0.5 y 1.7 % molar en
manganeso. Por otra parte, basándose en distorsiones Jahn-Teller características de
varios estados de oxidación del Mn, se observa que el ión Mn(III) estabiliza la fase
tetragonal (y ortorrómbica) mientras que Mn(II) y Mn(IV) estabiliza la fase
cúbica153,165
.
Resultados de conductividad mostrados por diferentes autores166-168
evidencian
un mecanismo de conducción tipo p, iónico ó tipo n dependiendo de la concentración de
Mn y de la 2
O
P durante la sinterización (figura 11.1); esto es debido a los múltiples
estados de oxidación del manganeso asociados con las vacantes de oxígeno. Al
aumentar el contenido de manganeso, la conductividad en la región tipo p aumenta y
disminuye en la región tipo n. El mínimo de conductividad no depende del contenido de
Mn, pero si de la temperatura de sinterización.
Figura 11.1. Conductividad eléctrica (σ) de una muestra de BaTiO3 dopada con 1 % molar en Mn vs la
presión parcial de oxígeno a diferentes temperaturas. Figura adaptada de la ref. [167].
Con el objetivo de estudiar el efecto de pequeñas cantidades de manganeso en
los diferentes polimorfos del BaTiO3 y construir el diagrama de fases parcial para este
sistema, así como analizar la respuesta eléctrica de las disoluciones sólidas formadas, se
procedió a la síntesis de composiciones en el sistema BaTi1-xMnxO3-δ donde
163
A. Kirianow, N. Ozaki. H. Ohsato, N. Kohzu y H. Kishi, J. Appl. Phys. 40, 5619-5623 (2001)
164
H.T. Langhammer, T. Müller, K.H. Felgner y H.P. Abicht, J. Am. Ceram. Soc. 83 [3], 605-611 (2000)
165
S.B. Desu y E.C. Subbarao, Ferroelectrics 37, 665-668 (1981)
166
I Burn, J. Am. Ceram. Soc. 14 [10], 2453-2458 (1979)
167
J-Y Kim, C-R Song y H-I Yoo, J Electroceram. 1[1], 27-39 (1997)
168
S.I. Osawa, A. Furuzawa y N. Fujikawa, J. Am. Ceram. Soc. 76 [5], 1191-4 (1993)
tipo p
tipo n](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-173-320.jpg)
![Capítulo 11
- 172 -
0 ≤ x ≤ 0.05. Las muestras se sintetizaron mediante metodología sol-gel. Cabe destacar
que en la mayoría de los estudios realizados en BaTiO3 dopado con manganeso, las
muestras se han preparado por metodología tradicional cerámica.
11.2. PROCEDIMIENTO EXPERIMENTAL
Se prepararon, por metodología sol-gel, diferentes composiciones con estequiometría
BaTi1-xMnxO3-δ, con 0 ≤ x ≤ 0.05, siguiendo el procedimiento experimental descrito en
el apartado 6.2. Como precursor de Mn se utilizó el acetato de manganeso (II)
[Mn(CH3COO)2·4H2O 99.999%, Strem Chemicals].
En primer lugar, se preparó una disolución de 12.6 mg/mL de acetato de
manganeso (II) en metanol, ya que la cantidad de Mn incorporada era muy pequeña. El
acetato de bario se disolvió de la forma indicada anteriormente, utilizando las mismas
relaciones molares de Ba:H2O:CH3OH:CH3COOH que en los otros sistemas. A
continuación, se añadió la disolución de bario, gota a gota, sobre la disolución que
contenía el isopropóxido de Ti (IV), obteniéndose una disolución transparente de color
amarillento. Finalmente, para obtener la estequiometría deseada, se añadieron alícuotas
de la disolución del acetato de manganeso sobre la disolución anterior, obteniéndose
una disolución transparente de color amarillento.
Las composiciones preparadas se indican en la Tabla XI.1.
Tabla XI.1. Composiciones preparadas en la disolución sólida BaTi1-xMnxO3-δ.
x Composición
0 BaTiO3 *
0.003 BaTi0.997Mn0.003O3-δ
0.005 BaTi0.995Mn0.005O3-δ
0.007 BaTi0.993Mn0.007O3-δ
0.01 BaTi0.99Mn0.01O3-δ
0.014 BaTi0.986Mn0.014O3-δ
0.017 BaTi0.983Mn0.0017O3-δ
0.02 BaTi0.98Mn0.02O3-δ
0.03 BaTi0.97Mn0.03O3-δ
0.04 BaTi0.96Mn0.04O3-δ
0.05 BaTi0.95Mn0.05O3-δ
* Esta es la misma composición que en el Capítulo 7.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-174-320.jpg)









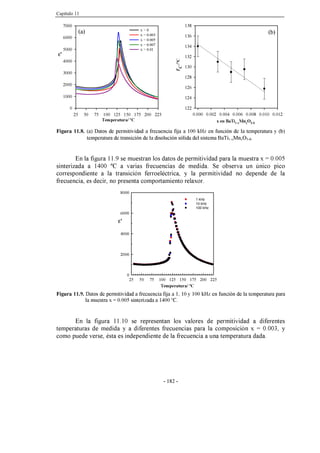
![BaTiO3 dopado con Mn
- 183 -
f / kHz
0.1 1 10 100 1000
ε'
1000
1500
2000
2500
3000
3500
80 ºC
100 ºC
121 ºC
141 ºC
131 ºC
Figura 11.10. Permitividad frente a la frecuencia a 80, 100, 121, 131 y 141 ºC para la muestra x = 0.003
sinterizada a 1300 ºC.
La permitividad del BaTiO3 puro sigue una dependencia con la temperatura
descrita por la ley de Curie-Weiss, en el estado paraeléctrico (por encima de TC):
0
'
T
T
Cw
−
=
ε [3.1]
donde Cw es la constante de Curie y T0 es la temperatura de Curie-Weiss. Para el
BaTiO3 la diferencia entre T0 y TC es generalmente de 8-10 ºC. Por otra parte, siguen el
comportamiento Curie-Weiss otros materiales ferroeléctricos, aunque en algunos de
ellos, muestran unos perfiles de ε’max amplios en función de la temperatura y
desviaciones de la ley de Curie-Weiss. Este efecto se conoce como “transición de fase
difusa” (diffuse phase transition).
Han sido varios los estudios acerca del grado de desviación entre T0 y TC.
Smolenskii170
sugirió que el grado de desviación indicaba el orden de la transición. Por
ejemplo, si TC-T0 0 es indicativo de una transición de primer orden y perfiles estrechos
de ε’ frente T cercanos a TC, mientras que una transición será de segundo orden si
TC = T0 y se obtienen valores de ε’max en un amplio intervalo de temperaturas. Otros
factores pueden afectar al grado de desviación son la porosidad, el tamaño de grano y
las regiones de límite de grano poco definidas. Smolenskii propuso una ecuación
cuadrática para diversos materiales ferroeléctricos que mostraron desviación del
comportamiento de Curie-Weiss:
2
)
(
'
1
c
T
T
B
A −
+
=
ε
[11.2]
170
G.A. Smolenskii, J. Phys. Soc. Japan. 28, 26-37 (1970)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-185-320.jpg)
![Capítulo 11
- 184 -
donde A = 1/ε’max y B = 1/2ε’maxδ; δ es un parámetro que describe el grado de
difusividad de la transición de fase.
Uchino y Nomura171
propusieron una expresión más general para los materiales
que muestran desviaciones de la ley de Curie-Weiss:
'
)
(
1
'
1
max
' c
T
T c γ
ε
ε
−
=
− [11.3]
donde c’ y γ son constantes 1 ≤ γ ≤ 2. Cuando γ = 1 se trata de la ley de Curie-Weiss,
mientras que si γ = 2 a la de Smolenskii. Smolenkii sugirió que la desviación de la ley
de Curie-Weiss se debe a que los cristales que exhiben transición de fase difusa pueden
considerarse como materiales que, a escala microscópica contienen variaciones
composicionales y, así pues, consisten en microvolúmenes cada uno de los cuales
presenta ligeras diferencias en el TC.
Para conocer el comportamiento de las todas las muestras y el orden de la
transición ferroeléctrica de éstas, se procedió al ajuste de los datos según las expresiones
mencionadas anteriormente. En la figura 11.11 se muestran las gráficas de Curie-Weiss,
de Smolenskii y de Uchino para la muestra con x = 0.003. Se observa una ligera
desviación del comportamiento Curie-Weiss a partir de ~140 ºC. Por ello, se procedió al
ajuste de los datos a las ecuaciones de Smolenskii y Uchino, para conocer el grado de
desviación de la ley de Curie-Weiss. Los datos no se ajustaron a la expresión de
Smolenskii ya que no se ajustaron a un comportamiento lineal, figura 11.11.b, mientras
que muestran una buena linealidad para la ecuación de Uchino (c). Del ajuste por
mínimos cuadrados, se obtuvo el exponente γ, que resultó ser de 1.1(8) para la muestra
x = 0.003. Este resultado corrobora la desviación del comportamiento de Curie-Weiss
(γ = 1) para estas muestras. Por tanto, a pesar que a escala macroscópica se obtuvieron
muestras de estequiometría BaTi1-xMnxO3-δ, se observó que presentaban variaciones
composicionales a escala microscópica asociadas al fenómeno de transición de fase
difusa. Para todas las composiciones, se observó la desviación del comportamiento
Curie-Weiss y se ajustaron los datos a la expresión de Uchino.
171
K. Uchino y S. Nomura, Ferroelectr. Lett. Sect. 44, 55-61 (1982)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-186-320.jpg)




![BaTiO3 dopado con Mn
- 189 -
Z' / kΩcm
0 20 40 60 80 100
Z
'
'
/
k
Ω
c
m
-100
-80
-60
-40
-20
0
aire
nitrogeno
oxígeno
Para comprobar si el electrodo influye en la respuesta eléctrica, se reemplazaron,
en la muestra x = 0.003, los electrodos de Pt por otros de Au y se volvió a medir. La
respuesta fue la misma, por lo que es independiente del electrodo utilizado.
Mecanismo de conducción
Se realizaron medidas de impedancia variando la atmósfera durante la medida, y
manteniendo constante la temperatura. Las atmósferas fueron aire, nitrógeno y oxígeno.
En la figura 11.15 se reflejan los resultados para la muestra x = 0.003. La respuesta
eléctrica es similar en las tres atmósferas, pero el valor de la resistencia de ambos
elementos varía en función de la atmósfera de medida. En la figura se observa que, tanto
la resistencia del elemento de alta frecuencia como la de baja frecuencia disminuyen al
cambiar la atmósfera de nitrógeno, a aire y a oxígeno. Este comportamiento se observó
en todas las muestras y fue totalmente reversible.
Al incrementar la presión parcial de oxígeno se provoca la adsorción de éste en
la superficie de la muestra, provocando la siguiente reacción:
½ O2 + 2e-
O2-
[10.3]
Como resultado de la adsorción de oxígeno, se produce una disminución del
número de electrones en ésta. Si los electrones participasen en el mecanismo de
conducción, al aumentar la presión parcial de oxígeno, disminuiría el número de
electrones en la muestra, con lo que la conductividad asociada disminuiría, es decir, la
resistencia aumentaría. En este caso, el mecanismo de conducción sería tipo n. En
nuestras muestras, como la resistencia disminuye al aumentar la presión parcial de
oxígeno, se concluye que el mecanismo de conducción es predominantemente tipo p, es
decir, los portadores de carga mayoritarios son los huecos.
Figura 11.15. Plano complejo de la impedancia, Z*, con los datos obtenidos a 555 ºC para la muestra
x = 0.003 medida usando diferentes atmósferas.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-191-320.jpg)
![Capítulo 11
- 190 -
Para un material aislante, según la estructura de bandas de energía de los sólidos,
todos los estados en la banda de valencia están completamente llenos con electrones
mientras que la banda de conducción está vacía. Mediante este mecanismo, cada
electrón promovido a través del gap (intervalo prohibido de energía), deja un hueco en
la banda de valencia. De esta forma, la conductividad en materiales bajo estas
condiciones de presión parcial de oxígeno no debería variar mucho, ya que existirían
dos tipos de portadores: electrones y huecos. Este sería el caso en que cada átomo de
Ti(IV) fuera reemplazado por un átomo de Mn(III), según la disolución sólida
BaTi1-xMn3+
xO3-3x/2. El hecho de que el mecanismo de conducción sea tipo p, es decir,
los portadores son los huecos, sugiere la posibilidad, como se ha explicado en los
sistemas anteriores, que la fuente de los portadores tipo p sean los iones óxido
débilmente unidos en la estructura defectuosa resultante.
Dependencia de la resistencia con el voltaje
Atendiendo a los resultados presentados anteriormente en los sistemas aceptores
estudiados, en cuanto a la dependencia de la resistencia con el voltaje se refiere, en este
caso, nos propusimos analizar dicha dependencia en función de los estados de oxidación
que puede presentar el Mn, ya que puede estar presente como Mn(II), Mn(III) y
Mn(IV). Si éste actúa como aceptor (Mn(II) ó Mn(III)) se prevé una respuesta
semejante con el voltaje, pero sin embargo, si actúa como ión isovalente al sustituir al
Ti(IV), puede que no presente la misma dependencia.
Por simplicidad en cuanto a la respuesta eléctrica estudiada, se comprobó el
efecto del voltaje aplicado en la composición x = 0.005 sinterizada a 1400 ºC, la cual
presenta un único componente asociado al bulk ferroeléctrico de la muestra. En la figura
11.16 se muestra el efecto de la aplicación de un voltaje dc de 10V hasta alcanzar el
estado estacionario en esta muestra.
Figura 11.16. (a) Plano complejo de la impedancia y (b) gráficas espectroscópicas de Z’’/M’’ para la
muestra x = 0.005 sinterizada a 1400 ºC, antes y después de aplicar un voltaje de 10V
[160 Vcm-1
] durante 2h.
Z' / kΩcm
0 3 6 9 12 15 18
Z
'
'
/
k
Ω
c
m
-18
-15
-12
-9
-6
-3
0
0V
10v
Z
'
'
/
k
Ω
c
m
-8
-6
-4
-2
0
f / Hz
102 103 104 105 106 107
1
0
-
9
M
e0
-
1
/F
-
1
c
m
0
5
10
15
20
25
30
707 ºC 707 ºC
(a) (b)
0V
10v](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-192-320.jpg)

![Capítulo 11
- 192 -
Z' / kΩcm
0 1000 2000 3000 4000 5000 6000
Z
'
'
/
k
Ω
c
m
-6000
-5000
-4000
-3000
-2000
-1000
0
0V
10V 5min
10V 82min
10V 1205min
10V 1497min
Z' / kΩcm
0 100 200 300 400
Z''
/
kΩcm
-400
-300
-200
-100
0
f / Hz
102 103 104 105 106 107
1
0
-
9
M
e0
-
1
/F
-
1
c
m
0
3
6
9
12
15
18
0V
10V 5min
10V 82min
10V 1205min
10V 1497min
diferentes tiempos para analizar la dependencia de la resistencia con el voltaje. En la
figura 11.18 se muestran las medidas de impedancia tras la aplicación de 10V a
diferentes tiempos.
Figura 11.18. (a) Plano complejo de la impedancia y (b) gráfica espectroscópica M’’ para la muestra
x = 0.005, sinterizada a 1400 ºC y enfriada rápidamente sobre nitrógeno líquido, antes y
después de aplicar un voltaje de 10V [160Vcm-1
] a diferentes tiempos a 485 ºC. Las
medidas eléctricas se realizaron en atmósfera de nitrógeno.
Como puede verse en la figura 11.18, la aplicación del voltaje dc provocó un
aumento de la resistencia total de la muestra con el tiempo. Si se representan los
mismos datos en forma de gráficas de Z”/M” puede observarse que la muestra es
inhomogénea eléctricamente ya que contiene dos componentes tras la aplicación del
voltaje; específicamente, el componente de alta frecuencia aumenta su capacidad, como
se ve en la reducción del tamaño del pico en el espectro de M”, mientras que un nuevo
pico aparece a bajas frecuencias en ambas gráficas y representa la parte del componente
más resistivo. Como se ha discutido anteriormente, en las muestras de BT dopado con
Mg2+
tiene lugar un proceso de nucleación y crecimiento, semejante al observado en
este caso. La diferencia radica en que, en este caso, el nuevo componente es más
resistivo que el bulk original de la muestra. El aumento de la resistencia de la muestra es
reversible al suprimir el voltaje dc.
A continuación, se realizaron medidas de impedancia de esta muestra, x = 0.005,
enfriada rápidamente, pero utilizando una atmósfera reductora (5% H2 / 95% N2)
durante las medidas. En la tabla XI.3 se indican los valores de conductividad, a una
misma temperatura, para la muestra medida tras el enfriamiento lento y tras el
enfriamiento rápido. Como puede verse, al realizar las medidas bajo atmósfera
reductora se produjo un gran aumento de la conductividad, indicativo del mayor grado
de reducción.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-194-320.jpg)
![BaTiO3 dopado con Mn
- 193 -
Tabla XI.3. Conductividad de la muestra x = 0.005 a 456 ºC.
Enfriamiento lento Enfriamiento rápido
Atmósfera de medida Aire N2 H2/N2
σ (Scm-1
) 1.24x10-7
1.75x10-6
1.00x10-4
Posteriormente, se aplicó un voltaje dc manteniendo la atmósfera reductora
durante las medidas. Los resultados obtenidos se presentan en la figura 11.19.
Figura 11.19. (a) Plano complejo de la impedancia y (b) gráfica espectroscópica M’’ para la muestra
x = 0.005, sinterizada a 1400 ºC y enfriada rápidamente sobre nitrógeno líquido, antes y
después de aplicar un voltaje de 10V [160Vcm-1
] durante 3h a 379 ºC. Las medidas
eléctricas se realizaron en atmósfera reductora (5% H2 / 95% N2).
El efecto de la aplicación del voltaje en la atmósfera reductora fue claramente el
aumento de la resistencia de la muestra varios órdenes de magnitud, apareciendo de
nuevo dos componentes eléctricos al igual que la muestra medida con nitrógeno.
Además el proceso fue reversible al suprimir la aplicación del voltaje.
En la figura 11.20 se ilustran dichos resultados en forma de gráficas de
Arrhenius, donde se representa la conductividad total de la muestra de la muestra
x = 0.005 enfriada lentamente y para la muestra enfriada rápidamente, tanto medida en
atmósfera de nitrógeno como de N2/H2. Como puede verse el efecto de realizar un
enfriamiento rápido es aumentar la conductividad de la muestra y disminuir la energía
de activación, siendo todavía más acusado este efecto bajo la atmósfera reductora.
Z' / kΩcm
0 100 200 300 400
Z
'
'
/
k
Ω
c
m
-400
-300
-200
-100
0
Z' / kWcm
0 10 20 30 40 50
Z
'
'
/
k
W
c
m
-50
-40
-30
-20
-10
0
f / Hz
102 103 104 105 106 107
1
0
-
9
M
e0
-
1
/F
-
1
c
m
0
3
6
9
12
15
18
21
• 0V
ο 10V
• 0V
ο 10V
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-195-320.jpg)

![BaTiO3 dopado con Mn
- 195 -
Figura 11.21. (a) Gráficas de Arrhenius para la conductividad total para la muestra x = 0.005 sinterizada
a 1400 ºC y enfriada lentamente, y enfriada rápidamente sobre nitrógeno líquido y medida
en atmósfera de N2 o H2/N2, (mismos datos mostrados en la figura 11.20) y para R1 y R2
después de aplicar un voltaje dc de 10V [160Vcm-1
]; volumen relativo de los
componentes en función del tiempo tras la aplicación de un voltaje dc de 10V, medida en
atmósfera de nitrógeno y a la temperatura de 485 ºC (b) y medida en atmósfera de H2/N2
y a la temperatura de 379 ºC (c).
Nota: los valores de R1 y R2 en la figura 11.21.a están corregidos por el volumen relativo
de los dos componentes.
Según los resultados presentados en la figura 11.21.a, tanto R1 como R2
disminuyen su conductividad al aplicar un voltaje bajo la atmósfera de N2/H2. Como
puede verse R2 disminuye considerablemente su conductividad debido a que el volumen
asociado a dicho componente es muy pequeño, y por tanto, la resistencia asociada es
muy elevada. Resultados semejantes se observan para las medidas llevadas a cabo en
atmósfera de nitrógeno, donde sólo se ha representado un punto.
1000 K/ T
0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4
lo
g
σ
/S
c
m
-
1
-8
-7
-6
-5
-4
-3
0.50
1.32
R
1,10V
R
2,10V
(a)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-197-320.jpg)



![Antecedentes de los bronces de tungsteno
- 203 -
12. ANTECEDENTES DEL LOS BRONCES DE
TUNSTENO
12.1. ASPECTOS GENERALES DE LOS BRONCES DE
TUNSGTENO
El nombre de bronce, dado originariamente por Wohler en 1824 a los compuestos de
W, se aplica actualmente a fases sólidas de óxidos con las siguientes características:
color vivo y lustre metálico, conductividad metálica o semiconductividad y resistencia
al ataque de los ácidos no oxidantes172
. La mayoría de los bronces, aunque no todos,
están constituidos por una matriz de composición MO2 ó MO3 en que M es un metal de
transición capaz de presentar un estado de oxidación inferior a 4 ó 6, respectivamente.
Se han preparado bronces en los que M era Ti, V, Nb, Ta, Mo, W ó Re.
Las estructuras de los bronces de tungsteno se basan en la formación de redes
tridimensionales MO3 por unión de octaedros MO6 a través de todos sus vértices. La
estructura de mayor simplicidad y de mayor simetría de esta clase, es la estructura del
ReO3; por adición de átomos de metales alcalinos a los centros de las celdas elementales
se obtiene la estructura de tipo perovsquita (figura 12.1.a y b). Dos estructuras
totalmente diferentes se encuentran para el bronce de K, que es tetragonal, y para el
bronce formado por K, Rb y Cs que es hexagonal. En la figura 12.1.c y d se muestran
las proyecciones de estas dos estructuras, donde se observa que los iones alcalinos, más
grandes, se encuentran en túneles limitados por anillos de cinco y seis octaedros WO6,
en vez de cuatro.
Figura 12.1. Proyecciones de las estructuras de los bronces de tungsteno: (a) estructura de perovsquita de
los bronces cúbicos, (b) la misma mostrando solamente los iones alcalinos (círculos
sombreados) y los átomos W (círculos pequeños), (c) y (d) armazones de W y de los iones
alcalinos de los bronces tetragonal y hexagonal. Figura adaptada de la referencia [172].
A continuación, se tratará con más detalle la estructura de los bronces
tetragonales. La estructura tetragonal de bronces de tungsteno (TTB) está formada por
octaedros MO6 (donde M es normalmente Ti, Nb, Ta ó W) compartiendo vértices en el
172
A. F. Wells, “Química Inorgánica Estructural” Ed. Reverté, Barcelona, 1978
(a) (b)
(c) (d)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-201-320.jpg)
![Capítulo 12
- 204 -
que se generan tres tipos de intersticios en los que se pueden acomodar diferentes
metales. Un gran número de compuestos cristalizan en esta estructura, con una gran
variedad de propiedades, dependiendo del número de posiciones ocupadas y del tamaño
y carga de los átomos173
. Estos compuestos pueden dividirse en tres categorías, como se
ilustra en la tabla XII.1.
Tabla XII.1. Algunos compuestos con estructura tipo “tetragonal de bronce de tungsteno”. Tabla
adaptada de la referencia [173].
Fórmula Composición a (Å) b (Å) c (Å) Z
1. Bronces no estequiométricos, conductores y altamente coloreados
KxW2O6 x = 0.9 - 1.1 12.31 - 3.84 5
NaxW2O6 x = 0.56 - 0.76 12.10 - 3.75 5
PbxW2O6 x = 0.3 - 0.7 12.20 - 3.78 5
BaxW2O6 x = 0.22 - 0.44 12.15 - 3.84 5
KxMo2O6 x ≈ 1.0 12.32 - 3.86 5
BaNb2O5 12.60 - 3.95 5
BaTa2O5 12.60 - 3.95 5
B2xW2O6 x = 0.01- 0.08 - - -
2. Compuestos del tipo (AO)·x(B2O5)
NaO·4Nb2O5 12.45 3x12.32 3.91 *
K2O·3Nb2O5 3x12.57 - 3.94 *
K2O·2Ta2O5 3x12.43 - 3.88 *
PbO·xNb2O5 x = 1 - 3 17.52 17.59 2x3.94 *
BaO·2Nb2O5 12.46 - 3.97 *
SrO·2½(Nb2O5) 12.34 - 3.94 *
BaO·2Ta2O5 17.55 17.65 3.91 *
Nb16W18O94 12.25 3x12.21 3.94 *
3. Materiales ferroeléctricos con fórmula (A1)2(A2)4(C)4(B1)2(B2)8O30
Pb5Nb10O30 17.65 17.91 2x3.84 4
Pb5Ta10O30 17.61 17.91 2x3.87 4
Sr5Ta10O30 12.45 - 2x3.85 2
Ba5Ta10O30 12.59 - 2x3.92 2
(Pb,X)5Nb10O30 X = Ca, Sr, Ba 17.85 18.14 2x3.90 4
Ba4R2Fe2Nb8O30 R = Nd, Sm, Gd 12.47 - 3.93 1
BaxSr5-xNb10O30 x = 1.25 - 3.75 12.43 - 3.91 1
Ba5.7Nb8.5Zr1.5O30 12.67 12.67 4.02 1
Ba6Nb8Ti2O30 12.54 - 4.01 1
Ba4Na2Nb10O30 17.59 17.63 4.00 2
K6Li4Nb10O30 12.58 - 4.01 1
* El valor de Z depende de la composición y si el compuesto es deficiente en oxígeno.
173
P. B. Jameison, S. C. Abrahams y J. L. Bernestein, J. Chem. Phys. 48 [11], 5048-57 (1968)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-202-320.jpg)
![Antecedentes de los bronces de tungsteno
- 205 -
El primer grupo consiste en bronces no estequiométricos con color
característico, lustre metálico y elevada conductividad eléctrica, como B2xW2O6.174
Los
compuestos del segundo grupo son aparentemente estequiométricos, aunque el intervalo
de composición en este segundo grupo no coincide exactamente con la fórmula base que
contiene grupos B2O6
2-
. Además esta estructura es deficiente en oxígeno y contiene
átomos B adicionales o grupos BO ocupando las cavidades mayores.
El tercer grupo contiene a los materiales ferroeléctricos, y la mayoría de ellos
son incoloros. La fórmula en este grupo es generalmente A5B10O30, donde A es un metal
divalente, y B es Nb ó Ta. Todos estos compuestos ferroeléctricos contienen cinco
unidades fórmula por celda unidad, en la que existen seis posiciones que pueden ser
ocupadas por átomos A. Por ello, hay cinco átomos que puede distribuirse en estas seis
posiciones. El número de átomos A por celda puede aumentar hasta un máximo de seis,
cumpliéndose en estos casos la fórmula general A6B10O30. Este aumento puede
producirse mediante la sustitución de Ti ó Zr por Nb ó Ta, o alternativamente por la
introducción de cationes monovalentes en el cristal, como Li, generándose en estos
casos una máxima ocupación.
Pequeñas diferencias en la estructura de estos compuestos con estructura
tetragonal de bronce de tungsteno, pueden provocar grandes diferencias en las
propiedades ferroeléctricas. Algunos cambios estructurales pueden ser: Pb5Ta10O30
presenta una simetría ortorrómbica, por encima y debajo del punto de Curie, mientras
que Pb5Nb10O30 es tetragonal sobre la TC y ortorrómbico por debajo de ésta, y los
compuestos Ba5xSr5-5xNb10O30 presentan estructura tetragonal por encima y debajo de la
TC.
12.2. MATERIALES FERROELÉCTRICOS CON ESTRUCTURA
TETRAGONAL DE BRONCES DE TUNGSTENO DEL TIPO
(A1)2(A2)4C4(B1)2(B2)8O30
Dentro del tercer grupo de materiales con estructura tetragonal de bronce de tungsteno
(TTB), la familia de compuestos del tipo (A1)2(A2)4C4(B1)2(B2)8O30 ha suscitado gran
interés debido a la gran variedad de propiedades que pueden presentar (ferroeléctricas,
piroeléctricas, piezoeléctricas y de óptica no lineal).
La estructura del bronce de tungsteno173
consiste en una serie compleja de
octaedros BO6 deformados compartiendo vértices, de tal modo que hay tres tipos
diferentes de intersticios (A, B y C), figura 12.2. Como se ha indicado en la tabla XII.1,
la fórmula general para esta familia de compuestos ferroeléctricos es
[(A1)2(A2)4C4] [(B1)2(B2)8]O30. Un catión de tipo A puede ser acomodado en las
posiciones A1, A2 y C, y los cationes de tipo B ocupan los sitios octaédricos B1 y B2.
En la fórmula dada, las posiciones A1 y A2 puede estar ocupados por cationes
divalentes o trivalentes, los sitios B1 y B2 pueden estar ocupados por cationes
174
J. Guo, Ch. Dong, L. Yang, G. Fu y H. Chen, Mater. Res. Bull. 42, 1384-9 (2007)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-203-320.jpg)
![Capítulo 12
- 206 -
tetravalentes o pentavalentes, y el sitio C, que es pequeño, a menudo deja el hueco
vacante. Esta situación dará lugar a la fórmula general A6B10O30.
Figura 12.2. Representación esquemática de la estructura del bronce de tungsteno. Se muestran dos
celdas unidad; los octaedros (B1,B2)O6 a la izquierda y los enlaces (B1,B2)-O a la derecha.
Las combinaciones posibles de iones en esta estructura son muy amplias,
pudiendo combinar numerosos iones generando diferentes formulaciones, algunas de las
cuales se han indicado en la tabla XII.1. Dentro de esta familia de materiales
ferroeléctricos con estructura tetragonal de bronce de tungsteno, variaciones en la
estructura y composición, originan propiedades muy diversas, y como consecuencia
generan una gran versatilidad de aplicaciones. Por este motivo, existen en la bibliografía
numerosos trabajos basados en el estudio de diferentes compuestos ferroeléctricos con
estructura de TTB172,175-189
.
175
P. B. Jamieson, S. C. Abrahams y J. L. Bernstein, J. Chem. Phys. 50 [10], 4352-63 (1969)
176
S. C. Abrahams, P. B. Jamieson y J. L. Bernstein, J. Chem. Phys. 54 [6], 2355-64 (1971)
177
B. Y. Jin, A. S. Bhalla, B. Ch. Choi y J. N. Kim, Phys. Stat. Sol. 140, 239-45 (1993)
178
L. Zhang, Y. G. Wang, P.L. Zhang, W. L. Zhong, Y. Y. Song y Y. X. Sun, Ferroelectrics 196, 43-46
(1997)
179
N. Wakiya, J. K. Wang, A. Saiki, K. Shinozaki y N. Mizutani, J. Eur. Ceram. Soc. 19, 1071-5 (1999)
180
J. Ravez y A. Simon, J. Sol. State. Chem. 162, 260-5 (2001)
181
Y. Guo, K. Kakimoto y H. Ohsato, Appl. Phys. Lett. 85 [18], 4121-3 (2004)
182
S. Fabbrici, E. Montanari, L. Righi, G. Calestani y A. Migliori, Chem. Mater. 16, 3007-19 (2004)
183
Y. Guo, K. Kakimoto y H. Ohsato, Mater. Lett. 59, 241-4 (2005)
184
M Josse, O. Bidault, F. Roulland, E. Castel, A. Simon, D. Michau, R. Von der Mühll, O. Nguyen y M.
Maglione, Sol. State Sci. 11[6], 1118-23 (2009)
185
T. Ikeda, T. Haraguchi, Y. Onodera y T. Saito, Japan J. Appl. Phys. 10 [8], 987-94 (1971)
186
P.V. Bijumon, V. Kohli, O. Parkash, M.R. Varma y M.T. Sebastian, Mat. Sci. And Engi. B 113, 13-8
(2004)
187
F.W. Ainger, W.P. Bickley, G.V. Smith, Proc. Brit. Ceram. Soc. 18, 221 (1970)
188
R.P. Neurgaonkar, J.G. Nelson y J.R. Oliver, Mat. Res. Bull. 27 [6], 677 (1992)
189
S. R. Shannigrahi, R. N. P. Choudhary, A. Kumar y H. N. Acharya, J. Phys. Chem. Solids 59 [5], 737-
42 (1998)
B1
A2
A1
B2
b
a
C](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-204-320.jpg)


![Procedimiento experimental de la síntesis de los bronces de tungsteno
- 211 -
13. PROCEDIMIENTO EXPERIMENTAL DE LA
SÍNTESIS DE LOS BRONCES DE TUNGSTENO
Como se ha comentado en el capítulo anterior, uno de los objetivos principales de esta
tesis fue estudiar cerámicas con estructura de bronce de tungsteno tetragonal dentro del
sistema BaO-Ln2O3-TiO2-Nb2O5, siendo Ln un ión lantánido. La síntesis de estos
materiales se realizó por dos metodologías de baja temperatura: sol-gel y solvotermal.
Se estudiaron composiciones alrededor de la Ba2LnTi2Nb3O15 [Ba4Ln2Ti4Nb6O30],
preparando, en primer lugar, las composiciones estequiométricas Ba2SmTi2Nb3O15 y
Ba2NdTi2Nb3O15, y posteriormente, estudiando disoluciones sólidas alrededor de estas
composiciones variando las relaciones Ba:Ln, Ti:Nb y el contenido de oxígeno.
Teniendo en cuenta estudios previos de solubilidad, los reactivos que se
utilizaron para la preparación de estos materiales fueron: acetato de bario
[Ba(CH3COO)2 99%], isopropóxido de titanio [Ti(OPri
)4 98%, 2% isopropanol] y
etóxido de niobio [Nb(OC2H5)5 +99.9%]. Como precursores de los iones lantánidos se
escogieron el isopropóxido de samario [Sm(OC3H7
i
)3 +99.9%] e isopropóxido de
neodimio [Nd(OC3H7
i
)3 +99.9%]. Todos estos reactivos son de Strem Chemicals. Como
disolventes se utilizó metanol [CH3OH 99%, Probus], ácido acético glaciar [CH3COOH
99.7%, J.B. Baker] y 2,4-pentadiona [CH3COCH2COCH3, acacH, 99.5%, Panreac].
13.1. ESTUDIO PREVIO
En primer lugar, se estudió la solubilidad del isopropóxido de samario (III). El uso de
metanol como único disolvente no permitió la total disolución del alcóxido, pero ésta
mejoraba al añadir previamente cantidades de acacH sobre el alcóxido y posteriormente
adicionar el metanol. Se realizaron diferentes ensayos para encontrar las condiciones de
solubilidad del isopropóxido de samario, manteniendo constante la cantidad de metanol.
En la tabla XIII.1 se indican las relaciones molares de Sm : acacH : CH3OH.
Tabla XIII.1. Estudio de solubilidad del isopropóxido de Sm en función de la cantidad de acetilacetona.
Ref. Sm : acacH : CH3OH Características
3a 1 : 2 : 350 Precipitado blanco
3b 1 : 4 : 350 Precipitado blanco
3c 1 : 8 : 350 Precipitado blanco
3d 1 : 14 : 350 Disolución transparente
Como puede verse, un factor importante en la solubilidad del isopropóxido de
samario fue la cantidad de acetilacetona utilizada, ya que ésta compleja el ión lantánido](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-207-320.jpg)



![Procedimiento experimental de la síntesis de los bronces de tungsteno
- 215 -
Figura 13.3. Imágenes de METAR de la muestra Ba2SmTi2Nb3O15 cruda (170 ºC) (a,c) y de la muestra
calcinada a 900 ºC (b,d).
A partir del patrón de difracción obtenido, se realizaron medidas experimentales
de las distancias interplanares y de los ángulos entre los planos. Teniendo en cuenta la
simetría de estos bronces de tungsteno (P4mm) y los patrones de difracción, se pudo
identificar, en primer lugar, el eje de zona. En la figura 13.4 se muestra el patrón de
difracción obtenido y el patrón de difracción a lo largo del eje de zona [2 3 7] para el
grupo espacial P4mm.
5 nm 2 nm
10 nm 200 nm
(c) (d)
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-211-320.jpg)
![Capítulo 13
- 216 -
Figura 13.4. (a) Patrón de difracción para la muestra Ba2SmTi2Nb3O15 calcinada a 900 ºC y (b) patrón de
difracción a lo largo del eje de zona [2 3 7] para el grupo espacial P4mm.
A continuación se compararon los valores experimentales de las distancias
interplanares y los ángulos, con los valores teóricos según la simetría. De esta forma se
pudieron asignar los valores (hkl) a cada familia de planos. En la tabla XIII.3 se indican
los valores experimentales determinados para las tres familias de planos observadas y
los valores teóricos extraídos de la simetría de estos bronces.
Tabla XIII.3. Distancias y ángulos interplanares, y valores de (hkl) calculados a partir de la muestra
calcinada a 900 ºC.
Valores experimentales Valores teóricos
planos d / Å ang d / Å (hkl) ang
1 3.44 3.44 -3 2 0
2 2.79 2.77 -1 3 1
3 3.10
58
50 3.19 2 1 -1
56.16
50.44
Según los resultados de DRX y METAR, la fase empieza a cristalizar a una
temperatura igual o inferior a 900 ºC. Por tanto, bajo estas condiciones experimentales
se consiguió una reactividad elevada, ya que habitualmente estas fases requieren
tratamientos prolongados a elevadas temperaturas. Por este motivo se establecieron éstas
como las condiciones óptimas a utilizar en la metodología solvotermal.
En resumen, la síntesis de estas cerámicas por el método solvotermal consistió
en la introducción del sol en un recipiente de teflón de 100 mL y la adición de la
cantidad necesaria de metanol para ajustar el volumen final a ~ 40 mL. La bomba de
(a) (b) [2 3 7]](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-212-320.jpg)


![Estudio de cerámicas con estequiometría Ba2LnTi2Nb3O15 (Ln = ión lantánido)
- 221 -
14. ESTUDIO DE CERÁMICAS CON
ESTEQUIOMETRÍA Ba2LnTi2Nb3O15 (Ln = ión
lantánido)
14.1. ANTECEDENTES DEL SISTEMA Ba2MTi2Nb3O15
En el sistema BaO-M2O3-TiO2-Nb2O5, donde M es ión lantánido ó Bi/Ta, los materiales
que presentan la estructura tetragonal de bronce de tungsteno (TTB) poseen unas
propiedades ferroeléctricas interesantes. En este sistema, el campo de existencia de la
fase tetragonal se limita a los siguientes compuestos: Ba4M2Ti4Nb6O30
(Ba2MTi2Nb3O15), Ba5MTi3Nb7O30 y Ba3M3Ti5Nb5O30. Sin embargo, hay pocos
estudios realizados con materiales de este tipo debido a la complejidad que presentan.
Dentro de este sistema cuaternario, la familia de materiales que presentan
estructura de bronce de tungsteno con fórmula general Ba2MTi2Nb3O15
[A1(A2)2(C)2B1(B2)4O15] ha sido estudiada recientemente incluyendo una gran
variedad de iones lantánidos, que van desde La a Dy, así como Bi, y Ta190-199
. Todos los
compuestos de esta familia muestran una transición ferroeléctrica/paraeléctrica
correspondiente a una transición de fase de P4bm (no centrosimétrica) a P4/mbm
(centrosimétrica). Para M = La y Bi, el compuesto Ba2MTi2Nb3O15 se comporta como
un material ferroeléctrico relaxor a baja temperatura, que depende de la frecuencia por
debajo del punto de Curie, mientras que altas temperaturas presenta una respuesta de
Curie-Weiss. Para M = La, el valor de la TC aumenta con la frecuencia desde -88 ºC a
100Hz a 27 ºC a 1 GHz. A medida que el tamaño del catión disminuye se observa, en
primer lugar, un aumento en la temperatura de transición, de -73 ºC para La(III)
(r = 103pm) a 327 ºC para Gd3+
(r = 94pm); y en segundo lugar, un cambio en la
transición de fase, de relaxor a una transición de primer orden.
Miles y col.193
realizaron estudios estructurales basados en difracción de
neutrones a -173 y 127 ºC para Ba2LaTi2Nb3O15, basándose en la celda unitaria estándar
de un bronce tetragonal. A -173 ºC, el grupo espacial polar es P4bm (no
190
C.A. Kirk, M.C. Stennett, I.M. Reaney y A.R. West, J. Mater. Chem. 12, 2609-2611 (2002)
191
G. C. Miles, M. C. Stennett, D. Pickthall, C. A. Kirk, I. M. Reaney y A. R. West, Powder Diffraction,
20 [1], 43-6 (2005)
192
M. C. Stennett, G. C. Miles, J. Sharman, I. M. Reaney y A. R. West, J. Eur. Ceram. Soc. 25, 2471-5
(2005)
193
G. C. Miles, M. C. Stennett, I. M. Reaney y A. R. West, J. Mater. Chem. 15, 798-802 (2005)
194
M. Stennett, I.M. Reaney, G.C. Miles, D.I. Woodward, A.R. West, C.A. Kirk y I. Levin, J. Appl. Phys.
101, 104114-1-7 (2007)
195
S. Kamba, S Veljko, M. Kempa, M. Savinov, V. Bovtun, P. Vanek, J. Petzelt, M.C. Stennett, I.M.
Reaney y A.R. West, J. Eur. Ceram. Soc. 25, 3069-73 (2005)
196
M.C. Stennett, I.M. Reaney, G.C. Miles y A.R. West, J. Am. Ceram. Soc. 90 [3], 980-2 (2007)
197
I. Levin, M.C. Stennett, G.C. Miles, D.I. Woodward, A.R. West y I.M. Reaney, Appl. Phys. Lett. 89,
122908-1-3 (2006)
198
R. Palai, R. N. P. Choudhary y H. S. Tewari, J. Phys. Chem. Solids 62, 659-700 (2001)
199
X. H. Zheng y X. M. Chen, Solid State Comm. 125, 449-54 (2003)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-215-320.jpg)
![Capítulo 14
- 222 -
centrosimétrico) donde el Ba (A1) y el La (A2) están completamente ordenados en las
posiciones A, mientras que el Ti y Nb están distribuidos de forma desordenada en las
dos posiciones octaédricas B1 y B2, ya que se detectaron pequeñas desviaciones en la
ocupación estadística para estas dos posiciones. El Nb muestra preferencia por la
posición B2, y el Ti por la posición B1. La estructura del bronce de tungsteno, figura
14.1, permite un pequeño desplazamiento de los átomos de Nb y Ti dentro del octaedro
(Nb/Ti)O6, mientras que no es posible determinar si están desplazados de igual forma en
ambos octaedros. A 127 ºC, el grupo espacial es P4/mbm (centrosimétrico) y no permite
el desplazamiento de los cationes del centro de los octaedros. Además, los estudios de
difracción mostraron que aparecía una supercelda débil paralela a la dirección [110] a
temperatura ambiente en la zona paraeléctrica.
Figura 14.1. Representación esquemática de la estructura del bronce de tungsteno a lo largo del eje c. Se
indican las posiciones B1/B2, las posiciones pentagonales (A1), cuadradas (A2) y triangular
(C).
Estudios posteriores194
por difracción de electrones de área seleccionada (DEAS)
mostraron que todas las fases presentan una superestructura compleja, que se caracteriza
por un doble eje c, así como la formación de una superestructura en el plano ab. La
naturaleza de esta superestructura en el plano ab, sin embargo, varía de
incommensurada en la dirección [110] para M = La, Bi (ferroeléctricos relaxores), a
commensurada en la misma dirección para iones lantánidos más pequeños como
Nd(III), Sm(III) y Ga(III) que son ferroeléctricos clásicos. Celdas inconmensuradas
similares han sido observadas en otras fases de bronces como Ba2NaNb5O15,200,171
BaxSr1-xNb2O6
169,201-202
y Pb1-xBaxNb2O6.203
Ambas superestructuras suponen diferentes
topologías de la rotación de los octaedros.
Levin y col.197,204
realizaron estudios por DEAS a diferentes temperaturas para la
fase Ba2NdTi2Nb3O15, mostrando una secuencia de cambios bastante compleja,
apareciendo de la misma forma una superestructura que cambia de inconmensurada a
200
P.J. Lin y L. A. Bursill, Acta Crystallogr. B43, 504-12 (1987)
201
L. A. Bursill y P.J. Lin, Acta Crystallogr. B43, 49-56 (1987)
202
J. Schneck, J. C. Toledano, R. Whatmore y F. W. Ainger, Ferroelectrics, 36 [1], 327-30 (1981)
203
C. A. Randall, R. Guo, A. S. Bhalla y L. E. Cross, J. Mater. Res. 6, 1720 (1991)
204
I. Levin, M. C. Stennett, G. C. Miles, D. I. Woodard, A. R. West y I. M. Reaney, IEEE International
Symposium on Applications of Ferroelectrics, 4393236, 266-268 (2007)
B2
B1](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-216-320.jpg)

![Capítulo 14
- 224 -
14.2. PROCEDIMIENTO EXPERIMENTAL
Se estudiaron las composiciones Ba2SmTi2Nb3O15 (BSTN) y Ba2NdTi2Nb3O15 (BNTN)
dentro del sistema BaO-Ln2O3-TiO2-Nb2O5. Para ello se utilizaron dos vías de síntesis
de baja temperatura alternativas al método cerámico tradicional: sol-gel y solvotermal.
En primer lugar, se preparó la composición Ba2SmTi2Nb3O15 (BSTN) por
metodología sol-gel. Posteriormente, se preparó, por metodología solvotermal, las dos
composiciones: BSTN y BNTN.
El procedimiento experimental seguido para la preparación de soles
transparentes se ha descrito en el capítulo 13. Como se ha indicado, ambas rutas
sintéticas tuvieron en común la preparación de los soles, aunque el tratamiento posterior
de éstos fue diferente. Los precursores de samario y neodimio utilizados fueron
isopropóxido de samario [Sm(OC3H7
i
)3 +99.9%, Strem Chemicals] e isopropóxido de
neodimio [Nd(OC3H7
i
)3 +99.9%, Strem Chemicals], respectivamente.
Tras la preparación del sol siguiendo el procedimiento anteriormente descrito,
éste se mantuvo en agitación durante 48h, y posteriormente, tras la eliminación de parte
del disolvente se obtuvo un gel homogéneo y transparente. La evaporación del
disolvente se realizó a temperatura ambiente en un desecador. Finalmente, el gel se secó
totalmente bajo las lámparas IR.
Para la síntesis solvotermal, al sol se le añadió metanol hasta un volumen total de
40 mL y se introdujo en un recipiente de teflón de 100 mL. La bomba de digestión se
introdujo en una estufa manteniendo la reacción a 170 ºC durante 24h (condiciones
óptimas que se obtuvieron de estudios previos descritos en el apartado 13.2),
obteniéndose un precipitado que tras la centrifugación, se lavó varias veces con acetona.
14.2.1. Análisis termogravimétrico y térmico diferencial
Los geles de las muestras BSTN y BNTN, una vez secos, se sometieron a un análisis
termogravimétrico (ATG) y térmico diferencial (ATD) con el fin de encontrar las
condiciones de calcinación más adecuadas para cada metodología. En las figuras 14.2 y
14.3 se muestran los resultados de la evolución de los productos crudos para BSTN,
preparado por sol-gel y solvotermal, y BNTN preparado por solvotermal.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-218-320.jpg)






![Estudio de cerámicas con estequiometría Ba2LnTi2Nb3O15 (Ln = ión lantánido)
- 231 -
Figura 14.8. Difractogramas de rayos X de la muestra BSTN sinterizada a 1400 ºC preparada por ambos
métodos.
A partir de los difractogramas y mediante una rutina de minimización por
mínimos cuadrados, se obtuvieron los parámetros de celda que se muestran en la tabla
XIV.1. Se han comparado con valores extraídos de la bibliografía para la misma
muestra Ba2SmTi2Nb3O15 preparada por el método cerámico tradicional, y como vemos,
los valores son semejantes.
Tabla XIV.1. Parámetros de celda para el compuesto Ba2SmTi2Nb3O15.
Para estudiar la homogeneidad de la muestra que presentaba fase única por
DRX, se sometió a un análisis microestructural por MEB/AXED. La micrografía para la
muestra BSTN preparada por vía solvotermal y sinterizada a 1400 ºC se muestra en la
figura 14.9, y como puede observarse el tamaño de partícula oscila entre 1 y 5 μm.
Mediante el uso del detector de electrones retrodispersados se pudieron observar
las diferentes regiones de la muestra de BSTN por su diferente intensidad de color. Las
regiones más oscuras corresponden a la fase mayoritaria, con un crecimiento de los
granos en forma de agujas. Las partículas más pequeñas, con tamaños incluso
nanométricos, corresponden a la fase minoritaria.
Los resultados por AXED indican que las regiones mayoritarias tienen una
relación molar Ba:Sm:Ti:Nb cercana a 2:1:2:3 y las minoritarias poseen una relación
Ba:Sm:Ti:Nb de 0:1:0:1. La relación en la zona mayoritaria podría corresponder a
a/ Å c/ Å V/ Å3
BSTN 12.3560(3) 3.9175(23) 598.1(3)
Ref. [195] 12.3587(5) 3.9295(3) 597.20
º2θ
24 26 28 30 32 34
I
n
t
e
n
s
i
d
a
d
r
e
l
a
t
i
v
a
(
u
.
a
.
)
solvotermal
(
4
1
0
)
(
3
2
0
)
(
2
1
1
)
(
4
0
0
)
(
2
2
1
)
(
1
1
1
)
BSTN
*
*
*Ba3Ti4Nb4O21
sol-gel
*
(
3
1
1
)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-225-320.jpg)

![Estudio de cerámicas con estequiometría Ba2LnTi2Nb3O15 (Ln = ión lantánido)
- 233 -
Figura 14.10. Difractogramas de rayos X de la muestra BNTN preparada por el método solvotermal y
sinterizada a varias temperaturas.
Se calcularon los parámetros de celda para la muestra BNTN a partir de los
difractogramas, obteniendo valores semejantes a los extraídos de la bibliografía (tabla
XIV.3).
Tabla XIV.3. Parámetros de celda para el compuesto Ba2NdTi2Nb3O15.
La micrografía para la muestra BNTN sinterizada a 1300 ºC se muestra en la
figura 14.11. Se observa que el tamaño de partícula oscila entre 1 y 5 μm, y que la
muestra es totalmente homogénea, sin detectar la presencia de fases secundarias.
Los resultados por AXED mostraron una relación Ba:Nd:Ti:Nb cercana a
2:1:2:3 en toda la muestra, relación que podría corresponder a la fase Ba2NdTi2Nb3O15.
Este resultado corrobora el obtenido por difracción de rayos X.
Tabla XIV.4. % molar de las fases presentes en la
superficie de la pastilla analizada por AXED.
Figura 14.11. Micrografías usando el detector de electrones retrodispersados y análisis semicuantitativos
de las superficies de las pastillas BNTN sinterizada a 1300 ºC.
a/ Å c/ Å V/ Å3
BNTN 12.3884(8) 3.9219(4) 601.90(6)
Ref. [195] 12.3781(5) 3.9317((3) 602.40
% molar 1 2
BaO 34.4 31.9
Nd2O3 8.2 7.9
TiO2 33.0 34.7
Nb2O5 24.4 25.5
º2θ
24 26 28 30 32 34
I
n
t
e
n
s
i
d
a
d
r
e
l
a
t
i
v
a
(
u
.
a
.
)
1400ºC
(
4
1
0
)
(
3
2
0
)
(
2
1
1
)
(
4
0
0
) (
2
2
1
)
(
1
1
1
)
BNTN
(
3
1
1
)
1300ºC
1100ºC
1
2
1 μm](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-227-320.jpg)
![Capítulo 14
- 234 -
Debido a que el grado de sinterización influye en gran medida en las
propiedades eléctricas, se calculó la densidad de las pastillas a las distintas temperaturas
de acuerdo con la ecuación [A3.3]. En la tabla XIV.5 se muestran los resultados
obtenidos.
Tabla XIV.5. Densidad relativa de las composiciones preparadas.
Referencia Método de síntesis Tsinterización ρrelativa /%
Sol-gel 1300 ºC/48h 84
Sol-gel 1400 ºC/48h 87
Solvotermal 1000 ºC/2h 56
Solvotermal 1100 ºC/2h 69
BSTN
Solvotermal 1400 ºC/2h 76
Solvotermal 1100 ºC/2h 79
Solvotermal 1300 ºC/2h 84
BNTN
Solvotermal 1400 ºC/2h 89
La densidad de las pastillas, en todos los casos, aumenta al aumentar la
temperatura de sinterización. Uno de los inconvenientes de utilizar métodos de síntesis
de baja temperatura y tiempos de sinterización cortos, es que no se obtienen densidades
elevadas, comparadas con las obtenidas por el método cerámico.
14.3.2. Caracterización eléctrica
Con el fin de analizar el comportamiento eléctrico de estos materiales, las pastillas de
BSTN y BNTN sinterizadas a las distintas temperaturas se caracterizaron por
espectroscopia de impedancia compleja a diferentes temperaturas en función de la
frecuencia, obteniendo también valores de capacidad a frecuencias fijas.
14.3.2.1. Medidas de impedancia a frecuencia variable
Para conocer la microestructura eléctrica de las muestras, se llevaron a cabo medidas de
impedancia desde temperatura ambiente hasta 900 ºC en el intervalo de 40 Hz a
13 MHz.
Las muestras fueron aislantes a temperatura ambiente con un valor de
conductividad (σ) menor de 10-7
Scm-1
, pero mostraron unos niveles de
semiconductividad muy pequeños a temperaturas elevadas. Como ejemplo, en la figura
14.12, se muestra una selección de datos de impedancia para la muestra BNTN](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-228-320.jpg)














![Estudio de disoluciones sólidas cercanas a la composición Ba2NdTi2Nb3O15
- 251 -
15. ESTUDIO DE DISOLUCIONES SÓLIDAS
CERCANAS A LA COMPOSICIÓN
Ba2NdTi2Nb3O15
15.1. INTRODUCCIÓN
En la bibliografía hay pocos estudios en los que se modifique la estequiometría de
compuestos con estructura tetragonal de bronce de tungsteno y que lleven asociada una
variación en el contenido de oxígeno. Uno de ellos se basa en el estudio del compuesto
Sr0.255La0.03Ba0.7Nb2-yTiyO6-y/2, en el que se ha comprobado que el Ti(IV)puede sustituir
al Nb(V) en las posiciones B manteniendo la electroneutralidad por generación de
vacantes de oxígeno208
, observándose una disminución en la temperatura de transición
al aumentar el contenido de Ti.
Por otra parte, un estudio sobre la disolución sólida Ba6-xLaxNb10O30+δ, también
con estructura de bronce de tungsteno, muestra que esta estructura es capaz de albergar
un exceso de oxígeno para compensar la carga209
.
McCabe y col.210
estudiaron la formación de disoluciones sólidas entorno a la
composición Ba2LaTi2Nb3O15 por sustitución del Ti(IV) por Mn(III) ó Fe(III) y Nb(V),
sin la formación de vacantes de oxígeno. El efecto de esta sustitución fue reducir las
propiedades ferroeléctricas relaxoras de este compuesto, y por ello propusieron que
probablemente el catión ferroeléctricamente activo fuera el Ti(IV), y que bajas
concentraciones de cationes paramagnéticos en la posición B disminuye
considerablemente el comportamiento ferroeléctrico de estos materiales.
En vista a los resultados detallados en el capítulo anterior, no está claro si la
composición Ba2LnTi2Nb3O15 existe como tal, o si por el contrario, existe un intervalo
de disolución sólida. Algunos autores, apuntan que en la fase Ba2LaTi2Nb3O15 puede
existir una relación Ba:La, Ti:Nb variable, así como el contenido de oxígeno190
.
Además, parece ser que estas relaciones y el contenido de oxígeno pueden tener una
influencia notable en las propiedades de los compuestos con estructura de bronce de
tungsteno.
Por tanto, y con el fin de determinar si es posible la modificación del contenido
de oxígeno y/o la formación de disolución sólida en nuestros compuestos, nos
planteamos estudiar disoluciones sólidas entorno a la composición estequiométrica
Ba2LnTiNb3O15 presentada en el capítulo anterior. Atendiendo a los resultados
obtenidos en cuanto a la formación de fase pura se refiere, se eligió como ión lantánido
el Nd y la metodología solvotermal. El objetivo fue estudiar la posible formación de
disoluciones sólidas variando las relaciones Ba:Nd, Ti:Nb y el contenido de oxígeno y,
en caso que se formasen, analizar las propiedades eléctricas de estos materiales.
208
H. Amorín, J. Portelles, F. Guerrero, A. Fundora y J.M. Sequeiros, J. Electroceram. 3 [4], 371-5
(1999)
209
Y. K. Hwang y Y. Kwon, Materials Research Bulletin, 32 [11], 1495-1502 (1997)
210
E. E. McCabe y A. R. West, J. Solid State Chem. 183, 624-30 (2010)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-243-320.jpg)
![Capítulo 15
- 252 -
Así pues, se estudiaron las siguientes disoluciones sólidas:
Ba2NdTi2+xNb3-xO15±x/2 y Ba3-yNdyTi1+yNb4-yO15. Los mecanismos implicados en éstas
son diferentes. En la primera disolución, se propone la sustitución de parte de los iones
Nb(V) por Ti(IV) en las posiciones B, con la correspondiente creación de vacantes de
oxígeno para mantener la electroneutralidad. En el caso de x 0, ocurriría lo contrario,
es decir, se sustituiría parte de los iones Ti(IV) por Nb(V) en las posiciones B y por lo
tanto, aumentaría el contenido de oxígeno en el retículo. El mecanismo propuesto es:
2Ti4+
↔ 2Nb5+
+ O2-
[15.1]
En la segunda disolución sólida Ba3-yNdyTi1+yNb4-yO15 tiene lugar una doble
sustitución. Por una parte, los iones Nd(III) sustituyen parte del Ba(II) en las posiciones
A, y al mismo tiempo, los iones Ti(IV) sustituyen al Nb(V) en las posiciones B. En este
caso, se mantiene la electroneutralidad como consecuencia de la doble sustitución sin la
necesidad de modificar el contenido de oxígeno en el retículo. El mecanismo que se
propone es:
Ba2+
+ Nb5+
↔ Nd3+
+ Ti4+
[15.2]
Según la bibliografía, sólo uno de los extremos de las disoluciones sólidas
propuestas presenta una fase conocida. Se trata del compuesto Ba3TiNb4O15, y
corresponde con la composición con y=0 en la disolución sólida Ba3-yNdyTi1+yNb4-yO15.
A continuación, se detallan los antecedentes más relevantes existentes en la bibliografía
sobre el compuesto Ba3TiNb4O15.
Ba3TiNb4O15
La ferroelectricidad en Ba3TiNb4O15 fue descubierta por Fang y col.
211
y su estructura
fue determinada posteriormente por Stephenson212
usando crecimiento de monocristales
por el método de fusión a la llama. La red cristalina es tetragonal y los parámetros de
celda son a = 12.54 ± 0.05 Å y c = 4.01 ± 0.05 Å.
Itoh y col.
213
encontraron que la constante dieléctrica en el eje c para
Ba3TiNb4O15 muestra un pico estrecho con un máximo de 2x104
a la temperatura de
transición de 245 ºC y una constante de Curie de 2.8x105
K, demostrando que la
transición de fase era de primer orden. Zellmer y col.
214
realizaron refinamientos en la
estructura de Ba3TiNb4O15 y determinaron el valor la temperatura de transición.
Andriamampianina y col.
215
estudiaron las propiedades eléctricas de Ba3TiNb4O15 y
vieron que éstas eran muy dependientes del tratamiento térmico seguido. Así,
determinaron que las muestras calcinadas en aire eran conductores mixtos electrónicos-
iónicos y presentaban una fuerte dispersión en la zona paraeléctrica. Las propiedades
211
P. H. Fang, R. S. Roth y F. Forrat, Comp. Rend. 253, 1039- (1961)
212
N. C. Stephenson, Acta Cryst. 18, 496 (1965)
213
Y. Itoh, S. Miyazawa, T. Yantada y H. Iwasaki, Japan J. App. Phys. 9, 157 (1970)
214
L. A. Zellmer, D. K. Smith, D. Nelson y B. E. Scheetz, Powder Diffraction, 3, 222-33 (1988)
215
V. Andriamampianina, J. Ravez, D. Ming y J. M. Reau, Ferroelectrics, 195, 39-42 (1997)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-244-320.jpg)
![Estudio de disoluciones sólidas cercanas a la composición Ba2NdTi2Nb3O15
- 253 -
dieléctricas y ópticas en monocristales fueron estudiadas por Itoh y col.
216
, confirmando
que este compuesto pertenece a la familia de materiales ferroeléctricos bronces de
tungsteno.
Existen además estudios basados en la sustitución en la posición A por
diferentes iones lantánidos217
, donde se indica que estos dopantes actúan como
inhibidores del crecimiento de grano y que la temperatura de transición disminuye a
medida que el radio del ión lantánido aumenta. Se han estudiado otras sustituciones de
Ti y Nb con iones isovalentes, como Hf o Zr y Ta, respectivamente218,219
, siendo todos
ellos ferroeléctricos. Massaroti y col.
220
estudiaron la influencia del dopado en la
estructura local y las propiedades dieléctricas de Ba3TiNb4O15. Se estudió la sustitución
de Cr, Mn ó Fe en las posiciones del Ti, y la sustitución de Y y Fe en las posiciones del
Ba y del Ti. En algunos casos, se encontró que era posible formar disolución sólida en
un amplio intervalo de composiciones, mientras que en otros componentes de esta
familia la estructura de bronce de tungsteno resultó inestable. Como es habitual para
este tipo de fases, en todos los estudios sobre Ba3TiNb4O15, la síntesis se realiza por el
método cerámico tradicional requiriéndose prolongados tratamientos a altas
temperaturas.
Aunque existen diferentes estudios en la bibliografía sobre las propiedades
eléctricas del compuesto Ba3TiNb4O15, hay una gran controversia sobre el
comportamiento ferroeléctrico y la temperatura de Curie de esta fase. Varios autores
muestran un comportamiento ferroeléctrico relaxor221,222
, pero otros autores indican que
éste es un ferroeléctrico clásico218
. Además, la temperatura de transición difiere
significativamente de unos trabajos a otros, de 135 a 245 ºC. 214,216, 218,221,222
216
Y. Itoh y H. Iwasaki, J. Phys. Chem. Solids 34, 1639-45 (1973)
217
K. S. Rao, A. S. V. Subrahmanyan y P. Viswarupachary, Ferroelectrics, 215, 95-102 (1998)
218
E. O. Chi, A. Gandini, K.M. Ok, L. Zhang y P.S. Halasyamani, Chem. Mater. 16, 3616-22 (2004)
219
G. L. Roberts, R. J. Cava, W. F. Peck y J. J. Krajewski, J. Mater. Res. 12 [2], 526-30 (1997)
220
V. Massarotti, D. Capsoni, M. Bini, C. B. Azzoni, M. C. Mozzati, P. Galinetto y G. Chiodelli, J. Phys.
Chem. B 110, 17798-805 (2006)
221
Y. Yuan, X. M. Chen y Y. J. Wu, J. Appl. Phys. 98, 084110-1-5 (2005)
222
D. C. Arnold y F. D. Morrison, J. Mater. Chem. 19, 6485-8 (2009)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-245-320.jpg)











![Estudio de disoluciones sólidas cercanas a la composición Ba2NdTi2Nb3O15
- 265 -
la relación de radios entre las posiciones A1 y A2 es la clave en la naturaleza
ferroeléctrica205,207
. Ello explicaría el comportamiento relaxor observado a baja
temperatura teniendo en cuenta que la diferencia de radios entre Ba2+
/Nd3+
es baja
(175/141).
En cuanto a las anomalías observadas en el perfil de permitividad (figura
15.13.a), cabe destacar que éstas son bastante comunes en materiales ferroeléctricos con
estructura de bronce de tungsteno, aunque existe gran controversia acerca de su
existencia y origen. Según algunos autores223
, estos efectos pueden deberse a la
fluctuación y congelación de clusters micropolares en la zona ferroeléctrica, asociados
con el desplazamientos de los centros Nb/Ti y el desorden de los cationes en ambas
posiciones (A y B), que aumenta al aumentar la diferencia de radios entre A1 y A2, así
como a la modulación conmensurada/inconmensurada de los octaedros del oxígeno.
Otros autores201
atribuyen estas anomalías al acoplamiento entre la polarizabilidad en el
plano ab y el desplazamiento del eje c. Sin embargo, teniendo en cuenta que en algunos
materiales la posición A está ocupada por un solo ión, como PbNb2O6,224
parece
improbable que las anomalías dieléctricas puedan asociarse al desorden local en las
posiciones A y B, sino que más bien parece ser un comportamiento genérico
característico de los materiales con estructura tetragonal de bronce de tungsteno.
Figura 15.13. Datos de permitividad en función de la temperatura para la composición x = 0.16
sinterizada a 1100 ºC a 100 kHz (a) y a la frecuencia fija de 1, 5, 10, 50 y 100 kHz (b).
x = 0.33
Los perfiles de permitividad para la composición x = 0.33 se ilustran en la figura 15.14.
En ésta pueden distinguirse dos picos en la permitividad. Los datos de permitividad a
diferentes frecuencias, evidencian que la capacidad es independiente de la frecuencia a
alta temperatura, mientras que presenta comportamiento relaxor a baja temperatura.
223
X. L. Zhu, X. M. Chen y X. Q. Liu, J. Mater. Res. 23 [11], 3112-21 (2008)
224
J. Guerra, M. Venet, D. Garcia, A. A Eiras y F. Guerrero, Appl. Phys. Let. 91, 062915-1-3 (2007)
Temperatura/ ºC
-150 -100 -50 0 50 100 150 200 250
ε'
50
60
70
80
90
100
110
100kHz
Temperatura/ ºC
-150 -100 -50 0
ε'
55
60
65
70
75
80
1 kHz
10 kHz
100 kHz
(a) (b)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-257-320.jpg)













![Fenómenos eléctricos
- 287 -
V
Q
C =
V
Q
V
V
Q
C =
−
=
2
1
+Q -Q
V1 V2
APÉNDICE 1. FENÓMENOS ELÉCTRICOS
En este apartado se definen diferentes conceptos que son de interés para las aplicaciones
cerámicas.
A1.1. CONCEPTO DE CAPACIDAD
La capacidad de un conductor aislado está definida como el cociente entre su carga (Q)
y su potencial (V)225
:
[A1.1]
La capacidad de un conductor se expresa en CV-1
, unidad denominada faradio
(símbolo, F) en honor a Michael Faraday. El faradio se define como la capacidad de un
conductor aislado el potencial eléctrico del cual, después de recibir una carga de un
culombio, es de un voltio; 1 F = 1 C V-1
= 1 m2
kg-1
s2
C2
.
El concepto de capacidad se puede extender a un sistema de conductores. Si se
considera el caso de dos conductores con cargas +Q y –Q (figura A1.1), siendo V1 y V2
sus potenciales respectivos, de manera que V = V1 - V2 sea su diferencia de potencial, la
capacidad del sistema se define como
[A1.2]
Figura A1.1. Sistema de dos conductores con cargas +Q y –Q. Figura adaptada de la ref. [225].
Esta disposición constituye aquello que se denomina condensador. Un
condensador típico está formado por dos conductores planos y paralelos separados por
una distancia l, con el espacio entre los conductores ocupado por un dieléctrico, figura
A1.2.
225
V. Martinez Sancho, “Fonaments de Física I”, Enciclopedia Catalana, Barcelona (1991)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-271-320.jpg)
![Apéndice 1
- 288 -
l
A
V
V
Q
C 0
2
1
ε
=
−
=
0
0
'
C
C
=
=
ε
ε
ε
dieléctrico
E
+Q -Q
V1 V2
Figura A1.2. Condensador de láminas paralelas. Figura adaptada de la ref. [225].
Suponiendo inicialmente que no existe ningún material entre las láminas, el
campo eléctrico en el espacio entre los conductores es uniforme y viene dado por
E0 = (V1 – V2)/l. Pero si σ es la densidad superficial de carga, la intensidad del campo
eléctrico en el espacio entre la placas es E0 = σ /ε0, siendo ε0 la permitividad del vacío
(ε0 =8.854 x 10-14
Fcm-1
). Por lo tanto:
V1 – V2 = E0l = σ l/ε0 [A1.3]
Si A es el área de las placas metálicas, entonces Q= σA. Por lo tanto, se obtiene
para la capacidad del sistema la expresión:
[A1.4]
Si entre las láminas hay un material, entonces
C = ε A/l [A1.5]
donde ε es la permitividad del material. Comparando [A1.4] y [A1.5], se deduce
que la permitividad relativa o constante dieléctrica relativa viene dada por
[A1.6]
Hay que notar que la capacidad de un condensador sólo depende de su geometría
y del material que existe entre sus láminas. Así pues, el uso de un material con una
constante dieléctrica muy elevada, permite desarrollar condensadores más pequeños con
valores de capacidad muy altos.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-272-320.jpg)

![Apéndice 1
- 290 -
A1.3. TANGENTE DE PÉRDIDAS, tan δ. FACTOR DE PÉRDIDAS
DIELÉCTRICAS
La tangente de pérdidas es una medida de la energía pérdida como energía calorífica por
un condensador en un circuito de corriente alterna. La carga almacenada en un
dieléctrico al aplicar una corriente consta de una componente real y una imaginaria,
producidas por su pérdida resistiva o por la absorción dieléctrica. Si representamos el
campo eléctrico y el desplazamiento (densidad de flujo de corriente) en notación
compleja:
E = E0 eiωt
[A1.7]
D = D0 ei(ωt-δ)
[A1.8]
y haciendo uso de la relación
D = k* E [A1.9]
se obtiene
k* = k0 e-iδ
= k0 (cos δ - i senδ ) [A1.10]
En términos de constante dieléctrica compleja
k* = k’ – i k’’ = ε* / ε0 = 1/ε0 (ε’- i ε’’) [A1.11]
si comparamos con la ecuación [A1.10] tenemos
k’ = k0 cos δ [A1.12]
k’’ = k0 sen δ [A1.13]
por lo tanto, la tangente de pérdidas se expresa como:
tan δ = k’’ / k’ = ε’’ / ε’ [A1.14]
considerando ε’’ como el factor de pérdidas dieléctricas (medida de la
conductancia o pérdida dieléctrica en el material) y ε’ la constante dieléctrica. La](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-274-320.jpg)
![Fenómenos eléctricos
- 291 -
tangente de pérdidas también se conoce con el nombre de factor de disipación del
material (D).
En un condensador ideal, tanto al aplicar un voltaje continuo como alterno, no
hay pérdida de energía, sin embargo en un condenador real, un incremento del flujo de
corriente continua durante la absorción no es recuperable en la descarga, produciéndose
pérdida de energía. Además, si se aplica un campo alterno, el ángulo de fase entre la
corriente y el voltaje es algo menor de 90º. Esa desviación angular de ese valor es lo que
se conoce como el ángulo de pérdidas (δ). La tan δ es la medida de las pérdidas
dieléctricas del condensador y se denomina factor de disipación.
A1.4. POLARIZACIÓN
Un material dieléctrico en presencia de un campo eléctrico se comporta de manera
diferente a como lo hace el vacío, porque contiene portadores de carga que pueden ser
desplazados, y el desplazamiento de carga dentro del dieléctrico puede neutralizar una
parte del campo aplicado. Es decir, cuando aplicamos un campo eléctrico externo,
generando un potencial a través de las dos láminas del condensador de un material
dieléctrico, se produce una alineación de las moléculas cargadas con el campo eléctrico.
Esta alineación de cargas produce dipolos donde las cargas positivas están en la
dirección del campo aplicado (figura A1.3). Como consecuencia se puede producir un
campo eléctrico interno opuesto al campo aplicado, con la reducción del potencial total.
Este fenómeno se conoce como polarización.
Figura A1.3. Representación esquemática de la polarización. Figura adaptada de la ref.[226]
Así pues, la magnitud de la constante dieléctrica (ε’) depende del grado de
polarización o desplazamiento de carga que ocurre en el material. A partir de V = Q/C y
C = ε’Co, podemos escribir para un condensador que contiene un dieléctrico:
226
Héctor Beltrán Mir, Tesis Doctoral, 2001
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
V
Láminas del capacitor
Orientación al azar de los
dipolos antes de aplicar un
campo eléctrico
Alineación de dipolos tras la
aplicación del campo eléctrico
+
-
Dipolos
E
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
+
+ +
+ +](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-275-320.jpg)
![Apéndice 1
- 292 -
V = (Q/ε’) / C0 [A1.15]
Esto es sólo una fracción de la carga total, la carga libre Q/ε’, formada por un
campo eléctrico y un voltaje cerca de la superficie; el resto, la carga enlazada, es
neutralizada por la polarización del dieléctrico. Podemos representar la densidad de
flujo eléctrico total D como la suma del campo eléctrico E y la carga de los dipolos P:
D = ε0 E + P = ε’ E [A1.16]
donde la polarización es la densidad de carga superficial de la carga enlace, igual
al momento dipolar por unidad de volumen de material:
P = N μ [A1.17]
siendo N el número de dipolos por unidad de volumen y μ el momento dipolar
promedio. El momento dipolar eléctrico corresponde a dos cargas eléctricas de
polaridad opuesta ±Q separadas por la distancia d:
μ = Q d [A1.18]
La polarización puede designarse de manera equivalente, según la ecuación
[A1.17], como:
P = ε’ E - ε0 E = ε0 (k’-1) E [A1.19]
Otra ecuación para la polarización teniendo en cuenta el factor de
proporcionalidad α, denominado polarizabilidad, que es una medida del momento
dipolar promedio por unidad de intensidad de campo local, viene dada por:
P = N α E’ [A1.20]
Hay cuatro posibles mecanismos para la polarización en un material dieléctrico,
que conducen a cuatro posibles componentes de la polarizabilidad:](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-276-320.jpg)
![Fenómenos eléctricos
- 293 -
(a) El primero es la polarización electrónica, o pequeño desplazamiento del
centro de gravedad de la nube de electrones cargada negativamente en relación a los
núcleos atómicos positivos, al aplicar un campo eléctrico. Esto provoca la aparición de
la primera componente de la polarizabilidad, la electrónica, αe. Ésta se presenta en
todos los sólidos y en algunos, tales como el diamante, es la única contribución a la
constante dieléctrica.
(b) El segundo mecanismo ocurre cuando se produce un desplazamiento relativo
o separación de iones positivos (cationes) y negativos (aniones) en un sólido, en
relación a otro. Es la llamada polarización atómica, que da lugar a la polarizabilidad
iónica, αi. Es la principal fuente de polarización en cristales iónicos.
(c) El tercer mecanismo es la polarización por orientación, que está asociada con
la presencia de dipolos eléctricos permanentes, que existen aún en ausencia de campo
eléctrico. Estos dipolos pueden cambiar su orientación y tienden a alinearse cuando se
aplica un campo eléctrico externo, siendo normalmente este fenómeno muy dependiente
de la temperatura. Esta última polarización es la que conduce a la aparición de la
polarizabilidad dipolar, αd.
(d) Por último, tenemos la polarización por carga espacio, que genera la
polarizabilidad carga espacio, αs, y que ocurre en materiales que no son dieléctricos
perfectos, pero en los cuales puede ocurrir alguna migración de cargas a través del
material al aplicar un campo eléctrico. En NaCl por ejemplo, los cationes migran
preferentemente hacia los electrodos negativos por medio de defectos cristalinos como
vacantes catiónicas.
Así pues, la polarizabilidad, teniendo en cuenta las cuatro posibles componentes
vendrá dada por la suma:
α = αe + αi + αd + αs [A1.21]
La magnitud de α normalmente decrece en el orden 4 3 2 1, aunque,
naturalmente, no todos los materiales muestran todos los tipos de polarización.
Experimentalmente, las cuatro contribuciones de α y ε’r pueden ser separadas haciendo
medidas a diferentes frecuencias. El resultado se muestra en la figura A1.4.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-277-320.jpg)
![Apéndice 1
- 294 -
10
6
10
5
10
4
10
3
10
2
10
1
1
10
3 10
6 10
9 10
12
αe + αi + αd + αs
αe + αi + αd
αe + αi
αe
ε’
0
ε’
∞
Frecuencia, f
P
e
r
m
i
t
i
v
i
d
a
d
,
ε
’
Figura A1.4. Efectos de la polarización en un dieléctrico. Figura adaptada de las ref. [226] y [227].
A bajas frecuencias, por ejemplo audiofrecuencias (~103
Hz), aparecen las cuatro
contribuciones. A radio frecuencias, (~106
Hz), los efectos de carga espacio pueden no
tener tiempo para producirse. A frecuencias de microondas (~109
Hz), los dipolos
normalmente no tienen tiempo a reorientarse y ese tipo de polarización se disipa. La
polarización iónica no ocurre a frecuencia más elevadas que el infrarrojo (≈ 1012
Hz).
Esto hace que la polarización electrónica pueda observarse en el UV pero se disipe fuera
de la frecuencia de rayos X. El valor de ε0’ es la denominada constante dieléctrica
estática, y el valor de ε∞’ es conocido como la constante dieléctrica óptica. Este último
contiene contribuciones de αe y sólo puede ser obtenido a partir de medidas de índice de
refracción, usando la relación:
n2
= ε∞’ [A1.22]
Cabe señalar un comportamiento especial de algunos materiales en los cuales
desarrollan una polarización espontánea o alineación de dipolos eléctricos y magnéticos
sin la aplicación de campo eléctrico externo. Esto puede ocurrir si la polarización
resultante de dipolos cercanos ejerce una fuerza suficientemente grande. Este proceso se
observa en los materiales ferromagnéticos y ferroeléctricos.
227
A. R. West, “Solid State Chemistry and its Applications”, John Wiley Sons, 1984](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-278-320.jpg)
![Fenómenos eléctricos
- 295 -
f
ε’
ε’’
tanδ
ε∞’
ε0’
f
ε’’
ε’
tanδ
f
max
2
2
0
τ
ω
1
ε
ε
ε
ε
+
′
−
′
+
′
=
′ ∞
∞
A1.5. RELAJACIÓN DIELÉCTRICA
En el proceso de polarización de un material, se produce una polarización instantánea
(P∞), que no alcanza el valor nominal de la polarización (Pe), pero si continua el proceso
de polarización, el tiempo que transcurre hasta que el material pasa al estado excitado es
lo que se denomina tiempo de relajación (τ) y la respuesta del material se conoce como
relajación dieléctrica. Para explicar este fenómeno, Debye construyó un modelo de
relajación cuyas ecuaciones relacionan la constante dieléctrica con el tiempo de
relajación, partiendo de que las frecuencias a las cuales δ es significativa corresponden a
la región donde ε’ no es constante pero varía entre ε0’ y ε∞’. En esta zona podemos
expresar la permitividad en forma compleja como:
ε*
= ε’- i ε’’ [A1.23]
siendo la parte real ε’ equivalente a una medida de la constante dieléctrica y la parte
imaginaria ε’’ el factor de pérdidas; tan δ, viene dada por la relación ε’’/ε’.
La variación de ε’’, ε’ y tan δ con la frecuencia puede observarse en la figura
A1.5.
Figura A1.5. Representación ε’’, ε’ y tanδ frente a la frecuencia. Figura adaptada de las ref. [226] y
[227].
Podemos ver que ε’’ tiene una dependencia característica con la frecuencia,
pasando por un valor máximo a la frecuencia, en donde ε’ experimenta el cambio
máximo en relación a la frecuencia. A partir de esta representación Debye plantea las
siguientes ecuaciones:
[A1.24]](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-279-320.jpg)
![Apéndice 1
- 296 -
ε’
ε'0
ω
ε’’
ε∞
ε0’-ε∞’
2
( )
2
2
0
τ
ω
1
ωτ
ε
ε
ε
+
′
−
′
=
′
′ ∞
( )
2
2
0
0
τ
ω
ε
ε
ωτ
ε
ε
ε
ε
δ
tan
∞
∞
′
+
′
′
−
′
=
′
′
′
=
[A1.25]
[A1.26]
siendo ω = 2πf y τ el tiempo de relajación o tiempo de decadencia de la
polarización iónica; el máximo de ε’’ ocurre cuando ωτ = 1, quedando
ε’’max = ½ (ε0’- ε∞’) [A1.27]
ε0’ es la constante dieléctrica estática cuando (ωt) = 0, y ε∞’ la constante
dieléctrica óptica, cuando (ωt) = ∞.
Los resultados pueden también presentarse como se observa en la figura A1.6,
en la llamada representación Cole-Cole, en la cual ε’’ se representa frente a ε’.
Figura A1.6. Representación de ε” frente ε’ para un material Debye puro. Figura adaptada de las ref.
[226] y [227].
En la práctica, la representación Cole-Cole a menudo no es exactamente
semicircular; de igual modo pasa con los picos de las pérdidas dieléctricas ε’’ que no
son simétricos. Es decir, esta representación implicaría un único tiempo de relajación,
mientras que la situación real es la existencia de una distribución de tiempos de
relajación, lo que conduce a la necesidad de modificar las ecuaciones de Debye. El
fenómeno de la relajación dieléctrica es aplicable a todo tipo de materiales en general,
excluyéndose los metales y algunas aleaciones.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-280-320.jpg)


![Métodos de síntesis
- 301 -
simultánea: [M(OR)n]x + [M'(OR')n']x' consiguiendo una homogeneidad a nivel
molecular, de ahí que a menudo se denomine como gel polimérico.
Las reacciones que tienen lugar son:
1) Reacción de hidrólisis
Esta reacción implica el ataque de un grupo hidroxilo de la molécula de agua a
un átomo metálico que conlleva la sustitución de un grupo OR (del alcóxido) por el OH
(del H2O):
M(OR)n + x H2O → M(OH)x(OR)n-x + x ROH [A2.1]
donde R denota al grupo alquilo y ROH a un alcohol. Dependiendo de la
cantidad de agua y del tipo de catálisis, la hidrólisis puede ser completa (todos los
grupos OR son remplazados por OH):
M(OR)n + n H2O → M(OH)n + n ROH [A2.2]
o parcial, obteniéndose: M(OH)x(OR)n-x.
2) Condensación / polimerización
En el proceso de condensación dos moléculas parcialmente hidrolizadas pueden
unirse. La condensación puede ocurrir de maneras distintas:
- Oxolación:
-M-OH + HO-M- → -M-O-M- + H2O [A2.3]
- Alcoxolación:
-M-OR + HO-M- → -M-O-M- + ROH [A2.4]
Si estas reacciones continúan se puede formar una macromolécula polimérica, o
gel polimérico. Este tipo de reacciones continuadas para formar polímeros o
macromoléculas de cientos y cientos de monómeros se denomina proceso de
polimerización. Un gel se denomina monolítico cuando su tamaño es mayor de unos
pocos milímetros.
Cuando se trabaja con sistemas multicomponentes, con alcóxidos de M, M’,
M’’etc., el objetivo es conseguir enlaces M-O-M’ donde los cationes estén enlazados a
nivel molecular. Esta es la forma de conseguir una buena homogeneidad molecular.
Las principales características que deben presentar los alcóxidos son:
· poseer un grupo OR lábil
· presentar solubilidades elevadas en disolventes orgánicos
· ser fácilmente hidrolizables y, si los distintos alcóxidos ([M(OR)n]x,
[M'(OR')n']x') hidrolizan a velocidades diferentes, se puedan armonizar
las cinéticas de hidrólisis con la adición de modificadores para
conseguir enlaces M-O-M'.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-283-320.jpg)


![Apéndice 2
- 304 -
A2.3. MÉTODO HIDROTERMAL / SOLVOTERMAL
Los procesos hidrotermales/solvotermales pueden definirse como transformaciones o
reacciones químicas en un disolvente bajo o cerca de sus condiciones supercríticas de
presión-temperatura228
.
La técnica hidrotermal ha sido muy popular suscitando el interés de científicos y
tecnólogos de diferentes disciplinas particularmente en los últimos años. El desarrollo
de la síntesis hidrotermal para la preparación de sólidos inorgánicos fue ya descrito por
Rabenau229
que definió la síntesis hidrotermal como el uso de agua como disolvente en
un recipiente sellado de reacción, cuando se alcanza la temperatura de 100 ºC. Con el
nombre general de síntesis solvotermal se agrupan una serie de técnicas en las que un
líquido, en un recipiente cerrado, es calentado por encima de su punto de ebullición, lo
que genera una presión superior a la atmosférica. El líquido habitual es el agua, y de ahí
el nombre de “hidrotermal”; sin embargo, cada vez se van utilizando con mayor
frecuencia otros medios líquidos como disolventes orgánicos, amoníaco líquido,
hidracina, etc. y se refiere entonces a la síntesis solvotermal. El objetivo de la técnica es
lograr una mejor disolución de los componentes de un sistema y así hacer reaccionar
especies muy poco solubles en condiciones habituales.
Bajo estas condiciones supercríticas, las propiedades físicas de los disolventes se
ven afectadas considerablemente. Para el caso del agua, por ejemplo, el producto iónico
crece acusadamente con la presión y la temperatura; la viscosidad del agua disminuye al
aumentar la temperatura, siendo a 500 ºC y 10 bares de presión sólo el 10 % del valor
de viscosidad en condiciones normales; la densidad aumenta al aumentar la presión y la
temperatura, mientras que la constante dieléctrica disminuye.
La presión existente en condiciones de trabajo hidrotermales está determinada
por dos factores: la temperatura y el grado de llenado del recipiente de reacción. En la
figura A2.3, se representa la presión en el recipiente de reacción en función de la
temperatura alcanzada para diferentes porcentajes de llenado para el caso del agua230
.
Como puede verse la presión aumenta a medida que lo hace el llenado del recipiente de
reacción.
Un aspecto importante a tener en cuenta es si la temperatura excede o no el
denominado “punto crítico” del disolvente (374.1 ºC para el agua; 239.5 ºC para el
metanol), ya que, por encima de dicho punto tan especial del diagrama de fases del
disolvente, el comportamiento del disolvente será muy distinto (será un fluido
“supercrítico”, distinto tanto del vapor como del líquido) y el aumento de la presión con
la temperatura será exponencial. En general, puede decirse que la síntesis solvotermal
en condiciones subcríticas dará lugar a sólidos con estructuras más abiertas, mientras
que en condiciones supercríticas, el gran aumento de la presión producirá estructuras
mucho más compactas.
228
G. Demazeau, J. Mater. Chem. 9, 15-18 (1998)
229
A. Rabeneau, Angew. Chem. Int. Ed. Engl. 24 [12], 1026 (1985)
230
R.I. Walton, Chem. Soc. Rev. 31, 230-238, (2002)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-286-320.jpg)
![Métodos de síntesis
- 305 -
Por lo tanto, debido a que la presión alcanzada dentro del recipiente es muy
dependiente de estos factores, y a su vez, la presión influye en gran medida en la
reactividad y solubilidad de los precursores, es muy importante controlar estas
variables, y establecer unas condiciones óptimas para la realización de la síntesis
solvotermal.
Figura A2.3. Presión en función de la temperatura y del porcentaje de llenado de agua en un recipiente de
teflón para la síntesis hidrotermal.
El método hidrotermal se relaciona con otros métodos de activación231
como la
electroquímica y microondas en la fabricación de láminas delgadas, cerámicas,
nanopartículas y nanocristales. Especialmente, como un nuevo método emergente y
complementario al método hidrotermal convencional, el método solvotermal juega un
papel muy importante en la síntesis de materiales avanzados mediante reacciones en
disoluciones no acuosas. De esta forma, el método solvotermal es similar al hidrotermal
a excepción que se utilizan disolventes orgánicos en lugar de agua230
. Históricamente, la
síntesis hidrotermal utilizaba temperaturas sobre 300 ºC, mientras que actualmente, la
mayoría de las síntesis solvotermal de materiales inorgánicos utilizan condiciones
subcríticas con temperaturas 250 ºC.
En el método solvotermal, los disolventes orgánicos juegan un papel importante
en el control de la nucleación y crecimiento de materiales nanocristalinos. Con
disolventes orgánicos adecuados, puede llevarse a cabo nuevas reacciones y se puede
controlar la morfología y las propiedades de estos materiales. La composición y
concentración del disolvente son fundamentales en el control de la forma y la fase
formada232
.
La síntesis solvotermal se realiza normalmente usando un recipiente de teflón
dentro de un autoclave de acero inoxidable, como se muestra en la figura A2.4. Se
231
S.H. Yu, J. Ceram. Soc. Jpn. 109, 565-575 (2001)
232
H.G. Choi, Y.H. Jung y D.K. Kim, J. Am. Ceram. Soc. 88 [6], 1684-1686 (2005)
Temperatura /ºC
P
r
e
s
i
ó
n
/
b
a
r
Temperatura crítica
90%
80%
70%
60%
50%
40%
30%
20%
10%
0 100 200 300 400 500 600 700 800 900
400
0
3200
2800
2400
2000
1600
1200
800
400](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-287-320.jpg)






![Apéndice 3
- 314 -
la densidad relativa (ρr) de las pastillas sinterizadas se obtuvo a partir de la siguiente
ecuación:
ρr = (ρ experimental / ρ teórica) x 100 [A3.1]
donde:
)
(
)
(
)
(
2
exp
cm
espesor
cm
area
g
pastilla
masa
erimental
⋅
=
ρ [A3.2]
)
(
)
(
)
º
(
)
(
Avogadro
de
número
N
celda
volumen
V
unidad
celda
por
atomos
n
Z
molecular
peso
PM
teorica
⋅
⋅
=
ρ [A3.3]
A3.2. ANÁLISIS TÉRMICO DIFERENCIAL (ATD) Y
TERMOGRAVIMÉTRICO (TG)
Muchos materiales sufren cambios bruscos en su estructura y/o propiedades al
calentarlos. Estos cambios pueden estudiarse fácilmente por Análisis Térmico
Diferencial (ATD) ya que estos cambios llevan asociados una entalpía de transición
apreciable. Esta técnica es una vía muy sensible para el estudio de la evolución con la
temperatura de diferentes fases cristalinas así como para el seguimiento de la ruptura y
formación de enlaces en las diferentes fases del material que se sintetiza. Con el
Análisis Termogravimétrico (TG) se estudia las pérdidas de masa de la muestra con la
temperatura, que pueden deberse a la evaporación del disolvente utilizado, combustión
de la materia orgánica, pérdidas de otros componentes, etc.
La combinación de ambas técnicas junto con la difracción de rayos X nos dará
una valiosa información para el diseño del ciclo de calcinación adecuado en cada
muestra.
El equipo utilizado para realizar los análisis, tanto ATD como TG, ya que los
realiza al mismo tiempo, ha sido un TGA/SDTA 850e
de la marca Mettler Toledo. En
los análisis de todas las muestras se ha utilizado atmósfera de aire.
A3.3. TRATAMIENTOS TÉRMICOS
En este trabajo las muestras se calcinaron y sinterizaron a las diferentes temperaturas en
hornos eléctricos, tipo mufla y tubular, en diferentes atmósferas (aire, oxígeno,
nitrógeno e hidrógeno) y en crisoles de platino. El enfriamiento de las muestras fue libre
en el interior del horno o rápido, sobre una lámina de cobre o sobre nitrógeno líquido al
utilizar el horno tubular. Tras la calcinación del polvo, las muestras se molturaron hasta
conseguir una buena homogeneidad, y posteriormente se prensaron en forma de pastilla.
Los ciclos de calcinación y sinterización se describen en cada síntesis.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-294-320.jpg)




![Apéndice 3
- 320 -
)
t)
sin(
t)
sin(
Z
)
t)
sin(
I
t)
sin(
E
I
E
Z 0
0
0
t
t
φ
+
ω
ω
=
φ
+
ω
ω
=
=
La señal de excitación, expresada en función del tiempo, tiene la forma
Et = E0 sin (ωt) [A3.4]
donde Et es el voltaje a un tiempo t, E0 es la amplitud de la señal y ω es la frecuencia
angular. La relación entre la frecuencia angular ω (expresada en radianes/segundo) y la
frecuencia f (expresada en Hertz) es:
ω = 2 π f [A3.5]
En un sistema lineal, la señal respuesta, It, está fuera de fase (φ) y tiene una
amplitud diferente, I0.
It = I0 sin (ωt + φ) [A3.6]
Una expresión análoga a la ley de Ohm permite calcular la impedancia del
sistema como:
[A3.7]
Por lo tanto, la impedancia se expresa en términos de una magnitud Z0
y un desfase φ.
Mediante la relación de Euler,
exp(jφ) = cos φ +j sin φ [A3.8]
(j = 1
− ) es posible expresar la impedancia como una función compleja. De
acuerdo con esta notación el voltaje se describe como
Et = E0 exp(jωt) [A3.9]
y la corriente como](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-300-320.jpg)
![Técnicas de caracterización
- 321 -
Z'
-
Z
ω
IZI
φ
It = I0 exp (jωt + φ) [A3.10]
Así pues, la impedancia se representa como un número complejo
Z(ω) = E/I = Z0 exp(jφ) = Z0 (cos φ +j sin φ) = Z’ + j Z” [A3.11]
A3.6.1. Representación de datos
Como puede observarse en la ecuación A3.11, la expresión de Z(ω) se compone de una
parte real Z’ (resistiva) y de una parte imaginaria Z” (capacitiva). Representando la
parte imaginaria (eje de ordenadas) frente a la parte real (eje de abscisas) se obtiene la
representación de Nyquist o del plano complejo de la impedancia (figura A3.3). Hay
que destacar que en este tipo de representación el eje de ordenadas es negativo para que
así la gráfica resultante se encuentre en el primer cuadrante y facilite la interpretación.
En esta gráfica cada punto representa la impedancia a una frecuencia determinada.
Figura A3.3. Representación de Nyquist o del plano complejo de la impedancia.
En la representación de Nyquist, la impedancia se puede representar por un
vector (flecha en la figura A3.3) de longitud |Z|. El ángulo entre este vector y el eje de
abscisas es φ.
Las diferentes regiones de la muestra son caracterizadas de acuerdo a sus
tiempos de relajación eléctrica o constantes de tiempo. Cuando un sistema se encuentra
en el estado estacionario y es perturbado, por ejemplo con una señal de corriente alterna,
tenderá a relajarse de nuevo al estado estacionario. El tiempo necesario para que tenga
lugar esa relajación se denomina constante de tiempo (τ). El análisis de estos procesos](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-301-320.jpg)
![Apéndice 3
- 322 -
πτ
2
1
=
f
1
max =
ω
RC
RC
=
τ
de relajación proporciona información acerca del sistema. Los procesos rápidos, es
decir, con τ bajas tienen lugar a frecuencias elevadas. Por el contrario, los procesos
lentos, con τ altas, tendrán lugar a frecuencias bajas. Por tanto, cada proceso se
relaciona con una frecuencia característica:
[A3.12]
Las diferentes regiones de una muestra cerámica se caracterizan mediante una
resistencia (R) y una capacidad (C), normalmente ubicados en paralelo. El tiempo de
relajación o constante de tiempo (τ) de cada elemento RC en paralelo está determinado
por el producto de R y C (ecuación A3.13).
[A3.13]
Los datos de impedancia se pueden analizar usando cuatro formalismos
complejos diferentes: impedancia, Z*; admitancia, Y* o A*; permitividad, ε*; y módulo
eléctrico, M*. Cada uno está compuesto de una parte real y otra imaginaria. Los cuatro
formalismos están relacionados mediante,
M* = 1/ε* = jωCoZ* = jωCo(1/Y*) [A3.14]
A partir de la representación del plano complejo de la impedancia (Z*), es
posible identificar diferentes elementos RC y asignarlos a las diferentes regiones de la
muestra. Cada elemento paralelo RC (dos en la figura A3.4) da lugar a un semicírculo
(idealmente) a partir del cual se pueden obtener los valores de R y C. En el dominio de
frecuencias, los elementos RC están separados, debido a que en el máximo del
semicírculo se cumple la relación
[A3.15]
Los valores de R se obtienen a partir del punto de corte sobre el eje Z', como se
muestra en la figura; los valores de C se obtienen aplicando la ecuación A3.15 a la
frecuencia en el máximo de cada semicírculo. En este caso en particular, los dos valores
de capacidad calculados son ~ 1 x 10-12
F y 4 x 10-9
F y las correspondientes resistencias
500 kΩ y 1 MΩ. El circuito equivalente utilizado para interpretar los datos se muestra
en el margen superior derecho.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-302-320.jpg)
![Técnicas de caracterización
- 323 -
Figura A3.4. Datos de impedancia representados en forma de plano complejo de la impedancia, Z” frente
a Z’ donde Z* = Z’ – j Z”, j = 1
− , ω = 2πf (frecuencia angular). El circuito equivalente
utilizado para interpretar los datos se muestra en el margen superior derecho.
Una vez obtenidos los valores de los componentes R y C, el próximo paso es
asignarlos a las diferentes regiones de la muestra. La asignación más inmediata se basa
en la magnitud de los valores de capacidad (tabla A3.1).
Tabla A3.1. Valores de capacidad y su posible interpretación.
Capacidad/ F Fenómeno responsable
10-12
Interior de grano (bulk)
10-11
Segundas fases minoritarias
10-11
– 10-8
Borde de grano
10-10
- 10-9 Interior de grano en
ferroeléctricos
10-9
- 10-7
Capas superficiales
10-7
– 10-5
Interfase electrodo-muestra
10-4
Reacciones electroquímicas
Para un condensador de láminas paralelas con una área A, una separación entre
placas l y un medio de permitividad ε' entre las placas, la capacidad viene dada por la
siguiente ecuación:
)
/
(
'
0 l
A
C ε
ε
= [A3.16]
Z' / kΩ cm
0 200 400 600 800 1000 1200 1400 1600
Z
/
kΩ
cm
-1200
-1000
-800
-600
-400
-200
0
Z' (a) vs Z'' (b)
39.4877 Hz
309852.3 Hz
ω
R1
RT = R1 + R2
ω
C1 = 1 x 10-12
F
C2 = 4 x 10-9
F
R1
C1
R2
C2](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-303-320.jpg)
![Apéndice 3
- 324 -
l1
l2
b
l3
gb
1
2
l
l
C
C
gb
b
=
donde ε0 es la permitividad del vacío, 8.854 x 10-14
Fcm-1
. Para un material con una
constante de celda de valor unidad (l/A = 1 cm-1
) y una permitividad de ~10, se obtiene
un valor de capacidad de ~1 x 10-12
F. Este sería un valor típico de capacidad del
interior de grano (bulk) de la muestra.
Para asignar el segundo semicírculo a una región de la muestra, es necesario
tener una imagen de una cerámica ideal, con granos y fronteras de grano, y considerar
los factores que controlan la magnitud de la impedancia de la frontera de grano. El
modelo de ladrillos (brickwork model) mostrado en la figura A3.5 representa una
cerámica compuesta de granos cúbicos de dimensiones l1, separados unos de otros
mediante límites de espesor l2.
Figura A3.5. Modelo de ladrillos (brickwork model). Interior de grano (b) y límite de grano (gb).
Para este caso idealizado, se cumple la ecuación A3.17.
[A3.17]
Esta se obtiene a partir de la relación inversa entre el espesor y la capacidad dada
por la ecuación A3.9. En la práctica, existe una gran variedad de microestructuras
cerámicas, observándose que la capacidad del límite de grano se extiende en el intervalo
de capacidades de 10-11
– 10-8
F; las capacidades más elevadas aparecen en materiales
que están bien sinterizados, con regiones intergranulares estrechas. Las capacidades más
pequeñas se obtienen a menudo en muestras poco sinterizadas que contienen
“constriction resistances” o cuellos de botella entre granos.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-304-320.jpg)
![Técnicas de caracterización
- 325 -
A3.6.2. Procesado de datos
A pesar que la representación del plano complejo de la impedancia, Z” frente a Z’, es un
método adecuado para la interpretación de los resultados, existen formalismos
alternativos (Y*, ε* y M*) de procesado de datos que pueden proporcionar información
adicional, la cual no es fácilmente accesible a partir del plano complejo debido a la
complejidad de la muestra. Hay casos en los cuales no necesariamente se van a observar
dos elementos bien definidos. El tamaño de los semicírculos es directamente
proporcional a la resistencia del elemento, por tanto, si un elemento es mucho más
resistivo que el otro, su semicírculo va a ser muy pequeño y puede estar dentro del que
tiene resistencia mucho mayor, y en consecuencia observarse únicamente un
semicírculo. Generalmente, en estos casos el semicírculo se ve un poco deformado en
uno de sus extremos, figura A3.6.a. También puede ocurrir que el arco no intercepte en
el origen, con lo cual nos estaría indicando que, aunque no aparezca el arco, existe otro
elemento a frecuencias muy altas. Si los datos de impedancia se procesan y se
representan en la forma de gráfica espectroscópica de los componentes imaginarios Z” y
M” (figura A3.6.b) se puede estudiar por separado la respuesta del límite del grano y de
los granos.
La representación espectroscópica de los componentes imaginarios Z” y M” se
compone de dos gráficas individuales, Z” frente a la frecuencia y M” frente a la
frecuencia. Debido a que tienen en común el eje de abscisas, se suele representar ambas
conjuntamente en una misma gráfica común. Debido a que
M* = jωC0Z* = M’ + j M” [A3.18]
donde j = 1
− , ω = 2πf (frecuencia angular), Co es la capacidad en el vacío,
M’ = ωCoZ” y M” = ωC0Z’, la representación espectroscópica de Z” y M” se puede
considerar en realidad la representación de la parte real y imaginaria de la impedancia,
Z*, frente a la frecuencia.
El interés en representar los datos en forma espectroscópica de Z” y M” es
debido a que ponen de relieve diferentes características de la muestra. La gráfica de
impedancia (Z”) destaca los elementos más resistivos en la muestra mientras que la del
módulo (M”) destaca aquellos elementos con la menor capacidad.
Volviendo al ejemplo de la figura A3.6, mientras en el plano de impedancia
compleja se observa un único semicírculo (figura A3.6.a) que muestra una ligera
desviación de la idealidad a altas frecuencias, en la gráfica espectroscópica de Z” se
observa un único pico, correspondiente al semicírculo único semicírculo observado en
Z* mientras que la gráfica de M” se observan dos. El pico de alta frecuencia de M”
corresponde a la respuesta eléctrica del interior de grano mientras que el de baja
frecuencia corresponde a la respuesta eléctrica del límite de grano.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-305-320.jpg)
![Apéndice 3
- 326 -
RC
j
1
R
C
j
R
1
Z
1
Z
1
Z
1
C
R
T ω
+
=
ω
+
=
+
=
( )2
RC
1
R
Z'
ω
+
=
( )
⎥
⎦
⎤
⎢
⎣
⎡
ω
+
ω
−
= 2
RC
1
RC
R
Z
Figura A3.6. Datos de impedancia representados en formato de plano complejo de la impedancia (a) y de
gráficas espectroscópicas de los componentes imaginarios M” y Z” (b). El circuito
equivalente utilizado para interpretar los datos se muestra en el margen superior derecho de
la figura (a).
Los valores de C y R de cada componente se obtienen, a partir de las gráficas
espectroscópicas de Z”/M”, teniendo en cuenta las siguientes consideraciones. En un
circuito RC en paralelo la impedancia total es la suma de los inversos de la impedancia
de la resistencia (ZR = R) y de la impedancia del condensador (ZC=1/jωC),
[A3.19]
donde la parte real y la imaginaria de Z* (Z* = Z’ + jZ”) son:
[A3.20]
[A3.21]
Z' / Ω cm
0 100000 200000 300000 400000 500000
Z
/
Ω
cm
-350000
-300000
-250000
-200000
-150000
-100000
-50000
0
(a) R1
C1
R2
C2
f / Hz
102 103 104 105 106 107
Z
/
Ω
cm
-200000
-150000
-100000
-50000
0
10
-10
Me
0
-1
/
F
-1
cm
0.0
0.5
1.0
1.5
2.0
2.5
(b)
(b)
(a)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-306-320.jpg)
![Técnicas de caracterización
- 327 -
( )
( )
⎥
⎦
⎤
⎢
⎣
⎡
ω
+
ω
= 2
2
0
RC
1
RC
C
C
M'
( )
( )
⎥
⎦
⎤
⎢
⎣
⎡
ω
+
ω
= 2
0
RC
1
RC
C
C
M
2
R
Zmax =
2C
C
M
o
max =
teniendo en cuenta la ecuación [A3.19] se obtiene que la parte real y imaginaria de M*:
[A3.22]
[A3.23]
El término entre corchetes describe la forma del pico de M”. Idealmente, tiene
forma de pico de Debye, que se caracteriza porque la anchura a la mitad de la altura de
pico es igual a 1.14 décadas y en el máximo del pico de Z” (Z”max) y de M” (M”max) se
cumple la relación RCωmax = 1. Sustituyendo esta relación en la ecuación A3.20 y
A3.23 se obtiene la relación entre los valores de Z”max y la resistencia, y los valores de
M”max y de capacidad.
[A3.24]
[A3.25]
siendo Co = ε0 (permitividad del vacío, 8.854 x 10-14
F cm-1
). De la ecuación A3.25 se
deduce que la altura del pico de M” es inversamente proporcional a su capacidad.
Generalmente, los software de impedancias representan M”/C0, con lo cual del máximo
del pico podremos extraer directamente la capacitancia del elemento. Las unidades de
éste sería F.
A3.6.3. Gráficas dependientes de la temperatura
Obtenidos los valores de R y C para cada elemento a diferentes temperaturas, se puede
analizar la dependencia de estos con la temperatura. Estas representaciones pueden dar
un conocimiento mayor del comportamiento físico de los componentes del material de
manera individual.
A3.6.3.1. Gráficas de Arrhenius
Un método comúnmente empleado para estudiar la dependencia de la resistencia o
conductividad (σ = R-1
) con la temperatura se hace uso de gráficas de Arrhenius. Estas
representaciones se basan en la ecuación de Arrhenius:
⎟
⎠
⎞
⎜
⎝
⎛ −
=
kT
Ea
Aexp
σ [A3.26]](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-307-320.jpg)









































![From the impedance data, Fig 3(a,b,d,e), values of the bulk, σ1 and grain boundary, σ2 conductivities were
extracted and are shown in Arrhenius format in Fig 4. There is a significant difference in the bulk
conductivities of the sol-gel and solid state samples but for both samples the application of a dc bias had
almost no effect on the magnitudes of either bulk or grain boundary conductivities. The reason for the
difference in bulk conductivities of sol-gel and solid state samples is not known.
For non-stoichiometric BaTiO3, the impedance data are very different with and without dc bias, Figs 5-
10; both R1 and R2 are much reduced and are time-dependent with a dc bias, Figs 5,8. The temperature-
dependence of the bulk capacitance C1, was readily obtained by replotting impedance data as log C′ vs
log f, Figs 5(c,f),8(c,f); although the real, resistive part of the impedance was too high to measure with the
available instrumentation for temperatures below ∼300 ºC, capacitance data were readily obtained and
show temperature dependence characteristic of paraelectric behaviour above Tc, Fig 2. For the grain
boundary, it was unclear from the impedance data whether C2 was ferroelectric or non-ferroelectric since
data could be obtained only at high temperatures and were not sufficiently sensitive, within experimental
errors, to show whether or not a Curie–Weiss temperature dependence was apparent.
Conductivity data as a function of time at constant temperature are shown in Figs 6a,9a for a selection of
temperatures after a bias voltage of 10V [~14.5 Vmm-1
] was applied; conductivities rise rapidly at first
but gradually level off after sufficiently long times. The difference between initial and final
conductivities was at least two orders of magnitude at lower temperatures but decreased with increasing
temperature. The initial increase in conductivity occurred more rapidly with increasing temperature and
the time required to achieve the final value decreased. Conductivity as a function of time for different dc
biases at constant temperature is shown in Figs 6b,9b. Again, steady state conductivities are reached after
a sufficient time and the magnitude of the steady state conductivity increases with dc bias, Figs 6c,9c.
On removing the dc bias, conductivity values gradually decreased with time, Figs 6d,9d, and eventually
reached steady state values at measuring temperatures 450 o
C. These steady state values were,
however, higher than the initial values before application of the dc bias. With increasing temperature, the
difference between these steady state and initial values decreased and the initial values could be fully
recovered by raising the temperature to e.g. 800 ºC for 1 hour. This shows that there are two excited
states which can be separated on removal of the dc bias although, on application of the dc bias a clear
separation of the two excited states is not seen.
Data for R1 (i.e. σ1
-1
) are shown in Arrhenius format in Figs 7a,10a for non-stoichiometric samples that
are both TiO2-deficient and BaO-deficient. The data show linear Arrhenius behaviour of both final and
initial conductivities, with and without a dc bias. The activation energy decreased significantly with dc
bias and as a consequence, the conductivity increased by 2-3 orders of magnitude, depending on
temperature. Similar effects were seen for R2 (i.e. σ2
-1
), Figs 7b,10b; activation energy data, together with
conductivities (R1
-1
and R2
-1
) at an example temperature, are summarised in Table II.
Confirmation that the conduction mechanism in both sets of non-stoichiometric samples is p-type is
shown by measurements in different atmospheres, Fig 11. In both cases, the conductivity decreases with
decreasing 2
O
P in the measuring atmosphere since electrons are injected into the sample as a
consequence of desorption of oxygen from the sample surface according to:
e
4
O
O
2 2
2
+
→
−
(1)
Discussion
The results presented here on non-stoichiometric BT extend significantly those recently reported for BT
ceramics doped with divalent cations,4-6
Mg2+
, Zn2+
and Ca2+
. The dc bias-dependence of the bulk (and
grain boundary) conductivity at low bias fields in acceptor-doped and non-stoichiometric BT is, we](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-349-320.jpg)


![Non-linear low field bulk resistivity is not a phenomenon that is usually found, or expected, with
moderately resistive materials that conduct by a mechanism of ion or electron hopping. Its occurrence in
both nonstoichiometric and Mg, Zn, Ca-doped BT, but not in undoped, stoichiometric BT, is believed to
be a consequence of the acceptor doping mechanism [i.e. doping with lower valence cation and associated
creation of oxygen vacancies]; in the case of non-stoichiometric-BT, the mechanism is the same because
the acceptor dopants are the zero-valent cation vacancies.
The electrical properties of Ba-deficient and TiO2-deficient BT are similar. This indicates that the
electron transfer mechanism within the BT defect structure is more important than the nature of the
acceptor dopant ( '
'
Ba
V or '
'
'
'
Ti
V ). Since underbonded oxygens appear to be the critical component of the
defect structure that are responsible for the non-linearity, similar effects may be anticipated with other
ceramic materials containing acceptor dopants which have an oxygen vacancy charge compensation
mechanism.
Evidence for non-stoichiometric in BaTiO3 is obtained from TC data of both BaO- and TiO2- deficient
samples, which are consistently a few degrees lower than that of stoichiometric BaTiO3. This is
supported by the observed non-linear phenomena for which non-stoichiometry appears to be a necessary
pre-requisite.
Acknowledgments
ARW thanks the EPSRC for financial support. MP, HB, EC thank the “Bancaja-Universitat Jaume I”-
project No. P1 1B2006-25 for financial support and the Generalitat Valenciana for a fellowship
BFPI/2007/174 for MP.
References
[1] A. J. Moulson and J. M. Herbert, Electroceramics, Second Edition, Wiley, 2003.
[2] R. A. Huggins, Diffusion in Solids, Recent Development. Edited by A. S. Nowick and J. J. Burton,
Academic Press, 1975.
[3] D. B. Strukov, G. S. Snider, D. R Stewart, and R. S Williams, “The Missing Memristor Found”,
Nature, 2008, 453, 80.
[4] H. Beltrán, M. Prades, N. Masó, E. Cordoncillo, and A. R. West,” Voltage-Dependent Low-Field
Bulk Resistivity in BaTiO3:Zn Ceramics”, J. Am. Ceram. Soc., 93[2], 500–505 (2010).
[5] M. Prades, N. Masó, H. Beltrán, E. Cordoncillo, and A. R. West, “Field enhanced bulk conductivity of
BaTiO3 : Mg ceramics”, J. Mater. Chem., 20[25], 5335–5344, (2010).
[6] N. Masó, M. Prades, H. Beltrán, E. Cordoncillo, D. C. Sinclair and A. R. West, “Field enhanced bulk
conductivity of acceptor-doped BaTi1−xCaxO3−x ceramics”, Appl. Phys. Lett., 97[6], 062907 (2010).
[7] H. Beltrán, E. Cordoncillo, P. Escribano, D. C. Sinclair, and A. R. West, “Insulating properties of
lanthanum-doped BaTiO3 ceramics prepared by low-temperature synthesis”, J. Am. Ceram. Soc., 87[11],
2132–2134 (2004).
[8] J.T.S. Irvine, D.C. Sinclair, and A.R. West, “Electroceramics: Characterization by impedance
spectroscopy”, Adv. Mater., 2[3] 132–138 (1990).
[9] A. Branwood and R.H. Tredgold, “The electrical conductivity of barium titanate single crystals”,
Proc. Phys. Soc., 76[1] 93–98 (1960).
[10] A. Branwood, O.H. Hughes, J.D. Hurd and R.H. Tredgold, “Evidence for space charge conduction in
barium titanate single crystals”, Proc. Phys. Soc., 79[6] 1161– 1165 (1962).
[11] G.A. Cox and R.H. Tredgold, “Double space charge injection in solids”, Phys. Letters, 4[3] 199–200
(1963).
[12] G.A. Cox and R.H. Tredgold, “Time dependence of the electrical conductivity in strontium titanate
single crystals”, Brit. J. Appl. Phys., 16[4] 427–430 (1965).
[13] C. A. McDowell, Physical Chemistry, Edited by H. Eyring, D. Henderson and W. Jost, Vol. 3,
Academic Press, 1969.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-352-320.jpg)


![Fig 3. Impedance complex plane plots, M” spectroscopic plots and capacitance data at 472ºC for
stoichiometric BaTiO3 prepared by sol-gel (a, b, c) and solid state reaction (d, e, f), before and after a
voltage of 10V [6.7 and 7.1 Vmm-1
, respectively] was applied.
Z' / kΩcm
0 100 200 300 400
Z
'
'
/
k
Ω
c
m
-400
-300
-200
-100
0
0V
10V
Z' / kΩcm
0 5 10
Z
'
'
/
k
Ω
c
m
-10
-5
0
R1+R2
(a)
f / Hz
102 103 104 105 106 107
10
-10
Me
0
-1
/F
-1
cm
0.0
0.5
1.0
1.5
0 V
10 V
Z''
/
kΩcm
-150
-100
-50
0
(b)
f/ Hz
102 103 104 105 106 107
C'
/
Fcm
-1
10-11
10-10
10-9
10-8
(c)
R1
Z' / kΩcm
0 100 200 300 400 500
Z
'
'
/
k
Ω
c
m
-500
-400
-300
-200
-100
0
R1+R2
(d)
f / Hz
102 103 104 105 106 107
10
-10
Me
0
-1
/F
-1
cm
0.0
0.5
1.0
1.5
Z''
/
kΩcm
-125
-100
-75
-50
-25
0
(e)
f/ Hz
102 103 104 105 106 107
C'
/
Fcm
-1
10-11
10-10
10-9
(f)
0V
10V
0V
10V
0V
10V
0 V
10 V](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-355-320.jpg)
![Fig 4. Arrhenius plots of (a) σ1 and (b) σ2 for stoichiometric BaTiO3 measured without a dc bias and with
an applied voltage of 10V [6.7 and 7.1 Vmm-1
for solid state and sol-gel samples, respectively] after a
steady state had been reached. Activation energies in eV, with errors in the range 0.01–0.05 eV, are
shown beside each data set.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-356-320.jpg)
![Z' /KΩcm
0 50 100 150 200 250 300
Z
/KΩcm
-300
-250
-200
-150
-100
-50
0
0V
10V
R1+R2
Z' /KΩcm
0 5 10 15 20
Z
/KΩcm
-20
-15
-10
-5
0
R1
R1
R1
+R2
(a)
f /Hz
102
103
104
105
106
107
Z
/KΩcm
-120
-100
-80
-60
-40
-20
0
0V
10V
10
-10
Me
0
-1
/F
-1
cm
0.0
0.5
1.0
1.5
2.0
2.5
3.0
(b)
f /Hz
102 103 104 105 106 107
C'
/Fcm
-1
10-11
10-10
10-9
10-8
0V
10V
(c)
Z' /KΩcm
0 5 10 15 20 25 30
Z
/KΩcm
-30
-25
-20
-15
-10
-5
0
0V
10V
R1
(d)
f /Hz
102 103 104 105 106 107
Z
/KΩcm
-12
-10
-8
-6
-4
-2
0
0V
10V
10
-10
Me
0
-1
/F
-1
cm
0.0
0.4
0.8
1.2
1.6
(e)
f /Hz
102 103 104 105 106 107
C'
/Fcm
-1
10-11
10-10
10-9
0V
10V
(f)
Fig 5. Impedance complex plane plots, M” spectroscopic plots and capacitance data at 485ºC and 477ºC
for BaTi0.99O2.98 prepared by sol-gel (a, b, c) and solid state reaction (d, e, f), before and after a voltage of
10V [15.1 and 9.52 Vmm-1
, respectively] was applied. Note: for the sample prepared by solid state
reaction, there is no evidence for a separate grain boundary resistance R2.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-357-320.jpg)
![Fig 6. BaTi0.99O2.98, sol-gel sample: (a) Bulk conductivity, σ1, at different temperatures vs time after a
voltage 10V [15.1 Vmm-1
] was applied; (b) σ1 vs time for different applied voltages at constant
temperature, 335 o
C; (c) limiting bulk conductivity vs bias voltage measured at 335 ºC; and (d) σ1 at
different measuring times after removal of the dc bias measured at 385 ºC, 432 ºC and 482ºC (lines
indicate the ground state for each temperature).
(d)
time /min
0 200 400 600 800 1000 1200 1400 1600
σ
1
/Scm
-1
10-6
10-5
10-4
10-3
10-2
10-1
385ºC
432ºC
482ºC
time /min
0 50 100 150 200
σ
1
/Scm
-1
10-6
10-5
10-4
10-3
(a)
Vmm-1
0 2 4 6 8 10 12 14 16 18
σ
1
/Scm
-1
10-7
10-6
10-5
10-4
10-3
(c)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-358-320.jpg)
![Fig 7. Arrhenius plots of (a) σ1 and (b) σ2 for BaTi0.99O2.98 measured without a dc bias and with an
applied voltage of 10V [9.52 and 15.1 Vmm-1
for solid state and sol-gel samples, respectively] after a
steady state had been reached. Activation energies in eV, with errors in the range 0.01–0.05 eV, are
shown beside each data set.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-359-320.jpg)
![Z' /KΩcm
0 20 40 60 80 100 120
Z
/KΩcm
-120
-100
-80
-60
-40
-20
0
0V
10V
R1
+R2
Z' /KΩcm
0 2 4 6 8 10
Z
/KΩcm
-10
-8
-6
-4
-2
0
R1
R1+R2
(a)
f /Hz
102
103
104
105
106
107
Z
/KΩcm-35
-30
-25
-20
-15
-10
-5
0
0V
10V
10
-10
Me
0
-1
/F
-1
cm
0.0
0.5
1.0
1.5
2.0
2.5
(b)
f /Hz
102 103 104 105 106 107
C'
/Fcm
-1
10-11
10-10
10-9
10-8
10-7
0V
10V
(c)
R1
Z' /KΩcm
0 30 60 90 120 150 180
Z
/KΩcm
-180
-150
-120
-90
-60
-30
0
0V
10V
R1+R2
Z' /KΩcm
0 5 10 15 20
Z
/KΩcm
-20
-15
-10
-5
0
R1
R1
+R2
(d)
f /Hz
102 103 104 105 106 107
Z
/KΩcm
-50
-40
-30
-20
-10
0
0V
10V
10
-10
Me
0
-1
/F
-1
cm
0.0
0.6
1.2
1.8
(e)
f /Hz
102 103 104 105 106 107
C'
/Fcm
-1
10-11
10-10
10-9
10-8
10-7
0V
10V
(f)
R1
Fig 8. Impedance complex plane plots, M” spectroscopic plots and capacitance data at 469ºC and 475ºC
for Ba0.99TiO2.99 prepared by sol-gel (a, b, c) and solid state reaction (d, e, f), before and after a voltage of
10V [13.7 and 8.7 Vmm-1
, respectively] was applied.](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-360-320.jpg)
![Fig 9. Ba0.99TiO2.99, sol-gel sample: (a) Bulk conductivity, σ1, at different temperatures vs time after a
voltage 10V [13.7 Vmm-1
] was applied; (b) σ1 vs time for different applied voltages at constant
temperature, 306 o
C; (c) limiting bulk conductivity vs bias voltage measured at 306 ºC; and (d) σ1 at
different measuring times after removal of the dc bias measured at 386 ºC, 431 ºC and 486ºC (lines
indicate the ground state for each temperature).
Fig 10. Arrhenius plots of (a) σ1 and (b) σ2 for Ba0.99TiO2.99 measured without a dc bias and with an
applied voltage of 10V [8.7 and 13.7 Vmm-1
for solid state and sol-gel samples, respectively] after a
steady state had been reached. Activation energies in eV, with errors in the range 0.01–0.05 eV, are
shown beside each data set.
(b)
time /min
0 200 400 600 800 1000 1200 1400 1600
σ
1
/Scm
-1
10-7
10-6
10-5
10-4
0.68 Vmm-1
1.37 Vmm
-1
2.73 Vmm
-1
time /min
0 200 400 600 800 1000 1200 1400 1600
σ
1
/Scm
-1
10-7
10-6
10-5
10-4
10-3
431ºC
386ºC
335ºC
(a
time /min
0 200 400 600 800 1000 1200 1400 1600
σ
1
/Scm
-1
10-6
10-5
10-4
10-3
10-2
10-1
386ºC
431ºC
486ºC
time /min
0 50 100 150 200
σ
1
/Scm
-1
10-6
10-5
10-4
10-3
(d
Vmm-1
0 2 4 6 8 10 12 14 16 18
σ
1
/Scm
-1
10-7
10-6
10-5
10-4
10-3
(c](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-361-320.jpg)





![since they are not surrounded fully by a cationic coordination sphere and under appropriate conditions
may act as either electron traps or electron donors. Recent studies on oxygen surface exchange kinetics
of erbia-stabilised bismuth oxide8
have shown the existence of oxygen species with intermediate
oxidation states at sample surfaces. It seems likely, therefore, that the occurrence of oxygen species in
various states of reduction is widespread in both bulk materials and at surfaces.
Acknowledgement
We thank EPSRC for financial support. MP, HB, EC thank the “Bancaja-Universitat Jaume I”- project
No. P1 1B2010-22 for financial support and the Generalitat Valenciana for a fellowship BFPI/2007/174
for MP.
References
1
H. Beltrán, M. Prades, N. Masó, E. Cordoncillo, and A. R. West,” Voltage-Dependent Low-Field Bulk
Resistivity in BaTiO3:Zn Ceramics”, J. Am. Ceram. Soc., 93[2], 500–505 (2010).
2
M. Prades, N. Masó, H. Beltrán, E. Cordoncillo, and A. R. West, “Field enhanced bulk conductivity of
BaTiO3 : Mg ceramics”, J. Mater. Chem., 20[25], 5335–5344, (2010).
3
N. Masó, M. Prades, H. Beltrán, E. Cordoncillo, D. C. Sinclair and A. R. West, “Field enhanced bulk
conductivity of acceptor-doped BaTi1−xCaxO3−x ceramics”, Appl. Phys. Lett., 97[6], 062907 (2010).
4
H. Beltrán, M. Prades, N. Masó, E. Cordoncillo and Anthony R West, “Enhanced Conductivity and
Non-linear Voltage-Current Characteristics of Non-stoichiometric BaTiO3 Ceramics”, J. Am. Ceram.
Soc., in press.
5
D. M. Smyth in The Defect Chemistry of Metals Oxides, Oxford University Press Inc, New York, 2000.
6
H.-H. Chan, R. K. Sharma and D. M. Smyth, “Nonstoichiometry in undoped BaTiO3”, J. Amer. Ceram.
Soc., 64[9], 556–562 (1981).
7
M. Prades, Nahum Masó, H Beltrán, E. Cordoncillo and A. R. West, “Polymorphism of BaTiO3
Acceptor Doped with Mn3+
, Fe3+
, and Ti3+
”, J. Am. Ceram. Soc., 91 [7], 2364–2366 (2008).
8
C.-Y. Yoo, B. A. Boukamp and H. J. M. Bouwmeester, “Oxygen surface exchange kinetics of erbia-
stabilized bismuth oxide”, J. Solid State Electrochem., DOI: 10.1007/S10008-010-1168-8 (2010).](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-367-320.jpg)

![Figure 3. (a) Impedance complex plane plot, Z*, and (b) M” spectroscopic plots at 707 ºC before (•) and
after (○) a voltage of 10V was applied [16 Vmm–1
] for the sample sintered at 1400 ºC and
slow cooled in air; (c) Impedance complex plane plot, Z*, (d) M” spectroscopic plots and (e)
relative volume of the regions (in %) after a voltage of 10V [16 Vmm–1
] was applied at
different measuring times for the sample sintered at 1400 ºC, quenched in liquid nitrogen and
measured in N2.
f / Hz
102
103
104
105
106
107
10
-9
Mε
0
-1
/
F
-1
cm
0
5
10
15
20
25
30
Z' / kΩcm
0 3 6 9 12 15 18
Z''
/
kΩcm
-18
-15
-12
-9
-6
-3
0
(a) (b)
Z' / kΩcm
0 1000 2000 3000 4000 5000 6000
Z''
/
kΩcm
-6000
-5000
-4000
-3000
-2000
-1000
0
0V
10V 5min
10V 82min
10V 1205min
10V 1497min
Z' / kΩcm
0 100 200 300 400
Z''
/
kΩcm
-400
-300
-200
-100
0
(c)
0V
10V 0V
10V
(e)
f / Hz
102
103
104
105
106
107
10
-9
Mε
0
-1
/
F
-1
cm
0
3
6
9
12
15
18
0V
10V 5min
10V 82min
10V 1205min
10V 1497min
(d
)](https://image.slidesharecdn.com/prades-240213163400-9de3b8c3/85/prades-pdf-369-320.jpg)
