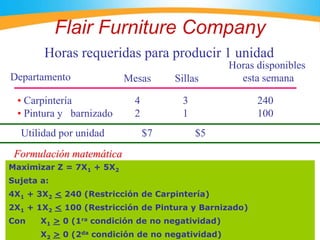
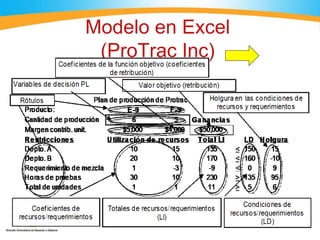
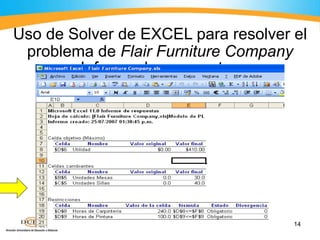
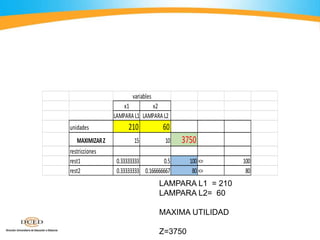
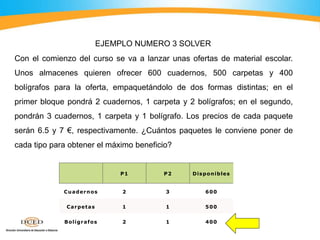
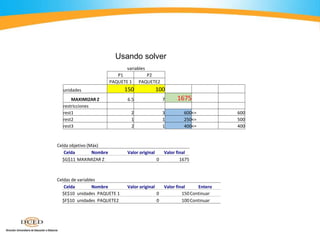
El documento describe cómo usar el programa Solver de Excel para resolver problemas de optimización lineal. Explica los pasos para ingresar los datos de una función objetivo y restricciones, ejecutar Solver para encontrar la solución óptima, e interpretar los resultados. También incluye ejemplos numéricos para ilustrar el proceso.

1. SIMULACION PROCESOS
USANDO
SOLVER

2. 2
Solución de problemas
usando computadora
Solver de EXCEL

3. 3
Para usar Solver, abra una hoja de Excel y:
1. Ingrese los nombres de las variables y los
coeficientes de la función objetivo y las
restricciones.
2. Especifique las celdas donde se localizarán los
valores de las variables. La solución será puesta
ahí.
3. Escriba una fórmula para calcular el valor de la
función objetivo. La función SUMAPRODUCTO
ayuda en esta tarea.
Uso de Solver de EXCEL

4. 4
4. Escriba fórmulas para calcular los lados
izquierdos de las restricciones. Las fórmulas
pueden ser copiadas y pegadas en estas celdas.
5. Indicar los signos de restricción (≤, =, y ≥) sólo
para propósitos de despliegue en pantalla. Los
signos reales deben ser ingresados en Solver
más adelante, pero mostrarlos en pantalla es
conveniente.
6. Ingresar los valores al lado derecho de cada
restricción.
Uso de Solver de EXCEL

5. Walter Silva Sotillo 5
Horas requeridas para producir 1 unidad
Departamento Mesas Sillas
Horas disponibles
esta semana
• Carpintería
• Pintura y barnizado
4
2
3
1
240
100
Formulación matemática
Utilidad por unidad $7 $5
Maximizar Z = 7X1 + 5X2
Sujeta a:
4X1 + 3X2 < 240 (Restricción de Carpintería)
2X1 + 1X2 < 100 (Restricción de Pintura y Barnizado)
Con X1 > 0 (1ra condición de no negatividad)
X2 > 0 (2da condición de no negatividad)
Flair Furniture Company

6. 6
Uso de Solver de EXCEL para resolver el
problema de Flair Furniture Company
Pantalla de ingreso de datos
=B6*B5+C6*C5
=B8*B5+C8*C5
=B9*B5+C9*C5

7. Modelo en Excel
(ProTrac Inc)
7

8. 8
Una vez que el problema es ingresado en una hoja de
cálculo Excel, para usar el Solver se deben seguir los
siguientes pasos:
1. La opción Solver de Excel estará, según la versión del
programa: En Excel 2003 y anteriores en el menú
Herramientas. A partir de la versión 2007 la opción Solver
estará en el menú Datos. Si Solver no aparece, habrá que
activarlo en la opción Archivo-Opciones-Complementos-IR.
2. Una vez que Solver ha sido seleccionado, se abrirá una
ventana para el ingreso de los parámetros Solver.
3. Función objetivo: Mueva el cursor a la casilla Celda
Objetivo y llene la celda para calcular el valor de la función
objetivo.
Uso de Solver de EXCEL

9. 9
3. Variables de decisión: Mueva el cursor a la casilla
Cambiando las celdas y elija las celdas que contendrán los
valores de las variables.
4. Restricciones: Mueva el cursor a la casilla Sujeta a las
siguientes restricciones: y luego seleccione Agregar. La
casilla Referencia de la celda es para el rango de celdas
que contienen los lados izquierdos (totales calculados) de
las restricciones.
Uso de Solver de EXCEL

10. 10
5. Seleccione el símbolo ≤ ó ≥ ó = para cambiar el tipo de
restricción si es necesario. Cuando hay restricciones de
más de un tipo, deben ingresarse todas las de un tipo
primero, y entonces seleccionar Agregar para ingresar otro
tipo de restricción.
6. Mueva el cursor a la casilla Restricción para ingresar los lados
derechos de las restricciones. Elija Aceptar al finalizar este
conjunto de restricciones y Agregar si desea agregar otra
restricción.
Uso de Solver de EXCEL

11. 11
7. Calcular solución: En la ventana Parámetros de
Solver elija Opciones… y marque Adoptar modelo
lineal y Asumir no negativos; entonces haga clic en
Aceptar.
8. Revise la información en la ventana Solver para
asegurarse de que está correcta y haga clic en Resolver.
10. La ventana Resultados de Solver es mostrada e indica la
solución encontrada. Los valores de las variables, la
función objetivo, y las holguras son mostradas.
11. Seleccione Aceptar y los valores se mantendrán en la
solución óptima.
12. Puede seleccionar que clase de información adicional será
presentada en la ventana Informes. Puede seleccionar
cualesquiera de ellos y seleccionar Aceptar para
generarlos automáticamente.
Uso de Solver de EXCEL

12. 12
Uso de Solver de EXCEL para resolver el
problema de Flair Furniture Company
Pantalla de parámetros

13. 13
Uso de Solver de EXCEL para resolver el
problema de Flair Furniture Company
Pantalla de solución

14. Walter Silva Sotillo 14
Uso de Solver de EXCEL para resolver el
problema de Flair Furniture Company
Informe de respuestas

15. 2Una compañía fabrica y venden dos modelos de
lámpara L1 y L2. Para su fabricación se necesita un
trabajo manual de 20 minutos para el modelo L1 y de 30
minutos para el L2; y un trabajo de 20 minutos de
máquina para L1 y de 10 minutos para L2. Se dispone
para el trabajo manual de 100 horas al mes y para la
máquina 80 horas al mes. Sabiendo que el beneficio por
unidad es de 15 y 10 euros para L1 y L2, respectivamente,
planificar la producción para obtener el máximo
L1 L2 Tiempo
Manual 1/3 1/2 100
Máquina 1/3 1/6 80
EJERCICIO NUMERO 2 :USANDO SOLVER
20MINUTOS= 1/3
30 MINUTOS= ½
10 MINUTOS= 1/6
MAXIMIZAR Z= 15X1 + 10X2
1/3 X1 + ½ X2 <=100
1/3 X1 + 1/6 X2 <= 80
X1>=0
X2>=0

17. x1 x2
LAMPARAL1 LAMPARAL2
unidades 210 60
MAXIMIZARZ 15 10 3750
restricciones
rest1 0.33333333 0.5 100 <= 100
rest2 0.33333333 0.166666667 80 <= 80
variables
LAMPARA L1 = 210
LAMPARA L2= 60
MAXIMA UTILIDAD
Z=3750

18. Con el comienzo del curso se va a lanzar unas ofertas de material escolar.
Unos almacenes quieren ofrecer 600 cuadernos, 500 carpetas y 400
bolígrafos para la oferta, empaquetándolo de dos formas distintas; en el
primer bloque pondrá 2 cuadernos, 1 carpeta y 2 bolígrafos; en el segundo,
pondrán 3 cuadernos, 1 carpeta y 1 bolígrafo. Los precios de cada paquete
serán 6.5 y 7 €, respectivamente. ¿Cuántos paquetes le conviene poner de
cada tipo para obtener el máximo beneficio?
EJEMPLO NUMERO 3 SOLVER
P1 P2 Disponibles
Cuadernos 2 3 600
Carpetas 1 1 500
Bolígrafos 2 1 400

19. P1 P2 Disponibles
Cuadernos 2 3 600
Carpetas 1 1 500
Bolígrafos 2 1 400

20. variables
P1 P2
PAQUETE 1 PAQUETE2
unidades 150 100
MAXIMIZAR Z 6.5 7 1675
restricciones
rest1 2 3 600<= 600
rest2 1 1 250<= 500
rest3 2 1 400<= 400
Celda objetivo (Máx)
Celda Nombre Valor original Valor final
$G$11 MAXIMIZAR Z 0 1675
Celdas de variables
Celda Nombre Valor original Valor final Entero
$E$10 unidades PAQUETE 1 0 150Continuar
$F$10 unidades PAQUETE2 0 100Continuar
Usando solver

21. Unos grandes almacenes desean liquidar 200 camisas y 100 pantalones de la temporada
anterior. Para ello lanzan, dos ofertas, A y B. La oferta A consiste en un lote de una camisa y
un pantalón, que se venden a 30 €; la oferta B consiste en un lote de tres camisas y un
pantalón, que se vende a 50 €. No se desea ofrecer menos de 20 lotes de la oferta A ni menos
de 10 de la B. ¿Cuántos lotes ha de vender de cada tipo para maximizar la ganancia?
A B Mínimo
Camisas 1 3 200
Pantalones 1 1 100
EJEMPLO NUMERO 4 USANDO SOLVER

23. variables
X Y
OFERTA A OFERTA B
unidades 50 50
MAXIMIZAR Z 30 50 4000
restricciones
rest1 1 3 200<= 200
rest2 1 1 100<= 100
rest3 1 0 50>= 20
rest4 0 1 50>= 10
Celda objetivo (Máx)
Celda Nombre Valor original Valor final
$G$11 MAXIMIZAR Z 4000 4000
Celdas de variables
Celda Nombre Valor original Valor final Entero
$E$10 unidades OFERTA A 50 50Continuar
$F$10 unidades OFERTA B 50 50Continuar

25. Se dispone de 600 g de un determinado fármaco para elaborar
pastillas grandes y pequeñas. Las grandes pesan 40 g y las
pequeñas 30 g. Se necesitan al menos tres pastillas grandes, y
al menos el doble de pequeñas que de las grandes. Cada
pastilla grande proporciona un beneficio de 2 € y la pequeña de
1 €. ¿Cuántas pastillas se han de elaborar de cada clase para
que el beneficio sea máximo?
Resolver en solver

26. Se dispone de 600 g de un determinado fármaco para elaborar
pastillas grandes y pequeñas. Las grandes pesan 40 g y las pequeñas
30 g. Se necesitan al menos tres pastillas grandes, y al menos el doble
de pequeñas que de las grandes. Cada pastilla grande proporciona un
beneficio de 2 € y la pequeña de 1 €. ¿Cuántas pastillas se han de
elaborar de cada clase para que el beneficio sea máximo?
Resolver en solver
X= PASTILLAS GRANDES
Y = PASTILLAS PEQUEÑAS
FUNCION OBJETIVO :
max Z = 2X + Y
RESTRICCIONES
40X + 30Y <=600
X >=3
Y >=2X
X>=0
Y>=0

27. Una escuela prepara una excursión para 400 alumnos.
La empresa de transporte tiene 8 autobuses de 40
plazas y 10 de 50 plazas, pero sólo dispone de 9
conductores. El alquiler de un autocar grande cuesta
800 € y el de uno pequeño 600 €. Calcular cuántos
autobuses de cada tipo hay que utilizar para que la
excursión resulte lo más económica posible para la
escuela.
Resolver en solver

28. Una escuela prepara una excursión para 400 alumnos. La
empresa de transporte tiene 8 autobuses de 40 plazas y 10
de 50 plazas, pero sólo dispone de 9 conductores. El alquiler
de un autocar grande cuesta 800 € y el de uno pequeño 600
€. Calcular cuántos autobuses de cada tipo hay que utilizar
para que la excursión resulte lo más económica posible para
la escuela.
Resolver en solver
X = AUTOBUS PEQUEÑO
Y = AUTOBUS GRANDE
MINIMIZAR Z = 600 X + 800 Y
RESTRICCIONES
40X + 50Y >= 400
X + Y <= 9
X>=0
Y>=0