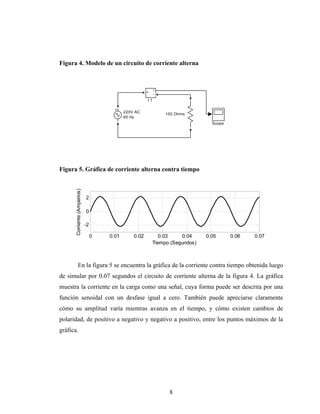
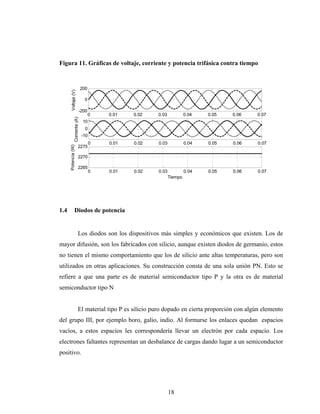
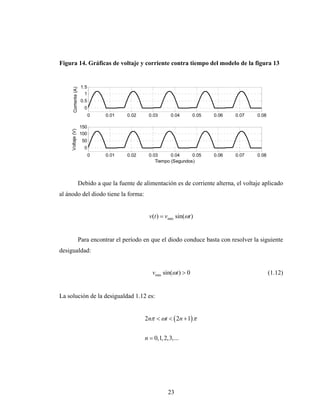
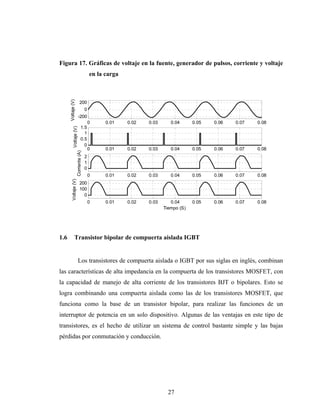
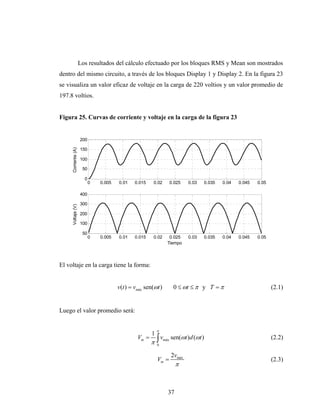
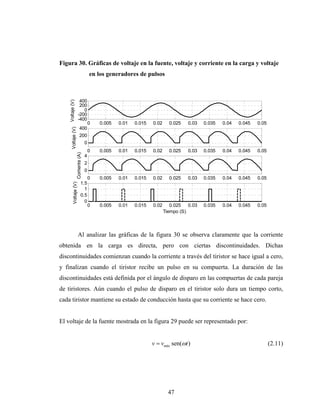
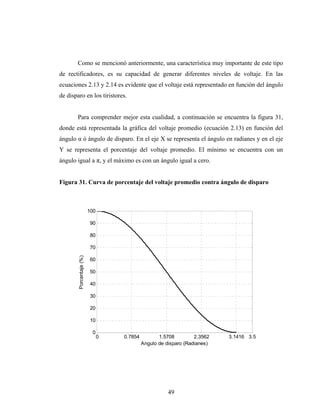
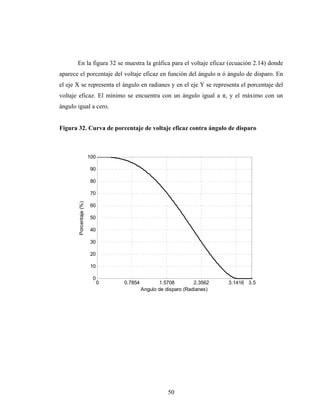
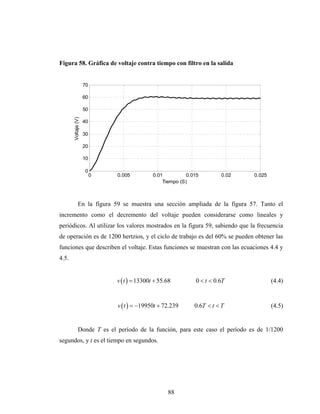
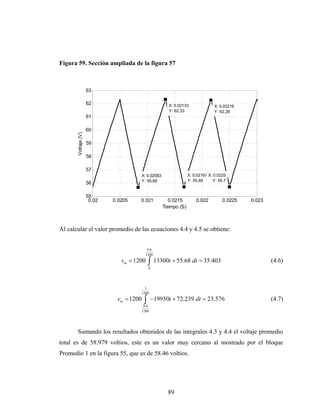
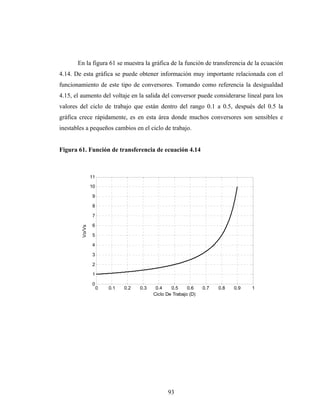
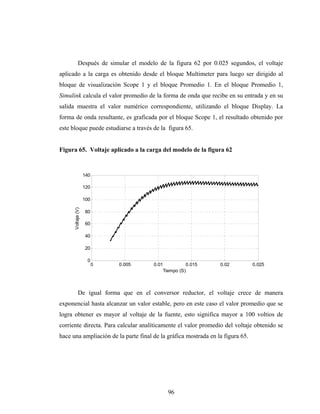
Este documento presenta el trabajo de graduación de Héctor Mendoza para obtener el título de Ingeniero Electricista de la Universidad de San Carlos de Guatemala. El trabajo consiste en un estudio sobre elementos de electrónica de potencia, incluyendo diodos, tiristores, transistores IGBT y diferentes tipos de conversores de corriente. Se describen modelos de circuitos y aplicaciones como el control de máquinas, generación eólica y sistemas fotovoltaicos. El documento contiene 13 secciones con figuras y ecuaciones para respaldar los