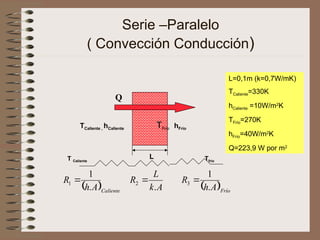
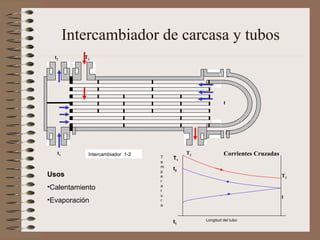
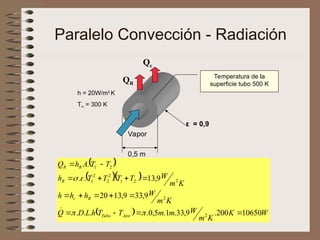
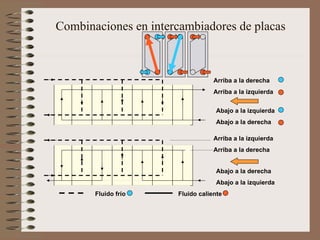
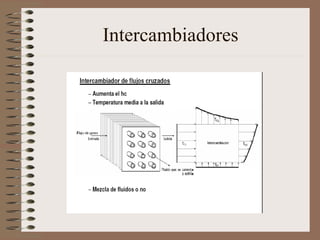
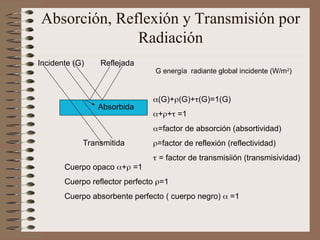
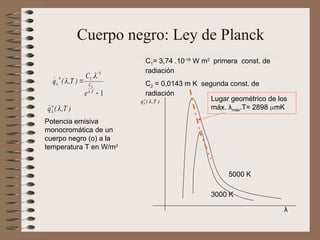
El documento aborda la transferencia de calor, destacando la Ley de Fourier, que establece que el flujo de calor es proporcional al gradiente de temperatura. Se presentan ejemplos de cálculos relacionados con la conducción y convección de calor en diferentes materiales y condiciones. Además, se discuten intercambiadores de calor y principios de radiación térmica.

1. Transferencia de Calor
Ing.Juan Montesano

2. Ley de Fourier
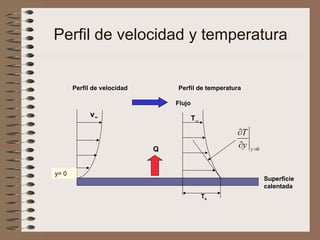
El flujo de calor , sin movimiento de materia, es
proporcional al gradiente de temperatura
Donde flujo de calor en dirección x [W]
k coeficiente de conducción [W/mºC]
A área normal a la dirección x[m2
]
T temperatura [ºC]
x distancia en [m]
dx
dT
A
k
Q
dx
dT
α
A
Q
x
x




-T
x
dx
dT

Tx
x
Q


3. Conducción en estado estacionario
en pared plana
dx
dT
A
k
Qx 


k
T1
T2
e
x =0 T=T1
x =e T=T2
A
k
e
T
T
Q
dT
k
dx
A
Q
2
1
x
T
T
e
0
x 2
1



 




4. k k1
k2
R1
= e / k A
T1
T2
T1
T2
T3
e e1 e2
Pared plana
R1=e1/k1A R2= e2/k2.A
Ejemplo :Calcular la resistencia térmica y Q a través de una hoja de vidrio
plano k=0,81 W/mK de 1 m de altura, 0,5m de ancho y 0,5 cm de espesor, si la
temperatura de la superficie externa es de 24 °C y la interna es de 24,5°C.
  W
W
K
C
R
T
T
Q
W
K
m
m
K
m
W
m
A
k
L
R
o
40
0123
,
0
.|
24
5
,
24
0123
,
0
5
,
0
.
1
.
.
81
,
0
005
,
0
.
2
1










5. Ejemplo 2
Placa de duraaluminio a
0°C (k=164 W/mK)
Paquete de
instrumentos
(con aislante )
Circuito integrado
2 cm
1 cm
10 cm
El circuito genera calor y su temperatura no debe exceder de 40°C.
La placa de acero inoxidable ( k=144 W/mK) se encuentra a 0°C
R1=Acero inoxidable R2= Duraaluminio
0,07 K/W 0,012 k/W
Fuente
a 40°C
Aislante Q= 487,80 W

6. Cilindros y Esferas
2
2
3
2
1
1
2
1
2
2
k
L
r
r
R
k
L
r
r
R




ln
ln
L
R1 R2
r3
r2
r1
k1
k2










2
1
1
1
4
1
r
r
k
R

r2
r1
Perfil
logarítmico
Perfil
hiperbólico

7. Serie - Paralelo
c
c
c
c
D
D
D
D
A
A
A
A
A
k
L
R
A
k
L
R
A
k
L
R
.
.
.



LA LB=LC LD
Material
A kA
Material
B, kB
Material
C,kC
Material
D, kD
T2
T1
B
B
B
B
A
k
L
R
.

T1 Q TX Ty Q T2

8. Convección

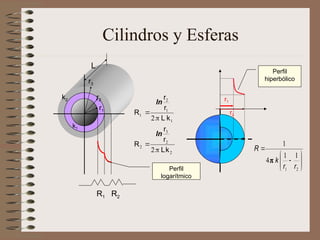
9. Capa límite
1
3
2
Laminar
Transición
Turbulento
T
1 3
2
T p
Q
e
= h A (T  - Tp)
Q

Donde h es el coeficiente de convección
[W/m2
K]



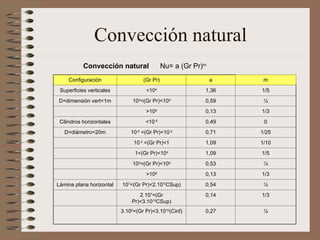
Forzada
Natural
Convección
h= f(v, ,,geometría,Cp,k)
h= f(v, ,,geometría,Cp,k, T,,g)

10. Perfil de velocidad y temperatura
y= 0
Perfil de velocidad Perfil de temperatura
Flujo
T∞
Superficie
calentada
Q
Ts
v∞
0



y
y
T

11. Coeficiente global de transferencia
T
hext
T2
T1
Tint.
hint
 
i
1
int
int
i
1
int
int
1
2
1
2
2
ext
ext
2
ext
ext
i
ext
ext
int
ext
ext
T
T
A
h
Q
)
T
(T
A
h
Q
T
T
d
D
ln
L
π
2
Q
r
D
ln
T
T
πL
2
k
Q
T
T
A
h
Q
)
T
(T
A
h
Q
T
T
A
U
Q
)
T
(T
A
U
Q
































ext
ext
int
int
ext
ext
ext
ext
int
int
ex
ex
h
1
d
D
ln
L
π
2
k
A
A
h
A
U
1
A
h
Q
d
D
ln
L
π
2
k
Q
A
h
Q
A
U
Q










D
d

12. Temperatura de la pared de un tubo
ext
ext
int
int
ext
ext h
1
d
D
ln
L
π
2
k
A
A
h
A
U
1



En tuberías se suele despreciar la
diferencia de temperaturas a través
del metal(T1 – T2) y se considera al
tubo en su totalidad está a la
temperatura de la superficie externa
de la pared T2
ext
ext
int
int
ext
int
int
ext
h
1
1
U
1
A
h
h
1
A
h
1
U
1





o
int,
o
int,
ext
ext
h
h
A
A
T1 T2
Text Tint
Rext Rint,o

13. Números adimensionales
Convección forzada en tuberías
0,14
p
f
,
L
D
Pr
Re
1,86
k
D
h

















33
0
Flujo dentro de tubos circulares con Re<2000( régimen laminar)
Nº de Reynolds = v..D/ Nº de Prandtl = cp. /k
Con Re>10000 (régimen turbulento)
0,14
p
f
0,33
f
0,8
f
μ
μ
Pr
Re
0,023
k
D
h









Nº de Nusselt






L
D
Pr
Re
para >100
0,14
p
f
0,66
μ
μ
L
D
Pr
Re
0,045
1
L
D
Pr
Re
0,085
3,66
k
D
h























para 





L
D
Pr
Re <100

14. Convección natural
Configuración (Gr Pr) a m
Superficies verticales <104
1,36 1/5
D=dimensión vert<1m 104
<(Gr Pr)<109
0,59 ¼
>109
0,13 1/3
Cilindros horizontales <10-5
0,49 0
D=diámetro<20m 10-5
<(Gr Pr)<10-3
0,71 1/25
10-3
<(Gr Pr)<1 1,09 1/10
1<(Gr Pr)<104
1,09 1/5
104
<(Gr Pr)<109
0,53 ¼
>109
0,13 1/3
Lámina plana horizontal 107
<(Gr Pr)<2.107(
CSup) 0,54 ¼
2.107
<(Gr
Pr)<3.1010
CSup)
0,14 1/3
3.105
<(Gr Pr)<3.1010
(Cinf) 0,27 ¼
Convección natural Nu= a (Gr Pr)m

15. Convección
Conductos no circulares
De= 4 . Área libre/ Perímetro mojado
De= 4 . L2
/4.L= L
De= 4 . (D2
-d2
) /4. (D+d) = D-d
L d
D
Ejemplo de convección:
Calcular Q por convección natural en un techo de área
20mX20m y el aire ambiental, si la temperatura del techo es de
27°C y del aire -3°C. el coeficiente promedio de transferencia
por convección es h = 10W/m2
K
    W
C
m
K
m
W
T
T
A
h
Q
o
techo
aire 120000
27
3
.
400
.
10
.
. 2
2 







16. Serie –Paralelo
( Convección Conducción)
TCaliente , hCaliente TFrío hFrío
   Frío
Caliente A
h
R
A
k
L
R
A
h
R
.
1
.
.
1
3
2
1 


T Caliente Tfrío
L
Q
L=0,1m (k=0,7W/mK)
TCaliente=330K
hCaliente =10W/m2
K
TFrío=270K
hFrío=40W/m2
K
Q=223,9 W por m2

17. Intercambiadores de calor
pA
pB
pA
pB
mL
ΔT
ΔT
Ln
ΔT
ΔT
ΔT


Tc
TpA
Tc
TpB
dx
L
m
m
T
dx
L
A
U
Q
L
A
dx
dA
T
dA
U
Q







 
     
pA
pB
p
B
A
p
p
p
p
p
p
c
p
p
p
p
T
T
c
m
T
d
c
m
Q
T
d
c
m
Q
d
dT
T
d
T
T
T
dT
c
m
Q
d















 






 
p
pA
pB
p
p
c
m
U
A
T
T
ln
dx
c
m
L
U
A
T
T
d
T
d
c
m
T
dx
L
A
U












 
  mL
pA
pB
pA
pB
pA
pB
p
pA
pB
p
T
A
U
T
T
T
T
ln
U
A
Q
T
T
ln
U
A
c
m
T
T
c
m
Q




















18. Intercambiadores de calor
Fluidos en contra-corriente
T2
t1
T1
t2
TubularHeat.exe
Fluidos en co-corriente T1
t1
T2
t2
Longitud del tubo

19. Intercambiador de carcasa y tubos
Intercambiador 1-2
t1 T2
t2 T1
t
T2
t
T1
t2
t1
Longitud del tubo
T
e
m
p
e
r
a
t
u
r
a
Usos
•Calentamiento
•Evaporación
Corrientes Cruzadas

20. Radiación

21. Radiación
Cavidad negra a
T2
Cuerpo negro de
área A1 a una T1
Qr1
Qr2
 















1
1
.
1
1
.
.
.
.
.
.
2
2
1
1
2
,
1
4
2
4
1
2
,
1
1
,
4
1
,
4
1
,






A
A
F
T
T
F
A
Q
T
A
Q
T
A
Q
neto
r
gris
r
negro
r
σ = Cte.Stefan-Boltzmann =
5,67 W/m2
K4
ε = emisividad

22. Ejemplo
• Una varilla larga y cilíndrica, 2 cm de diámetro y calentada mediante electricidad se
instala en un horno. La superficie de la varilla tiene un ε = 0,9 y se mantiene a 1000
K , mientras que las paredes internas del horno son negras y están a 800K. Calcular
Qneto perdido por la varilla por unidad de longitud.
    W
K
K
m
W
m
m
T
T
A
Q 1893
800
1000
.
.
67
,
5
.
9
,
0
.
1
.
02
,
0
.
.
.
. 4
4
4
4
2
4
2
4
1
1 



 



23. Paralelo Convección - Radiación
0,5 m
Qc
QR
Vapor
ε = 0,9
h = 20W/m2
K
T∞ = 300 K
Temperatura de la
superficie tubo 500 K
 
  
  W
K
K
m
W
m
m
T
T
h
L
D
Q
K
m
W
h
h
h
K
m
W
T
T
T
T
h
T
T
A
h
Q
Aire
Tubo
R
c
R
R
R
10650
200
.
9
,
33
.
1
.
5
,
0
.
.
.
.
9
,
33
9
,
13
20
9
,
13
.
.
.
.
2
2
2
2
1
2
2
2
1
2
1





















24. Intercambiadores

25. Combinaciones en intercambiadores de placas
Arriba a la derecha
Arriba a la izquierda
Abajo a la izquierda
Abajo a la derecha
Arriba a la izquierda
Arriba a la derecha
Abajo a la derecha
Abajo a la izquierda
Fluido frío Fluido caliente

26. Intercambiadores

27. Intercambiadores compactos
o de Placas
 Para flujos poco viscosos (< 5Pa s)
 Sólidos en suspensión < 0,3 cm
 Grandes áreas de transferencia
 U del orden de 2000- 5000 kcal/m2
h ºC
 Placas de acero inox. con relieve para prod. Turbulencia
 Capacidad:5000 – 20000 kg/h
 Mantenimiento simple
 Fácil desmontaje
 Higiénico
 Aumento de capacidad agregando placas
Usos : Ind. láctea y bebidas

28. Equipos y aparatos discontinuos
• Calentamiento/ enfriamiento por camisa
 U del orden de 250( pastas)- 1500(agua, eb.)
• Ídem por serpentín inmerso en el fluido
 Mayores áreas de transferencia
 Mayores coeficientes de transferencia
U del orden de 250 – 3000 kcal/ m2
h ºC

29. Atomización
Transporte neumática de polvo
4
1
5
3
6
2
Ventilador de
entrada
Ventilador de
salida
Ciclón
Turbina de atomización
Alimentación
Batería de
calentamiento
de aire
Ciclón de
envasado
Cámara de
atomización
Filtro
Envasado

30. Torre de enfriamiento (tiro inducido)

31. Instalación de torre de enfriamiento
(tiro forzado)
Tratamiento de agua
V. de purga V. descarga de caudal
Proceso
Depósito de dosificacióm química
Drenaje
Filtro
Agua de limpieza
Bombas
Vaciado

32. Absorción, Reflexión y Transmisión por
Radiación
Transmitida
Reflejada
Absorbida
Incidente (G)
(G)+(G)+(G)=1(G)
++ =1
=factor de absorción (absortividad)
=factor de reflexión (reflectividad)
 = factor de transmisiión (transmisividad)
Cuerpo opaco + =1
Cuerpo reflector perfecto =1
Cuerpo absorbente perfecto ( cuerpo negro)  =1
G energía radiante global incidente (W/m2
)

33. Cuerpo negro: Ley de Planck
1
2
5
1



T
.
C
o
e
.
C
)
T
,
(
q





)
T
,
(
qo



C1= 3,74 .10-16
W m2
primera const. de
radiación
C2 = 0,0143 m K segunda const. de
radiación
Potencia emisiva
monocromática de un
cuerpo negro (o) a la
temperatura T en W/m2
)
T
,
(
qo


 Lugar geométrico de los
máx. λmáx.T= 2898 mK
5000 K
3000 K
λ