Este documento describe los conceptos fundamentales de la convección, incluyendo los tipos de convección (libre y forzada), las propiedades que afectan la convección (viscosidad, conductividad térmica, densidad, velocidad del fluido, calor específico, configuración geométrica), y los regímenes de flujo (laminar y turbulento). También explica cómo calcular el coeficiente de transferencia de calor por convección y el número de Nusselt para diferentes geometrías y condiciones de flujo.

1. 200 Corte
Convección:Se necesita un fluido que esté
en movimi
ento. Para transportar la energia, puede ser conveccion
libre o Forzada.
El Fluido puede ser liquido o gaseoso.
La conveccion siempre implica conduccion,
ya que por ahi Incla
placa caliente
Si las placas y el fluido estan estaticas, se da
-
transferencia de calor por conduccion del más caliente
- -
al más Frio
Placa Frid
la convección depende de:
-
viscosidad dinamica, M
-
conductividad termica, k
-Densidad,
-
velocidad del Fluido, v
-
calor especifico, p
-
configuración geométrica
-
Aspereza
-
Régimen de Flujo
I
Ta
Local Q=
CTs -
Ta) SnxdAs
Promedio Q :
As ITs -
Tal
4a Ts
5
>
dAs i =
1,)nxxlocal dAs =
I nxx
X nx
-
h:coeficiente de transferencia de calor por conveccion [w/m2.]
Ts:Temperatura de la superficie

2. Econ=
q cona--
KFindotly=0 [wim-
h =
-
kFlvido (8424) y
=
0 Distribucion T °C
Ts -
Ta
capa
limite,térmica: T -
Ts =
0,99(Ty-
Ts)
- Placa Frid Ts =
0 +
T
=
0,99 To
x
PlaCA Frid placa callente Is-T =
0,99(Ts -
Tal
X
capa limite de velocidad
vy
-corriente libre
mis
*
Placa Frid
Re=
Fuertas denerca=
=fe
en
Re1
Flujo turbulento
Re-Pequeños Flujo laminar
Recror
-
Placa plana
5x105
Prandt:Pr:
DIFUSlvidad molecular de cantidad de movimiento
DIFUsividad molecular de calor
Pr = r
=
a =
E
Pr
=
L
k:conductividad térmica
Nusselt = 1 -
conduccion Dura
Nusselt-for=

3. C: constante que depende de la geometria, si se tienen placas, esteras, ductos
Nu =
CRemp,
Para placas: NO =
0,023 ReOop, o,
n =
0,4 +
calentamiento
n =
0,3 -
Enfriamiento
Tf:Temperatura promedio =
I
a
Placa plana isotérmica
Recr+ 1x105 -
3x
106
coeficiente de transferencia de calor
·laminar:
NV-asRewipi
-Pr0,6 -Res5e
·
Turbulento:
->
0,6<Pr260 +
5x10cRe<10t
Nux:Nusself
locales
Nusself promedio:Aproximadamente el doble que el local (enlaminar (
·
laminar:
Nut
=
0,664Re05p, -
Rec5x105 -Pr>0,6
·Turbulento sobre toda la placa:
Nu=
h=0,037Re0,8p,
13 +
0,6Prc60 +5x105<Re>1ot
k
·
Para region laminar + turbulenta:
n =
=))"caminar ax+nx turbuento ax)
Nr =
20,037 Re8-8+1)P."3 +
0,62Pr =
60 -
5x103 =
Re =
107

4. Propiedades del Fluido
T1 =
2Tr
=
1+20
-
80
Con la tabla A
15 (Se hallan las propiedades que no dependen de la presion (
·Cp =
1008 KJ/kg
·4
=
0,02953 WIm"C
-
M =
2,096 x
10-5 49/m.s
·
·
Pr =
0,7154
V=
2,097x10-5 m2 /s Se deben recalcular ya que si dependen de la presion
·
=
0,9994 kg/m3
183,44pa=
0,9994
83,4kPa.atkpa)
=
0,8226 kg
Para saber si hay transición de laminar a turbulento:

5. Conveccion Forzada externa:CFE
Es más efectiva la transferencia de calor por conveccion
Flujo de calor uniforme:As =
hx) Ts -
Tal
A
medida que se avanza en x:Ts varia;
Ts(x)
=
T
o +
hx
laminar:Nux=0,453 Rey" Pr"
A
bajas velocidades se puede mantener Fujo laminar después de
la esterd
En 0=0es un punto de estanca-
mien to
0 =
80 -
Es aproximadamente donde
Se separa la estela de la estera
<Para Re bajos)

6. Flujo cruzado sobre un cilindro (Churchill "Bernstein)
choca perpendicularmente el área transversal
NUGD
=
0,3 +
0,62 Repres
I =
(0)**)"para Rep. 0,2
[1 + 10,4/pr(43)
Flujo sobre una estera
NUesF- LD
k

7. Propiedades del Fluido
T =
25° Por tablas de 4
=
0,0255 WImoc
p =
1 at
m dire (A15)
M
=
1,849 x 10-5 kg/m.s
Pr =
0,7296
r=
1,562x10
- 5
m2/s
Re =
VD =
0,25 =
4,802x
e
Temperatura superficial es el:
30200
=
250
promedio aritmético
viscosidad dinamica del aire en la superficie de la estera:
M,soc= 2,76x758
No =
D
=
c +
[0,4(4,802x104)" +
0,00(4,802x10"43/10,7296)
0.49x0**5
4 =
13,8w/m2 °C
As =
HD
=
H10,25)
=
0,1963 m2
a =
hAs(T, -
Ta)
9=
13,8 (0,1963) (250 -25) =
610w
Q total
=
MC pAT =
PVCpA+ +
A
T =
300-200
①Total=
3 163000 [5] t=> WI
It =
2(ws
=
51855-1 hora 20 minaes

8. Flujo en tuberias
laminar Re-2300 RetomD
Turbulento Re > 10000 M
longitudes de entrada
Inlaminar
=
0,05 Re. D
It,laminar
=
0,05 Re.D.Pr
=
Pr. In, laminar
Ln,turbriento
Le,turbulento*
10D
Velocidad Promedio:Cambla respecto al radio
in =
PVpromAc=
Sa PUcrIdAc
vprom:
UridAc-ratrar=ucraer
!
Temperatura promedio.Exmpm =
SCATcalfi-SacCPTCrucr dAc
Cambia axialmente
Crespecto al movimiento im
=
(t(r18m_
pTaridvcrictr
del Fludo) PUprom (TRY CP
2
R
Tm=
UpromR
!TcrIU(rIrdr

9. Para valores de No mayores a
>10 el perfil esta
completament
te desarrollado.
No no depende la Frontera termica
Esta grafica es sólo para Flujo
-> TURBULENTO 5
Flujo de calor constante
El Fluido entra a T: y sale a te
En la region totalmente desarrollada la
variacion es constante y is varia con el
cambio de la temperatura del Fluido
calor que entrega la superficie por
Unidad de area:
=
9,As=mCp(Te-Ti)
minGlimaen el
Temperatura promedio de Salida
Te=
T: +
A
Temperatura de la superficie
&s=
nCTs -
Tm) -
Ts=
Tm
+
Conveccion Forzada Interna (CFI) Flujo de calor constante
Nr=
3,60 +
0,65(D/c) PePr -
Transferencia en regimen laminar y
region de
1 +
0.04[(D/L) RePr32/3
entrada térmica

10. Nr=
D =
4,36 -
Tubo circular -> Región completamente desarrollada
k
Ec. DiHas-Boelter -
Nu=0,023Re"op,
"
-> n
=
0,4 calentamiento
h=
0,3 enfriamiento
Si la Temperatura superficial es constante:
La temperatura nunca va a alcanzar la temperatura superficial,
pero va a tratar de acercarse.
Te =
Ts-
(Ts-
Tilexp(As
is
p
Uprom Flujo laminar
ucrI--)) (1-
vprom = -
2/(*)-rdr=-(*)
Ucrl=2Vprom(1-2)
+
r =
0 cenlasparedes):Umax =
2 Uprom
V =
Vmáx
Im Temperatura promedio
Perfil de Tadimensional
(Tx-T(rx)
=
0
T, (x)
-
Tm(x)
I
Pr=1 Gases

11. .
Adicionando calor
Si el flujo de calor es constante: la temper
ratura debe cambiar
sio
=
0 la temperatura del Fluido se mantiene
constante:Proceso de cambio de Fase
Flujo de calor en la superficie:
Is=
hx (Ts -
Tm)
i
Debe ser igual a la energia que entrega la superficie
mobatmas(od,a
no
e
Im temperatura promedio:
lii) =
Im( -
et)=-
2
=
2:am =
EP
te
Am=P
-
Tm=
Ti
+
Tm=
Ti
->
X =
L
Im:
Tentrada Te=
Ti+
Región de entrada dinámica
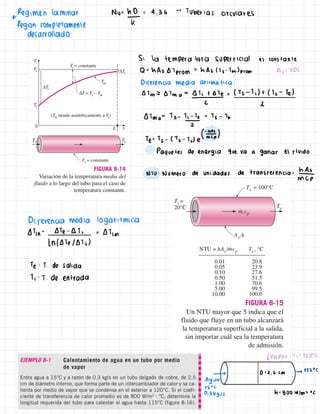
Tubos circulares:No=3,66 + 0,065(D/L) RePr
(2) 1 +
0,04[(D/1)RePr]23
Placas paralelas NU=7,54+0,03 (Dh/L) RePr
1 +
0,016 [ (Dr/L) RePr]43

12. -
Regimen laminar
Nu=hP
=
4,36- Tuberias arculares
Region completamente
desarrollado
Si la temperatura superficial es constante
a =
hAsATprom=
hAs (Ts -Tm) prom As =
HDL
Diferencia media aritmética:
ATm= DTma=
I+DTe
=
(Ts -
Ti) + (Ts -
Te
2
Atmattsctenien
Paquetes de energia que va a
ganar el fluido
NTU:Numero de unidades de
transferencia
Diferencia media logaritmica
ATin =
A
T
e -
A Ti =
ATim
(n(DTe/DTi)
Te:T. de Salida
Ti:T. de entrada
↓VAPOr:Ts
=
1200
-
->
1=
2,5cm
-
1750
Agua
15°
0,3 K9/S
h =
800 w/m2 oc

13. Propledades del agua
·
Ty =
1,75
=
650 ·
Cp=4187 J/kg.k
·
k
=
0,659 W/m.k
·
=
980,4kg/m3 ·Pr =
2,75
·
M
=
0,433 x
10
-
3
kg/m. S
a =
hAsATim =
in <p(Te-Til ->
As =
TDL
=
tim
- >
DTe =
Ts-
Te =
120-115=
50C
ATcm=
e
il ATi=
Ts -
Ti =
120-15=
105°C
ATcm =