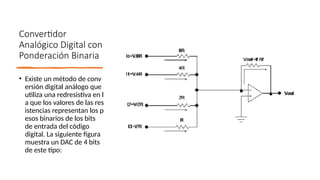
El documento describe métodos de conversión de señales analógicas a digitales utilizando circuitos resistivos, donde las resistencias representan los pesos binarios de los bits de entrada. Se analizan dos tipos de convertidores DAC: uno basado en resistencias ponderadas y otro en una red escalonada R/2R, mostrando cómo las tensiones de salida dependen de las corrientes generadas por las resistencias en relación a los valores binarios de entrada. Además, se explica el funcionamiento de un amplificador operacional en estos circuitos, que mantiene la entrada inversora en un potencial cercano a cero mediante realimentación negativa.

1. Información
Yaselga Christopher

2. Convertidor
Analógico Digital con
Ponderación Binaria
• Existe un método de conv
ersión digital análogo que
utiliza una redresistiva en l
a que los valores de las res
istencias representan los p
esos binarios de los bits
de entrada del código
digital. La siguiente figura
muestra un DAC de 4 bits
de este tipo:

3. • La corriente en cada resistencia de entrada depende del nivel de tensión aplicado: si es 0 (binario), no hay
corriente; si es 1 (binario), la corriente varía según el valor de la resistencia. Dado que no hay corriente en la
entrada inversora del opamp, la suma de las corrientes de entrada pasa por Rf, generando una caída igual a la
tensión de salida, Vout = If Rf.
• Las resistencias de entrada se eligen inversamente proporcionales a los pesos binarios de los bits de
entrada. La menor resistencia, R, corresponde al peso más alto (2³), y las demás son múltiplos de R (2R,
4R, 8R) según los pesos binarios 2¹, 2², 2³. Las corrientes de entrada también siguen esta proporción, por
lo que la tensión de salida depende de la suma ponderada de los pesos binarios, siendo la suma de las
corrientes de entrada multiplicada por Rf.

4. • . A continuación se
muestra el diagrama que
fue analizado e
implementado,los valores
que arrojo se muestran po
steriormente en una tabla
y en un pequeño análisis
que se hace:

5. Convertidor
digital analógico
en escalera R-2R
• Otro método para realizar
la conversión digital-
analógica es utilizar la red
escalonada R/2R

6. • Comencemos asumiendo que la entrada D3 está a nivel ALTO (+5 V) y las demás a nivel
BAJO (tierra, 0 V). Esta condición representa el número binario 1000. Un análisis del
circuito demostraría que este circuito es equivalente al mostrado:
• A través de la resistencia equivalente 2R prácticamente no circula corriente, ya que la
entrada inversora está a tierra virtual. Luego toda la corriente (I = 5 V/2R) que circula a
través de R7 pasa también por Rf , y la tensión de salida es −5 V. El amplificador
operacional mantiene la entrada inversora (−) a casi cero voltios (≈ 0V) debido a la
realimentación negativa. Por tanto, toda la corriente pasa a través de Rf en lugar de por
la entrada inversora

7. • Aquí se muestra el circuito equivalente cuando la entrada D2 está a
+5 V y las demás están a tierra. Esta condición representa 0100. Si se
aplica el equivalente de Thevenin* mirando desde R8 , se obtienen
2,5 V en serie con R, como se indica. Esto da lugar a una corriente a
través de Rf de I = 2,5 V/2R, lo que determina una tensión de salida de
−2,5 V. No olvide que no circula corriente por la entrada inversora ni
por la resistencia equivalente conectada a tierra, ya que caen 0 V en
ella debido a la tierra virtual.

8. • Aquí se muestra el circuito equivalente cuando la entrada D1 está a +
5V y las demás están a tierra. Esta condición representa el código
0010. De nuevo, aplicando el teorema de Thevenin al circuito a la
izquierda de R8, se obtienen 1,25 V en serie con R, como se indica.
Esto da lugar a una corriente a través de Rf de I = 1,25 V/2R, lo que
genera una tensión de salida de −1,25 V.

9. • Por último en la figura se representa el circuito equivalente para el
caso en que D0 está a + 5V y las demás entradas están a tierra. Esta
condición representa el código 0001. Aplicando el teorema de
Thevenin desde R8, se obtienen 0,625 V en serie con R, como se
indica. Esto da lugar a una corriente a través de Rf de I = 0,625 V/2R,
lo que genera una tensión de salida de −0,625 V. Observe que cada
entrada de menor peso sucesiva produce una tensión de salida que es
la mitad de la anterior, por lo que la tensión de salida es proporcional
al peso binario de los bits de entrada.