Matriz asociada a una composición de funciones
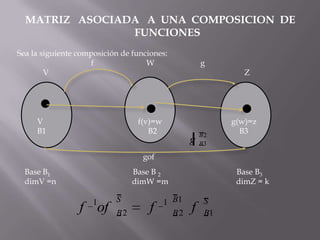
- 1. MATRIZ ASOCIADA A UNA COMPOSICION DE FUNCIONES Sea la siguiente composición de funciones: fW g V Z V B1 f(v)=w B2 g(w)=z B3 gof Base B1 Base B 2 Base B3 dimV =n dimW =m dimZ = k
- 2. MATRIZ CAMBIO DE BASE DE UNA COMPOSICION DE FUNCIONES DATO: = [ f]B1B2 CALCULO: = [ f]S1S2 [ f]S1S2= [Id]B2S2[ f]B1B2 [Id]S1B1 Id f Id F(v) S2 v S1 v B1 F(v) B2 [Id]S1B1 [ f]B1B2 [Id]B2S2
- 4. Matriz asociada a la aplicación lineal inversa V W V U S U B2 f(u) B1
- 5. EJERCICIOS: Comprobar que la matriz es diagonalizable, utilizando como la matriz de paso SOLUCIÓN Definiendo en DERIVE dichas matrices
- 7. Como A=P.D.P-1 , siendo D la matriz diagonal, entonces despejando matricialmente se obtiene que D=P-1.A.P, de tal forma que efectuando esta operación en DERIVE resulta Donde obtenemos la matriz diagonal
- 8. Sea la aplicación lineal Donde f(x,y,z)=(6x-6y+2z, -x-y+z, 7x+3y+z) ¿Cuál es la matriz asociada respecto de las bases canónicas? Por tanto la matriz asociada respecto de las bases canónicas se obtiene con:
- 9. Consideremos ahora una nueva base de R3 determinada por los vectores Para obtener la matriz asociada a la aplicación lineal f1 respecto de dicha base tendremos que calcular la coordenadas de las imágenes de dichos vectores en la citada base, es decir realizaremos las siguientes operaciones Para v1 se obtiene:
- 10. Para v2 resulta que: Y para v3 obtenemos: Por tanto la nueva matriz asociada es: Que se trata de una matriz diagonal.