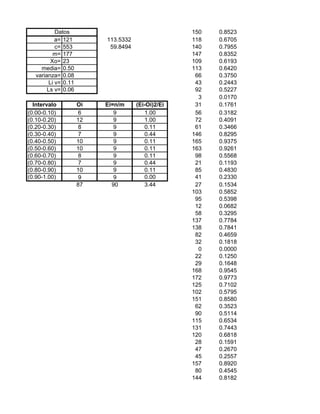
1. Datos 150 0.8523
a= 121 113.5332 118 0.6705
c= 553 59.8494 140 0.7955
m= 177 147 0.8352
Xo= 23 109 0.6193
media= 0.50 113 0.6420
varianza= 0.08 66 0.3750
Li v= 0.11 43 0.2443
Ls v= 0.06 92 0.5227
3 0.0170
Intervalo Oi Ei=n/m (Ei-Oi)2/Ei 31 0.1761
(0.00-0.10) 6 9 1.00 56 0.3182
(0.10-0.20) 12 9 1.00 72 0.4091
(0.20-0.30) 8 9 0.11 61 0.3466
(0.30-0.40) 7 9 0.44 146 0.8295
(0.40-0.50) 10 9 0.11 165 0.9375
(0.50-0.60) 10 9 0.11 163 0.9261
(0.60-0.70) 8 9 0.11 98 0.5568
(0.70-0.80) 7 9 0.44 21 0.1193
(0.80-0.90) 10 9 0.11 85 0.4830
(0.90-1.00) 9 9 0.00 41 0.2330
87 90 3.44 27 0.1534
103 0.5852
95 0.5398
12 0.0682
58 0.3295
137 0.7784
138 0.7841
82 0.4659
32 0.1818
0 0.0000
22 0.1250
29 0.1648
168 0.9545
172 0.9773
125 0.7102
102 0.5795
151 0.8580
62 0.3523
90 0.5114
115 0.6534
131 0.7443
120 0.6818
28 0.1591
47 0.2670
45 0.2557
157 0.8920
80 0.4545
144 0.8182

2. 100 0.5682
86 0.4886
162 0.9205
154 0.8750
71 0.4034
117 0.6648
19 0.1080
20 0.1136
141 0.8011
91 0.5170
59 0.3352
81 0.4602
88 0.5000
50 0.2841
54 0.3068
7 0.0398
161 0.9148
33 0.1875
121 0.6875
149 0.8466
174 0.9886
13 0.0739
2 0.0114
87 0.4943
106 0.6023
104 0.5909
39 0.2216
139 0.7898
26 0.1477
159 0.9034
145 0.8239
44 0.2500
36 0.2045
130 0.7386
176 1.0000
78 0.4432
79 0.4489
23 0.1307

3. 0.8797 0.3884 0.6289 0.8750 0.5999 0.8589 0.9996
0.9848 0.3469 0.7977 0.5844 0.8147 0.6431 0.7387
0.4557 0.1592 0.8536 0.8846 0.3410 0.1492 0.8681
0.9170 0.2204 0.5991 0.5461 0.5739 0.3254 0.0856
0.8376 0.6235 0.3681 0.2088 0.1525 0.2006 0.4720
Datos Intervalo Oi
media= 0.52 70.2122 (0.00-0.10) 4
LI= 0.42 31.5646 (0.10-0.20) 3
LS= 0.58 (0.20-0.30) 4
varianza= 0.07 (0.30-0.40) 7
Li v= 0.12 (0.40-0.50) 4
Ls v= 0.05 (0.50-0.60) 9
(0.60-0.70) 4
(0.70-0.80) 3
(0.80-0.90) 8
(0.90-1.00) 4
50

4. 0.2415 0.3808 0.9606
0.5613 0.0318 0.7401
0.5291 0.3188 0.5992
0.2258 0.4603 0.5027
0.4272 0.6360 0.0954
Ei=n/m (Ei-Oi)2/Ei
5 0.20
5 0.80
5 0.20
5 0.80
5 0.20
5 3.20
5 0.20
5 0.80
5 1.80
5 0.20
50 8.40

5. 0.78 0.98 0.24 0.73 0.43 0.16 0.78
0.04 0.29 0.68 0.77 0.16 0.03 0.79
0.96 0.26 0.91 0.55 0.75 0.55 0.64
0.61 0.14 0.38 0.12 0.4 0.74 0.78
0.43 0.67 0.62 0.32 0.53 0.54 0.24
0.82 0.94 0.19 0.98 0.41 1 0.74
0.83 0.88 0.18 0.21 0.5 0.13 0.43
0.22 0.5 0.16 0.11 0.18 0.89 0.8
0.83 0.79 0.65 0.28 0.78 0.49 0.36
0.51 0.07 0.18 0.94 0.5 0.22 0.66
Intervalo Oi Ei=n/m (Ei-Oi)2/Ei
(0.00-0.10) 5 10 2.50
(0.10-0.20) 15 10 2.50
(0.20-0.30) 13 10 0.90
(0.30-0.40) 5 10 2.50
(0.40-0.50) 11 10 0.10
(0.50-0.60) 11 10 0.10
(0.60-0.70) 9 10 0.10
(0.70-0.80) 11 10 0.10
(0.80-0.90) 10 10 0.00
(0.90-1.00) 10 10 0.00
100 100 8.80

6. 0.47 0.18 0.55
0.22 0.37 0.8
0.39 0.53 0.45
0.98 0.27 0.6
0.29 0.18 0.08
0.92 0.14 0.43
0.69 0.08 0.12
0.42 0.29 0.87
0.86 0.87 0.64
0.91 0.48 0.24

7. 0.78 0.98 0.24 0.73 0.43 0.16 0.78
0.04 0.29 0.68 0.77 0.16 0.03 0.79
0.96 0.26 0.91 0.55 0.75 0.55 0.64
0.61 0.14 0.38 0.12 0.4 0.74 0.78
0.43 0.67 0.62 0.32 0.53 0.54 0.24
0.82 0.94 0.19 0.98 0.41 1 0.74
0.83 0.88 0.18 0.21 0.5 0.13 0.43
0.22 0.5 0.16 0.11 0.18 0.89 0.8
0.83 0.79 0.65 0.28 0.78 0.49 0.36
0.51 0.07 0.18 0.94 0.5 0.22 0.66
x y Intervalo Oi Ei x2
0.78 0.04 1 5 3.96 0.2731313
0.04 0.96 2 3 3.96 0.2327273
0.96 0.61 3 6 3.96 1.0509091
0.61 0.43 4 4 3.96 0.000404
0.43 0.82 5 2 3.96 0.970101
0.82 0.83 6 5 3.96 0.2731313
0.83 0.22 7 2 3.96 0.970101
0.22 0.83 8 3 3.96 0.2327273
0.83 0.51 9 4 3.96 0.000404
0.51 0.98 10 4 3.96 0.000404
0.98 0.29 11 2 3.96 0.970101
0.29 0.26 12 2 3.96 0.970101
0.26 0.14 13 4 3.96 0.000404
0.14 0.67 14 8 3.96 4.1216162
0.67 0.94 15 5 3.96 0.2731313
0.94 0.88 16 5 3.96 0.2731313
0.88 0.5 17 5 3.96 0.2731313
0.5 0.79 18 5 3.96 0.2731313
0.79 0.07 19 4 3.96 0.000404
0.07 0.24 20 3 3.96 0.2327273
0.24 0.68 21 3 3.96 0.2327273
0.68 0.91 22 6 3.96 1.0509091
0.91 0.38 23 4 3.96 0.000404
0.38 0.62 24 2 3.96 0.970101
0.62 0.19 25 3 3.96 0.2327273
0.19 0.18 99 99 13.88
0.18 0.16
0.16 0.65 x2 de tablas= 33.196
0.65 0.18
0.18 0.73
0.73 0.77
0.77 0.55
0.55 0.12
0.12 0.32
0.32 0.98
0.98 0.21
0.21 0.11

8. 0.11 0.28
0.28 0.94
0.94 0.43
0.43 0.16
0.16 0.75
0.75 0.4
0.4 0.53
0.53 0.41
0.41 0.5
0.5 0.18
0.18 0.78
0.78 0.5
0.5 0.16
0.16 0.03
0.03 0.55
0.55 0.74
0.74 0.54
0.54 1
1 0.13
0.13 0.89
0.89 0.49
0.49 0.22
0.22 0.78
0.78 0.79
0.79 0.64
0.64 0.78
0.78 0.24
0.24 0.74
0.74 0.43
0.43 0.8
0.8 0.36
0.36 0.66
0.66 0.47
0.47 0.22
0.22 0.39
0.39 0.98
0.98 0.29
0.29 0.92
0.92 0.69
0.69 0.42
0.42 0.86
0.86 0.91
0.91 0.18
0.18 0.37
0.37 0.53
0.53 0.27
0.27 0.18
0.18 0.14
0.14 0.08
0.08 0.29

9. 0.29 0.87
0.87 0.48
0.48 0.55
0.55 0.8
0.8 0.45
0.45 0.6
0.6 0.08
0.08 0.43
0.43 0.12
0.12 0.87
0.87 0.64
0.64 0.24

10. 0.47 0.18 0.55
0.22 0.37 0.8
0.39 0.53 0.45
0.98 0.27 0.6
0.29 0.18 0.08
0.92 0.14 0.43
0.69 0.08 0.12
0.42 0.29 0.87
0.86 0.87 0.64
0.91 0.48 0.24
como la calculada es menor Ho se acepta por lo cual los numeros son independientes

11. 0.6069 0.5316 0.0529 0.4131 0.2991 0.6848 0.8291
0.4411 0.8195 0.3521 0.8068 0.1062 0.5384 0.9287
0.4029 0.2549 0.1003 0.5523 0.1897 0.8725 0.4439
0.1926 0.0266 0.5696 0.7504 0.8542 0.6045 0.2269
0.6367 0.9543 0.5385 0.2574 0.2396 0.3468 0.4105
s= 0 0 1 0 1 1
0 1 0 1 0 1
0 0 0 1 0 1
0 0 1 1 1 0
1 1 0 0 0 1
Co= 28
α= 90
μo= 33
σ 8.57
Zo= 0.58
Ztab= 1.655
Como Zo es menor nos er puede rechazar que los numeros son independientes

12. 0.1233 0.2497 0.9481
0.7954 0.7271 0.5739
0.6056 0.831 0.4709
0.797 0.3738 0.1284
0.5143 0.2014 0.99
0 1 1
1 0 0 0
0 1 1 0
0 1 0 0
1 1 0 1

13. 0.5858 0.8863 0.8378 0.3203 0.4115 0.271 0.9238
0.6213 0.436 0.6279 0.8415 0.5786 0.0543 0.3567
0.1931 0.0843 0.9152 0.6093 0.7587 0.4515 0.3203
0.1242 0.8826 0.9921 0.8523 0.6723 0.854 0.4722
0.8658 0.4028 0.6136 0.872 0.1126 0.5857 0.9172
x y Intervalo Oi Ei x2
0.5858 0.6213 1 2 1.96 0.00
0.6213 0.1931 2 1 1.96 0.47
0.1931 0.1242 3 1 1.96 0.47
0.1242 0.8658 4 3 1.96 0.55
0.8658 0.8863 5 2 1.96 0.00
0.8863 0.436 6 1 1.96 0.47
0.436 0.0843 7 1 1.96 0.47
0.0843 0.8826 8 0 1.96 1.96
0.8826 0.4028 9 1 1.96 0.47
0.4028 0.8378 10 5 1.96 4.72
0.8378 0.6279 11 2 1.96 0.00
0.6279 0.9152 12 1 1.96 0.47
0.9152 0.9921 13 2 1.96 0.00
0.9921 0.6136 14 0 1.96 1.96
0.6136 0.3203 15 3 1.96 0.55
0.3203 0.8415 16 1 1.96 0.47
0.8415 0.6093 17 2 1.96 0.00
0.6093 0.8523 18 2 1.96 0.00
0.8523 0.872 19 2 1.96 0.00
0.872 0.4115 20 2 1.96 0.00
0.4115 0.5786 21 2 1.96 0.00
0.5786 0.7587 22 2 1.96 0.00
0.7587 0.6723 23 4 1.96 2.12
0.6723 0.1126 24 3 1.96 0.55
0.1126 0.271 25 4 1.96 2.12
0.271 0.0543 49 49 17.84
0.0543 0.4515 X2= 33.193
0.4515 0.854 como Xo2<X2 se deduce que los numeros son independientes
0.854 0.5857
0.5857 0.9238
0.9238 0.3567
0.3567 0.3203
0.3203 0.4722
0.4722 0.9172
0.9172 0.1959
0.1959 0.1655
0.1655 0.5139
0.5139 0.4781
0.4781 0.8943

14. 0.8943 0.9268
0.9268 0.338
0.338 0.707
0.707 0.2101
0.2101 0.8095
0.8095 0.6702
0.6702 0.808
0.808 0.9123
0.9123 0.168
0.168 0.6408

15. 0.1959 0.9268 0.6702
0.1655 0.338 0.808
0.5139 0.707 0.9123
0.4781 0.2101 0.168
0.8943 0.8095 0.6408
x
1.2
1
0.8
0.6
0.4
0.2
0
0 0.2 0.4 0.6 0.8 1 1.2
x
os son independientes

16. 0.5858 0.8863 0.8378 0.3203 0.4115 0.271 0.9238
0.6213 0.436 0.6279 0.8415 0.5786 0.0543 0.3567
0.1931 0.0843 0.9152 0.6093 0.7587 0.4515 0.3203
0.1242 0.8826 0.9921 0.8523 0.6723 0.854 0.4722
0.8658 0.4028 0.6136 0.872 0.1126 0.5857 0.9172
media= 0.57486
var= 0.0784
No son los mismos que los de uan distribucion uniforme de numeros pseudoaleatorios, se atribuye la diferencia a l
que fueron concevidos quizas

17. 0.1959 0.9268 0.6702
0.1655 0.338 0.808
0.5139 0.707 0.9123
0.4781 0.2101 0.168
0.8943 0.8095 0.6408
s, se atribuye la diferencia a la forma empirica en

18. n= 71500
D= 4
2 pares= 3500
Categoria Prob Oi Ei Error
2P 0.027 3500 1930.5 1276.0063

19. N= x
D= 6
2 pares= 17500
Xo2= 15.51
alfa= 5%
X2= 12.592
ya que Xo2> X2 se rechazan que los núemros son independientes

20. A) No necesariamente se puede hacer con numeros de 3,4 y 5 y quizas hasta mas pero utilizando solo 5 digistos
b)Falso, pues para estar completamente seguros que son numeros aleatorios deben de pasar las 4 pruebas, medi
c) Cierto, esto quiere decir que los nuemros estan dispersos en todo el espacio disponible.
d) Cierto, pues al tener una media de 0.5 y una varianza de 1/12 se dice que los numeros tienen una priobabilidad

21. ero utilizando solo 5 digistos
de pasar las 4 pruebas, media, varianza, uniformidad e independencia
eros tienen una priobabilidad uniforme continua

22. Tamaño del Frecuencia Ei=(h)(β-α)(β-α)i
Observada (Ei-Oi)2/Ei
hueco Ei=(40)(0.1)(1-0.1)
0 5 4.00 0.25
1 4 3.60 0.04
2 3 3.24 0.02
3 3 2.92 0.00
>3 25 26.24 0.06
Total 40 40 0.37
β-α= 0.1
a) 0.37
b)
α= 10%
X2,0.1,3= 6.251
R=La muestra es pseudoaleatoria ya que Xo2 es menor que X2
n= 17000
alfa= 5%
alfa2= 0%
media= 11333
var= 3021.9
Zo=|(Co-media)/var|
Co=Zo*Var+media
Comin= 11484
Comax= 11333

23. n= 17000
alfa= 5%
alfa2= 0%
media= 11333
var= 3021.9
Zo=|(Co-media)/var|
Co=Zo*Var+media
Comin= 11484
Comax= 11333