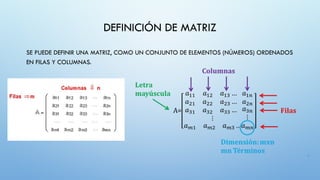
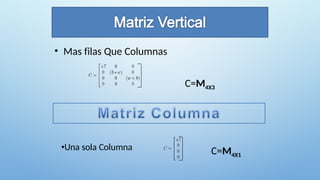
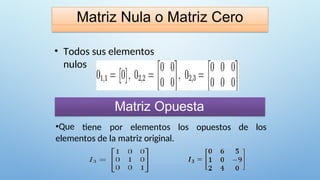
El documento aborda la definición y clasificación de matrices, presentando varios tipos, incluyendo matrices cuadradas, diagonales, identidad y simétricas, entre otras. También se explican las operaciones básicas con matrices, como la adición, resta y multiplicación, así como conceptos como matriz traspuesta y opuesta. Finalmente, se incluyen referencias para el estudio de álgebra lineal.














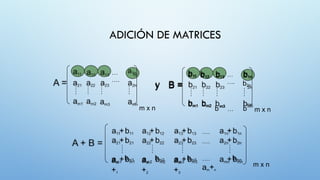
![Si A=
[ aij ]
y B=
[ bij ]
A + B = [ aij + bij ]
ADICIÓN DE MATRICES](https://image.slidesharecdn.com/1-250120034635-7faffa4e/85/1-2-Introduccion-algebra-lineal-aplicada-pptx-18-320.jpg)

![SUMA Y RESTA DE MATRICES
Diferencia se define como:
A - B = A + (-B) = [ aij -
bij ]
A
= 2 x 3
8 -4 0
1 2 -1 y B =
5 4 2
-1 -3 -1
2 x 3
8 - 5 -4- 4
1 - (-1) 2 - (-
3)
0 - 2
-1- (-1)
2 x 3
3
2
-8
5
-2
0
2 x 3](https://image.slidesharecdn.com/1-250120034635-7faffa4e/85/1-2-Introduccion-algebra-lineal-aplicada-pptx-21-320.jpg)
![Si A es una matriz cualquiera y k es un
número cualquiera, el producto kA el la
matriz obtenida de multiplicar cada
elemento de A por k:
Es decir si A= [ a ] kA= [ka ]
ij ij
m x n
…
….
m x n
ka ka ka
11 12 ka1n
….
ka2n
m1 m2 m3
…
…
MULTIPLICACIÓN DE UNA MATRIZ Y UN ESCALAR](https://image.slidesharecdn.com/1-250120034635-7faffa4e/85/1-2-Introduccion-algebra-lineal-aplicada-pptx-22-320.jpg)




