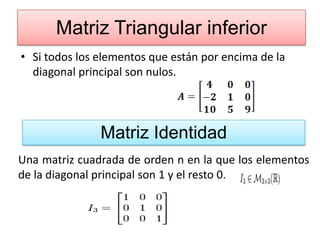
Este documento describe 27 tipos diferentes de matrices, incluyendo matrices cuadradas, rectangulares, diagonales, triangulares, identidad, nulas, opuestas, traspuestas, simétricas, antisimétricas y submatrices. Explica las características clave de cada tipo de matriz y cómo se definen y diferencian entre sí.

1. I.U. POLITECNICO
SANTIAGO MARIÑO
JESÚS RAMIREZ
C.I.:
14.794.388
ALGEBRA
LINEAL
TIPOS DE
MATRICES

2. 1. Matriz cuadrada
2. Matriz Rectangular
3. Matriz Vertical
4. Matriz Columna
5. Matriz Horizontal
6. Matriz Fila
7. Matriz Diagonal
8. Matriz Escalonada
9. Matriz Triangular superior
10. Matriz Triangular inferior
11. Matriz Identidad
12. Matriz Nula o Matriz Cero
13. Matriz Opuesta
14. Matriz Traspuesta
15. Matriz Simétrica
16. Matriz Antisimétrica
17. Matriz Ortogonal
18. Matriz Normal
19. Matriz Conjugada
20. Matriz Invertible
21. Matriz Singular o Degenerada
22. Matriz Permutación
23. Matrices iguales
24. Matriz Hermitiana
25. Matriz definida positiva
26. Matriz Unitaria
27. Submatriz
28. Resto del capítulo Matrices

3. • Número de filas igual que de columnas
FILAS
COLUMNAS

4. • Numero de Filas diferentes de Columnas
A=M3X2

5. • Mas filas Que Columnas
C=M4X3
•Una sola Columna C=M4X1

6. • Mas columnas Que Filas
A=M2X3
•Una sola Fila A=M1X3

7. Matriz Diagonal
• Puede ser una matriz con valores
•O también una matriz con subíndices (Genérica)

8. Matriz Escalonada
• El número de ceros que precede al primer elemento no nulo,
de cada fila o de cada columna, es mayor que el de la
precedente.
Matriz Triangular Superior
•Si todos los elementos que están por debajo de la diagonal
principal son nulos.

9. Matriz Triangular inferior
• Si todos los elementos que están por encima de la
diagonal principal son nulos.
Matriz Identidad
Una matriz cuadrada de orden n en la que los elementos
de la diagonal principal son 1 y el resto 0.

10. Matriz Nula o Matriz Cero
• Todos sus elementos nulos
Matriz Opuesta
•Que tiene por elementos los opuestos de los
elementos de la matriz original.

11. Matriz Traspuesta
• Matriz cuyas filas coinciden con las columnas de A y
las columnas coinciden con las filas de A.
Matriz Simétrica
• Cuando es una matriz cuadrada, y es igual a su
traspuesta.

12. • Cuando es una matriz cuadrada, y es igual a la
opuesta de su traspuesta.
• Matriz inversa coincide con su matriz traspuesta
Anti simétrica

13. • Sea A matriz compleja cuadrada, entonces es
una matriz normal si y sólo si
• donde A* es la matriz traspuesta conjugada de
A (también llamado hermitiano)
• La parte imaginaria de los elementos de la
matriz cambian su signo.

14. Matriz Invertible
• Es invertible si existe otra matriz cuadrada de orden
n, llamada matriz inversa de A y representada como
A−1, tal que AA−1 = A−1A = In,
• Donde In es la matriz identidad de orden n y el
producto utilizado es el producto de matrices usual.
Una matriz tiene inversa siempre que su
determinante no sea cero.
Matriz Singular o Degenerada
• Una matriz es singular si y solo si su determinante es
cero

15. Matriz Permutación
• Es la matriz cuadrada con todos sus n×n
elementos iguales a 0, excepto uno cualquiera
por cada fila y columna, el cual debe ser igual
a 1.
Matrices iguales
• Se dice que dos matrices A y B son iguales si tienen
la misma dimensión y son iguales elemento a
elemento, es decir, aij=bij i=1,...,n j=1,2,...,m.

16. Matriz Hermitiana
• Una matriz Hermitiana (o Hermítica) es una matriz cuadrada de elementos
complejos que tiene la característica de ser igual a su propia traspuesta
conjugada. Es decir, el elemento en la i-ésima fila y j-ésima columna es
igual al conjugado del elemento en la j-ésima fila e i-ésima columna, para
todos los índices i y j.
• Una matriz definida positiva es una matriz hermitiana que en muchos
aspectos es similar a un número real positivo.
• Es una matriz compleja U, de n por n elementos, que satisface la condición:
• Donde es la matriz identidad y es el traspuesto conjugado (también llamado el
hermitiano adjunto o la hermítica) de U. Esta condición implica que una matriz U
es unitaria si tiene inversa igual a su traspuesta conjugada .

17. Submatriz
• A partir de una Matriz M, se llama submatriz M' a
toda matriz obtenida suprimiendo p filas y q
columnas en M. Si M es de orden mxn, M' será de
orden (m-p)x(n-q), es decir con p filas menos y q
columnas menos. Es evidente que p < m ; q < n.