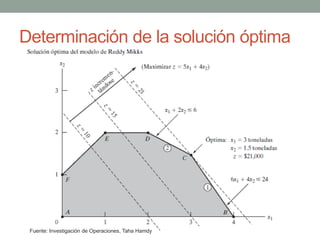
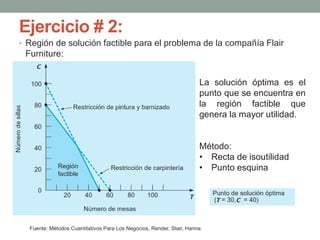
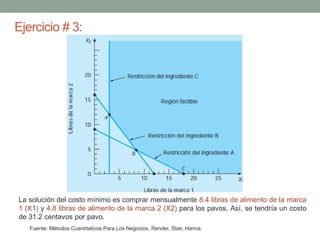
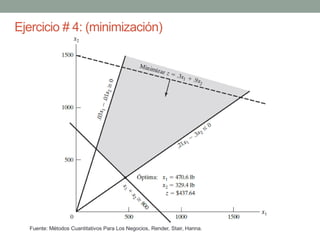
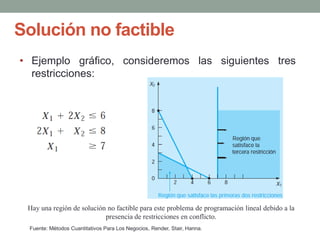
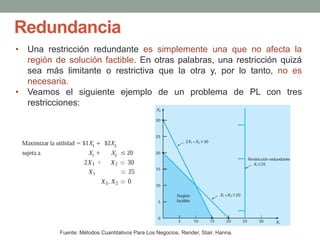
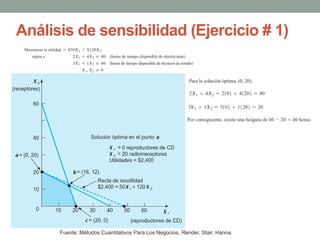
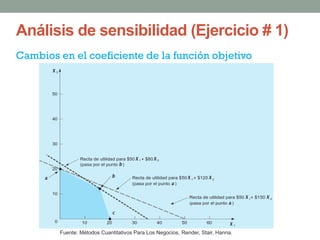
El documento describe la programación lineal (PL) como una técnica matemática para optimizar la asignación de recursos en decisiones administrativas, enfocándose en maximizar o minimizar funciones objetivo bajo ciertas restricciones. Se presentan ejemplos prácticos de PL, incluyendo un modelo de maximización de utilidad para una empresa de pinturas y un modelo de minimización de costos para la alimentación animal, además de discutir situaciones como soluciones no factibles y redundancia. También se menciona la importancia del análisis de sensibilidad en contextos inciertos del mundo real.

1. PROGRAMACION
MATEMATICA
Modelos de Programación Lineal

2. Introducción
• Muchas decisiones administrativas implican tratar de hacer un uso
más eficaz de los recursos de una organización.
• En general, los recursos incluyen maquinaria, mano de obra,
dinero, tiempo, espacio de almacenamiento y materia prima.
Tales recursos se utilizan para elaborar productos (como maquinaria,
mobiliario, alimentos o ropa) o servicios (como horarios para
aerolíneas o producción, políticas de publicidad o decisiones de
inversión).
• La programación lineal (PL) es una técnica de modelado
matemático ampliamente utilizada, que está diseñada para ayudar a
los gerentes en la planeación y toma de decisiones respecto a la
asignación de recursos.
Fuente: Investigación de Operaciones, Taha Hamdy

3. Requerimientos de un problema de
programación lineal
• Todos los problemas buscan maximizar o minimizar alguna cantidad,
por lo general la utilidad o el costo. Nos referimos a esta propiedad
como la función objetivo de un problema de PL.
• La segunda propiedad que los problemas de PL tienen en común es
la presencia de limitaciones o restricciones, que acotan el grado
en que se puede alcanzar el objetivo. (Por ejemplo, la decisión de cuántas
unidades de cada producto fabricar en la línea de productos de una empresa está restringida tanto
por el personal como por la maquinaria disponibles.)
• Tienen que existir cursos de acción alternativos para elegir. Por
ejemplo, si una organización fabrica tres productos diferentes, la gerencia puede utilizar la PL para
decidir cómo distribuir entre ellos sus recursos de producción limitados (de personal, maquinaria,
etcétera).
Fuente: Investigación de Operaciones, Taha Hamdy

4. Requerimientos de un problema de
programación lineal
• Los objetivos y las restricciones en los problemas de PL se deben
expresar en términos de ecuaciones o desigualdades lineales.
Las relaciones matemáticas lineales tan solo significan que todos los
términos utilizados en la función objetivo y en las restricciones son
de primer grado (es decir, no se elevan al cuadrado, al cubo o a una
potencia mayor, ni se presentan más de una vez).
Fuente: Investigación de Operaciones, Taha Hamdy

5. Modelo de PL con dos variables
Ejercicio # 1: (La compañía Reddy Mikks)
• Reddy Mikks produce pinturas para interiores y exteriores
con dos materias primas, M1 y M2. La tabla siguiente
proporciona los datos básicos del problema.
Fuente: Investigación de Operaciones, Taha Hamdy

6. Continuación …
• Una encuesta de mercado indica que la demanda diaria
de pintura para interiores no puede exceder la de pintura
para exteriores en más de una tonelada. Asimismo, que
la demanda diaria máxima de pintura para interiores es
de dos toneladas.
• Reddy Mikks se propone determinar la (mejor)
combinación óptima de pinturas para interiores y
exteriores que maximice la utilidad diaria total
Fuente: Investigación de Operaciones, Taha Hamdy

7. Solución
• Variables de Decisión:
• 𝑋1: Ton diarias producidas de pinturas para exteriores
• 𝑋2: Ton diarias producidas de pinturas para interiores
• Función Objetivo
• Maximizar la utilidad diaria total de la venta de los dos tipos de
pinturas
Maximizar 𝒁 = 𝟓𝑿𝟏 + 𝟒𝑿𝟐
• Restricciones (<=, =, >=)
Definir las restricciones que limitan el consumo de las materias primas y la
demanda del producto. Las restricciones en las materias primas se
expresan verbalmente como:
• Materia prima M1 disponible
• 𝟔𝑿𝟏 + 𝟒𝑿𝟐 ≤ 𝟐𝟒
• Materia prima M2 disponible
• 𝑿𝟏 + 𝟐𝑿𝟐 ≤ 𝟔
Fuente: Investigación de Operaciones, Taha Hamdy

8. Solución
• La producción diaria de pintura para interiores no debe
exceder a la de pintura para exteriores en más de 1
tonelada, lo cual se traduce en:
• Límite del mercado:
𝑿𝟐 − 𝑿𝟏 ≤ 𝟏
• La segunda restricción limita la demanda diaria de pintura
para interiores a 2 toneladas.
• Límite de la demanda:
𝑿𝟐 ≤ 𝟐
Las restricciones obvias de no negatividad deben incluirse
𝑿𝟏 ≥ 𝟎; 𝑿𝟐 ≥ 𝟎
Fuente: Investigación de Operaciones, Taha Hamdy

9. Modelo Matemático
𝑀𝑎𝑥 𝑍 = 5𝑋1 + 4𝑋2
Sujeto a
6𝑋1 + 4𝑋2 ≤ 24
𝑋1 + 2𝑋2 ≤ 6
𝑋2 − 𝑋1 ≤ 1
𝑋2 ≤ 2
𝑋1 ≥ 0
𝑋2 ≥ 0
• Una solución factible 𝑋1, 𝑋2 es aquella que satisface las cinco
restricciones del modelo.
• Caso contrario se dice que son infactibles o no factible, así por
ejemplo, 𝑋1 = 3; 𝑋2 = 1 es una solución factible.
Fuente: Investigación de Operaciones, Taha Hamdy

10. Solución gráfica del problema
1. Determinar el espacio de soluciones factibles.
2. Determinar la solución óptima dentro del espacio de
soluciones factibles.
• En la gráfica se muestra la intersección de las rectas
correspondientes a cada una de las restricciones del
modelo del ejemplo considerado.
• El espacio de soluciones factibles corresponde a la región
sombreada, el polígono de extremos: A, B, C, D, E, F.
• Los valores de los puntos extremos del polígono se
obtienen resolviendo las ecuaciones que resultan de la
intersección de las rectas correspondientes.
Fuente: Investigación de Operaciones, Taha Hamdy

11. La meta del problema es?
Fuente: Investigación de Operaciones, Taha Hamdy
• La meta del problema es determinar la solución
óptima, es decir la mejor solución factible que
maximice la utilidad total Z.
• Primero utilizamos el método gráfico para demostrar
que el problema (Reddy Mikks) tiene una cantidad
infinita de soluciones factibles, una propiedad
compartida por todas las PL no triviales.
• Esto significa que el problema no puede ser resuelto
por enumeración. En vez de eso, necesitamos un
algoritmo que determine la solución óptima en una
cantidad finita de pasos.

12. Espacio de soluciones factibles
Fuente: Investigación de Operaciones, Taha Hamdy
Solución factible:
𝑋1 = 3; 𝑋2 = 1
Solución NO factible:
𝑋1 = 4; 𝑋2 = 1
no satisface todas las restricciones
Las restricciones de no
negatividad limitan las variables
al primer cuadrante (sobre el eje
x1 y a la derecha del eje x2).
El espacio de soluciones
factibles corresponde a la región
sombreada, el polígono de
extremos: A, B, C, D, E, F.

13. Procedimiento para encontrar la solución óptima
• Encuentre el gradiente de Z
𝛻𝑍 =
𝜕𝑍
𝜕𝑋1
,
𝜕𝑍
𝜕𝑋2
• El gradiente indica el sentido de crecimiento más rápido
de una función en un punto dado.
• Trazar el vector gradiente en la gráfica de la región
factible
• Trazar paralelas perpendiculares al vector gradiente
hasta que el último punto de la región factible se
intersecte con la paralela.
• El último punto será el de la solución óptima.
Fuente: Investigación de Operaciones, Taha Hamdy

14. Determinación de la solución óptima
Fuente: Investigación de Operaciones, Taha Hamdy

15. Solución óptima
• La solución óptima de un problema PL siempre será un
punto extremo de la región factible. En el caso del
ejemplo el punto C es la solución óptima.
• Para encontrar el punto C hay que resolver el sistema de
ecuaciones siguiente:
6𝑋1 + 4𝑋2 = 24
𝑋1 + 2𝑋2 = 6
La solución óptima es : 𝑋1 = 3 𝑦 𝑋2 = 1.5
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

16. Ejercicio # 2: Compañía Flair Furniture
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

17. Ejercicio # 2:
• El objetivo es: Maximizar la utilidad
• Las variables de decisión que representan las decisiones reales
que tomarán se definen como:
T  número de mesas producidas por semana
C  número de sillas producidas por semana
• Las restricciones son:
1. Las horas de tiempo de carpintería utilizadas no pueden exceder
las 240 horas por semana.
2. Las horas de tiempo de pintura y barnizado utilizadas no pueden
exceder las 100 horas por semana.
• Ahora se crea la función objetivo de PL en términos de T y C:
Maximizar la utilidad = $70T + $50C.
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

18. Ejercicio # 2:
• Para obtener soluciones significativas, los valores de T y C deben
ser números no negativos. Es decir, todas las posibles soluciones
tienen que representar mesas y sillas reales. Matemáticamente, esto
significa que:
• T >= 0 (el número de mesas producidas es mayor que o igual a 0)
• C >= 0 (el número de sillas producidas es mayor que o igual a 0)
• Ahora el problema completo se reexpresa matemáticamente como:
Maximizar utilidad = $70T + $50C
• sujeto a las restricciones:
4T + 3C <= 240 (restricción de carpintería)
2T + 1C <= 100 (restricción de pintura y barnizado)
T >= 0 (primera restricción de no negatividad)
C >= 0 (segunda restricción de no negatividad)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

19. Ejercicio # 2:
• Región de solución factible para el problema de la compañía Flair
Furniture:
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
La solución óptima es el
punto que se encuentra en
la región factible que
genera la mayor utilidad.
Método:
• Recta de isoutilidad
• Punto esquina

20. Ejercicios complementarios:
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

21. Programación Lineal: Solución gráfica (minimización)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Muchos de los problemas de PL incluyen minimizar un objetivo
como el costo, en vez de maximizar una función de utilidad.
• Un restaurante, por ejemplo, tal vez quiera desarrollar un
horario de trabajo para satisfacer las necesidades de personal
y reducir al mínimo el número total de empleados.
• Un fabricante puede buscar la forma de distribuir sus
productos elaborados en diferentes fábricas a sus almacenes
regionales, de manera que minimice los costos de envío
totales.
Problemas típicos en PL:
• Problema de la dieta (minimización)
• Control de la producción
• Plan de producción de varios períodos

22. Resúmenes de los métodos de solución gráfica
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

23. Ejercicio # 3: (minimización)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

24. Ejercicio # 3:
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Variables de decisión:
• X1  número de libras de la marca 1 de alimento comprada
• X2  número de libras de la marca 2 de alimento comprada
• Función Objetivo:
• Minimizar los costos (en centavos) = 2X1 + 3X2
• Restricciones:
• 5X1 + 10X2 >= 90 onzas (restricción del ingrediente A)
• 4X1 + 3X2 >= 48 onzas (restricción del ingrediente B)
• 0.5X1 >= 1.5 onzas (restricción del ingrediente C)
• X1 >= 0 (restricción de no negatividad)
• X2 >= 0 (restricción de no negatividad)

25. Ejercicio # 3:
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
La solución del costo mínimo es comprar mensualmente 8.4 libras de alimento de la marca
1 (X1) y 4.8 libras de alimento de la marca 2 (X2) para los pavos. Así, se tendría un costo
de 31.2 centavos por pavo.

26. Ejercicio # 4: (minimización)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
Ozark Farms consume diariamente un mínimo de 800 lb
de un alimento especial, el cual es una mezcla de maíz y
soya con las siguientes composiciones:
Las necesidades dietéticas del alimento especial son un mínimo de
30% de proteína y un máximo de 5% de fibra. El objetivo es
determinar la mezcla diaria de alimento a un costo mínimo.

27. Ejercicio # 4: (minimización)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
Las variables de decisión del modelo son:
• X1 libras de maíz en la mezcla diaria
• X2 libras de soya en la mezcla diaria
El objetivo es minimizar el costo diario total (en dólares) de la mezcla
de alimento:
Minimizar z = 0.3x1 + 0.9x2
Las restricciones:
• Ozark Farms requiere un mínimo de 800 lb de alimento al día, es
decir:
x1 + x2 >= 800
• La cantidad de proteína contenida en x1 libras de maíz y en x2
libras de soya es (0.09x1 + 0.6x2) lb. Esta cantidad debe ser al
menos igual al 30% de la mezcla de alimentos total (x1 + x2) lb, es
decir:
0.09x1 + 0.6x2 >= 0.3(x1 + x2)

28. Ejercicio # 4: (minimización)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
Asimismo, la necesidad de fibra de 5% máximo se representa como
sigue:
0.02x1 + 0.06x2 <= 0.05(x1 + x2)
Las restricciones se simplifican:
Minimizar z = 0.3x1 + 0.9x2
sujeto a:
x1 + x2 >= 800
0.21x1 - 0.30x2 <= 0
0.03x1 - 0.01x2 >= 0
x1, x2 >= 0

29. Ejercicio # 4: (minimización)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

30. Casos especiales de PL
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
Algunas veces surgen cuatro casos especiales y dificultades
cuando se utiliza el método gráfico para resolver problemas de
PL:
1. Solución no factible,
2. Región no acotada,
3. Redundancia y
4. Soluciones óptimas múltiples.

31. Solución no factible
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Cuando no hay solución a un problema de PL que satisfaga todas
las restricciones dadas, entonces existe una solución no factible.
• Gráficamente, esto significa que no hay una región de solución
factible: una situación que ocurriría si el problema se formuló con
restricciones en conflicto.
Por ejemplo: Si el director de ventas proporciona:
• Una restricción que establece que al menos se deben fabricar 300
mesas (es decir, X1 >=300) para satisfacer la demanda de ventas.
• Una segunda restricción la da el gerente de producción, quien
insiste en que no se fabriquen más de 220 mesas (es decir, X1 <=
220) debido a la escasez de madera. No se obtiene una región de
solución factible.

32. Solución no factible
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Ejemplo gráfico, consideremos las siguientes tres
restricciones:
Hay una región de solución no factible para este problema de programación lineal debido a la
presencia de restricciones en conflicto.

33. Región no acotada
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Cuando la utilidad en un problema de maximización puede ser
infinitamente grande, el problema es no acotado y faltan una o más
restricciones.
• Consideremos lo siguiente para ilustrar la situación. Una empresa
formuló el siguiente problema de PL:
En un problema de maximización y la región factible
se extiende infinitamente hacia la derecha, es
ilimitada o existe una solución no acotada. Esto
implica que el problema se ha formulado
incorrectamente.

34. Redundancia
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Una restricción redundante es simplemente una que no afecta la
región de solución factible. En otras palabras, una restricción quizá
sea más limitante o restrictiva que la otra y, por lo tanto, no es
necesaria.
• Veamos el siguiente ejemplo de un problema de PL con tres
restricciones:

35. Soluciones óptimas múltiples
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Un problema de PL puede, en ocasiones, tener dos o más soluciones
óptimas múltiples. Gráficamente, este es el caso cuando la recta de
isoutilidad de la función objetivo corre perfectamente paralela a una
de las restricciones del problema o, en otras palabras, cuando tienen
la misma pendiente.
La recta entre A y B ofrece una combinación óptima de X1 y X2.
Lejos de causar problemas, la existencia de más de una
solución óptima permite una mayor flexibilidad en la
administración para decidir qué combinación seleccionar.

36. Análisis de sensibilidad
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Hasta ahora, las soluciones óptimas a los problemas de PL se han
encontrado en lo que se llaman suposiciones deterministas, que
significa que suponemos toda la certeza en los datos y las relaciones
de un problema. es decir, los precios son fijos, se conocen los
recursos y se ha establecido el tiempo necesario para producir
exactamente una unidad.
• No obstante, en el mundo real las condiciones son dinámicas y
cambiantes.
¿Cómo se manejaría esta
aparente discrepancia?

37. Análisis de sensibilidad
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Una forma de hacerlo es seguir tratando cada problema de PL en
particular como una situación determinista.
• Sin embargo, cuando se encuentra la solución óptima, se reconoce
la importancia de ver qué tan sensible es la solución ante los datos y
las suposiciones del modelo.
• Por ejemplo, si una organización se da cuenta de que la utilidad por
unidad no es de $5 como se había estimado, sino que está más
cerca de $5.50.
• ¿cómo sería la combinación de la solución final y cómo cambiaría la
utilidad total?

38. Análisis de sensibilidad
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• Una función importante del análisis de sensibilidad es permitir a los
gerentes experimentar con los valores de los parámetros de entrada.
• Estos análisis se utilizan para examinar los efectos de los cambios
en tres áreas:
• 1. tasas de contribución de cada variable,
• 2. coeficientes tecnológicos (los números en las ecuaciones de
restricción) y
• 3. recursos disponibles (las cantidades en el lado derecho de
cada restricción).
Análisis de sensibilidad, análisis de posoptimalidad,
programación paramétrica o análisis de optimalidad.

39. Análisis de sensibilidad
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
• El análisis de sensibilidad también implica a menudo una serie de
preguntas del tipo:
• ¿qué pasaría si?
• ¿Qué ocurriría si la utilidad del producto 1 se incrementa en un
10%? ¿Qué sucedería si hay menos dinero disponible en la
restricción del presupuesto de publicidad?
• ¿Qué pasaría si los trabajadores se quedan una hora más todos
los días a una tasa de pago de 1?, con la finalidad de aumentar
• la capacidad de producción?
El análisis de sensibilidad se utiliza para:
• Tratar los errores en la estimación de los parámetros de entrada
para el modelo de PL,
• sino también con experimentos administrativos con posibles
cambios futuros en la empresa, los cuales afectarían las
utilidades.

40. Análisis de sensibilidad
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
Métodos para
determinar qué tan
sensible es una
solución óptima ante
los cambios.
Método de ensayo y error:
El cual por lo general implica la
resolución de todo el problema,
cada vez que cambia un
parámetro o un elemento de los
datos de entrada.
El método analítico:
Después de que se haya resuelto
un problema de PL, se pretende
determinar una serie de cambios
en los parámetros del problema,
que no afectarán la solución
óptima ni cambiarán las variables
en la solución.

41. Análisis de sensibilidad (Ejercicio # 1)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

42. Análisis de sensibilidad (Ejercicio # 1)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.

43. Análisis de sensibilidad (Ejercicio # 1)
Fuente: Métodos Cuantitativos Para Los Negocios, Render, Stair, Hanna.
Cambios en el coeficiente de la función objetivo