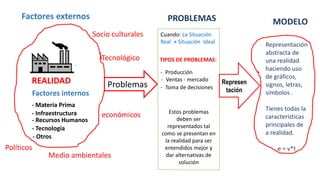
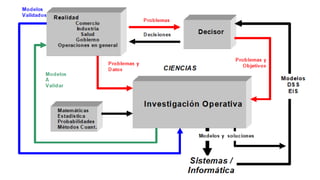
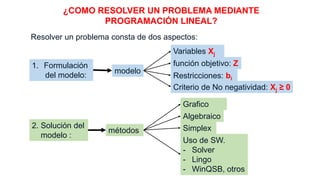
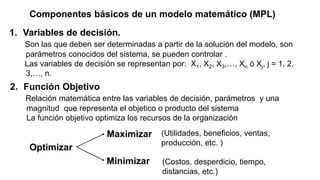
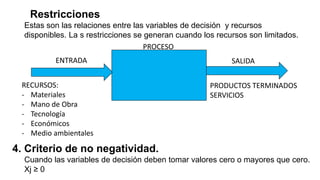
El documento aborda la investigación operativa, destacando varios tipos de modelos utilizados para representar problemas del mundo real, incluyendo modelos físicos, descriptivos, analógicos y simbólicos. Se explica cómo resolver problemas a través de la programación lineal, que implica la formulación y solución de modelos matemáticos, y se discuten las variables de decisión, funciones objetivo y restricciones. Además, se presenta un ejemplo práctico relacionado con la producción de tejidos para ilustrar la aplicación de estos conceptos en la optimización de recursos.

1. Investigación Operativa I
Escuela Profesional de Ingeniería de Sistemas
Carlos A. Bruno Romero
Introducción- Modelos utilizados en Investigación
Operativa – Clases de modelos –Alternativas
Universidad Nacional
José Faustino Sánchez Carrión

2. REALIDAD
Medio ambientales
Socio culturales
Factores externos
Políticos
económicos
Tecnológico
Problemas
PROBLEMAS
Represen
tación
MODELO
Representación
abstracta de
una realidad
haciendo uso
de gráficos,
signos, letras,
símbolos .
Tienes todas la
características
principales de
a realidad.
e = v*t
Factores internos
- Materia Prima
- Infraestructura
- Recursos Humanos
- Tecnología
- Otros
Cuando: La Situación
Real ≠ Situación Ideal
TIPOS DE PROBLEMAS:
- Producción
- Ventas - mercado
- Toma de decisiones
Estos problemas
deben ser
representados tal
como se presentan en
la realidad para ser
entendidos mejor y
dar alternativas de
solución

4. Clases o Tipos de Modelos
1. Modelos Físicos o Icónicos
Son representaciones hechas a escala de una realidad. Como por ejemplo: El
mapamundi, el plano de una casa, una foto, una maqueta de una fabrica
2. Modelos Descriptivos
Son representaciones habladas o escritas de una realidad. Como por ejemplo: El
relato como ha pasado esta cuarentena a causa de la pandemia
3. Modelos Analógicos
Son representaciones hechas de modelos ya existentes que tienen características
similares. Como por ejemplo: Desarrollar un SW de control de personal a la
empresa X similar al de la empresa Y
4. Modelos Simbólicos
son representaciones de la realidad con símbolos, letras, números, etc. Dentro de
ellos tenemos los modelos matemáticos, por ejemplo: v = e/t

5. ¿COMO RESOLVER UN PROBLEMA MEDIANTE
PROGRAMACIÓN LINEAL?
Resolver un problema consta de dos aspectos:
1. Formulación
del modelo:
2. Solución del
modelo :
modelo
Variables Xj
función objetivo: Z
Restricciones: bi
Criterio de No negatividad: Xj ≥ 0
Grafico
Algebraico
Simplex
Uso de SW.
- Solver
- Lingo
- WinQSB, otros
métodos

6. Componentes básicos de un modelo matemático (MPL)
1. Variables de decisión.
Son las que deben ser determinadas a partir de la solución del modelo, son
parámetros conocidos del sistema, se pueden controlar .
Las variables de decisión se representan por: X1, X2, X3,…, Xn ó Xj, j = 1, 2,
3,…, n.
2. Función Objetivo
Relación matemática entre las variables de decisión, parámetros y una
magnitud que representa el objetico o producto del sistema
La función objetivo optimiza los recursos de la organización
Optimizar
Maximizar
Minimizar
(Utilidades, beneficios, ventas,
producción, etc. )
(Costos, desperdicio, tiempo,
distancias, etc.)

7. 3. Restricciones
Son los diferentes requisitos cumplir cualquier solución para que pueda llevarse
a cabo. En cierta manera son las limitantes en los valores de los niveles de las
diferentes actividades (variables). Las restricciones más comunes son:.
Restricciones de capacidad. Limitan el valor de las variables debido a la
disponibilidad de horas-hombre, horas-máquina, espacio, etc.
Restricciones de mercado. Surgen de los valores máximos y/o mínimos de la
demanda o el uso del producto o actividad a realizar
Restricciones de entradas. Son limitantes debido a la escasez de materias
primas, mano de obra, dinero, etc.
Restricciones de calidad. Limitan las mezclas de componentes, que definen la
calidad de los productos a producir, mezcla de ingredientes, etc
Restricciones de balance de materiales. Son las que definen las salidas de un
proceso en función de las entradas, teniendo en cuenta el porcentaje de mermas

8. 4. Criterio de no negatividad.
Cuando las variables de decisión deben tomar valores cero o mayores que cero.
Xj ≥ 0
Restricciones
Estas son las relaciones entre las variables de decisión y recursos
disponibles. La s restricciones se generan cuando los recursos son limitados.
ENTRADA
PROCESO
SALIDA
RECURSOS:
- Materiales
- Mano de Obra
- Tecnología
- Económicos
- Medio ambientales
PRODUCTOS TERMINADOS
SERVICIOS

9. PROPIEDADES DEL M.P.L.
Proporcionalidad:
Significa cual es la contribución al valor de la función objetivo y el consumo o
requerimiento de los recursos utilizados
Aditividad:
Se puede valorar la función objetivo (Z) como los recursos utilizados, sumando
las contribuciones de cada uno de los términos y las restricciones .
Divisibilidad:
Las variables de decisión son continuas , por lo tanto aceptan valores no enteros
positivo
Certidumbre
Significa que los parámetros o constantes son estimados con certeza, es decir no
interviene una función de probabilidad para obtenerlas

10. Tipos de problemas
 Planeación de la producción e inventarios
 Mezcla de Alimentos
 Transporte y asignación
 Planeación financiera
 Mercadotecnia
 Asignación de recursos
 Redes de optimización

11. EJEMPLO:
La fábrica de Hilados y Tejidos “LA ARAÑITA" requiere fabricar dos
tejidos de calidad diferente T y T’; se dispone de 500 Kg de hilo a, 300
Kg de hilo b y 108 Kg de hilo c. Para obtener un metro de T
diariamente se necesitan 125 gr de a, 150 gr de b y 72 gr de c; para
producir un metro de T’ por día se necesitan 200 gr de a, 100 gr de b y
27 gr de c.
El T se vende a $4000 el metro y el T’ se vende a $5000 el metro. Si
se debe obtener el máximo beneficio, ¿cuántos metros de T y T’ se
deben fabricar?

12. PASO 1: "FORMULAR EL PROBLEMA"
Para realizar este paso partimos de la pregunta central del problema.
¿cuántos metros de T y T’ se deben fabricar?
PASO 2: DETERMINAR LAS VARIABLES DE DECISIÓN
Basándonos en la formulación del problema nuestras variables de decisión son:
X1 : Cantidad de metros diarios de tejido tipo T a fabricar
X2 : Cantidad de metros diarios de tejido tipo T’ a fabricar
Función Objetivo
Z Max = 4000X1 + 5000X2
PASO 3: DETERMINAR LA FUNCIÓN OBJETIVO
En este paso es de vital importancia establecer el contexto operativo del problema
para de esta forma determinar si es de Maximización o Minimización. En este caso
abordamos el contexto de beneficio por ende lo ideal es Maximizar.

13. PASO 4: DETERMINAR LAS RESTRICCIONES DEL PROBLEMA
Determinamos las funciones que limitan el problema, estas están dadas por capacidad,
disponibilidad, proporción, no negatividad entre otras.
PASO 5: CEITERIO DE NO NEGATIVIDAD
X1, X2 ≥ 0
De disponibilidad de materia prima:
0,12X1 + 0,2X2 <= 500 Hilo “a”
0,15X1 + 0,1X2 <= 300 Hilo “b”
0,072X1 + 0,027X2 <= 108 Hilo “c”
Z Max = 4000X1 + 5000X2
X1, X2 ≥ 0
S.a:
0,12X1 + 0,2X2 <= 500 Hilo “a”
0,15X1 + 0,1X2 <= 300 Hilo “b”
0,072X1 + 0,027X2 <= 108 Hilo “c”
Resumen

14. Formular los ejercicios propuestos
GRACIAS