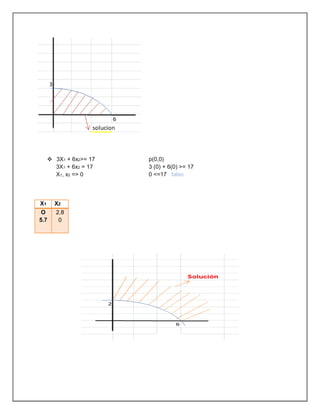
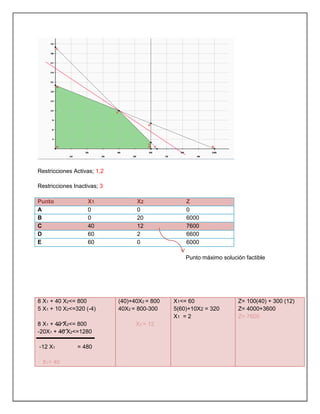
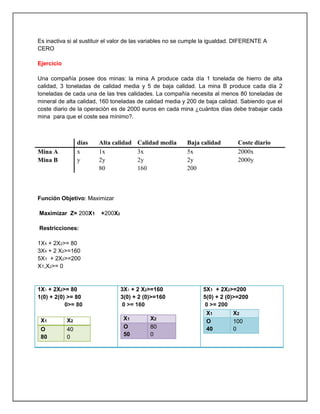
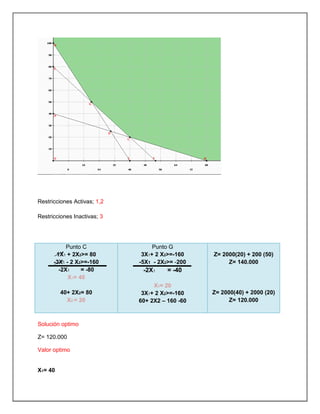
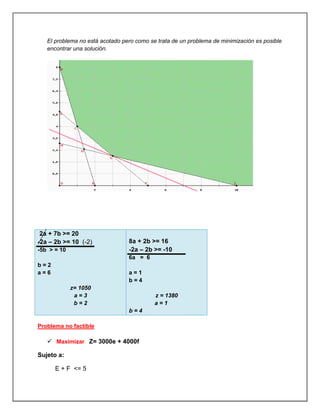
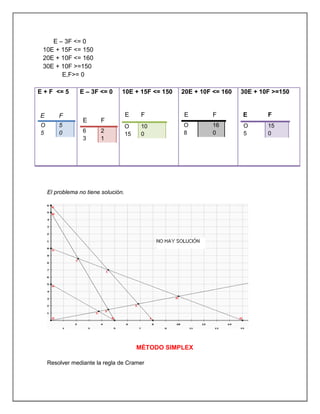
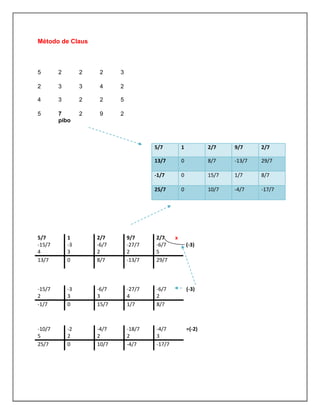
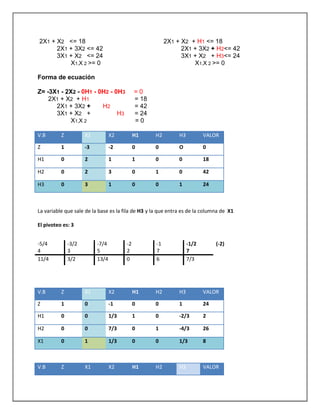
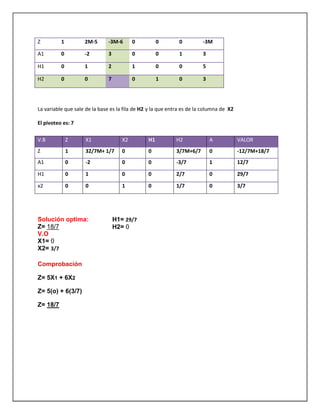
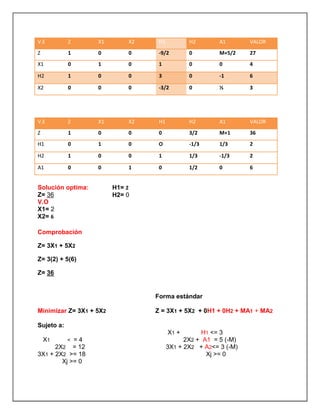
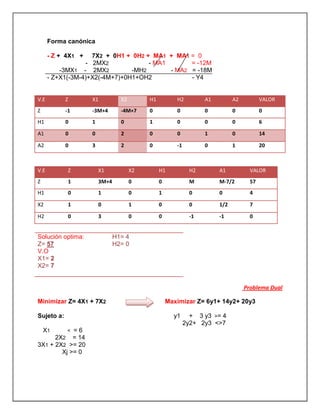
El documento trata sobre investigación operativa y programación lineal. Explica que la investigación operativa se aplica a problemas de coordinación de actividades dentro de una empresa y provee conclusiones claras para la toma de decisiones. La programación lineal busca optimizar un resultado mediante el planeamiento de actividades sujetas a restricciones, donde todas las funciones matemáticas deben ser lineales.

1. INVESTIGACIÓN OPERATIVA
Se aplica a los problemas que se refiere a la coordinación de actividades dentro de la empresa,
también proporcionan conclusiones claras para tomar decisiones.
PROGRAMACION LINEAL
El adjetivo lineal significa que todas las funciones matemáticas del modelo deber ser funciones
lineales. En este caso, las palabra programación no se refiere a programación en
computadoras; en esencia es un sinónimo de planeación. Así, la programación lineal trata la
planeación de las actividades para obtener un resultado óptimo.
Variables de decisión:
Z= ax1 + Bx2 +………………………n
Restricciones:
a11x1 + a12x2+… + a1nxn ≤ b1
a21x1 + a22x2+ …+ a2nxn>= b2
a31x1 + a32x2 + … + a3nxn≤ b3
………………………………
am1x1 + am2x2 + … + amnxn = bm
Aunque el problema no lo diga llevara las restricciones:
x1; x2; xn>= 0
Planteamiento de un problema
1. Definir las variables de decisión
2. Construir el modelo matemático
3. Plantear las limitaciones
4. Plantear las condiciones de no negatividad
Planteamiento de un problema de la investigación operativa
1. Definir el problema
2. C.MOD
3. Resolver MO
4. S.O
5. Revalorización
Condiciones de no negatividad

2. Z = valor de la medida global de efectividad
Xj =nivel de la actividad j (para j = 1,2,...,n)
Cj =incremento en Z que resulta al aumentar una unidad en el nivel de la actividad j
bi = cantidad de recurso i disponible para asignar a las actividades (para i = 1,2,...,m)
aij = cantidad del recurso i consumido por cada unidad de la actividad j
GRAFICA DE DESIGUALDADES
Para graficar desigualdades realice los siguientes pasos
 Gráfica de la igualdad. Convierta la desigualdad en igualdad y grafique la recta
 Escoja un punto de ensayo
 Evalúe el primer miembro de la expresión
 Determine si el punto de ensayo satisface la desigualdad.
Ejercicios
 2X1 + 4x2<= 12 p(0,0)
2X1 + 4x2 = 12 2 (0) + 4(0) <= 2
X1, x2 => 0 0 <=12 verdad
X1 X2
O
6
3
3

3.  3X1 + 6x2>= 17 p(0,0)
3X1 + 6x2 = 17 3 (0) + 6(0) >= 17
X1, x2 => 0 0 <=17 falso
X1 X2
O
5.7
2.8
0

4. MÉTODO GRÁFICO
Es una forma fácil para resolver problemas de Programación Lineal, siempre y cuando el
modelo conste de dos variables. Para modelos con tres o más variables, el método gráfico es
imposible.
Estructura Matemática
 Variables de decisión; (x1 + x2 + x3…….. xn )
 Función objetivo:(Max o min) f(x1 + x2 +x3… ………………..xn)
 Restricciones:
1. (x1 + x2 +x3… ………………..xn) ≤ b
2. (x1 + x2 + x3… ………………..xn) ≤ b2
3. (x1 + x2 + x3… ………………..xn) ≤ bm
 Condiciones de no negatividad
Ejercicio
Una compañía de auditores se especializa en preparar liquidaciones y auditorías de empresas
pequeñas. Tienen interés en saber cuántas auditorías y liquidaciones pueden realizar
mensualmente para maximizar sus ingresos. Se dispone de 800 horas de trabajo directo y 320
horas para revisión. Una auditoría en promedio requiere de 40 horas de trabajo directo y 10
horas de revisión, además aporta un ingreso de 300 dls. Una liquidación de impuesto requiere
de 8 horas de trabajo directo y de 5 horas de revisión, produce un ingreso de 100 dls. El
máximo de liquidaciones mensuales disponibles es de 60.
Incógnitas: auditorias, liquidaciones
Variables de decisión:
 cantidad de auditorías (x1)
 Cantidad de liquidaciones (x2)
Restricciones:
 tiempo disponible de trabajo directo
 Tiempo disponible de revisión
 Número máximo de liquidaciones
Liquidaciones
X1
Auditorias
X2
Dispongo
Horas de trabajo 8 40 800
Horas de revisión 5 10 320

5. utilidad 100 300 60
Función Objetivo: Maximizar el ingreso total.
Maximizar Z= 100 X1 +300 X2
Restricciones:
8X1 + 40X2<= 800
5X1 + 10 X2<=320
X1<=60
X1,X2>= 0
8X1 + 40X2<= 800
8(0) + 40(0) <= 800
0<= 800
X1 X2
O
5
10
0
5X1 + 10 X2<=320
5(0) + 10 (0)<=320
0 <= 320
X1 X2
O
8
4
0
X1<= 60

6. Restricciones Activas; 1,2
Restricciones Inactivas; 3
Punto X1 X2 Z
A 0 0 0
B 0 20 6000
C 40 12 7600
D 60 2 6600
E 60 0 6000
Punto máximo solución factible
8 X1 + 40 X2<= 800
5 X1 + 10 X2<=320 (-4)
8 X1 + 40 X2<= 800
-20X1 + 40 X2<=1280
-12 X1 = 480
X1= 40
(40)+40X2 = 800
40X2 = 800-300
X2 = 12
X1<= 60
5(60)+10X2 = 320
X1 = 2
Z= 100(40) + 300 (12)
Z= 4000+3600
Z= 7600

7. Valor optimo
X1= 40
X2 = 12
NOTA: Maximizar 40 liquidaciones y 12 auditorías para tener un ingreso de 7600
Comprobación
8X1 + 40X2 <= 800
8(40) + 40(12) <= 800
800 <=800
5X1 + 10 X2<=320
5(40) + 10 (12) <= 320
320>= 320
X1<= 60
40 < = 60
H1 = 20
VARIABLES DE HOLGURA Y VARIABLES DE EXCEDENTE
Variable de holgura.
Puede interpretarse como la cantidad de recurso no usado.
6X + 3Y ≤ 12 6X+3Y+h=24
Variable de Excedente.
Es la cantidad por encima de algún nivel mínimo requerido.
2X + 3Y ≥14 2X+3Y-h =14
Ambos tipos de variables tienen que cumplir con la restricción de NO NEGATIVIDAD
Restricción activa.
Dada una solución factible, una restricción es activa si al sustituir el valor de las variables se
cumple la igualdad. Sea CERO
Restricción Inactiva.

8. Es inactiva si al sustituir el valor de las variables no se cumple la igualdad. DIFERENTE A
CERO
Ejercicio
Una compañía posee dos minas: la mina A produce cada día 1 tonelada de hierro de alta
calidad, 3 toneladas de calidad media y 5 de baja calidad. La mina B produce cada día 2
toneladas de cada una de las tres calidades. La compañía necesita al menos 80 toneladas de
mineral de alta calidad, 160 toneladas de calidad media y 200 de baja calidad. Sabiendo que el
coste diario de la operación es de 2000 euros en cada mina ¿cuántos días debe trabajar cada
mina para que el coste sea mínimo?.
días Alta calidad Calidad media Baja calidad Coste diario
Mina A x 1x 3x 5x 2000x
Mina B y 2y 2y 2y 2000y
80 160 200
Función Objetivo: Maximizar
Maximizar Z= 200X1 +200X2
Restricciones:
1X1 + 2X2>= 80
3X1 + 2 X2>=160
5X1 + 2X2>=200
X1,X2>= 0
1X1 + 2X2>= 80
1(0) + 2(0) >= 80
0>= 80
X1 X2
O
80
40
0
3X1 + 2 X2>=160
3(0) + 2 (0)>=160
0 >= 160
X1 X2
O
50
80
0
5X1 + 2X2>=200
5(0) + 2 (0)>=200
0 >= 200
X1 X2
O
40
100
0

9. Restricciones Activas; 1,2
Restricciones Inactivas; 3
Punto C
1X1 + 2X2>= 80
-3X1 - 2 X2>=-160
-2X1 = -80
X1= 40
40+ 2X2= 80
X2 = 20
Punto G
3X1+ 2 X2>=-160
-5X1 - 2X2>= -200
-2X1 = -40
X1= 20
3X1+ 2 X2>=-160
60+ 2X2 – 160 -60
Z= 2000(20) + 200 (50)
Z= 140.000
Z= 2000(40) + 2000 (20)
Z= 120.000
Solución optimo
Z= 120.000
Valor optimo
X1= 40

10. X2 = 20
NOTA:debe trabajar X1= 40 y X2 = 20 para que el costo sea mínimo de 120.000
Comprobación
1 X1 + 2 X2 >= 80
40 + 2 (20) >= 80
40 +40>= 80
80>= 80
3X1 + 2 X2>=160
3(40) + 2 (20)>=160
120 + 40 >=160
160 >= 160
5X1 + 2X2>=200
5(40) + 2 (20)>=200
200+40 >=200
240>= 200
Variables De Holgura Y Variables De Excedente
1 X1 + 2 X2 + h>= 80
40 + 2 (20) +h>= 80
H1>= 0
3X1 + 2 X2 + h>=160
3(40) + 2 (20) + h>=160
H2>= 0
5X1 + 2X2 - h>=200
5(40) + 2 (20) - h>=200
240 - h3>=200
h3>=200
TIPOS DE REGIONES FACTIBLES
Un problema de programación lineal puede ser de dos tipos :
 Que tenga una región limitada o acotada
 Que tenga una región no acotada o limitada
 Región acotada
Calidad Disponibilidad Holgura Excedente
Alta 80
Media 160
Baja 200 40

11. 1. Puede ser que tenga una sola solución
2. Puede ser que tenga múltiples soluciones
 Región no acotada
3. que tenga una solución
4. No existe solución
Ejercicios

12.  Minimizar Z= 2x + 3y
Sujeto a:
-3x + 2y <= 6
X + y <= 10.5
-x + 2y >= 4
X,y>= 0
3x + 2y <= 6
X Y
O
-3
-3
0
X + y <= 10.5
X Y
O
10.5
10.5
0
-x + 2y >= 4
X Y
O
-4
2
0

13. -3x + 2y <= 6
-3x - 2y <= 30.5
6x = 6.5
X= 1.3
Z= 2x + 3 y
Z= 2 + 6
Z= 8
Solución optimo
Z= 6
Valor optimo
X= 0
y= 2
Restricciones Activas; 3
Restricciones Inactivas; 1,2
 Maximizar Z= 5/ 2x1 + X2
Sujeto a:
3X1 + 5X2<= 15
5X1 + 2X2<= 10
X1,X2>= 0
3X1 + 5X2<= 15
X Y
O
5
3
0
5X1 + 2X2<= 10
X Y
O
2
5
0

14. 3X1 + 5X2<= 15 (-2)
10X1 - 4X2<= 20 (5)
7x1< = 5
-6X1 - 10X2<= -30
-25X1 + 10X2<= 50
19x1< = 20
X1= 20/19
X1 = 2.37
3 (20/19)+ 5X2 =15
60/19 +5X2 = 15
5X2 = 45/19
X2
Z = 5/2(20/10) +45/19
Z = 2.5 + 2.37
Z =5
Solución optimo
Z= 5
Valor optimo
X1= 2
X2= 0
La solución es: todas las parejas de puntos que se encuentran en el intervalo

15. Problemas no acotadas
 Maximizar Z= 5000A + 4000B
Sujeto a:
a + b >= 5
a - 3b <= 0
3a + 10b >= 135
a,b>= 0
a + b >= 5
a b
O
5
5
0
a - 3b <= 0
a b
O
3
0
1
3a + 10b >= 135
a b
O
4.5
13.5
0

16.  Un frutero necesita 16 cajas de naranjas, 5 de platantas
 Maximizar Z= 150A + 300B
Sujeto a:
8a +2 b >= 16
a + b >= 5
2a + 7b >= 20
a,b>= 0
8a +2 b >= 16
a b
O
2
8
0
a + b >= 5
a b
O
5
5
0
2a + 7b >= 20
a b
O
10
3
0

17. El problema no está acotado pero como se trata de un problema de minimización es posible
encontrar una solución.
2a + 7b >= 20
-2a – 2b >= 10 (-2)
-5b > = 10
b = 2
a = 6
z= 1050
a = 3
b = 2
8a + 2b >= 16
-2a – 2b >= -10
6a = 6
a = 1
b = 4
z = 1380
a = 1
b = 4
Problema no factible
 Maximizar Z= 3000e + 4000f
Sujeto a:
E + F <= 5

18. E – 3F <= 0
10E + 15F <= 150
20E + 10F <= 160
30E + 10F >=150
E,F>= 0
E + F <= 5
E F
O
5
5
0
E – 3F <= 0
E F
6
3
2
1
10E + 15F <= 150
E F
O
15
10
0
20E + 10F <= 160
E F
O
8
16
0
30E + 10F >=150
E F
O
5
15
0
El problema no tiene solución.
MÉTODO SIMPLEX
Resolver mediante la regla de Cramer

19. Método de Claus
5 2 2 2 3
2 3 3 4 2
4 3 2 2 5
5 7
pibo
2 9 2
5/7 1 2/7 9/7 2/7
13/7 0 8/7 -13/7 29/7
-1/7 0 15/7 1/7 8/7
25/7 0 10/7 -4/7 -17/7
5/7
-15/7
4
1
-3
3
2/7
-6/7
2
9/7
-27/7
2
2/7 x
-6/7
5
(-3)
13/7 0 8/7 -13/7 29/7
-15/7
2
-3
3
-6/7
3
-27/7
4
-6/7
2
(-3)
-1/7 0 15/7 1/7 8/7
-10/7
5
-2
2
-4/7
2
-18/7
2
-4/7
3
=(-2)
25/7 0 10/7 -4/7 -17/7

20. 7 2 4 6 5 3
4 3 3 5 2 3
5 6 7 8
pibo
4 2
8 9 7 6 3 3
4 3 5 2 7 7
13/4 -5/2 -5/4 0 2 3/2
7/8 -6/8 -11/8 0 1/2 7/4
5/8 6/8 7/8 1 1/2 7/2
17/4 9/2 7/4 0 0 3/2
11/4 3/2 13/4 0 6 7/3
5/8
-25/8
4
6/8
-30/8
3
7/8
-35/8
3
1
-5
5
1/2
-5/2
2
7/2
-5/2
3
x
(-5)
7/8 -6/8 -11/8 0 1/2 7/4
-15/4
7
-9/2
2
-21/4
4
-6
6
-3
5
-3/2
3
(-6)
13/4 -5/2 -5/4 0 2 3/2
-15/4
8
-9/4
9
-21/4
7
-6
6
-3
3
-3/2
3
(-6)
17/4 9/2 7/4 0 0 3/2
-5/4
4
-3/2
3
-7/4
5
-2
2
-1
7
-1/2
7
(-2)
11/4 3/2 13/4 0 6 7/3

21.  Maximizar Z= 20a + 30b
Sujeto a:
2a + 2b + h1 <= 5
a + b + h2<= 150
a,b >= 0
Valor entrante: el número más alto
Valor saliente: el número más pequeño que existe
Pivoteo: se encuentra entre el valor entrante y valor saliente
La variable que sale de la base es la fila de H1 y la que entra es de la columna de B
El pivoteo es: 2
NOTA: Para encontrar el valor saliente dividimos los número de la columna de valor con la columna de
valor entrante (5/2), y es el menor número
Z= 3X1 + 4X2 + 9X3
Sujeto a:
2X1 + 2X2 <= 10
2X2 + 5X3 <= 16
3X1 - 2X2 - 7X3 <= 9
Xj >= 0
Forma de ecuación
Z= -3X1 - 4X2 - 9X3 = 0
s.a
2X1 + 2X2 = 10
2X2 + 5X3 = 16
3X1 - 2X2 - 7X3 = 9
Xj >= 0
F.S
V.E A B H1 H2 VALOR
Z 20 30 0 0 0
H1 2 2 1 o 5 2.3
H2 1 1 0 1 3 3

22. Z= -3X1 - 4X2 - 9X3 = 0
s.a
2X1 + 2X2 + H1 = 10
2X2 + 5X3 + H2 = 16
3X1 - 2X2 - 7X3 + H3 = 9
Xj, Hj >= 0
V.B E.C Z X1 X2 X3 H1 H2 H3 VALOR
Z 0 1 -3 -4 -9 0 O O 0
H1 1 0 2 2 0 1 0 0 10
H2 2 0 0 2 5 0 1 0 10
H3 3 0 3 -2 -7 0 0 1 9
La variable que sale de la base es la fila de H3 y la que entra es de la columna de X3
El pivoteo es: -7
MÉTODO SIMPLEX
Valor entrante: el más negativo, en la fila de z
Valor saliente: el menor valor, divido para cada valor de la derecha
Pivoteo: el número que se encuentra en la intersección entre el valor entrante y valor
saliente
Si es < = se debe agregar + H (horgura)
Si es = se debe agregar + A (artificial)
Si es > = se debe agregar + A –H
Maximizar Z= 3X1 + 2X2
Sujeto a:
Forma estándar
Z= 3X1 + 2X2 + 0H1 + 0H2 + 0H3
Sujeto a:

23. 2X1 + X2 <= 18
2X1 + 3X2 <= 42
3X1 + X2 <= 24
X1,X 2 >= 0
2X1 + X2 + H1 <= 18
2X1 + 3X2 + H2<= 42
3X1 + X2 + H3<= 24
X1,X 2 >= 0
Forma de ecuación
Z= -3X1 - 2X2 - 0H1 - 0H2 - 0H3 = 0
2X1 + X2 + H1 = 18
2X1 + 3X2 + H2 = 42
3X1 + X2 + H3 = 24
X1,X 2 = 0
V.B Z X1 X2 H1 H2 H3 VALOR
Z 1 -3 -2 0 0 O 0
H1 0 2 1 1 0 0 18
H2 0 2 3 0 1 0 42
H3 0 3 1 0 0 1 24
La variable que sale de la base es la fila de H3 y la que entra es de la columna de X1
El pivoteo es: 3
V.B Z X1 X2 H1 H2 H3 VALOR
Z 1 0 -1 0 0 1 24
H1 0 0 1/3 1 0 -2/3 2
H2 0 0 7/3 0 1 -4/3 26
X1 0 1 1/3 0 0 1/3 8
V.B Z X1 X2 H1 H2 H3 VALOR
-5/4
4
-3/2
3
-7/4
5
-2
2
-1
7
-1/2
7
(-2)
11/4 3/2 13/4 0 6 7/3

24. Z 1 0 0 3 0 -1 30
H1 0 0 1 3 0 -2 6
H2 0 0 0 -7 1 4 12
X1 0 1 0 -1 0 1 6
V.B Z X1 X2 H1 H2 H3 VALOR
Z 1 0 0 5/4 ¼ 0 33
H1 0 0 1 -1/2 ½ 0 12
H2 0 0 0 -7/4 ¼ 1 3
X1 0 1 0 3/4 3/4 0 3
Sujeto a:
Z= 33
V.O
X1= 3
X2= 12
H1= 0
H2= 0
H3= 3
Maximizar Z= 3000X1 + 4000X2
Sujeto a:
X1 + X2 <= 5
X1 - 3X2 <= 0
10X1 + 15X2 <= 150
20X1 + 10X2 <= 160
30X1 + 10X2 <= 150
Forma estándar
Z= -3000X1 - 4000X2 + 0H1 + 0H2 + 0H3
+H4+H5
X1 + X2 + H1 <= 5
X1 - 3X2 + H2<= 0
10X1 + 15X2 + H3<= 24
20X1 + 10X2 + H4<= 160
30X1 + 10X2 + H5 <= 150
V.B Z X1 X2 H1 H2 H3 H4 H5 VALOR
Z 1 -300 -400 0 0 0 0 0 0

25. H1 0 1 1 1 0 0 0 0 5
H2 0 1 3 0 1 0 0 0 0
H3 0 10 15 0 0 1 0 0 150
H4 0 20 10 0 0 0 1 0 160
H5 0 30 10 0 0 0 0 1 150
V.B Z X1 X2 H1 H2 H3 H4 H5 VALOR
Z 1 100 0 4000 0 0 0 0 2000
H1 0 1 1 1 0 0 0 0 5
H2 0 4 0 3 1 0 0 0 15
H3 0 -5 0 -15 1 1 0 0 75
H4 0 10 0 -10 0 0 1 10 110
H5 0 20 0 0 10 0 0 1 100
Maximizar Z= X1 + X2
Sujeto a:
X1 + 3X2 <= 26
4X1 + 3X2 <= 44
2X1 + 3X2 <= 28
Forma estándar
Z- X1 - X2 + 0H1 + 0H2 + 0H3
X1 + X2 + H1 <= 26
4X1 + 3X2 + H2<= 44
2X1 + 3X2 + H3<= 28
V.B Z X1 X2 H1 H2 H3 VALOR
Z -1 -1 -1 0 0 0 0
H1 0 1 3 1 0 0 26
H2 0 4 3 0 1 0 44
H3 0 2 3 0 0 1 28

26. MÉTODO SIMPLEX DE PENALIZACIÓN
V.B Z X1 X2 H1 H2 H3 VALOR
Z 1 2/3 0 -1/3 0 0 26/3
X2 0 1/3 1 1/3 0 0 26/3
H2 0 3 0 -1 1 0 18
H3 0 1 0 -1 0 1 2
V.B Z X1 X2 H1 H2 H3 VALOR
Z 1 0 0 2/3 0 2/3 10
H1 0 0 1 2/3 0 -1/3 8
H2 0 0 0 2 1 -3 12
H3 0 1 0 1 0 1 2
Maximizar Z= 5X1 + 6X2
Sujeto a:
-2X1 + 3X2 = 3
X1 + 2X2 <= 5
6X1 + 7X2 <= 3
Forma estándar
Z = 5X1 + 6X2 – M1 + 0H1 + 0H2
-2X1 + 3X2 + A1 <= 3
X1 + 2X2 + H1 <= 5
6X1 + 7X2 + H2<= 3
Z= 5X1 - 6X2 – M1- OHI –OH2 = 0
-2X1 + 3X2 + A1 = 3
X1 + 2X2 + H1<= 5
6X1 + 7X2 + H2<= 3
V.B Z X1 X2 H1 H2 A VALOR

27. La variable que sale de la base es la fila de H2 y la que entra es de la columna de X2
El pivoteo es: 7
Comprobación
Z= 5X1 + 6X2
Z= 5(o) + 6(3/7)
Z= 18/7
Z 1 2M-5 -3M-6 0 0 0 -3M
A1 0 -2 3 0 0 1 3
H1 0 1 2 1 0 0 5
H2 0 0 7 0 1 0 3
V.B Z X1 X2 H1 H2 A VALOR
Z 1 32/7M+ 1/7 0 0 3/7M+6/7 0 -12/7M+18/7
A1 0 -2 0 0 -3/7 1 12/7
H1 0 1 0 0 2/7 0 29/7
x2 0 0 1 0 1/7 0 3/7
Solución optima:
Z= 18/7
V.O
X1= 0
X2= 3/7
H1= 29/7
H2= 0

28. V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 -3M-3 -5-2M 0 0 0 -18M
H1 0 1 0 1 0 0 4
H2 1 0 2 0 1 0 12
A1 0 3 2 0 0 1 18
V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 0 -2M-5 3M+3 0 0 -6M+12
X1 0 1 0 1 0 0 4
H2 1 0 2 0 1 0 12
A1 0 0 2 3 0 1 6
Maximizar Z= 3X1 + 5X2
Sujeto a:
X1 < = 4
2X2 <= 12
3X1 + 2X2 <= 18
Xj >= 0
Forma estándar
Z = 3X1 + 5X2 + 0H1 + 0H2 - MA1
X1 + H1 <= 3
2X2 + H2 <= 5
3X1 + 2X2 + A<= 3
Xj >= 0
Forma canónica
Z - 3X1 - 5X2 - 0H1 - 0H2 + MA1 = 0
-3MX1 - 2M2 - MA1 – 18M
Z+X1(-3M-3)+X2(-5-2M) 0 - 18M
X1 + H1 <= 3
2X2 + H2 <= 5
3X1 + 2X2 + A<= 3
X1,x2 >= 0

29. V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 0 0 -9/2 0 M+5/2 27
X1 0 1 0 1 0 0 4
H2 1 0 0 3 0 -1 6
X2 0 0 0 -3/2 0 ½ 3
V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 0 0 0 3/2 M+1 36
H1 0 1 0 O -1/3 1/3 2
H2 1 0 0 1 1/3 -1/3 2
A1 0 0 1 0 1/2 0 6
Comprobación
Z= 3X1 + 5X2
Z= 3(2) + 5(6)
Z= 36
Solución optima:
Z= 36
V.O
X1= 2
X2= 6
H1= 2
H2= 0
Minimizar Z= 3X1 + 5X2
Sujeto a:
X1 < = 4
2X2 = 12
3X1 + 2X2 >= 18
Xj >= 0
Forma estándar
Z = 3X1 + 5X2 + 0H1 + 0H2 + MA1 + MA2
X1 + H1 <= 3
2X2 + A1 = 5 (-M)
3X1 + 2X2 + A2<= 3 (-M)
Xj >= 0

30. V.E Z X1 X2 H1 H2 A1 A2 VALOR
Z -1 -3M+3 -4M+5 0 0 0 0 -30M
H1 0 1 0 1 0 0 0 4
A1 0 0 2 0 0 1 0 12
A2 0 3 2 0 -1 0 1 18
V.E Z X1 X2 H1 H2 A1 VALOR
Z -1 -3M+3 0 0 M -2M-5/2 -6M+ 30
X1 0 1 0 1 0 0 4
X2 1 0 1 0 0 1/2 6
A2 0 3 0 0 -1 -1 6
V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 0 0 1 M-3/2 M-1 36
X1 0 0 0 1/3 1/3 -1/3 2
H2 1 0 1 0 ½ 0 6
X2 0 1 0 -1/3 -1/3 1/3 2(3M-3)
Forma canónica
- Z + 3X1 + 5X2 + 0H1 + 0H2 + MA1 + MA1 = 0
- 2MX2 - MA1 = -12M
-3MX1 - 2MX2 -MH2 - MA2 = -18M
- Z+X1(-3M-3)+X2(-4M+5)+0H1+OH2 - 30M
X1 + H1 <= 2
2X2 + A1 <= 12
3X1 + 2X2 + A2-H2<= 18
X1,x2 >= 0

31. PROBLEMA DUAL
EJERCICIOS
Problema Primal
V.E Z A B H1 H2 A1 VALOR
Z 1 -400 -300 0 0 0 0
H1 0 2 1 1 0 0 60
H2 0 1 3 0 1 0 40
H3 0 1 1 0 0 1 30
V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 0 100 0 0 400 12000
X1 0 0 -1 1 0 0 0
H2 0 0 -2 0 1 0 10
X2 0 1 1 0 0 1 30
Maximizar Z= 400A+ 300B
Sujeto a:
2A + B <= 60
A + 3B <= 40
A + B <= 30
Forma estándar
Z = 3X1 + 5X2 + 0H1 + 0H2 + MA1 + MA2
2A + B + H1 <= 3
A + 3B + H2 <= 40
A + B + H3<= 30
Solución optima:
Z= 12000
V.O
A= 30
B= 0
H1= 0
H2= 10
H3= 0

32. PROBLEMA DUAL
Problema Dual
Maximizar Z= 400A+ 300B
Sujeto a:
2A + B <= 60
A + 3B <= 40
A + B <= 30
Minimizar Z= 60y1+ 40y2+ 30y3
2y1 + y2 +y3 >= 400
y1+ 3y2 + y3 >= 3OO
Yj >=0
100+ Y3 =300
Y3 =200
2y1 +y3 = 400
y1+ y3 = 3OO
2y1 +y3 = 400
-y1 - y3 = -3OO
Y1 = 100
Solución optima:
Z= 12000
V.O
Y1= 100
Y2= 0
Y3 = 200
Z= 60y1+ 40y2+ 30y3
Z = 6000 + 6000
Z = 12000
Minimizar Z= 4X1 + 7X2
Sujeto a:
X1 < = 6
2X2 = 14
3X1 + 2X2 >= 20
Xj >= 0
Forma estándar
Z = 3X1 + 5X2 + 0H1 + 0H2 + MA1 + MA2
X1 + H1 <= 6
2X2 + A1 = 14 (-M)
3X1 + 2X2 - H2 + A2<= 20 (-M)
Xj >= 0

33. V.E Z X1 X2 H1 H2 A1 A2 VALOR
Z -1 -3M+4 -4M+7 0 0 0 0 0
H1 0 1 0 1 0 0 0 6
A1 0 0 2 0 0 1 0 14
A2 0 3 2 0 -1 0 1 20
V.E Z X1 X2 H1 H2 A1 VALOR
Z 1 3M+4 0 0 M M-7/2 57
H1 0 1 0 1 0 0 4
X2 1 0 1 0 0 1/2 7
H2 0 3 0 0 -1 -1 0
Problema Dual
Minimizar Z= 4X1 + 7X2
Sujeto a:
X1 < = 6
2X2 = 14
3X1 + 2X2 >= 20
Xj >= 0
Maximizar Z= 6y1+ 14y2+ 20y3
y1 + 3 y3 >= 4
2y2+ 2y3 <>7
Forma canónica
- Z + 4X1 + 7X2 + 0H1 + 0H2 + MA1 + MA1 = 0
- 2MX2 - MA1 = -12M
-3MX1 - 2MX2 -MH2 - MA2 = -18M
- Z+X1(-3M-4)+X2(-4M+7)+0H1+OH2 - Y4
Solución optima:
Z= 57
V.O
X1= 2
X2= 7
H1= 4
H2= 0

34. 100+ Y3 =300
Y3 =200
3y3 >= 4
Y3 = 4/3
2y2 + 2(4/3) = 7
2y2 + 8/3 = 7
Y2 = 7-8/3 /2
Y2 = 13/6
Solución optima:
Z= 63
V.O
Y1= 0
Y2= 13/6
Y3 = 4/3
Z= 6(0) +14(13/6)+20(4/3)
Z = 6 +91/3 +80/3
Z = 63