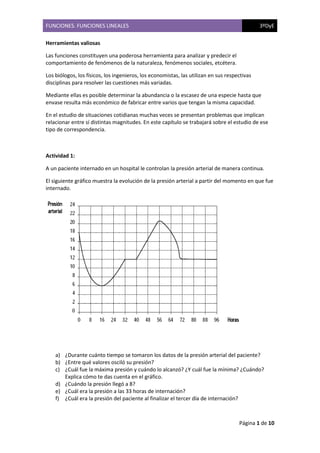
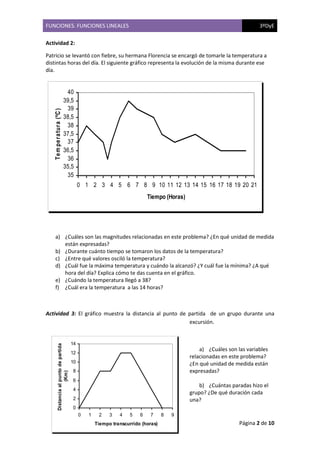
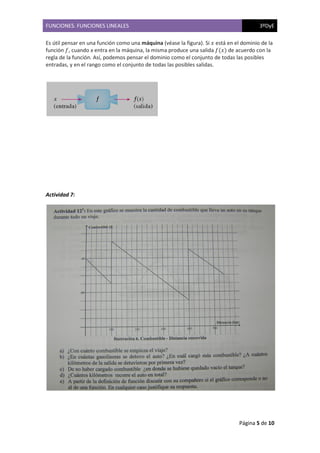
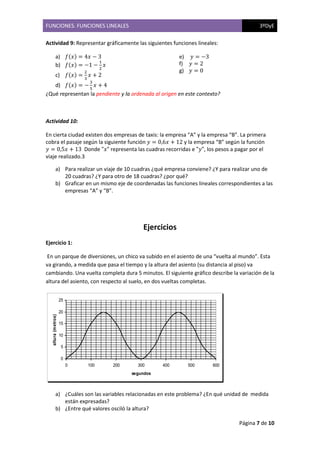
El documento trata sobre funciones lineales y presenta varias actividades para analizar situaciones que involucran la relación entre distintas magnitudes. Se analizan gráficos que representan la evolución de variables como presión arterial, temperatura y distancia recorrida en función del tiempo. También se presentan ejemplos sobre precios de viajes en taxi, valor de automóviles a lo largo de los años y costos de internet.