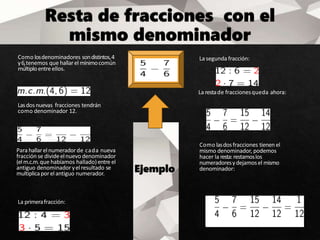
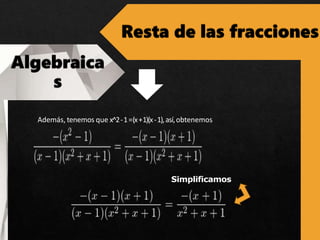
El documento trata sobre expresiones algebraicas y operaciones con fracciones. Explica cómo simplificar fracciones poniéndolas a común denominador y cómo realizar operaciones como suma, resta, multiplicación y división con fracciones algebraicas. También cubre temas como factorización de polinomios, cuadrados de binomios y trinomios, y la regla de Ruffini para dividir un polinomio por un binomio.

2. Cada producto notable corresponde a una fórmula de
factorización. Por ejemplo, la factorización de una diferencia
de cuadrados perfectos es un producto de dos binomios
conjugados, y recíprocamente
En matemática diremos que la simplificación o
reducción de fracciones es la acción de dividirse el
numerador y el denominador de una fracción por otro
mismo número con el fin de obtener otra fracción
equivalente, cuyo cociente tenga el mismo valor
numérico.
Podemos decir que una fracción está reducida a sus
términos más simples o completamente simplificados
cuando no existe ningún factor común al numerador y
el denominador

3. Calculamos el común denominador que
será el m.c.m. de los denominadores
Dividimos el común denominador entre los
denominadores de las fracciones dadas y el resultado
lo multiplicamos por el numerador correspondiente
Quitamos paréntesis
Realizamoslasoperacionesenelnumerador
Sacamosfactorcomún2enelnumerador
Simplificamos

4. En este caso, se mantiene el denominador y se
opera con los numeradores. Podemos dejar una
sola fracción con el denominador común y con
los términos de ambos numeradores:
Y después agrupar términos semejantes en el
numerador:

5. Como losdenominadores sondistintos,4
y6,tenemos que hallarel mínimocomún
múltiploentre ellos.
Lasdosnuevas fracciones tendrán
como denominador 12.
Para hallarelnumeradorde cada nueva
fracción se divideelnuevo denominador
(elm.c.m.que habíamos hallado)entre el
antiguo denominador yelresultado se
multiplicaporelantiguo numerador.
La primerafracción:
La segunda fracción:
La restade fraccionesqueda ahora:
Como lasdosfracciones tienen el
mismo denominador, podemos
hacer la resta:restamoslos
numeradoresydejamosel mismo
denominador:

6. Tenemos que poner a común denominador, para ello tenemos que hallar el m.c.m. de
los denominadores.
Por lo tanto
Dividimos el común denominador entre los denominadores de las fracciones dadas y el
resultado lo multiplicamos por el numerador correspondiente y operamos

7. Simplificamos
Además, tenemos que x^2-1=(x+1)(x-1),así,obtenemos

8. El producto de dos fracciones
algebraicas es otra fracción
algebraica donde el
numerador es el producto de
los numeradores y el
denominador es el producto
de los denominadores
Vamos a descomponer en factores para poder
simplificar
En el primer factor del numerador sacamos
factor común y el segundo factor que es un
trinomio cuadrado perfecto lo transformamos
en un binomio al cuadrado
El trinomio del denominador lo factorizamos
utilizando la fórmula general
También tenemos una diferencia de
cuadrados en el denominador
Sustituyendo todo lo anterior en nuestra
multiplicación tenemos
Simplificamos

9. La división de dos fracciones algebraicas es otra fracción algebraica cuyo numerador es el producto
del numerador de la primera por el denominador de la segunda, y como denominador el producto
del denominador de la primera por el numerador de la segunda.
El segundo binomio es una suma al cubo
El trinomio del denominador es un trinomio
cuadrado perfecto y el binomio es una
diferencia de cuadrados que factoriza como
una suma por diferencia.
Simplificamos
O bien

10. Solamente pueden sumarse (o restarse) dos
radicales cuando son radicales semejantes, es
decir, si son radicales con el mismo índice e igual
radicando.
Para sumar radicales con el mismo índice e igual
radicando se se suman los coeficientes de los
radicales.
Ejemplos
Sumamos los coeficientes de los radicales
Sumamos los coeficientes de los radicales

11. CUADRO DE UN BINOMIO
El producto de un binomio por sí mismo recibe el nombre de cuadrado de un
binomio.
El desarrollo del cuadrado del binomio a +b se puede obtener multiplicando
término a término:
“El cuadrado de un binomio a +b es igual al cuadrado del primer término más el
doble del producto de
los términos más el cuadrado del segundo término”.
Ahora, al elevar al cuadrado el binomio a −b , también multiplicando
término a término, se obtiene:
“El cuadrado de un binomio a −b es igual al cuadrado del primer
término menos el doble del producto
de los términos más el cuadrado del segundo término”.
En las fórmulas anteriores a y b pueden ser cualquier expresión algebraica y tener
cualquier signo. Por
lo tanto, segunda la fórmula es un caso particular de la primera ya que:

12. El producto de un trinomio por sí mismo recibe el nombre de cuadrado de un
trinomio.
El desarrollo del cuadrado del trinomio a +b +c se puede obtener de la siguiente forma:
ordenando se tiene
Por su parte, el desarrollo del cuadrado del polinomio de cuatro términos a +b +c +d
se puede obtener
de la siguiente forma:
ordenando se llega a:

13. El valor numérico de esta expresión algebraica
cuando
En primer lugar, sustituimos las incógnitas
(letras) por el valor dado.
Ahora, resolvemos las operaciones indicadas.
Primero hacemos las potencias:
En segundo lugar, las multiplicaciones
Por último, las sumas y restas
El valor numérico de esta expresión algebraica
cuando
En primer lugar, sustituimos las letras por los
valores que nos han indicado, en este
caso, se cambia por un -1
Ahora, simplificamos esta expresión
numérica según el orden de las
operaciones combinadas.
Primero hacemos las potencias:
Y, multiplicando, obtenemos

14. La regla de Ruffini (división sintética)
nos permite dividir fácilmente un
polinomio por un binomio de la forma
(x - a).
Teorema del Resto: El resto de
dividir P(x) entre (x - a) es igual a
P(a), valor númerico del polinomio
en x = a.
Teorema del Factor: Si x = a es una
raíz de P(x), entonces (x - a) es un
factor.
Modifica en el panel izquierdo los
coeficientes de P(x) y del divisor y
observa lo que sucede en el panel
derecho. Identifica todas las raíces del
polinomio que se muestra.
Puedes cambiar el tamaño de los
paneles moviendo la barra de
separación.

15. Álgebra
https://edu.gcfglobal.org/es/algebra/expresiones-
algebraicas/1/
Expresiones Algebraicas
https://sanfrancisco.utn.edu.ar/documentos/archivos/ing
reso/Cap%C3%ADtulo%202_Ingenier%C3%ADas.pdf
Expresiones Algebraicas Polinomios
https://ele.chaco.gob.ar/mod/book/view.php?id=70297
Regla de Ruffini
www.geogebra.org/m/YadfrN42#:~:text=La%20regla%20d
e%20Ruffini%20(divisi%C3%B3n,del%20polinomi
o%20en%20x%20%3D%20a.