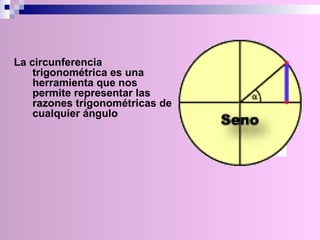
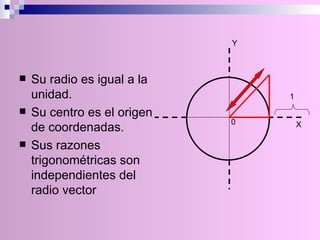
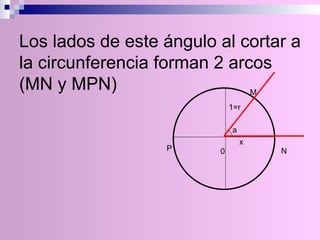
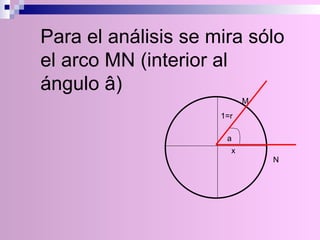
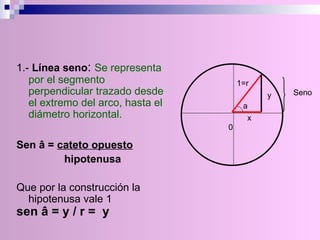
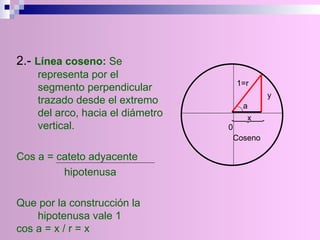
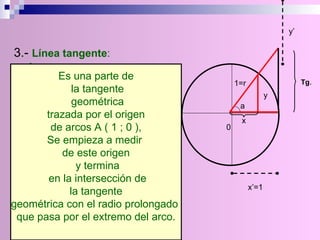
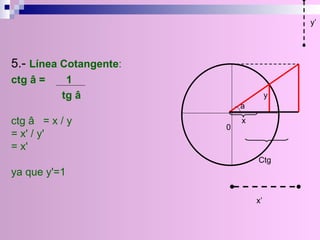
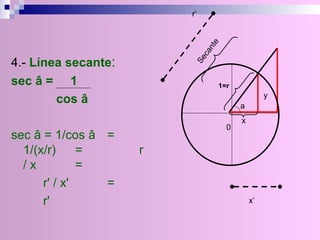
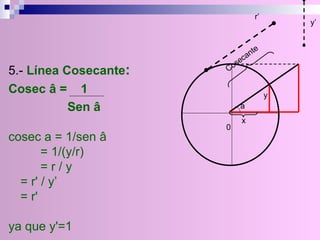
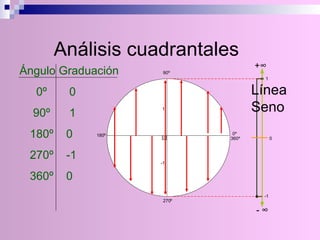
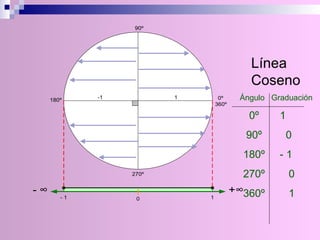
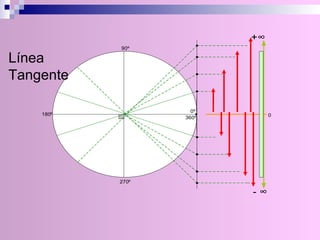
El documento describe la circunferencia trigonométrica y las líneas trigonométricas. La circunferencia trigonométrica tiene un radio de 1 unidad y se usa para representar las razones trigonométricas de cualquier ángulo. Las líneas trigonométricas (seno, coseno, tangente, cotangente, secante y cosecante) se definen en términos de los catetos y la hipotenusa de triángulos formados por los lados del ángulo y la circunferencia. También se describen los áng

1. CIRCUNFERENCIA TRIGONOMETRICA

2. Concepto

3. La circunferencia trigonométrica es una herramienta que nos permite representar las razones trigonométricas de cualquier ángulo

4. Características

5. Su radio es igual a la unidad. Su centro es el origen de coordenadas. Sus razones trigonométricas son independientes del radio vector 0 Y X 1

6. Líneas trigonométricas

7. Se considera un ángulo (â) en el cual un lado es el semieje positivo de abscisas (x) y el otro es “libre” (se mueve por los cuadrantes).

8. Los lados de este ángulo al cortar a la circunferencia forman 2 arcos (MN y MPN) 0 a 1=r x M N P

9. Para el análisis se mira sólo el arco MN (interior al ángulo â) 1=r x M N a

10. 1.- Línea seno : Se representa por el segmento perpendicular trazado desde el extremo del arco, hasta el diámetro horizontal. Sen â = cateto opuesto hipotenusa Que por la construcción la hipotenusa vale 1 sen â = y / r = y Seno 0 1=r x y a

11. 2.- Línea coseno: Se representa por el segmento perpendicular trazado desde el extremo del arco, hacia el diámetro vertical. Cos a = cateto adyacente hipotenusa Que por la construcción la hipotenusa vale 1 cos a = x / r = x Coseno 0 1=r x y a

12. 3.- Línea tangente : tg  = cateto opuesto cateto adyacente tg a = y / x = y' / x‘ = y' Es una parte de la tangente geométrica trazada por el origen de arcos A ( 1 ; 0 ), Se empieza a medir de este origen y termina en la intersección de la tangente geométrica con el radio prolongado que pasa por el extremo del arco. Tg . x’=1 0 1=r x y a y’ x x’ y y’ Teorema de Semejanza de triangulos (Teorema de Tales) y/x=y’/x’

13. 5.- Línea Cotangente : ctg â = 1 tg â ctg â = x / y = x' / y' = x' ya que y'=1 0 x y a x’ y’ Ctg

14. 4.- Línea secante : sec â = 1 cos â sec â = 1/cos â = 1/(x/r) = r / x = r' / x' = r' 0 1=r x y a r’ x’ Secante

15. 0 x y 5.- Línea Cosecante : Cosec â = 1 Sen â cosec a = 1/sen â = 1/(y/r) = r / y = r' / y’ = r' ya que y'=1 a r’ y’ Cosecante

16. RT de ángulos cuadrantales

17. Ángulos cuadrantales Son aquellos que están en posición normal y cuyo lado final (el libre) coincide con alguno de los semiejes del sistema de coordenadas cartesianas. Representación: 90° n ó π/2n rad (n pertenece a Z).

18. Análisis cuadrantales Ángulo Graduación 0º 0 90º 1 180º 0 270º -1 360º 0 Línea Seno

19. Línea Coseno 0º 1 90º 0 180º - 1 270º 0 360º 1 Ángulo Graduación

20. Línea Tangente