Este documento presenta apuntes sobre control robusto y multiobjetivos de sistemas. Se divide en cuatro capítulos que tratan sobre análisis de sistemas con múltiples objetivos, análisis y síntesis de controladores para sistemas con saturaciones, síntesis de controladores mediante programación semidefinida y sintonización robusta de controladores industriales. El documento proporciona una introducción a cada uno de estos temas y sus aplicaciones en el diseño de controladores.








![CAP´
ITULO I
An´lisis de sistemas con m´ltiples objetivos
a u
I.1. Controladores multiobjetivo
El dise˜o de estrategias de control que aseguren un n´mero de objetivos (especificaciones) en un lazo de control
n u
ha sido objeto de intensa investigaci´n y estudio, pasando en los ultimos 50 a˜os de ser un campo intuitivo y
o ´ n
de sentido com´n (“de ingenio”) [Cor96], [AH95], a uno riguroso y formal en el que matem´ticos e ingenieros
u a
encuentran tierra f´rtil.
e
Dentro de las disciplinas que conforman los sistemas de control, el estudio de los sistemas lineales invariantes en
el tiempo ha conocido enormes avances y cambios en los paradigmas de su estudio, en parte por su simplicidad y
propiedades que permiten la aplicaci´n de poderosas herramientas matem´ticas y en parte porque esos resultados
o a
pueden ser aplicados a un importante n´mero de sistemas, incluyendo algunos muy complejos (e.g., multimodelos
u
[CGP98], no lineales [BA95], etc).
De esta manera, el dise˜o de controladores para sistemas lineales ha evolucionado desde reglas muy simples de
n
sintonizaci´n [ZN42], ajustes de margen de fase y de ganancia [Kuo95], [PH96], dise˜o basado en representaciones
o n
de estado como ubicaci´n de polos [PH96], control ´ptimo, [AM89], LQG/LTR [DS81], dise˜o basado en el margen
o o n
del m´dulo (u operador diferencia de retorno) [DFT92], basado en los valores singulares y control robusto [San89],
o
[MZ89], [DGK89], llegando hasta los paradigmas basados en la manipulaci´n de normas (de se˜ales o de sistemas)
o n
y dentro de los que podemos mencionar H∞ , H2 , L1 , 1 . Este enfoque se ve fortalecido con la posibilidad de
ubicar los modos de un sistema, no en puntos exactos del plano “s”, sino m´s bien en regiones del mismo (t´cnicas
a e
denominadas de root clustering) y a lo que tambi´n denominaremos ubicaci´n de polos [CGP96].
e o
Todo ello encuentra adem´s un medio integrado de formulaci´n en las desigualdades matriciales lineales (LMIs)
a o
[Boy94] que surgen de la f´rmula del complemento de Schur, esto es, los problemas antes mencionados pueden
o
formularse como un conjunto de esas desigualdades (LMIs).
Si, como demostraremos, los controladores H2 aseguran un buen rechazo al ruido y los controladores H∞
funcionan bien, aun en presencia de incertidumbre asociada con din´micas no modeladas y reflejadas sobre todo
a
en altas frecuencias o en presencia de perturbaciones no conocidas pero acotadas en energ´ y si el agrupamiento
ıa,
de polos permite especificar algunas caracter´ ısticas de la respuesta temporal del sistema, entonces entenderemos](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-9-320.jpg)


![Observe que Y H (jω) = Y (−jω)T . Si Y (s) ∈ Lm×n entonces
2
Y (s) ∞ = sup σ (Y (jω))
¯ (I.3)
ω
donde σ es el valor singular m´ximo, esto es:
¯ a
σ (Y (jω)) = m´x
¯ a λi (Y (jω)H Y (jω)).
i
El siguiente teorema establece que la norma infinita es la norma inducida de la norma 2.
Teorema I.1 ([MZ89] y [San89]) Sea el sistema (I.1) en el que la perturbaci´n –w(t)– es cero y sean Y (s)
o
y U (s) las transformadas de y(t) y u(t). Sabemos que Y (s) = G(s)U (s), con, G(s) = C(sI − A) −1 B y g(t) la
transformada inversa de G(s). Consideremos igualmente que deseamos conocer la cota m´ ınima superior de la
salida cuando u 2 ≤ 1. Entonces:
G(s) ∞ = sup y(t) 2 . (I.4)
u(t) 2 ≤1
G(s) 2 = sup y(t) ∞. (I.5)
u(t) 2 ≤1
La demostraci´n de este teorema puede encontrarse en las referencias mencionadas en el enunciado y se basa en
o
el hecho de que el lado izquierdo de (I.4) y (I.5) en general sobreestima las normas y(t) 2 y y(t) ∞ , pero si no
hay restricci´n en la se˜al de control u(t) salvo la de su cota en la norma 2, siempre puede construirse una se˜al
o n n
u(t) ∈ Lm (de hecho, para el caso de la norma infinito, escogiendo u(t) como una sinusoide cuyo espectro sean
2
dos pulsos centrados en −ω0 y ω0 , la frecuencia de la norma infinito, de ancho 2ε y altura π/2ε y en el caso
de la norma 2, como g(−t)/ G 2 ) tal que esa cota superior sea alcanzada.
Observaci´n I.1 Observe que (I.4) puede interpretarse como que la norma infinita y dos de la funci´n de
o o
transferencia entre “u(t)” y “y(t)” en el sistema (I.1) da la m´xima amplificaci´n de la energ´ de la se˜al de
a o ıa n
entrada u(t) medidas como energ´ y valor pico respectivamente.
ıa
Observaci´n I.2 En este libro nos concentraremos en las normas dos e infinito que son las de uso m´s com´n.
o a u
Ellas, sin embargo, son s´lo un subconjunto de restricciones que de forma gen´rica se denominan Restricciones
o e
Integrales Cuadr´ticas (ICQ por sus siglas en ingl´s) [Boy94]. Estas restricciones pueden igualmente ser descrita
a e
como LMIs.
Ejemplo normas 2 e infinito
Se desea calcular la norma infinito y 2 del siguiente sistema:
1
G(s) =
s+5
Para el c´lculo de la norma 2 se puede usar el teorema de Parseval, esto es:
a
G(s) 2 = g(t) 2
4](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-12-320.jpg)
![donde g(t) es la respuesta al impulso de G(s), esto es:
g(t) = e−5t t≥0
entonces
∞ 1/2 ∞
1 −10t 1
G(s) 2 = {e−5t e−5t }dt =− e =√ .
0 10 0 10
En el caso de la norma infinito, se sabe que:
1
G(s) ∞ = sup |G(jω)| = sup √ = 0,2.
ω ω ω 2 + 52
Ejemplo valores singulares
Considere el sistema:
1 s
G(s) =
s2 + 9 −5
y se desea dibujar la evoluci´n de sus valores singulares cuando ω toma valores en el intervalo [0, ∞). Igualmente,
o
se desean esos mismos valores para G11 (s) y G12 (s). Hay que determinar tambi´n el valor de la norma infinito.
e
Note que en el caso de las transferencias G11 (s) y G22 (s) la respuesta graficada es simplemente el diagrama de
Bode, siendo como son funciones de transferencia SISO.
Un programa en Matlab que calcula y grafica los valores singulares se lista a continuaci´n:
o
s=tf(’s’)
g11=s/(s^2+9)
g12=-5/(s^2+9)
G=[g11;g12]
sigma(G,’k’,g11,’r’,g12,’b’)
y la gr´fica de los valores singulares vs frecuencia se muestra en la figura (I.1).
a
Observe que en ω = 3 los valores singulares no est´n definidos, i.e.,
a
G(s) ∞ = G11 (s) = G12 (s) = ∞.
En realidad hemos abusado del lenguaje, porque para ese sistema la norma infinita no existe, siendo que no es
finita o, dicho de otra manera, la norma infinita no es de ninguna utilidad para este sistema.
Consideremos ahora sistemas discretos lineales invariantes en el tiempo y sea x(k) una funci´n (secuencia) de
o
II → IRn . La norma p de x se define como [DD95]:
1
∞ p
x p = |x(k)|p )
p
k=0
si esa cantidad es finita. En la ecuaci´n anterior, | · |p es la norma p del vector x(k) e II es el conjunto de los
o
n´meros enteros. De particular inter´s son las normas donde p = 1, 2, ∞ y, en el caso de que p = ∞, esa norma
u e
se define como:
x ∞ = sup m´x |xi (k)|.
a
ω i
Finalmente, enunciamos sin demostraci´n el lema sobre la descomposici´n en valores singulares tomado de
o o
[GL95]:
5](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-13-320.jpg)
![60
40
G(ω) y G (ω)
12
20
G(ω) y G (ω)
Valores singulares
11
0
−20
−40
G11(ω)
−60 G12(ω)
−80
−1 0 1 2
10 10 10 10
Frecuencia (rad/s)
Figura I.1.: Evoluci´n de los valores singulares.
o
Lema I.1 Para cualquier matriz compleja Q ∈ IRm×p , existen matrices unitarias Y y U en m × x y p × p y una
matriz real Σ tal que:
Σ 0
Q=Y UH (I.6)
0 0
en el que Σ = diag(σ1 , . . . , σr ) con σ1 ≥ σ2 ≥ . . . ≥ σr ≥ 0 y m´ ın(m, p) ≥ r. Adem´s σi son los valores
a
singulares de Q. Cuando Q es real, el par (Y, U ) pueden escogerse ortonormales. La expresi´n (I.6) es com´nmente
o u
denominada descomposici´n en valores singulares de Q.
o
I.3. Evaluaci´n de las normas 2 e infinito de un sistema
o
En la secci´n previa hemos introducido brevemente las definiciones de normas 2 e infinito de se˜ales y sistemas.
o n
Salvo en muy pocos casos, estas definiciones no nos proporcionan un medio eficaz para el c´lculo de tales normas.
a
En esta secci´n presentamos un conjunto de medios que nos permiten el c´lculo de esas normas, en sistemas
o a
lineales con representaci´n de estados.
o
Con este prop´sito, consideremos una representaci´n simplificada del sistema (I.1) y tengamos al sistema lineal
o o
invariante en el tiempo (LTI):
x(t) = Ax(t) + Bu(t)
˙
(I.7)
y(t) = Cx(t)
donde x(t) ∈ IRn es el vector de estados, u(t) ∈ IRm es el vector de entradas (control) y y(t) ∈ IRp es el vector de
salidas medibles del sistema. A, B, C son matrices constantes de dimensiones apropiadas.
Es f´cil demostrar que la funci´n de transferencia del sistema [PH96] es:
a o
Y (s)
G(s) = = C(sI − A)−1 B. (I.8)
U (s)
Los siguientes teoremas nos dan las herramienta de c´lculo de esas normas que buscamos.
a
6](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-14-320.jpg)
![Teorema I.2 ([ZK88]) Para el sistema (I.7), las siguientes proposiciones son equivalentes:
1. A es una matriz estable y G(s) ∞ ≤γ
2. Existe una matriz P definida positiva tal que
AT P + P A + γ −2 P BB T P + C T C < 0. (I.9)
Demostraci´n: Una comprobaci´n muy sencilla de que (2) ⇒ (1) est´ inspirada en las propiedades del operador
o o a
diferencia de retorno (return difference operator) que se hace en [AM89] y es como sigue: cambiando el signo de
la desigualdad (I.9) y sumando y restando sP con s = jω y ω la frecuencia en la que ocurre la norma infinito de
G, tenemos que:
(−sI − A)T P + P (sI − A) − γ −2 P BB T P − C T C > 0, (I.10)
multiplicando la derecha de (I.10) por (sI − A)−1 B y a la izquierda por su transpuesto complejo conjugado
(hermitiano) resulta en:
B T P (sI − A)−1 B + B T (−sI − AT )−1 P B
−γ −2 B T (−sI − AT )−1 P BB T P (sI − A)−1 B ≥ (I.11)
B T (−sI − AT )−1 C T C(sI − A)−1 B
2
a la derecha de la desigualdad (I.11) reconocemos G(s) ∞ y recordando que:
[γI − γ −1 B T P (sI − A)−1 B]H [γI − γ −1 B T P (sI − A)−1 B] ≥ 0,
la proposici´n (1) sigue. La demostraci´n de que (1) ⇒ (2) puede encontrarse en la cita antes enunciada.
o o
Teorema I.3 ([San89] [PSG92]) Consideremos al sistema (I.7) y sea A una matriz hurwitz (estable), entonces
2
G(s) 2 = T r(CLc C T ) = T r(B T Lo B) (I.12)
donde Lc es el gramiano de controlabilidad y Lo es el gramiano de observabilidad y satisfacen:
ALc + Lc AT + BB T = 0
(I.13)
A T Lo + L o A + C T C = 0.
Demostraci´n: Sin p´rdida de generalidad, nos limitaremos a los sistemas de una entrada y una salida (SISO).
o e
Igualmente, como ambas demostraciones son similares nos limitaremos a la asociada al gramiano de controlabi-
lidad. En tal sentido, recordemos que:
∞
T
Lc = eAt BB T eA t dt
0
donde
A n tn
eAt = I + At + . . . + + ...
n!
luego se cumple que:
d(eAt )
= AeAt = eAt A
dt
ahora bien,
∞
T
CLc C T = CeAt BB T eA t C T dt
0
pero recordemos que la transformada inversa de G(s) es
L−1 (G(s)) = g(t) = CeAt B
y entonces
∞
CLc C T = g(t)g(t)T dt = g(t) 2
2
0
7](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-15-320.jpg)
![y por el teorema de Parseval
2 2
G(s) 2 = g(t) 2 = CLc C T
por otra parte
ALc + Lc AT + BB T =
∞ T ∞ At T
0
AeAt BB T eA t dt + 0
e BB T eA t AT dt + BB T =
∞ d T T
0 dt
eAt BB T eA t dt + BB T = eAt BB T eA t |∞
0 + BB T
T T
−BB + BB = 0.
Ejemplo
En el sistema que se describe a continuaci´n, se desea calcular las normas 2 e infinito de:
o
s
G(s) =
s2 + s + 1
el listado de un programa de MATLAB que las calcula se muestra a continuaci´n
o
s=tf(’s’)
G_tf=s/(s^2+s+1)
G=ss(G_tf)
Lc=gram(G,’c’)
[a,b,c]=ssdata(G)
Norma2=c*Lc*c’
Lo=gram(G,’o’)
OtraN2=b’*Lo*b
Respuesta=bode(G);
NormaInf=max(Respuesta)
obteni´ndose:
e
G(s) 2 = 0,5 y G(s) ∞ = 1.
I.4. Desigualdades matriciales lineales
Una desigualdad matricial lineal (LMI por sus siglas en ingl´s, Linear Matrix Inequality) tiene la forma [Boy94]:
e
m
F (x) = F0 + x i Fi > 0 (I.14)
i=1
donde x ∈ IRm es la variable y las matrices sim´tricas Fi (=FiT ∈ IRn×n ), i = 0, . . . , m son dadas. La desigualdad
e
en (I.14), entendi´ndose como que F (x) es una matriz definida positiva, i.e., u T F (x)u > 0 para todo u ∈ IRn
e
diferente de cero.
Observaci´n I.3 Hay que se˜alar que pueden tenerse desigualdades matriciales lineales no estrictas si la des-
o n
igualdad es del tipo ≥.
Una caracter´ıstica interesante es que desigualdades matriciales (convexas) no lineales pueden ser convertidas
a LMIs a trav´s de la f´rmula del complemento de Schur y que detallamos a continuaci´n.
e o o
Lema I.2 ([Boy94]) Las siguientes proposiciones son equivalentes:
8](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-16-320.jpg)
![1.
P Q
S1 = >0 (I.15)
QT R
2. P > 0 y R − QT P −1 Q > 0 o
´
3. R > 0 y P − QR−1 QT > 0.
Demostraci´n: Surge del hecho de que siendo (I.15) definida positiva (> 0), entonces P y R tambi´n lo son.
o e
Construyendo la matriz de transformaci´n T1 regular (con autovalores todos diferentes de cero, de hecho todos
o
iguales a uno):
I −P −1 Q
T1 = (I.16)
0 I
entonces
P 0 T
S2 = = T 1 S1 T1 . (I.17)
0 R − QT P −1 Q
siendo que S1 es definida positiva y T1 regular (de hecho tambi´n definida positiva), entonces S2 > 0. Por otro
e
lado, si S2 > 0 entonces P y R son definidas positivas, siendo que T1 es regular, entonces:
−1
S1 = (T1 )−1 S2 T1
T
(I.18)
de donde surge que S1 > 0 y la primera proposici´n del lema (I.15) queda demostrada.
o
Podemos proceder de manera similar con la proposici´n 2 del Lemma (I.15) si definimos la matriz de transfor-
o
maci´n:
o
I 0
T2 = . (I.19)
−R−1 QT I
Dejamos al lector tal demostraci´n
o
Es interesante describir al lema (I.15) en su forma dual.
Lema I.3 Las siguientes proposiciones son equivalentes:
1.
−P Q
<0 (I.20)
QT −R
2. P > 0 y QT P −1 Q − R < 0 o
´
3. R > 0 y QR−1 QT − P < 0.
En conclusi´n, las LMI (I.15) y (I.20) son equivalentes a sus contrapartes no lineales.
o
Observaci´n I.4 Hacemos notar que en una LMI las variables son matrices que aparecen en forma lineal en la
o
desigualdad. Una vez escrita como una LMI, podemos invocar con certeza la convexidad de la desigualdad, lo que
muchas veces no es aparente de las desigualdades no lineales.
Observaci´n I.5 Una vez escrita una desigualdad matricial como una LMI, existen herramientas poderosas
o
para la resoluci´n de tales problemas, como por ejemplo el “Toolbox de LMIs de Matlab”, [GNL95], que utiliza
o
m´todos (e.g., del elipsoide [Win94]) que aprovechan la estructura particular de las LMI para su resoluci´n.
e o
9](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-17-320.jpg)
![En un sentido m´s amplio, los problemas formulados en t´rminos de desigualdades matriciales lineales no son
a e
m´s que problemas de programaci´n semidefinida, los que a su vez son una generalizaci´n de los muy conocidos
a o o
problemas de programaci´n lineal en las que las restricciones de desigualdad son reemplazadas por desigualdades
o
generalizadas, correspondientes al cono de matrices semidefinidas [PL03].
En su forma primal pura, un problema de programaci´n semidefinida se define como el problema de optimiza-
o
ci´n:
o
m´ın traza(CX)
sujeto a traza(Ai X) = bi ∀i = 1, . . . , m, (I.21)
X≥0
donde X ∈ Sn , el espacio de matrices reales y sim´tricas en n × n, b ∈ IRm y C, A1 , . . . , Am ∈ Sn , son matrices
e
sim´tricas dadas.
e
En este libro presentaremos una serie de resultados sobre el an´lisis y s´
a ıntesis de controladores H ∞ , H2 y de
ubicaci´n de polos en regiones que encuentran un marco com´n en su formulaci´n a trav´s de LMIs, esto es,
o u o e
como un problema de programaci´n semidefinida. As´ por ejemplo, la desigualdad (I.9) puede escribirse como la
o ı,
siguiente LMI en P > 0:
AT P + P A + C T C P B
<0 (I.22)
BT P −γ 2 I
o en su forma dual si definimos S = P −1 ,
AS + SAT + γ −2 BB T SC T
< 0.
CS −I
La demostraci´n sigue de una aplicaci´n directa del complemento de Schur.
o o
De la misma forma, el problema de costo garantizado [CP72] y [PSG92] que brevemente significa que:
2
G(s) 2 <γ
puede escribirse como un problema de factibilidad, esto es, encontrar P > 0 tal que:
1.
γI CP
>0 (I.23)
P CT P
2.
AP + P AT + BB T < 0 (I.24)
Demostraci´n: En efecto, si la segunda condici´n (I.24) es satisfecha, se cumple que P > L c , por lo que
o o
2
G 2 = CLc C T ≤ CP C T
pero la LMI de la condici´n (I.23) implica que CP C T < γI.
o
Observaci´n I.6 Cuando no hay incertidumbre en el modelo se puede, con la introducci´n de una variable
o o
matricial adicional W , conseguir el m´ınimo de esa norma [GPS92] y que por supuesto coincide con el que arroja
el enfoque, digamos cl´sico, del control optimo [AM89].
a ´
En lo sucesivo nos referiremos a un controlador H2 (o H∞ ) como aquel que hace que la norma 2 (o infinito) de la
funci´n de transferencia del sistema a lazo cerrado cumpla con alguna especificaci´n (usualmente cota superior)
o o
dada. Ambas normas no son m´s que un subconjunto de una clase m´s amplia de restricciones denominadas
a a
Restricciones integrales cuadr´ticas (o IQC por sus siglas en ingl´s) que pueden igualmente representarse por
a e
conjuntos de LMIs.
Podemos notar que el problema de dise˜o de un controlador que satisfaga criterios en ambas normas (H 2 y
n
H∞ ) puede formularse como una colecci´n de LMIs.
o
10](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-18-320.jpg)
![Ejemplo
Consideremos una vez m´s el sistema del ejemplo de la secci´n (I.3) y calculemos cotas para sus normas 2 e
a o
infinito.
El listado MATLAB, destinado al c´lculo de una matriz P para una cota superior —digamos 1.01— de la
a
norma infinito, se muestra a continuaci´n. Se hace uso del toolbox de desigualdades matriciales lineales.
o
num=[1 0];
den=[1 1 1];
[a,b,c,d]=tf2ss(num,den);
gamma=1.01;
setlmis([]);
p=lmivar(1,[2 1]);
lmiterm([1 1 1 p],a’,1,’s’); % LMI #1: a’*p+p*a
lmiterm([1 1 1 0],c’*c); % LMI #1: c’*c
lmiterm([1 2 1 p],b’,1); % LMI #1: b’*p
lmiterm([1 2 2 0],-gamma^2); % LMI #1: -gamma
lmiterm([-2 1 1 p],1,1); % LMI #2: p
eje14=getlmis;
[tmin,popt]=feasp(eje14);
p=dec2mat(eje14,popt,1)
y una matriz P que verifica la condici´n (I.22) esta dada por
o
1,0047 0,0037
P = .
0,0037 1,0054
√
Por otra parte, el listado MATLAB del c´lculo de una matriz P > 0, para una cota superior de 0,501 de la
a
norma 2, se muestra a continuaci´n. De nuevo se utiliza el toolbox de desigualdades matriciales lineales.
o
num=[1 0];
den=[1 1 1];
[a,b,c,d]=tf2ss(num,den);
gamma=0.501;
setlmis([]);
p=lmivar(1,[2 1]);
lmiterm([-1 1 1 0],gamma); % LMI #1: gamma^2
lmiterm([-1 2 1 p],1,c’); % LMI #1: p*c’
lmiterm([-1 2 2 p],1,1); % LMI #1: p
lmiterm([2 1 1 p],a,1,’s’); % LMI #2: a*p+p*a’
lmiterm([2 1 1 0],b*b’); % LMI #2: b*b’
lmiterm([-3 1 1 p],1,1); % LMI #3: p
eje142=getlmis;
[tmin,popt]=feasp(eje142);
p=dec2mat(eje142,popt,1)
siendo una matriz P > 0 que verifica (I.23) y (I.24):
0,5006 −0,0003
P = .
−0,0003 0,5008
11](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-19-320.jpg)

![Consideremos ahora cualquier realizaci´n m´
o ınima de T (s) de la forma:
x
˙ = Acl x + Bcl r
y = Ccl x + Dcl r
Lema I.4 ([San89]) El sistema de la figura (I.2) es internamente estable si y s´lo si los autovalores de la matriz
o
Acl est´n en el semiplano izquierdo abierto. Esto es, que la matriz Acl es hurwitz.
a
Siendo Acl la matriz de estados (o din´mica) de cualquier funci´n de transferencia del lazo de la figura (I.2),
a o
la ubicaci´n de sus autovalores determina la de los polos de cualquier funci´n de transferencia.
o o
Si entendemos por robustez la capacidad de un sistema a lazo cerrado para responder adecuadamente ante
perturbaciones externas y/o variaciones en el modelo de la planta, tradicionalmente dicha robustez se asegura
ante incertidumbre en el modelo dise˜ando sistemas con amplios m´rgenes de fase (φ m ) y de ganancia (gm )
n a
[PH96].
En la figura (I.3) se muestran sobre un diagrama de Nyquist, en forma gr´fica, tales m´rgenes.
a a
Figura I.3.: Margen de fase φm y de ganancia gm de un sistema SISO.
El margen de ganancia (gm ) permite afrontar incertidumbre en la ganancia del proceso a controlar. En relaci´n
o
con la figura (I.4), esto significa alg´n escalar β del que s´lo se conocen sus cotas m´ximas. El margen de fase
u o a
(φm ) permite hacer frente a cambios —incertidumbre— en la fase. En relaci´n con la figura (I.4), alg´n escalar φ
o u
del que s´lo se conocen sus valores extremos. De modo que la planta real es la suma de la planta nominal (p(s))
o
y la incertidumbre (βe−φs ).
sistema real
r(t) y(t)
+ c(s) βe−φs p(s)
u(t)
(-)
Figura I.4.: Representaci´n cl´sica de lazo incierto.
o a
Hay que hacer notar que los enfoques de margen de fase o de ganancia presuponen que s´lo hay desconocimiento
o
en uno de los dos par´metros, i.e., la magnitud (β) o la fase (φ), no en ambos. En general se presenta incertidumbre
a
en los dos y es f´cil generar casos en los que, aun teniendo excelentes m´rgenes de fase y ganancia, una peque˜a
a a n
variaci´n simult´nea en ambos —magnitud y fase– sobre los valores nominales, genera plantas inestables.
o a
13](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-21-320.jpg)

![descripci´n m´s com´n de la incertidumbre y equivale a suponer que se conocen los l´
o a u ımites m´ximos de desviaci´n
a o
de la magnitud sobre un valor nominal, pero se desconoce totalmente la fase.
En relaci´n con el diagrama de la figura (I.2) supondremos que la planta real es descrita por:
o
p(s) = pn (s) + la (s) (I.27)
y entonces,
|p(jω) − pn (jω)| ≤ l¯ (ω).
a (I.28)
Esquem´ticamente podemos llevar esta incertidumbre al diagrama de Nyquist del sistema, tal como se muestra
a
en (I.6).
Figura I.6.: Modelo de la incertidumbre.
Se desprende de la descripci´n de la incertidumbre que, para una frecuencia ω dada, ¯a (ω) es la cota m´xima
o l a
de la magnitud de la incertidumbre y que no hay informaci´n sobre la fase (incertidumbre total en la fase).
o
A t´
ıtulo de ejemplo, consideremos un sistema de control de temperatura de un tanque de agua, que tenga
circulaci´n de agua permanente y nivel constante. El agua es calentada a trav´s de unas resistencias el´ctricas.
o e e
El ejemplo lo tomamos de [Qui04]. La funci´n de transferencia entre la potencia suministrada y la temperatura
o
del agua se determinan de manera experimental, dando escalones de potencia en la entrada y observando la
respuesta en la salida. Se realizan 4 pruebas, dos escalones positivos y dos negativos, resultando las 4 funciones
de transferencia que describimos a continuaci´n:
o
0,6125 −32s
G1 (s) = 254s+1 e
0,75 −25s
G2 (s) = 215s+1 e
0,7 −20s
G3 (s) = 100s+1 e
0,6 −34s
G4 (s) = 200s+1 e .
Promediando las ganancias, las constantes de tiempo y los retrasos obtenemos como sistema nominal:
0, 6656 −28s
Gn (s) = e
192s + 1
de donde es muy f´cil generar una funci´n m´xima de desviaci´n —en magnitud— para cada frecuencia.
a o a o
En la figura (I.7) hemos incluido la respuesta en frecuencia de magnitud de los sistemas encontrados con
ensayos y la respuesta del sistema nominal obtenido promediando los par´metros.
a
En la figura (I.8) se muestra, para el ejemplo anterior, la diferencia entre la magnitud de la respuesta en
frecuencia de los sistemas obtenidos en las pruebas menos la del sistema nominal. Ello para determinar una cota
superior al error en todo el rango de frecuencias.
15](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-23-320.jpg)
![0
−10
−20
|G (jω)|
n
Magnitud (dB)
−30
−40
−50
−60
−6 −5 −4 −3 −2 −1 0
10 10 10 10 10 10 10
Frecuencia (rad/s)
Figura I.7.: Diagramas de Bode de sistema de calentamiento.
En forma normalizada, com´nmente denominada descripci´n multiplicativa de la incertidumbre, la expresi´n
u o o
(I.27) puede escribirse como:
p(s) = pn (s)(1 + δ(s)W (s)) (I.29)
donde |δ(s)| < 1 es una funci´n de transferencia que representa la incertidumbre, de la que s´lo se conoce que su
o o
magnitud es menor que uno y W (s) es la funci´n de peso que recoge, para cada frecuencia y de forma normalizada,
o
la cota m´xima de la magnitud de la incertidumbre. Observe que cuando δ(s) es cero, no hay incertidumbre y la
a
planta p(s) es precisamente la nominal —pn (s).
De (I.29) es claro que:
¯a (ω)
l p(jω)
|W (jω)| = ≥ −1 .
|pn (jω)| pn (jω)
En la figura (I.9) hemos colocado los valores normalizados del error, esto es: (l a (w)/|Gn (jω)|).
Observamos que, bajo esta descripci´n de incertidumbre, ya no tenemos un solo modelo del sistema (digamos
o
el nominal) sino, m´s bien, una familia (infinita) de ellos.
a
La condici´n de estabilidad para toda la familia de sistemas, estabilidad robusta, viene dada por el siguiente
o
resultado:
Teorema I.4 ([San89] y [MZ89]) Consideremos al sistema de la figura (I.2) en el que la planta p(s) es descrita
por la familia de modelos (I.29) y los cuales tienen el mismo n´mero de polos en el semiplano derecho. Adem´s, sea
u a
c(s) un controlador que estabiliza la planta nominal pn (s). Entonces toda la familia de modelos ser´ estabilizado
a
por el controlador c(s) si y s´lo si
o
W (s)T (s) ∞ = sup |W (jω)T (jω)| ≤ 1 (I.30)
ω
donde T (s) es la funci´n complementaria definida en (I.25).
o
Demostraci´n: Es conveniente considerar que la familia de modelos del sistema de la figura (I.2), que satisfacen
o
(I.29), forman un conjunto representado por P. El sistema de la figura (I.2) es estable si y s´lo si para todo
o
16](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-24-320.jpg)
![0.2
0.18
0.16 |G (jω)−G (jω)|
3 n
Magnitud del error. la(ω)=|Gi(jω)−Gnjω)|
0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
−6 −5 −4 −3 −2 −1 0
10 10 10 10 10 10 10
Frecuencia (rad/s)
Figura I.8.: Magnitud de la incertidumbre para cada frecuencia.
miembro p(s) ∈ P se cumple que la ecuaci´n 1 + p(s)c(s) = 0 no tiene ra´
o ıces en el semiplano derecho cerrado
(que denominaremos C+ ). Luego ello es equivalente a:
1 + pn (s)c(s)[1 + W (s)δ(s)] = 0 ∀|δ| < 1 y s ∈ C+
⇐⇒ 1 + pn (s)c(s) = δ(s)W (s)pn (s)c(s) ∀|δ| < 1 y s ∈ C+
⇐⇒ |1 + pn (s)c(s)| ≥ |W (s)pn (s)c(s)| s = jω; ω ∈ [0, ∞) (I.31)
⇐⇒ |T (s)W (s)| ≤ 1 s = jω; ω ∈ [0, ∞)
⇐⇒ W (s)T (s) ∞ ≤ 1
Este resultado, fundamental para la teor´ de control robusto, tiene una interpretaci´n gr´fica en el diagrama
ıa o a
de Nyquist (ver figura (I.10)). En efecto, en (I.31) el t´rmino |W (s)pn (s)c(s)| = ¯a (ω)|c(s)| no es m´s que el radio
e l a
de la circunferencia que determina el tama˜o de la incertidumbre (para cada frecuencia) y entonces se infiere que
n
una condici´n necesaria y suficiente para estabilidad robusta es que, para cualquier frecuencia, la distancia del
o
−1 al diagrama nominal de Nyquist, i.e. la magnitud del Operador diferencia de retorno, sea mayor que ese radio
(que acota la incertidumbre en esa frecuencia). En otros t´rminos y visto que toda la familia de sistemas tiene el
e
mismo n´mero de polos en el semiplano derecho, la condici´n de estabilidad robusta implica que la “banda” de
u o
Nyquist, determinada por la familia de sistemas, no encierra al −1.
En (I.31) se us´ el hecho derivado del teorema del m´ximo m´dulo que se˜ala que:
o a o n
F (s) ∞ = sup |F (s)| = sup |F (jω)|,
Re{s}>0 ω
es decir, que el m´ximo de una funci´n continua en un conjunto cerrado y acotado ocurre en su frontera.
a o
Podemos incluir esquem´ticamente la representaci´n de la incertidumbre multiplicativa en la descripci´n cl´sica
a o o a
del lazo realimentado. Ello se muestra en la figura (I.11).
En relaci´n con la misma figura (I.11), observe que el resultado para la estabilidad robusta es equivalente a
o
“abrir” el lazo en los dos extremos del bloque de la incertidumbre (δ(s)) y verificar que la funci´n de transferencia
o
W (s)T (s) entre d(t) y z(t), nuevas entrada y salida al abrir el lazo, est´ acotada en magnitud.
a
La incertidumbre multiplicativa, representada por W (s), es s´lo una forma entre muchas para describir lo que
o
desconocemos en un lazo. Las funciones W (s) tienen normalmente la forma mostrada en la figura (I.12). La
incertidumbre es m´s peque˜a en bajas frecuencias y crece a medida que la frecuencia aumenta. Es importante
a n
17](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-25-320.jpg)
![3.5
Magnitud del error normalizada. W(ω)=|Gi(jω)−Gn(jω)|/|Gn(jω)|
3
|G3(jω)/Gn(jω)−1|
2.5
2
1.5
1
0.5
0
−6 −5 −4 −3 −2 −1 0
10 10 10 10 10 10 10
Frecuencia (rad/s)
Figura I.9.: Magnitud de la incertidumbre para cada frecuencia, normalizada.
Figura I.10.: Condici´n de an´lisis de estabilidad robusta.
o a
mencionar que de la funci´n de incertidumbre W (s) lo unico importante es su magnitud. La consideramos como
o ´
una funci´n de transferencia s´lo por tener una representaci´n consistente de un lazo de control (figura I.11).
o o o
La condici´n de estabilidad robusta impone que la funci´n complementaria T (s) satisfaga:
o o
|T (jω)| < |W (jω)|−1 ∀ω.
Luego, un modelo poco ajustado de la incertidumbre puede imponer cotas extremadamente restrictivas (muy
peque˜as) en la funci´n complementaria y, por ende, en el controlador.
n o
De la misma forma que la magnitud de la incertidumbre debe ser lo m´s entallada posible, a fin de evitar ser
a
excesivamente conservadores en el dise˜o del control, el mismo razonamiento se extiende a la “topolog´ del
n ıa”
modelo de la incertidumbre.
Hasta ahora hemos mencionado dos tipos, a saber:
Aditiva: p(s) = pn (s) + δ(s)W (s) |δ(s)| < 1
Multiplicativa: p(s) = pn (s)(1 + δ(s)W (s)) |δ(s)| < 1.
Adem´s, entre otras, tambi´n podemos representar la incertidumbre como [San89], [DFT92]:
a e
18](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-26-320.jpg)
![z(t) d(t)
δ(s) W (s)
e(t)
r(t) u(t) y(t)
+ c(s) pn (s) +
(-)
Figura I.11.: Representaci´n del lazo con incertidumbre multiplicativa.
o
Figura I.12.: Modelo de variaci´n de la incertidumbre.
o
p(s) = pn (s)(1 + δ(s)W (s))−1
p(s) = pn (s)(1 + δ(s)W (s)pn (s))−1 ;
algunas son equivalentes y, en cualquiera que sea la representaci´n, la estabilidad robusta viene determinada
o
por la norma infinita de alguna funci´n de transferencia. En la tabla (I.1) se recogen las equivalencias [San89],
o
[DFT92].
Tabla I.1.: Equivalencias entre medidas de incertidumbre
p(s) = pn (s)(1 + δ(s)W (s)) W (s)T (s) ∞ ≤ 1
p(s) = pn (s) + δ(s)W (s) W (s)p−1 (s)T (s) ∞ ≤ 1
n
−1
p(s) = pn (s)(1 + δ(s)W (s)) W (s)S(s) ∞ ≤ 1
p(s) = pn (s)(1 + δ(s)W (s)pn (s))−1 W (s)pn (s)S(s) ∞ ≤ 1
Cualquiera que sea su representaci´n, la incertidumbre que afecta al sistema siempre lo hace de manera global
o
y de all´ que reciba com´nmente en la literatura ese nombre, i.e., incertidumbre global o no estructurada. Si, por
ı u
el contrario, podemos identificar c´mo las diferentes fuentes de incertidumbre afectan elementos particulares del
o
sistema, entonces estar´ıamos frente a una incertidumbre estructurada.
Como ejemplo podemos mencionar modelos de incertidumbre de baja y alta frecuencia y que se traducen en
una representaci´n de la forma:
o
1 + δ1 (s)W1 (s)
p(s) = pn (s)
1 + δ2 (s)W2 (s)
|δ1 (s)|, |δ2 (s)| < 1.
19](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-27-320.jpg)

![10
5
W(ω)
0
−5
Magnitud del error normalizada
−10
|e−j0,2ω−1|
−15
−20
−25
−30
−35
−40
−1 0 1 2 3
10 10 10 10 10
Frecuencia (rad/s)
Figura I.13.: Respuesta frecuencial de la incertidumbre y su umbral.
y
z(t) 0 1 x1 (t) 0
= + d(t).
e(t) 2 −1 x2 (t) −2
El control sugerido —que calculamos con una de las t´cnicas que desarrollaremos en cap´
e ıtulos posteriores—
es:
−5,012 × 10−8 s2 + 0,03328s − 0,003325
C(s) = .
s2 + 3,333 × 106 s + 65,84
El diagrama de bloques para efectos de la atenuaci´n de perturbaci´n queda como se muestra en la figura
o o
(I.14).
z(t) d(t)
W (s)
e(t)
r(t) u(t) y(t)
+ c(s) Gn (s) +
(-)
Figura I.14.: Atenuaci´n de perturbaciones.
o
La funci´n de transferencia entre d(s) y z(s) con el controlador propuesto es:
o
−W (s)C(s)Gn (s)
Tdz =
1 + C(s)Gn (s)
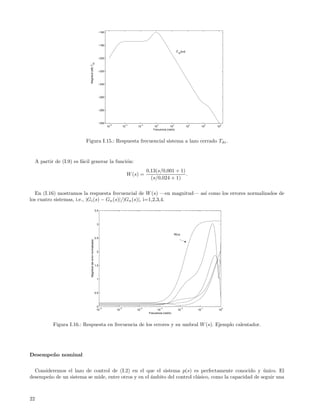
y la respuesta frecuencial de esa funci´n de transferencia se muestra en la figura (I.15).
o
Ejemplo caso calentador
Retomamos el ejemplo de [Qui04], s´lo en lo que respecta al c´lculo de la funci´n W (s).
o a o
21](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-29-320.jpg)
![referencia determinada r(t) o de rechazar una perturbaci´n de forma conocida d(t) en la salida del sistema y(t).
o
En el primer caso el desempe˜o podemos medirlo a trav´s de la se˜al de error:
n e n
r(s)
e(s) = = S(s)r(s)
1 + p(s)c(s)
y en el segundo a trav´s de la salida:
e
y(s) = S(s)d(s);
en ambos casos se desea hacer “peque˜a” la funci´n de sensibilidad a fin de tener el desempe˜o deseado.
n o n
En el marco del control cl´sico, la se˜al a seguir (o rechazar) es conocida —un escal´n, una rampa, una
a n o
par´bola, un impulso— y lo que es verdaderamente desconocido es el momento en el que la se˜al (de perturbaci´n)
a n o
ser´ aplicada al sistema. Recordemos, por ejemplo, la clasificaci´n en tipos de sistemas (0, 1, 2, . . .) para fines
a o
de eliminaci´n de las desviaciones en estado estacionario —tambi´n conocido como offset— [Kuo95] o el bien
o e
conocido hecho de que el modelo de la se˜al de referencia o perturbaci´n, seg´n sea el caso, debe estar incluido
n o u
en el controlador [AM89].
La suposici´n de que la se˜al externa (perturbaci´n o referencia) es conocida a priori es poco realista y, en
o n o
general, hay m´s conocimiento sobre la familia a la que pertenece la se˜al; v´ase por ejemplo [MZ89], p. 21.
a n e
Bajo esta perspectiva, en la que s´lo se conoce el conjunto al que pertenece la se˜al, el paradigma de control
o n
robusto plantea el rechazo de perturbaciones como la garant´ de atenuaci´n de esa caracter´
ıa o ıstica com´n del
u
conjunto de se˜ales (e.g., energ´ cota m´xima, etc.) En el marco del control robusto, la bien conocida teor´ de
n ıa, a ıa
H∞ , por ejemplo, eval´a el desempe˜o nominal en t´rminos de las energ´ de las se˜ales de perturbaci´n y de
u n e ıas n o
salida controlada. Es as´ que:
ı
Definici´n I.2 ([San89]) Sea γ un escalar mayor que cero, dado. El desempe˜o nominal del sistema de la figura
o n
(I.2) se eval´a como la capacidad del controlador c(s) de acotar la energ´ de la se˜al de salida del sistema a
u ıa n
lazo cerrado ( y(t) 2 < γ) para toda posible perturbaci´n con energ´ acotada d(t) 2 < β.
o ıa
La condici´n de existencia de un controlador que satisface la especificaci´n de desempe˜o nominal viene dada
o o n
por el siguiente teorema. Sin p´rdida de generalidad supondremos que γ y β son iguales a uno.
e
Teorema I.5 ([DD95]) El sistema de control de la figura (I.2) satisface la condici´n de desempe˜o nominal si
o n
y s´lo si
o
S(s) ∞ ≤ 1.
Demostraci´n: Surge de manera inmediata del hecho que la norma infinita es la norma inducida de la norma
o
2 (ver teorema (I.4)) y entonces
y(t) 2 = S(s) ∞ d(t) 2 .
En este punto se imponen algunas observaciones.
Observaci´n I.7 Resultar´ un problema “mal condicionado” en la mayor´ de los casos si dejamos el problema
o ıa ıa
de desempe˜o nominal tal y como fue formulado, esto es:
n
1
S(s) ∞ = ≤1 ∀ω
1 + p(s)c(s)
ya que en general el producto p(s)c(s) es estrictamente propio para sistemas f´
ısicos reales, i.e.,
l´ p(s)c(s) = 0
ım
s→∞
23](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-31-320.jpg)
![y entonces a muy altas frecuencias el problema de encontrar un controlador c(s) que haga el trabajo en toda la
gama de frecuencias puede resultar imposible. Por otra parte, en general s´lo interesa satisfacer el criterio de
o
desempe˜o en la gama de frecuencias asociadas al ancho de banda del sistema p(s) —siendo ´stas las se˜ales que
n e n
verdaderamente lo afectan— dejando “libre” al resto.
Adicionalmente, aunque s´lo hemos supuesto conocida la energ´ m´xima de las entradas (perturbaci´n o
o ıa a o
referencia) es posible que adem´s exista alg´n tipo de conocimiento del ancho de banda de ellas y que pudiera
a u
reflejarse como una funci´n de peso o filtro en la entrada de esas se˜ales.
o n
Esquem´ticamente, ambos pesos se pueden representar como lo ilustra la figura (I.17), lo que se traduce en el
a
nuevo criterio de desempe˜o nominal:
n
W1 (s)S(s)W2 (s) ∞ ≤1 o W (s)S(s) ∞ ≤ 1;
en W (s) se recogen lo que denominaremos las bandas de insensibilidad del dise˜o. Una buena selecci´n de los
n o
pesos puede resultar en un compensador m´s “suave” con ganancias m´s peque˜as.
a a n
d(t)
W1 (s)
r(t) u(t) y(t) y (s)
ˆ
+ c(s) p(s) + W2 (s)
(-)
Figura I.17.: Sistema con pesos (filtros) en entradas y salidas.
Observaci´n I.8 El criterio de desempe˜o nominal desarrollado no es gen´rico y est´ asociado con las se˜ales
o n e a n
de entrada y salida seleccionadas. Si hubi´semos escogido otras entradas y/o salidas, hubi´ramos obtenido la
e e
cota superior de la norma infinita de otra funci´n de transferencia. Esto ultimo s´ es un hecho general, es decir,
o ´ ı
al igual que la estabilidad robusta de un sistema, el desempe˜o nominal se eval´a —o analiza— calculando la
n u
norma infinita de alguna funci´n de transferencia asociada al lazo, siempre que los par´metros de medici´n
o a o
sean las energ´ de la se˜al de perturbaci´n y la se˜al de salida. Si los par´metros fuesen otros —diferentes de
ıas n o n a
energ´ıa— otra ser´ la norma (v´ase por ejemplo [SGC97]).
ıa e
Observaci´n I.9 En el caso de estabilidad robusta, si no se satisface el criterio (I.30) entonces existe un sub-
o
conjunto de modelos del sistema que no podr´n ser estabilizados por el compensador propuesto, i.e. el lazo cerrado
a
ser´ inestable para algunos modelos. En el caso del desempe˜o nominal, si no se satisface
a n
W (s)S(s) ∞ ≤γ
para un γ dado, s´lo implica que el criterio es muy restrictivo y no puede alcanzar ese nivel de desempe˜o. No
o n
obstante y asumiendo que el lazo puede estabilizarse, siempre existir´ alg´n γ s > γ a partir del cual s´ podr´ ob-
a u ı a
tenerse un controlador.
Ejemplo an´lisis de desempe˜ o
a n
Consideremos el sistema:
5e−3s
Gn (s) = .
10s + 1
Utilizando el criterio de sintonizaci´n de Ziegler y Nichols [Kuo95] se obtiene un controlador PI con K c = 0,6 y
o
Ti = 10. Se desea evaluar la atenuaci´n que presenta este controlador a perturbaciones d(t) que entran al sistema
o
tal como se muestra en la figura (I.18).
24](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-32-320.jpg)
![d(t)
r(t) y(t)
1
+ Kc (1 + Ti s ) + Gn (s)
(-)
Figura I.18.: Evaluaci´n de entonaci´n cl´sica.
o o a
La funci´n de transferencia entre d y y resulta:
o
Gn (s)
Tdy (s) =
1 + GP I (s)Gn (s)
donde
1
GP I (s) = Kc (1 + ).
Ti s
Aproximando el retardo por un Pade de primer orden ([Kuo95]) y dibujando el bode del sistema simplificado,
se obtiene la gr´fica de la figura (I.19), de donde es f´cil determinar que:
a a
2.5
|T (jω)|=|G (jω)|/|1+G (jω)PI(jω)|
dy n n
2
dy
1.5
Magnitud de T
1
0.5
0
−2 −1 0 1
10 10 10 10
Frecuencia (rad/sec)
Figura I.19.: Atenuaci´n con un PI.
o
Tdy (s) ∞ = 2,4657
Aunque en el caso de desempe˜o nominal no puede generalizarse sobre un resultado en particular, a simple
n
vista pareciera que el controlador propuesto no presentar´ un buen rechazo a perturbaciones para frecuencias
a
entre 0,1 y 1.
Un programa de Matlab para el c´lculo de esta norma infinito del sistema aproximado se muestra a continuaci´n:
a o
K=5;T=10;Td=3;
25](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-33-320.jpg)
![nn=K;dn=[T 1];
[nr,dr]=pade(Td,1);
ns=conv(nn,nr);ds=conv(dn,dr);
Kc=0.9*T/Td/K;Ti=Td/.3;
nc=Kc*[Ti 1];dc=[Ti 0];
[n,d]=feedback(ns,ds,nc,dc,-1);
[mag,pha,w]=bode(n,d);
Amplifica=max(mag)
semilogx(w,mag)
El paradigma de control robusto
En el caso de estabilidad robusta con incertidumbre multiplicativa a la salida del sistema a controlar, ubicaci´n
o
que no tiene ninguna importancia en sistemas SISO pero s´ la tiene en los MIMO, podemos representar al sistema
ı
como en la figura (I.11), con |δ(s)| < 1 y W (s) el modelo de la cota superior de la incertidumbre.
Para fines de an´lisis, sabemos que hay estabilidad robusta si y s´lo si
a o
W (jω)p(jω)c(jω)
W (s)T (s) ∞ = ≤1 ∀ω
1 + p(jω)c(jω)
lo que es equivalente a analizar el desempe˜o nominal entre d(t) y z(t) del sistema de la figura (I.14) y, entonces,
n
el problema de la estabilidad robusta (I.11) o el de desempe˜o nominal (I.17) pueden representarse esquem´ti-
n a
camente, como en la figura (I.20) donde p(s) es el sistema (multivariable) generalizado, e(t) es la salida medible
˜
d(t) z(t)
u(t) ˜
p(s) e(t)
c(s)
Figura I.20.: Paradigma de dise˜o de control robusto.
n
del sistema, y se desea determinar un compensador c(s) tal que:
Tdz (s) ∞ ≤1
siendo Tdz (s) la funci´n de transferencia entre d(t) (la perturbaci´n) y z(t). Observe que hemos preferido, como
o o
es usual en control robusto, usar la se˜al e(t) como salida medible, en lugar de y(t), por ser la primera la que
n
est´ directamente actuando sobre el controlador.
a
El esquema que se muestra en la figura (I.20) representa el paradigma cl´sico de dise˜o de control robusto,
a n
siendo adem´s el m´s usado.
a a
Si se dispone (o se ha calculado) un controlador y lo que se desea es analizar su desempe˜o, entonces el
n
paradigma pasa a ser el de la figura (I.21), donde, de nuevo, p(s) es la planta generalizada y |δ(s)| < 1 representa
˜
la incertidumbre. Es f´cil transformar el esquema de las figuras (I.11) y (I.14) a aquellos de las figuras (I.20) y
a
(I.21).
26](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-34-320.jpg)
![r(t) e(t)
d(t) ˜
p(s) z(t)
δ(s)
Figura I.21.: Paradigma de an´lisis de control robusto.
a
Sistemas con m´ ltiples entradas y m´ ltiples salidas
u u
Para el caso de los sistemas multivariables, nos serviremos del paradigma de control representado en (I.21).
Las relaciones entre la salida y la entrada del sistema son dadas por:
z(s) G11 (s) G12 (s) r(s)
= (I.34)
e(s) G21 (s) G22 (s) d(s)
˜
P
˜
siendo P la planta generalizada.
Para el caso multivariable, las salidas y/o las entradas pueden o no ser vectores. As´ por ejemplo, para el
ı,
sistema de la figura (I.22), si definimos a la dupla (r(t) y d(t)) como las entradas y a (z(t) y e(t)) como las
salidas, tendremos que:
z(s) T −T W1 r(s)
= (I.35)
e(s) W2 S −W2 SW1 d(s)
donde
S(s) = [I + p(s)c(s)]−1
T (s) = p(s)c(s)[I + p(s)c(s)]−1
con las correspondientes equivalencias en las ecuaciones (I.34) y (I.35).
e(t) z(t) d(t)
W2 (s) W1 (s)
r(t) u(t) y(t)
+ c(s) p(s) +
(-)
Figura I.22.: Sistema multivariables.
Desempe˜o nominal
n
Revisemos ahora los conceptos de estabilidad robusta y desempe˜o nominal a la luz del paradigma de control
n
y para sistemas multivariables, y para ello consideremos al sistema de la figura (I.21). En ese caso el desempe˜o
n
27](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-35-320.jpg)
![nominal est´ determinado por un controlador c(s) que asegura que:
a
e 2 <1 ∀r(t) : r 2 ≤1
cuando δ = 0.
Teorema I.6 ([San89]) La condici´n necesaria y suficiente para desempe˜o nominal es:
o n
G21 (s) ∞ <1
Demostraci´n: Cuando la incertidumbre es nula (δ = 0) tenemos que:
o
2 2
e 2 = G21 (s)r(s) 2 (I.36)
∞
= rH (jω)GH (jω)G21 (jω)r(jω)dω
21 (I.37)
−∞
∞
≤ σ 2 (G21 (jω ∗ ))
¯ rH (jω)r(jω)dω (I.38)
−∞
= σ 2 (G21 (jω ∗ ))
¯ (I.39)
con r H (jω) = r T (−jω) y σ (G21 (jω)) ocurre en w = w ∗ .
¯
Finalmente, la cota superior es alcanzada exactamente si escogemos, por ejemplo r(t) = e −εt cos w∗ t con ε > 0
para que r(t) ∈ L2 .
Estabilidad robusta
Para verificar la condici´n de estabilidad robusta, supondremos que el sistema es estable internamente y que
o
σ (δ) ≤ 1
¯ (I.40)
la condici´n de estabilidad robusta multivariable viene dada por:
o
Teorema I.7 ([San89]) El sistema de la figura (I.21) es estable para toda perturbaci´n δ que satisface (I.40) si
o
y s´lo si
o
G12 ∞ < 1.
Demostraci´n: La funci´n de transferencia entre r e y es (operando en (I.34)):
o o
Tre = G22 (I − G12 δ)−1 G11 + G21
y entonces, para un δ dado, la estabilidad del sistema es determinada por:
(I − G12 δ)−1
ya que, por hip´tesis, el sistema (I.34) es internamente estable.
o
Ahora bien, la estabilidad de (I − G12 δ)−1 es equivalente a:
det(I − G12 δ)) = 0 ∀s ∈ C+ . (I.41)
Supongamos que σ (G12 ) < 1. Recordando algunas propiedades de los valores singulares de una matriz, sabemos
¯
que:
σ(I − G12 δ) ≥ 1 − σ (G12 δ) > 1 − σ (G12 ),
¯ ¯
28](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-36-320.jpg)
![luego si
σ (G12 ) < 1
¯ ∀s ∈ C+
entonces
det(I − G12 δ) = 0 ∀s ∈ C+ .
Supongamos ahora que σ (G12 ) ≥ 1 para alguna s∗ y hagamos una descomposici´n en valores singulares
¯ o
G12 = U ΣV ∗ ,
1
tomemos δ = αV U ∗ y α = σ (G12 ) ,
¯ entonces
det(I − G12 (s∗ )δ = det[V (I − αΣ)U ∗ ] = 0
para el primer autovalor (recordando que los valores singulares est´n ordenados en Σ).
a
Finalmente, por el teorema del m´ximo m´dulo
a o
sup σ (G12 (s)) = sup σ (G(jω)) = G12
¯ ¯ ∞.
s∈C+ ω
Los sistemas multivariables, al igual que los SISO, pueden ser evaluados en su desempe˜o y estabilidad en el
n
marco de la norma infinita. Otras medidas de desempe˜o pueden igualmente imponerse al sistema. Algunas como
n
la norma 2 permiten evaluar el impacto de condiciones iniciales, al reflejar esas condiciones en el sistema como
una funci´n impulso δ(t) de magnitud adecuada [PH96]. Tambi´n la misma norma permite evaluar el efecto del
o e
ruido blanco, tambi´n cuantificable como una funci´n impulso con varianza conocida [San89].
e o
Las medidas de rechazo de perturbaciones presentadas, en modo alguno, no agotan las formas de evaluaci´n del
o
desempe˜o. Cl´sicamente, el desempe˜o se eval´a en t´rminos de los tiempos de establecimiento, de crecimiento,
n a n u e
m´ximo sobrepico, comportamientos sobre o subamortiguados, etc. [Kuo95], estando estas cualidades del sistema
a
´
ıntimamente relacionadas con la ubicaci´n de los polos del sistema de lazo cerrado.
o
La ubicaci´n de polos en regiones convexas ha recibido tambi´n la atenci´n de un n´mero de investigadores
o e o u
[GJ81] [ChG96] y ese problema tambi´n puede formularse como uno de desigualdades matriciales lineales (LMIs)
e
en la matriz de Lyapunov P , siempre que la regi´n pueda describirse como una regi´n LMI y que formalmente
o o
definimos de la forma:
Definici´n I.3 ([ChG96]) Una regi´n LMI es cualquier regi´n convexa R que pueda describirse de la forma:
o o o
R = {z ∈ C : L + zM + z M T < 0}
¯
donde L = LT y M son matrices constantes reales de las mismas dimensiones.
Ejemplos importantes de tales regiones LMI son:
1. Semiplano a la izquierda de x0 (figura (I.23)).
R = {z ∈ C : z + z + 2x0 < 0}.
¯
Cuando x0 = 0 da el semiplano izquierdo abierto.
2. Semiplano a la derecha de x0 (figura (I.24))
R = {z ∈ C : z + z + 2x0 > 0}.
¯
3. Cono con v´rtice en 0 (figura (I.25)).
e
sin θ(z + z )
¯ cos θ(z − z )
¯
R= z∈C: <0 .
cos θ(¯ − z)
z sin θ(z + z )
¯
29](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-37-320.jpg)
![Im(s)
Re(s)
xo
Figura I.23.: Semiplano a la izquierda.
Im(s)
Re(s)
xo
Figura I.24.: Semiplano a la derecha.
4. Regi´n circular centrada en −α y de radio r (figura (I.26)).
o
−r z+α
¯
R= z∈C: <0
z+α −r
El siguiente teorema establece la relaci´n entre la ubicaci´n de polos —autovalores de una matriz A— en una
o o
regi´n LMI y esa regi´n.
o o
Teorema I.8 Una matriz A tiene todos sus autovalores en una regi´n LMI de la forma:
o
R = {z ∈ C : L + zM + z M T < 0}
¯
si y s´lo si existe una matriz X > 0 tal que:
o
L ⊗ X + M ⊗ (AX) + M T ⊗ (AX)T < 0. (I.42)
La expresi´n (I.42) tambi´n puede escribirse de la forma
o e
(lkl X + Mkl AX + Mlk XAT )1≤k,l≤m
donde lkl (Mkl ) es el elemento kl de la matriz L (M ) y 1 ≤ k, l ≤ m indica los valores de k y l entre 1 y m.
La demostraci´n puede encontrarse en [ChG96] y no ser´ repetida aqu´
o a ı.
30](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-38-320.jpg)
![Im(s)
θ Re(s)
Figura I.25.: Cono centrado en cero.
Im(s)
r
Re(s)
-α
Figura I.26.: Circunferencia.
Como se ha visto, una cantidad de problemas cl´sicos y modernos pueden ser formulados en el marco com´n
a u
de las desigualdades matriciales. Hasta ahora hemos mencionado la estabilidad robusta, el desempe˜o nominal
n
y la ubicaci´n de polos en regiones. Todo esto tanto para sistemas SISO como MIMO, estos ultimos a trav´s de
o ´ e
los valores singulares.
La lista antes mencionada no es en modo alguno agotadora, y otros problemas tambi´n pueden o bien formularse
e
bajo el mismo marco o encontrar cotas superiores —l´ ımites seguros o conservadores— a esos problemas con las
mismas herramientas aportadas por las desigualdades matriciales. Mencionamos por ejemplo 1 , pasividad, etc.
V´ase [SGC97] para un recuento de otras formulaciones.
e
En este trabajo nos limitaremos a los tres primeros —H∞ , H2 y ubicaci´n de polos en regiones— m´s por una
o a
cuesti´n de no ser repetitivos. La extensi´n a esos otros problemas es, relativamente, sin dificultad.
o o
Resumen del cap´
ıtulo
En este cap´ ıtulo hemos presentado las definiciones, los t´rminos y resultados fundamentales de la teor´ de
e ıa
control robusto, de modo de sentar una base com´n e ilustrar la presentaci´n de los resultados que presentaremos
u o
en cap´
ıtulos subsiguientes. De igual forma hemos introducido las desigualdades matriciales lineales, la herramienta
que nos permitir´ desarrollar el marco com´n de las condiciones de s´
a u ıntesis de controladores multiobjetivo, nuestra
meta propuesta.
B´sicamente, hemos presentado condiciones de an´lisis de la estabilidad y desempe˜o bajo un n´mero de
a a n u
condiciones.
31](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-39-320.jpg)
![Esta breve revisi´n no pretende ser agotadora, f´
o ısicamente ser´ imposible incluirlos todos dada la enorme
ıa
cantidad de resultados que aparecen diariamente, pero s´ pretende ser lo suficiente como para sentar las bases
ı
del estudio de la formulaci´n multiobjetivo.
o
Finalmente, en este cap´ıtulo se ha fijado precisamente el alcance del trabajo, incluyendo otros paradigmas de la
teor´ de control robusto como los de factorizaci´n coprima [McF90] y L1 , 1 [DD95]. Todos ellos los revisaremos
ıa o
con m´s detalle en los cap´
a ıtulo siguientes. Enfoques no lineales quedan fuera del alcance de este trabajo.
32](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-40-320.jpg)
![CAP´
ITULO II
An´lisis y s´
a ıntesis de controladores para sistemas con saturaciones
II.1. Introducci´n
o
Frecuentemente, los sistemas a controlar con los que nos encontramos en la pr´ctica presentan alg´n tipo
a u
de restricciones sobre su comportamiento que lo limitan severamente. El caso m´s frecuente es la presencia
a
de saturaciones sobre la se˜al de control (pues los actuadores tienen un rango estrecho de actuaci´n), pero
n o
tambi´n pueden aparecer limitaciones sobre su velocidad o aceleraci´n m´ximas, efecto de las inercias de los
e o a
actuadores, as´ como limitaciones en variables secundarias. Para resolver estas dificultades en la etapa de dise˜o
ı n
del controlador se han propuesto varias soluciones, como los m´todos basados en la resoluci´n de problemas de
e o
programaci´n lineal, que tratan de optimizar la norma 1 , en vez de las normas H∞ o H2 que hemos presentado
o
en el cap´
ıtulo anterior [DD95].
En esta secci´n comprobaremos c´mo, utilizando una descripci´n adecuada del conjunto de se˜ales de entrada
o o o n
esperables, se puede, de forma natural, considerar problemas de control ´ptimo y control robusto, con el objetivo
o
ultimo de calcular controladores para m´ltiples tipos de restricciones (saturaciones, limitaciones en velocidad,
´ u
sobrepico, etc.) Como tal, esta soluci´n est´ basada en la evitaci´n de restricciones (“Constraint Avoidance”
o a o
[HTK01]): evitando las limitaciones, el sistema en lazo cerrado permanece en la regi´n de comportamiento lineal.
o
Aunque la soluci´n puede plantearse en el campo continuo utilizando la norma L 1 [DD87], los m´todos de
o e
dise˜o que resultan en el caso continuo no son adecuados para casos pr´cticos, pues es f´cil comprobar c´mo la
n a a o
soluci´n ´ptima de control ser´ una combinaci´n de impulsos. Por ello, en el resto del cap´
o o a o ıtulo trabajaremos con
sistemas discretos, en los que se utiliza la norma 1 y se dan soluciones que pueden aplicarse en sistemas reales.
Desde el punto de vista te´rico, una de las razones por las que se ha desarrollado una teor´ de control robusto
o ıa
basado en la norma 1 viene dada por el hecho de que en muchas aplicaciones pr´cticas tanto las perturbaciones
a
como el ruido de medida act´an de forma continua sobre el sistema, por lo que no es adecuado describirlas como
u
se˜ales acotadas en energ´ como se hace con los m´todos basados en la norma H ∞ . Por fortuna, normalmente
n ıa, e
se conoce la m´xima amplitud esperable de estas se˜ales, por lo que es posible describirlas como se˜ales acotadas
a n n
en magnitud: d ∞ , donde la norma es la denominada normal ∞ o norma pico-a-pico, que corresponde a la
m´xima amplitud de la se˜al: d ∞ = m´x(|u[i]|).
a n a](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-41-320.jpg)
![Otra raz´n m´s para desarrollar esta teor´ en vez de proseguir con la teor´ m´s popular de H ∞ , es el
o a ıa, ıa a
conocimiento que normalmente se tiene de las consignas que se aplican a cada sistema, que generalmente consisten
en una serie de saltos o rampas cuya magnitud o pendiente puede acotarse f´cilmente. Por ejemplo, si la entrada
a
es un salto siempre tiene una magnitud m´xima esperable: r ∞ ≤ rmax ; o si la consigna es una rampa, su
a
pendiente puede acotarse:
1 − z −1 r ∞ ≤ smax
donde z −1 es la funci´n retardo unitario: z −1 {u[i]} = {u[i − 1]}.
o
Para concluir con las ventajas de esta t´cnica, debemos mencionar su facilidad de c´lculo. As´ para un sistema
e a ı,
SISO, la norma 1 viene dada por la suma en valor absoluto de los t´rminos de la respuesta impulsional:
e
∞
Φ 1 = |Φ[i]|.
i=1
Si la norma es finita (esto es, el sistema estrictamente estable), basta con calcular la suma para un ´
ındice
suficientemente grande, para obtener una aproximaci´n con la precisi´n deseada.
o o
Antes de presentar el m´todo en detalle debemos puntualizar que, si las limitaciones sobre las se˜ales no fuesen
e n
sim´tricas en la mayor parte de los casos, basta con redefinir el punto de trabajo para que sean sim´tricas y
e e
la utilizaci´n de la norma sim´trica usual ( u ∞ ≤ umax ) no introduzca conservadurismo. Por ejemplo, si la
o e
´
unica limitaci´n es una saturaci´n no sim´trica sobre las se˜ales de control, basta redefinir el punto de trabajo
o o e n
en el punto medio de las restricciones: (xmean = xmax − xmin ; x(k) ∞ = m´xt (|x(k)|) = xmax +xmin ). Si esta
a 2
redefinici´n del punto de trabajo no resultase adecuada (por ejemplo, por cambiar las restricciones con el tiempo,
o
por haber m´ltiples restricciones o por modificarse el comportamiento nominal con el punto de trabajo), es posible
u
reformular todo el desarrollo presentado en esta secci´n para el caso no-sim´trico. Sin embargo, la notaci´n y la
o e o
soluci´n pasan a ser m´s engorrosas [NBT03].
o a
Esta teor´ fue planteada por primera vez por Vidyasagar [VI86], siendo resuelto el problema en un caso
ıa
bastante general por [DD88], que demostr´ c´mo pod´ convertirse dicho problema en uno de programaci´n
o o ıa o
lineal, f´cilmente resoluble. Comparado con otras t´cnicas propuestas de control con restricciones, hay resultados
a e
publicados sobre aplicaciones a sistemas reales (v´ase por ejemplo: [MK00], [TG02], [THV88]).
e
II.2. Especificaciones de funcionamiento
En la siguiente secci´n examinaremos tambi´n c´mo ciertas especificaciones de dise˜o pueden ponerse f´cil-
o e o n a
mente como l´ ımites sobre la amplitud m´xima de determinadas se˜ales, por lo que ser´ natural el describirlas
a n a
utilizando la norma pico-a-pico.
Saturaci´n
o
Supongamos que se desea comprobar si un determinado controlador K(z) satura el actuador del sistema de
control en la figura II.1. Como es bien sabido, este efecto se presenta frecuentemente en la pr´ctica: las v´lvulas
a a
tienen unos valores m´ximos y m´
a ınimos de apertura, los amplificadores electr´nicos se saturan, los alerones tienen
o
un ´ngulo m´ximo y una velocidad m´xima de giro, etc. Si la se˜al de control se satura pueden generarse ciclos
a a a n
l´
ımites o inestabilidades.
Vamos a ver c´mo tratar este problema dentro de una formulaci´n 1 . Supongamos que la saturaci´n del
o o o
controlador puede describirse matem´ticamente como:
a
−umax si u [i] < −umax
u[i] = u [i] si |u [i]| < −umax
umax si u [i] > umax .
34](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-42-320.jpg)
![Limitaci´n en la se˜al de
o n
control
r(z) e(z) u (z) u(z) y(z)
+ K(z) G(z)
(−)
Figura II.1.: Sistema de control con saturaci´n en la se˜al de control.
o n
Matem´ticamente se tratar´ de comprobar si la amplitud m´xima de la se˜al de control u[i] es menor que
a ıa a n
el valor de saturaci´n umax . Expres´ndolo en funci´n de normas, ser´ equivalente a comprobar que la norma
o a o ıa
pico-a-pico de la se˜al de control sea menor que el valor de saturaci´n, para el conjunto de consignas esperables:
n o
m´x
a u ∞ ≤ umax .
r posibles
Si la variaci´n m´xima de las referencias es rmax , por definici´n de la norma
o a o 1 esta comprobaci´n puede
o
expresarse como:
Tru 1 rmax ≤ umax .
Donde Tru denota la funci´n de transferencia de r a u , que en el caso del sistema realimentado de la figura II.1
o
es simplemente K(1 + KG)−1 , o sea, el sistema no se satura siempre que
umax
K(1 + KG)−1 1
≤ .
rmax
Resulta entonces que, dados una planta y un controlador, puede comprobarse de forma sencilla si el actuador
pudiera saturarse para un conjunto de consignas esperables. Para ello basta calcular la norma 1 de la funci´no
de transferencia K(1 + KG)−1 . Si esta norma es menor que el valor de saturaci´n no se alcanzar´ la saturaci´n.
o ıa o
Limitaciones de velocidad y aceleraci´n en actuadores
o
Adem´s de saturaci´n, muchos actuadores reales presentan adem´s (por razones f´
a o a ısicas o de seguridad) limita-
ciones en la velocidad y/o aceleraci´n m´xima que pueden alcanzar. En muchos casos resulta, entonces, necesario
o a
limitar el esfuerzo de control, entendiendo ´ste como la variaci´n de la se˜al de control. Estas limitaciones pueden
e o n
expresarse tambi´n en relaci´n con la norma 1 de determinadas funciones de transferencia:
e o
Limitaciones de velocidad
Si la variaci´n m´xima permitida de la se˜al de control recibida por el actuador es V max , en cada per´
o a n ıodo de
muestreo, el sistema no sobrepasar´ este l´
a ımite en la variaci´n de la se˜al de control si se cumple que:
o n
m´x
a u[i] − u[i − 1] ≤ Vmax .
r posibles
O lo que es lo mismo:
m´x
a (1 − z −1 )u ∞
≤ Vmax ,
r posibles
que puede convertirse a una condici´n sobre la norma
o 1 de la funci´n de transferencia de r a u = u[i] − u[i − 1]
o
(Tru = (1 − z −1 )K(1 + KG)−1 ) :
(1 − z −1 )K(1 + KG)−1 1
≤ Vmax .
35](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-43-320.jpg)
![Limitaciones de aceleraci´n
o
De forma an´loga al caso de la velocidad, si la variaci´n m´xima permitida de la variaci´n de la se˜al de control
a o a o n
recibida por el actuador es Amax en cada per´ ıodo de muestreo, no se superar´ este l´
a ımite siempre que:
m´x
a u[i] − 2u[i − 1] + u[i − 2] ≤ Amax .
r posibles
O lo que es lo mismo:
m´x
a (1 − z −1 )2 u ∞
≤ Amax ,
r posibles
que puede convertirse a una condici´n sobre la norma
o 1 de Tru = (1 − z −1 )2 K(1 + KG)−1 (funci´n de transfe-
o
rencia de r a u = u[i] − 2u[i − 1] + u[i − 2]):
(1 − z −1 )2 K(1 + KG)−1 1
≤ Amax .
Puede aplicarse un argumento similar a cualquier otra limitaci´n en la se˜al de control, que en general se
o n
expresar´ como:
a
H(z −1 )K(1 + KG)−1 1 ≤ Amax .
Rechazo de perturbaciones
Si en vez de un problema de seguimiento de una consigna variable, lo que tratamos de resolver es un problema
de regulaci´n en presencia de perturbaciones, puede plantearse matem´ticamente c´mo calcular la desviaci´n
o a o o
m´xima de la salida regulada para cualquier perturbaci´n posible (que supondremos acotada en magnitud).
a o
Si el sistema de control corresponde al de la figura II.2, el error de seguimiento m´ximo (e max ) ser´ el m´ximo
a a a
valor del error e[i] para el conjunto de perturbaciones posibles n[i]. Siguiendo el mismo razonamiento, puede
expresarse matem´ticamente este problema como calcular γ que cumple:
a
emax = m´x u
a ∞
que por definici´n de la norma
o 1 ser´
a
emax = Tne 1 n ∞ = Wd K(1 + KG)−1 1
nmax .
Es decir, el error de seguimiento m´ximo viene dado por el producto del tama˜o de la perturbaci´n m´xima, por
a n o a
la norma 1 de Wd K(1 + KG)−1 .
n(z)
Wd (z)
Limitaci´n en la
o
se˜al de control
n
y(z)
e(z) u (z) u(z)
K(z) G(z) +
(−)
Figura II.2.: Sistema de control con perturbaci´n a la salida y saturaci´n en la se˜al de control.
o o n
36](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-44-320.jpg)


![estos problemas de optimizaci´n, para dise˜adores no familiarizados con parametrizaciones de Youla. Sin embargo,
o n
debemos hacer constar que, al tener generalmente las respuestas impulsionales ´ptimas un n´mero infinito de
o u
t´rminos, nunca obtendremos el regulador ´ptimo, s´lo una aproximaci´n a ´l (por otra parte suficiente en la
e o o o e
mayor parte de los casos pr´cticos).
a
Conversi´n a un problema de programaci´n lineal
o o
Por simplicidad, comenzamos la presentaci´n para el caso de optimizaci´n de una unica funci´n de transfe-
o o ´ o
rencia SISO. La idea principal del m´todo se basa en trabajar directamente con los coeficientes de la respuesta
e
impulsional de la funci´n de transferencia a minimizar Φ = {Φ[i]}. Efectivamente, hemos visto c´mo los pro-
o o
blemas con restricciones se pueden expresar en funci´n de la suma (en valor absoluto) de los coeficientes de la
o
respuesta impulsional (que no es otra cosa que la norma 1 ).
El problema de optimizaci´n puede expresarse entonces como:
o
∞
m´
ın Φ 1 = m´
ın |Φ[i]|
K estabilizantes K estabilizantes
i=1
donde Φ[i] son los coeficientes de la respuesta impulsional que tratamos de optimizar, con la restricci´n adicional
o
de que el controlador K no puede cancelar ning´n cero inestable de la planta G (lo que har´ K inestable, que
u ıa
siempre es indeseable). Tampoco K deber´ cancelar ning´n polo inestable de la planta (pues la cancelaci´n no
ıa u o
ser´ efectiva en cuanto la planta sufriera una peque˜a variaci´n, haciendo el sistema en lazo cerrado inestable;
ıa n o
esto es, el sistema no tendr´ estabilidad interna). Esto lo representaremos matem´ticamente como la restricci´n
ıa a o
de que KG debe valer 0 en los ceros inestables de la planta e ∞ en los polos inestables de la planta.
Por ejemplo, en el caso de que quisi´ramos minimizar el error de seguimiento en presencia de perturbaciones,
e
el objetivo ser´ minimizar la sensibilidad S = 1/(1 + KG). Denotando los ceros inestables de la planta G como
ıa
{zk } y los polos inestables como {pk }, las restricciones de interpolaci´n ser´
o ıan:
S(zk ) = 1/(1 + 0) = 1 ∀k
S(pk ) = 1/(1 + ∞) = 0 ∀k.
(z−3)
Por ejemplo, si la planta fuese G = (z−2)(z−0,5) , entonces z1 = 3, p1 = 2 con lo que las restricciones de
interpolaci´n ser´
o ıan:
S(3) = 1
S(2) = 0.
En cambio, si la funci´n a optimizar resultase ser la sensibilidad complementaria T = KG/(1 + KG), las
o
restricciones de interpolaci´n ser´
o ıan:
T (zk ) = 0 ∀k
T (pk ) = 1 ∀k
que para nuestro ejemplo ser´
ıan
T (3) = 0
S(2) = 1.
En general, para asegurar la estabilidad interna del sistema de control a dise˜ar se deber´n cumplir las siguientes
n a
restricciones de interpolaci´n:
o
M (zk ) = αk ∀k
M (pk ) = βk ∀k
39](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-47-320.jpg)
![donde αk y βk corresponden a los valores (constantes) resultantes de sustituir los ceros o polos en la funci´n de
o
transferencia.
Como se ha mencionado antes, si expresamos esta funci´n de transferencia gen´rica Φ en t´rminos de su
o e e
∞
respuesta impulsional Φ = {Φ[i]}, por definici´n de la transformada z de un sistema (Φ(z) = i=0 Φ[i]z −i ) y
o
seg´n la f´rmula de c´lculo de una norma 1 como la suma en valor absoluto de los t´rminos de una respuesta
u o a e
impulsional, la norma ell1 resulta ser:
∞
m´
ın |Φ[i]|.
Φ[i]
i=0
Para tener en cuenta las restricciones de interpolaci´n, basta utilizar el hecho de que el valor de una funci´n
o o
de transferencia Φ en un punto ak , dada su respuesta impulsional {Φ[i]}, es:
∞
Φ[i]
Φ(ak ) = .
i=0
ai
k
Resulta entonces que el problema de optimizaci´n puede expresarse como:
o
∞
m´
ın |Φ[i]|
i=0
sujeto a
∞
Φ[i]
i
= αk ∀k
i=0
zk
∞
Φ[i]
= βk ∀k.
i=0
pi
k
Este problema de minimizaci´n puede transformarse a un problema de programaci´n lineal est´ndar haciendo
o o a
el cambio de variable Φ[i] = Φ[i]+ − Φ[i]− , donde aseguraremos que las nuevas variables sean siempre positivas:
Φ[i]− ≥ 0 y Φ[i]+ ≥ 0 y una de ellas siempre 0 (esto se conseguir´ normalmente pesando de alguna forma el valor
a
de estos nuevos coeficientes).
Resulta entonces el nuevo problema de optimizaci´n:
o
∞
m´
ın Φ[i]+ + Φ[i]−
i=0
sujeto a
∞ ∞
Φ[i]+ Φ[i]−
i
− i
= αk ∀k
i=0
zk i=0
zk
∞ ∞
Φ[i]+ Φ[i]−
i
− = βk ∀k.
i=0
pk i=0
pi
k
En principio ´ste es un problema de programaci´n lineal con infinitas variables, pero normalmente puede
e o
truncarse, suponiendo que la respuesta impulsional es finita. Para ello basta reemplazar el ∞ en la expresi´n o
anterior por un valor finito N (que puede aumentarse hasta obtener buena convergencia). Resulta entonces un
problema de programaci´n lineal de dimensi´n finita, que puede resolverse utilizando software de programaci´n
o o o
lineal (por ejemplo la funci´n lp o linprog en Matlab), como mostraremos posteriormente en el ejemplo detallado
o
del reformador de hidr´geno (II.6).
o
40](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-48-320.jpg)
![Una vez resuelto el problema de optimizaci´n lineal, basta deshacer los cambios de variables realizados para
o
obtener el controlador:
Primero los coeficientes de la respuesta impulsional ´ptima se obtendr´ a partir de la soluci´n ´ptima del
o ıan o o
problema de programaci´n lineal:
o
Φ[i] = Φ[i]+ − Φ[i]−
y el controlador ´ptimo se calcula despejando K de la f´rmula de la funci´n de transferencia caracter´
o o o ıstica
utilizada. As´ si la funci´n a optimizar es la sensibilidad S = 1/(1 + KG), el controlador ser´
ı, o ıa:
1−Φ
K= .
GΦ
Teniendo en cuenta que la funci´n de transferencia en z correspondiente a la respuesta impulsional es Φ[z] =
o
n
0 Φ[i]z
−k
, si la planta expresada como cociente de polinomios en z es G = nG [z] , resulta el controlador ´ptimo:
d
G [z]
o
dG (1 − Φ[i]z −k )
K= .
nG ( Φ[i]z −k )
Para obtener el controlador definitivo basta cancelar ceros y polos (si se ha realizado correctamente siempre
se cancelar´n los que hayamos introducido en las restricciones de interpolaci´n, con lo que desaparecen del
a o
controlador), y realizar la reducci´n de orden correspondiente, si fuese necesario.
o
Problema multibloque
Hemos visto c´mo es posible resolver el problema de dise˜o de controladores en presencia de restricciones, en
o n
el caso de que el objetivo sea minimizar una unica funci´n de transferencia. Sin embargo, en problemas pr´cticos
´ o a
el objetivo puede ser minimizar varias matrices de transferencia de forma simult´nea.
a
Presentaremos la t´cnica multibloque mediante un ejemplo num´rico basado en resolver un problema de sen-
e e
sibilidad mixta, donde el dise˜ador debe considerar situaciones de compromiso entre requerimientos a baja y
n
altas frecuencias, que se pueden transformar como un problema de optimizaci´n en paralelo de dos funciones de
o
transferencia caracter´ısticas, como pueden ser la sensibilidad, la sensibilidad al control o la sensibilidad comple-
mentaria. Por ejemplo, un problema de sensibilidad mixta que trate de minimizar la sensibilidad y la sensibilidad
al control puede expresarse como:
(I + KG)−1
m´ ın .
K K(I + KG)−1 1
Este problema de sensibilidad mixta presenta la ventaja frente a otros en que evita que el controlador cancele
los ceros y polos estables de la planta, como luego comprobaremos en un ejemplo.
Pues bien, la soluci´n se obtiene de forma an´loga al caso de un bloque, definiendo Φ 1 = (I + KG)−1 y
o a
Φ2 = K(I + KG)−1 :
Φ1
m´ın .
Φ2 1
La principal diferencia en este caso es que ser´ necesario a˜adir restricciones de factibilidad que aseguren que
a n
al optimizar se tenga en cuenta que el controlador K es el mismo para las dos funciones de transferencia. En el
ejemplo que estamos desarrollando esto significa que:
Φ1 + GΦ2 = 1.
pues (I + KG)−1 + GK(I + KG)−1 = 1.
41](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-49-320.jpg)
![Al sustituir Φ1 y Φ2 por sus respuestas impulsionales Φ1 [i] = Φ+ [i] − Φ− [i] y Φ2 [i] = Φ+ [i] − Φ− [i], estas
1 1 2 2
restricciones de factibilidad dan lugar a un n´mero infinito de restricciones. En efecto, si la planta expresada
u
como cociente de polinomios en z es G = nG [z] , resulta la siguiente relaci´n:
d
G [z]
o
dG ∗ (Φ+ + Φ− ) + nG ∗ (Φ+ + Φ− ) = dG
1 1 2 2
donde ∗ significa convoluci´n (producto de polinomios en z −1 ). Al desarrollar la convoluci´n se obtiene un con-
o o
junto infinito de restricciones, f´cilmente desarrollable en t´rmino de los coeficientes de numerador y denominador
a e
de la planta.
Ejemplo
En el caso de que nG = n0 z + n1 y dG = z + d1 , con p1 = d1 > 1, z1 = n1 /n0 > 1, en t´rminos de los
e
elementos de las respuestas impulsionales, esta relaci´n se transformar´ en el siguiente conjunto de restricciones
o ıa
de factibilidad:
(Φ+ [0] + Φ− [0]) + n0 (Φ+ [1] + Φ− [1]) = d0
2 2
d1 (Φ+ [0] + Φ1 [0]) + (Φ+ [1] + Φ− [1]) + n1 (Φ2 [0] + Φ− [0]) + n0 (Φ+ [1] + Φ− [1]) = d1
1
−
1 1
+
2 2 2
d1 (Φ+ [1] + Φ− [1]) + (Φ+ [2] + Φ− [2]) + n1 (Φ+ [1] + Φ− [1]) + n0 (Φ+ [2] + Φ− [2]) = 0
1 1 1 1 2 2 2 2
d1 (Φ+ [i] + Φ− [i]) + d1 (Φ+ [i + 1] + Φ− [i + 1]) + n1 (Φ+ [i] + Φ− [i]) + n0 (Φ+ [i + 1] + Φ− [i + 1]) = 0 ∀i > 1
1 1 1 1 2 2 2 2
En cuanto a las condiciones de interpolaci´n, en este caso inicialmente ser´ las siguientes:
o ıan
Φ1 (zk ) = 1 ∀k
Φ1 (pj ) = 0 ∀j
Φ2 (pj ) = 0 ∀j.
Sin embargo, en este caso las restricciones de interpolaci´n (Φ1 (zk ) y Φ2 (pj )) resultan ser redundantes, pues
o
las restricciones de factibilidad crean relaciones entre las restricciones de interpolaci´n. As´ en nuestro ejemplo,
o ı
al tener como restricci´n de factibilidad Φ1 + GΦ2 = 1, si la evaluamos en los ceros de la planta resulta autom´ti-
o a
camente que Φ1 (zk ) = 1, y si la evaluamos en los polos Φ2 (pj ) = 0, con lo que se comprueba que no hace falta
incluir estas restricciones de interpolaci´n, pues ya est´n incluidas autom´ticamente en las de factibilidad.
o a a
Esta redundancia hace que sea siempre recomendable comprobar si es posible eliminar algunas de las restric-
ciones (de hecho en la mayor parte de los problemas multibloque correctamente formulados las restricciones de
interpolaci´n resultan redundantes).
o
En definitiva, el problema de optimizaci´n resultante para este ejemplo, suponiendo que las respuestas impul-
o
sionales son finitas de longitud N , ser´
ıa
N
ın
m´ m´x
a Φ1 [i] + Φ− [i] + Φ+ [i] + Φ− [i]
+
1 2 2
Φ+ [i],Φ− [i],Φ+ [i],Φ− [i]
1 1 2 2 i=0
sujeto a
N N
Φ+ [i]
1 Φ− [i]
1
− = γj
i=0
pi1 i=0
pi1
(Φ [0] + Φ [0]) + n0 (Φ+ [1] + Φ− [1]) = d0
+ −
2 2
d1 (Φ+ [0] + Φ− [0]) + (Φ+ [1] + Φ− [1]) + n1 (Φ+ [0] + Φ− [0]) + n0 (Φ+ [1] + Φ− [1]) = d1
1 1 1 1 2 2 2 2
d1 (Φ1 [i] + Φ− [i]) + d1 (Φ+ [i + 1] + Φ1 [i + 1]) + n1 (Φ+ [i] + Φ− [i]) + n0 (Φ+ [i + 1] + Φ− [i + 1]) = 0 ∀i > 0.
+
1 1
−
2 2 2 2
42](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-50-320.jpg)
![II.6. Control de un reformador de hidr´geno
o
En esta secci´n presentamos el dise˜o de un controlador utilizando las t´cnicas de programaci´n lineal pre-
o n e o
sentadas en el cap´
ıtulo para un sistema industrial, lo que nos permitir´ comprobar las ventajas de utilizar estas
a
t´cnicas para resolver problemas reales.
e
Problema de control del reformador de hidr´geno
o
El problema a resolver es el control de un reformador de hidr´geno en una planta petroqu´
o ımica, cuyo esquema
se muestra en la figura II.5. El objetivo de este sistema es la producci´n de hidr´geno por cat´lisis a partir de
o o a
hidrocarburos a los que se ha eliminado previamente el azufre. Para generar el hidr´geno los hidrocarburos se
o
mezclan con vapor supercalentado justo antes de entrar en los tubos del reformador, donde un catalizador de
ıquel calentado a alta temperatura (sobre 750o C) produce el hidr´geno. La alta temperatura necesaria para
n´ o
acelerar la reacci´n se produce quemando combustible en el reformador [WV00], [AK01].
o
Figura II.5.: Esquema del reformador de hidr´geno.
o
El sistema de control trata de mantener la temperatura deseada del catalizador bas´ndose en modificar la
a
cantidad de combustible que alimenta al reformador. Para ello se dispone de medidas de temperatura del cata-
lizador y del flujo de combustible, y asimismo de una v´lvula controlada por ordenador que regula el flujo de
a
combustible. Al disponer de un unico actuador y dos medidas, la estructura de control se basa en la estructura
´
en cascada que se muestra en la figura II.6.
En el proceso real existen fuertes perturbaciones, tales como variaciones del flujo de combustible, variaciones
de su calidad, variaciones de la temperatura del vapor, etc. La perturbaci´n m´s dif´ de corregir corresponde
o a ıcil
a la temperatura del vapor, que modifica de una forma muy r´pida la temperatura del catalizador. El sistema
a
de control trata de atenuar lo m´s posible esta perturbaci´n actuando sobre la referencia del lazo de control de
a o
flujo de combustible.
En este ejemplo unicamente nos planteamos el dise˜o de un controlador para el lazo exterior que elimine
´ n
de forma adecuada las variaciones de la temperatura del catalizador, actuando sobre la referencia del lazo de
control de combustible. Este ultimo se considera adecuado, por lo que se mantendr´n sus valores y caracter´
´ a ısticas.
43](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-51-320.jpg)
![perturbaci´n
o
r(z) y(z)
control de
+ K(z) + v´lvula
a G(z) +
flujo
(−) (−)
Figura II.6.: Sistema de control en cascada del reformador de hidr´geno.
o
Debemos puntualizar que no se dispone de una medida fiable de la temperatura del vapor de entrada, lo que
hace inadecuado utilizar un compensador feedforward que elimine las perturbaciones; adem´s, la planta es de
a
fase no-m´
ınima. Esta reduci´n de las perturbaciones debe realizarse entonces por realimentaci´n.
o o
Modelo del sistema
Un modelo simplificado del sistema se obtuvo a partir de modelado e identificaci´n del sistema a partir de
o
medidas obtenidas del sistema real [Sh96]. El modelo calculado corresponde a la funci´n de transferencia entre
o
la referencia del flujo de combustible y la temperatura de salida, incluyendo las din´micas impuestas por el lazo
a
interior de control de flujo.
−0,032 [z + 0,2453] [z − 0,623257] [z + 0,999] [z − 15,4484] z 2 + 1,576432z + 3,074984
G= .
z [z + 0,58958] [z − 0,615995] [z + 0,81983] [z − 0,910085] [z 2 + 0,838534z + 0,320120]
Puede comprobarse en este modelo que la planta es estable, pero de fase no m´
ınima, con tres ceros fuera del
c´
ırculo unidad (en z = 15,45, y z = −0,79 + −1,57j).
El modelo de perturbaci´n se obtuvo por identificaci´n, resultando ser:
o o
0,03 [z + 0,1216]2 + 0,6900822 z 2
Wd = .
z 3 [z + 0,58958] [z − 0,615995] [z + 0,81983] [z − 0,910085] [z 2 + 0,838534z + 0,320120]
Sensibilidad mixta
Para resolver problemas pr´cticos basados en minimizaci´n de una norma
a o 1 el problema de sensibilidad mixta:
WS I + KG−1
ın
m´
WM KG I + KG−1 1
fue propuesto y resuelto en [DP87], luego estudiado en m´s detalle en [ST93]. En problemas reales, las principales
a
dificultades de esta soluci´n vienen dadas por la cancelaci´n de ceros y polos estables por el controlador, y el
o o
excesivo esfuerzo de control. Para resolver estos problemas hemos propuesto [TG02] la soluci´n del problema de
o
sensibilidad mixta alternativo:
WS I + GK −1
m´ın .
WM K I + GK −1 1
En efecto, con esta estrategia el controlador no cancela necesariamente los ceros y polos estables del controlador.
Adem´s, desde el punto de vista de la ingenier´ se sabe que es m´s adecuado considerar en la optimizaci´n los
a ıa a o
esfuerzos de control, que pueden reducirse directamente al a˜adir en la optimizaci´n un peso sobre la sensibilidad
n o
al control.
44](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-52-320.jpg)
![Este problema puede resolverse seg´n los m´todos vistos en la secci´n anterior, convirti´ndose a un problema
u e o e
de programaci´n lineal semi-infinita:
o
Φ1
m´
ın
Φ2 1
−1 −1
sujeto a WS Φ1 + GWM Φ2 = 1.
Dise˜ o del problema de optimizaci´n
n o
El objetivo principal del sistema de control a dise˜ar es reducir el efecto de las perturbaciones sobre la salida.
n
En t´rminos de se˜ales el objetivo puede expresarse como la minimizaci´n de la desviaci´n m´xima que alcanza
e n o o a
la salida por efecto de las perturbaciones, que es precisamente Sn ∞ . Si el efecto de la perturbaci´n sobre la
o
salida viene filtrado por la funci´n de transferencia Wd , el problema de dise˜o puede expresarse entonces como
o n
el problema de calcular un controlador que minimice SWd 1 .
Adem´s debemos asegurar que la se˜al de control sea razonable. Para ello incluimos en la minimizaci´n
a n o
el efecto de la perturbaci´n sobre la se˜al de control, que vendr´ determinada por la sensibilidad al control
o n a
M = K I + GK −1 . El controlador se calcula entonces resolviendo el problema de sensibilidad mixta:
WS I + GK −1
m´
ın .
WM K I + GK −1 1
Selecci´n de pesos
o
Observando las componentes en frecuencia del modelo de las perturbaciones se comprueba c´mo, en el sistema
o
objeto de estudio, las perturbaciones siguen siendo importantes hasta frecuencias cercanas a 0,02 rad/s, afectando
directamente a la salida. Con el fin de reducir las perturbaciones hasta una frecuencia cercana a 0,02 rad/s, ser´ ıa
necesario que la frecuencia de corte de la sensibilidad estuviera sobre esta frecuencia. Es decir, la funci´n de peso
o
a utilizar para dise˜ar S deber´ tener un cero cerca de esta frecuencia.
n a
El problema que presenta esta elecci´n es que esta frecuencia resulta ser superior al ancho de banda del sistema
o
en lazo abierto. Resulta entonces que el ancho de banda en lazo cerrado debe ser mayor que en lazo abierto, lo
que unicamente puede conseguirse haciendo la ganancia del controlador grande entre ambas frecuencias [GL95].
´
Significar´ esto que el controlador amplificar´ las frecuencias comprendidas entre las frecuencias de corte en lazo
a a
abierto y en lazo cerrado. Esto debe hacerse con precauci´n para evitar excesivos esfuerzos de control y asegurar
o
la estabilidad del sistema en lazo cerrado.
Se debe alcanzar entonces una soluci´n de compromiso entre la frecuencia de corte de S y la amplificaci´n de
o o
altas frecuencias que presentar´ M . Esta situaci´n es dif´ de conseguir por m´todos cl´sicos, por lo que un
a o ıcil e a
m´todo de dise˜o de controladores robustos mediante optimizaci´n (tal como la optimizaci´n 1 ) es ideal para
e n o o
resolver el problema. En este caso se puede conseguir estos requerimientos mediante la selecci´n adecuada de los
o
pesos sobre las funciones de transferencia a minimizar.
En este ejemplo en particular, los pesos se han elegido tal como se muestran en la figura II.7. La selecci´n
o
concreta se realiz´ de la siguiente manera:
o
Peso sobre la sensibilidad al control WM
:
45](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-53-320.jpg)

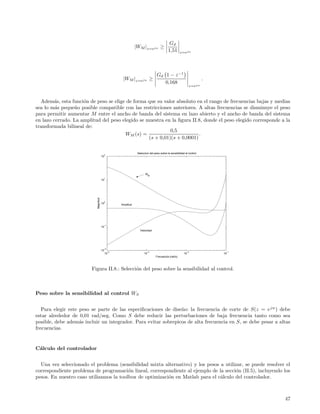
![El controlador resultante se redujo de orden hasta un controlador de orden 4, con funci´n de transferencia:
o
[z − 1,03795] [z − 0,88451] [z − 0,65138] [z + 0,20540]
K= .
[z − 1] [z − 0,390547] [z 2 − 0,097448z + 0,280517]
La respuesta en frecuencia del controlador resultante se compara con la del controlador completo en la figura
II.9. En la figura II.10 se comparan las respuestas salto en lazo cerrado. Puede comprobarse c´mo la aproximaci´n
o o
realizada es correcta, afectando s´lo a altas frecuencias y no significativamente a la respuesta salto.
o
Respuesta en frecuencia del controlador
1
10
0
10
control original
−1
10
control reducido
−2
10
−4 −3 −2 −1
10 10 10 10
Frecuencia (rad/s)
Figura II.9.: Respuesta en frecuencia del controlador.
Respuesta salto en lazo cerrado
1.2
1
controlador reducido
0.8
0.6
0.4
0.2
0
−0.2
0 10 20 30 40 50 60
Tiempo (muestras)
Figura II.10.: Respuesta salto en lazo cerrado.
Las funciones de transferencia caracter´ısticas del sistema en lazo cerrado se muestran en la figura II.11. Es
posible comprobar c´mo la forma de estas funciones de transferencia es adecuada: el ancho de banda del sistema
o
es ahora de 0,000218 rad/s, lo que significa que se filtrar´n las perturbaciones por debajo de esta frecuencia, como
a
48](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-56-320.jpg)
![est´bamos buscando. Adem´s, la sensibilidad complementaria no presenta sobrepico, por lo que no lo presentar´ la
a a a
respuesta salto del sistema. El sobrepico que presenta la sensibilidad al control se debe a la necesidad de aumentar
el ancho de banda del sistema en lazo cerrado respecto al de lazo abierto, para poder rechazar las perturbaciones.
Funciones de transferencia características
1
10
T=KG/(1+KG) S=1/(1+KG)
0
10
−1
10
M=K/(1+KG)
−2
10
−4 −3 −2 −1
10 10 10 10
Frecuencia (rad/s)
Figura II.11.: Funciones de transferencia caracter´
ısticas.
El c´digo en Matlab que permite calcular este controlador se muestra a continuaci´n:
o o
m=20; %Longitud de la respuesta impulsional
tol=1e-5;
% Definici´n de la planta
o
kg=-0.032
zg=[-0.2453 0.623257 -0.9999 15.4484 -0.788216+1.566429j ...
-0.788216-1.566429j]’;
pg=[-0.58958 0.615995 -0.81983 0.910085 -0.419267+0.379915j ...
-0.419267-0.379915j]’;
% Planta G=ng/dg
[ng,dg]=zp2tf(zg,pg,kg)
% Definici´n de los ceros fuera del c´rculo unidad
o ı
zi=[15.4484 -0.788216+1.566429j]’;
Ts=30; w=logspace(-4,-1,256);
% Peso de S
[nw2,dw2]=c2dm(5*[1/0.01 1],[1/10 1],Ts,’matched’)
% Peso de M
[nw1,dw1]=c2dm(0.5*[1 0.01],[1 1e-6],Ts,’matched’)
% Polinomios auxiliares para evaluar las restricciones de factibilidad
pol1=conv(conv(dw1,nw2),dg); mpol1=length(pol1);
pol2=conv(conv(nw1,dw2),ng); mpol2=length(pol2);
pol3=conv(conv(nw1,nw2),dg); mpol3=length(pol3);
% Restricciones sobre la NORMA
A=[-1 ones(1,m) ones(1,m) zeros(1,m) zeros(1,m)
-1 zeros(1,m) zeros(1,m) ones(1,m) ones(1,m)];
49](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-57-320.jpg)
![b=[0;0];
Aeq=[];beq=[];
% restricciones de FACTIBILIDAD: S+GM=I
Apol1=zeros(m+mpol1-1,m); Apol2=zeros(m+mpol2-1,m);
for i=1:m,
Apol1(i:i+mpol1-1,i)=pol1’;
Apol2(i:i+mpol2-1,i)=pol2’;
end
Aeq= [Aeq
zeros(size(Apol1,1),1) Apol1 -Apol1 Apol2 -Apol2];
beq=[beq
pol3’
zeros(size(Apol1,1)-mpol3,1)];
% funcion de coste a minimizar
f=eye(1,4*m+1);
% RESOLUCION DEL PROBLEMA DE PROGRAMACION LINEAL
[phiopt,FVAL,EXITFLAG,OUTPUT,LAMBDA]=linprog(f,A,b,Aeq,beq,zeros(size(f)),...
Inf*ones(size(f))’,zeros(size(f))); gamma=phiopt(1);
% C´lculo de la Sensibilidad ´ptima S=(phi(+)-phi(-))/W1
a o
phi1=phiopt(2:m+1)’-phiopt(m+2:2*m+1)’;
% Eliminaci´n de coeficientes esp´reos en phi1
o u
while (abs(phi1(length(phi1)))<=tol*max (abs(phi1)))
phi1=phi1(1:length(phi1)-1);
end
nsopt=conv(dw1,phi1);
dsopt=[nw1,zeros(1,length(nsopt)-length(nw1))];
% C´lculo de la Sensibilidad al Control ´ptima M=(phi(+)-phi(-))/W2
a o
phi2=phiopt(2*m+2:3*m+1)’-phiopt(3*m+2:4*m+1)’;
while (abs(phi2(length(phi2)))<=tol* max(abs(phi2)))
phi2=phi2(1:length(phi2)-1);
end
nmopt=conv(dw2,phi2);
dmopt=[nw2,zeros(1,length(nsopt)-length(nw1))];
% Calculo del Controlador a partir de S y el modelo de la planta G
nkopt=conv(dg,(dsopt-nsopt)); dkopt=conv(ng,nsopt);
while (abs(nkopt(1))<=tol* max(abs(nkopt)) & ...
abs(dkopt(1))<=tol*max(abs(nkopt)))
nkopt=nkopt(2:length(nkopt));
dkopt=dkopt(2:length(dkopt));
end
% cancelaci´n de los ceros/polos interpolados (los inestables)
o
[nk,dk]=minreal(nkopt,dkopt,5e-3);
% Reducci´n ad-hoc del orden del controlador:
o
%Controlador ´ptimo es K=nk/dk; Controlador Reducido es K=nkr/dkr
o
[mag,f]=freqz(nk,dk,128); nb=6; na=6; ft=1./(0.01+f);
[nkr,dkr]=invfreqz(mag,f,nb,na,ft);
50](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-58-320.jpg)
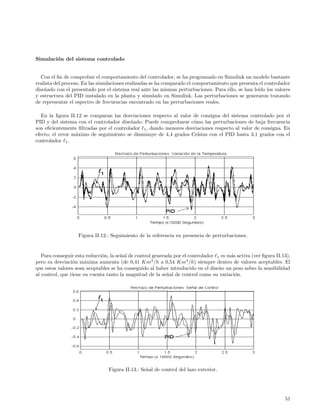
![Conclusiones del ejemplo
Como aplicaci´n pr´ctica de estas t´cnicas se ha visto que es posible solucionar el problema de control del
o a e
reformador de hidr´geno objeto de estudio mediante un controlador lineal dise˜ado utilizando el m´todo de
o n e
optimizaci´n 1 . Tal controlador fue dise˜ado solucionando un problema de minimizaci´n mixta. Se ha mostrado
o n o
c´mo pueden escogerse los pesos de las funciones caracter´
o ısticas a minimizar a partir de las especificaciones
de dise˜o. En particular se han tenido en cuenta las limitaciones sobre el tama˜o de la se˜al de control y sus
n n n
variaciones entre per´ıodos de muestreo.
El rendimiento del controlador ha sido comprobado utilizando un modelo no-lineal del sistema de control en
cascada utilizado en la planta real, comprobando c´mo se disminuye la variaci´n en la variable controlada, que
o o
es la temperatura del catalizador. El controlador dise˜ado ha sido comparado con el situado actualmente en la
n
planta, del tipo PID, comprobando que se puede obtener un control m´s preciso de la temperatura del reformador
a
(se disminuyen las variaciones de 4,4 grados hasta 3,1 grados Celsius), con una se˜al de control adecuada. Adem´s
n a
el controlador dise˜ado, al ser de par´metros fijos y de bajo orden, puede integrarse adecuadamente en el sistema
n a
de control.
II.7. M´todo de c´lculo basado en LMIs
e a
El problema de dise˜o 1 no es posible expresarlo directamente como un conjunto de LMIs. Sin embargo, s´ es
n ı
posible expresar un conjunto de LMIs que se aproximen a la soluci´n ´ptima, acotando superior e inferiormente
o o
la soluci´n. Presentamos unicamente las ideas generales; los detalles aparecen en [ED98].
o ´
Pasos preliminares
Utilizando la parametrizaci´n de Youla (ver ap´ndice A), podemos convertir el problema de optimizaci´n
o e o 1
al siguiente problema de equivalencia de modelos en el par´metro de Youla Q:
a
m´ H − U Q
ın 1 .
Q
Para poder plantearlo como un problema LMI, hacemos primero el cambio de variable Φ = H − U Q:
m´ Φ
ın 1
Q
sujeto a:
Φ = H − U Q.
Ahora descomponemos la respuesta impulsional de Φ en dos fragmentos: Φ 1 , que contendr´ los N primeros
a
t´rminos de la respuesta impulsional, y Φ2 , que contendr´ el resto de los t´rminos de la respuesta impulsional:
e a e
Φ1 = {Φ[0], Φ[1], ..., Φ[N − 1], 0, 0, ...} ;
Φ2 = {0, 0, ..., 0, Φ[N ], Φ[N + 1], ...} .
Si tenemos en cuenta que Φ = H − U Q, vamos a ver qu´ parte de las respuestas impulsionales de H, U y Q
e
afectan a Φ1 y Φ2 .
En primer lugar supongamos que las respuestas impulsionales de H y Q son:
H = {h[0], h[1], h[2], ...}
U = {u[0], u[1], u[2], ...}
Q = {q[0], q[1], q[2], ...} .
52](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-60-320.jpg)
![H puede descomponerse directamente en los mismos dos fragmentos que Φ:
H1 = {h[0], h[1], ..., h[N − 1], 0, 0, ...}
H2 = {0, 0, ..., 0, h[N ], h[N + 1], ...}
Q tambi´n puede descomponerse en los mismos fragmentos que Φ:
e
Q1 = {q[0], q[1], ..., q[N − 1], 0, 0, ...}
Q2 = {0, 0, ..., 0, q[N ], q[N + 1], ...}
Para poder multiplicar U y Q debemos convolucionarlas, lo que equivale a premultiplicar el vector de res-
puestas impulsionales de Q por la matriz de Toeplitz, formada por repeticiones desplazadas de la respuesta
impulsional:
u[0] 0 0 ...
u[1] u[0] 0 ...
U = u[2] u[1] u[0] ... (infinitas filas e infinitas columnas).
... ... ... ...
U puede descomponerse en 4 fragmentos, a saber:
u[0] 0 ... 0
u[1] u[0] ... 0
• U11 = (N filas y N columnas)
... ... ... ...
u[N − 1] u[N − 2] ... u[0]
• U12 = 0 (por ser U causal)
u[N ] u[N − 1] ... u[1]
• U21 = u[N + 1] u[N ] ... u[2] (infinitas filas y N columnas)
... ... ... ...
u[0] 0 ...
• U22 = u[1] u[0] ... (infinitas filas e infinitas columnas)
... ... ...
Puede observarse adem´s que U22 = U (que matem´ticamente viene dado por ser U una matriz de Toeplitz).
a a
Resulta entonces que
Φ1 = H1 − U1 Q1
Φ2 = H2 − U12 Q1 − U Q2 .
M´todo aproximado
e
Una vez descompuesto el problema en bloques vamos a plantear un problema de optimizaci´n que pueda
o
resolverse utilizando LMIs y que aproxime al problema 1 .
Por ejemplo, puede plantearse el correspondiente problema de optimizaci´n como la media geom´trica de:
o e
La norma 1 de los N primeros t´rminos de la respuesta impulsional de Φ (que son precisamente los que
e
est´n en Φ1 )
a
la norma H2 de los restantes t´rminos de la respuesta impulsional de Φ (que son los que hemos incluido en
e
Φ2 ).
53](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-61-320.jpg)
![2 2
Es decir, tratamos de calcular un Q que minimice Φ1 1 + Φ2 2 .
Esta funci´n a optimizar se elige porque, para un N fijo, corresponde a una norma que puede minimizarse
o
mediante LMIs, y adem´s, a medida que se aumenta N la soluci´n se aproxima a la del problema original. Para
a o
tener una estimaci´n bastar´ entonces resolver este problema de optimizaci´n modificado, aumentando N hasta
o a o
converger a una soluci´n. Como veremos en la pr´xima secci´n, dependiendo de las restricciones consideradas
o o o
nos aproximaremos al ´ptimo, bien por arriba, bien por abajo.
o
Aproximaci´n inferior por LMIs
o
Una aproximaci´n inferior puede calcularse utilizando Φ2 2 .
o
2 2
m´
ın Φ1 1 + Φ2 2
Q
sujeto a: Φ1 = H1 − U1 Q1 ; Φ2 = H2 − U12 Q1 − U Q2 .
2 2 1
Φ2 2 = H2 − U12 Q1 − U Q2 2 = Trace 1 Q1 T B T Lo B .
Q1
Los par´metros Lo y B se obtienen a partir de la representaci´n de espacios de estados de
a o
H2 − U12 Q1 − U Q2 .
Lo es el Gramiano de observabilidad, que puede calcularse resolviendo una ecuaci´n de Lyapunov (en Matlab
o
se calcula inmediatamente con el comando gram).
Aproximaci´n superior
o
Para obtener una aproximaci´n superior basta imponer una restricci´n adicional al problema utilizado para
o o
la aproximaci´n inferior, que resulte redundante cuando N sea muy grande, y que adem´s no complique el
o a
procedimiento de resoluci´n.
o
Por ejemplo, a medida que N va haci´ndose m´s grande Q2 ir´ tendiendo a 0, por lo que podemos buscar una
e a a
soluci´n imponiendo que Q2 = 0. Es decir:
o
2 2
m´
ın Φ1 1 + Φ2 2
Q
sujeto a:
Φ1 = H1 − U1 Q1 ; Φ2 = H2 − U12 Q1 − U Q2 y Q2 = 0
o lo que es lo mismo:
2 2
m´
ın Φ1 1 + Φ2 2
Q
sujeto a:
Φ1 = H1 − U1 Q1 ; Φ2 = H2 − U12 Q1 .
Al tener una restricci´n adicional este problema de optimizaci´n, su valor ´ptimo ser´ mayor. Adem´s puede
o o o a a
demostrarse [ED98] que, a medida que N va haci´ndose m´s grande, las aproximaciones, superior e inferior,
e a
convergen (de forma d´bil).
e
54](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-62-320.jpg)



![III.2. Estabilidad cuadr´tica
a
Consideremos al sistema
x = A(r)x + B(s)u
˙ (III.1)
n m n×n n×m
donde x ∈ IR es el vector de estados, u ∈ IR es el vector de control, A(r) ∈ IR y B(s) ∈ IR son las
matrices de din´mica y de entrada del sistema, funciones de r ∈ IRnr y s ∈ IRns , los cuales son vectores no
a
conocidos que representan la incertidumbre, que puede o no ser variante en el tiempo.
Nuestro objetivo, en un primer momento, ser´ el de calcular una ley de control que asegure la estabilidad del
a
sistema para toda perturbaci´n factible r ∈ R y s ∈ S.
o
Para tal fin utilizaremos el enfoque cuadr´tico, que pasamos a definir.
a
Definici´n III.1 ([Bar83], [Pet87]) El sistema III.1 es cuadr´ticamente estabilizable si existe una ley de con-
o a
trol, funci´n continua de los estados p(·) : IRn → IRm tal que p(0) = 0, una matriz P sim´trica, definida positiva,
o e
y una constante real α > 0 que verifican, para toda incertidumbre posible:
xT [AT (r)P + P A(r)]x + 2xT P B(s)p(x) ≤ −α x 2
(III.2)
para todo x ∈ IRn = 0 y para todo t.
Observaci´n III.1 Hay que se˜alar que el sistema III.1 es en realidad no un sistema sino una familia de ellos
o n
que bien puede ser infinita.
Observaci´n III.2 Si la condici´n III.2 es satisfecha, toda la familia de sistemas III.1 comparten la funci´n
o o o
—cuadr´tica— de Lyapunov:
a
V (x) = xT P x
al cerrar el lazo. En adelante denominaremos a P como matriz de Lyapunov.
Observaci´n III.3 La condici´n de que toda la familia de sistemas comparta una misma funci´n (matriz)
o o o
de Lyapunov puede hacer que el controlador sea extremadamente conservador. A cambio, ofrece gran poder de
c´lculo del mismo y, como veremos m´s adelante, la misma puede ser reformulada en t´rminos mucho menos
a a e
conservadores.
En relaci´n con el tipo de incertidumbre, ser´ imposible tratar de extraer ning´n resultado para un tipo cualquiera
o ıa u
de ella. Al igual que en el enfoque frecuencial, nos concretaremos al estudio de 2 tipos de ellas, a saber:
1. Incertidumbre acotada en norma
2. Incertidumbre poli´drica.
e
Ambos tipos de conjuntos son convexos y de su representaci´n pueden extraerse soluciones.
o
Incertidumbre acotada en norma
Sea An una matriz constante en IRn×n . D y E matrices constantes y conocidas de dimensiones n × q y q × n
respectivamente. F ∈ IRq×q es una matriz que puede variar en el tiempo y de la que s´lo se conoce que:
o
F T F ≤ I.
58](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-66-320.jpg)

![A
1 A
2 B
3
B
2
B
B
Ar 4
A A3
B
1
B
5
A A Bs
5 4
C5
C
t
C
4
C
1
C
C
3 C
2
Figura III.2.: Incertidumbre poli´drica
e
III.3. Sistemas con incertidumbre acotada en norma
Consideremos el sistema
x
˙ = (An + DF E1 )x + (Bn + DF E2 )u + B1 w
(III.3)
z = C1 x
donde x ∈ IRn es el vector de estados, u ∈ IRm es el vector de control, w ∈ IRnw es la perturbaci´n externa
o
y z ∈ IRnz es el vector de salidas a controlar —salida controlable—. An y Bn son las matrices (constantes y
conocidas) de din´mica y entrada del sistema, D, E1 y E2 son matrices constantes (y conocidas) de dimensiones
a
adecuadas, que determinan la forma como la incertidumbre afecta al sistema y F es una matriz de la que s´lo se
o
sabe que:
F T F ≤ I.
Se desea encontrar una ley de control u = Kx —realimentaci´n lineal de los estados— tal que el sistema a lazo
o
cerrado sea internamente estable y que la norma infinita de la funci´n de transferencia entre w y z sea menor
o
que un escalar positivo γ, esto es:
Twz ∞ < γ ∀A ∈ A y B ∈ B (III.4)
donde
A = {A : A = An + DF E1 ∀ F T F ≤ I}
y
B = {B : B = Bn + DF E2 ∀ F T F ≤ I}.
Si la condici´n III.4 se satisface, entonces diremos que el control u, γ-aten´a la perturbaci´n w [XFS92].
o u o
El siguiente teorema da las condiciones que deben cumplirse para la existencia de u.
Teorema III.1 ([KPZ90]) Sea γ > 0 un escalar dado. El sistema III.3 es cuadr´ticamente estabilizable por
a
una ley de control u = Kx con atenuaci´n γ de la perturbaci´n w sobre z si y s´lo si existen matrices S > 0 y
o o o
R, y un escalar ε > 0, soluciones de la LMI:
An S + SAT + Bn RT + RBn + εDDT + γ −2 B1 B1 SC1 SE1 + RE2
n
T T T T T
C1 S −I 0 <0 (III.5)
T
E2 R + E 1 S 0 −εI
60](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-68-320.jpg)
![M´s a´n, una ley de control estabilizante (cuadr´ticamente) est´ dada por:
a u a a
K = RT S −1 .
Demostraci´n: El sistema III.3 es cuadr´ticamente estabilizable con atenuaci´n γ > 0 de perturbaci´n si y s´lo
o a o o o
si existen matrices P > 0 y K tales que
(An + Bn K + DF E1 + DF E2 K)T P + P (An + Bn K + DF E1 + DF E2 K)+
γ −2 P B1 B1 P + C1 C1 < 0
T T
pero ello es equivalente, denominando a E = E1 + E2 K, [Pet87]:
1
(An + Bn K)T P + P (An + Bn K) + εP DD T P + E T E + γ −2 P B1 B1 P + C1 C1 < 0
T T
(III.6)
ε
para alg´n ε > 0. En su forma dual III.6 toma la forma (S = P −1 y R = SK T ):
u
1
An S + SAT + RBn + Bn RT + εDDT + SE T ES + γ −2 B1 B1 + SC1 C1 S < 0.
n
T T T
(III.7)
ε
III.7 puede escribirse como una LMI de la forma:
An S + SAT + RBn + Bn RT + γ −2 B1 B1 + εDDT
n
T T T T
SE1 + RE2 SC1T
T
E2 R + E 1 S −εI 0 <0 (III.8)
C1 S 0 −I
Observaci´n III.4 La desigualdad III.8 es lineal (convexa) con respecto a sus inc´gnitas S, R, ε y aun con
o o
respecto a γ −2 . Por lo tanto, puede ser resuelta con herramientas est´ndar, e.g., el LMI Toolbox de Matlab
a
[GNL95].
Observaci´n III.5 Si s´lo se impone estabilidad cuadr´tica, la LMI se reduce a las 2 primeras filas y columnas
o o a
de III.8.
Observaci´n III.6 Si se trata de sistemas ciertos, la LMI se reduce a la 1ra y 3ra filas y columnas de III.8 con
o
D = 0.
A continuaci´n, presentamos la extensi´n del teorema III.1 a los casos de costo garantizado (H 2 ) y de ubicaci´n
o o o
de polos.
Corolario III.1 Definamos el siguiente problema convexo:
m´ Tr W
ın
sujeto a
W C1 S
T >0 (III.9)
SC1 S
An S + SAT + εDDT + Bn RT + RBn + B1 B1
n
T T T T
SE1 + RE2
T <0 (III.10)
E2 R + E 1 S −εI
Sea W ∗ la soluci´n —si existe una— del problema convexo definido. Existe una ley de control u = Kx tal que
o
Twz 2 < γ 1/2 = Tr W ∗
para toda la familia de sistemas III.3 si y s´lo si existen matrices W y S definidas positivas, una matriz R y un
o
escalar ε > 0 tales que el problema de optimizaci´n tiene soluci´n. M´s a´n, la ley de control viene dada por
o o a u
u = Kx con K = RT S −1 .
61](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-69-320.jpg)



![III.5. Condiciones menos conservadoras
Trat´ndose de sistemas con incertidumbre, la condici´n cuadr´tica de existencia de una matriz de Lyapunov
a o a
P , com´n a todo miembro de la familia incierta, introduce cierto conservadurismo que se ve contrastado con el
u
hecho de poder calcular un controlador unico para todos los sistemas. Sin embargo, la condici´n de existencia de
´ o
una matrix de Lyapunov com´n puede ser relajada y por ende obtener mejores controladores. En lo que sigue
u
damos condiciones de estabilidad para sistemas con incertidumbre poli´drica (continuos y discretos), y dejamos
e
para el lector las extensiones a los casos de ubicaci´n de polos, H∞ y H2 y los casos con incertidumbre acotada
o
en norma.
Teorema III.3 [SS01], [Sh01]. Con relaci´n al sistema (III.13), existe una ley de control u(t) = Kx(t) que
o
estabiliza al sistema en cualquiera de sus representaciones, i.e., ∀A ∈ A y ∀B ∈ B, si existen matrices definidas
positivas Sq , q = 1, . . . , r × s y G, todas en IRn×n tales que:
Ai G + G T AT + B j R + R T Bj
i
T
Ai G + B j R − G T + S q
T T < 0. (III.20)
G Ai − G + S q −G − GT
i = 1, . . . , r, y j = 1, . . . , s. M´s a´n, K = RG−1 .
a u
Demostraci´n-necesidad: ([DB01]) El sistema (III.13) es estabilizable por una ley de control u(t) = Kx(t) si
o
existen matrices definidas positivas SA , posiblemente dependientes de A y una ganancia K tales que:
(A + BK)SA + SA (A + BK)T < 0 ∀A ∈ A y B ∈ B
0 SA I
= ( I (A + BK) ) < 0 ∀A ∈ A y B ∈ B
SA 0 (A + BK)T
0 SA A + BK
= ( I (A + BK) ) + ( F G )+
SA 0 −I
(III.21)
FT I
((A + BK)T − I) <0
GT (A + BK)T
∀A ∈ A, ∀B ∈ B y cualesquiera F, G
(A + BK)F + F T (A + BK)T (A + BK)G − F T + SA
=⇒ < 0.
GT (A + BK)T − F + SA −G − GT
Haciendo F = G, ya que no existe ninguna restricci´n en F , definiendo R = KG y observando que las matrices
o
A y B aparecen linealmente en (III.21), es decir, que la satisfacci´n en los v´rtices garantiza la satisfacci´n en
o e o
cualquiera de sus combinaciones convexas, queda demostrada la necesidad.
Suficiencia: Si la condici´n (III.20) es satisfecha, entonces tambi´n se cumple para toda A ∈ A y B ∈ B, de
o e
hecho la matriz (SA ) de Lyapunov asociada a cada a cada par (A, B) no es m´s que la combinaci´n convexa de
a o
las matrices Sq asociadas a los v´rtices. En consecuencia, si definimos la matriz regular:
e
I (A + BK)
Γ=
0 I
se cumple que:
(A + BK)G + GT (A + BK)T (A + BK)G − GT + SA
Γ ΓT < 0, (III.22)
GT (A + BK)T − G + SA −G − GT
pero (III.22) es igual a:
(A + BK)SA + SA (A + BK)T SA − AGT − GT
< 0, (III.23)
SA − GAT − G −G − GT
y el t´rmino (1,1) de (III.23) asegura que K es una ganancia estabilizante y S A la matriz de Lyapunov, i.e., que
e
la primera de las condiciones de (III.21) es satisfecha
65](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-73-320.jpg)
![Para el caso de sistemas discretos, consideraremos el sistema:
xk+1 = Axk + Buk (III.24)
con las matrices A, B en A, B respectivamente.
Recordemos ahora la condici´n de estabilidad para sistemas discretos, equivalente a que los polos del sistema
o
(III.24) est´n dentro del c´
e ırculo unitario.
Definici´n III.2 El sistema (III.24) es estabilizable por una ley de control de la forma u k = Kxk , si existen
o
matrices definidas positivas SA y una ganancia K tales que:
(A + BK)T SA (A + BK) − SA < 0, ∀A ∈ A y B ∈ B. (III.25)
La demostraci´n es muy similar a la de los sistemas discretos ya que (III.25) es equivalente a:
o
−SA 0 I
(I (A + BK) ) <0
0 SA (A + BK)T
y dejamos para el lector tal demostraci´n.
o
III.6. Dise˜ o por realimentaci´n de la salida
n o
En las secciones anteriores se presentaron resultados para sistemas inciertos —incertidumbre acotada en norma
y poli´drica—, basados en la realimentaci´n lineal de todos los estados del sistema.
e o
Muchas veces esos estados no est´n f´
a ısicamente disponibles para su medici´n porque no son medibles o porque
o
no pueden serlo de manera confiable, y s´lo una parte de entre ellos puede usarse para control. A estos ultimos
o ´
los llamaremos “salida medible” del sistema.
Lo que resta de este cap´ıtulo ser´ consagrado a la s´
a ıntesis de controladores que satisfacen cierto criterio de
desempe˜o —H∞ , H2 , etc.— y que usan solamente la salida medible. Las implicaciones pr´cticas de tal objetivo
n a
son obvias. No tan obvio, sin embargo, es el grado de dificultad que implica la tarea de estimaci´n de estados
o
para sistemas con incertidumbre.
De igual manera, trataremos primero sistemas lineales invariantes en el tiempo sin incertidumbre para los
que demostraremos que podemos alcanzar el objetivo propuesto. Para los sistemas con incertidumbre acotada
en norma tambi´n encontraremos la soluci´n a trav´s de la extensi´n del resultado de [Pet87] a sistemas con
e o e o
realimentaci´n de la salida pero, desafortunadamente, s´lo para el caso de estabilidad —cuadr´tica—, no pudiendo
o o a
extender esos resultados al caso H∞ o H2 . Los sistemas con incertidumbre poli´drica, por el contrario, no conocen
e
de soluci´n total ni siquiera en el caso de estabilidad y para ellos s´lo presentaremos soluciones parciales.
o o
Como en los cap´ ıtulos anteriores, toda la formulaci´n est´ basada en una representaci´n del sistema en variables
o a o
de estado y las soluciones ser´n formuladas como desigualdades matriciales lineales.
a
III.7. Sistemas ciertos
Consideremos al sistema
x
˙ = Ax + Bu + B1 w
y = Cx + Dw (III.26)
z = C1 x + D 1 u
66](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-74-320.jpg)
![donde x ∈ IRn es el vector de estados, u ∈ IRm es el vector de controles, w ∈ IRnw es el vector de perturbaciones
externas que afectan al sistema, z ∈ IRnz es el vector de salidas controlables, y ∈ IRp es el vector de salidas
medibles.
A, B, B1 , C, C1 y D1 son matrices constantes de dimensiones apropiadas.
Se desea dise˜ar un compensador din´mico de la forma:
n a
xc
˙ = A c xc + B c y
(III.27)
u = C c xc
que asegure que el sistema a lazo cerrado cumpla con ciertas condiciones de desempe˜o medidas como una norma
n
2, infinita, ubicaci´n de polos.
o
El controlador escogido es uno estrictamente propio, lo que, sin p´rdida de generalidad, simplifica considera-
e
blemente las demostraciones. La extensi´n al caso propio es s´lo m´s agotadora desde el punto de desarrollo y
o o a
demostraci´n.
o
En principio, nos planteamos unicamente la b´squeda de controladores estabilizantes para luego extender esos
´ u
resultados a los otros casos que hemos venido estudiando, incluyendo a los sistemas discretos.
El siguiente teorema caracteriza los controladores buscados.
Teorema III.4 ([SGC97]) El sistema III.26 puede ser estabilizado por un controlador din´mico de la forma
a
III.27 si y s´lo si existen matrices sim´tricas X, Y > 0 y matrices U y V en IR n×n soluciones del conjunto de
o e
desigualdades matriciales
AY + Y AT + BCc V T + V Cc B T
T
Φ
T <0
Φ AT X + XA + U Bc C + C T Bc U T
T
(III.28)
Y I
>0
I X
donde Φ = V AT U T + A + Y AT X + V Cc B T X + Y C T Bc U T .
c
T T
Demostraci´n: El sistema a lazo cerrado —aut´nomo— resultante de aplicar el compensador din´mico III.27
o o a
es:
x˙ A BCc x B1
= + w
xe
˙ Bc C A c xc Bc D
˜
A ˜
B (III.29)
x
z = (C1 D1 Cc )
xc
˜
C
o o ˜
y el sistema es asint´ticamente estable si y s´lo si existe una matriz P > 0 tal que
˜ ˜ ˜˜
AT P + P A < 0. (III.30)
˜
Particionemos ahora la matriz P de la forma:
˜ X U ˜ Y V
P = ˆ P −1 = ˆ .
UT X VT Y
˜ ˜
Con relaci´n a los elementos de la matriz P y P −1 se cumple que:
o
XY + U V T = I
XV + U Yˆ = 0
T ˆ T (III.31)
U Y + XV = 0
Y ˆ
= (X − U XU T )−1 > X −1 .
67](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-75-320.jpg)
![Definamos T de la forma:
Y V
T = .
I 0
Sin p´rdida de generalidad, podemos asumir que V = 0 ya que, de tener V autovalores iguales a cero, siempre
e
podr´ hacerse una descomposici´n en valores singulares de V :
ıa o
V = Mv ΣMu
reemplazando Σ por Σ∗ donde se han reemplazado los autovalores en cero por ε > 0 suficientemente peque˜os,
n
de modo que
V ∗ = Mv Σ∗ Mu
˜
y la nueva matriz P ∗ tambi´n cumplir´ con la desigualdad III.30 para alg´n ε suficientemente peque˜o [IS94].
e a u n
Si V = 0 entonces T es una matriz regular, i.e., tiene inversa. Si multiplicamos a la derecha de III.30 por T T
y a la izquierda por T , lo cual preserva la desigualdad, obtenemos:
T
Y V A BCc X U Y I
+ΥT
ˆ <0
VT
I 0 Bc C Ac UT X 0
Υ
y que resulta en:
Y V XA + AT X + U BCc + Cc Bc U
T T
∆ Y I
T <0 (III.32)
I 0 ∆ Ω VT 0
ˆ ˆ T ˆ
donde ∆ = XBCc + U Ac + AT U + Cc B T X y Ω = XAc + Ac X + U T BCc + Cc B T U y de donde se obtiene, a
T T
trav´s de las relaciones III.31, la desigualdad matricial III.28.
e
Definamos ahora las variables intermedias,
L = Cc V T ; F = U B c y M = V A T U T
c
(III.33)
Z = A + Y AT X + Y C T F T + LT B T X,
entonces tenemos que:
Corolario III.5 El sistema (III.26) es estabilizable por un compensador din´mico de la forma (III.27) si y s´lo
a o
si existen matrices X, Y > 0 y Φ ∈ IRn×n , L ∈ IRm×n y F ∈ IRn×r tales que
AY + Y AT + BL + LT B T Φ
< 0. (III.34)
ΦT AT X + XA + F C + C T F T
Observaci´n III.21 La desigualdad matricial es lineal —convexa— con respecto a sus variables X, Y, L, F, Φ y,
o
de nuevo, herramientas de programaci´n lineal pueden utilizarse para la b´squeda de su soluci´n.
o u o
Observaci´n III.22 Una vez que X, Y, L, F y Φ son calculadas, es f´cil calcular A c , Bc , Cc de la siguiente
o a
forma:
1. Tomemos cualquier matriz regular V
2. Hagamos Cc = L(V T )−1 y
3. U = (I − XY )(V T )−1
4. Bc = U −1 F
68](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-76-320.jpg)
![5. M =Φ−Z
6. Ac = U −1 M T (V T )−1 ,
si V = 0 entonces U = 0.
Aunque parece que los controladores estabilizantes est´n parametrizados por V , ello no es cierto. Si calculamos
a
la funci´n de transferencia del compensador tenemos que:
o
Tc (s) = Cc (sI − Ac )−1 Bc
= L(V T )−1 [sI − U −1 M T (V T )−1 ]−1 U F =
= L[s(U V T ) − M T ]−1 F =
= L[s(I − XY ) − M T ]−1 F
con lo que queda demostrado que la soluci´n de III.34 determina totalmente al controlador estabilizante, y la
o
verdadera parametrizaci´n est´ determinada por la tripleta (Φ, F, L). De hecho, si no existe ninguna restricci´n
o a o
sobre la estructura de la din´mica del compensador Ac , podemos tomar Φ = 0 recobrando los resultados de
a
[DGK89] y [GA94].
Pasemos ahora a la aplicaci´n de los resultados a H2 y sistemas discretos, que surgen de peque˜as extensiones
o n
del resultado previo.
Corolario III.6 ([GPS92], [PSG92]) Consideremos el sistema III.26 para el que deseamos conseguir un con-
trolador de la forma III.27 que asegure:
m´ Twz 2 .
ın
Tal problema tiene soluci´n, si y s´lo si el siguiente problema de optimizaci´n la tiene:
o o o
m´ Tr W
ın
sujeto a
Y I B1
I X XB1 + F D > 0 (III.35)
T
B1 B1 X + D T F T
T
W
y
AY + Y AT + BL + LT B T Φ Y C 1 + L T D1
T T
ΦT AT X + XA + F C + C T F T T
C1 <0 (III.36)
C1 Y + D 1 L C1 −I
con L, Φ, Z, F tal como se definieron anteriormente.
o o ˆ
Para la obtenci´n del resultado anterior se us´ el hecho de que (sea P una matriz definida positiva):
m´ Twz
ın 2 = m´ ˜ ˜˜ ˜ ˜ ˜˜ ˜ ˜
ın{Tr[B T P B] : AT P + P A + C T C = 0} (III.37)
˜ ˜ ˜
con A, B, C definidos en III.29. Adem´s, la restricci´n de igualdad puede reemplazarse por una de desigualdad
a o
usando la propiedad de no decrecimiento de la soluci´n de la ecuaci´n de Lyapunov.
o o
De esta manera la ecuaci´n III.37 puede escribirse de la forma:
o
m´ Tr W
ın
sujeto a:
˜
P ˜˜
PB
>0 (III.38)
B ˜
˜T P W
69](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-77-320.jpg)

![La demostraci´n est´ basada en que el sistema a lazo cerrado debe cumplir que:
o a
˜
−P ˜ ˜
AT P
˜˜ ˜ <0
PA −P
˜ ˜ ˜
con A, P tal como fueron descritas en III.29 y III.30, utilizando la partici´n descrita de P y multiplicando por la
o
matriz Γ antes definida.
Observaci´n III.23 Como en los casos anteriores, la soluci´n del problema de factibilidad conlleva la determi-
o o
naci´n de los par´metros del compensador estabilizante Ac , Bc , Cc . Igualmente, la extensi´n del resultado a otras
o a o
circunferencias con radio r y centrada en −α es inmediata.
III.8. Sistemas con incertidumbre acotada en norma
Pasemos ahora al estudio de los sistemas con incertidumbre acotada en norma, para los que, en una primera
instancia y para simplificar las demostraciones, s´lo consideraremos incertidumbre en la matriz de din´mica del
o a
sistema. Igualmente, buscaremos un controlador estabilizante que adem´s asegure atenuaci´n de una perturbaci´n
a o o
externa w en la salida medible del sistema z, medida la atenuaci´n como la ganancia en la energ´
o ıa.
Sistemas continuos. Controladores H∞
Formalmente, consideremos al sistema incierto definido por:
x
˙ = (A + DF E)x + B1 w + Bu
z = C1 x (III.43)
y = Cx
donde x ∈ IRn es el vector de estados, u ∈ IRm es el vector de comandos o controles, w ∈ IRnw es la perturbaci´n,
o
y ∈ IRp es la salida medible y z ∈ IRnz es la salida a controlar. A, B1 , B y C son matrices constantes reales de
dimensiones apropiadas. D, F, E caracterizan la incertidumbre que puede o no ser variante en el tiempo. Adem´s:
a
F T F ≤ I.
El problema planteado es aquel de la determinaci´n de un compensador din´mico de la forma:
o a
xc
˙ = A c xc + B c y
(III.44)
u = −Cc xc
que estabiliza cuadr´ticamente el sistema incierto (III.43) con atenuaci´n γ > 0 de perturbaci´n, esto ultimo
a o o ´
siendo:
Twz ∞ < γ.
El teorema siguiente propone las condiciones necesarias y suficientes de la existencia de un tal compensador
din´mico del tipo (III.44).
a
Teorema III.5 ([CGP97]) Sea γ > 0 un escalar dado. El sistema (III.43) es cuadr´ticamente estabilizable con
a
atenuaci´n γ por un compensador de la forma (III.44) si y s´lo si existen R 1 , R2 definidas positivas, un escalar
o o
ε > 0 y matrices P y W definidas positivas tales que las expresiones siguientes se verifican
−1
1) AT P + P A − P BR1 B T P + εP DD T P + 1 E T E + γ −2 P B1 B1 P + C1 C1 < 0
ε
T T
T T −1 1 T T −2 T T (III.45)
2) AW + W A − W C R2 CW + ε W E EW + εDD + γ B1 B1 + W C1 C1 W < 0
−1
3) S = W − P > 0.
71](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-79-320.jpg)

![recordando que
Q1 = −{AT P + P A − P BR1 −1 B T P + εP DD T P + 1 E T E + γ −2 P B1 B1 P + C1 C1 }
ε
T T
y si definimos:
H = {W −1 A + AT W −1 − C T Bc S − SBc C + 1 E T E + εW −1 DDT W −1 +
T
ε
γ W B1 B1 W −1 + C1 C1 }
−2 −1 T T
entonces
(A − Bc C)T S + S(A − Bc C) + Cc B T P + P BCc + εSDD T P + εP DD T S+
T
T −2 T
εSDD S − 2Q1 + γ SB1 B1 P + γ −2 P B1 B1 SP + γ −2 SB1 B1 S = H − Q1
T T
y podemos escribir III.48 bajo la forma:
−Q1 Q1
.
Q1 H − Q1
Esta matriz es definida negativa si Q1 > 0 y H < 0. En consecuencia, la desigualdad III.47 se satisface si
(A − BCc )T P + P (A − BCc ) + εP DD T P + 1 E T E + γ −2 P B1 B1 P + C1 C1 < 0
ε
T T
(III.49)
AT W −1 + W −1 A − C T Bc S − SBc C + εW −1 DDT W −1 +
T
1 T −2 (III.50)
εE E + γ W B1 B1 W −1 + C1 C1 < 0.
−1 T T
Utilizando argumentos sacados del teorema de Finsler [Pet87], III.49 y III.50 son, respectivamente, equivalentes
a las condiciones 1 y 2 del teorema III.5 con Bc y Cc , las expresiones “cl´sicas” de las ganancias de control y de
a
filtraje.
Necesidad: Sea
T T
˜ A −BCc ˜ B1 B1 0 ˜ C1 C1 0
A= B1 = C1 = .
Bc C Ac 0 0 0 0
El sistema en lazo cerrado III.43 y III.44 resulta
x˙ ˜ DF E 0 x B1
= A+ + w
xc
˙ 0 0 xc 0 (III.51)
y= (C1 0)
y en consecuencia III.43 es cuadr´ticamente estable con atenuaci´n γ > 0 de perturbaci´n si y solamente si
a o o
existen matrices
−1
˜ W1 W2 ˜ P1 P2
W = T = P −1 = T >0
W2 W3 P2 P3
tales que
˜ ˜ ˜˜ ˜ DF E 0 E T F T DT 0 ˜ ˜ ˜ ˜ ˜
AT P + P A + P + P + γ −2 P B1 P + C1 < 0. (III.52)
0 0 0 0
Si III.52 es satisfecha, entonces [Pet87]
˜ ˜ ˜˜ ˜ D ˜ 1 ET ˜ ˜ ˜ ˜
AT P + P A + ε P (DT 0)P + (E 0) + γ −2 P B1 P + C1 < 0, (III.53)
0 ε 0
˜ ˜
si multiplicamos III.53 a ambos lados por W = P −1 ,
˜ ˜ ˜˜ 1 ˜ ET ˜ D ˜ ˜ ˜ ˜
W AT + A W + W (E 0)W + ε (DT 0) + γ −2 B1 + W C1 W < 0. (III.54)
ε 0 0
ˆ
Extrayendo los t´rminos superior izquierdo de las matrices III.53 y III.54, colocando P = W1 −1 > 0 y W =
e ˆ
ˆ
P1 −1 > 0 y utilizando el teorema de Finsler, recobramos la primera y segunda condici´n del teorema III.5 en P
o
ˆ
y W . Ahora bien, seg´n el lema de inversi´n de matrices [AM89], tenemos que:
u o
P1 − W1 −1 = P2 P3 −1 P2 T ≥ 0
ˆ ˆ
y por lo tanto W −1 − P ≥ 0. Esta ultima desigualdad puede ser satisfecha estrictamente. De hecho, seg´n el lema
´ u
ˆ ˆ
2 de [SMN90], si las condiciones (1) y (2) del teorema III.5 son satisfechas en P y W , ellas lo ser´n igualmente
a
ˆ
para las matrices W < W y P < P . ˆ
73](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-81-320.jpg)
![Observaci´n III.24 Las condiciones enunciadas en el teorema III.5 no nos proveen de un medio de c´lculo
o a
para la determinaci´n del compensador dado en III.46. Sin embargo, podemos notar que la primera condici´n es
o o
−1 −1
convexa con respecto a (P −1 , R1 , ε) o, igualmente, con respecto a (ε−1 P −1 , R1 , ε−1 ). La segunda es convexa
−1 −1
con respecto a (W −1 , R2 , ε−1 ) o con respecto a (εW −1 , R2 , ε). La ultima es convexa con respecto a (W −1 ,
´
−1
P ). Desgraciadamente, el conjunto de las 3 desigualdades no forma una “representaci´n” convexa y otros
o
m´todos, como por ejemplo [Gar93] [GSK94] o [IS95], que toman en cuenta la naturaleza particular (convexidad
e
con respecto a ε y ε−1 ) de este problema, deben ser utilizados.
Observaci´n III.25 Una condici´n necesaria y suficiente puede encontrase tambi´n en el trabajo [XFS92], pero
o o e
bajo la hip´tesis de que el compensador din´mico es dado.
o a
Observaci´n III.26 Para la demostraci´n del teorema III.5, nos hemos alejado un poco de las LMIs, y hemos
o o
seguido un enfoque m´s bien constructivo, siguiendo la demostraci´n original de [CGP97]. Igual comentario se
a o
aplica a la forma del compensador III.44 en el que se introdujo un signo (-).
Las condiciones III.45 del teorema III.5 tambi´n pueden escribirse bajo la forma de LMIs, las cuales recogemos
e
en el siguiente corolario (con X = P −1 y Y = W −1 ):
Corolario III.8 Sea γ > 0 un escalar dado. El sistema III.43 es cuadr´ticamente estabilizable con atenuaci´n
a o
−1 −1
γ de perturbaci´n, si y solamente si existen matrices X, Y, R1 , R2 definidas positivas y un escalar ε > 0 tales
o
que el siguiente conjunto de LMIs es satisfecho:
−1
AX + XAT − BR1 + εDDT + γ −2 B1 B1 XE T XC1
T T
1) EX −εI 0 <0
T C1 X 0 −I
−1
A Y + Y A + C T R2 C + ε−1 E T E + C1 C1
T
YD Y B1
(III.55)
2) DT −ε−1 I 0 <0
T 2
B1 Y 0 −γ I
Y I
3) > 0.
I X
Observamos que la convexidad del conjunto de matrices se pierde a causa del escalar ε.
Finalmente, en el caso de que solamente se desee asegurar la estabilidad —cuadr´tica— del sistema, las dos
a
primeras condiciones de III.55 se reducen a las dos primeras filas y columnas de las LMIs respectivas. Hay que
se˜alar que en este caso es f´cil eliminar ε de las variables multiplicando la primera LMI por
n a
ε−1/2 I 0
0 I
a ambos lados del lado izquierdo de la desigualdad y luego por
I 0
0 ε−1/2
y la segunda por
ε1/2 I 0
0 I
y luego por
I 0
0 ε1/2
74](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-82-320.jpg)
![para finalmente hacer un cambio de variable
X
X= y Y = εY
ε
que no afecta la tercera LMI.
Al eliminar ε recuperamos la convexidad del problema y, por ende, su soluci´n total.
o
Ejemplo
En esta secci´n presentamos un ejemplo tomado de [HF93] ligeramente modificado para incluir los requisitos
o
H∞ que impondremos al problema.
El sistema considerado es:
−1 −1 2
x=
˙ + k(4 − 1) x+
0 2 −2
1 0
u+
−3 1
y = (−3 1)x
z = (1 0)x;
k es la incertidumbre con rango −1 ≤ k ≤ 1.
El compensador obtenido usando el LMI Toolbox de Matlab con γ = 1 y ε = 0,1 fue:
−169,9767 43,4919
Ac =
598,2483 −161,0055
−7,8010
Bc = Cc = (148,9342 − 37,3479).
51,6630
La respuesta al escal´n unitario en la perturbaci´n w se muestra en la figura III.4 para valores de k =
o o
1, −1, 0, 0,5, −0,5. En la figura III.5 se muestra una ubicaci´n de los polos del sistema para una discretizaci´n
o o
uniforme del intervalo de la incertidumbre.
Los resultados obtenidos son equivalentes a aquellos para sistemas con incertidumbre estructurada en 2 bloques.
Otros resultados para un n´mero mayor de bloques pueden encontrarse en [CH95].
u
La extensi´n a incertidumbre en otras matrices del sistema podemos encontrarla en [GCG97].
o
Sistemas discretos
En esta secci´n derivaremos condiciones para la existencia de controladores H 2 en sistemas lineales discretos,
o
con incertidumbre acotada en norma. El problema ser´ formulado como una colecci´n de desigualdades matriciales
a o
lineales donde, de nuevo, encontraremos la similitud con problemas con incertidumbre estructurada en 2 bloques.
Los resultados estar´n basados en el resultado [SGC97], en el que se introduce un elegante cambio en las variables
a
del controlador —de hecho un cambio matricial de variables.
Consideraremos los sistemas lineales discretos:
xt+1 = (A + DF E1 )xt + (B + DF E2 )ut + B1 wt
yt = Cxt (III.56)
zt = C1 xt + D12 ut
75](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-83-320.jpg)
![0.14
0.12
0.1
0.08
0.06
0.04
0.02
0
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Figura III.4.: Desempe˜o ante la perturbaci´n.
n o
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−2.8 −2.6 −2.4 −2.2 −2 −1.8 −1.6 −1.4 −1.2 −1 −0.8
Figura III.5.: Ubicaci´n de polos.
o
donde xt ∈ IRn , ut ∈ IRm y yt ∈ IRp son respectivamente los vectores de estado, el control y la salida “medible”.
wt ∈ IRnw es la perturbaci´n externa y zt ∈ IRnz es la salida “controlable”. Todas las matrices tienen dimensiones
o
apropiadas. F ∈ IRnD ×nE representa la incertidumbre —acotada en norma [Pet87]— y que pertenece a:
F = {F ∈ IRnD ×nE : FT F ≤ I}.
Buscamos un controlador (del tipo observador) de la forma:
xt+1
ˆ = A c x t + B c yt
ˆ
(III.57)
ut = Cc xt
ˆ
de manera que, cuando el lazo es cerrado –con (III.57)–, la norma H2 de la funci´n de transferencia desde w a z
o
√
sea menor o igual que alg´n valor γ > 0 dado, para todo posible F ∈ F, i.e.,
u
2
Twz 2 ≤γ ∀F ∈ F
lo que normalmente conocemos como costo garantizado [EP98].
76](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-84-320.jpg)
![Todos los resultados que presentaremos pueden ser extendidos a la ubicaci´n de polos en discos centrados en
o
alg´n escalar real α con radios r. Adem´s, todas las matrices asociadas con la salida medible y t pueden incluir
u a
incertidumbre (con algunas condiciones sobre la forma como afectan al sistema –matrices D y F –). Igualmente
pueden ser considerados controladores no estrictamente propios. Hemos escogido la estructura del sistema y la
del controlador como en (III.56) y (III.57) para mantener las demostraciones mucho m´s simples.
a
Cuando aplicamos el control (III.57) para cerrar el lazo, obtenemos:
xt+1 A BCc D xt B1
= + F (E1 E2 Cc ) + wt
xt+1
ˆ Bc C A c
0
xt
ˆ 0
˜
˜ ˜
E
x
˜ ˜
(III.58)
A D B1
xt
zt = (C1 D12 Cc )
xt
ˆ
˜
C1
o agrupando t´rminos:
e
xt+1
˜ = ˜ ˜ ˜ x ˜
(A + DF E)˜t + B1 wt
˜ ˜ (III.59)
zt = C1 x t
Nuestra soluci´n del problema est´ basada en el concepto de disco-estabilidad cuadr´tica, cuya definici´n es:
o a a o
Definici´n III.3 ([GB95]) El sistema (III.59) es cuadr´ticamente disco estabilizable (d − estabilizable), si
o a
existe una matriz sim´trica definida negativa P > 0 tal que:
e
˜ ˜ ˜ ˜ ˜ ˜
(A + DF E)T P (A + DF E) − P < 0
∀F ∈ F.
El costo H2 garantizado viene dado por:
Definici´n III.4 ([GGB94]) Sea {Ac , Bc , Cc } un controlador dado que d−estabiliza cuadr´ticamente a (III.59).
o a
Entonces, el sistema (III.59) tiene un costo γ > 0, H2 garantizado si:
2
Twz 2 ≤γ ∀F ∈ F
donde Twz es la funci´n de transferencia entre w - z en (III.59), dada por:
o
˜ ˜ ˜ ˜ ˜
Twz = C1 (δI − A − DF E)−1 B1 , δ = el operador de retardo.
Recordemos ahora que:
Twz 2 ˜T ˜
= Traza(B1 Lo (F )B1 )
2
donde Lo (F ) satisface:
˜ ˜ ˜ ˜ ˜ ˜ ˜T ˜
(A + DF E)T Lo (F )(A + DF E) − Lo (F ) + C1 C1 = 0. (III.60)
El siguiente teorema nos aporta condiciones equivalentes “ciertas” de la existencia de l´
ımites superiores de la
norma H2 de sistema (III.59).
Teorema III.6 ([GB95]) El sistema(III.59) es cuadr´ticamente d−estable si existe una matriz sim´trica P > 0
a e
y un escalar ε > 0 tal que
˜ ˜˜ ˜ ˜ ˜ ˜T ˜
AT (P −1 − εDDT )−1 A − P + ε−1 E T E + C1 C1 . < 0 (III.61)
˜
Q
77](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-85-320.jpg)
![Observaci´n III.27 En [GB95] el resultado es formulado en t´rminos de una matriz Q que puede ser escogida
o e
o o ˜
arbitrariamente y de una ecuaci´n discreta de Riccati. Con una selecci´n apropiada de Q (e.g., = Q + cualquier
matriz definida positiva “peque˜a”) se obtiene (III.61).
n
El l´
ımite superior de la norma H2 es funci´n de la soluci´n P de la desigualdad de Riccati (III.61).
o o
De hecho, la satisfacci´n de (III.61) es equivalente a [GB95]:
o
˜ ˜ ˜ ˜ ˜ ˜ ˜T ˜
(A + DF E)T P (A + DF E) − P + C1 C1 < 0 (III.62)
al comparar (III.60) y (III.62) P > Lo , y por lo tanto:
T T
Traza(B1 Lo (F )B1 ) ≤ Traza(B1 P B1 )
En t´rminos de desigualdades matriciales, la existencia de una matriz P > 0 y un escalar ε > 0 tal que:
e
P −1 ˜
B1
˜T >0 y (III.63)
B1 γI
˜˜
−P −1 + εDDT ˜
A
˜T <0 (III.64)
A −P + ε −1
E ˜
˜ T E + C T C1
˜ ˜
1
implica que:
2
Twz 2 ≤γ ∀F ∈ F.
Con estos resultados previos, podemos presentar el resultado principal de esta secci´n.
o
A continuaci´n presentaremos condiciones –necesarias y suficientes– de existencia de un controlador cuadr´tico
o a
d − estabilizante con costo H2 garantizado.
Para facilitar la presentaci´n del resultado principal, introduciremos manipulaciones elementales de los resul-
o
tados previos.
Lema III.1 La desigualdad (III.64) es satisfecha si y s´lo si existe una matriz sim´trica, definida positiva S tal
o e
que:
˜˜
−S + DDT ˜
AS
˜T ˜ T ˜ ˜ ˜ .<0 (III.65)
SA −S + S E ES + εS C T C1 S 1
Demostraci´n: Pre y post multiplicando el lado izquierdo de la desigualdad (III.64) por la matriz regular
o
sim´trica:
e
I 0
0 P −1
y definiendo S = ε−1 P −1 , obtenemos (III.65).
Observe que, con este cambio de variable, la desigualdad (III.63) resulta:
S ˜
B1
˜T > 0. (III.66)
B1 εγI
Lema III.2 Sea T cualquier matriz regular de dimensiones apropiadas, entonces la desigualdad (III.65) se sa-
tisface si y s´lo si existe una matriz sim´trica, positiva definida S tal que:
o e
˜
−I 0 EST T 0 0
0 ˜
−ε−1 I C1 ST T 0 0
T SE ˜ T ˜ ˜
T S C1 −T ST T T S AT T T
T
0 < 0. (III.67)
0 0 ˜
T AST T −T ST T T D ˜
0 0 0 ˜
DT T T −I
78](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-86-320.jpg)
![Demostraci´n: (III.67) se obtiene pre y post multiplicando el lado izquierdo de la desigualdad (III.65) por la
o
matriz regular:
T 0
0 T
y su transpuesta respectivamente, y luego aplicando el teorema del complemento de Schur para expandir las
dimensiones de la matriz.
Lema III.3 Sea T una matriz regular cualquiera de dimensiones apropiadas, entonces la desigualdad (III.66) se
satisface si y s´lo si existe una matriz definida positiva S tal que:
o
T ST T T B1
< 0. (III.68)
B1 T T
T
εγI
Demostraci´n: (III.68) se obtiene al pre y post multiplicar el lado izquierdo de (III.66) por la matriz regular:
o
T 0
0 I
y su transpuesta respectivamente.
Presentamos ahora el resultado principal de esta secci´n:
o
Teorema III.7 ([CP99]) El sistema(III.59) es cuadr´ticamente d − estable con costo H 2 γ > 0 garantizado,
a
si y s´lo si existen matrices X y Y sim´tricas, definidas positivas y matrices H, L, Z y un escalar ε > 0 tal que
o e
el siguiente conjunto de desigualdades matriciales lineales tiene soluci´n:
o
Y I Y B1
I X B1 > 0 y (III.69)
T T
B1 Y B 1 εγI
−I 0 E 1 E1 X + E 2 L 0 0 0
−ε−1 I C1 C1 X + D12 L 0 0 0
T T T T
−Y −I A Y +C H A 0
−X Z XAT + LT B T 0 < 0.
(III.70)
−Y −I YD
−X D
−I
M´s a´n, un controlador de costo H2 garantizado viene dado por:
a u
Bc = V −1 H
Cc = L(U T )−1
Ac = V −1 (Z T − Y AX − HCX − Y BL)(U T )−1
en el que V es cualquier matriz regular (escogida arbitrariamente por el dise˜ador) y U satisface XY + U V T = I.
n
Observe que siendo el lado izquierdo de (III.70) una matriz sim´trica, hemos introducido una “ ” para evitar
e
una descripci´n m´s complicada de la matriz.
o a
Demostraci´n: Para obtener (III.70) particionamos S en (III.67) de la forma:
o
X U Y V
S= ˆ S −1 = P = ˆ
UT X VT Y
y definimos a la matriz:
Y V
T =
I 0
79](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-87-320.jpg)
![donde podemos suponer, sin p´rdida de generalidad, que la matriz V es una matriz regular [SGC97].
e
Obtenemos los resultados de (III.69) y (III.70) con esta selecci´n de la matriz T en (III.67) y definiendo:
o
H = V Bc ; L = Cc U T ; Z = (Y AX + HCX + Y BL + V Ac U T )T
el conjunto de desigualdades matriciales lineales (III.69) y (III.70) aseguran d − estabilidad con desempe˜o del
n
sistema asegurado a trav´s del costo H2 garantizado del sistema (III.59).
e
Ejemplo
En esta secci´n presentamos un ejemplo num´rico tomado de Huei & Fong [HF93], ligeramente modificado.
o e
El sistema que consideramos es:
−1,00 −1,20 0,1 1 0
xt+1 = + F 1 0 xt + ut + wt
0,10 −0,15 0,2 0 0,1
(III.71)
yt = 1,2 −1,5 xt
zt = 0 1 xt + u t .
Colocando ε = γ = 1, la soluci´n al conjunto de desigualdades matriciales (III.69) y (III.70) viene dada por:
o
0,8229 −0,2671 3,5096 −1,5866
X= ; Y = ; y
−0,2671 0,3179 −1,5866 23,9678
−0,0765 0,0598 2,4053
L= 0,3194 0,0178 ; Z= ; H= .
−0,3870 0,1364 −2,9949
Con este conjunto de valores y simplemente escogiendo V como la matriz identidad, obtenemos para el con-
trolador:
0,9017 −0,0642 2,4053
xt+1
ˆ = xt +
ˆ yt
−0,4275 0,0008 −2,9949
ut = −0,4616 −0,0970 xt .
ˆ
Resulta sencillo construir una matriz de Lyapunov P para el sistema de lazo cerrado, como una funci´n de
o
X, Y y V o U .
III.9. Sistemas con incertidumbre poli´drica
e
En esta secci´n nos interesaremos particularmente en los sistemas con incertidumbre poli´drica. Buscamos
o e
soluciones que se basen en la realimentaci´n de la salida del sistema. En un primer momento, buscamos un
o
controlador que asegure la estabilidad del sistema, para luego avanzar en las especificaciones del controlador.
El problema de los sistemas con incertidumbre poli´drica es la ausencia de un sistema nominal, lo que lo
e
diferencia del caso con incertidumbre acotada en norma en el que el enfoque de generar un controlador din´mico,
a
basado en un observador del sistema con los elementos nominales “ligeramente” compensados en funci´n de la
o
incertidumbre, es inmediato y a de partir dichos elementos se construye una condici´n suficiente.
o
80](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-88-320.jpg)
![Para solventar este problema, proponemos en esta secci´n un enfoque iterativo para determinar un dominio
o
de incertidumbre polit´pico “lo m´s grande posible” alrededor de un sistema inicial fijo, proporcion´ndonos de
o a a
esta manera con una especie de sistema nominal de arranque. En cierta forma estamos evaluando un margen de
robustez en el sentido definido en [Bar94] y [MZ89].
La estrategia que utilizaremos se basa en una condici´n necesaria, a saber: si un sistema es cuadr´ticamente
o a
estabilizable y detectable —esta ultima noci´n dual del concepto de estabilidad cuadr´tica— siempre existe una
´ o a
cierta vecindad alrededor de no importa qu´ punto (modelo) dentro del dominio incierto que podr´ estabilizarse
e a
con un compensador din´mico del tipo “observador de Luenberger” [ORe83].
a
Esta vecindad puede ser —y lo ser´ en nuestro enfoque— definida a trav´s de una matriz de Lyapunov del tipo
a e
diagonal, la cual servir´, de manera cl´sica en el enfoque cuadr´tico, igualmente para la s´
a a a ıntesis del controlador
y viceversa.
El algoritmo que desarrollaremos se basa en la t´cnica de iteraciones “D-K” [MZ89], en el que explotaremos
e
la naturaleza biconvexa con respecto a la matriz de Lyapunov y con respecto al controlador.
En el enfoque que vamos a presentar se puede incluir incertidumbre en todas las matrices del sistema, esto es,
las matrices de din´mica, entrada y salida.
a
Estabilidad local de sistemas inciertos
En vista de que el algoritmo que propondremos se basa en la propiedad de estabilidad local de sistemas
inciertos, perm´
ıtasenos pasar a demostrar tal propiedad y para ello consideremos el sistema:
x = Ax + Bu
˙
(III.72)
y = Cx
donde x, u, y son respectivamente los vectores de estado, de control y de salida medible del sistema perteneciendo
a IRn , IRm y IRp respectivamente. Las matrices A, B, C son matrices no conocidas que pertenecen a los conjuntos:
A ∈ A = {An + ∆A : ∆A ≤ ρ1 }
B ∈ B = {Bn + ∆B : ∆B ≤ ρ2 } (III.73)
C ∈ C = {Cn + ∆C : ∆C ≤ ρ3 }
donde · es una norma matricial cualquiera. Para la demostraci´n de la estabilizabilidad local supondremos que
o
el sistema (III.72) es estabilizable y detectable. La definici´n de detectabilidad cuadr´tica es dual de la estabilidad
o a
cuadr´tica y concierne al par (C T , AT ). As´ la detectabilidad cuadr´tica del par (C T , AT ) est´ definida por la
a ı, a a
existencia de una matriz de Lyapunov unica W = W T > 0 y de una ganancia L, de manera que:
´
(A − LC)T W + W (A − LC) < 0.
Recordemos que la estabilidad cuadr´tica est´ determinada por la existencia de P = P T > 0 y K tales que
a a
(A − BK)P + P (A − BK)T < 0
para todo el dominio de la incertidumbre.
Consideremos ahora un observador de Luenberger [ORe83] para el sistema III.72 “nominal”
z
˙ = An z + Bn u + L(y − Cn z)
(III.74)
u = −Kz
donde z ∈ IRn . Definiendo e = x − z, tenemos
e = (An − LCn + ∆B K)e + (∆A − ∆B K − L∆C )x.
˙ (III.75)
81](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-89-320.jpg)
![Sea ∆ = ∆A − ∆B K − L∆C , el sistema a lazo cerrado puede escribirse como:
x
˙ A − BK BK x
= (III.76)
e
˙ ∆ An − LCn + ∆B K e
donde, de acuerdo con nuestra hip´tesis de estabilidad y detectabilidad, las ganancias L y K son tales que existen
o
matrices P > 0 y W > 0 tales que
FS (P, A, B) = (A − BK)T P + P (A − BK) < 0; ∀A, B ∈ A, B
(III.77)
FO (W, A, C, ) = (A − LC)T W + W (A − LC) < 0; ∀A, C ∈ A, C.
Notamos que ∀α > 1,
FS (αP, A, B) < FS (P, A, B) y
(III.78)
FO (αW, A, C) < FO (W, A, C).
Podemos ahora caracterizar la estabilidad local del sistema (III.72).
Teorema III.8 ([CPM94]) Si el par incierto (A, B) es cuadr´ticamente estabilizable y el par incierto (C T , AT )
a
es cuadr´ticamente detectable, entonces siempre existe una vecindad alrededor de la tripleta (A n , Bn , Cn ) tal que
a
el sistema (III.72) es cuadr´ticamente estabilizable por un compensador de la forma (III.74).
a
Demostraci´n:
o
Supongamos que existe una matriz de Lyapunov del sistema (III.76) de la forma
˜
P 0
Pg = ˜ (III.79)
0 W
por lo tanto
T
A − BK BK
(xT eT ) Pg
∆ An − LCn − ∆B K
(III.80)
A − BK BK x
+Pg < 0,
∆ An − LCn − ∆B K e
lo que podemos escribir como
˜ ˜
xT {(A − BK)T P + P (A − BK)}x + eT {(An − LCn − ∆B K)T W ˜
˜ (An − LCn + ∆B K)}e + 2eT {K T B T P + W ∆}x < 0.
˜ (III.81)
+W
Sin embargo,
˜ ˜
(P BKe + x)T (P BKe + x) ≥ 0
y entonces
˜ ˜˜
2eT {K T B T P }x ≤ xT x + eT K T B T P P BKe (III.82)
teniendo adem´s que:
a
˜ ˜ ˜
2eT {W ∆}x ≤ xT x + eT W ∆∆T W e (III.83)
y de all´ que la desigualdad (III.80) se satisface si
ı
1) ˜ ˜
(A − BK)T P + P (A − BK) + 2I < 0 y
2) ˜ ˜ ˜˜
(An − LCn )T W + W (An − LCn ) + K T B T P P BK (III.84)
+W˜ ∆∆W + W ∆B K + K T ∆B W < 0.
˜ ˜ ˜
Pero dado que el sistema es estabilizable y detectable cuadr´ticamente, siempre existen β > 0, γ > 0 y ρ m > 0
a
tales que
(A − BK)T βP + βP (A − BK) + 2I < 0 y
(An − LCn )T γW + γW (An − LCn ) + β 2 K T B T P P BK+ (III.85)
ρm (γ 2 W ∆∆W + γW ∆B K + K T ∆B T γW ) < 0.
82](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-90-320.jpg)

![donde x ∈ IRn , u ∈ IRm e y ∈ IRp representan, respectivamente, los vectores de estado, control y salida medible.
A ∈ A, B ∈ B y C ∈ C donde A, B, C son subconjuntos poli´dricos no vac´ de IR n×n , IRn×m y IRp×n respectiva-
e ıos
mente. Los v´rtices de esos poliedros son {A1 , A2 , . . . , Ar }, {B 1 , B 2 , . . . , B s } y {C 1 , C 2 , . . . , C t }. D est´ definido
e a
como el poliedro en el que los v´rtices son todas las combinaciones posibles de la tripleta (A j , B k , C l ) con
e
j = 1, . . . , r, k = 1, . . . , s, l = 1, . . . , t. Para simplificar la notaci´n, indexaremos los v´rtices con i = 1, . . . , q,
o e
q = rst y en consecuencia D es el envoltorio convexo (Convex Hull Co) de las tripletas (A i , Bi , Ci ), es decir
D = Co{(Ai , Bi , Ci ), i = 1, . . . , q}.
Sea (Ac , Bc , Cc ) un punto cualquiera en D y finalmente definimos al subconjunto θ(·, ·) de D como
θ(D, ε) = Co {((1 − ε)(Ac , Bc , Cc ) + ε(Ai , Bi , Ci )) i = 1, . . . , q} 0 ≤ ε ≤ 1. (III.87)
Claramente, tenemos
θ(D, 0) = (Ac , Bc , Cc ) y
θ(D, 1) = D.
El problema que abordamos es el siguiente:
m´x ε
a
tal que el sistema
x = Ax + Bu
˙
y = Cx
(III.88)
z = F z + Gy
˙
u = −Kz
es cuadr´ticamente estable para todo (A, B, C) ∈ θ(D, ε), esto es, encontraremos matrices F ∈ IR n×n , G ∈ IRn×p
a
y K ∈ IRm×n que estabilizan el subconjunto “m´ximo” de D (y que medimos en este caso con la ayuda de ε).
a
El sistema III.88 puede ser escrito en funci´n de las variables
o
x
x=
˜ (III.89)
e
donde e = x − z, de la forma
˙ ˜ ˜˜˜
x = (A + B F C)
˜ (III.90)
donde
˜ A 0 ˜ 0 −B ˜ I −I ˜ F G
A= B= C= F = . (III.91)
A 0 −I −B C 0 K 0
˜
Por lo tanto el sistema es cuadr´ticamente estabilizable si y solamente si existen matrices W > 0 y F tales que
a
˜ ˜ ˜˜˜ ˜ ˜˜˜
H(F , W ) = (A + B F C)T W + W (A + B F C) < 0 (III.92)
˜ ˜ ˜ ˜ ˜
∀˜ ∈ IR2n y ∀(A, B, C) ∈ θ(D, ε). D definido como el poliedro
x
˜ ˜ ˜ ˜
D = Co {(Ai , Bi , Ci ), i = 1, . . . , q}
Ai 0 0 −Bi I −I (III.93)
˜
Ai = ˜
Bi = ˜
Ci = .
Ai 0 −I −Bi Ci 0
˜ ˜
Resaltamos que la funci´n H(F , W ) es biconvexa en F y W —es decir, convexa con respecto a una de las dos
o
˜ ˜ ˜ ˜
matrices una vez que la otra es fijada—. Adem´s, notamos que ∀(A, B, C) ∈ θ(D, ε),
a
q
˜ ˜˜˜ ˜ ˜˜˜
(A + B F C)T W + W (A + B F C) = ˜ ˜ ˜˜ ˜ ˜ ˜˜
αi [(Ai + Bi F Ci )T W + W (Ai + Bi F Ci )] (III.94)
i=1
q
donde αi ≥ 0 y αi = 1. Es, por lo tanto, suficiente (y necesario) que la condici´n (III.92) sea satisfecha en los
o
i=1
˜ ˜ ˜
v´rtices (Ai , Bi , Ci ), i = 1, . . . , q.
e
84](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-92-320.jpg)
![˜
Dada la convexidad del problema respecto a una de las variables (W o F ) cuando la otra se fija, el enfoque que
utilizaremos para determinar el domino m´ximo ser´ escoger un ε y una de las variables (por ejemplo W ) y luego
a a
˜
calcular la otra (F ) si es que ella existe y verifica (III.92). Al obtener una soluci´n, aumentamos ε y repetimos
o
˜
el procedimiento, e.g. fijamos F y calculamos una nueva matriz W . El proceso continua hasta el momento en
el que cualquier incremento de ε no permite calcular la variable que no hemos fijado, esto es, que el problema
convexo resultante al fijar una de las variables no tiene soluci´n. En ese momento tendremos un m´ximo local y
o a
˜
un controlador que estabiliza F ese m´ximo de incertidumbre [CGP96], [CGH95].
a
En este momento ya podemos exponer el algoritmo de c´lculo del controlador y el margen de robustez. Como se
a
ha dicho, la estrategia calcula un compensador o una matriz de Lyapunov usando los algoritmos a continuaci´n.
o
C´lculo de la din´mica del compensador
a a
e o ˜ ˜ ˜
Paso 0: Consideremos que los v´rtices de la regi´n incierta (Ai , Bi , Ci ), i = 1, . . . , q y que una matriz de
Lyapunov W son dados y sea
˜ ˜ ˜ ˜˜ ˜ ˜ ˜˜
Hi (F ) = (Ai + Bi F Ci )T W + W (Ai + Bi F Ci ). (III.95)
a u e ˜
M´s a´n, sea fij el elemento ij i-´simo de la matriz F que puede efectivamente ser diferente de cero.
˜0 una matriz inicial —por ejemplo, nula— y ζ 0 un subconjunto de IR(n+m)×(n+p)
Finalmente, sea k = 0, F
˜
compacto y “suficientemente grande” (de tal manera que F0 ∈ ζ 0 ).
Paso 1: Calcular el autovalor m´ximo
a
a a
˜
λk ax = m´x {λm´x (Hi (Fk )), i = 1, . . . , q}. (III.96)
m´
˜
Si λk ax < 0, pare: F es un compensador din´mico estabilizante —cuadr´ticamente— al sistema extendido,
a a
m´
si no vaya al paso 2.
˜
Paso 2: Sea vk el autovector asociado a λk ax y H k (F ) la funci´n Hi asociada al v´rtice correspondiente a
o e
m´
k ˜k+1 a trav´s del problema
λm´x . Calcular F e
a
m´ ρ
ın
tal que
−ρ ≤ fij ≤ ρ
˜ ˜
Fk+1 ∈ ζ k+1 = ζ k ∩ {vk T H k (F )vk < 0}.
Paso 3 : Hacer k = k + 1 y volver al paso 1.
C´lculo de la matriz de Lyapunov
a
e o ˜ ˜ ˜
Paso 0: Consideremos que los v´rtices de la regi´n incierta (Ai , Bi , Ci ), i = 1, . . . , q y un controlador
˜
din´mico F son dados y sea
a
˜ ˜ ˜˜ ˜ ˜ ˜˜
Hi (W ) = (Ai + Bi F Ci )T W + W (Ai + Bi F Ci ), i = 1, . . . , q
(III.97)
Hq+1 (W ) = −W.
M´s a´n, sea k = 0, W0 la matriz identidad y ζ 0 un subconjunto compacto de IR2n×2n “suficientemente
a u
grande”, tal que W0 ∈ ζ 0 .
Paso 1: Calcular el autovalor m´ximo
a
λk ax = m´x {λm´x (Hi (W )), i = 1, . . . , q + 1}.
m´ a a (III.98)
Si λk ax < 0 pare: W es un matriz de Lyapunov, si no vaya al paso 2.
m´
85](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-93-320.jpg)
![Paso 2: Sea vk el autovector asociado a λm´x y H k (W ) la funci´n Hi (W ) asociada al v´rtice correspondiente
k
a o e
k
a λm´x . Calcular Wk+1 a trav´s de
a e
m´ Tr(W )
ın
tal que
Wk+1 ∈ ζ k+1 = ζ k ∩ {vk T H k (W )vk < 0}.
Paso 3: Haga k = k + 1 y vuelva al paso 1.
Algunas observaciones a prop´sito de los algoritmos propuestos
o
Observemos que en los dos algoritmos propuestos los v´rtices de la regi´n de incertidumbre son calculados a
e o
partir de (III.87) para valores crecientes de ε.
Los dos algoritmos explotan igualmente la naturaleza convexa del problema que queda cuando una de las
variables se fija en un valor. En ambos casos generamos hiperplanos de corte que excluyen el punto no factible
˜
(Fk o Wk ), obteniendo de esta manera un subconjunto reducido.
En todos los casos podemos asegurar convergencia hacia una soluci´n si el paso 2 es reemplazado por:
o
ζ k+1 = ζ k ∩ {vk T H k (.)vk ≤ −γ} (III.99)
con γ > 0 “suficientemente peque˜a”. La escogencia de una regi´n inicial ζ “suficientemente grande” no presenta
n o
ninguna dificultad pr´ctica. En general podemos escoger todo el espacio (abierto) y luego de un n´mero peque˜o
a u n
de iteraciones se generar´ una regi´n ζ compacta, siendo ´sta lo que necesitamos para asegurar la convergencia
a o e
que demostraremos un poco m´s adelante.
a
˜
A fin de asegurar el ´xito, los dos algoritmos deben disponer de una de las dos variables (W o F ) y de la
e
certidumbre que esa variable funcionar´ para un dominio de incertidumbre ligeramente m´s grande que aquel
a a
para el que ella fue calculada (teorema III.8), en tanto que ´l sea un subconjunto de D.
e
Para iniciar el algoritmo debemos, sin embargo, tener un compensador o una matriz de Lyapunov. Si el
sistema es cuadr´ticamente estabilizable y detectable siempre podemos construir un compensador estabilizante
a
del sistema cierto, de la forma expuesta en (III.74) y con las ganancias L y K calculadas del problema convexo
asociado. Por otra parte, es f´cil demostrar con las mismas hip´tesis —detectabilidad y estabilizabilidad— que
a o
bajo la representaci´n (xT eT )T siempre existe una matriz de Lyapunov de la forma
o
P 0
(III.100)
0 αW −1 − P
para todo α ≥ k para una cierta k > 0.
En ambos casos disponemos de valores que nos permiten inicializar los procedimientos de c´lculo.
a
La estrategia propuesta en III.9 puede igualmente utilizarse para determinar el margen de robustez de un
controlador dado de un sistema. Este t´pico ha sido tambi´n estudiado por un n´mero de autores —[Yed86],
o e u
[YL86], [Soh94], [HL93]— siendo las cotas superiores de la incertidumbre dada. La estrategia presentada en III.9
calcula el l´
ımite de robustez (cuadr´tica) de tal compensador.
a
Hay que se˜alar que el enfoque num´rico precedente no impone de ninguna manera la restricci´n de diagonali-
n e o
dad en bloques de la matriz de Lyapunov, y esta forma se utiliza unicamente para demostrar que la estabilidad en
´
una cierta vecindad es verificada. Por otra parte, esta forma diagonal es util para la inicializaci´n del algoritmo.
´ o
En fin, con respecto a la implementaci´n num´rica del algoritmo, el enfoque general propuesto ha sido ilus-
o e
trado usando t´cnicas de hiperplanos de corte y programaci´n lineal, y debe remarcarse que tal enfoque puede
e o
igualmente ser realizado utilizando LMIs y t´cnicas de punto interior.
e
86](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-94-320.jpg)
![Convergencia del esquema iterativo
Sea ζ el conjunto factible; la convergencia de los algoritmos propuestos est´ asegurada por los hechos siguientes:
a
El conjunto —compacto— de b´squeda ζ k se reduce de iteraci´n a iteraci´n. En efecto,
u o o
ζ ⊂ . . . ⊂ ζ k+1 ⊂ ζ k . (III.101)
El algoritmo genera un problema de optimizaci´n (minimizaci´n) en conjuntos en los que la talla se reduce
o o
y que son todos incluidos en el precedente; por ejemplo, lo que implica la existencia de un punto l´
ımite si
el conjunto inicial ζ no est´ vac´ [Hof81].
a ıo
En la iteraci´n k se a˜ade la restricci´n
o n o
vk T H k (.)vk ≤ −γ (III.102)
para γ > 0 dada “suficientemente peque˜a”. Esta restricci´n ser´, de seguro, satisfecha para cualquier
n o a
soluci´n obtenida por los algoritmos en la iteraci´n l > k, es decir
o o
vk T H k (Sl )vk ≤ −γ (III.103)
donde Sl = Wl o Fl en funci´n del problema que estemos resolviendo en la iteraci´n l. (III.103) se puede
o o
escribir
λm´x (Sk ) − vk T H k (Sl − Sk )vk ≤ −γ.
k
a (III.104)
Dada la existencia de un punto l´
ımite,
l´ vk T H k (Sl − Sk )vk = 0
ım (III.105)
l,k→∞
y, por lo tanto, si S = l´ k→∞ Sk ,
ım
λk ax (S) ≤ −γ.
m´ (III.106)
Si el conjunto factible ζ(= l´ k→∞ ζ k ) no est´ vac´ tenemos que S ∈ ζ.
ım a ıo,
Si el conjunto factible es vac´ existir´ una iteraci´n l para la que ζ l ser´ vac´
ıo a o a ıo.
Sobre las condiciones de estabilizabilidad y detectabilidad cuadr´tica
a
En la secci´n precedente hemos propuesto algoritmos que requieren de un punto inicial de partida, por ejemplo,
o
un compensador estabilizante del sistema nominal. Ahora bien, un punto inicial se puede calcular a partir de
(III.77) si el sistema es cuadr´ticamente estabilizable y detectable. Recordamos ahora que las condiciones de
a
estabilizabilidad y detectabilidad son necesarias para la existencia de un controlador din´mico del sistema III.72
a
a lazo cerrado.
En efecto, el sistema (III.88) es cuadr´ticamente estabilizable si existe una matriz:
a
P1 P2
P = > 0,
P2 T P3
tal que:
T
A −BK P1 P2 P1 P2 A −BK
+ <0 (III.107)
GC F P2 T P3 P2 T P3 GC F
∀(A, B, C) ∈ D. En consecuencia, el bloque (1,1) de la desigualdad (III.107) debe igualmente ser definido negativo,
i.e.,
AT P1 + P1 A + P2 GC + C T GT P2 T < 0,
87](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-95-320.jpg)
![lo que es equivalente a la detectabilidad cuadr´tica del sistema III.72.
a
Para demostrar la necesidad de la estabilizabilidad procedemos de manera similar sobre el sistema dual, ya
que:
˜ ˜˜˜ ˜ ˜˜˜ ˜ ˜˜˜ ˜ ˜˜˜
(A + B F C)W + W (A + B F C)T < 0 ⇐⇒ (A + B F C)T P + P (A + B F C) < 0
donde P = W −1 . Por lo que tambi´n se debe cumplir que:
e
T
A −BK W1 W2 W1 W2 A −BK
T + T <0
GC F W2 W3 W2 W3 GC F
∀(A, B, C) ∈ D. El bloque (1, 1):
AW1 + W1 AT − BKW2 − W2 K T B T < 0
T
traduce la condici´n de estabilizabilidad.
o
Ejemplos num´ricos
e
En los ejemplos que siguen consideraremos sistemas de la forma:
x = Ax + Bu
˙
(III.108)
y = Cx.
En todos los casos iniciamos el proceso iterativo con un compensador din´mico que estabiliza el sistema sin
a
incertidumbre.
Primer ejemplo
Consideremos al sistema tomado de [CPM94] con 4 par´metros inciertos, a saber q 1 , q2 , q3 y q4 .
a
−1 + q1 + 0,3q4 0,1q4 0,1q4 −q3 + 0,01q4
A= 1 − q1 1 1 B= 1 + q3
4 − q 1 + q2 2 + q2 1 1 + q3
T
2 + 0,003q4
C = 1 + 0,001q4 .
1 + 0,001q4
Para −0,3 ≤ q1 , q2 ≤ 0,3, −0,66 ≤ q3 , q4 ≤ 0,66. El algoritmo converge en las matrices siguientes:
−9,4837 −17,6611 −8,2820 −5,4260
F = −17,6611 −14,3579 −17,2162 G = 17,2915
−10,5445 −7,8590 −11,1210 9,6483
T
10,0238
K = 14,0324
9,8226
y el autovalor m´ximo sobre el conjunto de todos los v´rtices es: −0,0014. El lugar de las ra´
a e ıces para una
discretizaci´n de la incertidumbre se muestra en la figura III.6:
o
88](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-96-320.jpg)
![10
8
6
4
2
0
−2
−4
−6
−8
−10
−18 −16 −14 −12 −10 −8 −6 −4 −2 0
Figura III.6.: Lugar de los polos para −0,3 ≤ q1 , q2 ≤ 0,3 y −0,66 ≤ q3 , q4 ≤ 0,66.
Segundo ejemplo
Se trata de un sistema presentado en [HF93] con un solo par´metro incierto k, constituido por las matrices
a
T
−1 + 5k −1 − 2k 1+k −3k
A= B= C= .
−8k 2 + 3k −3 1+k
Con |k| ≤ 1,145, el algoritmo converge a las matrices
T
−5,4819 5,0269 −5,4708 2,0472
F = G= F =
5,2405 −5,4819 5,4819 −1,0203
y el autovalor m´ximo sobre el conjunto de v´rtices es −0,0104. El lugar de las ra´
a e ıces del sistema a lazo cerrado
para una discretizaci´n del rango de la incertidumbre se muestra en la figura III.7.
o
15
10
5
0
−5
−10
−15
−14 −12 −10 −8 −6 −4 −2 0
Figura III.7.: Lugar de las ra´
ıces de una discretizaci´n del rango de incertidumbre.
o
Aplicaciones pr´cticas del esquema presentado, espec´
a ıficamente al control del pH y de procesos de neutraliza-
ci´n, pueden encontrarse en [CGP98] y [PCG97].
o
89](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-97-320.jpg)

![CAP´
ITULO IV
Sintonizaci´n robusta de controladores industriales
o
IV.1. Introducci´n
o
En la ultima d´cada la teor´ de control robusto ha experimentado avances considerables, alcanzando un
´ e ıa
elevado grado de madurez [MZ89], [Bar94]. La teor´ es particularmente atractiva, ya que, como hemos mostrado
ıa
en cap´ıtulos anteriores, permite considerar de manera expl´
ıcita los elementos desconocidos que afectan al lazo
de control, esto es, perturbaciones externas y/o imperfecciones de modelado, que en adelante denominaremos
incertidumbre.
Sin embargo, y a pesar de lo poderosa que puede resultar esta teor´ para la s´
ıa ıntesis de controladores, son muy
pocas las aplicaciones industriales que funcionan actualmente. La raz´n es que, en la mayor´ de los casos, los
o ıa
controladores robustos calculados son de orden elevado y poseen estructuras dif´ ıciles de implementar o manipular
por el operador. En contraste, el muy conocido controlador proporcional, integral, derivativo (PID), se ha con-
vertido en el est´ndar de facto para el control de lazos de una entrada y una salida (SISO), siendo sumamente
a
familiar su manipulaci´n (entonamiento) para los t´cnicos de control y operadores del sistema [Ast02]. Aparte
o e
de su versatilidad y amplio espectro de uso que va desde aplicaciones en procesos qu´ ımicos hasta la avi´nica y
o
aeron´utica [GCS01], este controlador incorpora elementos atractivos en el lazo de control como son: robustez,
a
eliminaci´n de error y perturbaci´n estacionaria. El ajuste de sus tres par´metros, sin embargo, no es transparente
o o a
y ha sido objeto numerosos estudios ([ZN42],[AH95], [RMS86], [Sko03], [HHC95]).
En este cap´ ıtulo se proponen dos metodolog´ para la sintonizaci´n (entonaci´n) de controladores PID. La
ıas o o
primera se basa en un peque˜o cambio en las variables de estado, incorporando la integral de la salida como una
n
de ellas, y en un esquema iterativo, denominado ILMI que explota la naturaleza bilineal del problema resultante.
Una segunda se basa en el controlador multiobjetivo (robusto) obtenido para el mismo lazo. Notablemente, el
controlador PID tratar´ de aproximar las caracter´
a ısticas frecuenciales del controlador robusto, y en este ultimo
´
caso las prestaciones del lazo s´lo pueden verificarse a posteriori.
o
En el enfoque frecuencial, como en la mayor´ de los controladores PID comerciales, se cuenta tambi´n con un
ıa e
filtro a la salida del PID, y para mejorar la aproximaci´n del PID al controlador robusto nuestro dise˜o incorpora
o n
el filtro al PID en serie.](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-99-320.jpg)
![Para facilitar la comprensi´n de las ideas que se proponen, se ha escogido aplicar esta metodolog´ a varios
o ıa
casos de estudio, en el caso de las ILMI compar´ndola con los resultados presentados en [Sko03] y en el caso
a
frecuencial a un esquema de control de presi´n de una tuber´ de gas, siendo la variable manipulada el flujo de
o ıa
gas que se alivia a un mechurrio para lograr el objetivo de control. Para todos los sistemas en estudio se dispone
de un buen modelo, aunque el enfoque ILMI puede igualmente aceptar incertidumbre en la matriz de din´mica a
del sistema [GCB03].
En este cap´ıtulo consideraremos un lazo de control de una entrada y una salida como el que se muestra en la
figura (IV.1).
Figura IV.1.: Lazo cerrado de control.
IV.2. Los algoritmos PID
En general hablamos de controladores PID, porque cada controlador tiene una componente proporcional, una
integral y una derivativa, pero su estructura puede variar. Las expresiones m´s comunes son:
a
PID paralelo. En t´rminos de la expresi´n temporal.
e o
1 de(t)
u(t) = Kp (e(t) + e(t)dt + Td ) (IV.1)
Ti dt
donde e(t) es la se˜al de error (ver figura IV.1) y
n
PID interactivo. En t´rminos de la funci´n de transferencia.
e o
1
U (s) = Kp (1 + )(1 + Td s)E(s) (IV.2)
Ti s
Es posible pasar de una forma a la otra, siempre que el polinomio: Ti Td s2 + Ti s + 1, tenga ra´ reales [DM95].
ıces
De igual forma, pueden encontrase ligeras variaciones sobre las estructuras antes mencionadas para resolver pro-
blemas espec´ ıficos como saturaci´n y evitar que cambios en la consigna afecten sensiblemente al controlador,
o
entre otros [Ast02].
Para el c´lculo de los par´metros del PID mediante LMIs, hemos considerado la forma paralela o ideal (IV.1),
a a
en el entendido de que la mayor´ de los controladores industriales aceptan esta estructura y que si no fuese el
ıa
caso, en general se puede pasar de una forma a la otra.
IV.3. PID v´ LMIs iterativas
ıa
En esta secci´n desarrollaremos una estrategia de c´lculo de los par´metros (K p , Ti , Td ) basada en LMIs,
o a a
siguiendo la estrategia propuesta en [CLS98]. Para ello consideremos el sistema:
x(t) = Ax(t) + Bu(t)
˙
(IV.3)
y(t) = Cx(t)
92](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-100-320.jpg)

![Paso 1: Dado Pi , determine Ki y α∗ de la forma:
α∗ = m´ α
ın (IV.9)
sujeto a:
(A + BKi C)Pi + Pi (A + BKi C)T − αPi < 0; Pi > 0. (IV.10)
Si α ≤ 0 habremos encontrado una ganancia Ki que estabiliza al sistema, si no, vaya al paso 2.
Paso 2: Dado Ki y un borde superior α∗ que es el valor de α obtenido en el paso 1, calcule Pi+1 y un nuevo
α ´ptimo (ˆ ), partir de:
o α
α = m´ α
ˆ ın (IV.11)
sujeto a:
(A + BKi C)Pi+1 + Pi+1 (A + BKi C)T − αPi+1 < 0; Pi+1 > 0. (IV.12)
Si α ≤ 0, entonces Ki es una ganancia estabilizante y si no haga i = i + 1 y vaya al paso 1.
ˆ
Debemos ahora realizar algunos comentarios a prop´sito del algoritmo.
o
Observaci´n IV.1 El algoritmo propuesto est´ basado en el hecho de que la condici´n de Lyapunov, que asegura
o a o
la estabilidad para el sistema con realimentaci´n est´tica de la salida (IV.7), es bilineal en las inc´gnitas K y P ,
o a o
y por ende, cuando una se fija, lo que resulta es una desigualdad matricial lineal (LMI) en la otra variable y, en
consecuencia, un problema convexo.
Observaci´n IV.2 En el paso 0, lo que hacemos es suministrar al algoritmo un punto de arranque, a partir
o
de la condici´n de estabilidad con realimentaci´n de los estados, que es una LMI en P y R(= K −1 P ). Si no
o o
existe tal matriz P que asegure estabilidad con realimentaci´n de estados, tampoco existir´ un PID que haga el
o a
trabajo. Observe que en el paso 0 simplemente damos un punto de inicio a partir de una condici´n necesaria, pero
o
hubi´ramos podido arrancar desde otro punto, e.g., desde la matriz P asociada a un PID ajustado por Ziegler y
e
Nichols, que sabemos estabiliza al sistema original.
Observaci´n IV.3 En el paso 1, conocida una matriz Pi , se inicia la b´squeda de una ganancia Ki que pudiera
o u
estabilizar al sistema. Ella (Ki ) ser´ una ganancia estabilizante, si la soluci´n del problema (convexo) de opti-
a o
mizaci´n que se formula en el paso 1 termina con un valor de α ∗ ≤ 0. Observe que el problema en el paso 1 es
o
una LMI en las inc´gnitas (Ki , α).
o
Observaci´n IV.4 En el paso 2, conocida una ganancia Ki , lo que se busca es verificar si ella es, en efecto, una
o
ganancia estabilizante, lo que se certifica si la condici´n (IV.12) es satisfecha o, lo que es lo mismo, se obtiene
o
una matriz Pi+1 . Observe igualmente que la condici´n (IV.12) es biconvexa en α y P i+1 ; sin embargo, siendo α
o
un escalar y conociendo un l´ ımite superior (α∗ ) es f´cil obtener ese m´
a ınimo de α porque (siendo escalar) s´lo
o
tiene una forma de descenso. Luego, en el paso 2 lo que se hace es fijar el α en un valor, resolver la LMI para
Pi+1 y si tiene soluci´n se hace α m´s peque˜o y, si no, se vuelve al paso 1.
o a n
Observaci´n IV.5 La satisfacci´n de la condici´n (IV.10) o la (IV.12) no s´lo asegura una ganancia estabili-
o o o o
zante sino que adem´s da una medida de calidad del controlador obtenido, ya que su satisfacci´n garantiza que
a o
los polos del sistema a lazo cerrado est´n ubicados a la izquierda de α/2 [SGC97].
e
Observaci´n IV.6 En el paso 2, no se requiere calcular el m´
o ınimo de α; bastar´ verificar que con α = 0 se
ıa
satisface (IV.12), lo que certificar´ la estabilidad. Se ha incluido el m´
ıa ınimo, s´lo para determinar la bondad
o
del controlador medido como lo descrito en el comentario anterior (IV.5). De hecho, en algunas circunstancias
y para ubicar un mejor PID y evitar los problemas num´ricos, no se vuelve al paso 1 con la P i+1 asociada al
e
m´ınimo sino m´s bien con una menos extrema.
a
94](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-102-320.jpg)
![Observaci´n IV.7 La variable escalar α asegura que los problemas formulados en los pasos 1 y 2 siempre
o
tendr´n soluci´n. Ello no asegura, sin embargo, que siempre se encontrar´ un PID estabilizante. El algoritmo
a o a
falla en encontrar un PID si α∗ , α ≥ 0 y |α∗ − α| ≤ ε, con ε un valor predeterminado de convergencia.
ˆ ˆ
Observaci´n IV.8 Por ultimo, este algoritmo puede igualmente ser aplicado para el c´lculo de controladores
o ´ a
PI de sistemas continuos y discretos, para sistemas multivariables y para sistemas con incertidumbre poli´drica
e
o acotada en norma en las matrices A y C del sistema original (v´ase [Pet87] y [BGP89] para la definici´n de la
e o
incertidumbre y [GCB03] para las extensiones referidas).
IV.5. Comparaci´n de t´cnicas de entonaci´n
o e o
En esta secci´n, hacemos una comparaci´n de la estrategia de entonaci´n ILMI presentada en la secci´n anterior
o o o o
(secci´n (IV.4)) con otras t´cnicas ampliamente conocidas.
o e
Hemos escogido dos casos tomados de [Sko03]. Ellos son: uno de fase no m´
ınima y otro con retardo. En [CMR05]
pueden encontrarse comparaciones m´s detalladas del enfoque propuesto con otros y en [GCB03] la extensi´n a
a o
sistemas multivariables.
Debemos se˜alar que en el caso de los m´todos de IMC y de Ziegler y Nichols, al igual que para la mayor´ de
n e ıa
los m´todos de ajuste de PIDs, aunque se da una funci´n de transferencia del sistema para los ejemplos num´ricos,
e o e
la misma es ajustada, sea a una de primer orden m´s retardo o a una de segundo orden m´s retardo. En el caso
a a
de ajuste con LMIs que hemos propuesto, la unica simplificaci´n realizada es la aproximaci´n del retardo a una
´ o o
de Pade de primer orden. Ello porque el m´todo se basa en una representaci´n en variables de estado.
e o
A continuaci´n presentamos los resultados para cada caso.
o
Fase no m´
ınima
La funci´n de transferencia del sistema es:
o
(1 − 0, 3s)(1 + 0, 08)
G2 (s) = (IV.13)
(2s + 1)(s + 1)(0, 4s + 1)(0, 2s + 1)(0, 05s + 1)3
El ajuste de los par´metros por los diferentes m´todos se muestra en la tabla (IV.1).
a e
M´todo
e Kp Ki Kd
LMI1 2,092 0,5543 2,0673
IMC2 1,3 0,65 1,56
Z & N2 2,56 0,966 1,6896
Tabla IV.1.: Par´metros de los PID de la fase no m´
a ınima.
(1 ) PID paralelo y (2 ) PID interactivo.
En la figura (IV.2) se muestran los resultados del sistema para una perturbaci´n tipo escal´n unitario, aplicada
o o
a los 30 segundos.
Los m´rgenes de fase y de ganancia comparados se muestran en la tabla (IV.2).
a
95](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-103-320.jpg)
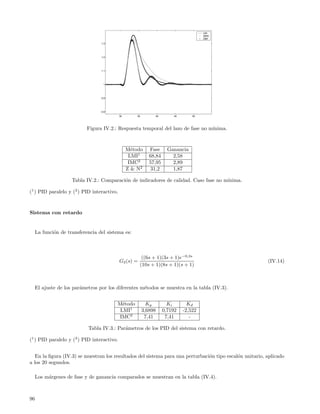
![LMI
1.25 SIMC−PI
1.2
1.15
1.1
1.05
1
0.95
0.9
0.85
0.8
15 20 25 30 35 40 45
Figura IV.3.: Respuesta temporal del sistema con retardo.
M´todo
e Fase Ganancia
LMI1 78,47 1,58
IMC-PI 51,67 3,05
Tabla IV.4.: Comparaci´n de indicadores de calidad. Caso retardo.
o
IV.6. Enfoque frecuencial
En esta secci´n presentamos el enfoque frecuencial al c´lculo de PIDs, y ello lo haremos con un caso de estudio.
o a
Primero presentamos el modelo del sistema a considerar, en la secci´n siguiente se calcula el controlador y el PID
o
aproximado y finalmente en la ultima secci´n, para fines de comparaci´n, el PID calculado se compara con uno
´ o o
entonado por Ziegler-Nichols [ZN42].
El sistema que consideraremos tiene la siguiente funci´n de transferencia:
o
−0,7136 −s
G(s) = e (IV.15)
s+1
sobre este sistema se desea que no tenga offset a cambios en la entrada tipo escal´n (salto) y que sea r´pido en su
o a
respuesta (que se medir´ como un tiempo de respuesta inferior a 10 seg.). Todas las especificaciones impuestas son
a
muy comunes para lazos de control. Una especificaci´n adicional fue que el sistema se vea poco afectado (rechace)
o
por perturbaciones que entran al sistema de la misma forma que el control. Esta ultima especificaci´n, de tipo
´ o
robusto, toma en cuenta cambios en la presi´n del sistema producto de agentes externos, como movimientos en
o
la demanda, etc.
Para eliminar el offset “a priori” se incluye un integrador 1 en la trayectoria directa del lazo, de esta manera
s
se dise˜ar´ un compensador para el sistema (G(s)) que ha incorporado de manera directa el integrador. Una
n a
vez calculado el control robusto, el compensador final ser´ el control robusto m´s el integrador. El problema se
a a
muestra esquem´ticamente en la figura IV.4.
a
Todo el dise˜o de controladores robustos se realiza en el ´mbito de los sistemas lineales y en representaci´n
n a o
de variables de estado, por lo tanto, el retardo del sistema —e−s — es modelado como un sistema lineal con una
aproximaci´n de Pade de 1er orden [Kuo95]:
o
1 − 0,5s
e−s = .
1 + 0, 5s
97](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-105-320.jpg)
![w
∧
r(s) u -0.7136 e -s y(s)
Control 1/s
s+1
(-)
Figura IV.4.: Esquema con integrador.
Con esta representaci´n del retardo, el sistema lineal resulta:
o
−3 −2 0 0
x =
˙ x+ u+ w
1 0 1 1
y = [0,7136 − 1,4271]
al incluir el integrador el sistema “aumentado” resulta:
−3 −2 0 0 0
xa = 1
˙ 0 1 xa + 0 u + 1 w
ˆ
0 0 0 1 0
(IV.16)
Aa Ba Bp
y = [0,7136 − 1,4272 0] xa con
Ca
x
xa =
u
y u como en la figura IV.4.
ˆ
El objetivo de rapidez de respuesta puede traducirse en que todos los polos del sistema compensado est´n a
e
la izquierda de un cierto valor, en este caso se impuso a la izquierda de −1. De igual manera, el objetivo de
atenuaci´n a las perturbaciones w puede ser descrito como:
o
Twz ∞ <1
esto es, que la norma infinita de la funci´n de transferencia entre w y y sea menor que 1. M´s adelante formali-
o a
zaremos las condiciones que deben cumplirse, pero antes debemos describir el tipo de control que ser´ utilizado,
a
a saber:
x c = A c xc + B c y
˙
(IV.17)
u = Cc xc + Dc u.
ˆ
El sistema a lazo cerrado resulta:
xa
˙ A a + B a Dc Ca B a Cc xa Bp
= + w
xc
˙ B c Ca Ac xc 0
A B (IV.18)
xa
y = [Ca 0] .
xc
C
Para satisfacer las condiciones de dise˜o se debe cumplir que exista una matriz X definida positiva tal que:
n
AX + XAT + 2 · 1 · X < 0 Condici´n de rapidez
o
AX + X T + BB T XC T
<0 Condici´n de atenuaci´n
o o
CX −I
98](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-106-320.jpg)
![Evidentemente, las ecuaciones no son lineales en ambos, la matriz de Lyapunov X y los par´metros del
a
compensador IV.17. Con una transformaci´n de variable apropiada, que describimos en el cap´
o ıtulo 2 (ver tambi´n
e
[SGC97]), pueden determinarse —con operaciones lineales y a trav´s de variables intermedias— A c , Bc , Cc y
e
Dc . El “LMI Tooolbox” de Matlab [GNL95] puede de manera est´ndar calcular esas matrices para el sistema
a
mencionado —funci´n hinfmix— en vista de que no hay incertidumbre en el sistema.
o
Al aplicar ese toolbox el resultado obtenido es:
−21,4544 −0,6575 59,2912
Ac = −26,1471 −30,3823 −166,9874
95,9493 32,5594 −84,0687
11,5249
Bc = 15,41,42 Cc = [0,3007 38,3535 357,8518]
−56,3364
y Dc = −0,1882. La funci´n de transferencia del controlador resulta:
o
0,188s3 + 19,519 × 103 s2 + 59,589 × 103 s + 40,704 × 103
Gc (s) = .
s3 + 136s2 + 4,741 × 103 s + 37,101 × 103
Incorporando el integrador al controlador y cambiando el signo del numerador —por la tradici´n hist´rica de que
o o
la realimentaci´n sea negativa— resulta, en el compensador multiobjetivo:
o
0,188s3 + 19,519 × 103 s2 + 59,589 × 103 s + 40,704 × 103
Gc (s) = −
s4 + 136s3 + 4,741 × 103 s2 + 37,101 × 103 s
La respuesta ante una entrada escal´n de este sistema se muestra en la figura IV.5:
o
1.4
1.2
1
Salida del lazo (y(t))
0.8
0.6
0.4
0.2
0
0 1 2 3 4 5 6 7 8 9 10
Tiempo (s)
Figura IV.5.: Respuesta con control robusto.
El diagrama de Bode de magnitud se muestra en la figura IV.6.
En la representaci´n de magnitud, se puede observar el efecto del integrador en las bajas frecuencias y que
o
(aproximadamente) las frecuencias de w = 1 y w = 100 son puntos significativos en los que obviamente existen
un cero y un polo, respectivamente, en la descripci´n del sistema. Teniendo en cuenta que un controlador (PI +
o
F) posee una funci´n de transferencia de la forma:
o
s+z
GP I+F = Kc
s(s + p)
99](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-107-320.jpg)
![20
0
Magnitud (dB) a lazo abierto. |Gn(jω)Gc(jω)|
−20
−40
−60
−80
−100
−1 0 1 2 3
10 10 10 10 10
Frecuencia (rad/s)
Figura IV.6.: Respuesta frecuencial del lazo.
se escogieron z = 1 y p = 100 para la aproximaci´n. La ganancia Kc del compensador se calcul´ de tal manera
o o
que el diagrama de magnitud coincida en bajas frecuencias. Ello se logra haciendo K c = 100.
El controlador obtenido resulta:
s+1
GP I+F = −100
s(s + 100)
y la respuesta que se obtiene del sistema se puede observar en la figura IV.7.
1.4
1.2
Salida del lazo (y(t)) con controlador PI
1
0.8
0.6
0.4
0.2
0
0 1 2 3 4 5 6 7 8 9 10
Tiempo (s)
Figura IV.7.: Respuesta con PI+F robusto.
A fin de evaluar el desempe˜o de controlador calculado GP I+F contra uno de selecci´n est´ndar, se sintoniz´ por
n o a o
Ziegler-Nichols [ZN42] un PID para el sistema en cuesti´n, obteni´ndose:
o e
s + 0,3
GZN = −1,26
s
y cuyo desempe˜o se muestra en la figura IV.8.
n
100](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-108-320.jpg)






![Bibliograf´
ıa
[AA90] A. Abdul-Amir y A. Abdul-Wahab, “Lyapunov Bounds for Root Clustering in the Presence of System
Uncertainty”, International Journal of Systems Science, Vol. 21(12), pp. 2.603–2.611, 1990.
[AK01] S. Ahmed y M. Krumpelt, “Hydrogen from hydrocarbon fuels for fuel cells”, International Journal of
Hydrogen Energy, Vo. 26, pp 291-301, 2001.
[AM89] B.D.O. Anderson y J.B. Moore, Optimal Control: Linear Quadratic Methods, Prentice-Hall Interna-
tional Editions, 1989.
[Ast02] K. J. Astrom, “Control System Design. Lecture Notes”, Dpt. Mech. and Envirom. Eng., U. of Cali-
fornia. (2002) http://www.cds.caltech.edu/ murray/courses/cds101/fa02/caltech/astrom.html.
[AH95] K. Astrom y T. Hagglung, PID controllers: theory, design and tunning, 2da Edici´n ISA, 1995.
o
[BA95] A. Banerjee y Y. Arkun, “H∞ control of nonlinear processes using multiple linear models”, Proceedings
of European Control Conference, Roma, 1995.
[Bar83] B.R. Barmish, “Stabilization of Uncertain Systems via Linear Control”, IEEE Transactions on Auto-
matic Control, Vol. 28(8), pp. 848–850, 1983.
[Bar85] B.R. Barmish, “Necessary and Sufficient Conditions for the Quadratic Stability of an Uncertain Sys-
tem”, Journal of Optimization Theory and Application, Vol. 46(4), pp. 399–408, 1985.
[Bar94] B.R. Barmish, New Tools for Robustness of Linear Systems, Maxwell Macmillan International, 1994.
[BB88] A. Benzaouia y C. Burgat, “Regulator problem for linear discrete-time systems with non symmetrical
constrained control”, International Journal of Control, Vol. 48(6), pp. 2.441–2.451, 1988.
[BGP89] J. Bernussou, J.C. Geromel y P.L.D. Peres, “A Linear Programming Oriented Procedure for Quadratic
Stabilization of Uncertain Systems”, Systems and Control Letters, Vol. 13, pp. 65–72, 1989.
[Boy94] S. Boyd, L. El Ghaoui, E. Feron y V. Balakrishnan, Linear Matrix Inequalities in Systems and Control
Theory, SIAM Studies in Applied Mathematics, Vol. 15, 1994.
[CLS98] Y.-Y. Cao, J. Lam, y Y.-X. Sun, “Static Output Feedback Stabilization: An ILMI Approach”, Auto-
matica, Vol. 34, pp. 1.641–1.645, 1998.
[CP72] S.S.L. Chang y T.K.C. Peng, “Adaptive Guaranteed Cost Control of Systems with Uncertain Para-
meters”, IEEE Transactions on Automatic Control, Vol. AC-17(4), pp. 474–483, 1972.
107](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-115-320.jpg)
![[ChG96] M. Chilali y P. Gahinet, “H∞ Design with pole placement constraints: an LMI approach”, IEEE
Transactions on Automatic Control Vol. 41(3), pp. 358–367, 1996.
[ChS92] R. Chiang y M. Safonov, Robust Control Toolbox for Use with MATLAB: User’s Guide, The Math
Works Inc., 1992.
[CGY98] W. Colmenares, K. Garrido, A. Yong, E. Granado y O. P´rez, “Sintonizaci´n robusta de controladores
e o
PID”, Memorias III Jornadas Panamericanas de Automatizaci´n, Caracas, mayo 1998. Tambi´n en
o e
InTech Venezuela, diciembre 1998.
[CGP98] W. Colmenares, E. Granado, O. P´rez y F. Tadeo, “Robust Multimodel Control of a pH Process”,
e
Proceedings of II World Automation Congress, Anchorage, Alaska, mayo 1998.
[CGP97] W. Colmenares, E. Granado, O. P´rez y K. Garrido, “H∞ control of Systems with Norm Bounded
e
Uncertainties”, Proceedings of IASTED International Conference in Control (Control ´97), Cancun,
M´xico, mayo 1997.
e
[CGP96] W. Colmenares, E. Granado, O. P´rez y K. Garrido, “Synthesis and Robustness Evaluation Of Dy-
e
namic Controllers for Uncertain Systems”, Proceedings of III IEEE International Conference on Elec-
tronics, Circuits and Systems, Rodas, Grecia, octubre 1996.
[CGH95] W. Colmenares, E. Granado, D. Henrion, J. Bernussou y O. P´rez, “Synthesis of Feedback Controllers
e
for Uncertain Discrete Linear Systems by Linear Programming”, Proceedings of 4 th IFAC Symposium
on Low Cost Automation, Buenos Aires, Argentina, septiembre 1995.
[CH95] W. Colmenares y D. Henrion, “Necessary Conditions and Sufficient Conditions for the Quadratic
Stabilization by Dynamic Feedback of a Class of Uncertain Systems”, Proceedings of Latin American
Seminar on Advanced Control, Santiago, 1995.
[CMR05] W. Colmenares, E. Mata, S. Revollar, E. Granado y O. P´rez, “Entonaci´n de controladores indus-
e o
triales tipo PID”, Revista Ciencia e Ingenieria, ULA, 2005.
[CP99] W. Colmenares y O. P´rez, “H2 Guaranteed Cost Output Feedback Control of Uncertain Discre-
e
te Linear Systems”, Proceedings of International Conference on Dynamics and Control of Systems,
Ottawa, agosto 1999.
[CPH96] W. Colmenares, O. P´rez, J. Bernussou y E. Granado, “Synthesis of Output Feedback Controllers for
e
Uncertain Linear Systems”, Proceedings of the 1st IEEE Caracas Conference on Devices, Circuits and
Systems, Caracas, diciembre 1995.
[CPM94] W. Colmenares, O. P´rez y E. Margaglio, “On the Local Stabilizability of Uncertain Linear Systems”,
e
Proceedings of 6th Latin American Control Conference, Rio de Janeiro, Brasil, pp. 337–339, septiembre
1994.
[CTG00] W. Colmenares, F. Tadeo, E. Granado, O. P´rez y F. Del Valle, “H2 Guaranteed cost control of
e
uncertain discrete linear systems”, Math. Problems in Engineering, Vol. 6, pp. 425–437, 2000.
[Cor96] A. Corripio, “Tunning of industrial control systems”, 2da edici´n, ILM ISA, 1990.
o
[DB01] J. Daafouz y J. Bernussou, “Parameter dependent Lyapunov functions for discrete time systems with
time varying parametric uncertainties”, Systems and Control Letters, Vol. 43, pp. 355–359, 2001.
[DD87] M. A. Dahleh y M. Dahleh, ”L1 optimal feeddback compensators for continuous-time systems”, IEEE
Transactions on Automatic Control, Vol. 32, pp. 889–895, 1987.
[DD88] M. A. Dahleh y M. Dahleh, ”Optimal rejection of persistent disturbances, robust stability and mixed
sensitivity minimization”, IEEE Transactions on Automatic Control, Vol. 33, pp. 722–731, 1988.
[DD95] M. Dahleh e I. Diaz-Bobillo, Control of uncertain systems: a linear programming approach, Prentice
Hall, 1995.
108](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-116-320.jpg)
![[DP87] M. A. Dahleh y J. B. Pearson, “ 1 Optimal Feedback Controllers for MIMO Discrete-time Systems”.
IEEE Transactions on Automatic Control, Vol. 32, 1987.
[DV75] C. A. Desoer y M. Vidyasagar, “Feedback Systems: Input-Output Properties” Academic Press Inc.,
New York, 1975.
[DM95] S. Dormido y F. Morilla, Autosintonia y m´todos de antiwindup en los Reguladores PID, Apuntes del
e
XV Curso de Autom´tica en la Industria, AEIA, 1995.
a
[DFT92] J. Doyle, B. Francis y A. Tannenbaum, “Feedback control theory”, Maxwell Macmillan Int., 1992.
[DGK89] J. Doyle, K. Glover, P. Khargonekar y B. Francis, “State Space Solutions to Standard H 2 and H∞
Control Problems”, IEEE Transactions on Automatic Control, Vol. 34, pp. 831–847, 1989.
[DS81] J. Doyle y G. Stein, “Multivariable feedback design: concepts for a classical/modern synthesis”, IEEE
Transactions on Automatic Control, Vol. 26, No. 1, pp. 4–16, 1981.
[ED98] N. Elia y M.A. Dahleh, “Computational Methods for Controller Design”, Lecture Notes in Control
and Information Sciences 238, Springer Verlag, London, 1998.
[EP98] S. Esfahani and I. Petersen “Optimal Output Feedback Guaranteed Cost Control of Uncertain Linear
Systems”, Control and Decision Conference CDC ’98, 1998.
[GA94] P. Gahinet y P. Apkarian, “A Linear Matrix Inequality Approach to H∞ Control”, International
Journal of Robust and Nonlinear Control, Vol. 4, pp. 421–448, 1994.
[GNL95] P. Gahinet, A. Nemirovski, A. Luab y M. Chillali, LMI control toolbox, The MathWorks Inc., 1995.
[GB86] A. Galimidi y B. Barmish, “The Constrained Lyapunov Problem and its Application to Robust Output
Feedback Stabilization”, IEEE Transactions on Automatic Control, Vol. 31(5), pp. 410–419, 1986.
[GAB92] G. Garcia, D. Arzelier y J. Bernussou, “Stabilization of Uncertain Linear Dynamic Systems by State
and Output Feedback: a Quadratic Stabilizability Approach”, Rapport Interne du LAAS, Toulouse,
France, 1992.
[GB91] G. Garcia y J. Bernussou, “Stabilit´ et D´tectabilit´ Quadratique: Lien avec l’Approche LQG”, Comp-
e e e
tes Rendus de l’Acad´mie des Sciences de Paris, t. 312, s´rie I, pp. 193–198, 1991.
e e
[GB95] G. Garcia y J. Bernussou, “Pole Assignment for Uncertain Systems in a Specified Disk by State
Feedback”, IEEE Transactions on Automatic Control, Vol. 40(1), 1995.
[GBA93] G. Garcia, J. Bernussou y D. Arzelier, “Robust Stabilization of Discrete Time Linear Systems with
Norm Bounded Time Varying Uncertainty”, Systems and Control Letters, 1993.
[GBA95] G. Garcia, J. Bernussou y D. Arzelier, “A LMI Solution for Disk Pole Location with H 2 Guaranteed
Cost”, Proceedings of European Control Conference, Rome, 1995.
[GB96] G. Garcia, J. Bernussou y D. Arzelier, “Robust Pole Assingment by Dynamic Output Feedback”,
Mathematics of Control, Signals and Systems, No. 9, pp. 152–161. 1996.
[Gar93] U. Garcia Palomares, “Parallel Projected Agregation Methods for Solving Convex Feasibility Pro-
blems”, SIAM Journal of Optimization, Vol. 3, No. 4, pp. 882–900, 1993.
[GCG97] K. Garrido, W. Colmenares, E. Granado y O. P´rez, “H∞ output feedback control for Uncertain Sys-
e
tems”, Proceedings of IEEE International Symposium on Industrial Electronics (ISIE97), Guimaraes,
Portugal, julio 1997.
[GGB94] J.C. Geromel, G. Garcia y J. Bernussou, “H2 Robust Control with Pole Placement”, Proceedings of
the 12th IFAC World Congress, Sidney, Australia, 1994.
[GPB91] J.C. Geromel, P.L.D. Peres y J. Bernussou, “On a Convex Parameter Space Method for Linear Control
Design of Uncertain Systems”, SIAM Journal of Control and Optimization, Vol. 29(2), 1991.
109](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-117-320.jpg)
![[GPS92] J.C. Geromel, P.L.D. Peres y S.R. Souza, “H2 Guaranteed Cost Control for Uncertain Continous-Time
Linear Systems”, Systems and Control Letters, Vol. 19, pp. 23–27, 1992.
[GSK94] J.C. Geromel, C.C. de Souza y R.E. Skelton, “LMI Numerical Solution for Output Feedback Stabili-
zation”, Proceedings of the American Control Conference, Baltimore, 1994.
[GCS01] G. Goodwin, S. Graebe y M. Salgado, Control System Design, Prentice Hall, 2001.
[GCB03] E. Granado, W. Colmenares, J. Bernussou y G. Garcia, “A Robust multivariable PID controller with
constraints via LMI approach”, Proceedings of 4th IFAC Symposium on Robust Control Design.
Milan, Italy, 2003.
[GL95] M. Green y D. Limebeer, Linear Robust Control, Prentice Hall Inc., 1995.
[GJ81] S. Gutman y E. Jury, “A General Theory for Matrix Root-Clustering in Subregions of the Complex
Plane”, IEEE Transactions on Automatic Control, Vol. 26, pp. 853–863, 1981.
[HB92] W. Haddad y D. Bernstein, “Controller Design with Regional Pole Constraints”, IEEE Transactions
on Automatic Control, Vol. 37(1), 1992.
[HL93] H.S. Han y J.G. Lee, “ Stability Analysis of Interval Matrices by Lyapunov Function Approach Inclu-
ding ARE”, Control Theory and Advanced Technology, Vol. 9, pp. 745–757, 1993.
[HTK01] D. Henrion, S. Tarbouriech, V. Kucera. “Control of linear systems subject to input constraints: a
polynomial approach”, Automatica, Vol. 36, pp. 597–604, 2001.
[HHC95] W.K. Ho, C.C. Hang, L.S. Cao, “Tuning of PID controllers based on gain and phase margin specifi-
cation”, Automatica, Vol. 31(3), pp. 497–502, 1995.
[Hof81] K. Hoffman, “A Method for Globally Minimizing Concave Functions over Convex Sets”, Mathematical
Programming, Vol. 20, pp. 22–32, 1981.
[HF93] J. Huei y K. Fong, “Robust Stability Analysis of Linear Continuous/Discrete Time Systems with
Output Feedback Controllers”, IEEE Transactions on Automatic Control, Vol. 38, pp. 1.154–1.158,
1993.
[IS94] T. Iwasaki y R. E. Skelton, “All Controllers for General Control Problems: LMI Existence and Con-
ditions and State Space Formulas”, Automatica, Vol. 30, pp. 1.307–1.317, 1994.
[IS95] T. Iwasaki y R.E. Skelton, “The XY-centring Algorithm for the Dual LMI Problem: A New Approach
to Fixed-order Control Design”, International Journal of Control, Vol. 62(6), pp. 1.257–1.272, 1995.
[JS93] F. Jabbari y W. Schmitendorf, “Effects of Using Observers on the Stabilization of Uncertain Linear
Systems”, IEEE Transactions on Automatic Control, Vol. 38(2), pp. 266–271, 1993.
[Jua91] Y. Juang, “ Robust Stability and Robust Pole Assignment of Linear Systems with Structured Uncer-
tainty”, IEEE Transactions on Automatic Control, Vol. 36(5), 1991.
[KPZ90] P. Khargonekar, I. Petersen y K. Zhou, “Robust Stabilization of Uncertain Linear Systems: Quadratic
Satbilizability and H ∞ Control Theory”, IEEE Transactions on Automatic Control, Vol. 35(3), pp.
356–361, 1990.
[Kuo95] B. Kuo, Automatic Control Systems, 7ma Edici´n Prentice Hall, 1995.
o
[MK00] P. O. Malaterre, M. Khammash. “ 1 controller design for a high-order 5-pool irrigation canal system”,
Proceedings of the Conference on Decision and Control CDC 2000, Sydney, Australia, 2000.
[McF90] D. McFarlane y K. Glover, Robust controller design using normalized coprime factor descriptions,
Springer Verlag, 1990.
[ME89] M. A. Mendlovitz, “A Simple Solution to the 1 Optimization Problem”, Systems and Control Letters,
Vol. 12, 1989.
110](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-118-320.jpg)
![[MTB04] F. Mesquine, F. Tadeo, A. Benzaouia. “Regulator problem for linear systems with constraints on
control and its increment or rate ”, Automatica, Vol. 40(8), pp. 1.378–1.395, 2004.
[MZ89] M. Morari y E. Zafirou, Robust Process Control, Prentice Hall Inc., 1989.
[NBT03] M. Naib, A. Benzaouia, F. Tadeo. “Nonsymmetrical approach for l1-optimal control”, Proceedings of
the European Control Conference ECC 2003, Cambridge, Reino Unido, 2003.
[OC97] P. Ollero, E. Camacho, Control e Instrumentacion de Procesos Quimicos, Sintesis, 1997
[ORe83] J. O’Really, Observers for Linear Systems, Academic Press, 1983.
[PL03] P. A. Parrilo y S. Lall, “Semidefinite Programming Relaxations and Algebraic Optimization in Con-
trol”, European Journal of Control, Vol. 9, pp. 307–321, 2003.
[Per89] P.L.D. Peres, Sur la Robustesse des Syst`mes Lin´aires: Approche par Programmation Lin´aire, Th`se
e e e e
de doctorat, Universit´ Paul Sabatier - LAAS du CNRS, Toulouse, France, 1989.
e
[PSG92] P.L.D. Peres, S.R. Souza y J.C. Geromel, “Optimal H2 Control for Uncertain Systems”, Proceedings
of American Control Conference - ACC ’92, 1992.
[PCG97] O. P´rez, W. Colmenares, E. Granado y K. Garrido, “Robust Control of a Neutraliation Process”,
e
4th. Proceedings of IEEE International Conference on Electronics, Circuits and Systems, Cairo, Egipto
diciembre 1997.
[Pet87] I.R. Petersen, “A Stabilization Algorithm for a Class of Uncertain Linear Systems”, Systems and
Control Letters, Vol. 8, pp. 351–357, 1987.
[PH86] I.R. Petersen y C. Hollot, “A Riccati Equation Approach to the Stabilization of Uncertain Linear
Systems”, Automatica, Vol. 22, No.4, pp. 397-411, 1986.
[PH96] C. Phillips y R. Harbor, Feedback Control Systems, 3ra Edici´n, Prentice Hall Int., 1996.
o
[Qui04] M. V. Quintero G., Control multivariable de una planta piloto con tecnologias FieldBus y t´cnicas
e
predictivas, proyecto de grado USB, ingenieria electr´nica, 2004.
o
[RMS86] D.E. Rivera, M. Morari, S. Skogestad, “Internal model control. 4. PID controller design”, Ind. Eng.
Chem. Res. 25 (1) pp. 252–265, 1986.
[Rot93] M.A. Rotea, M. Corless, D. Da y I.R. Petersen, “Systems with Structured Uncertainty: Relations
between Quadratic and Robust Stability”, IEEE Transactions on Automatic Control, Vol. 38(5), pp.
799–803, 1993.
[SMN90] M. Sampei, T. Mita y M. Nakamachi, “An Algebraic Approach to H ∞ Output Feedback Control
Problems”, Systems and Control Letters, Vol. 14, pp. 13–24, 1990.
[San89] R. S´nchez Pe˜a, Introducci´n a la teoria de control robusto, Asociaci´n Argentina de Control Au-
a n o o
tom´tico (AADECA), 1989.
a
[SS98] R.S. S´nchez-Pe˜a, M. Sznaier Robust Systems Theory and Applications, Wiley Interscience, New
a n
York, 1998.
[SGC97] C. Scherer, P. Gahinet y M. Chilali, “Multiobjective Output-Feedback Control via LMI Optimization”,
IEEE Transactions on Automatic Control, Vol. 42, pp. 896–911, 1997.
[Sh01] U. Shaked “Improved LMI representations for the analysis and design of continuous-time systems with
polytopic uncertainty”, IEEE Transactions on Automatic Control, Vol. 46(4), pp. 652–656, 2001.
[SS01] U. Shaked y V. Suplin “A new bounded real lemma representation for the continuous time case”,
IEEE Transactions on Automatic Control, Vol. 46(9), pp. 1.420-1.426, 2001.
[Sh96] A. S. Shakoor “Industrial Uses of Predictive Control”, MSc. Dissertation, University of Strathclyde,
1996.
111](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-119-320.jpg)
![[Sko03] S. Skogestad, “Simple analytic rules for model reduction and PID controller tuning”, Journal of Process
Control, Vol. 13, pp. 291–309, 2003.
[SK96] S. Skogestad, I. Postlethwaite, Multivariable Feedback Control, Analysis and Design, John Wiley &
Sons, 1996
[Soh94] C.B. Soh, “Robust Stability of Dynamic Interval Systems”, Control Theory and Advanced Technology,
Vol. 10, pp. 73–80, 1994.
[ST93] O.J. Staffans “On the Four-Block Model Matching Problem in 1 and Infinite-Dimensional Linear
Programming” SIAM J. Control and Optimization, Vol. 38, pp. 747–779, 1993.
[Str82] G. Strang, Algebra lineal y sus aplicaciones, Fondo Educativo Interamericano, S.A. de C.V. 2da.
edici´n, 1982.
o
[TG96] F. Tadeo y M. J. Grimble, Design of 1 Optimal Controllers for a Hydrogen Reformer Plant, Internal
Report Industrial Control Centre, University of Strathclyde, 1996.
[TG02] F. Tadeo y M. J. Grimble. “Advanced Control of a Hydrogen Reformer”, IEE Computing and Control
Engineering Journal, Vol. 13, pp. 305–314, 2002.
[TG03] F. Tadeo y M. J. Grimble. “Controller design using linear programming for systems with constraints.
Part 1: Tutorial Introduction; Part 2: Controller Design; Part 3: Design Examples”, IEE Computing
and Control Engineering Journal, Vol. 12, pp. 273–276, (2002), Vol. 13, pp. 49–52, 89–93, 2003.
[TG00] F. Tadeo, M. J. Grimble y P. Vega, “Design of an 1 Optimal Controller for a Hydrogen Reformer
Plant”, Proceedings of American Control Conference, Chicago, June 2000.
[THV88] F. Tadeo, A. Holohan y P. Vega, “ 1 -Optimal control of a pH plant”, Computers and Chemical
Engineering, pp. S459–S466, 1998.
[TVP95] F. Tadeo, P. Vega y C. Prada, “Dise˜o de controladores robustos para una caldera industrial”, I
n
Congreso de Usuarios de Matlab, 1995.
[VI85] M. Vidyasagar Control system Synthesis: a Factorization Approach, MIT Press, Cambridge, Mass.,
1985.
[VI86] M. Vidyasagar, “Optimal Rejection of Persistent Bounded Disturbances” IEEE Transactions on Au-
tomatic Control, Vol. 31, 1986.
[WV00] P.J. de Wild y M.J.F.M. Verhaak, “Catalytic production of hydrogen from methanol”, Catalysis
Today, Vol. 60, pp 3-10, 2000.
[Win94] W. Winston, Operation Research: Applications & Algorithms, Duxbury Press, 3ra Edici´n, 1994.
o
[XFS92] L. Xie, M. Fu y C. E. de Sousa, “H∞ Control and Quadratic Stabilization of Systems with Parameter
Uncertainty Via Output feedback”, IEEE Transactions on Automatic Control, Vol. 37(8), pp. 1253–
1256, 1992.
[Yed86] R.K. Yedavalli, “Stability Analysis of Interval Matrices: Another Sufficient Condition”, International
Journal of Control, Vol. 43, pp. 767–772, 1986.
[YL86] R.K. Yedavalli y Z. Liang, “Reduced Conservatism in Stability Robustness Bounds by State Trans-
formation ”, IEEE Transactions on Automatic Control, Vol. 31, pp. 863–866, 1986.
[YJB76] D .C. Youla, H. A. Jabr, J. J. Bongiorno. “Modern Wiener-Hopf design of optimal controllers. Part
2: The multivariable case” IEEE Transactions on Automatic Control, Vol. 21, pp. 319–338, 1976.
[Zam81] G. Zames, “Feedback and Optimal Sensitivity: Model Reference Transformations, Multiplicative Se-
minorms and Approximate Inverses”, IEEE Transactions on Automatic Control, Vol. 26, pp. 301–320,
1981.
112](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-120-320.jpg)
![[ZN42] J. Ziegler y N. Nichols, “Optimum Settings for Automatic Controllers”, ASME Transactions, Vol. 64,
pp. 759–768, 1942.
[ZK88] K. Zhou y P. Khargonekar, “An Algebraic Riccati Equation Approach to H ∞ Optimization”, Systems
and Control Letters, Vol. 11, pp. 85–91, 1988.
113](https://image.slidesharecdn.com/multiobjetivos-120416173122-phpapp02/85/Diseno-Robusto-y-Multiobjetivos-de-Sistemas-121-320.jpg)