Apuntes ic4

Depto. de Ingenier´ıa de Sistemas y Automática
APUNTES DE INGENIERÍA DE CONTROL
ANÁLISIS Y CONTROL DE SISTEMAS EN ESPACIO DE ESTADO
IDENTIFICACIÓN DE SISTEMAS
CONTROL ADAPTATIVO
CONTROL PREDICTIVO
Daniel Rodr´ıguez Ram´ırez
Carlos Bordóns Alba
Rev. 5/05/2005

Índice general
Lista de figuras IX
1. Control de sistemas discretos en el espacio de estados 1
1.1. Representación de sistemas discretos en el espacio de estados . . . . . . 1
1.2. Obtención de la representación de en espacio de estados de sistemas
discretos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2.1. Método de programación directa . . . . . . . . . . . . . . . . . . 3
1.2.2. Método de programación anidada . . . . . . . . . . . . . . . . . 5
1.3. La representación en espacio de estados de un sistema no es única . . . 6
1.4. Resolución de las ecuaciones del espacio de estados . . . . . . . . . . . 7
1.4.1. Procedimiento recursivo . . . . . . . . . . . . . . . . . . . . . . 7
1.4.2. Matriz de transición de estados . . . . . . . . . . . . . . . . . . 8
1.4.3. Método basado en la transformada Z . . . . . . . . . . . . . . . 9
1.4.3.1. Procedimiento alternativo para calcular (zI − G)−1
. . 10
1.5. Discretización de las ecuaciones de estado continuas . . . . . . . . . . . 12
1.6. Controlabilidad y Observabilidad . . . . . . . . . . . . . . . . . . . . . 15
i

ii ÍNDICE GENERAL
1.6.1. Controlabilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.6.2. Controlabilidad de la salida completa . . . . . . . . . . . . . . . 17
1.6.3. Observabilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.6.4. Principio de Dualidad . . . . . . . . . . . . . . . . . . . . . . . 19
1.7. Transformación de un sistema en formas canónicas . . . . . . . . . . . 19
1.7.1. Obtención de la forma canónica controlable . . . . . . . . . . . 20
1.7.2. Obtención de la forma canónica observable . . . . . . . . . . . . 20
1.8. Colocación de polos mediante realimentación del vector de estados . . . 21
1.8.1. Condición necesaria y suficiente para la colocación arbitraria de
polos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.8.2. Procedimientos para calcular K . . . . . . . . . . . . . . . . . . 22
1.8.2.1. Procedimiento alternativo: la fórmula de Ackermann . 24
1.8.3. Control Dead-Beat . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.9. Observadores del estado . . . . . . . . . . . . . . . . . . . . . . . . . . 27
1.9.1. Procedimiento iterativo para la estimación del estado . . . . . . 28
1.9.2. Observador del estado completo . . . . . . . . . . . . . . . . . . 30
1.9.2.1. Cálculo de Ke . . . . . . . . . . . . . . . . . . . . . . . 32
1.9.2.2. Comentarios acerca del papel de Ke . . . . . . . . . . 34
1.9.2.3. Efectos de la adición del observador . . . . . . . . . . . 35
1.9.3. Observador de orden m´ınimo . . . . . . . . . . . . . . . . . . . . 36
1.10. Control óptimo LQR . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

ÍNDICE GENERAL iii
1.10.1. Solución de la ecuación de Riccatti . . . . . . . . . . . . . . . . 43
1.11. Filtro de Kalman . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
2. Modelos de procesos y perturbaciones 45
2.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
2.2. Perturbaciones deterministas a trozos . . . . . . . . . . . . . . . . . . . 46
2.3. Procesos estocásticos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
2.4. Modelos de procesos con ruidos . . . . . . . . . . . . . . . . . . . . . . 48
3. Introducción a la identificación de sistemas 51
3.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
3.2. Ideas básicas sobre identificación de sistemas . . . . . . . . . . . . . . . 52
3.2.1. Planificación de los experimentos . . . . . . . . . . . . . . . . . 52
3.2.2. Selección del tipo de modelo . . . . . . . . . . . . . . . . . . . . 53
3.2.3. Elección de un criterio . . . . . . . . . . . . . . . . . . . . . . . 54
3.2.4. Estimación de los parámetros . . . . . . . . . . . . . . . . . . . 54
3.2.4.1. Identificación en l´ınea . . . . . . . . . . . . . . . . . . 54
3.2.4.2. Identificación fuera de l´ınea . . . . . . . . . . . . . . . 55
3.2.5. Validación del modelo . . . . . . . . . . . . . . . . . . . . . . . 55
3.2.6. Resumen del proceso de identificación . . . . . . . . . . . . . . . 57
3.3. Algunas propiedades . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58

iv ÍNDICE GENERAL
3.3.1. Excitación persistente . . . . . . . . . . . . . . . . . . . . . . . 58
3.3.2. Convergencia e identificabilidad . . . . . . . . . . . . . . . . . . 59
3.3.2.1. Identificación en bucle cerrado . . . . . . . . . . . . . . 60
3.3.3. Niveles de supervisión y acondicionamiento . . . . . . . . . . . . 62
4. Identificación por m´ınimos cuadrados 63
4.1. El método de los m´ınimos cuadrados . . . . . . . . . . . . . . . . . . . 63
4.2. Algoritmo recursivo para identificación en linea . . . . . . . . . . . . . 65
4.3. Interpretación estad´ıstica . . . . . . . . . . . . . . . . . . . . . . . . . . 67
4.4. M´ınimos cuadrados ponderados . . . . . . . . . . . . . . . . . . . . . . 70
4.5. M´ınimos cuadrados extendidos y generalizados . . . . . . . . . . . . . . 71
4.6. Estimación de los valores de continua . . . . . . . . . . . . . . . . . . . 72
4.6.1. Utilización de los incrementos de las variables . . . . . . . . . . 73
4.6.2. Cálculo de los valores medios . . . . . . . . . . . . . . . . . . . 73
4.6.3. Estimación de una constante . . . . . . . . . . . . . . . . . . . . 73
4.7. Importancia del orden del modelo . . . . . . . . . . . . . . . . . . . . . 74
4.8. Identificación de sistemas con retardo o no lineales . . . . . . . . . . . . 77
4.9. Consideraciones finales . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
5. Introducción al control adaptativo 81
5.1. Planteamiento del problema . . . . . . . . . . . . . . . . . . . . . . . . 81

ÍNDICE GENERAL v
5.1.1. Clasificación grosso modo de los sistemas de control adaptativo . 82
5.2. Justificación del uso de control adaptativo . . . . . . . . . . . . . . . . 84
5.3. Control adaptativo por modelo de referencia (MRAC) . . . . . . . . . . 87
5.3.1. La regla del MIT . . . . . . . . . . . . . . . . . . . . . . . . . . 89
6. Reguladores Autoajustables (STR) 93
6.1. Introducción. Estructura general de los STR . . . . . . . . . . . . . . . 93
6.1.1. Algoritmos con estructura impl´ıcita y expl´ıcita . . . . . . . . . . 95
6.2. Control por M´ınima Varianza . . . . . . . . . . . . . . . . . . . . . . . 96
6.2.1. El regulador de m´ınima varianza generalizado . . . . . . . . . . 99
6.3. Asignación de polos y ceros . . . . . . . . . . . . . . . . . . . . . . . . 100
6.3.1. Algoritmo con estructura impl´ıcita. . . . . . . . . . . . . . . . . 103
6.3.2. Algoritmo con estructura expl´ıcita . . . . . . . . . . . . . . . . . 104
7. Controladores PID con autoajuste y Ajuste por tabla 105
7.1. Introducción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
7.2. Función de autoajuste (autotuning) . . . . . . . . . . . . . . . . . . . . 105
7.3. Funciones de autoajuste para PIDs . . . . . . . . . . . . . . . . . . . . 107
7.3.1. Técnicas de ajuste basadas en la respuesta transitoria . . . . . . 108
7.3.2. Métodos basados en las oscilaciones producidas al realimentar
con un relé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
7.4. La técnica de ajuste por tabla o gain scheduling . . . . . . . . . . . . . 110

vi ÍNDICE GENERAL
7.5. Controladores adaptativos industriales . . . . . . . . . . . . . . . . . . 113
7.5.1. SattControl ECA40 y Fisher-Rosemount DPR900 . . . . . . . . 115
7.5.2. Foxboro EXACT . . . . . . . . . . . . . . . . . . . . . . . . . . 115
7.5.3. ABB Novatune . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
8. Control Predictivo Basado en Modelo (MPC) 117
8.1. Perspectiva histórica . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
8.2. Conceptos básicos de control predictivo . . . . . . . . . . . . . . . . . . 118
8.3. Estrategia de los controladores predictivos . . . . . . . . . . . . . . . . 119
8.4. Elementos básicos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
8.4.1. Modelo de predicción . . . . . . . . . . . . . . . . . . . . . . . . 122
8.4.1.1. Respuestas libre y forzada . . . . . . . . . . . . . . . . 125
8.4.2. Función objetivo . . . . . . . . . . . . . . . . . . . . . . . . . . 126
8.4.3. Obtención de la ley de control . . . . . . . . . . . . . . . . . . . 129
8.5. Revisión de los principales algoritmos . . . . . . . . . . . . . . . . . . . 130
8.5.0.1. Dynamic Matrix Control . . . . . . . . . . . . . . . . . 130
8.5.0.2. Model Algorithmic Control . . . . . . . . . . . . . . . 131
8.5.0.3. Predictive Functional Control . . . . . . . . . . . . . . 131
8.5.0.4. Extended Prediction Self Adaptive Control . . . . . . 132
8.5.0.5. Extended Horizon Adaptive Control . . . . . . . . . . 133
8.5.0.6. Generalized Predictive Control . . . . . . . . . . . . . 134

ÍNDICE GENERAL vii
9. Controladores predictivos 135
9.1. Dynamic Matrix Control . . . . . . . . . . . . . . . . . . . . . . . . . . 135
9.1.1. Predicción . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
9.1.2. Perturbaciones medibles . . . . . . . . . . . . . . . . . . . . . . 137
9.1.3. Algoritmo de control . . . . . . . . . . . . . . . . . . . . . . . . 138
9.1.3.1. El caso con restricciones . . . . . . . . . . . . . . . . . 140
9.1.3.2. Extensión al caso multivariable . . . . . . . . . . . . . 141
9.2. Control Predictivo Generalizado . . . . . . . . . . . . . . . . . . . . . . 141
9.2.1. Formulación del Control Predictivo Generalizado . . . . . . . . 142
9.2.1.1. Predicción óptima . . . . . . . . . . . . . . . . . . . . 143
9.2.1.2. Obtención de la ley de control . . . . . . . . . . . . . . 146
9.2.2. Ejemplo de cálculo . . . . . . . . . . . . . . . . . . . . . . . . . 147
9.2.3. Caso multivariable . . . . . . . . . . . . . . . . . . . . . . . . . 149
10.Otros aspectos del Control Predictivo 151
10.1. Restricciones en Control Predictivo . . . . . . . . . . . . . . . . . . . . 151
10.1.1. Tratamiento convencional de restricciones . . . . . . . . . . . . 151
10.1.2. Restricciones en Control Predictivo . . . . . . . . . . . . . . . . 153
10.1.3. Resolución del problema . . . . . . . . . . . . . . . . . . . . . . 155
10.1.4. Gestión de restricciones . . . . . . . . . . . . . . . . . . . . . . 156
10.1.4.1. Técnicas de búsqueda de soluciones factibles . . . . . . 157

Índice de figuras
1.1. Diagrama de bloques de la representación en espacio de estados de un
sistema LTI. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2. Diagrama de bloques de un sistema controlado por una realimentación
del vector de estados. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
1.3. Diagrama de bloques de un sistema LTI controlado mediante una reali-
mentación del vector de estados que estima el estado con un observador. 31
1.4. Diagrama de bloques de un observador de orden completo. . . . . . . . 31
2.1. Procesos estocásticos: realizaciones y variables aleatorias. . . . . . . . 47
2.2. Modelo de Box-Jenkins. . . . . . . . . . . . . . . . . . . . . . . . . . . 48
3.1. Esquema de la identificación en l´ınea. . . . . . . . . . . . . . . . . . . 55
3.2. Diagrama de flujo del proceso de identificación. . . . . . . . . . . . . . 57
3.3. Ejemplo de señal de entrada del tipo PRBSS. . . . . . . . . . . . . . . 59
4.1. Diagrama de flujo del proceso de identificación mediante m´ınimos cuadra-
dos recursivos. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
4.2. Diagrama de Bode de un sistema de segundo orden (linea continua) y
de un modelo de primer orden estimado para una entrada senoidal de
frecuencia ω = 0,2 rad × s−1
. . . . . . . . . . . . . . . . . . . . . . . . 75
ix

x ÍNDICE DE FIGURAS
4.3. Misma situación que en la figura 4.2 pero con una señal de entrada
senoidal de frecuencia ω = 1 rad × s−1
. . . . . . . . . . . . . . . . . . . 75
4.4. Evolución de los parámetros identificados en un caso de sobreparametrización.
76
4.5. Evolución de unos parámetros frente a otros para el modelo sobreparametriza-
do. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
5.1. Configuración genérica de un controlador adaptativo. . . . . . . . . . . 82
5.2. Sistema realimentado con actuador con caracter´ıstica v = f(u). . . . . 84
5.3. Sistema realimentado con actuador con caracter´ıstica v = f(u). . . . . 85
5.4. Respuestas en bucle abierto (izquierda) y cerrado (derecha) del sistema
dado en (5.1). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86
5.5. Respuestas en bucle abierto (izquierda) y cerrado (derecha) del sistema
dado en (5.2). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
5.6. Configuración genérica de un controlador adaptativo por modelo de re-
ferencia (MRAC). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
6.1. Configuración genérica de un regulador o controlador autoajustable. . 94
6.2. Configuración genérica de un regulador o controlador autoajustable. . 95
6.3. División de polinomios para el ejemplo 6.2. . . . . . . . . . . . . . . . 99
6.4. Estructura para la asignación de polos y ceros. . . . . . . . . . . . . . 101
7.1. PID industrial moderno con función de autoajuste (ABB modelo ECA). 107
7.2. Determinación de T y L por áreas. . . . . . . . . . . . . . . . . . . . . 109
7.3. Estructura usada en el método basado en oscilaciones de relé. . . . . . 110

ÍNDICE DE FIGURAS xi
7.4. Configuración genérica de un controlador adaptativo con adaptación en
bucle abierto. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
7.5. Curva de pH para una solución de HCl 0.001 M y NaOH 0.001 M. . . 112
7.6. Caracter´ıstica aproximada de una sonda lambda . . . . . . . . . . . . 113
7.7. La herramienta Novatune se comercializa actualmente con el sistema
Advant 410 de ABB. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
8.1. Estrategia del Control Predictivo . . . . . . . . . . . . . . . . . . . . . 120
8.2. Estructura básica del MPC . . . . . . . . . . . . . . . . . . . . . . . . . 121
8.3. Respuesta impulsional y ante escalón . . . . . . . . . . . . . . . . . . . 123
8.4. Respuestas libre y forzada . . . . . . . . . . . . . . . . . . . . . . . . . 126
8.5. Trayectoria de referencia . . . . . . . . . . . . . . . . . . . . . . . . . . 128
8.6. Puntos de coincidencia . . . . . . . . . . . . . . . . . . . . . . . . . . . 132
9.1. Ley de control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
9.2. Punto de operación óptimo de un proceso t´ıpico . . . . . . . . . . . . . 140
10.1. Restricciones y punto de operación óptimo . . . . . . . . . . . . . . . . 152
10.2. Restricciones en la señal de control . . . . . . . . . . . . . . . . . . . . 153
10.3. Gestión de restricciones . . . . . . . . . . . . . . . . . . . . . . . . . . . 157

Cap´ıtulo 1
Control de sistemas discretos en el
espacio de estados
1.1. Representación de sistemas discretos en el es-
pacio de estados
El método de espacio de estados está basado en la descripción del sistema mediante
n ecuaciones en diferencias, que se agrupan en una ecuación vectorial matricial en
diferencias.
Definición 1.1 Concepto de estado: El estado de un sistema dinámico es el con-
junto más pequeño de variables (llamadas variables de estado) tal que, el conocimiento
de esas variables en un determinado instante t0 junto con el conocimiento de los valores
de la señal de entrada para los instantes t ≥ t0, permite determinar el comportamiento
y evolución del sistema para cualquier instante de tiempo t ≥ t0.
Las variables de estado se agrupan en el llamado vector de estado y el espacio n-
dimensional que determinan los posibles valores de esas variables, se denomina espacio
de estados.
La dinámica de un sistema se puede describir en función del valor del vector de
estados y de la señal de entrada (asumiendo que el sistema es no autónomo mediante
1

2OBTENCI ÓN DE LA REPRESENTACI ÓN DE EN ESPACIO DE ESTADOS DE SISTEMAS DISCRETOS
unas ecuaciones que tendrán la forma:
x(k + 1) = f(x(k), u(k), k)
y(k) = g(x(k), u(k), k)
donde la notación ξ(k) indica el valor tomado por ξ en el instante de tiempo tk y f y g
pueden ser cualquier tipo de función. No obstante en esta asignatura nos centraremos
en los Sistemas Lineales e Invariantes en el tiempo (LTI). Este tipo de sistemas son
descritos mediante las siguientes ecuaciones:
x(k + 1) = Gx(k) + Hu(k) (1.1)
y(k) = Cx(k) + Du(k)
que corresponder´ıan al diagrama de bloques:
x(k+1) +
+
D
H
u(k)
z-1 C
G
+
+
x(k)
Figura 1.1: Diagrama de bloques de la representación en espacio de estados de un sistema LTI.
1.2. Obtención de la representación de en espacio
de estados de sistemas discretos
Partiremos de un sistema discreto descrito por:
y(k)+a1y(k−1)+a2y(k−2)+· · ·+any(k−n) = b0u(k)+b1u(k−1)+· · ·+bnu(k−n) (1.2)
Es bien conocido de anteriores temas de la asignatura que este sistema puede ser
descrito por la siguiente función de transferencia:
G(z) =
Y (z)
U(z)
=
b0 + b1z−1
+ b2z−2
+ · · · + bnz−n
1 + a1z−1 + a2z−2 + · · · + anz−n
(1.3)
A continuación se expondrán dos de los métodos disponibles para obtener la repre-
sentación en espacio de estados del sistema descrito por (1.3).

CAPÍTULO 1. CONTROL DE SISTEMAS DISCRETOS EN EL ESPACIO DE ESTADOS 3
1.2.1. Método de programación directa
Parte de la premisa que la función de transferencia (1.3) puede reescribirse como:
G(z) = b0 +
(b1 − a1b0)z−1
+ (b2 − a2b0)z−2
+ · · · + (bn − anb0)z−n
1 + a1z−1 + a2z−2 + · · · + anz−n
(1.4)
teniendo en cuenta que G(z) = Y (z)
U(z)
se obtiene:
Y (z) = b0U(z) +
(b1 − a1b0)z−1
+ (b2 − a2b0)z−2
+ · · · + (bn − anb0)z−n
1 + a1z−1 + a2z−2 + · · · + anz−n
U(z) (1.5)
que a su vez se puede expresar como:
Y (z) = b0U(z) + ˜Y (z)U(z) (1.6)
con:
˜Y (z) =
(b1 − a1b0)z−1
+ (b2 − a2b0)z−2
+ · · · + (bn − anb0)z−n
1 + a1z−1 + a2z−2 + · · · + anz−n
(1.7)
Por otra parte, teniendo en cuenta la expresión de ˜Y (z) se puede definir un Q(z) que
cumple que:
Q(z) =
˜Y (z)
(b1 − a1b0)z−1 + · · · + (bn − anb0)z−n
=
U(z)
1 + a1z−1 + · · · + anz−n
(1.8)
De ah´ı se obtiene que:
Q(z) = −a1z−1
Q(z) − a2z−2
Q(z) − · · · − anz−n
Q(z) + U(z) (1.9)
˜Y (z) = (b1 − a1b0)z−1
Q(z) + (b2 − a2b0)z−2
Q(z) + · · · + (bn − anb0)z−n
Q(z) (1.10)
A continuación se eligen las variables de estado como:
X1(z) = z−n
Q(z) (1.11)
X2(z) = z−(n−1)
Q(z)
· · ·
Xn(z) = z−1
Q(z)
lo que teniendo en cuenta las propiedades de la transformada Z, implica que:
zX1(z) = X2(z)
zX2(z) = X3(z)
· · ·
zXn−1(z) = Xn(z)

4OBTENCI ÓN DE LA REPRESENTACI ÓN DE EN ESPACIO DE ESTADOS DE SISTEMAS DISCRETOS
lo que a su vez equivale a:
x1(k + 1) = x2(k) (1.12)
x2(k + 1) = x3(k)
· · ·
xn−1(k + 1) = xn(k)
Nótese que según la última igualdad de (1.11) se tiene que Q(z) = zXn(z), luego
teniendo en cuenta esto y el resto de las igualdades de (1.11) podemos reescribir la
expresión de Q(z) en (1.9) como:
zXn(z) = −a1Xn(z) − a2Xn−1(z) − · · · − anX1(z) + U(z) (1.13)
o lo que es lo mismo:
xn(k + 1) = −anx1(k) − an−1x2(k) − · · · − a1xn(k) + u(k) (1.14)
De esta manera y si tenemos en cuenta (1.12) obtenemos la siguiente expresión de la
ecuación de estado:







x1(k + 1)
x2(k + 1)
...
xn−1(k + 1)
xn(k + 1)







=







0 1 0 · · · 0
0 0 1 · · · 0
...
...
...
...
0 0 0 · · · 1
−an −an−1 −an−2 · · · −a1














x1(k)
x2(k)
...
xn−1(k)
xn(k)







+







0
0
...
0
1







u(k)
(1.15)
Por otra parte, podemos reescribir también (1.10) teniendo en cuenta las igualdades
de (1.11) de manera que:
˜Y (z) = (b1 − a1b0)Xn(z) + (b2 − a2b0)Xn−1(z) + · · · + (bn − anb0)X1(z) (1.16)
Esto se puede llevar a la ecuación (1.6) de manera que antitransformando se obtiene:
y(k) = (bn −anb0)x1(k)+(bn−1 −an−1b0)x2(k)+· · ·+(b1 −a1b0)xn(k)+b0u(k) (1.17)
lo cual se puede escribir como:
y(k) = bn − anb0 bn−1 − an−1b0 · · · b1 − a1b0







x1(k)
x2(k)
...
xn−1(k)
xn(k)







+ b0u(k) (1.18)
Las ecuaciones (1.15) y (1.18) forman una representación en espacio de estados del
sistema descrito por la función de transferencia (1.3) que se denomina forma canónica
controlable.

1.2.2. Método de programación anidada
En este caso se parte de que de la función de transferencia (1.3) se obtiene la
siguiente ecuación:
Y (z) − b0U(z) + z−1
(a1Y (z) − b1U(z)) + · · · + z−n
(anY (z) − bnU(z)) = 0 (1.19)
que a su vez se puede reescribir como:
Y (z) = b0U(z) + z−1
b1U(z) − a1Y (z) + z−1
(b2U(z) − a2Y (z) (1.20)
+z−1
(b3U(z) − a3Y (z) + · · ·)
Teniendo en cuenta esto se definen las siguientes variables de estado:
Xn(z) = z−1
(b1U(z) − a1Y (z) + Xn−1(z)) (1.21)
Xn−1(z) = z−1
(b2U(z) − a2Y (z) + Xn−2(z))
...
X2(z) = z−1
(bn−1U(z) − an−1Y (z) + X1(z))
X1(z) = z−1
(bnU(z) − anY (z))
Nótese que según esta definición de las variables de estado la expresión (1.20) se puede
reescribir en forma condensada como:
Y (z) = b0U(z) + Xn(z) (1.22)
Sustituyendo esta expresión en la definición de las variables de estado (1.21) y multi-
plicando por z en ambos lados de cada igualdad se obtiene:
zXn(z) = Xn−1(z) − a1Xn(z) + (b1 − a1b0)U(z)
zXn−1(z) = Xn−2(z) − a2Xn(z) + (b2 − a2b0)U(z)
...
zX2(z) = X1(z) − an−1Xn(z) + (bn−1 − an−1b0)U(z)
zX1(z) = −anXn(z) + (bn − anb0)U(z)
Antitransformando lo anterior:
x1(k + 1) = −anxn(k) + (bn − anb0)u(k) (1.23)
x2(k + 1) = x1(k) − an−1xn(k) + (bn−1 − an−1b0)u(k)
...
xn−1(k + 1) = xn−2(k) − a2xn(k) + (b2 − a2b0)u(k)
xn(k + 1) = xn−1(k) − a1xn(k) + (b1 − a1b0)u(k)

6 LA REPRESENTACI ÓN EN ESPACIO DE ESTADOS DE UN SISTEMA NO ES ÚNICA
Antitransformando también la expresión (1.22) se obtiene:
y(k) = xn(k) + b0u(k) (1.24)
Finalmente, agrupando las dos expresiones anteriores se obtiene:







x1(k + 1)
x2(k + 1)
...
xn−1(k + 1)
xn(k + 1)







=







0 0 · · · 0 0 −an
1 0 · · · 0 0 −an−1
...
...
...
...
...
0 0 · · · 1 0 −a2
0 0 · · · 0 1 −a1














x1(k)
x2(k)
...
xn−1(k)
xn(k)







+







bn − anb0
bn−1 − an−1b0
...
b2 − a2b0
b1 − a1b0







u(k)
y(k) = 0 0 · · · 0 1







x1(k)
x2(k)
...
xn−1(k)
xn(k)







+ b0u(k) (1.25)
A esta representación en espacio de estados del sistema descrito por la función de
transferencia (1.3) se la denomina forma canónica observable.
1.3. La representación en espacio de estados de un
sistema no es única
Se ha comprobado que a un mismo sistema descrito por su función de transferencia
le corresponden, al menos, dos representaciones en espacio de estado distintas. De
hecho, la representación en espacio de estados de un sistema no es única. Por ejemplo,
podemos tomar otras variables de estado que describan la dinámica del sistema que
sean a su vez combinaciones lineales de las variables de estado originales, o considerar
que éstas son a su vez combinaciones lineales de otras. Dicho de otro modo, dado un
sistema LTI como el descrito en (1.1) podemos considerar que el vector de estado x(k)
está relacionado con otro vector ˜x(k) con variables de estado distintas mediante una
transformación:
x(k) = P ˜x(k) (1.26)
donde P es una matriz invertible. Esto se puede llevar a la ecuación de estado del
sistema de manera que obtendr´ıamos:
P ˜x(k + 1) = GP ˜x(k) + Hu(k)
Premultiplicando por P−1
:
˜x(k + 1) = P−1
GP ˜x(k) + P−1
Hu(k)

por lo que la ecuación de estado se puede expresar como:
˜x(k + 1) = ˜G˜x(k) + ˜Hu(k) (1.27)
con ˜G = P−1
GP y ˜H = P−1
H. De la misma manera la ecuación, de la salida del
sistema se puede expresar como:
y(k) = ˜C˜x(k) + ˜Du(k) (1.28)
con ˜C = CP y ˜D = D. As´ı pues, las ecuaciones (1.27) y (1.28) describen una repre-
sentación del sistema en espacio de estados que es diferente de la original pero equiva-
lente a ella1
.
1.4. Resolución de las ecuaciones del espacio de es-
tados
En esta sección se trata el tema de la resolución de las ecuaciones de estado. Es
decir, se presentarán procedimientos para obtener el valor del vector de estado para
un determinado instante de tiempo k > 0 a partir del valor de x(0), es decir, del valor
inicial del vector de estados.
1.4.1. Procedimiento recursivo
Iterando las ecuaciones del estado para un sistema LTI como (1.1) a partir de k = 0:
x(1) = Gx(0) + Hu(0)
x(2) = Gx(1) + Hu(1) = G2
x(0) + GHu(0) + Hu(1)
x(3) = Gx(2) + Hu(2) = G3
x(0) + G2
Hu(0) + GHu(1) + Hu(2)
...
generalizando para cualquier k > 0:
x(k) = Gk
x(0) +
k−1
j=0
Gk−j−1
Hu(j) (1.29)
1
Obsérvese que en la ecuación (1.28) el estado aparece con ˜, indicando que el vector de estados
es diferente al original. La salida sin embargo si coincide con la del sistema original pues ambas
representaciones son equivalentes.

8 RESOLUCI ÓN DE LAS ECUACIONES DEL ESPACIO DE ESTADOS
Obsérvese que x(k) depende del estado inicial y de los valores de la entrada. Por otra
parte, la salida se puede expresar como:
y(k) = CGk
x(0) + C
k−1
j=0
Gk−j−1
Hu(j) + Du(k) (1.30)
1.4.2. Matriz de transición de estados
Considérese la ecuación:
x(k + 1) = Gx(k) (1.31)
En este caso, al no tener señal de entrada la solución de la ecuación viene dada por:
x(k) = Ψ(k)x(0)
con:
Ψ(k + 1) = GΨ(k) Ψ(0) = I
es decir:
Ψ(k) = Gk
A Ψ(k) se le llama la matriz de transición de estados y contiene toda la información
sobre los movimientos libres del sistema descrito por (1.31). Estos movimientos libres
se refieren a los cambios de estado o evolución del estado del sistema en ausencia de
entrada.
En términos de Ψ(k) la solución de la ecuación de estados para el sistema (1.1)
viene dada por:
x(k) = Ψ(k)x(0) +
k−1
j=0
Ψ(k − j − 1)Hu(j) (1.32)
= Ψ(k)x(0) +
k−1
j=0
Ψ(j)Hu(k − j − 1)
lo que lleva a:
y(k) = CΨ(k)x(0) + C
k−1
j=0
Ψ(j)Hu(k − j − 1) + Du(k) (1.33)

1.4.3. Método basado en la transformada Z
Aplicando la transformada Z a ambos lados de la ecuación de estados del sistema
(1.1) se obtiene:
zX(z) − zx(0) = GX(z) + HU(z)
y de ah´ı:
(zI − G)X(z) = zx(0) + HU(Z)
Premultiplicando por (zI − G)−1
:
X(z) = (zI − G)−1
zx(0) + (zI − G)−1
HU(Z)
y antitransformando:
x(k) = Z−1
(zI − G)−1
z x(0) + Z−1
(zI − G)−1
HU(z)
Esta ecuación la podemos comparar con la solución mediante el procedimiento recursivo
indicado en la ecuación (1.29), e identificando términos tenemos que:
Gk
= Z−1
(zI − G)−1
z y
k−1
j=0
Gk−j−1
Hu(j) = Z−1
(zI − G)−1
HU(z) (1.34)
La dificultad de este método consiste en realizar la transformada Z de las expresiones
anteriores. Para ilustrar el procedimiento considérese el siguiente ejemplo:
Ejemplo 1.1
Dado un sistema LTI como (1.1) con:
G =
0 1
−0,16 −1
H =
1
1
C = 1 0
Se pide calcular Ψ(k) = GK
= Z−1
{(zI − G)−1
z}. En primer lugar calculamos:
(zI − G)−1
=
z −1
0,16 z + 1
=
z+1
(z+0,2)(z+0,8)
1
(z+0,2)(z+0,8)
−0,16
(z+0,2)(z+0,8)
z
(z+0,2)(z+0,8)
=
4
3
1
z+0,2
− 1
3
1
z+0,8
5
3
1
z+0,2
− 5
3
1
z+0,8
−0,8
3
1
z+0,2
+ 0,8
3
1
z+0,8
−1
3
1
z+0,2
+ 4
3
1
z+0,8
(1.35)

10 RESOLUCI ÓN DE LAS ECUACIONES DEL ESPACIO DE ESTADOS
Multiplicando lo anterior por z y antitransformando se obtiene:
Ψ(k) = Gk
= Z−1
(zI − G)−1
z =
4
3
(−0,2)k
− 1
3
(−0,8)k 5
3
(−0,2)k
− 5
3
(−0,8)k
−0,8
3
(−0,2)k
+ 0,8
3
(−0,8)k
−1
3
(−0,2)k
+ 4
3
(−0,8)k
(1.36)
El ejemplo se puede completar resolviendo completamente la ecuación de estado y la
de la salida para una señal de entrada dada por:
u(k) = 1 k = 0, 1, 2, · · · x(0) =
1
−1
Teniendo en cuenta la transformada Z de la entrada (escalón unitario) y que se sabe
que:
X(z) = (zI − G)−1
[zx(0) + HU(z)]
se calcula:
zx(0) + HU(z) =
z
−z
+
z
z−1
z
z−1
=
z2
z−1
−z2+2z
z−1
que premultiplicado por el resultado de la ecuación (1.35) lleva a:
X(z) =
− 17
6
z
z+0,2
+
22
9
z
z+0,8
+
25
18
z
z−1
3,4
6
z
z+0,2
+
− 17,6
9
z
z+0,8
+
7
18
z
z−1
y de ahi, antitransformando:
x(k) =
−17
6
(−0,2)k
+ 22
9
(−0,8)k
+ 25
18
3,4
6
(−0,2)k
− 17,6
9
(−0,8)k
+ 7
18
Finalmente la ecuación de salida será:
y(k) = 1 0 x(k)
= −
17
6
(−0,2)k
+
22
9
(−0,8)k
+
25
18
1.4.3.1. Procedimiento alternativo para calcular (zI − G)−1
Se observa en el ejemplo 1.1 que gran parte del cálculo se emplea en calcular (zI −
G)−1
. Esto puede ser muy engorroso cuando el orden de las matrices involucradas es
superior a 3. A continuación se detalla un procedimiento alternativo para esos casos.
En primer lugar es conocido que, por definición de matriz inversa:
(zI − G)−1
=
Adj(zI − G)
|zI − G|

donde ((Adj)) indica la matriz adjunta. El determinante |zI − G| se puede expresar
como:
|zI − G| = zn
+ a1zn−1
+ a2zn−2
+ · · · + an
Por otra parte se puede demostrar que:
Adj(zI − G) = Izn−1
+ H1zn−2
+ H2zn−3
+ · · · + Hn−1
donde las matrices Hi se calculan mediante:
H1 = G + a1I
H2 = GH1 + a2I
...
Hn−1 = GHn−1 + an−1I
Hn = GHn−1 + anI = 0
y los ai se calculan a su vez como:
a1 = −traza(G)
a2 = −
1
2
traza(GH1)
a3 = −
1
3
traza(GH2)
...
an = −
1
n
traza(GHn−1)
Ejemplo 1.2
A continuaci´on se calcular´a la inversa de (zI − G) para el ejemplo 1.1 mediante este
procedimiento alternativo. Dado que el orden de la matriz es n = 2, se tiene que:
|zI − G| = z2
+ a1z + a2
Adj(zI − G) = Iz + H1
donde:
a1 = −traza(G)
a2 = −1
2
traza(GH1)
H1 = G + a1I
La traza de G es igual a 1, luego a1 = 1 y de ah´ı se obtiene que H1 = G + I, con lo
que se puede calcular:
a2 = −
1
2
traza
0 1
−0,16 −1
1 1
−0,16 0
= 0,16

12 DISCRETIZACI ÓN DE LAS ECUACIONES DE ESTADO CONTINUAS
con lo que se obtiene:
Adj(zI − G) = Iz +
1 1
−0,16 0
=
z + 1 1
−0,16 z
|zI −G| = z2
+z+0,16 = (z+0,2)(z+0,8)
Finalmente:
(zI − G)−1
=
z + 1 1
−0,16 z
(z + 0,2)(z + 0,8)
que evidentemente es el mismo resultado obtenido en el ejemplo 1.1.
1.5. Discretización de las ecuaciones de estado con-
tinuas
En esta sección veremos cómo se puede pasar de un modelo en espacio de estado
continuo a discreto. Se partirá de un sistema lineal e invariante en el tiempo continuo:
˙x = Ax + Bu
y = Cx + Du
(1.37)
Supondremos que la entrada sólo cambia en ciertos instantes igualmente espaciados en
el tiempo, es decir, sólo puede cambiar en t = kT, para k = 0, 1, 2, · · ·. Al discretizar
la ecuación de estado ésta tomará la forma:
x((k + 1)T) = G(T)x(kT) + H(T)u(kT) (1.38)
donde puede observarse que las matrices G y H dependen del tiempo de muestreo T.
Para determinar el valor de G(T) y H(T) usaremos la solución de la ecuación de estado
en tiempo continuo:
x(t) = eAt
x(0) + eAt
t
0
e−Aτ
Bu(τ)dτ (1.39)
Supondremos que la entrada u(t) es muestreada mediante un mantenedor de orden
cero, por lo que se cumple que:
u(t) = u(kT) para kT ≤ t ≤ kT + T (1.40)

Se tiene que:
x((k + 1)T) = eA(k+1)T
x(0) + eA(k+1)T
(k+1)T
0
e−Aτ
Bu(τ)dτ (1.41)
x(kT) = eAkT
x(0) + eAkT
kT
0
e−Aτ
Bu(τ)dτ (1.42)
Mutiplicando la ecuación (1.42) por eAT
y restándola de la ecuación (1.41) se obtiene:
x((k + 1)T) = eAT
x(kT) + eA(k+1)T
(k+1)T
kT
e−Aτ
Bu(τ)dτ (1.43)
Teniendo en cuenta la suposición de que u(t) es constante en el intervalo de integración
(ver (1.40)) se puede sustituir u(τ) por u(kT). Aplicando esto y operando se llega a:
x((k + 1)T) = eAT
x(kT) + eAT
T
0
e−Aτ
Bu(kT)dτ
= eAT
x(kT) +
T
0
e−Aλ
Bu(kT)dλ (1.44)
donde λ = T − τ. Sea:
G(T) = eAT
H(T) =
T
0
eAλ
dλ B
(1.45)
entonces la ecuación (1.44) queda:
x((k + 1)T) = G(T)x(kT) + H(T)u(kT) (1.46)
que es la ecuación a la que ten´ıamos que llegar y por tanto se ha obtenido la ecuación
de estado continuo discretizada.
En el caso particular (aunque muy común, y por tanto interesante) de que A sea
una matriz invertible se tiene que:
H(T) = eAT
− I A−1
B
Por otra parte, la ecuación de la salida al ser discretizada queda:
y(kT) = Cx(kT) + Du(kT) (1.47)
con C, D matrices constantes e iguales a la de la ecuación en tiempo continuo.
Existen diferentes métodos para calcular eAT
. Quizás el más sencillo de aplicar
cuando se trata de calcular la exponencial con papel y lápiz sea utilizar la equivalencia:
eAt
= L−1
(sI − A)−1
(1.48)

14 DISCRETIZACI ÓN DE LAS ECUACIONES DE ESTADO CONTINUAS
donde L−1
indica la transformada de Laplace inversa. Desde el punto de vista práctico
el método consistir´ıa en calcular (sI−A)−1
(nótese que puede emplearse el método para
calcular (zI − G)−1
dado en la sección 1.4.3.1) y aplicar a posteriori la transformada
de Laplace inversa a cada elemento de la matriz.
Ejemplo 1.3
Se ilustrará en este ejemplo el cálculo de eAt
siendo:
A =
0 1
0 −2
Para ello se calcula:
(sI − A) =
s 0
0 s
−
0 1
0 −2
=
s −1
0 s + 2
y aplicando los métodos vistos en la sección 1.5 y subsiguientes se calcula la inversa:
(sI − A)−1
=
1
s
1
s(s+2)
0 1
(s+2)
Finalmente se aplica la transformada inversa de Laplace a cada elemento de la matriz
anterior de manera que se obtiene:
eAt
= L−1
(sI − A)−1
=
1 1
2
(1 − e−2t
)
0 e−2t
Ejemplo 1.4
Como ejemplo de discretización de las ecuaciones de estado en tiempo continuo, con-
sidérese el siguiente sistema:
˙x = −ax + u
y = x
Usando las expresiones de (1.45) se obtiene:
G(T) = eAT
= e−aT
y
H(T) =
T
0
eAλ
dλ B
=
T
0
e−aλ
dλ
= 1−e−aT
a

Luego:
x(k + 1) = e−aT
x(k) + 1−e−aT
a
u(k)
y(k) = x(k)
1.6. Controlabilidad y Observabilidad
En esta sección se pasan a tratar dos conceptos clave en el estudio de sistemas
dinámicos, la controlabilidad y la observabilidad. El primero se refiere a la existencia
de una secuencia de actuaciones para llevar el sistema a un estado arbitrario. Por
otro lado, la observabilidad tiene que ver con la posibilidad de determinar el valor del
vector de estados de un sistema a partir de observaciones de las salidas y la entradas
de dicho sistema. Ambos conceptos se deben a Kalman y son claves en estrategias de
control como la colocación de polos por realimentación del vector de estados o el control
óptimo.
1.6.1. Controlabilidad
Definición 1.2 Un sistema de control es completamente controlable o de estado com-
pletamente controlable, si es posible transferir al sistema desde un estado inicial ar-
bitrario a cualquier estado deseado en un tiempo finito. También puede decirse que
será completamente controlable, si cada variable de estado se puede controlar en un
tiempo finito por una señal de control que no esté sujeta a ningún tipo de restricción.
Como es habitual nos centraremos en el estudio de la controlabilidad de sistemas
LTI:
x((k + 1)T) = Gx(kT) + Hu(kT) (1.49)
siendo la señal u(kT) constante en el intervalo de tiempo kT ≤ t ≤ (k + 1)T. En este
caso, la controlabilidad de estado completo implica que existe una señal de control
constante entre cada tiempo de muestreo que transfiere al sistema, desde un estado
x(kT) cualquiera a un estado deseado xf en como mucho n periodos de muestreo,
donde n es el tamaño del vector de estados.
Recordemos que la solución de la ecuación de estados es:
x(nT) = Gn
x(0) +
n−1
j=0
Gn−j−1
Hu(jT)

16 CONTROLABILIDAD Y OBSERVABILIDAD
= Gn
x(0) + Gn−1
Hu(0) + Gn−2
Hu(T) + · · · + Hu((n − 1)T)
de ah´ı se obtiene:
x(nT) − Gn
x(0) = H
... GH
... · · ·
... Gn−1
H





u((n − 1)T)
u((n − 2)T)
...
u(0)





(1.50)
donde la matriz
Mc = H
... GH
... · · ·
... Gn−1
H (1.51)
es la llamada matriz de controlabilidad.
Supóngase un estado final arbitrario x(nT) = xf . Si el sistema fuera controlable
deber´ıa existir un vector de actuaciones que al multiplicarlo por la matriz de controla-
bilidad (1.51) diese como resultado xf − Gn
x(0). Como xf y x(0) pueden ser cualquier
par de valores del vector de estado, es fácil entender que xf −Gn
x(0) puede ser cualquier
vector de Rn
. De esto se desprende que para que el sistema sea controlable, el espa-
cio de vectores generado por los vectores que forman la matriz de controlabilidad (es
decir, sus columnas) debe ser todo Rn
. La condición necesaria y suficiente para que
se cumpla esto es que el rango de la matriz de controlabilidad sea n. Este resultado
permite enunciar el siguiente lema.
Lema 1.1 Dado un sistema LTI de orden n representado por (1.49), es condición
necesaria y suficiente para que el sistema sea completamente controlable que el rango
de la matriz de controlabilidad (1.51) sea igual a n.
Comentario 1.1 El sistema que cumpla la condición establecida en el lema 1.1 po-
drá alcanzar cualquier estado como máximo en n periodos de muestreo, pero sólo si no
existen restricciones sobre la señal de control. En caso contrario, se tardar´ıa más.
Si el sistema es controlable, se podrá determinar la secuencia de valores de la entrada
necesaria para llevar al sistema a xf resolviendo el sistema de ecuaciones (1.50).
Por otra parte, la controlabilidad se puede comprobar a partir de la función de
transferencia de un sistema observando si hay cancelaciones de polos y ceros. En el
caso de que las hubiese, el sistema no ser´ıa controlable. Por tanto, el sistema
Y (z)
U(z)
=
z + 0,2
(z + 0,8)(z + 0,2)
no ser´ıa controlable pues existe una cancelación de un polo con un cero.

1.6.2. Controlabilidad de la salida completa
En control automático el objetivo más común es controlar la evolución de la salida
del sistema. Se puede demostrar que la controlabilidad del estado no implica la contro-
labilidad de la salida. Sin embargo, podemos comprobar dicha controlabilidad de una
manera análoga a la de la controlabilidad del estado completo. Sea un sistema cuya
ecuación de estado es (1.49) y la ecuación de la salida es:
y(kT) = Cx(kT) (1.52)
La condición para comprobar la controlabilidad de la salida completa ser´ıa que
Rango CH
... CGH
... · · ·
... CGn−1
H = m (1.53)
donde m es el número de salidas. Por otra parte, si la ecuación de la salida es:
y(kT) = Cx(kT) + Du(kT) (1.54)
la condición a comprobar ser´ıa:
Rango D
... CH
... CGH
... · · ·
... CGn−1
H = m (1.55)
Nótese que en esta segunda forma de la ecuación de salida, la presencia del término
Du(kT) no empeora la controlabidad del sistema, sino justo lo contrario. De hecho, al
introducirse una columna extra en la matriz de controlabilidad (la correspondiente a
D), se puede dar el caso que se pase de tener m−1 columnas linealmente independientes
a tener m, por lo que se lograr´ıa la controlabilidad de la salida. Dicho de otra manera,
encontrar m vectores linealmente independientes siempre será igual o más fácil entre
n + 1 vectores que entre sólo n de esos vectores.
1.6.3. Observabilidad
Considérese un sistema autónomo:
x((k + 1)T) = Gx(kT)
y(kT) = Cx(kT)
(1.56)
Definición 1.3 El sistema autónomo (1.56) es completamente observable si todo es-
tado inicial x(0) se puede determinar de la observación de y(kT) durante un número
finito de intervalos de muestreo. Para que ello ocurra, cada transición del estado debe
afectar a todos los elementos del vector de salida.

18 CONTROLABILIDAD Y OBSERVABILIDAD
La observabilidad juega un papel esencial en el control de aquellos sistemas en los
que algunas de las variables de estado no son accesibles, es decir, no son medibles
directamente. Nótese que se ha considerado un sistema autónomo. La razón de esto es
que la observabilidad de un sistema no autónomo se reduce a la del sistema autónomo
equivalente.
Se sabe que la solución de la ecuación de estado para el sistema autónomo (1.56)
es:
x(kT) = Gk
x(0)
y de ah´ı
y(kT) = CGk
x(0)
La observabilidad completa implica que usando
y(0), y(T), y(2T), · · · , y((n − 1)T)
se pueden determinar
x1(0), x2(0), · · · , xn(0)
donde xi(0) indica la iésima componente de x(0). Es decir el sistema es completamente
observable si las ecuaciones:
y(0) = Cx(0)
y(T) = CGx(0)
...
y((n − 1)T) = CGn−1
x(0)
permiten determinar x1(0), x2(0), · · · , xn(0). Como y(kT) es un m-vector (asumiendo
que el sistema tiene m salidas) el sistema de ecuaciones anterior es en realidad un
sistema de n × m ecuaciones, en las que las incógnitas son las n componentes de x(0).
Para que la solución de este sistema sea única debe haber entre ellas n ecuaciones
linealmente independientes. Esto se traduce en la siguiente condición de observabilidad
completa:
Rango C∗ ... G∗
C∗ ... · · ·
... (G∗
)n−1
C∗ = n (1.57)
donde ∗
indica la conjugada traspuesta de una matriz y a la matriz que aparece en la
condición se la llama matriz de observabilidad.
Por otra parte, de una manera análoga a la de la controlabilidad, la observabilidad
de un sistema a partir de su función de transferencia se puede asegurar si ésta no
presenta cancelaciones de polos y ceros.

Finalmente, se enuncia a continuación una propiedad que será útil para poder obte–
ner la representación de un sistema en forma canónica, sin que por ello pueda argu-
mentarse que existe la posibilidad de variar la controlabilidad u observabilidad del
mismo.
Propiedad 1.1 Sea un sistema LTI dado en la forma usual (1.1), cuya matriz de
controlabilidad es M y la de observabilidad es N. Si se define una transformación
como (1.26) con:
ˆG = P−1
GP
ˆH = P−1
H
ˆC = CP
siendo P una matriz invertible, entonces las matrices de controlabilidad y observabilidad
del sistema equivalente tienen el mismo rango que M y N.
1.6.4. Principio de Dualidad
Este principio, que es debido a Kalman, relaciona la controlabilidad y observabilidad
de un sistema con la de otro sistema llamado dual del primero. Sea un sistema S1:
S1 :
x((k + 1)T) = Gx(kT) + Hu(kT)
y(kT) = Cx(kT)
(1.58)
Sea S2 el sistema dual de S1:
S2 :
ˆx((k + 1)T) = G∗
ˆx(kT) + C∗
û(kT)
ˆy(kT) = H∗
ˆx(kT)
(1.59)
Entonces se puede afirmar que2
:
SI S1
CONTROLABLE
OBSERVABLE
ENTONCES S2
OBSERVABLE
CONTROLABLE
1.7. Transformación de un sistema en formas canónicas
Sea un sistema controlable y observable:
x(k + 1) = Gx(k) + Hu(k)
y(k) = Cx(k) + Du(k)
(1.60)
2
Nótese que los sistemas S1 y S2 son diferentes, es decir, S2 no es una representación alternativa
de S1.

20 TRANSFORMACI ÓN DE UN SISTEMA EN FORMAS CAN ÓNICAS
A continuación, se verá el procedimiento para obtener las formas canónicas a partir de
ese sistema.
1.7.1. Obtención de la forma canónica controlable
Sea una matriz de transformación T = MW con:
M = H
... GH
... · · ·
... Gn−1
H W =







an−1 an−2 · · · a1 1
an−2 an−3 · · · 1 0
...
...
...
...
a1 1 · · · 0 0
1 0 · · · 0 0







donde los coeficientes ai son los coeficientes de la ecuación caracter´ıstica del sistema,
es decir:
|zI − G| = zn
+ a1zn−1
+ · · · + an−1z + an = 0
Se define el estado x(k) en función de la transformación de otro vector de estados ˆx(k):
x(k) = T ˆx(k)
Entonces el sistema:
ˆx(k + 1) = ˆGˆx(k) + ˆHu(k)
y(k) = ˆCx(k) + ˆDu(k)
(1.61)
con ˆG = T−1
GT, ˆH = T−1
H, ˆC = CT, ˆD = D está en forma canónica controlable.
1.7.2. Obtención de la forma canónica observable
En este caso la matriz de transformación es:
Q = (WN∗
)−1
con
N = C∗ ... G∗
C∗ ... · · ·
... (G∗
)n−1
C∗
Sea ˆG = Q−1
GQ, ˆH = Q−1
H, ˆC = CQ, ˆD = D y def´ınase el estado x(k) como
x(k) = Qˆx(k). Entonces el sistema (1.61) está en forma canónica observable.

1.8. Colocación de polos mediante realimentación
del vector de estados
En esta sección se presentará una estrategia de control que permite elegir la situación
de los polos de bucle cerrado del sistema, mediante la realimentación lineal del vector
de estados. Se verá que la condición necesaria para que esto se pueda conseguir es que
el sistema sea controlable. Por otra parte, se asumirá que todas las variables de estados
son accesibles, es decir, podemos medirlas directamente sin tener que estimarlas por
otros procedimientos.
1.8.1. Condición necesaria y suficiente para la colocación ar-
bitraria de polos
Sea un sistema LTI:
x(k + 1) = Gx(k) + Hu(k)
Se escoge una ley de control que tiene la forma:
u(k) = −Kx(k)
es decir, la señal de control se obtiene de la realimentación negativa del vector de
estados multiplicado por una cierta matriz de ganancias K. Este tipo de ley de control
se la denomina usualmente realimentación del vector de estados. Con esta ley de control
el sistema en bucle cerrado quedar´ıa:
x(k+1)
H z-1¡
G
+
+
x(k)
-K
u(k)
Figura 1.2: Diagrama de bloques de un sistema controlado por una realimentación del vector de
estados.
y la ecuación de estado del sistema en bucle cerrado resultar´ıa ser:
x(k + 1) = (G − HK)x(k)

22 COLOCACI ÓN DE POLOS MEDIANTE REALIMENTACI ÓN DEL VECTOR DE ESTADOS
De manera análoga a lo que se da en sistemas continuos, los autovalores de (G − HK)
son (o coinciden con) los polos de bucle cerrado del sistema. Por tanto, lo que buscamos
es ver que condición es necesario cumplir para que exista una matriz de ganancias K
determinada, que nos permita colocar los autovalores de (G − HK) en unos valores
elegidos a voluntad.
Lema 1.2 Se demuestra que la condición necesaria y suficiente para que por medio de
una realimentación del vector de estados puedan escogerse los polos de bucle cerrado
(es decir, los autovalores de (G−HK)) es que el sistema en bucle abierto sea de estado
completamente controlable. Si esta condición no se cumple, no se podrán elegir todos
los polos de bucle cerrado.
1.8.2. Procedimientos para calcular K
Sean µ1,µ2,· · ·,µn los valores deseados para los polos de bucle cerrado, es decir,
para los autovalores de (G−HK). Aquellos que sean complejos siempre irán por pares
conjugados. La ecuación caracter´ıstica del sistema en bucle abierto es:
|zI − G| = zn
+ a1zn−1
+ · · · + an = 0
Se define una matriz de transformación T = MW exactamente igual que la matriz
de transformación necesaria para obtener la forma canónica controlable descrita en la
sección 1.7.1. Se obtiene:
T−1
GT = ˆG =







0 1 0 · · · 0
0 0 1 · · · 0
...
...
...
...
0 0 0 · · · 1
−an −an−1 −an−2 · · · −a1







T−1
H = ˆH =







0
0
...
0
1







Se define a continuación:
ˆK = KT = δn δn−1 · · · δ1
Entonces:
ˆH ˆK =





0
0
...
1





δn δn−1 · · · δ1 =







0 0 · · · 0
0 0 · · · 0
...
...
...
0 0 · · · 0
δn δn−1 · · · δ1








Por otra parte, la ecuación caracter´ıstica del sistema en B.C. es:
|zI − G − HK| = |zI − ˆG + ˆHK|
= z







1 0 · · · 0
0 1 · · · 0
...
...
...
0 0 · · · 0
0 0 · · · 1







−







0 1 0 · · · 0
0 0 1 · · · 0
...
...
...
...
0 0 0 · · · 1
−an −an−1 −an−2 · · · −a1







+







0 0 · · · 0
0 0 · · · 0
...
...
...
0 0 · · · 0
δn δn−1 · · · δ1







=
z −1 · · · 0
0 z · · · 0
...
...
...
0 0 · · · −1
an + δn an−1 + δn−1 · · · z + a1 + δ1
= zn
+ (a1 + δ1)zn−1
+ · · · + (an−1 + δn−1)z + (an + δn) = 0
A su vez, la ecuación caracter´ıstica correspondiente a los autovalores deseados será:
(z − µ1)(z − µ2) · · · (z − µn) = zn
+ α1zn−1
+ α2zn−2
+ · · · + αn−1 + αn = 0
Igualando los coeficientes de ambas ecuaciones caracter´ısticas:
α1 = a1 + δ1
α2 = a2 + δ2
...
αn = an + δn
se obtiene la siguiente expresión para K:
K = ˆKT−1
= δn δn−1 · · · δ1 T−1
= αn − an
...αn−1 − an−1
... · · ·
...α1 − a1
T−1
(1.62)
que coloca los polos de bucle cerrado del sistema en los valores deseados. Nótese
que si el sistema en bucle abierto viene dado en forma canónica controlable, se verifica
que T = I = T−1
.

1.8.2.1. Procedimiento alternativo: la fórmula de Ackermann
Existen otros procedimientos alternativos para el cálculo de la matriz K. Aqu´ı men-
cionaremos uno muy conocido, el que emplea la fórmula de Ackermann. Según esto, la
expresión para K tomar´ıa la forma:
K = 0 0 · · · 0 1 H
... GH
... · · ·
... Gn−1
H
−1
φ(G)
donde:
φ(G) = Gn
+ α1Gn−1
+ · · · + αn−1G + αnI
Los coeficientes αi se calcularán como en el apartado anterior.
Finalmente, otro procedimiento que puede ser útil para sistemas de bajo orden
consiste en tomar
K = k1 k2 · · · kn
plantear la ecuación caracter´ıstica en función de los ki:
|zI − G + HK| = 0
e igualar a los coeficientes de
zn
+ α1zn−1
+ α2zn−2
+ · · · + αn−1 + αn = 0
1.8.3. Control Dead-Beat
Este es un tipo de control que resulta ser un caso particular del control por colo-
cación de polos.
Definición 1.4 Dado un sistema LTI, entenderemos como control dead-beat aquel que
consigue llevar el estado a cero en como máximo n intervalos de muestreo, donde n es
el orden del sistema.
Para obtener este tipo de control se deben especificar los polos de bucle cerrado con-
forme a lo que se establece en el siguiente lema.
Lema 1.3 Se demuestra que si se escogen los polos de bucle cerrado de manera que
estén todos en el origen (es decir, todos los autovalores de (G − HK) igual a cero) se
consigue un control dead-beat.

Esto se lleva a la práctica con una matriz de realimentación del vector de estados
calculada mediante:
K = −an −an−1 · · · −a1 T−1
Este tipo de control no goza de una reputación excesivamente favorable porque habit-
ualmente se precisa de una señal de control de amplitud muy grande para obtener la
respuesta dead-beat. De hecho en este tipo de control, el único parámetro de diseño
que se ha de elegir es el tiempo de muestreo. Si éste es muy pequeño, los n intervalos
de muestreo supondrán un tiempo total muy corto, de manera que para llevar el estado
a cero partiendo de un estado inicial arbitrario se precisará un valor muy alto de la
señal.
Ejemplo 1.5
Sea un sistema
x(k + 1) = Gx(k) + Hu(k)
con
G =
0 1
−0,16 −1
0
1
Se desea determinar una matriz K, tal que los polos de bucle cerrado sean el par
complejo conjugado z = 0,5 ± j0,5.
En primer lugar hay que determinar la controlabilidad del sistema. Para ello, se
forma la matriz de controlabilidad:
H
... GH =
0 1
1 −1
cuyo rango es igual a dos (basta comprobar que su determinante es distinto de cero),
por lo que el sistema es controlable y se puede proceder a calcular K. La ecuación
caracter´ıstica de bucle cerrado deseada es:
|zI − G + HK| = (z − 0,5 − j0,5)(z − 0,5 + j0,5) = z2
− z + 0,5 = 0 (1.63)
por tanto, los coeficientes αi son en este caso α1 = −1 y α2 = 0,5. Por otra parte, la
ecuación caracter´ıstica de bucle abierto del sistema es:
|zI − G| =
z −1
0,16 z + 1
por lo que los coeficientes ai son a1 = 1 y a2 = 0,16. A partir de aqu´ı se puede aplicar
cualquiera de los métodos explicados anteriormente.

Método 1
K = α2 − a2
... α1 − a1
T−1
Obsérvese que el sistema viene dado en forma canónica controlable, por lo que T = I
y por tanto:
K = 0,34 −2
Método 2 (fórmula de Ackermann)
En este caso la fórmula de Ackermann ser´ıa:
K = 0 1 H
... GH
−1
φ(G)
donde φ(G) es
φ(G) = G2
− G + 0,5I
=
−0,16 −1
0,16 0,84
−
0 1
−0,16 −1
+
0,5 0
0 0,5
=
0,34 −2
0,32 2,34
por lo que
K = 0 1
0 1
1 −1
−1
0,34 −2
0,32 2,34
= 0,34 −2
Método 3
Este procedimiento es apropiado para sistemas de bajo orden como el que nos ocupa.
En primer lugar, se toma K = [k1 k2] y se formula la ecuación caracter´ıstica de bucle
cerrado en función de K:
|zI − G + HK| =
z 0
0 z
−
0 1
−0,16 −1
+
0
1
k1 k2
=
z −1
0,16 + k1 z + 1 + k2
= z2
+ (1 + k2)z + k1 + 0,16 = 0
la comparamos con la ecuación caracter´ıstica deseada (1.63) e identificamos coeficientes:
1 + k2 = −1
k1 + 0,16 = 0,5

de donde se obtiene que k1 = 0,34 y k2 = −2, por lo que se tiene ya el valor de K, que
evidentemente coincide con el obtenido mediante los dos métodos anteriores.
Ejemplo 1.6
Calcular para el mismo sistema del ejemplo anterior la matriz K que conlleva un
control dead-beat, y comprobarlo calculando la evolución del sistema a partir de un
estado inicial arbitrario.
En este caso:
K = −a2 −a1 T−1
= −0,16 −1
Vamos a verificar que el control es dead-beat. Para ello, obtenemos la ecuación de
estado del sistema en bucle cerrado:
x1(k + 1)
x2(k + 1)
=
0 1
−0,16 − 1
x1(k)
x2(k)
+
0
1
0,16 1
x1(k)
x2(k)
=
0 1
0 0
x1(k)
x2(k)
Supongamos ahora que el estado inicial es
x1(0)
x2(0)
=
a
b
entonces se tiene que:
x1(1)
x2(1)
=
0 1
0 0
a
b
=
b
0
e iterando una vez más:
x1(2)
x2(2)
=
0 1
0 0
b
0
=
0
0
luego este control lleva al estado a cero en 2 pasos y es efectivamente un control dead-
beat.
1.9. Observadores del estado
En el control por colocación de polos se asume que el estado se puede medir direc-
tamente. En ocasiones, sin embargo, puede que esta suposición no se cumpla y todas

28 OBSERVADORES DEL ESTADO
o algunas de las variables de estado no puedan ser medidas. Es decir, puede que haya
variables de estado no accesibles. En cualquier caso, para poder controlar el sistema se
deberán estimar los valores de esas variables de estado no accesibles. Este proceso de
estimación es lo que se conoce como observación.
Un observador del estado es un subsistema del sistema de control, que realiza la
estimación de las variables de estado basándose en los valores medidos (observados) de
las salidas y la señal de control. Se distinguen tres tipos de observadores, en función
de las variables de estado que se estimen:
1. Observador del estado completo. Es aquél que estima todas las variables de esta-
do.
2. Observador de orden m´ınimo. En este caso sólo se estiman aquellas variables de
estado que no son accesibles.
3. Observador de orden reducido. Este tipo de observador estima todas las variables
no accesibles y algunas de las accesibles.
En esta asignatura nos centraremos en los dos primeros tipos de observadores. Como
en el caso de la colocación de polos, formularemos en primer lugar las condiciones para
que se pueda llevar a cabo la observación.
Lema 1.4 Condición necesaria y suficiente para la observación del estado. Dado un
sistema LTI, se puede determinar x(k + 1) a partir de y(k), y(k − 1),· · ·,y(k − n + 1) y
u(k),u(k − 1),· · ·,u(k − n + 1), donde n es el orden del sistema, s´ı y sólo s´ı, el sistema
es completamente observable.
Por tanto x(k + 1) se puede determinar, si el sistema es observable, en n pasos. Sin
embargo, no debe olvidarse que sobre el sistema actúan ruidos y perturbaciones. Por
esta razón no es posible utilizar un procedimiento algebraico para determinar el estado,
sino que se ha de acudir a un procedimiento iterativo para estimarlo.
1.9.1. Procedimiento iterativo para la estimación del estado
Sea un sistema LTI
x(k + 1) = Gx(k) + Hu(k)
y(k) = Cx(k)
(1.64)

Si se dispone de una aproximación del estado en k, que denotaremos ˆx(k), ésta evolu-
cionará según la dinámica del sistema
ˆx(k + 1) = Gˆx(k) + Hu(k)
ˆy(k) = Cˆx(k)
(1.65)
Si las condiciones iniciales son las mismas, es decir, si x(0) = ˆx(0) entonces se verifica
que x(k) = ˆx(k). Sin embargo, si las condiciones iniciales son diferentes entonces, de
manera general, x(k) = ˆx(k). Podemos pues, definir el error de estimación en k como:
e(k) = x(k) − ˆx(k)
Restando la ecuación de estado aproximada (1.65) de la real (1.64):
x(k + 1) − ˆx(k + 1) = G (x(k) − ˆx(k))
que teniendo en cuenta la definición del error de aproximación es equivalente a:
e(k + 1) = Ge(k)
que se puede considerar como un sistema dinámico autónomo. Si G es una matriz
estable (es decir, si sus autovalores están dentro del c´ırculo unidad) el ((estado)) de este
sistema tiende a cero, es decir:
e(k) → 0 ⇒ ˆx(k) → x(k)
Por tanto, si el sistema es estable, la propia dinámica del sistema hace que la aproxi-
mación del estado tienda al valor real del mismo. Esto quiere decir que podr´ıamos usar
la propia ecuación del sistema para obtener en cualquier instante k una aproximación
del estado, cuyo error ir´ıa decayendo a lo largo del tiempo. Esta convergencia al valor
real, sin embargo, puede ser muy lenta, y por otra parte no siempre se tratará con
sistemas estables. Por tanto, esta estrategia no es muy aconsejable.
Nótese que en el esquema que se ha presentado, no se hace uso de la salida del sis-
tema, que siempre será accesible. Esto puede ser aprovechado para mejorar el rendimien-
to del observador introduciéndose un término corrector, de manera que la ecuación para
obtener la aproximación del estado para el instante k + 1 ser´ıa:
ˆx(k + 1) = Gˆx(k) + Hu(k) + Ke (y(k) − Cˆx(k))
donde Ke es una matriz de ponderación o ganancia. Este término se puede elegir de
manera que se mejore el rendimiento, incluso si existen discrepancias entre las matrices
del sistema y las del proceso real al que dicho sistema representa.

1.9.2. Observador del estado completo
Sea un sistema LTI observable (1.64) con una ley de control por realimentación
negativa del vector de estados,
u(k) = −Kx(k)
siendo el estado del sistema x(k) no accesible pero s´ı observable. Por tanto, podemos
sustituir el valor del estado por una aproximación de manera que
u(k) = −Kˆx(k)
y de ah´ı, aplicando las consideraciones de la sección 1.9.1 se obtiene
ˆx(k + 1) = Gˆx(k) + Hu(k) + Ke (y(k) − ˆy(k))
= (G − KeC)ˆx(k) + Hu(k) + Key(k)
= (G − KeC − HK)ˆx(k) + Key(k)
(1.66)
Ésta es la llamada ecuación del observador predictivo. La palabra predictivo se utiliza
para indicar que la estimación del valor futuro del estado en k +1, se realiza utilizando
información disponible en el instante k. A los autovalores de la matriz (G − KeC)
se les suele denominar polos del observador, y como se hizo en la sección 1.9.1, se
verá a continuación que marcan la dinámica de la evolución del error de observación.
En efecto, si se resta la ecuación del observador de la del sistema real (1.64) se llega a
que
e(k + 1) = (G − KeC)e(k)
de lo que puede observarse que los polos del observador determinan la dinámica del
error. Si G − KeC es estable, el error convergerá a cero independientemente de la
estimación del estado inicial ˆx(0).
La ecuación del observador y del propio sistema en espacio de estados controlado
por la realimentación lineal del vector de estados, pueden representarse mediante un
diagrama de bloques que se ilustra en las figuras 1.3 y 1.4.
Finalmente, es evidente que interesa que la estimación del estado converja rápida-
mente al valor real de dicho estado. Una manera evidente de lograr esto es colocar todos
los polos del observador en cero, de manera que se consiga que el error de aproximación
muestre una respuesta dead-beat. Esto se consigue eligiendo de manera apropiada Ke.

x(k+1)
+
H
u(k)
z-1¢ C
G
+
+
x(k)
OBSERVADOR
y(k)
y(k)
-K
u(k)
(k)x£
u(k)
Figura 1.3: Diagrama de bloques de un sistema LTI controlado mediante una realimentaci´on del vector
de estados que estima el estado con un observador.
x(k+1) +
Hu(k)
z-1¤ C
G
+
+
Ke
(k)x¥
(k)y¦
y(k)-+
+
(k)x§
Figura 1.4: Diagrama de bloques de un observador de orden completo.

1.9.2.1. Cálculo de Ke
El procedimiento para elegir Ke de manera que se coloquen los polos del observador
en unos valores especificados es análogo al de la colocación de polos vista en la sección
1.8. Si la ecuación caracter´ıstica deseada del observador es:
zn
+ α1zn−1
+ · · · + αn−1z + αn = 0
y la del sistema es
zn
+ +a1zn−1
+ · · · + an−1z + an = 0
entonces
Ke = (WN∗
)−1





αn − an
αn−1 − an−1
...
α1 − a1





(1.67)
donde
W =







an−1 an−2 · · · a1 1
an−2 an−3 · · · 1 0
...
...
...
...
a1 1 · · · 0 0
1 0 · · · 0 0







N = C∗ ... G∗
C∗ ... · · ·
... (G∗
)n−1
C∗
es decir, la misma matriz W empleada en la colocación de polos y la matriz de ob-
servabilidad3
. Nótese que si el sistema viene indicado en forma canónica observable
(WN∗
)−1
= I. También puede emplearse la fórmula de Ackermann, que para este caso
es:
Ke = φ(G)





C
CG
...
CGn−1





−1 




0
0
...
1





donde
φ(G) = Gn
+ α1Gn−1
+ · · · + αn−1G + αnI = 0
Ejemplo 1.7
Considérese un sistema como (1.64) con
G =
1 1
0 1
H =
0,5
1
C = 1 0
3
A fin de obtener un texto más legible se evita en lo posible hacer referencias a material anterior,
aún a pesar de que esto pueda alargar la exposición del tema al repetirse ecuaciones y expresiones.

diseñaremos un observador del estado. En primer lugar, se ha de comprobar que el
sistema es observable. Para ello se comprueba que
rango C∗ ... G∗
C∗ = rango
1 1
0 1
= 2
luego el sistema es completamente observable. El siguiente paso es hallar la ecuación
caracter´ıstica del sistema en bucle abierto:
|zI − G| =
z 0
0 z
−
1 1
0 1
= z2
− 2z + 1 = 0
luego a1 = −2 y a2 = 1. Deseamos que el observador tenga una respuesta dead-beat,
luego la ecuación caracter´ıstica deseada del observador será:
z2
= 0 ⇒ α1 = α2 = 0
A continuación se calculará Ke:
Ke = (WN∗
)−1 −1
2
con
N =
1 1
0 1
W =
a1 1
1 0
=
−2 1
1 0
resultando
Ke =
2
1
Cálculo de Ke mediante la fórmula de Ackermann
En este caso la fórmula de Ackermann es:
Ke = φ(G)
C
CG
−1
0
1
con
φ(G) = G2
+ α1G + α2I = G2
resultando
Ke =
1 1
0 1
2
1 0
1 1
−1
0
1
=
2
1
que evidentemente es el mismo resultado que el obtenido con el procedimiento anterior.

Estudio de la evolución del error de estimación
Vamos a comprobar que el error cae a cero según una respuesta dead-beat. Sea
x(0) =
a1
b1
ˆx(0) =
a2
b2
entonces
e(0) = x(0) − ˆx(0) =
a1 − a2
b1 − b2
=
a
b
además se tiene que
G − KeC =
−1 1
−1 1
el error evoluciona, por tanto, según
e1(k + 1)
e2(k + 1)
=
−1 1
−1 1
e1(k)
e2(k)
por lo que se calcula la evolución de este error:
e1(1)
e2(1)
=
−1 1
−1 1
a
b
=
−a + b
−a + b
e1(2)
e2(2)
=
−1 1
−1 1
−a + b
−a + b
=
0
0
luego, tal y como se pretend´ıa, la estimación del vector de estados coincide con el
valor real de dicho vector dos tiempos de muestreo después de iniciarse la estimación.
Finalmente, la ecuación del observador es:
ˆx1(k + 1)
ˆx1(k + 1)
=
−1 1
−1 1
ˆx1(k)
ˆx1(k)
+
0,5
1
u(k) +
2
1
y(k)
1.9.2.2. Comentarios acerca del papel de Ke
Se ha visto que Ke se utiliza para corregir la estimación, disminuyendo el efecto de
las incertidumbres que se tengan sobre la dinámica real de la planta. Si estas incer-
tidumbres son importantes (es decir, si se tiene poca confianza en que el modelo de la

planta coincida con la dinámica real de la misma) este término corrector deber´ıa tomar
un valor alto. Sin embargo, si la señal de salida está contaminada por perturbaciones y
ruido en general procedente, por ejemplo, de los sensores de medida, entonces la señal
de salida no es fiable en el sentido de que no proviene únicamente de la dinámica real de
la planta. Por tanto, en estas situaciones el término corrector deber´ıa ser más pequeño.
Al seleccionar Ke se debe pensar no sólo en reducir el error en base a una corrección
enérgica, sino que hay que tener en cuenta que cuando hay ruidos o perturbaciones,
una ganancia Ke alta no contribuir´ıa a reducir el error, porque las correcciones no ir´ıan
en la ((dirección)) correcta. Es decir, hay que llegar a un compromiso entre la velocidad
de respuesta y la sensibilidad a ruidos y perturbaciones.
1.9.2.3. Efectos de la adición del observador
Hemos supuesto que al no disponerse de x(k) para calcular la señal de control, se
usa el observador para producir una estimación ˆx(k), de manera que
u(k) = −Kˆx(k) (1.68)
Cabe preguntarse si al usar el observador, se colocan los polos del sistema en el sitio
que se pretende al calcularse la ganancia de realimentación del vector de estado K.
¿Que efectos tiene el observador sobre los polos de bucle cerrado? Para estudiar esto,
se analizará el efecto que tiene la adición del observador sobre la ecuación caracter´ıstica
del sistema en bucle cerrado.
Sea el sistema (1.64) controlado mediante (1.68). La ecuación de estado puede
reescribirse como:
x(k + 1) = Gx(k) − HKˆx(k)
= (G − HK)x(k) + HK(x(k) − ˆx(k))
= (G − HK)x(k) + HKe(k)
donde e(k) es el error de observación en el instante k. Recordemos que el error de
observación viene dado por:
e(k + 1) = (G − KeC)e(k)
La ecuación de estado y la del error, se pueden combinar en la ecuación de un sistema
autónomo aumentado que describe la dinámica del sistema observado (es decir, de todo
el conjunto sistema-controlador-observador):
x(k + 1)
e(k + 1)
=
G − HK HK
0 G − KeC
x(k)
e(k)

La ecuación caracter´ıstica de este sistema es
zI − G + HK −HK
0 zI − G + KeC
= 0
es decir,
|zI − G + HK||zI − G + KeC| = 0
Dado que las ra´ıces de esta ecuación son las ra´ıces de cada uno de los dos determinantes
que aparecen, esto implica que los polos del sistema completo son los polos del sistema
en bucle cerrado, tal y como se han colocado mediante el diseño de K junto con los
polos del observador. Por tanto, la colocación de polos y la observación son dos cosas
independientes, porque la adición del observador no modifica los polos de bucle cerrado
del sistema tal y como se eligieron al diseñar K. Por tanto:
Los polos del sistema se eligen para que se cumplan las especificaciones del sistema
de control.
Los polos del observador se escogen de manera que la respuesta del observador
sea más rápida que la del sistema (para que esta última resulte dominante),
t´ıpicamente 4 o 5 veces más rápida.
1.9.3. Observador de orden m´ınimo
Supóngase que x(k) es un n-vector y que y(k) es un m-vector. Como las m salidas
son combinaciones lineales del estado, hay m variables que no necesitan ser estimadas.
El observador de orden m´ınimo será el que estime las n − m restantes.
Para diseñar el observador de orden m´ınimo estableceremos una partición del vector
de estados:
x(k) =


xa(k)
· · ·
xb(k)


donde el m-vector xa(k) son las variables medibles (accesibles) y el n − m-vector xb(k)
son las variables no medibles (no accesibles). Esta partición del vector de estados

determina una partición en la ecuación de estados:


xa(k + 1)
· · ·
xb(k + 1)

 =




Gaa
... Gab
· · ·
... · · ·
Gba
... Gbb






xa(k)
· · ·
xb(k)

 +


Ha
· · ·
Hb

 u(k)
y(k) = I
... 0


xa(k)
· · ·
xb(k)


donde Gaa ∈ Rm×m
, Gab ∈ Rm×(n−m)
, Gba ∈ R(n−m)×m
, Gbb ∈ R(n−m)×(n−m)
, Ha ∈
Rm×1
, Hb ∈ R(n−m)×1
. La ecuación de la parte del estado que es accesible (medible)
ser´ıa:
xa(k + 1) = Gaaxa(k) + Gabxb(k) + Hau(k)
Nótese que en esta ecuación hay términos que no son medibles, por lo tanto la podemos
reescribir agrupando los términos medibles a la izquierda y los no medibles a la derecha:
xa(k + 1) − Gaaxa(k) − Hau(k) = Gabxb(k) (1.69)
Por otro lado, la parte del vector de estados que no se puede medir se puede escribir
como:
xb(k + 1) = Gbaxa(k) + Gbbxb(k) + Hbu(k)
Obsérvese que en esta ecuación, los términos que dependen de xa(k) y u(k) son cono-
cidos mientras que el término que depende de xb(k) es desconocido. Esta ecuación la
podemos reescribir como
xb(k + 1) = Gbbxb(k) + [Gbaxa(k) + Hbu(k)] (1.70)
El diseño del observador de orden m´ınimo se realiza tomando como referencia el del
observador de orden completo, cuya ecuación de estados es
x(k + 1) = Gx(k) + Hu(k)
En el caso del observador de orden m´ınimo, la ecuación (1.70), es decir, la ecuación
que describe la evolución de la parte del estado no medible, es la que hace el papel
de ecuación de estado. Por otra parte, se conoce que la ecuación de salida para el
observador de orden completo es:
y(k) = Cx(k)
donde y(k) es medible y Cx(k) es no medible (por serlo x(k)). Obsérvese que se puede
establecer un paralelismo entre los términos de esta ecuación y los de la ecuación (1.69).
En el caso del observador de orden m´ınimo, por tanto, se considera como ecuación de
salida la ecuación (1.69).

Recordemos que la ecuación del observador de orden completo es
ˆx(k + 1) = (G − KeC)ˆx(k) + Hu(k) + Key(k)
Comparando las ecuaciones de estado y salida del observador de orden completo y las
del observador de orden m´ınimo, se establecen las siguientes analog´ıas:
Observador de orden completo Observador de orden m´ınimo
ˆx(k) ˆxb(k)
G Gbb
Hu(k) Gbaxa(k) + Hbu(k)
y(k) xa(k + 1) − Gaaxa(k) − Hau(k)
C Gab
Ke ∈ Rn×m
Ke ∈ R(n−m)×m
Teniendo en cuenta esto, se obtiene
ˆxb(k+1) = (Gbb−KeGab)ˆxb(k)+Gbaxa(k)+Hbu(k)+Ke [xa(k + 1) − Gaaxa(k) − Hau(k)]
(1.71)
Además, de la ecuación del sistema sabemos que
y(k) = xa(k)
luego, aplicando esto en la ecuación (1.71) se obtiene
ˆxb(k + 1) = (Gbb − KeGab)ˆxb(k) + Key(k + 1) + (Gba − KeGaa)y(k) + (Hb − KeHa)u(k)
que ser´ıa la ecuación del observador de orden m´ınimo. Los polos del observador de
orden m´ınimo ser´ıan los autovalores de (Gbb − KeGab). Obsérvese, sin embargo, que en
esta ecuación aparece un término que multiplica a y(k + 1). Como es lógico el valor
de la salida en k + 1 no está disponible en el instante k, por lo que esta ecuación ha
de ser modificada. Se puede demostrar (no se hará aqu´ı), que esta ecuación se puede
reescribir como:
ˆxb(k) = ˆη(k) + Kexa(k)
ˆη(k + 1) = (Gbb − KeGab)ˆη(k) + [(Gbb − KeGab)Ke + Gba − KeGaa] y(k)
+(Hb − KeHa)u(k)
(1.72)
La ecuación caracter´ıstica del observador de orden m´ınimo es:
|zI − Gbb + KeGab| = 0
y como en el caso del observador de orden completo, Ke se puede elegir para colocar
los polos del observador donde se desee mediante los métodos indicados en la sección

1.9.2.1. Por ejemplo, si la salida y(k) es un escalar, es decir m = 1, se tienen que estimar
n − 1 variables. La fórmula de Ackermann, por ejemplo, quedar´ıa:
Ke = φ(Gbb)





Gab
GabGbb
...
GabGn−2
bb





−1 




0
0
...
1





donde
φ(Gbb) = Gn−1
bb + α1Gn−2
bb + · · · + αn−1I
De manera análoga a la del observador de orden completo, se comprueba que la ecuación
caracter´ıstica del conjunto formado por el observador de orden m´ınimo y el sistema
controlado por una realimentación lineal del vector de estados es:
|zI − G + HK||zI − Gbb + KeGab| = 0
por lo que, nuevamente se ve que los problemas de diseño del controlador y del obser-
vador son independientes.
Ejemplo 1.8
Sea un sistema LTI cuyas matrices son
G =
1 0,2
0 1
H =
0,02
0,2
C = 1 0
se pide
1. Diseñar un controlador que coloque los polos de bucle cerrado en z = 0,6 ± j0,4.
2. Asumiendo que y(k) = x1(k) es el único estado accesible, diseñar un observador
de orden m´ınimo con respuesta dead-beat.
En primer lugar, se ha de comprobar la controlabilidad y observabilidad del sistema:
rango H
... GH = rango
0,02 0,06
0,2 0,2
= 2
rango C∗ ... G∗
C∗ = rango
1 1
0 0,2
= 2
Luego el sistema cumple ambas condiciones. La ecuación caracter´ıstica del controlador
es:
|zI − G| =
z − 1 −0,2
0 z − 1
= z2
− 2z + 1

luego a1 = −2 y a2 = 1. La ecuación caracter´ıstica de bucle cerrado deseada es:
(z − 0,6 − j0,4)(z − 0,6 + j0,4) = z2
− 1,2z + 0,52
luego α1 = −1,2 y α2 = 0,52. Por tanto,
K = α2 − a2 α1 − a1 T−1
= −0,48 0,8 T−1
donde la matriz T se calcula como
T = H
... GH
a1 1
1 0
=
0,02 0,02
−0,2 0,2
y
T−1
=
25 −2,5
25 2,5
lo que lleva a
K = 8 3,2
la ley de control se formulará por tanto, como
u(k) = −Kˆx(k)
= − 8 3,2
x1(k)
ˆx2(k)
= − 8 3,2
y(k)
ˆx2(k)
En cuanto al observador de orden m´ınimo, éste estimará una sola variable, por lo
que es de orden 1. La partición de la ecuación de estado en este caso será:




Gaa
... Gab
· · ·
... · · ·
Gba
... Gbb



 =




1
... 0,2
· · ·
... · · ·
0
... 1






Ha
· · ·
Hb

 =


0,02
· · ·
0,2


La ecuación caracter´ıstica deseada del observador es
Φ(z) = z = 0
luego
Ke = φ(Gbb)[Gab]−1
[1] = (1)(0,2)−1
(1) = 5
Las ecuaciones del observador ser´ıan
ˆη(k + 1) = (Gbb − KeGab)ˆη(k) + [(Gbb − KeGab)Ke + Gba − KeGaa] y(k)
+(Hb − KeHa)u(k)
= (1 − 5 × 0,2)ˆη(k) + [(1 − 5 × 0,2) × 5 + 0 − 5 × 1] y(k) + (0,2 − 5 × 0,02)u(k)
= −5y(k) + 0,1u(k)
ˆx2(k) = Key(k) + ˆη(k)
= 5y(k) + ˆη(k)

y la ley de control será por tanto,
u(k) = −Kˆx(k)
= −8y(k) − 3,2ˆx2(k)
= −8y(k) − 3,2(5y(k) + ˆη(k))
= −24y(k) − 3,2ˆη(k)
1.10. Control óptimo LQR
Las técnicas de control óptimo conforman una de las ramas del control automático
más importantes en el desarrollo de las estrategias modernas de control más utilizadas
hoy en d´ıa. Se han escrito numerosas monograf´ıas dedicadas a su estudio, y se ha
publicado una ingente cantidad de art´ıculos en revistas especializadas. No obstante,
en estos apuntes sólo se dará una pincelada sobre este particular, centrándonos en el
caso particular del control LQR con horizonte infinito, también conocido como LQR
de régimen permanente.
Las estrategias de control óptimo calculan la ley de control de manera que se opti-
miza una cierta medida del rendimiento del controlador. Se parte de un sistema descrito
por
x(k + 1) = Gx(k) + Hu(k)
El objetivo es calcular una ley de control
u(k) = −Kx(k)
de tal manera que se minimiza el funcional (que expresa un ´ındice de funcionamiento)
J =
1
2
∞
k=0
(x∗
(k)Qx(k) + u∗
(k)Ru(k)) (1.73)
siendo Q y R matrices de ponderación que cumplen que Q∗
= Q > 0, R∗
= R > 0.
Nótese que este ´ındice de funcionamiento pondera la diferencia entre el estado y el ori-
gen el instante inicial, hasta un tiempo infinito. Por tanto, cuanto más rápido se llegue
al origen menor valor de J se tendrá. Esto implica que al minimizarse J, se encon-
trará la ley de control que lleva el estado al origen más rápidamente y manteniéndolo

42 CONTROL ÓPTIMO LQR
siempre lo más cerca posible del origen4
. Por otra parte, se observa que en el funcional
hay otro término que pondera el valor de la secuencia de señales de actuación. Este
término impide que se obtenga una ley de control que lleve el estado al origen a expen-
sas de una actuación muy grande. Al minimizarse J, por tanto, se conseguirá una ley de
control que por una parte acerque el estado al origen lo mas rápido posible, pero man-
teniendo un nivel de actuaciones moderado, encontrándose por tanto, una solución de
compromiso entre el rendimiento del controlador y su nivel de actuación. El sentido de
este compromiso puede venir dictado por diferentes razones, como por ejemplo moderar
el gasto de energ´ıa o combustible necesario para proporcionar la señal de actuación.
Existen razones más sutiles pero no por ello menos importantes para incorporar esta
ponderación del esfuerzo de control. Por ejemplo, cuando existen discrepancias entre
el modelo del sistema y su dinámica real (algo que ocurre casi siempre, pues los mode-
los matemáticos no pueden recoger todas las complejidades de los sistemas o procesos
reales) esta ponderación del esfuerzo de control resulta en un sistema más estable.
Para calcular la ley de control que minimiza el ´ındice (1.73) se define una matriz P
que satisface la siguiente ecuación de Riccatti:
P = Q + G∗
PG − G∗
PH(R + H∗
PH)−1
H∗
PG (1.74)
La solución de esta ecuación es una matriz P que es herm´ıtica y definida positiva. Se
demuestra que la matriz
K = (R + H∗
PH)−1
H∗
PG
es la que minimiza el ´ındice (1.73) mediante la ley de control
u(k) = −(R + H∗
PH)−1
H∗
PGx(k)
La ecuación de estado del sistema en bucle cerrado será por tanto:
x(k + 1) = (G − H(R + H∗
PH)−1
H∗
PG) x(k)
= (I + HR−1
H∗
P)−1
Gx(k)
Para este desarrollo se ha empleado el lema de inversión
(A + BC)−1
= A−1
− A−1
B(I + CA−1
B)−1
CA
con A = I, B = H y C = R−1
H∗
P.
4 Ésta es una interpretación que hay que tomar con cierto cuidado, pues puede que se obtenga una
ley de control que provoque que el estado no se acerque al origen todo lo posible al principio pero que
lo lleve a dicho origen muy rápidamente en los instantes siguientes, manteniendo pues el valor de J
muy bajo.

1.10.1. Solución de la ecuación de Riccatti
Para calcular la ley de control óptima LQR en régimen permanente es necesario
resolver la ecuación de Riccatti (1.74). Esto no es algo trivial en general, pero si pode-
mos resolverla fácilmente si se dispone de un computador. Para ello formularemos un
proceso iterativo en que tomando como valor inicial de P = 0 (es decir una matriz de
ceros) se calculará el valor de la matriz P en el paso i + 1 como
Pi+1 = Q + G∗
PiG − G∗
PiH (R + H∗
PiH)−1
H∗
PiG
La condición de parada del bucle o proceso iterativo será que Pi+1 − Pi ≈ 0, esto es,
que la diferencia entre Pi+1 y Pi sea una matriz cuyos elementos estén todos cerca del
cero.
1.11. Filtro de Kalman
El filtro de Kalman es un estimador del estado (en realidad también se puede
interpretar como filtro y como predictor), que tiene en cuenta la presencia de ruidos
en la ecuación de estados y la salida. En este sentido es un estimador óptimo, pues
la estimación obtenida tiene el menor error posible teniendo en cuenta que al haber
ruidos actuando, nunca se podrá obtener una estimación perfecta. Al igual que en el
caso del control LQR no se entrará en profundidad en el estudio de este estimador, sino
que sólo se presentará la formulación de un caso particular, el filtro de Kalman para
régimen permanente.
Sea un sistema:
x(k + 1) = Gx(k) + Hu(k) + ω(k)
y(k) = Cx(k) + (k)
donde ω(k) y (k) son variables aleatorios que actúan como ruidos aditivos. Se de-
muestra que se puede obtener una estimación óptima del vector de estados mediante
el siguiente esquema:
ˆx(k + 1) = Gˆx(k) + Hu(k) + Ke(k) (y(k) − Cˆx(k))
Ke(k) = GPkC∗
(R + CPkC∗
)−1
Pk+1 = Q + (G − Ke(k)C) PkG∗
(1.75)
donde
R = E { (k) ∗
(k)}
Q = E {ω(k)ω∗
(k)}
P0 = E { (0) ∗
(0)}

44 FILTRO DE KALMAN
donde E {·} denota la esperanza matemática y R,Q se asumen constantes. Se demuestra
que conforme k → ∞:
Pk+1 → P
Ke(k) → Ke
donde P y Ke son matrices constantes y además P es semidefinida positiva. Usando
esto, las ecuaciones de estimación (1.75) se pueden reescribir como:
ˆx(k + 1) = Gˆx(k) + Hu(k) + Ke (y(k) − Cˆx(k))
Ke = GPC∗
(R + CPC∗
)−1
P = Q + GPG∗
− GPC∗
(R + CPC∗
)−1
CPG∗
(1.76)
que son las ecuaciones del filtro de Kalman de régimen permanente. Nótese que para
resolver la ecuación de Riccatti se puede usar el mismo método usado en el LQR.

Cap´ıtulo 2
Modelos de procesos y
perturbaciones
2.1. Introducción
En este cap´ıtulo se expondrán diversos tipos de formas de modelar perturbaciones
y procesos cuya evolución se ve afectada por perturbaciones. Es importante tener en
cuenta que los modelos de procesos con perturbaciones tienen su origen en el modelado
de perturbaciones y no al revés.
En la teor´ıa clásica del control automático siempre se ha tenido en cuenta el com-
portamiento de los sistemas frente a perturbaciones a la hora de diseñar sistemas de
control. Dichas perturbaciones se modelaban siempre de manera muy simplificada. Es
por tanto común en esta teor´ıa el considerar que las perturbaciones van a tener la
forma de
Pulsos.
Escalones.
Rampas.
Sinusoides.
Todos estos modelos tienen en común que son absolutamente predecibles en su evolu-
ción en función de las condiciones iniciales. Es decir, en cuanto la perturbación aparece
45

46 PERTURBACIONES DETERMINISTAS A TROZOS
podemos predecir su evolución futura. Es una suposición común en estos casos, consi–
derar que estas perturbaciones vienen generadas por sistemas dinámicos.
2.2. Perturbaciones deterministas a trozos
Como fuente de perturbaciones con una mayor variabilidad que los modelos clásicos
antes comentados, se pueden considerar las perturbaciones deterministas a trozos. Sur-
gen de la necesidad de estudiar el efecto de perturbaciones más realistas en sistemas
de control que se basan en algún tipo de esquema predictivo para calcular la señal
de control. En este tipo de sistemas, el considerar una perturbación absolutamente
predecible (como en el caso de los modelos clásicos) no tiene utilidad alguna, pues se
pueden considerar directamente en el cálculo de la ley de control.
Los modelos de perturbaciones deterministas a trozos parten de la suposición de
que son generados por un sistema lineal, en el que la entrada es cero excepto en ciertos
instantes de tiempo separados por más de n tiempos de muestreo, donde n es el orden
del sistema:
y(k) =
C(z−1
)
A(z−1)
w(k)
suponiéndose que el grado de C(z−1
) es igual al grado de A(z−1
). Si la entrada es
cero excepto en ciertos instantes de tiempo que están separados, quiere decir que la
señal w(k) es un tren de pulsos. La amplitud y momento de aparición de esos pulsos
son desconocidos. Esto es lo que le da variabilidad a la fuente de perturbaciones. Sin
embargo, una vez que aparecen y se conoce la amplitud del pulso, la evolución de la
salida y(k) es perfectamente predecible pues la dinámica del sistema es conocida. De
ah´ı el nombre de determinista a trozos.
2.3. Procesos estocásticos
Es natural utilizar el concepto de aleatorio o estocástico1
para describir una amplia
clase de perturbaciones, suficientemente realistas para formular problemas de predic-
ción con postulados cercanos a la realidad.
1
Estocástico: relativo a una variable aleatoria; algo que sigue una determinada distribución de
probabilidad, usualmente con varianza finita.

CAPÍTULO 2. MODELOS DE PROCESOS Y PERTURBACIONES 47
El concepto de proceso estocástico es complejo y alcanza su madurez en los trabajos
de Kolmogorov (1930). Aqu´ı presentaremos sólo algunas ideas básicas. Un proceso
estocástico puede ser considerado como una función de dos variables
X(t, w)
donde t es la variable tiempo con su significado habitual y w es una variable aleatoria.
Si consideramos un valor fijo de w, esto es w = w0 y dejamos la variable t libre, lo que
denotaremos como
X(:, w0)
estaremos hablando de una ((realización)) del proceso. Esta realización es una función
temporal común sin ningún tipo de carácter aleatorio una vez que se conoce que w =
w0. Si por otra parte se considera un instante de tiempo fijo, es decir t = t0, que
denotaremos como
X(t0, :) X(t0)
tendremos una variable aleatoria. Se puede considerar por tanto, que la evolución del
proceso está dictada por un generador de señales aleatorias. En la figura 2.1 se ilustran
estos conceptos. Puede observarse que el valor de la función en cada instante es un
valor aleatorio que en la figura se considera variable en un determinado rango. Por
otra parte, cuando se habla de una realización no es más que una función común que
depende de t.
t0
t1
t2
t3
t4
w=w0
......
Figura 2.1: Procesos estocásticos: realizaciones y variables aleatorias.
Definición 2.1 Se denomina proceso estocástico determinista, a aquél cuya evolución
puede ser predicha exactamente con un predictor lineal 2
en base a medidas pasadas.
En estos procesos, el carácter estocástico sólo se manifiesta en la aleatoriedad de las
condiciones iniciales. Para aplicaciones basadas en predicción no son muy interesantes.
2
Es decir, haciendo evolucionar hacia delante un modelo lineal.

48 MODELOS DE PROCESOS CON RUIDOS
Definición 2.2 Se denomina proceso estocástico estacionario, a aquél cuya distribu-
ción estad´ıstica para X(t1), X(t2),...,X(tn) es la misma que para X(t1 + τ), X(t2 +
τ),...,X(tn + τ). Es decir, su distribución no var´ıa con el tiempo.
Definición 2.3 Se denomina ruido blanco discreto, a un proceso aleatorio que se puede
considerar como una secuencia cuyos elementos son variables aleatorias independientes
entre s´ı cuya distribución es idéntica. Se suele suponer que
E {x(k)} = 0
es decir, que el valor esperado es cero y además
E {x(i)x(j)} =
0 si i = j (por ser variables independientes)
σ2
si i = j
Al ruido blanco se le suele considerar prototipo de una señal impredecible.
2.4. Modelos de procesos con ruidos
En esta sección veremos cómo se pueden generar diversos tipos de procesos es-
tocásticos, cuando a un sistema lineal se le inyecta un ruido blanco v(k) además de
una entrada externa u(k) a través de sendas funciones de transferencia.
El caso más general es el llamado modelo de Box-Jenkins, el cual se ilustra en la
figura 2.2. Esta estructura es demasiado general, y normalmente se utilizan diversas
¨©
¨©

−
−

−
−

!

v(k)
u(k)
y(k)
Figura 2.2: Modelo de Box-Jenkins.
simplificaciones de las cuales veremos a continuación las más comunes:

CAPÍTULO 2. MODELOS DE PROCESOS Y PERTURBACIONES 49
Modelo de Media Móvil (MA : Moving Average). Es el caso más sencillo y viene
descrito por
y(k) = v(k) + c1v(k − 1) + c2v(k − 2) + · · · + cnv(k − n)
Con este modelo se pueden describir muchos tipos de perturbaciones aleato-
rias. Sin embargo, no incluye a los valores pasados de la salida por lo que no
servirá para modelar procesos que tengan dinámica.
Modelo Autoregresivo (AR). Viene descrito por
y(k) + d1y(k − 1) + d2y(k − 2) + · · · + dny(k − n) = v(k)
En este caso, la parte aleatoria correspondiente a la perturbación tiene una es-
tructura muy simple porque no depende de los valores pasados.
Modelo Autoregresivo de Media Móvil (ARMA). Es la combinación de los dos
anteriores, por lo que tomará la forma
y(k) + d1y(k − 1) + · · · + dny(k − n) = v(k) + c1v(k − 1)
+c2v(k − 2) + · · · + cnv(k − n)
Este modelo permite describir procesos más ricos que los anteriores. Sin embargo,
desde el punto de vista del control es interesante poder considerar el efecto de una
entrada externa, por lo que se considera el siguiente tipo de modelos de procesos
con ruidos.
Modelo Autoregresivo de Media Móvil con una entrada exógena (ARMAX). Tam-
bién llamado modelo CARMA (Controlled ARMA). Viene descrito por
y(k) + a1y(k − 1) + · · · + any(k − n) = b1u(k − 1) + · · · + bnu(k − n)
+v(k) + c1v(k − 1) + · · · + cnv(k − n)
Modelo Autoregresivo con entrada exógena para m´ınimos cuadrados (ARX-LS).
Este modelo surge como versión simplificada del anterior, para el caso en el que
no se necesita que la fuente de perturbaciones tenga una estructura tan compleja.
Viene descrito por
y(k) + a1y(k − 1) + · · · + any(k − n) = b1u(k − 1) + · · · + bnu(k − n) + v(k)
Como su nombre indica se utiliza en la identificación por el método de los m´ınimos
cuadrados (véase el tema 4).

50 MODELOS DE PROCESOS CON RUIDOS
Modelo Autoregresivo de Media Móvil integrada y con una entrada exógena
(ARIMAX o CARIMA). Este modelo incorpora un integrador en la fuente de
perturbaciones, por lo que viene descrito por
y(k) + a1y(k − 1) + · · · + any(k − n) = b1u(k − 1) + · · · + bnu(k − n)
+
v(k) + c1v(k − 1) + · · · + cnv(k − n)
∆
donde ∆ = 1−z−1
. Este tipo de modelos es útil en esquemas de control predictivo
para formular leyes de control que incorporen un efecto integral, de manera que
sean capaces de rechazar perturbaciones en escalón.
Los modelos anteriores pueden escribirse en forma condensada utilizando polinomios
en z−1
tal y como se muestra en la siguiente tabla resumen:
Modelo Expresión
MA y(k) = C(z−1
)v(k)
AR D(z−1
)y(k) = v(k)
ARMA D(z−1
)y(k) = C(z−1
)v(k)
ARMAX A(z−1
)y(k) = B(z−1
)u(k − 1) + C(z−1
)v(k)
ARX-LS A(z−1
)y(k) = B(z−1
)u(k − 1) + v(k)
ARIMAX A(z−1
)y(k) = B(z−1
)u(k − 1) + C(z−1)v(k)
∆
Cuando en los modelos anteriores el polinomio que convoluciona con la señal v(k) es
distinto de la unidad se habla de ruido coloreado, y en caso contrario, de ruido blanco.

Cap´ıtulo 3
Introducción a la identificación de
sistemas
3.1. Introducción
Un modelo de un proceso es una forma de resumir el conocimiento que se tiene
sobre su dinámica, y por tanto es una herramienta importante en el diseño y análisis
de sistemas de control. Sin embargo, al construir modelos estamos obteniendo repre-
sentaciones simplificadas de la dinámica real del proceso. Un solo modelo no suele ser
suficiente para describir un proceso. Por otra parte, según sea el uso destinado al mod-
elo este deberá ser mas o menos detallado. Por tanto, se establece una jerarqu´ıa de
modelos que describe al proceso con mayor o menor detalle.
Hay dos maneras de abordar la construcción de un modelo: obtenerlo mediante
principios y leyes f´ısicas que describan la dinámica del proceso, o bien obtenerlo me-
diante experimentación sobre el proceso que se quiere modelar. La primera opción
requiere un conocimiento muy preciso del proceso que se quiere modelar. Por ejemplo,
hay que elegir las variables que vayan a ser los estados del sistema, y esto puede ser un
problema. Es, en general un proceso complicado y muy arduo, excepto en casos muy
simples. Normalmente, se debe combinar con la otra estrategia que es la denominada
identificación de sistemas. Esta estrategia será el objeto de este tema.
51

52 IDEAS B ÁSICAS SOBRE IDENTIFICACI ÓN DE SISTEMAS
3.2. Ideas básicas sobre identificación de sistemas
La identificación de sistemas es la aproximación experimental al modelado de sis-
temas. Consiste en obtener un modelo a partir de observaciones obtenidas directamente
del propio sistema que se pretende modelar. La identificación de un sistema conlleva
una serie de actividades y herramientas, de las que podemos destacar:
Planificación de los experimentos.
Selección del tipo de modelo.
Elección de un criterio para expresar la bondad del modelo que se va a obtener.
Estimación de los parámetros del modelo.
Validación del modelo obtenido.
A continuación, se irán desglosando las principales ideas de cada uno de estos aspectos.
3.2.1. Planificación de los experimentos
Dado que la identificación de sistemas involucra experimentar con el proceso a mod-
elar, es necesario tener en cuenta que, en general, es muy costoso experimentar con pro-
cesos industriales. Por tanto, es necesario elegir una técnica que nos sea lo más rentable
desde el punto de vista del tipo de experimentos necesarios. Algunas técnicas son muy
sencillas, en el sentido de que una vez hecho el experimento es fácil obtener el modelo.
Estas técnicas, sin embargo, requieren que en los experimentos se utilicen señales de
entradas preestablecidas de manera muy precisa: pulsos, sinusoides, etc. . . Puede que
el proceso a modelar no pueda ser sometido a este tipo de entradas por consideraciones
de seguridad o motivos económicos. Otras técnicas de identificación pueden emplear
casi cualquier tipo de señal de entrada (es decir, son menos exigentes en el tipo de
experimentos necesarios), pero una vez realizado el experimento es más complicado
obtener el modelo. Como comentario general, es necesario que en el experimento se
utilicen señales de entrada que exciten todos los modos del sistema. Más allá de eso,
un buen método de identificación debe ser insensible a las caracter´ısticas de la entrada.
Otro aspecto es que a veces no se puede identificar en bucle abierto y hay que hacerlo
en bucle cerrado. Esto no es siempre posible, pues aunque el sistema sea identificable en

CAPÍTULO 3. INTRODUCCI ÓN A LA IDENTIFICACI ÓN DE SISTEMAS 53
bucle abierto esta propiedad puede perderse en bucle cerrado. Esto ocurre, por ejemplo,
si los perfiles de la consigna o referencia que se usan son muy simples. También, si los
lazos de control son demasiado simples. En general, cuanto más complejos sean los
lazos de control y más se mueva la consigna, más fácil será la identificación en bucle
cerrado.
3.2.2. Selección del tipo de modelo
En teor´ıa, la selección del tipo de modelo deber´ıa venir dada por un conocimiento
del proceso y de las perturbaciones que deban ser tenidas en cuenta. Dependiendo de
si conocemos mucho o poco la estructura del proceso elegiremos entre uno u otro tipo
de modelo. En general, los modelos los clasificaremos como:
Modelos de Caja Blanca. Son los obtenidos a partir de leyes f´ısicas (esto no ser´ıa
realmente identificación porque no se estar´ıan haciendo experimentos).
Modelos de Caja Negra. En estos modelos se postula una estructura matematica
con una serie de parámetros libres, a los cuales se les da valor a partir de los
datos obtenidos en los experimentos.
Modelos de Caja Gris. Corresponden a un tipo intermedio entre los dos anteriores.
Parte del modelo se obtiene mediante leyes f´ısicas y otra parte, se ajusta usando
medidas experimentales. Por ejemplo, mediante leyes f´ısicas podemos determinar
la estructura del modelo (o de parte de él) y usar experimentos para terminar de
caracterizar el modelo.
También se pueden clasificar los tipos de modelos en paramétricos y no paramétri-
cos. En los primeros se tienen una serie de parámetros que hay que ajustar. Por ejemplo,
en una función de transferencia se tendr´ıan que ajustar el orden y los coeficientes de
los polinomios. En modelos de espacio de estados tendr´ıamos la misma situación pero
con las matrices del sistema. En los modelos no paramétricos, el modelo no tiene una
serie de parámetros que definen la dinámica sino que se compone de una cantidad de
información sobre la misma, por ejemplo los modelos basados en la respuesta en fre-
cuencia de un sistema. En el caso que aqu´ı nos ocupa los modelos que emplearemos
serán de caja negra y paramétricos.

3.2.3. Elección de un criterio
En el proceso de estimación del modelo y su subsiguiente validación es necesario
contar con un criterio que exprese la bondad del ajuste del modelo a los datos, es
decir, que exprese la calidad del modelo obtenido. Normalmente, se utilizan criterios
que toman la forma:
J(θ) =
N
k=1
g(e(k))
donde θ es el vector de parámetros que se trata de ajustar, e(k) es el error de estimación
para la medida k, N es el número de observaciones o medidas disponibles y g(·) es una
función usualmente cuadrática.
Usualmente, el proceso de ajuste del modelo se realiza de manera que se busca el
valor del vector de parámetros θ que hace m´ınimo al ´ındice o criterio J(θ). El método
más antiguo que emplea esta estrategia es el de los m´ınimos cuadrados, debido a Gauss.
Por otra parte, cuando los procesos se describen mediante modelos estocásticos, el
problema es de estimación estad´ıstica. Un método muy popular en este caso, es el del
estimador de máxima verosimilitud.
3.2.4. Estimación de los parámetros
Para resolver el problema de estimación de los parámetros del modelo se requiere
de los elementos comentados anteriormente: datos experimentales, un tipo de modelo
y un criterio. Estimar los parámetros es resolver un problema de optimización en el
cual, el mejor modelo es el que hace m´ınimo el criterio. Es necesario tener en cuenta
que el modelo obtenido dependerá de los elementos anteriores, como por ejemplo de la
amplitud y contenido frecuencial de la señal de entrada. Hay diversas formas de llevar
a cabo el proceso de estimación. Una distinción amplia, es aquella que distingue entre
identificación en l´ınea e identificación fuera de l´ınea.
3.2.4.1. Identificación en l´ınea
En los métodos de identificación en l´ınea la estimación se efectúa usando medidas
que se van obteniendo en tiempo real, y normalmente se usan cálculos recursivos.
El esquema de este tipo de identificación ser´ıa el mostrado en la figura 3.1. En este
esquema aparece un nivel de supervisión que es necesario para evitar, por ejemplo, que

PLANTA
u(k) y(k)
IDENTIFICACIÓN
SUPERVISIÓN
MODELO
ACTUALIZADO
MODELO
CORREGIDO
Figura 3.1: Esquema de la identificación en l´ınea.
el modelo actualizado se salga de ciertos l´ımites o cambie bruscamente (esto no ser´ıa
bueno para ciertas leyes de control basadas en modelos). Este método suele ser el único
apropiado cuando se pretende usar una estrategia de control adaptativo, o el proceso
var´ıa su dinámica con el tiempo.
3.2.4.2. Identificación fuera de l´ınea
En este caso se toman los datos del experimento (es decir, series de medidas) y
posteriormente, se ajusta el modelo usando para ello todo el conjunto de datos. Este
tipo de procedimientos suelen obtener modelos más precisos y son más fiables en cuanto
a la convergencia de los parámetros estimados a los parámetros reales del proceso1
. En
cualquier caso, existe un consenso general en que no existe un método universalmente
bueno, por tanto, dependiendo de la situación unos funcionarán mejor que otros.
3.2.5. Validación del modelo
La validación del modelo consiste en comprobar la bondad del modelo que se ha
obtenido por el proceso de identificación. Una técnica muy común para comprobar la
bondad de un modelo identificado es la validación cruzada.
1
Nótese que aunque el proceso real no corresponderá en general exactamente con el modelo (pues
todo modelo implica un cierto grado de simplificación de la realidad) se asume que existe un valor del
vector de parámetros que es el que mejor describe al proceso.

La idea del método de validación cruzada es dividir el conjunto de datos disponible
en dos partes o subconjuntos:
Conjunto de estimación. Es usado para estimar el modelo mediante la resolución
de un problema de optimización, de tal manera que el vector de parámetros
estimados sobre el conjunto de estimación ˆθCE ser´ıa
ˆθCE = arg m´ın
θ
VCE(θ, CE)
donde VCE es el criterio de estimación.
Conjunto de prueba o validación. Con este modelo se evalúa el estimador obtenido
mediante un criterio de prueba, que puede ser el mismo que el usado en la esti-
mación u otro distinto:
ˆFCE = VCP(ˆθCE, CP)
La idea tras el concepto de validación del modelo es estimar distintos tipos de modelos
(por ejemplo con distintos órdenes) y quedarse con el que mejor ajusta (es decir, el que
dé menor ˆFCE). Mediante esta técnica de validación cruzada, lo que se trata de ver es
si el modelo es capaz de reproducir los datos de salida para entradas que no se han
empleado en la estimación.
Como se ha comentado anteriormente, el criterio VCP no tiene por qué ser el mismo
que el VCE. Por ejemplo, se puede usar como criterio para validación el conocido criterio
de Akaike o criterio AIC (Akaike’s Information Criterion), el cual asumiendo que las
perturbaciones siguen una distribución gaussiana se calcula mediante la fórmula
VCP(θ, CP) = 1 +
2dimensión(θ)
N
1
N
N
t=1
e2
(t, θ)
donde e(t, θ) = y(t) − ˆy(t, θ) es el error de estimación para los datos obtenidos en el
instante t.
Tampoco puede descartarse la posibilidad de no usar criterio de validación alguno y
efectuar una inspección visual sobre una simulación, en la que se usa el modelo estimado
para predecir la salida en base a datos de entradas experimentales.
Finalmente, la técnica de validación cruzada, aunque muy popular no es la única.
Otra técnica que a veces se utiliza es el análisis de residuos. Se entiende por residuos
los errores que comete el modelo una vez ajustado, es decir e(t) = y(t) − ˆy(t, θ). Si el
modelo estimado es suficientemente bueno, estos residuos tienen que ser independientes

de la información disponible en el instante anterior (es decir, el residuo en t tiene que
ser incorrelado con las medidas obtenidas en los instantes anteriores). Esto es as´ı por
que si existe correlación entre e(t) y alguna entrada pasada u(t − τ), quiere decir que
una parte del valor de y(t), que depende de u(t − τ) no ha sido reproducida por el
modelo en ˆy(t, θ). Por tanto, el modelo no estar´ıa reproduciendo toda la dinámica del
proceso.
3.2.6. Resumen del proceso de identificación
El proceso de identificación de un sistema rara vez se concluye con la sola ejecución
de los pasos anteriormente descritos. En lugar de esto, se realizan numerosas repeti-
ciones de esta secuencia de pasos, a veces variándose el tipo de modelo, o repitiéndose
los experimentos hasta que se obtenga un buen modelo. Por tanto, podemos ver el
proceso de identificación como un método iterativo que se puede describir mediante
el diagrama de flujo mostrado en la figura 3.2. En esa figura el hecho de que el flujo
INICIO
TOMA DE DATOS
ACONDICIONAMIENTO DE
DATOS
ELEGIR ESTRUCTURA DEL
MODELO
AJUSTAR MODELO
VALIDAR MODELO
¿ VALIDO ?
NO
SI
USAR MODELO
Figura 3.2: Diagrama de flujo del proceso de identificación.
pueda retornar a cualquiera de las pasos intermedios, indica que puede que en cada

58 ALGUNAS PROPIEDADES
iteración no se realicen todos los pasos. Por otra parte, aparece un paso sobre el que no
se ha comentado nada, el acondicionamiento de datos. Esta tarea consiste en manipu-
lar los datos de manera que sean apropiados para el método de ajuste elegido. Es algo
que es espec´ıfico para cada procedimiento. As´ı por ejemplo, una tarea muy común de
acondicionamiento de datos es la eliminación de los valores de continua de las señales
de entrada y salida. Esto será tratado en mayor profundidad en el tema 4. Finalmente,
en el caso de la identificación en linea el proceso es más simple, ya que por ejemplo
no es posible cambiar la estructura del modelo sin descartar el resultado que se ha
obtenido hasta ese momento. Además, los datos se toman según van llegando, pues
recordemos que en este tipo de identificación la identificación se hace como su propio
nombre indica en tiempo real, es decir, ((en l´ınea)).
3.3. Algunas propiedades
En esta sección, veremos algunas propiedades relacionadas con la identificación de
sistemas. Concretamente se tratarán los conceptos de excitación persistente, convergen-
cia e identificabilidad. Además, se verán las tareas de supervisión y acondicionamiento
que aparecen en las figuras 3.1 y 3.2.
3.3.1. Excitación persistente
Se ha comentado en la sección 3.2.1, que para poder identificar correctamente un
sistema la señal de entrada debe excitar (es decir, poner de manifiesto) todos los modos
del sistema (toda su dinámica). Formalmente, se dice que si el sistema es de orden n
se deber´ıa contar con una señal persistentemente excitadora de orden n.
Se puede probar que una señal de entrada u(k) es persistentemente excitadora de
orden n, s´ı y sólo s´ı se cumple que
l´ım
N→∞
1
N
N
k=1
A(z−1
)u(k)
2
0
para todo polinomio A(z−1
) no nulo de grado inferior a n. Usando este resultado se
pueden caracterizar las señales más comunes:
Pulso: no excita persistentemente para ningún orden n.

Escalón: excita persistentemente para orden 1.
Ruido blanco: excita persistentemente para todo orden n.
Esto quiere decir que el ruido blanco ser´ıa una señal de entrada muy buena para identi-
ficar sistemas. En la práctica, sin embargo, es muy dif´ıcil obtener una señal de entrada
que se comporte como un ruido blanco ideal, porque es muy dif´ıcil obtener una se-
cuencia de valores puramente aleatorios. Es posible obtener sin embargo, secuencias de
valores seudoaleatorios, por lo que en la práctica se recurre a secuencias seudoaleatorias
de escalores binarios (PRBSS: Pseudo Random Binary Step Sequence). En la figura
3.3 se muestra una de esas secuencias. Nótese que los escalones no tienen por qué tener
amplitud unitaria, el concepto de binario se refiere solamente a dos niveles de entrada
distintos. Por otra parte, la aleatoriedad está en la duración de los escalones y en el
momento de aparición de los mismos.
0 20 40 60 80 100 120 140 160 180 200
3
3.5
4
4.5
5
5.5
6
6.5
intervalos de muestreo
voltaje
Figura 3.3: Ejemplo de señal de entrada del tipo PRBSS.
3.3.2. Convergencia e identificabilidad
Se dice que un sistema es identificable cuando usando un método de identificación
adecuado se tiene que
l´ım
N→∞
E(ˆθ)) = θ0
y además la salida obtenida mediante el modelo estimado es posible. Es decir, para
un sistema identificable el valor del vector de parámetros estimado convergerá con un
número de observaciones suficientes al valor real de esos parámetros. No obstante, esta

convergencia tiene a su vez una serie de requisitos o condiciones que se pueden resumir
en:
El orden del modelo y el retardo deben ser conocidos.
Los valores de continua de la señal de entrada y la de salida deben ser conocidos.
Si el sistema es de orden n, la señal de entrada debe ser persistentemente excita-
dora de orden n o mayor.
Las perturbaciones sobre la salida deben ser ruidos estacionarios.
El error en el instante k debe ser incorrelado con los elementos de los que depende
la salida en el instante k (es decir, de los valores pasados de la entrada y la salida).
El valor esperado (esperanza matemática) del error en k debe ser cero, es decir
E{e(k)} = 0.
Finalmente, la convergencia también depende de los valores iniciales del esti-
mador.
3.3.2.1. Identificación en bucle cerrado
Como se comentó en la sección 3.2.1, a veces resulta bastante dif´ıcil identificar en
bucle cerrado. Esto es especialmente cierto cuando el lazo de control es simple, el regu-
lador lineal y además no se emplean señales externas (a modo de perturbaciones) para
excitar toda la dinámica del sistema. Existen una serie de condiciones para establecer
la identificabilidad de un sistema en bucle cerrado. Supóngase que se parte del siguiente
modelo para identificar un sistema:
A(z−1
)y(k + d) = B(z−1
)u(k) + C(z−1
)e(k + d)
donde d es el retraso del proceso, y los grados de los polinomios A(z−1
), B(z−1
), C(z−1
)
son ma, mb, mc respectivamente. Supóngase además que el sistema está gobernado por
un regulador que toma la expresión:
u(t) = −
Q(z−1
)
P(z−1)
y(t)
donde los grados de Q y P son v y w respectivamente. Teniendo en cuenta todo esto,
se formulan las siguientes condiciones de identificabilidad en bucle cerrado.

Primera condición de identificabilidad en bucle cerrado
Los órdenes del modelo del proceso y de las perturbaciones deben ser conocidos con
exactitud.
Segunda condición de identificabilidad en bucle cerrado
Si los polinomios A(z−1
) y C(z−1
) tienen p ceros comunes (en caso de que sean primos
entre si, p = 0) se ha de cumplir que
máx(w − mb, d + v − ma) ≥ p
Si esto no se cumpliese, la solución pasa por fijar alguno de los parámetros del modelo
a fin de bajar los grados ma o mb. Si fuera factible aumentar el retraso, también
podr´ıa usarse esto para lograr la identificabilidad en bucle cerrado. Nótese que por
estos procedimientos lo que se consigue es que el proceso de identificación converja a
un valor del vector de parámetros que corresponde con el que da un menor error. No
quiere decir que el sistema real se describa mejor por ese modelo. Es decir, puede que
exista otro modelo del mismo orden mejor, pero si no se toman las medidas indicadas
no se llegar´ıa a ese modelo ni probablemente se converger´ıa a ningún otro.
Un caso común es que p = 0 y ma = mb = n, por lo que esta condición se puede
expresar como
máx(w, v + d) ≥ n
Ejemplo 3.1
Supongamos que ma = mb = n y que
u(k) = −
G(z−1
)
zB(z−1)F(z−1)
y(k)
y que los ordenes de G(z−1
) y F(z−1
) son n − 1 y d respectivamente. Entonces se
cumple que
v = n − 1 w = n + d − 1
por lo que la condición de identificabilidad ser´ıa que
máx(n + d − 1, n − 1 + d) ≥ n
Esto implica que para que el sistema sea identificable en bucle cerrado, d ≥ 1. Otra
solución ser´ıa fijar un parámetro.

3.3.3. Niveles de supervisión y acondicionamiento
En la identificación en l´ınea es habitual introducir un nivel de supervisión y tratamien-
to de las señales a fin de evitar que se produzcan situaciones que desestabilicen la
identificación, es decir, que el valor del vector de parámetros identificado no converja
o converja a un valor incorrecto. Las tareas que se pueden realizar en estos niveles
incluyen:
Filtrado de datos a la entrada del identificador para evitar cambios bruscos en
los parámetros estimados.
Acondicionamiento de señales: eliminación de los valores de continua y escalado
de las variables.
Supervisar que la evolución de los parámetros esté dentro de unos rangos deter-
minados.
Monitorizar otros elementos del algoritmo de identificación.
Monitorizar la introducción de riqueza dinámica al sistema: paradas temporales
del identificador e inyección de perturbaciones.

Cap´ıtulo 4
Identificación por m´ınimos
cuadrados
4.1. El método de los m´ınimos cuadrados
Este método permite la identificación en tiempo real de modelos con el único req-
uisito de que estos sean lineales en los parámetros. Esto incluye, por tanto, a modelos
lineales y no lineales que sean lineales en los parámetros. El mayor interes práctico re-
side, sin embargo, en la identificación de los primeros, dado que son los más utilizados
en control.
Considerése el siguiente modelo paramétrico lineal monovariable1
:
y(k) + a1y(k − 1) + · · · + any(k − n) = b1u(k − 1) + · · · + bnu(k − n) (4.1)
Nótese que este modelo es determinista en el sentido de que no considera ruidos aleato-
rios como en los modelos vistos en el tema 2. Es inmediato comprobar que este modelo
corresponde a la siguiente función de transferencia:
G(z−1
) =
b1z−1
+ · · · + bnz−n
1 + a1z−1 + · · · + anz−n
El modelo (4.1) se puede reescribir como:
y(k) = m(k)θ (4.2)
1
Este método se puede aplicar sin cambios conceptuales a modelos multivariables. Sin embargo por
simplicidad nos ceñiremos al caso de modelos monovariables.
63

64 EL MÉTODO DE LOS MÍNIMOS CUADRADOS
donde el vector
m(k) = −y(k − 1) · · · −y(k − n) u(k − 1) · · · u(k − n) (4.3)
es llamado regresor y
θ = a1 · · · an b1 · · · bn
T
es el vector de parámetros. Dado un valor del vector de parámetros ˆθ, el error de
predicción para el instante k será
e(k, ˆθ) = y(k) − ˆy(k) = y(k) − m(k)ˆθ
Nótese que conocido el valor de los valores presentes y pasados de la salida y la entrada,
la expresión (4.2) es una ecuación en las que las 2n incognitas son los parámetros que
forman θ. Si el proceso a identificar correspondiese exactamente con un modelo como
(4.1) se podr´ıa determinar el valor del vector de parámetros a partir de 2n medidas u
observaciones de la salida para una serie de entradas conocidas. Es decir, se formar´ıa
un sistema de 2n ecuaciones con el que se podr´ıa determinar el valor ((real)) de θ.
El método de los m´ınimos cuadrados parte de N pares (y(k), m(k)) donde N es
generalmente mucho mayor de 2n (este ser´ıa el conjunto de estimación) y permite
ajustar un modelo del tipo (4.1). En el supuesto poco realista de que el proceso coincida
con un modelo como el que se intenta ajustar, se tendr´ıa un sistema de ecuaciones
sobredeterminado compatible, de manera que tendr´ıa solución y el error de predicción
alcanzado ser´ıa cero para todas las medidas del conjunto de estimación. Sin embargo,
en la práctica el proceso no se puede describir a la perfección mediante un modelo lineal
del tipo (4.1) por lo que el sistema de ecuaciones no tiene solución en el sentido de que
no existe un valor del vector de parámetros que haga que el error de predicción sea cero
para todas las medidas del conjunto de estimación. Es decir, el sistema de ecuaciones
es incompatible. Sin embargo si se puede encontrar un valor del vector de parámetros
que haga m´ınimo el error de predicción, de manera más precisa que haga m´ınima la
suma de los cuadrados de los errores de predicción del conjunto de estimación. Esta es
precisamente la estrategia del método de m´ınimos cuadrados2
.
Las medidas obtenidas desde k = n hasta k = N se agrupan en vectores de manera
que se obtiene:
E(N, θ) = Y (N) − M(N)θ
donde los vectores E(N) e Y (N) son
E(N, θ) = e(n, θ) · · · e(N, θ)
T
Y (N) = y(n) · · · y(N)
T
2
En un contexto matemático se dir´ıa que el vector de parámetros que se calcula es la pseudosolución
en el sentido de los m´ınimos cuadrados de un sistema sobredeterminado incompatible.

CAPÍTULO 4. IDENTIFICACI ÓN POR MÍNIMOS CUADRADOS 65
y la matriz M(N) está formada por los regresores correspondientes, es decir
M(N) =



m(n)
...
m(N)



Se define el ´ındice de bondad de ajuste como
J(θ) = E(N, θ) 2
=
N
k=n
e2
(k, θ)
Este ´ındice lo podemos reescribir como
J(θ) = (Y (N) − M(N)θ)T
(Y (N) − M(N)θ)
El m´ınimo valor de J(θ) se dará en el valor del vector de parámetros que cumpla que
dJ(θ)
dθ
= 0
es decir,
2(M(N)θ − Y (N))T
M(N) = 0
de donde se obtiene que el valor del vector de parámetros que hace m´ınimo el ´ındice
de bondad de ajuste es
θ∗
= [MT
(N)M(N)]−1
MT
(N)Y (N) (4.4)
y ese es por tanto el valor del vector de parámetros del modelo identificado.
Nótese que para que el problema de identificación tenga solución la matriz [MT
(N)M(N)]
tiene que ser invertible al igual que M(N). Sin entrar en demasiados detalles, tal condi-
ción se verifica cuando la entrada cumple las condiciones de excitación persistente del
sistema. Se deberá acudir por tanto a señales de entrada parecidas al ruido blanco (ver
tema 3).
4.2. Algoritmo recursivo para identificación en lin-
ea
La expresión (4.4) implica la inversión de una matriz que puede tener unas dimen-
siones apreciables, tanto más si se tiene en cuenta que para identificar correctamente

66 ALGORITMO RECURSIVO PARA IDENTIFICACI ÓN EN LINEA
un sistema se deben tener suficientes medidas para eliminar el efecto de ruidos y per-
turbaciones ajenas a la dinámica del sistema. Intentar efectuar estos cálculos en linea
es bastante ambicioso para el hardware de control habitual3
. Por tanto este algoritmo
se destina a la identificación fuera de linea. En linea se emplea otro procedimiento que
se muestra a continuación.
La estimación para el instante k usando las medidas obtenidas desde el instante n
vendrá dada por
ˆθ(k) = [MT
(k)M(k)]−1
MT
(k)Y (k)
= P(k)MT
(k)Y (k)
= P(k)(MT
(k − 1)Y (k − 1) + mT
(k)y(k))
(4.5)
donde
P(k) = [MT
(k)M(k)]−1
=
k
i=n
mT
(i)m(i)
−1
es la llamada matriz de covarianza. Se puede comprobar que
P−1
(k − 1) = P−1
(k) − mT
(k)m(k)
Por otra parte tambien se puede obtener que
MT
(k − 1)Y (k − 1) = P−1
(k − 1)ˆθ(k − 1)
= P−1
(k)ˆθ(k − 1) − mT
(k)m(k)ˆθ(k − 1)
Combinando las dos ultimas expresiones con (4.5) se obtiene
ˆθ(k) = ˆθ(k − 1) − P(k)mT
(k)m(k)ˆθ(k − 1) + P(k)mT
(k)y(k)
= ˆθ(k − 1) + P(k)mT
(k)(y(k) − m(k)ˆθ(k − 1))
= ˆθ(k − 1) + K(k)(y(k) − m(k)ˆθ(k − 1))
(4.6)
donde K(k) = P(k)mT
(k). Por tanto ˆθ(k) se puede expresar en forma recursiva, es
decir en función del valor del estimador en el instante anterior más un término corrector
que consiste en el error de predicción en el instante actual cometido por el estimador
calculado en el instante anterior multiplicado por una ganancia de adaptación K(k).
Esta formula da lugar al llamado algoritmo de minimos cuadrados recursivos, que
consiste en
1. Dar valores iniciales a la matriz P y al vector de parámetros θ.
3
Téngase en cuenta que el hardware industrial no se renueva tan rápidamente como el usado
en informática personal y que además tampoco se incorporan las últimas tecnologias con la misma
rapidez.

2. En cada instante k
a) Leer los valores de y(k) y u(k).
b) Formar el vector regresor m(k) según la expresión (4.3).
c) Calcular P(k) mediante
P(k) = P(k − 1) −
P(k − 1)mT
(k)m(k)P(k − 1)
1 + m(k)P(k − 1)mT (k)
d) Calcular K(k) segun la expresión
K(k) = P(k)mT
(k)
e) Calcular θ(k):
ˆθ(k) = ˆθ(k − 1) + K(k)[y(k) − m(k)ˆθ(k − 1)]
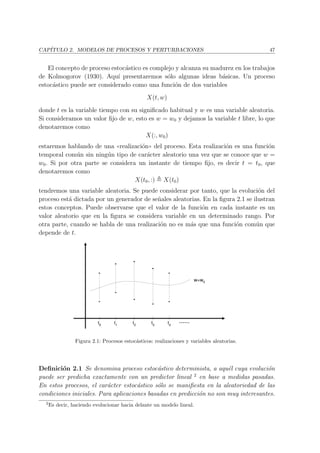
Este algoritmo puede intepretarse gráficamente como se ilustra en la figura 4.1.
PLANTA
FORMAR
REGRESOR
ALGORITMO
RECURSIVO
Z-1
Σ
+
- #$%'(
)102345 +
6879A@B879A@
CEDFAG
HPIQARISQARTUIQVR θ
Figura 4.1: Diagrama de flujo del proceso de identificación mediante m´ınimos cuadrados recursivos.
4.3. Interpretación estad´ıstica
En esta sección se presentan las propiedades estad´ısticas del estimador obtenido
por el método de m´ınimos cuadrados en función de las caracter´ısticas del proceso que
se trata de identificar.

68 INTERPRETACI ÓN ESTADÍSTICA
Supongase que el proceso que se pretende modelar responde bien a un modelo
ARMAX o bien a un modelo ARX-LS (vease la sección 2.4). Considerese que la variable
aleatoria v(k) corresponde a un ruido blanco. La diferencia entre estos dos tipos de
modelos es el grado del polinomio coloreador del ruido C(z−1
) que denotaremos por
cn. En el ARMAX cn 0 por lo que la variable aleatoria v(k) y sus valores pasados
hasta el instante k − cn afectan al valor de la salida en k. En el caso del ARX − LS el
grado de C(z−1
) es cero, por lo que la salida en k viene afectada por el valor de la señal
de ruido en el instante k exclusivamente. Esto implica que en el caso del ARMAX la
salida depende de los valores pasados de v(k) mientras que en el caso del ARX-LS esta
dependencia es exclusivamente con el valor actual de v(k).
Un hecho a tener en cuenta es que al ser v(k) una variable aleatoria, y(k) es a su
vez una variable aleatoria al ser el ruido aditivo. Esto implica a su vez que el valor
del vector de parametros estimado ˆθ tambien es una variable aleatoria que se puede
estudiar desde un punto de vista estad´ıstico. Por responder el proceso exactamente a
uno de los dos tipos de modelos considerados existe un valor del vector de parámetros
θ∗
que consideraremos como verdadero. Es decir
y(k) = mT
(k)θ∗
+ C(z−1
)v(k)
Resulta muy interesante saber si al aplicar el método de los m´ınimos cuadrados, el
vector de parámetros estimados ˆθ(k) coincide con θ∗
. Dado que ˆθ(k) es una variable
aleatoria estudiaremos su valor esperado, es decir su esperanza matemática. Se define
el sesgo de la estimación como
˜θ = E ˆθ(k) − θ∗
es decir como la diferencia entre el valor esperado de ˆθ(k) y el valor ((verdadero)) θ∗
. Se
comprueba que
˜θ = E [MT
(k)M(k)]−1
MT
(k)V (k) (4.7)
donde V (K) es una matriz donde la fila correspondiente al instante k está formada por
los valores v(k),· · ·,v(k − cn). Nótese además que la fila de M(k) correspondiente al
instante k contiene los valores de la salida y de la entrada en los instantes k−1,· · ·,k−n
pero no los del instante k (ver expresión (4.3)).
Considerese el caso del modelo ARMAX. Claramente existe relación entre los com-
ponentes de la matriz M(k) y V (k). En efecto, la matriz de regresores está formada por
valores de la salida y la entrada. Los primeros dependen de los valores de la señal de
ruido y los segundos son deterministas, por lo que existe una correlación entre la matriz
M(k) y V (K). Por lo tanto tambien existe esa correlación entre [MT
(k)M(k)]−1
MT
(k)
y V (k). Eso implica que según la expresión (4.7) ˜θ es distinto de cero. Por tanto no
está garantizada la convergencia del vector de parámetros estimados con el ((real)).

La situación es diferente con el modelo ARX-LS. En este caso los valores de M(k)
no pueden estar relacionados con V (k) (que, al ser cn = 0, solo está formada por los
valores presentes de v(k) para cada instante k). Por tanto, el estimador por m´ınimos
cuadrados es insesgado, es decir ˜θ = 0 y por tanto el valor esperado del estimador
coincide con el valor real del vector de parámetros, es decir
E ˆθ(k) = θ∗
Por otra parte, el hecho que de que el proceso responda a uno u otro tipo de
modelo tiene una interpretación f´ısica inmediata. En el caso del proceso ARMAX el
ruido presenta una cierta dinámica , mientras que en el caso del ARX-LS el ruido no
presenta dinámica alguna y responde únicamente a un ruido proveniente del sensor
de medida. Es en este último caso cuando el método de m´ınimos cuadrados produce
estimaciones consistentes.
Otra propiedad que resulta interesante conocer es la varianza del estimador. Clara-
mente interesa que esta varianza sea pequeña o por lo menos que disminuya conforme
se acumulan medidas disponibles para usarlas en la estimación. De esa manera, el vec-
tor de parámetros estimados estará con seguridad cerca del vector real. La varianza del
estimador se puede calcular como
varianza(ˆθ(k)) = E (ˆθ(k) − θ∗
)T
(ˆθ(k) − θ∗
)
= σ2
P(k)
donde σ = E{v(i)v(j)} para i = j. Nótese que para que la varianza sea pequeña
interesa que P(k) sea ((pequeña)) o que al menos decrezca a medida de que k aumenta.
Una medida del tamaño de P(k) es su traza, por lo que se usa como una medida de la
exactitud de la estimación, de manera que se busca que la traza vaya decreciendo.
Esta interpretación estadistica del tamaño de P(k) tambien proporciona una regla
para dar un valor inicial a la matriz P(k). En efecto, en general no se tendrá demasiada
confianza en que el valor inicial del vector de parámetros estimados, por lo que se
escogerá una matriz P(0) ((grande)) para reflejar esa desconfianza, por ejemplo P(0) =
pI donde p es un número muy alto (por ejemplo 10000). Este número será mas pequeño
si se sabe que el valor inicial del vector de parámetros está cerca de θ∗
.
Por otra parte, es evidente que a medida que el numero de observaciones N crece
la suma
N
k=n
mT
(k)m(k)

70 MÍNIMOS CUADRADOS PONDERADOS
crece. Recuerdese que, segun se definió en la sección 4.2
P(k) =
k
i=n
mT
(i)m(i)
−1
lo que implica que a medida que N crece P decrece. Se puede demostrar que si el
tamaño del regresor no cambia demasiado P decrece como 1
N
. Esto quiere decir que la
incertidumbre en la estimación decrece, es decir, que cada vez se obtiene un estimador
más cercano al valor real. Además la ganacia de adaptación K(k) tambien decrece
(vease su definición en la sección 4.2) lo cual es congruente con el hecho de que cuanto
más exacta es la estimación menos corrección de su valor se necesita. Esto es bueno
si la dinámica del proceso no cambia con el tiempo, pero si esto no es as´ı habrá que
modificar este esquema.
4.4. M´ınimos cuadrados ponderados
A veces es conveniente dar más peso a algunas medidas que a otras en la esti-
mación. Por ejemplo si se identifica un proceso cuya dinámica cambia con el tiempo
interesará dar mas peso a las medidas más recientes, pues estas serán las que reflejen la
dinámica más actualizada. Para conseguir esto hay que modificar el ´ındice de bondad
de ajuste, de manera que se use
J(θ) = E(N, θ)T
W(N)E(N, θ) 2
=
N
k=n
w(k)e2
(k, θ)
siendo W(N) la matriz diagonal de pesos
W(N) =



w(n)
...
w(N)



La solución del problema de ajuste es en este caso
θ∗
= [MT
(N)W(N)M(N)]−1
MT
(N)W(N)Y (N) (4.8)
El esquema de ponderación más habitual es el llamado olvido exponencial. En este
caso
w(k) = λN−K

, donde λ ∈ (0, 1) es el llamado factor de olvido. Es fácil entender por que se le llama
olvido exponencial: el peso dado a la medida disminuye exponencialmente cuanto más
antigua sea. De esta manera las medidas muy antiguas se olvidan, pues su peso es tan
pequeño que es como si no se contribuyesen a la estimación. Habitualmente se usa
λ ∈ [0,98, 1). Por ejemplo, si λ = 0,99 el estimador tendr´ıa una ((memoria)) de unas 100
muestras. En aquellos casos que la dinámica del proceso cambie muy rápidamente se
puede optar por valores más bajos (por ejemplo, λ = 0,95).
En el caso de la técnica de olvido la formulación recursiva puede aplicarse modifi-
cando las expresiones para el calculo de P(k) de manera que:
P(k) =
P(k − 1)
λ
−
P(k − 1)mT
(k)m(k)P(k − 1)
λ + m(k)P(k − 1)mT (k)
Puede observarse que, dado que K(k) = P(k)mT
(k), la ganancia de adaptación K(k)
depende de λ y a menor λ mayor ganancia de adaptación. Esto quiere decir que a menor
λ mejor se adaptará la identificación a una dinámica cambiante, ya que se considerar´ıa
en la optimización solo la información más reciente.
Sin embargo si en el sistema o en las medidas hay mucho ruido, es conveniente
que la dinámica se identifique sobre un conjunto amplio de medidas ya que si no se
identificar´ıa el ruido más que la dinámica del proceso. Por tanto en estos casos conviene
que λ no sea muy pequeño. Por tanto hay que llegar a un compromiso entre la capacidad
de seguir una dinámica cambiante y el rechazo del ruido en la identificación.
4.5. M´ınimos cuadrados extendidos y generalizados
Según se explicó en la sección 4.3 el estimador obtenido mediante m´ınimos cuadra-
dos es insesgado si el proceso responde a un modelo ARX-LS, pero no si responde a
un modelo ARMAX. En la práctica, si la relación señal-ruido es baja el proceso ha de
modelarse con un modelo de perturbaciones más complejo que el del ARX-LS ya que
la señal de ruido y su influencia sobre la dinámica son importantes. En estos casos se
debe recurrir a un modelo ARMAX.
El método de los m´ınimos cuadrados extendidos trata de resolver el problema del
sesgo en la estimación de modelos ARMAX. La solución es incluir los coeficientes del
polinomio C(z−1
) en el vector de parámetros del estimador, es decir
θ = a1 · · · an b1 · · · bn c1 · · · cn
T

72 ESTIMACI ÓN DE LOS VALORES DE CONTINUA
Sin embargo, los valores pasados de la señal de ruido v(k) no son medibles, por lo que
no se pueden incluir en el regresor. Lo que se hace es aproximarlos por los errores de
predicción, es decir
e(k) = y(k) − m(k)ˆθ(k − 1)
Si el proceso coincidiera exactamente con el modelo para algun valor del vector de
parámetros, entonces si los parametros evolucionasen en la dirección correcta la aprox-
imación de los valores de los ruidos por los errores cada vez ser´ıa más correcta y
eventualmente se igualar´ıan, es decir v(k) = e(k). El regresor se formará entonces
como,
m(k) = −y(k − 1) · · · −y(k − n) u(k − 1) · · · u(k − n) e(k − 1) · · · e(k − n)
El resto del procedimiento es exactamente igual, tanto en las formulaciones fuera de lin-
ea como en linea. Con este método se consiguen estimaciones insesgadas y consistentes
para procesos que respondan como un modelo ARMAX. Los problemas son un aumen-
to de la carga de calculo y una menor velocidad de convergencia en los parámetros ci
debido a que la señal de ruido no es la más preponderante.
Finalmente, existe otra variante de los m´ınimos cuadrados que son los m´ınimos
cuadrados generalizados. Sin entrar en demasiados detalles, esta formulación se usa
cuando se tiene algún conocimiento del valor real del polinomio C(z−1
) o de la matriz
P (matriz de covarianza). En este caso si la matriz N definida como
N = E vvT
es distinta de la matriz identidad se obtienen mejores resultados si el criterio que se
utiliza es
J(θ) = eT
(k, θ)N−1
e(k, θ)
4.6. Estimación de los valores de continua
Una de las condiciones necesarias para asegurar la convergencia que se mencionaron
en el tema 3 era que es necesario conocer los valores de continua de la señal y eliminarlos
de las medidas usadas en la identificación. Es decir para identificar un proceso hay que
utilizar señales sin componente continua:
u(k) = U(k) − U∞ y(k) = Y (k) − Y∞
donde U(k) e Y (k) son los valores reales de la salida y la entrada y U∞ e Y∞ son
los valores de continua de ambas señales. Para estimar dichos valores existen diversas
opciones.

4.6.1. Utilización de los incrementos de las variables
En este caso se toman los incrementos de las señales, es decir
uID(k) = u(k) − u(k − 1) = (U(k) − U∞) − (U(k − 1) − U∞) = U(k) − U(k − 1)
donde la señal uID(k) es la señal de entrada que se utiliza en la identificación. Como
se puede observar, al usarse el incremento, se resta de manera implicita la componente
continua. Lo mismo se hace con la salida
yID(k) = y(k) − y(k − 1) = (Y (k) − Y∞) − (Y (k − 1) − Y∞) = Y (k) − Y (k − 1)
Evidentemente, lo que se obtiene al identificar es un modelo incremental, es decir
formulado en incrementos de y(k) y u(k) y este incremento se tendrá que deshacer si
lo que se quiere son los valores no incrementales de dichas señales.
4.6.2. Cálculo de los valores medios
La idea es aproximar los valores de continua por los valores medios de las señales.
En el caso de la formulación fuera de linea estos valores medios se calculan mediante
las expresiones tradicionales, es decir
U∞ =
1
N
N
i=1
u(i) Y∞ =
1
N
N
i=1
y(i)
para la identificación en linea, es decir mediante algoritmos recursivos, se emplean las
siguientes expresiones
U∞(k) = U∞(k − 1) +
1
k
(U(k) − U∞(k − 1))
Y∞(k) = Y∞(k − 1) +
1
k
(Y (k) − Y∞(k − 1))
4.6.3. Estimación de una constante
La idea en este caso es que el modelo que se pretende identificar puede reescribirse
como
Y (k) − Y∞ = −a1(Y (k − 1) − Y∞) − a2(Y (k − 1) − Y∞) − · · · − an(Y (k − n) − Y∞)
+b1(U(k − d − 1) − U∞) + · · · + bn(U(k − d − n) − U∞)

74 IMPORTANCIA DEL ORDEN DEL MODELO
lo cual a su vez se puede poner como
Y (k) = −a1Y (k − 1) − · · · − anY (k − n)
+b1U(k − d − 1) + · · · + bnU(k − d − n) + K
siendo K una constante que vale
K = (1 + a1 + · · · + an)Y∞ − (b1 + · · · + bn)U∞ (4.9)
Para estimar la componente continua se modifica el algoritmo de manera que en el
vector de parámetros se incluye K
θ = a1 · · · an b1 · · · bn K
T
y en el regresor se incluye un 1
m(k) = −y(k − 1) · · · −y(k − n) u(k − 1) · · · u(k − n) 1
Una vez estimado el valor de K, lo que se hace es dar un valor arbitrario a Y∞, por
ejemplo igual al valor de la referencia o consigna. Con ese valor se calcula U∞ mediante
la expresión (4.9).
4.7. Importancia del orden del modelo
El orden del sistema a identificar es algo que debe ser conocido para asegurar la
convergencia e identificabilidad (ver tema 3). En la práctica esto no es sencillo, y se
debe recurrir a probar con varios modelos de ordenes y estructuras distintas a ver cual
resulta mejor. Esto quiere decir que se pueden dar situaciones de mala estimación del
orden del modelo por defecto (incurriendose en lo que se llama infraparametrización)
o por exceso (sobreparametrización).
Veamos que ocurre cuando se intenta aproximar un sistema por un modelo de
orden inferior. Si esto sucede se llega a una situación en la que el modelo solo puede
aproximar al sistema real en una banda de frecuencia relativamente estrecha. Si durante
el transcurso del proceso de identificación la señal de entrada cambia su contenido
frecuencial, el modelo estimado (es decir su vector de parámetros) evoluciona hasta
aproximar al sistema en torno a la nueva banda de frecuencias. Todo esto implica que
se obtendrá un modelo distinto dependiendo de la señal de entrada. Este problema se
ilustra en las figuras 4.2 y 4.3. En ambas se muestra el diagrama de bode de un sistema
de segundo orden sobre el que ha sido identificado un modelo de primer orden mediante
dos entradas senoidales de distinta frecuencia. Puede observarse en ambas figuras que

10
−1
10
0
10
1
−40
−30
−20
−10
0
10
20
amplituddB
10
−1
10
0
10
1
−250
−200
−150
−100
−50
0
frecuencia rad/s
desfase(grados)
Figura 4.2: Diagrama de Bode de un sistema de segundo orden (linea continua) y de un modelo de
primer orden estimado para una entrada senoidal de frecuencia ω = 0,2 rad × s−1
.
10
−1
10
0
10
1
−40
−30
−20
−10
0
10
20
amplituddB
10
−1
10
0
10
1
−250
−200
−150
−100
−50
0
frecuencia rad/s
desfase(grados)
Figura 4.3: Misma situación que en la figura 4.2 pero con una señal de entrada senoidal de frecuencia
ω = 1 rad × s−1
.

76 IMPORTANCIA DEL ORDEN DEL MODELO
el modelo obtenido no es sino una aproximación del sistema original en el entorno de
la frecuencia de la entrada. Esto ocasiona por tanto que ambos modelos sean distintos.
A la vista de lo que ocurre cuando existe infraparametrización, parecer´ıa lógico que
resulte mejor sobreestimar el orden del modelo para evitar el continuo cambio de los
parámetros del modelo estimado. Sin embargo esto no es una buena idea, pues puede
ocurrir que haya parámetros del modelo estimado que puedan tomar cualquier valor sin
que cambie la relación que liga las entradas del modelo con las salidas. Esto se manifiesta
en que algunos parámetros experimentan una deriva tomando valores arbitrarios muy
altos o muy bajos. Esto ocasionar´ıa problemas numéricos. Esta situación se ilustra
en la figura 4.4. En ella se muestra la evolución de los parámetros de un modelo de
cuarto orden identificado sobre el sistema de segundo orden utilizado en las figuras 4.2
y 4.3. Puede observarse que algunos de los ocho parámetros identificados convergen y
permanecen estables a lo largo del proceso de identificacion. Sin embargo otros no solo
no convergen sino que derivan hacia valores muy altos o muy bajos.
0 5 10 15 20 25 30 35 40
−1.5
−1
−0.5
0
0.5
1
1.5
uey
0 5 10 15 20 25 30 35 40
−2
−1.5
−1
−0.5
0
0.5
1
1.5
a
i
,b
i
estimados
tiempo (s)
Figura 4.4: Evolución de los parámetros identificados en un caso de sobreparametrización.
Matemáticamente el exceso de parámetros conduce a una situación en la que más
de una combinación de los valores del vector de parámetros producen la misma relación
entre la entrada y la salida. Por tanto la sobreparametrización se manifiesta también si
se traza la gráfica de un parámetro del modelo frente a otros por que aparecen relaciones
lineales. Esta situación se ilustra en la figura 4.5. En ella se muestran dos ejemplos en
los que se presentan los valores de un parámetro en función del otro a medida que
el proceso de identificación avanza. Puede observarse que existe un marcado patron
lineal, que indica una dependencia lineal entre ambos parámetros.

−2 −1.8 −1.6 −1.4 −1.2 −1 −0.8 −0.6
−0.005
0
0.005
0.01
0.015
0.02
0.025
a1
b
3
k=30
k=100
k=180
−2 −1.8 −1.6 −1.4 −1.2 −1 −0.8 −0.6
−0.5
0
0.5
1
1.5
a1
a
2
k=30
k=100
k=180
Figura 4.5: Evolución de unos parámetros frente a otros para el modelo sobreparametrizado.
4.8. Identificación de sistemas con retardo o no li-
neales
El método de los m´ınimos cuadrados puede aplicarse a procesos con retardo, siempre
que se tengan en cuenta algunas cuestiones. El modelo determinista de un sistema con
retardo puro de d periodos de muestreo se puede poner como
A(z−1
)y(k) = B(z−1
)u(k − d − 1)
Eso quiere decir que el regresor en el instante k debe contener valores pasados de la
entrada desde k − d − 1 a k − d − n donde n es el grado del polinomio B(z−1
). Por
tanto el regresor queda
m(k) = −y(k − 1) · · · −y(k − n) u(k − d − 1) · · · u(k − d − n)
Con esta modificación cualquiera de los algoritmos de m´ınimos cuadrados vistos ante-
riormente se puede aplicar a procesos con retardo. El problema estriba en que se ha
de conocer exactamente el retardo (vease tema 3). El método usual para conocer este
dato es provocar un cambio en la entrada y observar cuando se manifiesta dicho cam-
bio en la salida (ha de tenerse en cuenta que en todo sistema muestreado los cambios
en la entrada se manifestarán como mucho en el siguiente periodo de muestreo). Este
sencillo esquema se puede complicar por ejemplo si el retardo es variable. Esto es más
común de lo que se cree, pues el retardo as´ı como el resto de parámetros de un sistema
suele depender del punto de funcionamiento (por ejemplo, los retardos de transporte
ocasionados por tuberias dependen del caudal de material que se transporta). El pro-
blema es que, aunque los métodos de identificación propuestos puedan seguir cambios

78 CONSIDERACIONES FINALES
en los parametros del modelo (se adaptan a esos cambios) no recogen la posibilidad
de un retardo variable (existen remedios a este problema, pero no se tratarán aqu´ı).
Otro problema que puede suceder es que el retardo no sea multiplo exacto del tiempo
de muestreo. Aunque existen formas para describir retardos no enteros (por ejemplo,
el uso de una expansión de Padé) es mas sencillo y menos problemático emplear si es
posible otro tiempo de muestreo para hacer que el retardo sea entero.
Finalmente se comentó al principio del tema que el método de m´ınimos cuadrados
tambien permite la identificación de sistemas no lineales con la limitación de que el
modelo a identificar sea lineal en los parámetros. De este modo, si el sistema se pretende
identificar con un modelo que por ejemplo podr´ıa ser
y(k) + ay(k − 1) = bu2
(k − 1)
el regresor y el vector de parámetros ser´ıan
m(k) = −y(k − 1) u2
(k − 1) y θ(k) = a b
T
respectivamente.
4.9. Consideraciones finales
En esta sección se enunciarán algunas cuestiones prácticas a tener en cuenta cuando
se implementa alguno de los algoritmos presentados en este tema. En primer lugar si
no se emplea la técnica de factor de olvido, la ganancia de adaptación K(k) decrece
hasta hacerse casi cero, por lo que cuando eso ocurre ya no se pueden seguir cambios
posteriores de la dinámica. Por tanto para identificar sistemas cuya dinámica var´ıa
lentamente se ha de emplear m´ınimos cuadrados ponderados. Por otra parte, existen
situaciones en las que la matriz de covarianzas P puede crecer demasiado, por lo que
el identificador se har´ıa muy sensible a cualquier pequeño cambio de la dinámica o al
ruido. Esto ocurre por ejemplo cuando el punto de funcionamiento no var´ıa. Lo que se
puede hacer en este caso es utilizar un factor de olvido variable, de manera que si la
traza de P crece demasiado se toma λ = 1. Si la traza de P baja mucho se va bajando
λ, pero sin sobrepasar un cierto l´ımite que evita que el proceso de identificación se haga
demasiado sensible al ruido.
Otro aspecto es la elección del valor inicial de P. Se ha comentado que en el caso de
que no se tenga mucha confianza en el valor del vector de parámetros inicial, se propone
elegir P como una matriz diagonal pI siendo p un número arbitrariamente alto. Por

otra parte si antes de comenzar la identificación ya se dispone de 2n observaciones,
donde 2n es el número de parámetros a estimar, es posible tomar como valor inicial
P(0) = MT
(2n)M(2n)
−1
y como valor inicial del vector de parámetros se puede usar θ = P(0)M(2n)Y (2n).

Cap´ıtulo 5
Introducción al control adaptativo
5.1. Planteamiento del problema
En el contexto del control automático el término adaptativo se refiere a la facultad
de cambiar el comportamiento o parámetros del control en respuesta a cambios en las
circunstancias del sistema controlado. Un regulador adaptativo será aquel que pueda
modificar su comportamiento en respuesta a cambios en la dinámica del sistema y/o en
las perturbaciones a las que se ve sometido dicho sistema. En realidad esto es también
lo que se persigue cuando se introduce la realimentación en un sistema de control. En
efecto, el control realimentado fundamenta su efectividad en el hecho de que es capaz
de reaccionar a los cambios del estado o salida del proceso (los cuales pueden venir
motivados por perturbaciones o también cambios en la dinámica del proceso) actuando
de manera que dicho estado o salida se mantenga controlado.
En general se acepta que el control adaptativo es un tipo de control no lineal en el
que el estado del proceso puede ser separado en dos escalas de tiempo que evolucionan
a diferente velocidad. La escala lenta corresponde a los cambios en los parámetros del
regulador y la escala rápida a la dinámica del bucle ordinario de realimentación.
La configuración t´ıpica de un controlador adaptativo es la que se ilustra en la figura
5.1. Como se puede observar hay un bucle principal de realimentación negativa en el que
aparece un regulador ajustable y otro bucle que se utiliza para ajustar los parámetros de
dicho regulador. Para ello, se obtiene un cierto ´ındice de actuación en el cual se expresa
la bondad o comportamiento del controlador. Dicho´ındice de actuación se compara con
un cierto comportamiento deseado y según el resultado de dicha comparación se ajustan
81

82 PLANTEAMIENTO DEL PROBLEMA
WYXa`cbedfXhgpirqsXhd
iutwvyx€beir‚geƒ „ gpif`…b†i
‡ ƒˆqs‰qri‘qrƒˆg
‰`…qu‰’W“ƒ”qsƒ
iyWYbevriyWU‰–•Y`
‡ ƒ‚W“if`y‰’x ‡ X—qsƒ
irqui „ beiyW“‰–•Y`qrƒYW‚‰’x˜‰’•h`
COMPORTAMIENTO
DESEADO
y
u
+
++
-
REFERENCIA
Figura 5.1: Configuración genérica de un controlador adaptativo.
los parámetros del regulador. Para ello se utiliza un mecanismo de adaptación que en
algunos casos (no siempre) también puede actuar directamente sobre la actuación o
señal de control que recibe el proceso. En algunos casos se añade un tercer bucle que
tiene como tarea la supervisión del sistema de manera que, por ejemplo, se garantice la
estabilidad del sistema en bucle cerrado o se eviten ciertos comportamientos indeseados
tales como cambios demasiado abruptos en los parámetros del regulador ajustable.
Es fácil ver que en el esquema anterior el mecanismo de adaptación realiza la tarea
de resolver en tiempo real el problema de diseñar un regulador apropiado (en el caso
más sencillo con una estructura predefinida) para un sistema dado de manera que se
cumplan unas determinadas especificaciones de diseño (dadas por el ((comportamiento
deseado))).
Existen otros controladores que proporcionan una cierta capacidad de adaptación
pero que no encajan en la definición anterior ya que la adaptación se realiza en bucle
abierto, es decir, para adaptar la ley de control no se usan las medidas de la salida o
estado de la planta. Este es el caso de los controladores gain scheduling los cuales se
tratarán en la sección 7.4.
5.1.1. Clasificación grosso modo de los sistemas de control
adaptativo
De una manera general los sistemas de control adaptativo se pueden clasificar en
dos grandes grupos:

CAPÍTULO 5. INTRODUCCI ÓN AL CONTROL ADAPTATIVO 83
Controladores adaptativos por modelo de referencia (MRAC).
Reguladores autoajustables (STR).
Ambas estrategias suponen que para cualquier juego de valores de los parámetros del
sistema y las perturbaciones, existe un controlador lineal que hace que el sistema en
bucle cerrado cumpla los requisitos de diseño.
Los MRAC intentan alcanzar un comportamiento en bucle cerrado deseado que
viene especificado por un modelo de referencia. Por otra parte, los STR intentan alcan-
zar un control lo mejor posible (óptimo) a partir de un tipo de controlador prefijado y
la información obtenida del proceso (señales de entrada, salida, etc. . . ).
Las dos técnicas tienen sus ventajas e inconvenientes. Las ventajas del MRAC pasan
por una rápida adaptación y la posibilidad de utilizar formulaciones que garanticen
estabilidad (usando métodos de Lyapunov). Sin embargo, la capacidad de adaptación
de estas estrategias dependen en gran medida de la riqueza dinámica de la señal de
control (esto es análogo a lo que ocurre en la identificación de sistemas, véase el tema
3). Por otra parte, los STR se adaptan bien en casi todas las situaciones y son fáciles de
implementar pues admiten técnicas de programación modular. Sin embargo, también
presentan sus propios inconvenientes como se verá más adelante.
Otra posible clasificación de los sistemas de control adaptativos es aquella que
atiende a la forma de obtener los parámetros del controlador. En este esquema podemos
encontrarnos:
Controladores adaptativos con diseño mediante criterio óptimo.
Controladores adaptativos con diseño mediante criterio no óptimo.
En los primeros el valor de los parámetros se obtiene buscando entre los posibles valores
aquellos que hacen óptimo un cierto criterio de comportamiento del sistema. Es decir,
optimizan un criterio de comportamiento o funcionamiento. En este grupo estudiare-
mos los controladores de m´ınima varianza y m´ınima varianza generalizado. También
se puede considerar en este grupo el control predictivo basado en modelo (al que dedi-
caremos un amplio cap´ıtulo más adelante) cuando este tipo de control se utiliza como
controlador ajustable en alguno de los esquemas de control adaptativo referidos al
principio del tema.

84 JUSTIFICACI ÓN DEL USO DE CONTROL ADAPTATIVO
Los controladores adaptativos sin criterio óptimo buscan los parámetros del contro-
lador no mediante la optimización de un criterio de funcionamiento sino entre aquellos
que cumplen unas ciertas especificaciones, por ejemplo, la colocación de los ceros y los
polos de bucle cerrado. En estos esquemas el controlador ajustable puede ser por ejem-
plo un regulador PID, un controlador dead-beat como los estudiados anteriormente o
un controlador por asignación de polos o de ceros y polos. En tiempo real se resolverá el
problema de diseñar dichos controladores, de manera que a pesar de los cambios en el
proceso se sigan cumpliendo las especificaciones de diseño.
5.2. Justificación del uso de control adaptativo
El control adaptativo conlleva una serie de inconvenientes que pueden hacernos cues-
tionar su uso. Por ejemplo, su sinton´ıa no suele ser tan sencilla como la de los clásicos
controladores PID. Por tanto, hay que ver en que situaciones puede ser ventajoso su
uso y en que situaciones es mejor quedarse con controladores más sencillos.
En general un controlador convencional está pensando para controlar sistemas cuyos
parámetros permanecen constantes (es decir, su dinámica no var´ıa). Esta suposición se
corresponde más o menos con la de un sistema que suele operar siempre cerca de un
determinado punto de operación y cuyas perturbaciones no son grandes (en relación a
la variable controlada) y no var´ıan demasiado. Sin embargo, puede suceder que el punto
de trabajo var´ıe frecuentemente y en algunos sistemas puede suponer una variación de
su dinámica lo suficientemente importante para afectar al rendimiento del controlador.
Por ejemplo, supongamos un sistema realimentado en el que el actuador presenta una
caracter´ıstica de transferencia no lineal (figura 5.2). Esta situación corresponde por
G(s)f(u)
u v+
-
Figura 5.2: Sistema realimentado con actuador con caracter´ıstica v = f(u).
ejemplo a la caracter´ıstica instalada de un válvula que usualmente suele ser no lineal.
Supongamos que el caudal de salida de la válvula viene dado por una expresión C =
ξ ∗ A4
, donde ξ es una cierta constante y A la apertura porcentual de la válvula. En la
figura 5.3 se muestra dicha caracter´ıstica instalada (trazo sólido). A la hora de diseñar
el sistema de control se intentar´ıa obtener un modelo linealizado del actuador, que

evidentemente saldr´ıa diferente en función del punto de operación. Si el controlador
se ve forzado a trabajar en distintos puntos de operación su rendimiento no podrá ser
igual de bueno en todos, de manera que este esquema irá bien si el punto de operación
no se mueve demasiado. Una solución ser´ıa trabajar con un modelo linealizado a tramos
de la caracter´ıstica de la válvula (figura 5.3 trazo discontinuo), de manera que en cada
punto de funcionamiento el controlador adaptará su comportamiento (variando sus
parámetros de diseño) de acuerdo al modelo linealizado que se tenga en cada caso. En
0 10 20 30 40 50 60 70 80 90 100
0
2
4
6
8
10
12
14
16
apertura (%)
caudal(m
3
/h)
Figura 5.3: Sistema realimentado con actuador con caracter´ıstica v = f(u).
general, cuando la variación en los parámetros del sistema o los actuadores se conoce
de antemano y además se puede establecer una dependencia entre dichos parámetros
y el punto de operación (o una variable auxiliar) se puede recurrir a técnicas sencillas
de control adaptativo como el gain scheduling (véase la sección 7.4). En caso contrario
tendr´ıamos que recurrir a técnicas más sofisticadas.
Otro hecho a tener en cuenta es que no siempre es fácil juzgar la necesidad o
no de utilizar el control adaptativo. Considérese el sistema dado por la función de
transferencia
G(s) =
1
(s + 1)(s + a)
donde a = −0,01, 0, 0,01 (5.1)
La primera aproximación a este sistema ser´ıa hallar su respuesta ante escalón, para
los diversos valores de a. Como se ilustra en la figura 5.4 (izquierda), dicha respuesta
var´ıa mucho en función de los valores del parámetro a, pasando de hecho de ser un
sistema estable a otro inestable. Parecer´ıa que el sistema var´ıa lo suficiente como para
justificar el uso del control adaptativo. Sin embargo, la configuración que realmente
nos interesa es la del sistema realimentado. En la figura 5.4 (derecha) se muestra la

86 JUSTIFICACI ÓN DEL USO DE CONTROL ADAPTATIVO
respuesta del sistema en bucle cerrado (realimentación unitaria). En contra de lo que
podr´ıamos suponer la respuesta en bucle cerrado es más o menos la misma, por lo que,
siendo esta la configuración en la que se va a trabajar, no ser´ıa necesario usar control
adaptativo.
0 20 40 60 80 100 120 140 160 180 200
0
100
200
300
400
500
600
700
Step Response
Time (sec)
Amplitude
0 2 4 6 8 10 12
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Step Response
Time (sec)
Amplitude
Figura 5.4: Respuestas en bucle abierto (izquierda) y cerrado (derecha) del sistema dado en (5.1).
Es fácil poner un ejemplo en el que la situación sea la inversa de la anterior. Con-
sidérese el sistema dado por la función de transferencia
G(s) =
20(1 − Ts)
(s + 1)(s + 20)(Ts + 1)
donde T = 0, 0,015, 0,03 (5.2)
En este caso la respuesta en bucle abierto del sistema es muy parecida independiente-
mente de los valores de T (figura 5.5 izquierda). Cuando se le realimenta usando como
entrada u = 15(ref − y) se obtienen, sin embargo, comportamientos muy diferentes en
función del valor de T (figura 5.5 derecha). Es por tanto que en este caso s´ı estar´ıa
justificado el uso de técnicas de control adaptativo. El lector puede comprobar además
que no sólo hay que juzgar en función del comportamiento en bucle cerrado en general,
sino que hay que tener en cuenta cuáles van a ser las condiciones de operación particu-
lares en las que se va a trabajar. En efecto, si se obtiene la respuesta en bucle cerrado
para el sistema (5.2) pero utilizando una realimentación unitaria (esto es, u = (ref −y))
entonces las respuestas son esencialmente iguales independientemente del valor de T.

0 1 2 3 4 5 6
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Step Response
Time (sec)
Amplitude
0 0.5 1 1.5 2 2.5 3
0
0.5
1
1.5
Step Response
Time (sec)
Amplitude
Figura 5.5: Respuestas en bucle abierto (izquierda) y cerrado (derecha) del sistema dado en (5.2).
5.3. Control adaptativo por modelo de referencia
(MRAC)
Es una de las técnicas más antiguas de control adaptativo y se basa, como su nombre
indica, en disponer de un modelo de bucle cerrado que es el que se desea que describa al
conjunto controlador-planta. Es decir, se debe partir de un conjunto de especificaciones
deseadas de bucle cerrado que se expresan mediante el modelo de referencia. El con-
trolador ajustable deberá adaptar sus parámetros para que el modelo de bucle cerrado
del conjunto coincida o se acerque lo más posible al modelo de referencia. La figura
5.6 muestra la configuración más popular (no es la única sin embargo) para este tipo
de controladores. En dicha figura puede observarse un controlador primario ajustable
que en principio puede ser cualqier tipo de controlador. El mecanismo de adaptación
es el que se va a encargar de ajustar los parámetros del control primario para que la
diferencia entre la salida de la planta y el modelo de referencia sea lo más pequeña
posible (es decir, que independientemente del valor inicial de esa diferencia, ésta vaya
tendiendo a cero progresivamente).
Además de utilizar las señales tomadas de las salidas de la planta y el modelo,
el mecanismo de adaptación puede utilizar las señales de entrada, de referencia y si
estuviesen disponible las variables de estado. En suma, toda la información disponible
sobre la planta y el comportamiento del sistema en bucle cerrado.
Para diseñar un MRAC se ha de definir el modelo de referencia, el controlador y
la ley de adaptación. En cuanto al modelo de referencia, sabemos que éste especifica
el comportamiento en bucle cerrado deseado. Por tanto, el modelo ha de ser tal que

88 CONTROL ADAPTATIVO POR MODELO DE REFERENCIA (MRAC)
™pdfefg˜h“dî€jYkhdphjal’monPgpjYqfi†r s i€jUeogtj
u rf™ejUeovwn u dxk‚rjYk‚j s g˜jh™fvype
u+
-
REFERENCIA
yp
u dˆkYrzied{kYrhprz|Przhprtef™fvSj ym
+
-
+
Figura 5.6: Configuración genérica de un controlador adaptativo por modelo de referencia (MRAC).
el conjunto controlador ajustable-planta pueda reproducir dicho modelo. Es decir, no
se puede escoger el comportamiento deseado de bucle cerrado sin pensar si el contro-
lador ajustable es capaz de lograr (para alguna combinación de sus parámetros) dicho
comportamiento. Esto impone una serie de requisitos sobre el modelo, principalmente
sobre el orden del mismo. Tampoco es realista escoger un modelo de referencia con
una dinámica muy rápida en comparación con la de la planta en bucle abierto. Por
supuesto es normal escoger la dinámica de bucle cerrado más rápida que la de bu-
cle abierto, pero no se puede escoger de manera arbitrariamente rápida, ya que ello
desembocará en problemas de convergencia en los parámetros del controlador.
Por otra parte para el controlador primario se puede pensar en casi cualquier es-
tructura de control lineal, incluyendo los populares PI, PID, etc. . . Se deben cumplir
sin embargo varios requisitos, entre ellos que la señal de control debe ser una función
lineal de los parámetros. También (suponiéndose fijado el modelo) se debe escoger un
controlador ajustable que permita reproducir el modelo.
Finalmente, para la ley de adaptación existen diferentes estrategias en la literatura
de las cuales nombraremos el método de hiperestabilidad y la estrategia basada en la
teor´ıa de estabilidad de Lyapunov (ambas estrategias aseguran la estabilidad de bucle
cerrado del sistema) y la primera y más popular, el enfoque de sensibilidad o regla del
MIT.

5.3.1. La regla del MIT
Se basa en un ´ındice de actuación, usualmente cuadrático, que mide la bondad de
la adaptación en base a las discrepancias entre las salidas del modelo y la planta a lo
largo de un intervalo de tiempo:
J(t + T) =
t+T
t
e2
(τ)dτ con e(t) = yproceso(t) − ymodelo(t) (5.3)
donde T es un periodo fijo de tiempo. La idea de la regla del MIT es ajustar el vector
de parámetros del controlador en el instante t + T, de manera que haga decrecer J. Es
decir,
θ(t + T) = θ(t) − Γ
∂J
∂θ
= θ(t) − Γ
t+T
t
2e(τ)
∂e(τ)
∂θ
dτ (5.4)
donde Γ ∈ Rn×n
es una matriz definida positiva que actúa como ganancia de adaptación.
Es fácil entender que el controlador sólo tiene influencia sobre la salida de la planta,
no sobre la del modelo. Por tanto ymodelo(t) no depende de θ y al variar éste tampoco
lo hace ymodelo(t), luego
∂e(τ)
∂θ
=
∂yproceso(τ)
∂θ
Finalmente, podemos conocer la variación instantánea de los parámetros del contro-
lador tomando T → 0 en el segundo miembro de (5.4) y teniendo en cuenta lo anterior
se llega a
dθ
dt
= −2Γe(t)
∂yproceso
∂θ
(5.5)
Nótese que ∂yproceso
∂θ
representa cómo var´ıa la salida del proceso frente a variaciones del
vector de parámetros, es decir la sensibilidad de yproceso(t) frente a variaciones de θ, de
ah´ı el nombre alternativo de ((enfoque de sensibilidad)).
En la práctica la sensibilidad de la salida del proceso puede ser dif´ıcil de conocer.
Por tanto, se la suele sustituir por la del modelo de referencia (que s´ı es conocido). Este
esquema funciona porque después de un tiempo el comportamiento en bucle cerrado del
sistema acaba convergiendo al del modelo de referencia. En cualquier caso, la ganancia
de adaptación no debe ser muy grande pues si no puede aparecer un comportamiento
inestable (especialmente si hay discrepancias iniciales fuertes entre la sensibilidad del
proceso y la del modelo, porque las correcciones al valor de θ serán muy enérgicas y en
la dirección equivocada).
Finalmente hay que decir que esta regla presenta diversas formulaciones alternati-
vas. De hecho la formulación original del MIT se basaba en el ´ındice
J(t) =
1
2
e2
(T)

que resulta en la regla
dθ
dt
= −γe(t)
∂e(t)
∂θ
y hay otras posibilidades como
J(t) = |e(t)| que resulta en
dθ
dt
= −γ
∂e(t)
∂θ
signo(e(t))
o directamente ajustar mediante
dθ
dt
= −γ signo
∂e(t)
∂θ
signo(e(t))
Ejemplo 5.1
Supongamos que tenemos un proceso cuya función de transferencia viene dada por
G(s) = kF(s)
donde k es ganancia desconocida y F(s) es perfectamente conocida. Se pretende que
el sistema en bucle cerrado se comporte acorde al modelo de referencia
GM (s) = k0F(s) (5.6)
donde k0 es una ganancia conocida (es un dato de entrada del problema). El controlador
ajustable del que se dispone tiene la estructura
u = θuc
donde u es la entrada que se aplica a la planta y uc es la entrada al controlador (es
decir el parámetro θ que se ha de ajustar es simplemente una ganancia). Se supone una
configuración del sistema de control tal que θ es una ganancia feed-forward, es decir,
la función de transferencia desde uc a la salida del proceso yp es
Y (s)
UC(s)
= θkF(s)
Como se pretende que la función de transferencia sea como en (5.6), lo lógico ser´ıa
tomar
θ =
k0
k
pero es evidente que esto no se puede hacer, porque se desconoce el valor de k. Se
propone ajustar θ mediante la regla del MIT en el contexto de un control adaptativo
MRAC. El error es en este caso
e(t) = yp(t) − ym(t) = kF(s)θuc(t) − k0F(s)uc(t) (5.7)

La sensibilidad1
vendrá dada por
∂e(t)
∂θ
= kF(s)uc(t) (5.8)
ahora bien, de (5.7) se obtiene que
−ym(t) = −k0F(s)uc(t)
luego,
F(s)uc(t) =
ym(t)
k0
por lo que llevando esto a (5.8) se obtiene
∂e(t)
∂θ
=
k
k0
ym(t)
La variación de los parámetros según la regla del MIT será
dθ
dt
= −γ
k
k0
ym(t)e(t)
Nótese que se sigue desconociendo el valor de k0, sin embargo esto no plantea problema
alguno, pues como γ es una constante cualquiera podemos agrupar las constantes que
aparecen en una sola γ , de manera que la regla ser´ıa
dθ
dt
= −γ ym(t)e(t)
1
Con el objeto de simplificar las cosas en la ecuación (5.7) se ha abusado notablemente de la
notación pues se están incluyendo simultáneamente funciones en el dominio s (de la transformada de
Laplace) y señales en el dominio temporal. Esto no es correcto y quizás ser´ıa mejor utilizar la notación
F(p) donde p = d
dt , es decir, sustituir las funciones en s por su equivalente en el operador derivada.

Cap´ıtulo 6
Reguladores Autoajustables (STR)
6.1. Introducción. Estructura general de los STR
Los reguladores autoajustables (del inglés Self Tuning Regulator) constituyen un
tipo de control adaptativo muy popular en el que en función del conocimiento que se
tiene de la dinámica del proceso a controlar son capaces de ajustarse a si mismos. Este
conocimiento se va actualizando en tiempo real de manera que el ajuste se mantiene
lo más cercano posible al óptimo.
Los STR se basan en el principio de equivalencia cierta que consiste en suponer
que los parámetros del proceso coinciden con los que se obtienen por identificación
de manera que se diseña el controlador usando esos parámetros. Como el controlador
se recalcula en cada paso, y los parámetros se actualizan también en cada paso, el
principio de equivalencia cierta no es una suposición demasiado arriesgada.
La estructura general de un STR se ilustra en la figura 6.1. En esta se observa que
hay tres partes diferenciadas:
Algoritmo recursivo de identificación. Al tener que actualizarse los parámetros
en tiempo real es evidente que se debe utilizar un algoritmo recursivo (véase el
cap´ıtulo 4).
Mecanismo de adaptación que desarrolla la tarea de diseño del regulador. Para
ello se utilizará el modelo actualizado que se tenga de la planta. Nótese que al
ser la estructura del controlador fija, ((diseñar)) el controlador es equivalente a
93

94 INTRODUCCI ÓN. ESTRUCTURA GENERAL DE LOS STR
obtener los mejores valores de los parámetros de sinton´ıa en base al modelo.
Regulador con parámetros ajustables. Por lo general la estructura es fija y puede
ser cualquier tipo de controlador lineal en el que los parámetros se puedan ajustar.
REFERENCIA }†~†“€‚e~fƒ‚„p…ˆ~e„p†ˆ‡“‰V€‚„pŠ€ƒP‹ Œ ƒ‚„pˆ€P„
‹z‰A€‚Žu„“}tS†{…U‹ƒp„ Œ ƒ‚„fˆ€P„…p‰A‹‚‚~‘…ˆ‹pƒ}†~†“€‚e~fƒ‚„p…ˆ~eCOMPORTAMIENTO
DESEADO
y
u+
-
Figura 6.1: Configuración genérica de un regulador o controlador autoajustable.
En los STR clásicos se suele suponer que los procesos son deterministas (es decir no
se consideran fuentes de perturbaciones estocásticas como las vistas en el cap´ıtulo 2).
Por otra parte es común que el controlador ajustable sea del tipo PID. En realidad,
como es la estructura de un STR es modular, se puede usar cualquier combinación de
controlador/método de identificación.
También se pueden considerar procesos estocásticos en los STR. Es común entonces
que la estructura escogida para el modelo sea la de tipo ARMAX (véase el cap´ıtulo 2).
El diseño se podrá hacer, por tanto, utilizando un criterio estocástico o no estocástico.
En el caso de que sea un criterio estocástico normalmente se obtienen los parámetros
del regulador mediante la minimización de un cierto ´ındice de funcionamiento. Por
ejemplo en el regulador de m´ınima varianza (el cual se verá en la sección 6.2) se intentan
minimizar las variaciones con respecto a cero de la salida (se considera un problema de
regulación con referencia nula), que al ser una señal ruidosa se consigue minimizando
la esperanza matemática de la salida en k + d, es decir
J = E y2
(k + d)
siendo d el retraso.
Cuando el diseño ser realiza usando un planteamiento no estocástico, se está con-
siderando que las perturbaciones que inciden sobre el sistema son conocidas con exac-
titud de antemano, de tal manera que podemos usar modelos deterministas (véase el
cap´ıtulo 2). En este caso el ´ındice de actuación se da en función de unas especifica-
ciones que debe cumplir la salida del sistema, como por ejemplo el tiempo de subida y

CAPÍTULO 6. REGULADORES AUTOAJUSTABLES (STR) 95
establecimiento, etc. . . También se emplear´ıan especificaciones que definan la dinámica
resultante como la colocación de los polos de bucle cerrado.
6.1.1. Algoritmos con estructura impl´ıcita y expl´ıcita
Entre los STR podemos distinguir dos tipos de algoritmos, unos que identifican di-
rectamente los parámetros de la planta y luego diseñan el controlador para cumplir con
los requisitos (estructura expl´ıcita) y otros que lo que hacen es estimar el controlador
directamente sin pasar por la estimación previa de la planta (estructura impl´ıcita).
Un algoritmo con estructura expl´ıcita constar´ıa de los siguientes pasos:
1. Estimar los parámetros del modelo mediante un algoritmo de identificación re-
cursivo.
2. Calcular los parámetros del controlador.
3. Calcular la señal de control y aplicarla.
Estos pasos se repetir´ıan en cada tiempo de muestreo.
Los algoritmos de estructura impl´ıcita son más complicados desde el punto de vista
conceptual. Lo que se hace en ellos es reparametrizar el modelo de la planta y el
controlador en función de los parámetros del controlador. El esquema ser´ıa el mostrado
en la figura 6.2. Obsérvese en esta figura que no se está pasando por la fase de diseño del
REFERENCIA ’p“t”e•8–€“t—8˜z™†“t–˜†š›pœw•8˜z‚—Vž Ÿ —8˜z”†•V˜
™†ž8”f• ¡¢ ’p˜p’ £ ”™†ž¤—Y¥o“€™zž¤—‚“–˜ž Ÿ ˜z–˜˜z¥hžP•V– ¦ ˜†™e“
COMPORTAMIENTO
DESEADO
y
u+
-
Figura 6.2: Configuración genérica de un regulador o controlador autoajustable.
controlador sino que este se identifica, de manera que cumpla con las especificaciones de
diseño. Por eso en la figura 6.2 como la identificación toma como datos de entrada las

96 CONTROL POR MÍNIMA VARIANZA
medidas de la planta y además las especificaciones de diseño. En este tipo de algoritmo
los pasos suelen ser:
1. Estimar los parámetros del modelo reparametrizado.
2. Calcular y aplicar la señal de control.
Al igual que en caso anterior estos pasos se repiten cada tiempo de muestreo.
Ambos tipos tienen ventajas e inconvenientes. En el caso de los de estructura ex-
pl´ıcita, la carga computacional suele ser mayor pero a cambio, se obtiene un modelo de
la planta que puede ser utilizado para otras tareas diferentes de la de control, por ejem-
plo para simulación o supervisión. También se puede tener un banco de controladores
seleccionables en función del modelo obtenido. En el caso de los de estructura impl´ıcita
se necesitan menos cálculos, pero la identificación es más dif´ıcil (pueden aparecer prob-
lemas de convergencia con más facilidad). Por otra parte no siempre es posible obtener
el modelo reparametrizado.
6.2. Control por M´ınima Varianza
El regulador de m´ınima varianza es un regulador óptimo que pretende reducir el
efecto de las perturbaciones sobre la salida, minimizándose para ello un cierto ´ındice
de funcionamiento. Efectivamente, la señal de control que se aplica en el instante k, es
decir u(k), se calcula como una función de u(k−1) . . . u(k−nb) y(k)y(k−1) . . . y(k−na),
de manera que se minimice
J = E y2
(k + d|k)
donde E{} es el operador esperanza matemática, y la notación y(k + d|k) indica la
predicción del valor de y en el instante k + d hecha en base a la información disponible
en el instante k. El modelo del proceso que se considera es del tipo ARMAX, el cual
se indica a continuación
A(z−1
)y(k + d) = B(z−1
)u(k) + C(z−1
)v(k + d) (6.1)
donde
A(z−1
) = 1 + a1z−1
+ · · · + anz−n
B(z−1
) = b1z−1
+ b2z−2
+ · · · + bnz−n
C(z−1
) = 1 + c1z−1
+ · · · + cnz−n

y d es el retraso puro1
.
Supóngase que se desea dividir C(z−1
) entre A(z−1
). Dicha división de polinomios
producirá en general un polinomio cociente y un polinomio resto. El cociente lo deno-
taremos por F(z−1
) y el resto se factoriza de manera que se denote por z−(d+1)
G(z−1
).
Por tanto podremos reescribir la conocida expresión dividendo igual a divisor por co-
ciente más resto as´ı
C(z−1
) = A(z−1
)F(z−1
) + z−(d+1)
G(z−1
) (6.2)
donde
F(z−1
) = 1 + f1z−1
+ · · · + fdz−d
G(z−1
) = g0 + g1z−1
+ · · · + gn−1z−(n−1)
Nótese que el grado de F(z−1
) es d y el de G(z−1
) es n−1. A continuación dividiremos
ambos miembros de la ecuación (6.1) por A(z−1
) y usaremos (6.2) de manera que se
obtiene
y(k + d) =
B(z−1
)
A(z−1)
u(k) + F(z−1
)v(k + d) +
z−1
G(z−1
)
A(z−1)
v(k) (6.3)
en donde además se ha tenido en cuenta que z−d
v(k + d) = v(k). Veamos el significado
de algunos de los términos de (6.3). El término F(z−1
)v(k + d) es una combinación
lineal de los valores de v(k) a v(k + d) cuyo efecto sobre y(k + d) no depende de u(k).
Por otra parte el termino
z−1
G(z−1
)
A(z−1)
v(k)
representa el efecto sobre la salida de las perturbaciones en instantes anteriores a k.
Por otra parte si dividimos por C(z−1
) la expresión (6.2) se obtiene
1 =
A(z−1
)F(z−1
)
C(z−1)
+
z−(d+1)
G(z−1
)
C(z−1)
que se puede reescribir como
1 −
A(z−1
)F(z−1
)
C(z−1)
=
z−(d+1)
G(z−1
)
C(z−1)
(6.4)
Por otra parte según el modelo ARMAX
v(k) =
A(z−1
)
C(z−1)
y(k) −
B(z−1
)
C(z−1)
z−d
u(k)
1
Nótese que el polinomio B(z−1
) no tiene término independiente, lo que se refleja en la forma de
describir el proceso ARMAX en la ecuación (6.1).

98 CONTROL POR MÍNIMA VARIANZA
Esto se puede sustituir en la ecuación (6.3) de manera que se obtiene
y(k +d) =
B(z−1
)
A(z−1)
u(k)+F(z−1
)v(k +d)+
z−1
G(z−1
)
A(z−1)
A(z−1
)
C(z−1)
y(k) −
B(z−1
)
C(z−1)
z−d
u(k)
operando
y(k + d) =
B(z−1
)
A(z−1)
u(k) + F(z−1
)v(k + d) +
z−1
G(z−1
)
C(z−1)
y(k) −
G(z−1
)B(z−1
)
A(z−1)C(z−1)
z−(d+1)
u(k)
que, agrupando los términos que contienen u(k), es a su vez es igual a
y(k +d) = F(z−1
)v(k +d)+
z−1
G(z−1
)
C(z−1)
y(k)+
1
A(z−1)
1 −
G(z−1
)z−(d+1)
C(z−1)
B(z−1
)u(k)
Recuérdese ahora la ecuación (6.4) y sustitúyase en la anterior para obtener
y(k + d) = F(z−1
)v(k + d) +
z−1
G(z−1
)
C(z−1)
y(k) +
F(z−1
)B(z−1
)
C(z−1)
u(k)
A partir de esta ecuación podemos calcular J y ver que valor de u(k) hace m´ınimo J:
E y2
(k + d) = E F(z−1
)v(k + d)
2
+ E
F(z−1
)B(z−1
)
C(z−1)
u(k) +
z−1
G(z−1
)
C(z−1)
y(k)
2
+2E F(z−1
)v(k + d)
F(z−1
)B(z−1
)
C(z−1)
u(k) +
z−1
G(z−1
)
C(z−1)
y(k)
Si se intenta minimizar la expresión anterior se tiene que el primer término no depende
de u(k), por lo que no influye a la hora de calcular el valor de u(k) que hace m´ınimo
J. Por tanto, ese término puede ser descartado. Por otra parte, el tercer término es la
esperanza matemática de una expresión la que aparece términos en los que los valores
de la perturbación v(k + i) i = 0 . . . d multiplican valores actuales y pasados de y(k)
y u(k). Como los valores de v(k + i) i = 0 . . . d son independientes (incorrelados)
de los de y(k) y u(k) la esperanza matemática que aparece en ese tercer término es
cero. Por tanto, nos queda sólo el segundo término que es el que hay que minimizar.
Para ello basta con calcular el valor que hace cero lo que está dentro de las llaves y
as´ı el cuadrado será cero (que es el m´ınimo valor posible de una función cuadrática).
El resultado es
u(k) = −
z−1
G(z−1
)
F(z−1)B(z−1)
y(k) (6.5)
que se puede reescribir también como (y as´ı aparece en algunos textos)
u(k) = −
G(z−1
)
zB(z−1)F(z−1)
y(k) (6.6)

Ejemplo 6.1
Considérese el siguiente sistema lineal
yk = ayk−1 + buk−2
Se pide encontrar la expresión del regulador de m´ınima varianza.
En este caso es fácil ver que
A(z−1
) = 1 − az−1
B(z−1
) = bz−1
C(z−1
) = 1
y por otra parte d = 1. Recordemos que se ha de dividir C(z−1
) entre A(z−1
) hasta que
el grado del cociente F(z−1
) sea d, o sea en este caso F(z−1
) tiene la forma F(z−1
) = 1+
f1z−1
. La figura 6.3 nos muestra la división hecha paso a paso a la manera tradicional.
Por tanto F(z−1
) = 1 + az−1
. El resto que en este caso es a2
z−2
debe identificarse con
§ §w¨S©8ª¢«¬§w¨S©8ª¢«¬
©8ª «¬
§¢¤©8ª «¬
©8ª «¬¨© 8®ª «®
© ®ªA«®
Figura 6.3: División de polinomios para el ejemplo 6.2.
la expresión z−2
G(z−1
), por lo que es evidente que en este caso G(z−1
) = a2
. Luego
recordando la expresión (6.5) obtenemos que el regulador de m´ınima varianza para este
caso es
uk =
−z−1
a2
(1 + az−1)bz−1
yk = −
a2
(1 + az−1)b
yk
6.2.1. El regulador de m´ınima varianza generalizado
El control por m´ınima varianza tal y como se ha presentado aqu´ı presenta problemas
cuando el sistema es de fase no m´ınima ya que al tener ceros inestables estos se cance-
larán mediante polos inestables. Esta situación no es deseable, por que en la práctica
puede que los ceros cambien de posición, bien por imprecisión en el modelo del sistema
o por variaciones de la dinámica del sistema. En este caso los ceros no se cancelar´ıan
con los polos con lo cual añadir´ıamos polos inestables al sistema. Evidentemente esto
último llevar´ıa a la inestabilidad del sistema. Existen variaciones del regulador de m´ıni-
ma varianza que tratan este problema y además incorporan seguimiento de referencias
y ponderación del esfuerzo de control (es decir, que además de perseguir el objetivo de

100 ASIGNACI ÓN DE POLOS Y CEROS
m´ınimizar las variaciones de la salida con respecto a la referencia se intenta hacer esto
usando el menor esfuerzo de control posible). La más conocida es la del regulador de
m´ınima varianza generalizado. La idea de este regulador es la de considerar el siguiente
´ındice de funcionamiento
J = E Q(z−1
)y(k + d) + R(z−1
)u(t) − P(z−1
)ref(t + d)
2
donde Q(z−1
), R(z−1
) y P(z−1
) son funciones de ponderación estables que tienen la
forma
Q(z−1
) =
Qn(z−1
)
Qd(z−1)
R(z−1
) =
Rd(z−1
)
Rd(z−1)
P(z−1
) =
Pn(z−1
)
Pd(z−1)
Bajo estas condiciones la señal de control que minimiza J es
u(k) =
Rd(z−1
) (C(z−1
)P(z−1
)ref(t) − G(z−1
)y(t))
Qd(z−1)(Rd(z−1)F(z−1)zB(z−1) + C(z−1)Rd(z−1))
(6.7)
En las expresiones anterior R(z−1
) se utiliza para ajustar la velocidad de la respuesta
del controlador, con el objeto por ejemplo de prevenir la saturación de los actuadores.
Por otra parte se suele tomar Qd(z−1
) = 1 − z−1
de manera que la ley de control
resultante tiene un integrador por lo que se rechazan perturbaciones constantes.
Finalmente existen otras variaciones de la formulación presentada aqu´ı. Por ejemplo
una versión del regulador de m´ınima varianza que sólo soluciona el seguimiento de
referencia (no ir´ıa bien con sistemas de fase no m´ınima) resulta en la expresión
u(t) = −
G(z−1
)
zB(z−1)F(z−1)
y(t) −
C(z−1
)
zB(z−1)F(z−1)
ref(t + d) (6.8)
6.3. Asignación de polos y ceros
De entre los métodos basados en criterios no estocásticos se recoge aqu´ı el método
de asignación de polos y ceros debido a Aström y Wittenmark. En el cap´ıtulo 1 ya se
trató el problema de la asignación de polos mediante realimentación lineal del vector
de estados. Es conocido que con un sólo controlador no se pueden asignar polos y ceros
arbitrariamente, por lo que usualmente se prefiere asignar los polos. El método que
aqu´ı se presenta se basa por tanto en una estructura más compleja que permite colocar
los polos y los ceros en las posiciones deseadas. Dicha estructura se presenta en la figura
6.4.
El objetivo del procedimiento es que la función de transferencia de bucle cerrado

¯“°±² ³
ćµ’¶
³
¶· µˆ¶¹¸
º
»º
¸
¼
½¾À¿’Á
ÂÄÃ
Å
ÆÇ{È1ÉÀÊË
ÌÍpÎˆÏÑÐÒ Ó °S±¢²
Figura 6.4: Estructura para la asignación de polos y ceros.
sea igual a una dada, que supondremos denotada por
y(k) =
Rm(z−1
)
Pm(z−1)
z−d
w(k) (6.9)
donde se asume que Rm(z−1
) y Pm(z−1
) no tienen factores comunes y además el sistema
es causal por lo que el grado de Pm(z−1
) es mayor o igual al de Rm(z−1
).
A partir de la figura 6.4 y aplicando el álgebra de bloques se llega a la conclusión
de que la función de transferencia entre w(k) (la referencia a seguir) y y(k) es
y(k) =
S(z−1
)B(z−1
)z−d
A(z−1)M(z−1) + B(z−1)G(z−1)z−d
w(k)
Igualando esta expresión con la función de transferencia deseada (6.9) se llega a
(A(z−1
)M(z−1
) + B(z−1
)G(z−1
)z−d
)Rm(z−1
) = S(z−1
)B(z−1
)Pm(z−1
) (6.10)
Como se ha comentado en la sección 6.2.1 no es conveniente que se cancelen ceros
inestables con polos inestables, por lo que se imponen que las ra´ıces inestables de
B(z−1
) formen parte también de Rm(z−1
). Por tanto lo que se hace es que se factoriza
B(z−1
) como
B(z−1
) = B−
(z−1
)B+
(z−1
)
donde B−
(z−1
) contiene las ra´ıces inestables de B(z−1
) y B+
(z−1
) las estables. Como
las primeras deben estar en Rm(z−1
) factorizamos este último polinomio como
Rm(z−1
) = B−
(z−1
)Rm1(z−1
)
Impondremos además que las ra´ıces estables de B(z−1
) estén en M(z−1
), de manera
que tendremos
M(z−1
) = M1(z−1
)B+
(z−1
)

Por otra parte se asume que, además de especificarse el retraso y los polinomios que
definen la función de transferencia deseada, como parte de los datos de entrada del
problema, se tiene un polinomio A0(z−1
) que se utiliza para definir S(z−1
) mediante la
expresión
S(z−1
) = A0(z−1
)Rm1(z−1
)
Con todo lo anterior y la ecuación (6.10) se llega a
A(z−1
)M1(z−1
) + B−
(z−1
)G(z−1
)z−d
= A0(z−1
)Pm(z−1
) (6.11)
Esto es una ecuación polinomial, donde las incógnitas son M1(z−1
) y G(z−1
), que
puede resolverse mediante diferentes métodos2
. Quizás el más simple (pero no más
eficiente) sea plantear un sistema de ecuaciones lineales donde las incógnitas sean los
coeficientes de los polinomios M1(z−1
) y G(z−1
). En cualquier caso se deben imponer
condiciones sobre los grados de dichos polinomios para que la ecuación tenga solución
única. Aplicando consideraciones algebraicas que no mostraremos aqu´ı, se llega a que
existen dos posibles opciones para los grados de M1(z−1
) y G(z−1
),
1.
grado(G(z−1
)) = grado(A(z−1
)) − 1
grado(M1(z−1
)) = grado(A0(z−1
)) + grado(Pm(z−1
)) − grado(A(z−1
))
2.
grado(G(z−1
)) = grado(A0(z−1
)) + grado(Pm(z−1
)) − grado(B−
(z−1
)) − d
grado(M1(z−1
)) = grado(B−
(z−1
)) + d − 1
Se puede demostrar que el control por asignación de polos y ceros es equivalente al
MRAC. Por otra parte según el sistema podemos tener casos simplificados:
1. Cancelación de todos los ceros. Esto se puede hacer si el sistema es de fase m´ınima.
En este caso
B+
(z−1
) = B(z−1
) B−
(z−1
) = 1 Rm(z−1
) = Rm1(z−1
) = K
M(z−1
) = M1(z−1
)B(z−1
) S(z−1
) = KA0(z−1
)
por lo que la ecuación quedar´ıa como
A(z−1
)M1(z−1
) + G(z−1
)z−d
= A0(z−1
)Pm(z−1
)
2
De hecho es una ecuación polinomial diofántica. Este tipo de ecuaciones las encontraremos de
nuevo en el cap´ıtulo 9, donde se verán otros métodos para resolverla.

2. No se cancela ningún cero. Esto ocurre si todos las ra´ıces de B(z−1
) son inestables.
En este caso
B+
(z−1
) = 1 B−
(z−1
) = B(z−1
) S(z−1
) = KA0(z−1
)
M(z−1
) = M1(z−1
) Rm(z−1
) = KB(z−1
)
por lo que ahora la ecuación quedar´ıa como
A(z−1
)M(z−1
) + B(z−1
)G(z−1
)z−d
= A0(z−1
)Pm(z−1
)
Con este tipo de control se puede ilustrar la diferencia entre algoritmo con estructura
impl´ıcita y expl´ıcita. Comenzaremos derivando un algoritmo con estructura impl´ıcita,
para ver después el de estructura expl´ıcita.
6.3.1. Algoritmo con estructura impl´ıcita.
Nótese que multiplicando ambos miembros de la ecuación (6.11) por y(k) se obtiene
A(z−1
)M1(z−1
)y(k) + B−
(z−1
)G(z−1
)z−d
y(k) = A0(z−1
)Pm(z−1
)y(k)
que dado que A(z−1
)y(k) = B(z−1
)z−d
u(k) es equivalente a
M1(z−1
)B(z−1
)z−d
u(k) + B−
(z−1
)G(z−1
)y(k) = A0(z−1
)Pm(z−1
)y(k)
Por otra parte sabemos que M(z−1
) = M1(z−1
)B+
(z−1
) y B(z−1
) = B+
(z−1
)B−
(z−1
),
por lo que se llega a
A0(z−1
)Pm(z−1
)y(k) = B−
(z−1
)z−d
M(z−1
)u(k) + G(z−1
)y(k) (6.12)
La ecuación (6.12) expresa una relación entre la entrada y la salida que constituye
un modelo reparametrizado del sistema en bucle cerrado. En dicho modelo aparecen
polinomios conocidos de antemano (A0(z−1
), Pm(z−1
)), el retraso d que se supone
conocido, y tres polinomios (B−
(z−1
) , M(z−1
), G(z−1
)) que son los que deben ser
identificados (ajustados mediante un método de identificación recursivo), usando los
valores experimentales de la entrada y la salida. Obsérvese que al identificarse dicho
modelo reparametrizado se estarán identificando los parámetros del controlador además
de parte de los parámetros de la planta. Estos últimos no son sin embargo necesarios,
se pueden considerar un ((subproducto)) del proceso de identificación del controlador.
El algoritmo de control en s´ı, tomar´ıa como datos de entrada A0(z−1
), Pm(z−1
), el
retraso d y Rm1(z−1
). Los pasos de los que constar´ıa en cada instante de muestreo son
los siguientes

1. Obtener una estimación actualizada de M(z−1
), G(z−1
), B−
(z−1
) mediante la
identificación del modelo reparametrizado (6.12).
2. Calcular y aplicar
u(k) =
1
M(z−1)
S(z−1
)w(k) − G(z−1
)y(k)
donde S(z−1
) = A0(z−1
)Rm1(z−1
).
Este procedimiento puede presentar problemas para aquellos sistemas que sean de
fase no m´ınima. Esta mayor dificultad es inherente a los algoritmos con estructura
impl´ıcita, tal y como se ha comentado al comienzo del cap´ıtulo.
6.3.2. Algoritmo con estructura expl´ıcita
En este caso los datos de entradas al algoritmo ser´ıan A0(z−1
), Pm(z−1
), el retraso
d y Rm(z−1
). Los pasos de los que constar´ıa en cada instante de muestreo son los
siguientes
1. Obtener una estimación actualizada de A(z−1
) y B(z−1
) mediante la identifi-
cación del modelo
y(k) =
B(z−1
)
A(z−1)
z−d
u(k)
2. Factorizar B(z−1
) = B+
(z−1
)B−
(z−1
).
3. Resolver la ecuación (6.11).
4. Calcular y aplicar
u(k) =
1
M(z−1)
S(z−1
)w(k) − G(z−1
)y(k)
donde S(z−1
) = A0(z−1
)Rm1(z−1
) y M(z−1
) = M1(z−1
)B+
(z−1
).
Es fácil ver que este algoritmo tiene más cálculos que el anterior, en particular la
factorización de B(z−1
) y la resolución de la ecuación polinomial (6.11), tareas ambas
que pueden ser costosas en un hardware industrial no muy potente (además de más
complicadas de implementar). Sin embargo desde el punto de vista práctico suele tener
menos problemas.

Cap´ıtulo 7
Controladores PID con autoajuste
y Ajuste por tabla
7.1. Introducción
En este cap´ıtulo se revisaran algunas de las técnicas de control adaptativo con mayor
aplicación en la industria. Éstas no son tan ambiciosas como algunas de las presentadas
hasta ahora y sin embargo son definitivamente estrategias de control avanzado que han
demostrado ser útiles en la práctica. Además de las técnicas referidas en el t´ıtulo del
cap´ıtulo se concluirá el temario relativo a control adaptativo con un breve repaso a
algunos sistemas comerciales.
7.2. Función de autoajuste (autotuning)
Los reguladores adaptativos vistos hasta ahora, es decir los MRAC y STR, necesitan
para poder funcionar correctamente un conocimiento básico a priori de la planta. A fin
de poder obtener esa información lo mas fácilmente posible, los fabricantes introdujeron
en los controladores adaptativos comerciales un modo de sinton´ıa previa (pre-tune), que
obten´ıa dicha información básica.
Paralelamente, se estaban desarrollando técnicas para poder ajustar automática-
mente controladores de tipo PID sin necesidad de intervención del operario. Lo que
105

106 FUNCI ÓN DE AUTOAJUSTE (AUTOTUNING)
ocurrió, es que se vio que para poder ajustar un PID automáticamente bastaba con la
información básica que proporcionaban los modos pre-tune de los controladores adap-
tativos.
Por otra parte, desde el mundo industrial una de las caracter´ısticas más demandadas
era una función de autoajuste inicial. Al instalarse el controlador se activar´ıa dicha
función (apretando un botón en el panel de control) a lo que el controlador responder´ıa
realizando una bater´ıa de tests pre-programados que dar´ıan como resultado el ajuste
automático del controlador. Esta demanda surge de la dificultad y el engorro de ajustar
un controlador inicialmente. Lo que hicieron los fabricantes de PID fue aprovechar los
resultados obtenidos en el desarrollo de funciones pre-tune en controladores adaptativos
para dotar a sus PID de una función de autoajuste como la que demandaban los
usuarios.
Para conseguir el autoajuste se puede utilizar cualquier técnica de control adap-
tativo que permita estimar los parámetros adecuados, con el único requisito de que
los ensayos requeridos sean sencillos, a fin de poderse realizar de manera automática.
Desde el punto de vista práctico, los controladores con autoajuste tendrán dos modos
de funcionamiento, el modo normal en el cual funcionan como cualquier controlador
y el de ajuste. En el modo de ajuste el control se desconecta, se realizan los ensayos
necesarios y después se vuelve al modo normal con el controlador ajustado.
Por tanto un controlador con autoajuste realiza tareas de modelado (identificación),
y diseño del controlador, de manera transparente al usuario, por lo que se simplifican
mucho las tareas de instalación y puesta en marcha de los controladores. Por otra parte
no incrementan en mucho el coste final del controlador y son una manera de introducir
técnicas de control adaptativo en la industria.
Finalmente hay que hacer notar la diferencia fundamental entre un controlador
autoajustable del tipo STR y un controlador con autoajuste. En los primeros el con-
trolador de manera autónoma va adaptándose de una manera más o menos continuada.
En un controlador con función de autoajuste, dicho autoajuste sólo se realiza bajo de-
manda del operador, y usualmente sólo cuando se instala o se cambia sustancialmente
las condiciones del equipo a controlar.

CAPÍTULO 7. CONTROLADORES PID CON AUTOAJUSTE Y AJUSTE POR TABLA 107
7.3. Funciones de autoajuste para PIDs
Antes de tratar las distintas técnicas existentes para ajustar automáticamente PIDs
es importante hacer notar que los PIDs industriales (figura 7.1) no son exactamente
iguales a las formulaciones académicas que se enseñan en cursos básicos de control. Por
Figura 7.1: PID industrial moderno con función de autoajuste (ABB modelo ECA).
ejemplo, en lugar de considerarse la derivada del error se suele usar la derivada de la
salida y además a veces ni siquiera se emplea la derivada exacta de la salida, sino que se
usa una aproximación de la misma que reduce la ganancia en altas frecuencias, a fin de
minimizar los efectos del ruido. As´ı mismo a la hora de calcular la parte proporcional
de la acción de control no se suele usar el valor exacto de la referencia a seguir, sino
una fracción del mismo, a fin de evitar cambios bruscos en la salida del proceso. Otro
detalle muy importante es que se suele incorporar una función de anti-windup que,
básicamente, consiste en que cuando el actuador se satura (alcanza su l´ımite f´ısico de
operación), se deja de integrar el error. Con esto se consigue que, cuando empieza a
disminuir el error, el actuador deja de estar saturado, es decir que se consigue que el
descenso del error se manifieste en un decremento de la señal de actuación.
Sin entrar en demasiados detalles un PID más realista que la versión académica
vendr´ıa dado por la siguiente expresión:
u(t) = f(v(t))
donde u(t) es la señal de actuación que se aplica, f(·) es una posible (se suele dar casi
siempre) no-linealidad debida al actuador y
v(t) = P(t) + I(t) + D(t)

108 FUNCIONES DE AUTOAJUSTE PARA PIDS
donde P(t) es la acción proporcional que se calcula mediante
P(t) = Kc(βref(t) − y(t)) 0,7 ≤ β ≤ 1
I(t) es la acción integral que se calcula mediante
dI
dt
=
Kc
Ti
(ref(t) − y(t)) +
1
Tt
(u(t) − v(t))
En la expresión anterior el último término que se suma se usan para lograr el efecto
anti-windup de manera que la acción integral se mantenga acotada cuando el actuador
se sature. El parámetro Tt es una constante de tiempo para reinicializar la acción
integral cuando aparezca la saturación y suele ser una fracción del tiempo integral Ti.
Por otra parte la acción derivativa se calcula usando
Td
N
dD
dt
= −D − KcTd
dy
dt
donde el parámetro N es fijo y suele tomarse igual a 10.
En cuanto a las técnicas para sintonizar automáticamente PIDs, la gran mayor´ıa
están basadas en experimentos simples que el PID puede llevar a cabo por si solo. Estos
experimentos podrán ser en bucle abierto o cerrado, de ah´ı que luego distingamos dos
tipos de técnicas. Hay que mencionar que en los PID industriales el ajuste automático
viene realizado por el propio PID, o por un módulo separado que se coloca en lugar del
PID para realizar los experimentos, y que devuelve los valores de los parámetros del
PID. Este módulo deberá ser compatible con los distintos modelos de PID que se usen en
la planta, ya que para calcular los parámetros deben conocerse todas las peculiaridades
de los algoritmos usados por cada PID. Otros métodos más sofisticados son los que
se basan en técnicas de inteligencia artificial principalmente sistemas expertos. Estos
programas monitorizan en paralelo el funcionamiento de la planta y cuando se producen
cambios de referencia o perturbaciones importantes los aprovechan para analizar la
dinámica de la planta, estimándose valores para parámetros como ganancias, factores de
amortiguamiento, etc . . . Estos parámetros son los que luego se usarán para sintonizar
el PID. Esta técnica se utiliza por ejemplo en controladores de las marcas Foxboro o
Fenwal.
7.3.1. Técnicas de ajuste basadas en la respuesta transitoria
Estas son técnicas de ajuste en bucle abierto que se basan en aplicar un escalón en
la señal de entrada del lazo que se quiere sintonizar y ajustar un modelo simple del
tipo
G(s) =
k
1 + sT
e−sL
(7.1)

Conocidos los parámetros del modelo el PID se puede ajustar usando técnicas del
tipo Ziegler-Nichols de bucle abierto. Otros métodos están basados en medida de áreas
como la que se describe a continuación. Considérese la figura 7.2. El procedimiento
para calcular T y L comienza por el cálculo de A0. De ah´ı se determina
L + T =
A0
k
y de ah´ı se puede medir A1, la cual se usa para obtener T mediante
T =
eA1
k
donde e es la base de los logaritmos neperianos. Una vez que se conoce L + T y T se
puede obtener L y con eso ya están estimados todos los parámetros.
k
A0
A1
L+T
Figura 7.2: Determinación de T y L por áreas.
7.3.2. Métodos basados en las oscilaciones producidas al real-
imentar con un relé
Los métodos de ajuste basados en la respuesta transitoria son simples, pero muy
sensibles a las perturbaciones, ya que las pruebas se realizan en bucle abierto. Las
técnicas basadas en experimentos en bucle cerrado no tienen este problema. De estas
técnicas veremos la que está basada en las oscilaciones producidas al realimentar con
un relé. La estructura para realizar el ajuste es la que se muestra en la figura 7.3.
La idea clave es que la mayor´ıa de los procesos exhiben oscilaciones autosostenidas
(conocidas como ciclos l´ımite1
) cuando son realimentados con un relé en la cadena
1
El estudio de los ciclos l´ımite no pertenece a esta asignatura. Baste saber que son oscilaciones con
entrada nula o referencia constante que aparecen en ciertos sistemas y que pueden provocarse con la
estructura presentada aqu´ı.

110 LA TÉCNICA DE AJUSTE POR TABLA O GAIN SCHEDULING
PID
RELÉ
PROCESO
r u y+
-
Figura 7.3: Estructura usada en el método basado en oscilaciones de relé.
directa. Los parámetros del ciclo l´ımite contienen información suficiente para calcular
los parámetros de ajuste del PID.
El procedimiento consiste en desconectar el controlador a la hora de hacer el ajuste
y sustituirlo por el relé. En la salida comenzarán a aparecer oscilaciones que se em-
pezarán a repetir periódicamente cuando el ciclo l´ımite aparezca. Una vez que se han
determinado los parámetros del ciclo l´ımite se calculan los del PID y se vuelve a conec-
tar el controlador. El método más conocido para calcular los parámetros del PID es el
método de Ziegler-Nichols de bucle cerrado. Suponiendo una referencia nula, si el ciclo
l´ımite resultante tiene amplitud a y frecuencia ωu entonces los parámetros del método
de Ziegler-Nichols de bucle cerrado, es decir, la ganancia cr´ıtica Ku y el periodo cr´ıtico
Tu son iguales a
Ku =
4d
πa
Tu =
2π
ωu
donde d es la amplitud del relé.
7.4. La técnica de ajuste por tabla o gain schedul-
ing
Existen otros controladores que proporcionan una cierta capacidad de adaptación
pero que no encajan en el esquema t´ıpico discutido en el cap´ıtulo 5 ya que la adaptación
se realiza en bucle abierto. Este esquema, más limitado se ilustra en la figura 7.4. Puede
observarse que en este caso, el ajuste de los parámetros no se realiza en función del
comportamiento del sistema, sino que se utilizan los valores de una variable auxiliar
para decidir cuales son los mejores valores de los parámetros del regulador. De ah´ı que
se diga que la adaptación es en bucle abierto.
Un esquema de control t´ıpico que utiliza la estructura de la figura 7.4 es el popular
gain scheduling o ajuste por tabla. En este esquema, los parámetros del controlador que

ÔuÕuÖ{×UØyÕ…Ù‚ÚyÛÜÕuØ
Ú‘ÝAÞ{ße×UÚ‘àoÙ“á â Ù‚ÚyÖã×pÚ
ä áoÔoÚyÖãåæß ä ÕçÛèá
Ú‘Û‘Ú â ×UÚãÔfå’éfÖ
ä áYÛèå–Û‘ÚêÛ‘áëÙ“Ú
ì Ú‘ØuåˆÚ‘àfÙ‚á
Ú‘Þèí‘å–Ùaå–Ú‘ØMEDIO
AMBIENTE
u+
-
REFERENCIA
y
Figura 7.4: Configuración genérica de un controlador adaptativo con adaptación en bucle abierto.
se usan en cada instante vienen determinados por una tabla precalculada para varios
puntos de funcionamiento o valores de la variable auxiliar. Este tipo de control es muy
popular, por ejemplo, en sistemas de control de vuelo, en los que los parámetros del
controlador se seleccionan de un conjunto de parámetros precalculados en función de
la altura de vuelo. Por supuesto, este tipo de control funciona bien si entre la variable
auxiliar y la dinámica del sistema existe una fuerte relación, que permite determinar
el valor de los parámetros en función del valor observado de la variable auxiliar. Una
ventaja que tiene este esquema es que los parámetros del control se pueden cambiar
(adaptar) a la misma velocidad a la que cambia la dinámica del sistema pues estos
cambios se reflejan sobre la variable auxiliar a la vez que se producen. Esta rapidez en
el cambio de los parámetros puede ser, sin embargo, contraproducente. Por otra parte la
construcción de la tabla puede ser muy complicada. De hecho no existe una metodolog´ıa
universal, sino que para cada aplicación ha de verse como llevar a la práctica las ideas
del gain scheduling. Por último encontrar la variable auxiliar apropiada no siempre es
posible.
Estos controladores, sin embargo, se pueden encontrar en diversos sistemas t´ıpi-
cos de control, principalmente debido a su sencillez y efectividad cuando están bien
diseñados. Algunas de las aplicaciones t´ıpicas son:
Linealización de la caracter´ıstica de ciertos actuadores. Tal y como se vio en la
sección 5.2 la caracter´ıstica no lineal de un actuador se puede aproximar por un
modelo linealizado a trozos, de manera que en función del punto de operación del
actuador se escogerán unos valores u otros para el controlador.
Control de pH. En estos sistemas se presentan no linealidades originadas tanto
por los elementos de control (válvulas, bombas, sensores) como por las reacciones

112 LA TÉCNICA DE AJUSTE POR TABLA O GAIN SCHEDULING
qu´ımicas propias del proceso. La no linealidad principal proviene de la relación
entre las concentraciones de los reactivos y el pH de la solución resultante. Dicha
relación se representa en la llamada curva de pH2
. En dicha curva se representa
el pH en función de las diferencias en las concentraciones de los reactivos. En la
figura 7.5 se muestra dicha curva para una solución acuosa de ácido clorh´ıdrico
y sosa cáustica (es decir un par ácido-base). Puede observarse que en este caso
la no linealidad también se puede aproximar bien por un modelo linealizado a
tramos.
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
x 10
−3
2
3
4
5
6
7
8
9
10
11
12
Diferencia entre las concentraciones acido−base
pH
Figura 7.5: Curva de pH para una solución de HCl 0.001 M y NaOH 0.001 M.
Control de la mezcla aire combustible en un motor de combustión. En este caso se
utilizan como variables para decidir el ajuste del controlador (un PI usualmente)
la velocidad del motor y la cantidad de aire que entra. Usando dichas variables
se busca en una tabla (usualmente de 16x16 entradas) en la que se obtienen los
valores de los parámetros del controlador (si los valores de las variables no coin-
ciden con los de ninguna entrada se interpola con las más próximas). La variable
de control es el tiempo de apertura de la válvula de inyección de combustible.
En este caso se presenta otra no linealidad debida al sensor utilizado para medir
la proporción de aire y combustible. Este sensor denominado sonda lambda tiene
una caracter´ıstica que de manera aproximada viene representada por la figura
7.6. De hecho la señal de error que se env´ıa al PI se genera mediante la expresión
e =
1 si V 0,5
−1 si V ≤ 0,5
2
En realidad el nombre técnico es curva de titración, aunque tales detalles no son relevantes en
esta asignatura

0.5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Relación combustible − aire (λ)
Voltajedesalida(V)
Figura 7.6: Caracter´ıstica aproximada de una sonda lambda
Control de vuelo. Es el ejemplo clásico, en este caso, se puede encontrar una
relación entre los parámetros óptimos del controlador y la altura, la velocidad y
el número de Mach.
Control de la dirección de un barco. En este caso la dinámica considerada para
el control de la dirección depende de la velocidad del barco y de ciertas variables
relacionadas con el tiempo atmosférico, como la fuerza y dirección del viento (en
realidad dichas variables atmosféricas no afectan a la dinámica del barco en si,
sino a la de las perturbaciones que este sufre).
A modo de conclusión, podemos decir que la técnica de gain scheduling se puede
usar con éxito cuando las no linealidades que se pretendan compensar se conocen bien
a priori. Por otra parte como la adaptación es en bucle abierto, es necesario conocer
bien tanto la dinámica del proceso como la de las perturbaciones.
7.5. Controladores adaptativos industriales
Las técnicas de control adaptativo han llegado al mundo industrial en distintas
formas y capacidades, entre las cuales podemos distinguir las siguientes.
Herramientas para sintonizar controladores. Están basadas en experimentos como
los que se han descrito en la sección 7.3. A veces se encuentran como componentes

114 CONTROLADORES ADAPTATIVOS INDUSTRIALES
opcionales del controlador como en el caso de los sistemas Protonic (Hartman
Braun) o UDC 6000 (Honeywell). Estos combinan reglas emp´ıricas y técnicas
de colocación de polos usando experimentos en bucle abierto. Las estrategias de
oscilaciones mediante relé también son comunes como por ejemplo en el SattCon-
trol3
ECA40 y en el DPR900 (Fisher-Rosemount). Otra posibilidad es que estas
herramientas para sintonizar controladores sean módulos independientes, com-
patibles con determinadas familias de controladores. En este tipo encontramos
ejemplo como SIEPID (Siemens), Supertuner (Toyo), Protuner (Techmation) o
PIDWIZ (BST Control). Una tercera posibilidad es que estas herramientas for-
men parte de sistemas de control distribuido como en el caso de Looptune (Hon-
eywell) e Intelligent Tuner (Fisher-Rosemount).
Controladores adaptativos estandar. Estos controladores ajustan los parámetros
de manera más o menos continua. Los hay que están basados en la identificación
de un modelo mediante m´ınimos cuadrados recursivos como los CLC04 (Bailey
Controls) y SLPC-181/281 (Yokogawa) que además utilizan una estrategia de
control por colocación de polos. Algunos, como el SattControl ECA40, no identi-
fican un modelo paramétrico sino que usan reglas del tipo Ziegler-Nichols de bucle
cerrado, a partir de experimentos de realimentación con relé. Por otra parte exis-
ten otros más ambiciosos que están basados en sistemas expertos y en técnicas de
reconocimiento de patrones como EXACT (Foxboro), SLPC-171/271 (Yokogawa)
o UDC 6000 de Honeywell. Estos sistemas utilizan una base de reglas (100-200)
con las que se pretende reproducir el conocimiento de un experto (humano) en
sintonizar controladores. Finalmente, las capacidades de gain scheduling tam-
bién están presentes en ciertos controladores como el SattControl ECA 400 o el
DPR910 (Fisher-Rosemount).
Controladores adaptativos basados en autómatas programables. Los autómatas
programables ganan terreno d´ıa a d´ıa en cualquier aplicación industrial de control.
3M y General Electric tienen en su catálogo aplicaciones de control adaptativo
basados en sus autómatas.
Soluciones a medida. A veces en determinadas aplicaciones se encuentran contro-
ladores adaptativos a medida y que por tanto son exclusivos de cada sistema. Se
encuentran en barcos, aviones, automoción, y ciertas industrias.
A continuación se analizarán en mayor detalle algunos controladores especialmente
interesantes.
3
Mas tarde Alfa-Laval y actualmente ABB.

7.5.1. SattControl ECA40 y Fisher-Rosemount DPR900
Estos controladores están basados en oscilaciones inducidas mediante realimentación
con un relé. Incluyen una función de ”sinton´ıa pulsando un botón”. Además tiene ca-
pacidades limitadas de gain scheduling con una tabla de tres entradas. Previamente
al ajuste el proceso se deja evolucionar con una entrada constante. El procedimiento
de ajuste comienza con la detección del ciclo l´ımite. En cuanto se observa que las os-
cilaciones comienzan a repetirse, se calcula la amplitud y periodo de las mismas y a
partir de ah´ı se calculan los parámetros. Para ello se utilizan una versión modificada del
método de Ziegler-Nichols. Una vez se calculan los parámetros el controlador conmuta
a modo automático. El ajuste ofrece tres perfiles diferentes: control normal, lento o
rápido. La reacción de la comunidad industrial a estos productos ha sido muy buena,
encontrándose particularmente útil en industrias que no tienen personal especializado
en todos los turnos.
7.5.2. Foxboro EXACT
Este sistema está basado en la respuesta transitoria de bucle cerrado, es decir es
de bucle cerrado pero no usa las oscilaciones inducidas por un relé. Lo que se emplea
es un escalón o perturbación aplicada al sistema y de la evolución de la salida a par-
tir de ese instante se obtiene información que permite ajustar el controlador usando
Ziegler-Nichols. Este controlador requiere información previa para poder sintonizar au-
tomáticamente, concretamente una estimación previa de Kc, Ti y Td, as´ı como de la
escala de tiempos del proceso. Si esta información se desconoce se puede usar el modo
de pre-tune incorporado que la obtiene mediante la aplicación de un escalón. Es nece-
sario sin embargo que el proceso esté en regimen permanente. La aceptación comercial
de este producto ha sido excelente y se han vendido miles de unidades. A modo de
anécdota la planta de Atlantic Copper en Huelva utiliza este controlador en algunos
de sus procesos. El controlador adaptativo multivariable EXACT MV se distribuye ac-
tualmente en forma de software de control avanzado como parte del sistema I/A Series
de Foxboro.
7.5.3. ABB Novatune
Esta herramienta de control STR (figura 7.7) está basada entre otras cosas en el
control de m´ınima varianza y ofrece la capacidad de especificar la posición de 1 de los

116 CONTROLADORES ADAPTATIVOS INDUSTRIALES
polos de bucle cerrado. Utiliza m´ınimos cuadrados recursivos con factor de olvido para
Figura 7.7: La herramienta Novatune se comercializa actualmente con el sistema Advant 410 de ABB.
identificar un modelo que tiene la estructura
(1 − Plz−1
)y(t + kd) − (1 − Pl)y(t) = A(z−1
)∆y(t) + B(z−1
)∆u(t) + C(z−1
)∆v(t)
donde Pl es el polo que se puede especificar y kd es el horizonte de predicción. Por otra
parte la ley de control tiene la forma
(σ + B∗
(z−1
))∆u(t) = (1 − Pl)(ref(t) − y(t)) − A(z−1
)∆y(t) − C(z−1
)∆v(t)
donde σ es un factor de ponderación. La experiencia en el uso de esta herramienta
demuestra que da mejores resultados que el control PID convencional.

Cap´ıtulo 8
Control Predictivo Basado en
Modelo (MPC)
8.1. Perspectiva histórica
El Control Predictivo se desarrolló en base a dos l´ıneas básicas. Por un lado, a finales
de los años setenta surgieron diversos algoritmos que usaban expl´ıcitamente un modelo
dinámico del proceso para predecir el efecto de las acciones de control futuras en la
salida, las cuales eran determinadas minimizando el error predicho sujeto a restricciones
de operación. La optimización se repet´ıa en cada instante de muestreo con información
actualizada del proceso. Estas formulaciones eran de naturaleza heur´ıstica y algor´ıtmica
e intentaban aprovechar el creciente potencial de los computadores digitales por aquélla
época.
Rápidamente el mpc adquirió gran popularidad en las industrias de procesos qu´ımi-
cos principalmente debido a la simplicidad del algoritmo y al uso del modelo de re-
spuesta impulsional o en escalón, que aunque posea muchos más parámetros que las
formulaciones en el espacio de estados o función de transferencia suele ser preferido
por ser intuitivo y necesitar menos información a priori para identificar. La mayor´ıa
de las aplicaciones fueron llevadas a cabo sobre sistemas multivariables incluyendo
restricciones. Los algoritmos utilizados fueron principalmente el idcom (Identification-
Command) y el dmc (Control con Matriz Dinámica, Dynamic Matrix Control).
Independientemente fue surgiendo otra l´ınea de trabajo en torno a las ideas del con-
trol adaptativo, desarrollando estrategias esencialmente para procesos monovariables
117

118 CONCEPTOS B ÁSICOS DE CONTROL PREDICTIVO
formuladas con modelos entrada/salida. En este contexto se extendieron las ideas del
Controlador de M´ınima Varianza y se desarrolló el Control Predictivo Generalizado
(Generalized Predictive Control gpc) que es uno de los métodos más populares en la
actualidad.
8.2. Conceptos básicos de control predictivo
El Control Predictivo Basado en Modelo, Model (Based) Predictive Control (mbpc
ó mpc) constituye un campo muy amplio de métodos de control desarrollados en torno
a ciertas ideas comunes e integra diversas disciplinas como control óptimo, control
estocástico, control de procesos con tiempos muertos, control multivariable o control
con restricciones.
El Control Predictivo no es una estrategia de control espec´ıfica, sino que se trata
más bien de un campo muy amplio de métodos de control desarrollados en torno a
ciertas ideas comunes. Estos métodos de diseño conducen a controladores lineales que
poseen prácticamente la misma estructura y presentan suficientes grados de libertad.
Las ideas que aparecen en mayor o menor medida en toda la familia de controladores
predictivos son básicamente:
Uso expl´ıcito de un modelo para predecir la salida del proceso en futuros instantes
de tiempo (horizonte).
Cálculo de las señales de control minimizando una cierta función objetivo.
Estrategia deslizante, de forma que en cada instante el horizonte se va desplazan-
do hacia el futuro, lo que implica aplicar la primera señal de control en cada
instante y desechar el resto, repitiendo el cálculo en cada instante de muestreo.
Los distintos algoritmos de mpc difieren entre s´ı casi exclusivamente en el modelo
usado para representar el proceso y los ruidos y en la función de coste a minimizar.
Aunque las diferencias puedan parecer pequeñas a priori, pueden provocar distintos
comportamientos en bucle cerrado, siendo cr´ıticas para el éxito de un determinado
algoritmo en una determinada aplicación.
El Control Predictivo es un tipo de control de naturaleza abierta dentro del cual se
han desarrollado muchas realizaciones, encontrando gran aceptación tanto en aplica-
ciones industriales como en el mundo académico. En la actualidad existen numerosas

CAPÍTULO 8. CONTROL PREDICTIVO BASADO EN MODELO (MPC) 119
aplicaciones de controladores predictivos funcionando con éxito, tanto en la industria
de procesos como en control de motores o Robótica. El buen funcionamiento de estas
aplicaciones muestra la capacidad del mpc para conseguir sistemas de control de ele-
vadas prestaciones capaces de operar sin apenas intervención durante largos per´ıodos
de tiempo.
El mpc presenta una serie de ventajas sobre otros métodos, entre las que destacan:
Resulta particularmente atractivo para personal sin un conocimiento profundo
de control, puesto que los conceptos resultan muy intuitivos, a la vez que la
sintonización es relativamente fácil.
Puede ser usado para controlar una gran variedad de procesos, desde aquéllos con
dinámica relativamente simple hasta otros más complejos incluyendo sistemas con
grandes retardos, de fase no m´ınima o inestables.
Permite tratar con facilidad el caso multivariable.
Posee intr´ınsecamente compensación del retardo.
Resulta conceptualmente simple la extensión al tratamiento de restricciones, que
pueden ser incluidas de forma sistemática durante el proceso de diseño.
Es muy útil cuando se conocen las futuras referencias (robótica o procesos en
batch).
Es una metodolog´ıa completamente abierta basada en algunos principios básicos
que permite futuras extensiones.
Pero, lógicamente, también presenta inconvenientes. Unos de ellos es la carga de
cálculo necesaria para la resolución de algunos algoritmos. Pero quizás el mayor in-
conveniente venga marcado por la necesidad de disponer de un modelo apropiado del
proceso. El algoritmo de diseño está basado en el conocimiento previo del modelo y es
independiente de éste, pero resulta evidente que las prestaciones obtenidas dependerán
de las discrepancias existentes entre el proceso real y el modelo usado.
8.3. Estrategia de los controladores predictivos
La metodolog´ıa de todos los controladores pertenecientes a la familia del mpc se
caracteriza por la estrategia siguiente, representada en la figura 8.1:

120 ESTRATEGIA DE LOS CONTROLADORES PREDICTIVOS
N
y(t+k|t)^
u(t+k|t)
t t+1t-1 . . . t+N. . .t+k
y(t)
u(t)
Figura 8.1: Estrategia del Control Predictivo
1. En cada instante t y haciendo uso del modelo del proceso se predicen las futuras
salidas para un determinado horizonte N, llamado horizonte de predicción. Estas
salidas predichas, ˆy(t+k | t)1
para k = 1 . . . N dependen de los valores conocidos
hasta el instante t (entradas y salidas pasadas) y de las señales de control futuras
u(t + k | t), k = 0 . . . N − 1 que se pretenden mandar al sistema y que son las
que se quieren calcular.
2. El conjunto de señales de control futuras se calcula optimizando un determinado
criterio en el que se pretende mantener el proceso lo más próximo posible a la
trayectoria de referencia w(t + k) (que puede ser directamente el setpoint o una
suave aproximación a éste). Este criterio suele tomar la forma de una función
cuadrática de los errores entre la salida predicha y la trayectoria de referencia
también predicha, incluyendo en muchos casos el esfuerzo de control. Si el criterio
es cuadrático, el modelo lineal y no existen restricciones se puede obtener una
solución expl´ıcita, en otro caso se debe usar un método iterativo de optimización.
Adicionalmente se hace alguna suposición sobre la estructura de la ley de control
futura, como por ejemplo que va a ser constante a partir de cierto instante.
3. La señal de control u(t | t) es enviada al proceso mientras que las siguientes
señales de control calculadas son desechadas, puesto que en el siguiente instante
de muestreo ya se conoce y(t + 1) y se repite el paso 1 con este nuevo valor y
todas las secuencias son actualizadas. Se calcula por tanto u(t+1 | t+1) (que en
1
la notación indica el valor de la variable en el instante t + k calculado en el instante t.

+
-
futuros
Entradas y salidas
Funcion de coste Restricciones
Errores futuros
pasadas
Controles
de referencia
Trayectoria
predichas
Salidas
Optimizador
Modelo
Figura 8.2: Estructura básica del MPC
principio será diferente al u(t+1 | t) al disponer de nueva información), haciendo
uso del concepto de horizonte deslizante.
Para llevar a cabo esta estrategia, se usa una estructura como la mostrada en la
figura 8.2. Se hace uso de un modelo para predecir las salidas futuras del proceso,
basándose en las futuras señales de control propuestas. Estas señales son calculadas
por el optimizador teniendo en cuenta la función de coste (donde aparece el futuro
error de seguimiento) as´ı como las restricciones. Por tanto el modelo juega un papel
decisivo en el controlador. El modelo elegido debe ser capaz de capturar la dinámica del
proceso para poder predecir las salidas futuras al mismo tiempo que debe ser sencillo
de usar y de comprender.
El optimizador es otra parte fundamental de la estrategia pues proporciona las
acciones de control. Si la función de coste es cuadrática, el m´ınimo se puede obtener
como una función expl´ıcita de las entradas y salidas pasadas y de la trayectoria de
referencia. Sin embargo, cuando existen restricciones de desigualdad la solución debe
ser calculada por métodos numéricos con más carga de cálculo.
8.4. Elementos básicos
Todos los controladores predictivos poseen elementos comunes y para cada uno de
estos elementos se pueden elegir diversas opciones, dando lugar a distintos algoritmos.

122 ELEMENTOS B ÁSICOS
Estos elementos son:
Modelo de predicción
Función objetivo
Obtención de la ley de control
8.4.1. Modelo de predicción
La piedra angular del mpc es el modelo; un diseño completo debe incluir los mecan-
ismos necesarios para la obtención del mejor modelo posible, el cual debe ser lo sufi-
cientemente rico para capturar al maximo la dinámica del proceso y debe ser capaz de
permitir el cálculo de las predicciones a la vez que sea intuitivo y permita un análisis
teórico. El uso del modelo del proceso viene determinado por la necesidad del cálcu-
lo de la salida predicha en instantes futuros ˆy(t + k | t). Las diferentes estrategias
de mpc pueden usar distintos modelos para representar la relación de las salidas con
las entradas medibles, algunas de las cuales serán variables manipuladas y otras se
pueden considerar como perturbaciones medibles, que pueden ser compensadas por ac-
ción feedforward. Además se tendrá en cuenta un modelo de las perturbaciones, para
intentar describir el comportamiento que no aparece reflejado en el modelo del proce-
so, englobándose aqu´ı el efecto de las entradas no medibles, el ruido y los errores de
modelado.
Para el estudio se puede separar el modelo en dos partes: el modelo del proceso
propiamente dicho y el modelo de las perturbaciones. Cualquier método usará ambas
partes para la predicción.
Modelo del Proceso
Casi todas las formas posibles de modelar un proceso aparecen en alguna formu-
lación de mpc siendo las más usadas las siguientes:
Respuesta impulsional. También conocida por secuencia de ponderación o modelo
de convolución. La salida viene relacionada con la entrada por la ecuación
y(t) =
∞
i=1
hiu(t − i)

t t+1 t+2 . . . t+N t t+1 t+2 . . . t+N
y(t) y(t)
h
h
h
h
g
g
g
1
i
i
N
2
N
g1
2
a) b)
Figura 8.3: Respuesta impulsional y ante escalón
donde hi son los valores muestreados obtenidos al someter al proceso a un impulso
unitario de amplitud igual al per´ıodo de muestreo (ver figura 8.3a). Esta suma
es truncada y sólo se consideran N valores (por tanto sólo permite representar
procesos estables y sin integradores), teniendo
y(t) =
N
i=1
hiu(t − i) = H(z−1
)u(t) (8.1)
donde H(z−1
) = h1z−1
+ h2z−2
+ · · · + hN z−N
. Un inconveniente de este método
es el gran número de parámetros que necesita, ya que N suele ser un valor elevado
(del orden de 40-50). La predicción vendrá dada por:
ˆy(t + k | t) =
N
i=1
hiu(t + k − i | t) = H(z−1
)u(t + k | t)
Este método es ampliamente aceptado en la práctica industrial debido a que
es muy intuitivo y no requiere información previa sobre el proceso, con lo que
el procedimiento de identificación se simplifica, a la vez que permite describir
fácilmente dinámicas complejas como fase no m´ınima o retardos.
Respuesta ante escalón. Es muy similar al anterior sólo que ahora la señal de
entrada es un escalón. Para sistemas estables se tiene la respuesta truncada que
será
y(t) = y0 +
N
i=1
gi u(t − i) = y0 + G(z−1
)(1 − z−1
)u(t) (8.2)

donde las gi son los valores muestreados ante la entrada en escalón y u(t) =
u(t) − u(t − 1), según se muestra en la figura 8.3b. El valor de y0 puede tomarse
0 sin pérdida de generalidad, con lo cual el predictor será:
ˆy(t + k | t) =
N
i=1
gi u(t + k − i | t)
Este método presenta las mismas ventajas e inconvenientes que el anterior.
Función de transferencia. Se utiliza el concepto de función de transferencia G =
B/A con lo que la salida viene dada por:
A(z−1
)y(t) = B(z−1
)u(t)
A(z−1
) = 1 + a1z−1
+ a2z−2
+ · · · + anaz−na
B(z−1
) = b1z−1
+ b2z−2
+ · · · + bnbz−nb
Por tanto la predicción vendrá dada por
ˆy(t + k | t) =
B(z−1
)
A(z−1)
u(t + k | k)
Esta representación es válida también para procesos inestables y posee la ventaja
de necesitar pocos parámetros, aunque es fundamental un conocimiento a priori
del proceso sobre todo en cuanto al orden de los polinomios A y B.
Espacio de estados. Tiene la siguiente representación:
x(t) = Ax(t − 1) + Bu(t − 1)
y(t) = Cx(t)
siendo x el estado y A, B y C las matrices del sistema, de entrada y de salida
respectivamente. Para este modelo la predicción viene dada por
ˆy(t + k | t) = Cˆx(t + k | t) = C[Ak
x(t) +
k
i=1
Ai−1
Bu(t + k − i | t)]
Posee la ventaja de que sirve también para sistemas multivariables a la vez que
permite analizar la estructura interna del proceso (aunque a veces los estados
obtenidos al discretizar no tienen ningún significado f´ısico). Los cálculos pueden
ser complicados, con la necesidad adicional de incluir un observador si los estados
no son accesibles.

Modelo de las perturbaciones
De tanta importancia como la elección de un determinado modelo del proceso es la
elección del modelo utilizado para representar la perturbaciones. Un modelo bastante
extendido es el Autorregresivo Integrado de Media Móvil (Auto-Regressive and Inte-
grated Moving Average, arima), en el que las perturbaciones, es decir, las diferencias
entre la salida medida y la calculada por el modelo vienen dadas por
n(t) =
C(z−1
)e(t)
D(z−1)
donde el polinomio D(z−1
) incluye expl´ıcitamente el integrador = 1−z−1
, e(t) es un
ruido de media cero y normalmente el polinomio C se considera igual a uno. Este modelo
se considera apropiado para dos tipos de perturbaciones: cambios aleatorios ocurridos
en instantes aleatorios (por ejemplo cambio en la calidad del material) y movimiento
browniano (en procesos con balance de energ´ıa) y es usado en varios métodos. Nótese
que al incluir un integrador se consigue un control con error nulo en régimen permanente
(offset-free).
Como caso particular del arima se puede incluir la perturbación constante
n(t) =
e(t)
1 − z−1
cuya mejor predicción será ˆn(t + k | t) = n(t).
8.4.1.1. Respuestas libre y forzada
Una caracter´ıstica t´ıpica de la mayor´ıa de los controladores mpc es el empleo de los
conceptos de repuesta libre y forzada. La idea es expresar la secuencia de acciones de
control como la suma de dos señales:
u(t) = uf (t) + uc(t)
La señal uf (t) corresponde a las entradas pasadas (anteriores al instante t) y en el
futuro se mantiene constante e igual al último valor de la variable manipulada. Es
decir,
uf (t − j) = u(t − j) para j = 1, 2, · · ·
uf (t + j) = u(t − 1) para j = 0, 1, 2, · · ·

La señal uc(t) vale cero en el pasado y corresponde a las señales de control en los
instantes futuros:
uc(t − j) = 0 para j = 1, 2, · · ·
uc(t + j) = u(t + j) − u(t − 1) para j = 0, 1, 2, · · ·
La predicción de la secuencia se salida se separa en dos partes, como se ve en
la figura 8.4. Una de ellas (yf (t)), la respuesta libre, corresponde a la predicción de
la salida cuando la variable manipulada se hace igual a uf (t), y la otra, la repuesta
forzada (yc(t)), corresponde a la predicción de la salida cuando la señal de control es
uc(t). La respuesta libre corresponde a la evolución del proceso debido a su estado
actual (incluido por tanto el efecto de acciones pasadas) mientras que la respuesta
forzada es la debida a las acciones de control futuras.
t
uc
t
u
f
u
t
t
y
f
t
y
t
yc
Process
Figura 8.4: Respuestas libre y forzada
8.4.2. Función objetivo
Los diversos algoritmos de mpc proponen distintas funciones de coste para la ob-
tención de la ley de control. En general se persigue que la salida futura en el horizonte
considerado siga a una determinada señal de referencia al mismo tiempo que se puede
penalizar el esfuerzo de control requerido para hacerlo. La expresión general de tal
función objetivo será:
J(N1, N2, Nu) =
N2
j=N1
δ(j)[ˆy(t + j | t) − w(t + j)]2
+
Nu
j=1
λ(j)[ u(t + j − 1)]2
(8.3)
En algunos métodos el segundo sumando, que considera el esfuerzo de control, no

se tiene en cuenta, mientras que en otros también aparecen directamente los valores de
la señal de control (no sus incrementos). En la función de coste se pueden considerar:
Parámetros: N1 y N2 son los horizontes m´ınimo y máximo de coste (o de predic-
ción) y Nu es el horizonte de control, que no tiene por qué coincidir con el
horizonte máximo, como se verá posteriormente. El significado de N1 y N2 re-
sulta bastante intuitivo: marcan los l´ımites de los instantes en que se desea que
la salida siga a la referencia. As´ı, si se toma un valor grande de N1 es porque
no importa que haya errores en los primeros instantes, lo cual provocará una re-
spuesta suave del proceso. Nótese que para procesos con tiempo muerto d no tiene
sentido que N1 sea menor que dicho valor puesto que la salida no empezará a
evolucionar hasta el instante t + d. Además, si el proceso es de fase no m´ınima,
este parámetro permite eliminar de la función objetivo los primeros instantes de
respuesta inversa.
Los coeficientes δ(j) y λ(j) son secuencias que ponderan el comportamiento fu-
turo. Usualmente se consideran valores constantes o secuencias exponenciales. Por
ejemplo se puede conseguir un peso exponencial de δ(j) a lo largo del horizonte
usando:
δ(j) = αN2−j
Si α está comprendido entre 0 y 1 indica que se penaliza más a los errores más
alejados del instante t que a los más próximos, dando lugar a un control más
suave y con menor esfuerzo. Si, por el contrario, α 1 es que se penalizan más
los primeros errores, provocando un control más brusco.
Todos estos valores pueden ser usados como parámetros de sintonización, obte-
niendo un abanico muy amplio de posibilidades con las que se puede cubrir una ex-
tensa gama de opciones, desde un control estándar hasta una estrategia diseñada
a medida para un proceso en particular.
Trayectoria de referencia: Una de las ventajas del control predictivo es que si se
conoce a priori la evolución futura de la referencia, el sistema puede empezar
a reaccionar antes de que el cambio se haya efectivamente realizado, evitando
los efectos del retardo en la respuesta del proceso. En muchas aplicaciones la
evolución futura de la referencia r(t + k) es conocida de antemano, como en
Robótica, servos o procesos en batch; en otras aplicaciones aunque la referencia sea
constante, se puede conseguir una sensible mejora de prestaciones simplemente
conociendo el instante de cambio de valor y adelantándose a esa circunstancia.
En el criterio de minimización (8.3), la mayor´ıa de los métodos suelen usar una
trayectoria de referencia w(t + k) que no tiene por qué coincidir con la referencia
real. Normalmente será una suave aproximación desde el valor actual de la salida

y(t) a la referencia conocida mediante un sistema de primer orden:
w(t) = y(t) w(t + k) = αw(t + k − 1) + (1 − α)r(t + k) k = 1 . . . N (8.4)
α es un parámetro comprendido entre 0 y 1 (mientras más próximo a 1 más
suave será la aproximación) que constituye un valor ajustable que influirá en
la respuesta dinámica del sistema. En la figura 8.5 se muestra la forma de la
trayectoria cuando la referencia r(t + k) es constante y para dos valores distintos
de α; para valores pequeños de este parámetro se tiene un seguimiento rápido
(w1) mientras que si aumenta, la trayectoria de referencia será w2 dando lugar a
una respuesta más suave.
y(t)
r(t+k)
w (t+k)
w (t+k)
t
1
2
Figura 8.5: Trayectoria de referencia
Restricciones: En la práctica, todos los procesos están sujetos a restricciones. Los
actuadores tienen un campo limitado de acción as´ı como una determinada veloci-
dad de cambio (slew rate), como es el caso de las válvulas, limitadas por las posi-
ciones de totalmente abierta o cerrada y por la velocidad de respuesta. Razones
constructivas, de seguridad o medioambientales o bien los propios alcances de los
sensores pueden causar l´ımites en las variables de proceso, tales como niveles en
depósitos, caudales en tuber´ıas o temperaturas y presiones máximas. Además,
normalmente las condiciones de operación vienen definidas por la intersección
de ciertas restricciones por motivos fundamentalmente económicos, con lo que el
sistema de control operará cerca de los l´ımites. Todo lo expuesto anteriormente
hace necesaria la introducción de restricciones en la función a minimizar.
Muchos algoritmos predictivos tienen en cuenta el tema de las restricciones por lo
cual han tenido gran éxito en la industria. Normalmente se considerarán l´ımites
en la amplitud y el slew rate de la señal de control y l´ımites en las salidas:
umin ≤ u(t) ≤ umax ∀t

dumin ≤ u(t) − u(t − 1) ≤ dumax ∀t
ymin ≤ y(t) ≤ ymax ∀t
con la adición de estas restricciones a la función objetivo, la minimización resulta
más compleja, no pudiendo obtenerse la solución anal´ıticamente como en el caso
sin restringir.
8.4.3. Obtención de la ley de control
Para obtener los valores u(t + k | t) será necesario minimizar la funcional J de la
ecuación (8.3). Para ello se calculan los valores de las salidas predichas ˆy(t + k | t)
en función de valores pasados de entradas y salidas y de señales de control futuras,
haciendo uso del modelo que se haya elegido y se sustituyen en la función de coste,
obteniendo una expresión cuya minimización conduce a los valores buscados. Para el
criterio cuadrático si el modelo es lineal y no existen restricciones se puede obtener una
solución anal´ıtica, en otro caso se debe usar un método iterativo de optimización.
De cualquiera de las maneras la obtención de la solución no resulta trivial pues
existirán N2 − N1 + 1 variables independientes, valor que puede ser elevado (del orden
de 10 a 30). Con la idea de reducir estos grados de libertad se puede proponer cierta
estructura a la ley de control. Además se ha encontrado que esta estructuración de
la ley de control produce una mejora en la robustez y en el comportamiento general
del sistema, debido fundamentalmente a que el hecho de permitir la libre evolución de
las variables manipuladas (sin estructurar) puede conducir a señales de control de alta
frecuencia no deseables y que en el peor de los casos podr´ıan conducir a la inestabilidad.
Esta estructura de la ley de control se plasma en el uso del concepto de horizonte
de control (Nu), que consiste en considerar que tras un cierto intervalo Nu N2 no
hay variación en las señales de control propuestas, es decir:
u(t + j − 1) = 0 j Nu
lo cual es equivalente a dar pesos infinitos a las cambios en el control a partir de cierto
instante. El caso l´ımite ser´ıa considerar Nu igual a 1 con lo que todas las acciones
futuras ser´ıan iguales a u(t)2
.
2
Recuérdese que debido al horizonte deslizante, la señal de control se recalcula en el siguiente
muestreo.

130 REVISI ÓN DE LOS PRINCIPALES ALGORITMOS
8.5. Revisión de los principales algoritmos
Se presentan a continuación los principales algoritmos de control predictivo, mostran-
do sus principales caracter´ısticas pero sin entrar en detalles. En el tema siguiente se
estudiarán en detalle los dos métodos considerados más representativos: dmc y gpc.
8.5.0.1. Dynamic Matrix Control
Este método usa la respuesta ante escalón (8.2) para modelar el proceso, consideran-
do sólo los N primeros términos, asumiendo por tanto que el proceso es estable. En
cuanto a las perturbaciones, se considera que su valor permanence constante e igual al
existente en el instante actual durante todo el horizonte, es decir, igual al valor medido
de la salida (ym) menos el estimado por el modelo ˆy(t | t)).
ˆn(t + k | t) = ˆn(t | t) = ym(t) − ˆy(t | t)
y por tanto el valor predicho de la salida será:
ˆy(t + k | t) =
k
i=1
gi u(t + k − i) +
N
i=k+1
gi u(t + k − i) + ˆn(t + k | t)
donde el primer término contiene las acciones de control futuras (que serán calculadas),
el segundo los valores pasados de las acciones de control (conocidas) y el último rep-
resenta las perturbaciones. La función de coste puede considerar sólo errores futuros o
incluir también el esfuerzo de control, en cuyo caso toma la forma genérica (8.3).
Una de las caracter´ısticas de este método que lo ha hecho muy popular en la in-
dustria es la inclusión de restricciones, que se traduce en inecuaciones de la forma
genérica:
N
i=1
Cj
yi ˆy(t + k | t) + Cj
uiu(t + k − i) + cj
≤ 0 j = 1 . . . Nc
En este caso la optimización debe ser numérica y se lleva a cabo en cada periodo de
muestreo, enviándose la señal u(t) y recalculando todo en el nuevo periodo de muestreo,
como en todos los métodos mpc. Los principales inconvenientes de este método son el
tamaño del modelo empleado y la imposibilidad de tratar procesos inestables.

8.5.0.2. Model Algorithmic Control
Este método se conoce también como Model Predictive Heuristic Control y el pro-
ducto comercial se llama idcom (Identification-Command). Es muy similar al dmc con
la diferencia principal de usar un modelo de respuesta impulsional (8.1). Introduce el
concepto de trayectoria de referencia como un sistema de primer orden que evoluciona
desde la salida actual al setpoint según una determinada constante de tiempo. La var-
ianza del error entre esta trayectoria y la salida es lo que marca la minimización de la
función objetivo. Las perturbaciones se pueden tratar como en el método anterior o se
pueden estimar según la siguiente expresión:
ˆn(t + k | t) = αˆn(t + k − 1 | t) + (1 − α)(ym(t) − ˆy(t | t))
con ˆn(t | t) = 0. α es un parámetro ajustable (0 ≤ α 1) relacionado con el tiempo
de respuesta, el ancho de banda y la robustez del bucle cerrado. El método también
considera restricciones en los actuadores, en las variables internas o en salidas secun-
darias.
8.5.0.3. Predictive Functional Control
Este controlador fue desarrollado por Richalet para procesos rápidos. Emplea un
modelo en el espacio de estados, por lo que permite el manejo de procesos inestables,
y también la extensión al caso no lineal. Este esquema de control tiene dos carac-
ter´ısticas que lo distinguen del resto de controladores de la familia: el uso de puntos de
coincidencia y de funciones base.
El concepto de puntos de coincidencia (ver figura 8.6) se emplea para simplificar los
cálculos considerando sólo un subconjunto de puntos en el horizonte de predicción hj,
j = 1, . . . , nH. La salida deseada y la predicha deben coincidir en dichos puntos, no en
todo el horizonte de predicción.
La otra idea innovadora de este método es la parametrización de la señal de con-
trol como una combinación lineal de ciertas funciones base, que son elegidas según la
naturaleza del proceso y la referencia:
u(t + k) =
nB
i=1
µi(t)Bi(k)
Normalmente estas funciones son de tipo polinómico: escalones (B1(k) = 1), rampas
(B2(k) = k) o parábolas (B3(k) = k2
), ya que la mayor´ıa de referencias se pueden es-
pecificar como combinación de estas funciones. Con esta estrategia, un perfil de entrada

Puntos de coincidencia
Figura 8.6: Puntos de coincidencia
complejo se puede especificar usando un pequeño número de parámetros desconocidos
µi que son las incógnitas del problema de minimización.
La función a minimizar es:
J =
nH
j=1
[ˆy(t + hj) − w(t + hj)]2
El algoritmo pfc también puede manejar restricciones de máximo y m´ınimo en la
aceleración, que son prácticas en aplicaciones de servocontrol.
8.5.0.4. Extended Prediction Self Adaptive Control
El algoritmo epsac usa un modelo de función de transferencia
A(z−1
)y(t) = B(z−1
)u(t − d) + v(t)
donde d es el retardo y v(t) la perturbación. Este modelo puede ampliarse para tratar
perturbaciones medibles añadiendo un término D(z−1
)d(t) para incluir efecto feedfor-
ward. La estructura de la ley de control es muy simple, ya que se considera que la señal
de control permanecerá constante a partir del instante t (es decir, horizonte de control
igual a 1): u(t+k) = 0 para k 0. Para obtener la señal de control de minimiza una
función de coste de la forma:
N
k=d
γ(k)[w(t + k) − P(z−1
)ˆy(t + k | t)]2

donde P(z−1
) es un polinomio de diseño con ganancia unitaria y γ(k) es una secuencia
de ponderación. La señal de control se puede calcular anal´ıticamente de la forma:
u(t) =
N
k=d
hkγ(k)[w(t + k) − P(z−1
)ˆy(t + k | t)]
N
k=d
γ(k)h2
k
siendo hk los coeficientes de la respuesta impulsional del sistema.
8.5.0.5. Extended Horizon Adaptive Control
Esta formulación también emplea un modelo de función de transferencia y pretende
minimizar la discrepancia entre la salida calculada y la referencia en el instante t + N:
ˆy(t + N | t) − w(t + N), con N ≥ d. La solución a este problema no es única (a menos
que N = d); una posible estrategia es considerar horizonte de control igual a 1:
u(t + k − 1) = 0 1 k ≤ N − d
o minimizar el esfuerzo de control
J =
N−d
k=0
u2
(t + k)
Este método utiliza un predictor de N pasos de la forma
ˆy(t + N | t) = y(t) + F(z−1
) y(t) + E(z−1
)B(z−1
) u(t + N − d)
donde E(z−1
) y F(z−1
) son polinomios que satisfacen la relación
(1 − z−1
) = A(z−1
)E(z−1
)(1 − z−1
) + z−N
F(z−1
)(1 − z−1
)
con el grado de E igual a N −1. Una ventaja de este método es que se puede encontrar
fácilmente una solución expl´ıcita, dada por
u(t) = u(t − 1) +
α0(w(t + N) − ˆy(t + N | t))
N−d
k=0
α2
i
siendo αk el coeficiente correspondiente a u(t + k) en la ecuación de predicción. Por
tanto la ley de control depende sólo de los parámetros del proceso y puede hacerse
fácilmente adaptativa si se emplea un identificador en l´ınea. El único coeficiente de
ajuste es el horizonte de predicción N, lo cual simplifica el uso pero proporciona poca
libertad para el diseño. Obsérvese que no puede usarse trayectoria de referencia porque
el error se considera sólo en un instante (t+N), ni tampoco la ponderación del esfuerzo
de control.

8.5.0.6. Generalized Predictive Control
Este método propuesto por Clarke et al. emplea un modelo carima (Controlled
Auto-Regressive Integrated Moving Average) para la predicción de la salida:
A(z−1
)y(t) = B(z−1
)z−d
u(t − 1) + C(z−1
)
e(t)
donde la perturbación viene dada por un ruido blanco coloreado por el polinomio
C(z−1
). Como en la práctica es dif´ıcil encontrar el verdadero valor de este polinomio,
se puede emplear como parámetro de diseño para rechazo de perturbaciones o mejora de
la robustez. La predicción óptima se lleva a cabo resolviendo una ecuación diofántica,
lo cual puede hacerse eficazmente de forma recursiva.
Este algoritmo, al igual que otros que usan el modelo de función de transferencia,
se puede implementar fácilmente en forma adaptativa usando un algoritmo de identi-
ficación en l´ınea como los m´ınimos cuadrados recursivos.
gpc usa una función de coste cuadrática de la forma
J(N1, N2, Nu) =
N2
j=N1
δ(j)[ˆy(t + j | t) − w(t + j)]2
+
Nu
j=1
λ(j)[ u(t + j − 1)]2
donde las secuencia de ponderación δ(j) y λ(j) se eligen normalmente constantes o
exponenciales y la trayectoria de referencia w(t+j) se puede generar como una secuencia
que empieza en el valor actual de la salida y tiende exponencialmente al setpoint.
Las bases teóricas del algoritmo gpc has sido ampliamente estudiadas y se puede
demostrar que, para distintos conjuntos de parámetros, el algoritmo es estable y que
otros controladores como por ejemplo el dead beat son casos incluidos en éste.

Cap´ıtulo 9
Controladores predictivos
9.1. Dynamic Matrix Control
El método Dmc se desarrolló a finales de los setenta por Cutler y Ramaker de Shell
Oil Co. y ha sido aceptado ampliamente en el mundo industrial, principalmente por
las industrias petroqu´ımicas. Actualmente dmc es algo más que un algoritmo y parte
de su éxito se debe al hecho de que el producto comercial resuelve otros temas como
identificación u optimización global de la planta. En esta sección sólo se analiza el
algoritmo standard sin abordar detalles técnicos propios del producto de mercado que
no son de dominio público.
Pero a pesar de este éxito en la práctica, este método adolece quizás de la ausencia
de un análisis teórico ma´s completo que estudie la influencia de los parámetros de
diseño (horizontes, secuencias de ponderación) sobre la estabilidad del bucle cerrado
as´ı como de resultados de robustez.
9.1.1. Predicción
El modelo de proceso que se emplea es el de respuesta temporal, considerando la
perturbación como constante a lo largo del horizonte. El procedimiento para obtener
la predicción se describe a continuación.
135

136 DYNAMIC MATRIX CONTROL
Como se emplea un modelo de respuesta ante escalón:
y(t) =
∞
i=1
gi u(t − i)
los valores predichos a lo largo del horizonte serán:
ˆy(t + k | t) =
∞
i=1
gi u(t + k − i) + ˆn(t + k | t) =
=
k
i=1
gi u(t + k − i) +
∞
i=k+1
gi u(t + k − i) + ˆn(t + k | t)
Las perturbaciones se consideran constantes, ˆn(t+k | t) = ˆn(t | t) = ym(t)− ˆy(t | t),
por lo que se puede escribir:
ˆy(t + k | t) =
k
i=1
gi u(t + k − i) +
∞
i=k+1
gi u(t + k − i) + ym(t) −
−
∞
i=1
gi u(t − i) =
k
i=1
gi u(t + k − i) + f(t + k)
donde f(t + k) es la respuesta libre del proceso, es decir, la parte de la respuesta que
no depende de las acciones de control futuras, y viene dada por:
f(t + k) = ym(t) +
∞
i=1
(gk+i − gi) u(t − i) (9.1)
Si el proceso es asintóticamente estable, los coeficientes gi de la respuesta ante
escalón tienden a un valor constante después de N periodos de muestreo, por lo que se
puede considerar que
gk+i − gi ≈ 0, i N
y por tanto la respuesta libre se puede calcular como
f(t + k) = ym(t) +
N
i=1
(gk+i − gi) u(t − i)
Nótese que si el proceso no es estable, entonces no existe N y no se puede calcu-
lar f(t + k) (aunque existe una generalización en el caso de que la inestabilidad sea
producida por integradores puros).

CAPÍTULO 9. CONTROLADORES PREDICTIVOS 137
Ahora las predicciones se pueden calcular a lo largo del horizonte de predicción
(k = 1, . . . , p), considerando m acciones de control.
ˆy(t + 1 | t) = g1 u(t) + f(t + 1)
ˆy(t + 2 | t) = g2 u(t) + g1 u(t + 1) + f(t + 2)
...
ˆy(t + p | t) =
p
i=p−m+1
gi u(t + p − i) + f(t + p)
Si se define la matriz dinámica G como:
G =










g1 0 · · · 0
g2 g1 · · · 0
...
...
...
...
gm gm−1 · · · g1
...
...
...
...
gp gp−1 · · · gp−m+1










se puede escribir que:
ˆy = Gu + f (9.2)
Obsérvese que G está formada por m (horizonte de control) columnas de la respuesta
ante escalón apropiadamente desplazadas hacia abajo. ˆy es un vector de dimensión p
que contiene las predicciones de la salida, u representa el vector de incrementos de
control y f es el vector de respuestas libres. Esta es la expresión que relaciona las
respuestas futuras con los incrementos en las señales de control, por lo que usará para
calcular las acciones necesarias para conseguir el comportamiento deseado del sistema.
9.1.2. Perturbaciones medibles
El efecto de las perturbaciones medibles se puede añadir fácilmente a las anteriores
ecuaciones de predicción, ya que éstas se pueden tratar como entradas al sistema. La
expresión (9.2) se puede usar para calcular la predicción del efecto de las perturbaciones
en la salida de la siguiente forma:
ˆyd = D d + fd

donde ˆyd es la contribución de las perturbaciones medibles a la salida, D es una matriz
similar a G que contiene los coeficientes de la respuesta del sistema a un escalón en la
perturbación, d es el vector de incrementos en la perturbación y fd es la parte de la
respuesta que no depende de la perturbación.
En el caso más general de perturbaciones medibles y no medibles, la respuesta libre
completa del sistema (la fracción de la salida que no depende de la variable manipulada)
se puede considerar como la suma de cuatro efectos: la respuesta a la entrada u(t), a la
perturbación medible d(t), a la perturbación no medible y al estado actual del proceso:
f = fu + D d + fd + fn
Por tanto la predicción se puede expresar en la forma general
ˆy = Gu + f
9.1.3. Algoritmo de control
El éxito en la industria del dmc se ha debido principalmente a su aplicación a
sistemas multivariables de gran dimensión con la consideración de restricciones. En
esta sección se describe el algoritmo de control comenzando por el caso más simple
de un sistema monovariable sin restricciones y extendiéndolo posteriormente al caso
general multivariable con restricciones.
El objetivo del controlador dmc es llevar el proceso los más cerca posible al setpoint
en el sentido de m´ınimos cuadrados con la posibilidad de incluir una penalización en los
movimientos de la señal de control. Por ello se seleccionan las variables manipuladas de
forma que minimicen un objetivo cuadrático que puede incluir sólo los errores futuros
J =
p
j=1
[ˆy(t + j | t) − w(t + j)]2
o también el esfuerzo de control, presentando la forma genérica
J =
p
j=1
[ˆy(t + j | t) − w(t + j)]2
+
m
j=1
λ[ u(t + j − 1)]2
Si no existen restricciones, la minimización de la función de coste J = eeT
+ λuuT
,
donde e es el vector de errores futuros a lo largo del horizonte de predicción y u es el

w
f
+
K
u
Proceso
y
-
Calculo
Resp. libre
Figura 9.1: Ley de control
vector de futuros incrementos en la señal de control u(t), . . . , u(t + m), se puede
hacer de forma anal´ıtica calculando la derivada de J y haciéndola igual a 0, lo que
proporciona el resultado general:
u = (GT
G + λI)−1
GT
(w − f) (9.3)
Recuérdese que, como en todas las estrategias predictivas, sólo se env´ıa al proceso
el primer elemento del vector u ( u(t)). No es aconsejable implementar la secuencia
completa sobre los siguientes m intervalos, ya que al ser imposible estimar de forma
exacta las perturbaciones, no es posible anticiparse a las perturbaciones inevitables que
provocan que la salida real difiera de las predicciones que se emplean para calcular la
secuencia futura de acciones de control. Además, el setpoint puede cambiar durante los
próximos m intervalos.
Resulta interesante analizar en qué consiste realmente la ley de control. Analizan-
do la expresión 9.3 se observa que el primer elemento del vector u, que es la señal
que efectivamente se env´ıa a la planta, es el producto de la primera fila de la matriz
(GT
G+λI)−1
GT
(llamémosle K) por la diferencia entre la trayectoria de referencia y la
respuesta libre, que es el error futuro si no hubiera incrementos en la señal de control.
Se puede decir por tanto que el incremento de la señal de control es proporcional (por
medio de K) a los errores futuros y por tanto habrá cambios en la señal de control
siempre que el controlador detecte que va a haber una discrepancia en el futuro entre el
objetivo deseado y el comportamiento esperado del sistema. Esta idea queda reflejada
en la figura 9.1.

zona
P. operacion
optimo
segura 2
Zona segura 1
Punto operacion 1
Punto operacion 2
Restriccion
Restriccion
Figura 9.2: Punto de operación óptimo de un proceso t´ıpico
9.1.3.1. El caso con restricciones
Aunque computacionalmente más complicado que otros algoritmos más simples, la
capacidad de manejar restricciones que posee este método (y mpc en general) lo hace
muy atractivo para aplicaciones prácticas, ya que en general el punto de operación
óptimo según criterios económicos se encuentra normalmente en la intersección de las
restricciones, como se muestra en la figura 9.2. Por razones de seguridad, es necesario
mantener una zona segura alrededor del punto de operación, ya que el efecto de las
perturbaciones puede hacer que la salida del proceso viole las restricciones. Esta zona
se puede reducir (y por tanto aumentar los beneficios económicos) si el controlador es
capaz de manejar restricciones (punto de operación 1).
Las restricciones tanto en entrada como en salida se pueden reducir a desigualdades
de forma genérica
N
i=1
Cj
yi ˆy(t + k | t) + Cj
uiu(t + k − i) + cj
≤ 0 j = 1 . . . Nc
que deben tenerse en cuenta para la minimización. Como se ha visto, las salidas se
pueden expresar en función del vector de incrementos de control a través de la matriz
dinámica, por que las restricciones tanto en la entrada como en la salida se pueden
recoger en una desigualdad matricial de la forma Ru ≤ c, como se verá con más
detalle en el tema dedicado a restricciones. Ahora la minimización es un problema de
Programación Cuadrática qp, cuya solución es numérica.
Todo lo relacionado con las restricciones será abordado con mayor grado de detalle
en el tema dedicado a ello.

9.1.3.2. Extensión al caso multivariable
El esquema previo se puede extender fácilmente al caso de sistemas con varias
entradas y varias salidas. Las ecuaciones básicas se mantienen igual a excepción de que
las matrices y vectores cambian de dimensión para poder incluir todas las entradas y
salidas.
Al tratarse de modelos lineales, se puede aplicar el principio de superposición para
obtener el valor de las salidas ante las diversas entradas. Para ello se define el vector
de salidas futuras como:
ˆy = [y1(t + 1 | t), . . . , y1(t + p1 | t), . . . , yny(t + 1 | t), . . . , yny(t + pny | t)]T
y el de señales de control de la forma:
u = [ u1(t), . . . , u1(t + m1 − 1), . . . , unu(t), . . . , unu(t + mnu − 1)]T
as´ı como la respuesta libre:
f = [f1(t + 1 | t), . . . , f1(t + p1 | t), . . . , fny(t + 1 | t), . . . , fny(t + pny | t)]T
teniendo en cuenta que la respuesta libre de la salida i depende tanto de valores pasados
de yi como de valores pasados de todas las señales de control.
Con estas definiciones, la ecuación de predicción es igual que en el caso monovariable
simplemente considerando que la matriz G toma la forma:
G =





G11 G12 · · · G1nu
G21 G22 · · · G2nu
...
...
...
...
Gny1 Gny2 · · · Gnynu





Cada submatriz Gij contiene los coeficientes de la respuesta ante escalón i-ésima
correspondiente a la entrada j-ésima. El proceso de minimización es análogo sólo que la
ponderación tanto de los errores como de los esfuerzos de control se realiza con matrices
de peso.
9.2. Control Predictivo Generalizado
El Control Predictivo Generalizado gpc fue propuesto por Clarke et al. en 1987
y se ha convertido en uno de los métodos más populares en el ámbito del Control

142 CONTROL PREDICTIVO GENERALIZADO
Predictivo tanto en el mundo industrial como en el académico. Se ha empleado con
éxito en numerosas aplicaciones industriales, mostrando buenas prestaciones a la vez
que un cierto grado de robustez respecto a sobreparametrización o retardos mal cono-
cidos. Puede resolver muchos problemas de control diferentes para un amplio campo de
procesos con un número razonable de variables de diseño, que son especificadas por el
operario dependiendo del conocimiento previo del proceso y de los objetivos de control.
La idea básica del gpc es calcular una secuencia de futuras acciones de control
de tal forma que minimice una función de coste multipaso. El ´ındice a minimizar es
una función cuadrática que mide por un lado la distancia entre la salida predicha del
sistema y una cierta trayectoria de referencia hasta el horizonte de predicción, y por
otro el esfuerzo de control necesario para obtener dicha salida.
El Control Predictivo Generalizado tiene muchas ideas en común con otros con-
troladores predictivos previamente mencionados ya que está basado en las mismas
ideas pero posee a su vez algunas diferencias. Como se verá más adelante, es capaz de
proporcionar una solución expl´ıcita (en ausencia de restricciones), puede trabajar con
procesos inestables o de fase no m´ınima e incorpora el concepto de horizonte de control
as´ı como la consideración en la función de coste de ponderación de los incrementos en
las acciones de control. Las diversas posibilidades disponibles para el gpc conducen a
una gran variedad de objetivos de control comparado con otras realizaciones, algunas
de las cuales pueden ser consideradas como subconjuntos o casos l´ımites del gpc.
9.2.1. Formulación del Control Predictivo Generalizado
La mayor´ıa de los procesos de una sola entrada y una sola salida (single-input single-
output, siso), al ser considerados en torno a un determinado punto de trabajo y tras
ser linealizados, pueden ser descritos de la siguiente forma:
A(z−1
)y(t) = z−d
B(z−1
)u(t − 1) + C(z−1
)e(t)
donde u(t) y y(t) son respectivamente la señal de control y la salida del proceso y e(t)
es un ruido blanco de media cero. A, B y C son los siguientes polinomios en el operador
de desplazamiento hacia atrás z−1
:
A(z−1
) = 1 + a1z−1
+ a2z−2
+ ... + anaz−na
B(z−1
) = b0 + b1z−1
+ b2z−2
+ ... + bnbz−nb
C(z−1
) = 1 + c1z−1
+ a2z−2
+ ... + cncz−nc
donde d es el tiempo muerto del sistema.

Este modelo es conocido como Autorregresivo de Media Móvil (Controller Auto-
Regressive Moving-Average carma). En muchas aplicaciones industriales en las que
las perturbaciones son no-estacionarias resulta más conveniente el uso de un modelo
carma integrado, dando lugar al carima, que viene descrito por:
A(z−1
)y(t) = B(z−1
)z−d
u(t − 1) + C(z−1
)
e(t)
con = 1 − z−1
(9.4)
Por simplicidad, a partir de ahora el polinomio C se va a tomar igual a 1. Nótese
que en el caso de que C−1
pueda ser truncado se puede absorber en A y B.
El algoritmo del Control Predictivo Generalizado consiste en aplicar una secuencia
de señales de control que minimice una función de coste de la forma:
J(N1, N2, Nu) =
N2
j=N1
δ(j)[ˆy(t + j | t) − w(t + j)]2
+
Nu
j=1
λ(j)[ u(t + j − 1)]2
(9.5)
donde ˆy(t + j | t) es la predicción óptima j pasos hacia delante de la salida del proceso
con datos conocidos hasta el instante t, N1 y N2 son los horizontes m´ınimo y máximo
de coste, Nu es el horizonte de control y δ(j) y λ(j) son las secuencias de ponderación
mientras que w(t+j) es la futura trayectoria de referencia, que se puede calcular según
se muestra en la figura 8.5. En muchas situaciones se considera δ(j) igual a 1 y λ(j)
constante.
El objetivo es pues el cálculo de la futura secuencia de control u(t), u(t + 1),... de
tal manera que la salida futura del proceso y(t + j) permanezca próxima a w(t + j).
Esto se logra minimizando J(N1, N2, Nu).
9.2.1.1. Predicción óptima
Con la intención de minimizar la función de coste, se obtendrá previamente la
predicción óptima de y(t + j) para j ≥ N1 y j ≤ N2. Considérese la siguiente ecuación
diofántica:
1 = Ej(z−1
) A + z−j
Fj(z−1
) (9.6)
1 = Ej(z−1
) Ã + z−j
Fj(z−1
)
Los polinomios Ej y Fj están únicamente definidos con grados j − 1 y na respecti-
vamente. Se pueden obtener dividiendo 1 entre Ã(z−1
) hasta que el resto pueda ser fac-
torizado como z−j
Fj(z−1
). El cociente de la división es entonces el polinomio Ej(z−1
).

Si se multiplica la ecuación (9.4) por Ej(z−1
) zj
Ã(z−1
)Ej(z−1
)y(t + j) = Ej(z−1
)B(z−1
) u(t + j − d − 1) + Ej(z−1
)e(t + j) (9.7)
Teniendo en cuenta (9.6), la ecuación (9.7) queda:
(1 − z−j
Fj(z−1
))y(t + j) = Ej(z−1
)B(z−1
) u(t + j − d − 1) + Ej(z−1
)e(t + j)
La cual se puede escribir como
y(t + j) = Fj(z−1
)y(t) + Ej(z−1
)B(z−1
) u(t + j − d − 1) + Ej(z−1
)e(t + j) (9.8)
Al ser el grado del polinomio Ej(z−1
) igual a j − 1 los términos del ruido en la
ecuación (9.8) están todos en el futuro. La mejor predicción de y(t + j) será por con-
siguiente:
ˆy(t + j | t) = Gj(z−1
) u(t + j − d − 1) + Fj(z−1
)y(t)
donde Gj(z−1
) = Ej(z−1
)B(z−1
)
Resulta simple demostrar que los polinomios Ej y Fj se pueden obtener recursiva-
mente, de forma que los nuevos valores en el paso j + 1 (Ej+1 y Fj+1) sean función de
los del paso j. A continuación se muestra una demostración simple de la recursividad
de la ecuación diofántica. Existen otras formulaciones del gpc que no están basadas
en la recursividad de esta ecuación.
Considérense que los polinomios Ej y Fj se han obtenido dividiendo 1 entre Ã(z−1
)
hasta que el resto haya sido factorizado como z−j
Fj(z−1
) .
Con:
Fj(z−1
) = fj,0 + fj,1z−1
+ · · · + fj,naz−na
Ej(z−1
) = ej,0 + ej,1z−1
+ · · · + ej,j−1z−(j−1)
Supóngase que se utiliza el mismo procedimiento para obtener Ej+1 y Fj+1, es decir,
dividir 1 entre Ã(z−1
) hasta que el resto se pueda factorizar como z−(j+1)
Fj+1(z−1
) con
Fj+1(z−1
) = fj+1,0 + fj+1,1z−1
+ · · · + fj+1,naz−na
Está claro que solamente es necesario dar un paso más en la división para obtener
los polinomios Ej+1 y Fj+1. Al ser Ej+1 el nuevo cociente de la división, será igual al

cociente que hab´ıa hasta el momento (Ej) más un nuevo término, que será el fj,0 pues
el divisor ( Ã) es mónico. Por tanto:
Ej+1(z−1
) = Ej(z−1
) + ej+1,jz−j
con ej+1,j = fj,0
Teniendo en cuenta que el nuevo resto será el resto anterior menos el producto del
cociente por el divisor, los coeficientes del polinomio Fj+1 se pueden expresar como:
fj+1,i = fj,i+1 − fj,0 ãi+1 i = 0 · · · na
En resumen, la forma de obtener los polinmios Ej y Fj es la siguiente:
1. Comenzar con E1 = 1, F1 = z(1 − Ã)
2. Ir añadiendo nuevos términos a Ej con ej+1,j = fj,0
3. Calcular fj+1,i = fj,i+1 − fj,0 ãi+1 i = 0 · · · na, (siendo fj,na+1 = 0).
El polinomio Gj+1 puede ser obtenido recursivamente como sigue:
Gj+1 = Ej+1B = (Ej + fj,0z−j
)B = Gj + fj,0z−j
B
Es decir, los primeros j coeficientes de Gj+1 serán idénticos a los de Gj mientras
que el resto viene dado por:
gj+1,j+i = gj,j+i + fj,0 bi para i = 0 · · · nb
Para resolver el gpc es necesario obtener el conjunto de señales de control u(t),
u(t+1), ...,u(t+N) que minimizan la ecuación (9.5). Al tener el proceso un retardo de
d per´ıodos de muestreo, la salida sólo se verá influenciada por la señal u(t) después del
instante d+1. Los valores N1, N2 y Nu que marcan los horizontes pueden ser definidos
como N1 = d + 1, N2 = d + N y Nu = N. No tiene sentido hacer N1 d + 1 ya que
los términos de (9.5) sólo dependerán de las señales de control pasadas. Por otro lado,
haciendo N1 d + 1 los primeros puntos de la secuencia de salida, que serán los mejor
estimados, no se tendrán en cuenta.
El conjunto de las j predicciones óptimas:
ˆy(t + d + 1 | t) = Gd+1 u(t) + Fd+1y(t)
ˆy(t + d + 2 | t) = Gd+2 u(t + 1) + Fd+2y(t)
...
ˆy(t + d + N | t) = Gd+N u(t + N − 1) + Fd+N y(t)

puede ser escrito en forma matricial como:
y = Gu + F(z−1
)y(t) + G (z−1
) u(t − 1) (9.9)
Donde
y =





ˆy(t + d + 1 | t)
ˆy(t + d + 2 | t)
...
ˆy(t + d + N | t)





u =





u(t)
u(t + 1)
...
u(t + N − 1)





G =





g0 0 ... 0
g1 g0 ... 0
...
...
...
...
gN−1 gN−2 ... g0





G (z−1
) =





z(Gd+1(z−1
) − g0)
z2
(Gd+2(z−1
) − g0 − g1z−1
)
...
zN
(Gd+N (z−1
) − g0 − g1z−1
− · · · − gN−1z−(N−1)
)





F(z−1
) =





Fd+1(z−1
)
Fd+2(z−1
)
...
Fd+N (z−1
)





Al depender los últimos términos de la ecuación (9.9) sólo del pasado, pueden
agruparse en f, dando lugar a:
y = Gu + f (9.10)
Obsérvese que es la misma expresión que se obtuvo para el dmc, aunque en este
caso la respuesta libre es distinta.
9.2.1.2. Obtención de la ley de control
Entonces la ecuación (9.5) puede escribirse como:
J = (Gu + f − w)T
(Gu + f − w) + λuT
u (9.11)
donde:
w = w(t + d + 1) w(t + d + 2) · · · w(t + d + N)
T
(9.12)

La ecuación (9.11) se puede poner como:
J =
1
2
uT
Hu + bu + f0 (9.13)
donde:
H = 2(GT
G + λI)
b = 2(f − w)T
G
f0 = (f − w)T
(f − w)
El m´ınimo de J, siempre que no existan restricciones en la señal de control, puede
ser calculado igualando a cero el gradiente de J, lo cual conduce a:
u = −H−1
bT
(9.14)
Debido al uso de la estrategia deslizante, sólo se aplica realmente el primer elemento del
vector u, repitiendo de nuevo el mismo procedimiento al siguiente instante de muestreo.
La solución propuesta involucra la inversión (o al menos la triangularización) de una
matriz de dimensión N ×N, lo cual conlleva una gran carga de cálculo. El concepto ya
usado en otros métodos de horizonte de control se emplea con la finalidad de reducir
la cantidad de cálculo, asumiendo que las señales de control permanecerán en un valor
constante a partir del intervalo Nu N. Por tanto la dimensión de la matriz que hay
que invertir queda reducida a Nu × Nu, quedando la carga de cálculo reducida (en el
caso l´ımite de Nu = 1, se reduce al caso escalar) aunque restringiendo la optimalidad.
9.2.2. Ejemplo de cálculo
Se presenta a continuación un ejemplo de cálculo de un Controlador Predictivo
Generalizado en un caso sencillo. Se diseñará el controlador para un sistema de primer
orden.
Al discretizar el proceso continuo se obtiene el siguiente equivalente discreto:
(1 + az−1
)y(t) = (b0 + b1z−1
)u(t − 1) +
e(t)
Se va a considerar un retardo d igual a 0 y un polinomio de ruido C(z−1
) igual a 1.
Se usará el algoritmo descrito previamente para obtener la ley de control, obteniendo
resultados numéricos para valores de los paámetros a = 0,8, b0 = 0,4 y b1 = 0,6, siendo

los horizontes N1 = 1 y N = Nu = 3. Como se ha mostrado, se calcularán los valores
predichos de la salida del proceso en el horizonte haciendo uso de la ecuación (9.9),
obteniendo la ley de control de la expresión (9.14).
Resolviendo la ecuación (9.6) se obtienen los polinomios del predictor Ej(z−1
),
Fj(z−1
) desde j = 1 hasta j = 3, con
Ã(z−1
) = A(z−1
)(1 − z−1
) = 1 − 1,8z−1
+ 0,8z−2
En este caso sencillo donde el horizonte no es demasiado largo, estos polinomios se
pueden obtener directamente dividiendo 1 por Ã(z−1
). Como se ha explicado antes,
también se pueden calcular recursivamente, comenzando con los valores obtenidos en
el primer paso de la división, es decir:
E1(z−1
) = 1 F1(z−1
) = 1,8 − 0,8z−1
Cualquiera que sea el método empleado, los valores obtenidos son:
E2 = 1 + 1,8z−1
F2 = 2,44 − 1,44z−1
E3 = 1 + 1,8z−1
+ 2,44z−2
F3 = 2,952 − 1,952z−1
Con estos valores y el polinomio B(z−1
) = 0,4 + 0,6z−1
, los elementos Gi(z−1
) resultan
ser:
G1 = 0,4+0,6z−1
G2 = 0,4+1,32z−1
+1,08z−2
G3 = 0,4+1,32z−1
+2,056z−2
+1,464z−3
y por tanto se pueden escribir las salidas predichas como:


ˆy(t + 1 | t)
ˆy(t + 2 | t)
ˆy(t + 3 | t)

 =


0,4 0 0
1,32 0,4 0
2,056 1,32 0,4




u(t)
u(t + 1)
u(t + 2)

 +
+


0,6 u(t − 1) + 1,8y(t) − 0,8y(t − 1)
1,08 u(t − 1) + 2,44y(t) − 1,44y(t − 1)
1,464 u(t − 1) + 2,952y(t) − 1,952y(t − 1)


f
El paso siguiente es el cálculo de H−1
b. Tomando λ igual a 0,8 se tiene que:
(GT
G + λI)−1
GT
=


0,133 0,286 0,147
−0,154 −0,165 0,286
−0,029 −0,154 0,1334



Como sólo se necesita el valor de u(t) para los cálculos, sólo se emplea realmente la
primera fila de la matriz, con lo que resulta la siguiente expresión para la ley de control:
u(t) = −0,6042 u(t − 1) − 1,371y(t) + 0,805y(t − 1) +
+ 0,133w(t + 1) + 0,286w(t + 2) + 0,147w(t + 3)
donde w(t + i) es la trayectoria de referencia que se puede considerar bien constante
e igual a la referencia actual o bien una suave aproximación de primer orden a ésta.
Entonces la señal de control resulta ser una función de la referencia deseada y de
entradas y salidas pasadas, dada por:
u(t) = 0,3958u(t − 1) + 0,6042u(t − 2) − 1,371y(t) + 0,805y(t − 1) +
+ 0,133w(t + 1) + 0,286w(t + 2) + 0,147w(t + 3)
Al mismo resultado se puede llegar sin emplear la ecuación diofántica, calculando
G en base a los coeficientes de la respuesta ante escalón (que se pueden calcular en
función de los coeficientes de la función de transferencia) y calculando la respuesta
libre haciendo evolucionar hacia delante el modelo mientras la entrada se mantiene
constante.
9.2.3. Caso multivariable
Al igual que en el dmc todo lo visto para el caso de sistemas con una sola entrada
y una sola salida se puede extender al caso multivariable, aunque los cálculos son más
complejos.
En este caso el modelo carima para un sistema de m entradas y n salidas se puede
expresar como:
A(z−1
)y(t) = B(z−1
)u(t − 1) +
1
C(z−1
)e(t) (9.15)
donde A(z−1
) y C(z−1
) son matrices polinomiales mónicas de dimensión n×n y B(z−1
)
es una matriz polinomial de dimensión n × m, definidos como:
A(z−1
) = In×n + A1z−1
+ A2z−2
+ · · · + Ana z−na
B(z−1
) = B0 + B1z−1
+ B2z−2
+ · · · + Bnb
z−nb
C(z−1
) = In×n + C1z−1
+ C2z−2
+ · · · + Cnc z−nc

Las variablesy(t), u(t) y e(t) son de dimensión n × 1, m × 1 y n × 1 respectivamente.
La predicción conlleva la resolución de una ecuación diofantica matricial, que también
puede calcularse de forma recursiva.
En muchas ocasiones el problema radica en la obtención adecuada del modelo en
esta forma a partir de una matriz de transferencia en continuo que puede haberse
obtenido a partir de la curva de reacción.
Una vez obtenido el modelo, el criterio a minimizar tendrá la forma general
J(N1, N2, N3) =
N2
j=N1
ˆy(t + j | t) − w(t + j) 2
R +
N3
j=1
u(t + j − 1) 2
Q
donde R y Q son matrices de ponderación definidas positivas que normalmente se eligen
diagonales. La minimización se realiza igual que en el caso monovariable dando como
resultado un vector de señales de control a enviar a la planta en el instante actual:
u1(t), u2(t) . . . um(t).

Cap´ıtulo 10
Otros aspectos del Control
Predictivo
10.1. Restricciones en Control Predictivo
En la práctica todos los procesos están sujetos a restricciones. Los actuadores tienen
un campo limitado de acción impuesto por l´ımites f´ısicos (por ejemplo una válvula no
puede abrir más de un 100 % o un calentador no puede aportar más de su potencia
máxima. También existen l´ımites de seguridad (por ejemplo presiones o temperaturas
máximas), requerimientos tecnológicos (por ejemplo mantener temperaturas en un ran-
go dado), limitaciones de calidad del producto (no salirse de cierta zona) o normativa
medioambiental.
10.1.1. Tratamiento convencional de restricciones
El tratamiento convencional de restricciones en control de procesos se basa en que
las restricciones en la variable manipulada (entrada) se cumplen saturando la salida del
controlador. Sin embargo, las restricciones en la variable controlada (salida) no pueden
abordarse; se intenta evitar su violación trabajando alejados de los l´ımites (en zona
segura), operando lejos de la restricción. Por seguridad se trabaja con una consigna
inferior, más lejos del punto de operación óptimo, lo que normalmente equivale a una
disminución de la calidad y/o cantidad en la producción, ya que normalmente el punto
óptimo se encuentra en la intersección de las restricciones obligando a acercarse lo más
151

152 RESTRICCIONES EN CONTROL PREDICTIVO
Pmax
P
P
P
QQQ
1
2
1 2
t
Figura 10.1: Restricciones y punto de operación óptimo
posible a las éstas pero sin superarlas.
Si el controlador fuera capaz de tener en cuenta las restricciones y evitar su violación,
el proceso podr´ıa operar más cerca de éstas y por tanto de forma más eficiente. La figura
10.1 muestra un ejemplo donde existe una limitación de presión máxima y se observa
cómo al alejar el punto de operación del l´ımite la producción Q disminuye.
En cuanto a la forma de operar de un controlador predictivo que no considera restric-
ciones el procedimiento es similar: si la señal de control calculada viola la restricción,
se satura. Las señales futuras ni siquiera se tienen en cuenta, ya que normalmente no
se calculan. Esta forma de proceder no garantiza el carácter óptimo de la solución y en
ningún caso garantiza el cumplimiento de las restricciones en la salida. La violación de
los l´ımites de las variables controladas puede ser más costoso y peligroso, produciendo
daños en equipos y pérdidas en la producción.
La figura 10.2 muestra con claridad el fenómeno de pérdida de la solución óptima
cuando las variables manipuladas se mantienen en sus l´ımites por el programa de
control o por el propio actuador. Este hecho puede llevar a valores mayores de la
función objetivo y a un comportamiento no deseado (incluso inestabiliad). En 10.2a se
muestra un caso con horizonte de control igual a 2, donde se observa que si se satura
la señal de control u(t) a umax el valor de la función de coste no es el mejor que se
podr´ıa conseguir (que ser´ıa el correspondiente a uc). Incluso puede que no se viole la
restricción en el instante actual pero s´ı en el futuro (figura 10.2b) con lo que la señal
enviada al sistema (sin saturar) no es la mejor para el problema de dimensión 2 que se
está optimizando.

CAPÍTULO 10. OTROS ASPECTOS DEL CONTROL PREDICTIVO 153
u(t+1)
maxu
u max u(t)
u(t+1)
maxu
u max u(t)
cu u uc u
a) b)
Figura 10.2: Restricciones en la señal de control
10.1.2. Restricciones en Control Predictivo
En la actualidad el mpc es la única metodolog´ıa capaz de incorporar las restricciones
de forma sistemática en la fase de diseño del controlador, siendo esta caracter´ıstica una
de las razones de su gran éxito en la industria. Parece lógico que al disponer de un
modelo dinámico del proceso se pueda conocer la evolución futura de su salida y por
tanto se pueda saber si ésta va a violar o no las restricciones y actuar en consecuencia.
Para formular el algoritmo mpc con restricciones hay que expresar éstas en función
de la variable sobre la que se puede actuar, es decir, en función de u. Las restricciones
en la entrada están ya expresadas en función de u y para las restricciones en la salida
se hace uso de las ecuaciones de predicción que expresan el valor futuro de las salidas
en función de las señales de control futuras y valores conocidos en el instante t.
Cualquier controlador predictivo calcula la predicción como:
y = Gu + f
por lo que tanto entradas como salidas se pueden expresar en función del vector de
incrementos de la señal de control.
Las restricciones que aparecen serán básicamente amplitud y velocidad de cambio
en la señal de control y amplitud en la salida y se pueden expresar como:

U ≤ u(t) ≤ U ∀t
u ≤ u(t) − u(t − 1) ≤ u ∀t
y ≤ y(t) ≤ y ∀t
Para un proceso de m entradas y n salidas y restricciones en el horizonte N, las
restricciones se pueden expresar como:
1 U ≤ Tu + u(t − 1) 1 ≤ 1 U
1 u ≤ u ≤ 1 u
1 y ≤ Gu + f ≤ 1 y
donde l es una matriz de dimensión (N × n) × m formada por N m × m matrices
identidad y T es una matriz triangular inferior por bloques cuyos elementos no nulos
son matrices identidad de dimensión m × m. En forma condensada se pueden expresar
como:
R u ≤ c (10.1)
siendo
R =









IN×N
−IN×N
T
−T
G
−G









c =









l u
−l u
l U − lu(t − 1)
−l U + lu(t − 1)
l y − f
−l y + f









Aparte de las restricciones en amplitud, a la salida se le pueden aplicar otro tipo
de restricciones de para forzar un determinado comportamiento temporal (movimiento
dentro de una banda, comportamiento monótono, evitar respuesta inicial inversa, etc.),
pudiendo expresarlas también de la forma genérica (10.1).
Además de la clasificación en restricciones en la entrada y en la salida según a
qué tipo de variable se apliquen, se puede hacer otra clasificación atendiendo a la
forma de tratarlas. As´ı, se puede hablar de:
Restricciones duras como aquéllas que no se pueden violar bajo ningún concepto.
En este grupo se incluyen las restricciones relacionadas con la operación segura
del proceso.

Restricciones blandas, que son aquéllas que pueden ser violadas en un momento
dado por no ser cruciales, pero la violación se penaliza en la función objetivo
como un término más. Es una forma de relajar la restricción.
10.1.3. Resolución del problema
Con la adición de restricciones el problema general de control predictivo cambia se
puede formular como
minimizar J(u)
sujeto a Ru ≤ c
Es decir, el problema consiste en la minimización de una función cuadrática con
restricciones lineales, lo que se conoce como Programación Cuadrática, qp. En este
caso no se puede encontrar una solución anal´ıtica como en el caso sin restricciones,
sino que hay que recurrir a métodos iterativos.
Resulta evidente que la carga de cálculo será considerable, ya que hay que encontrar
la solución resolviendo el algoritmo iterativo en cada periodo de muestreo. Normalmente
el esfuerzo está justificado por el beneficio económico obtenido al trabajar más cerca del
punto de operación óptimo. Para resolver el problema qp existen diversos algoritmos
suficientemente probados.
Un problema asociado a la implementación del control con restricciones es el análisis
de la estabilidad del bucle cerrado. Como es necesario utilizar métodos numéricos para
resolver el problema de la optimización, la ley de control resultante no se puede describir
de forma expl´ıcita, haciendo el problema muy dif´ıcil de atacar mediante la teor´ıa clásica
de control.
En los últimos años se ha trabajado mucho sobre la estabilidad en estas circun-
stancias, proponiéndose soluciones basadas en la teor´ıa de Lyapunov. La idea básica
consiste en que la función de coste cuando el horizonte es infinito es monótona decre-
ciente (si existe solución factible) y se puede interpretar como función de Lyapunov
que garantiza por tanto la estabilidad. Sin embargo, como la solución tiene que ser
numérica, el número de variables de decisión tiene que ser finito, por lo que se han
propuesto dos ideas. En la primera, se descompone la función objetivo en dos partes:
una con horizonte finito y restricciones y otra con horizonte infinito y sin restricciones.
La segunda idea es en esencia equivalente y consiste en imponer restricciones terminales
al estado y usar un horizonte infinito.

En cualquier caso es un tema muy abierto, sobre todo si se quieren considerar las
incertidumbres en el modelo y los temas asociados con la factiblidad.
10.1.4. Gestión de restricciones
Durante la etapa de optimización puede aparecer problemas de no existencia de
solución óptima para unas restricciones dadas (no existe compatibilidad entre las re-
stricciones), por ejemplo por el planteamiento de unos objetivos inalcanzables para
unas restricciones dadas. Existen otras posibles causas de inexistencia de solución, co-
mo es el caso de que una perturbación saque al proceso fuera de la zona de trabajo
usual.
La factibilidad de un problema de optimización significa que la función objetivo
esté acotada y que todas las restricciones sean satisfechas.
La no factibilidad puede aparecer en régimen permanente o en el transitorio. El
problema de la falta de solución en régimen permanente puede venir provocado por
un objetivo de control irrealizable. Sin embargo, este tipo de no factibilidad puede ser
fácilmente eliminado en la etapa de diseño evitando la inclusión de tales objetivos.
También puede ser debido a cambios en referencias que hagan incompatibles las re-
stricciones (se quiera llevar alguna variable a un punto que es imposible de alcanzar
con una entrada que está acotada).
En el régimen transitorio puede aparecer no factibilidad incluso cuando las restric-
ciones impuestas parezcan razonables. Restricciones que no causan problemas en op-
eración normal pueden producir problemas bajo ciertas circunstancias. Puede que una
perturbación o cambio de referencia grande fuerce a una variable fuera de su l´ımite y sea
imposible introducirla de nuevo en su zona permitida con señales de control de energ´ıa
limitada. En estos casos las restricciones se hacen temporalmente incompatibles.
Las soluciones no factibles aparecen con mayor frecuencia en casos en que el óptimo
se encuentre cerca de las restricciones y el sistema esté sujeto a perturbaciones, llevando
a la salida a regiones prohibidas”.

Límites físicos
Restricciones reales
Límites de operación
Figura 10.3: Gestión de restricciones
10.1.4.1. Técnicas de búsqueda de soluciones factibles
Los métodos de gestión de restricciones tratan de recuperar la factibilidad actuando
sobre las restricciones según diferentes criterios.
Los l´ımites de las restricciones se pueden considerar de los siguientes tipos:
Limites fisicos: nunca se pueden sobrepasar, principalmente por motivos de se-
guridad o por la propia construcción de los equipos (p.ej. actuadores)
Limites de operación: son fijados por los operarios para mantener las condiciones
nominales de funcionamiento. Se pueden sobrepasar bajo ciertas circunstancias
Limites reales: son los que usa el algoritmo de control en cada instante. Son los
que proporciona el gestor de restricciones, quien debe calcularlos de forma que
nunca superen los limites f´ısicos.
Es decir, el gestor de restricciones calculará los l´ımites reales (los que se env´ıan al
algoritmo qp) en base a los l´ımites de operación pero sin salirse nunca de los l´ımites
f´ısicos, según se observa en la figura 10.3.
Se analizan a continuación posibles soluciones para este problema, que se pueden
agrupar en:
1. Desconexión del controlador.

2. Eliminación de restricciones.
3. Relajación de restricciones.
4. Otras técnicas.
1. Desconexión del controlador
La forma más sencilla de resolver de este tipo de problemas es pasar el controlador
a posición manual cuando aparecen las incompatibilidades de restricciones y volver a
operación automática cuando se recupera la admisibilidad de la solución.
Este método, como se puede comprender tiene serias desventajas. Normalmente,
cuando aparecen problemas de incompatibilidad de restricciones es porque el sistema
en bucle cerrado se encuentra en un estado cr´ıtico donde normalmente el operador
tendrá muy poca experiencia en la operación. Adicionalmente, si las restricciones están
relacionadas con aspectos de seguridad o económicos, las decisiones llevadas a cabo
cuando aparecen problemáticas de compatibilidad de restricciones suelen ser cr´ıticas
dado que en estos casos alguno de los objetivos del control no puede ser satisfecho.
El método suele ser utilizado cuando los problemas de incompatibilidad de restric-
ciones no son frecuentes.
2. Eliminación de restricciones
La factibilidad se analiza en cada periodo de muestreo, por lo que la eliminación
de restricciones se realiza de forma temporal. Periódicamente se chequea la factibilidad
para poder reinsertar restricciones eliminadas.
La eliminación de un grupo de restricciones ha de realizarse en aquellos casos en que
el conjunto completo de restricciones que se imponen sobre el sistema sea incompatible.
Cada vez que existe un problema de incompatibilidad de restricciones, se forma un
conjunto de restricciones no admisibles que no se tienen en cuenta en el proceso de
optimización. Se pueden distinguir en la metodolog´ıa de eliminación de restricciones
varios tipos.
Eliminación indiscriminada Con esta estrategia todas las restricciones se elimi-
nan cada vez que aparezcan problemas de existencia de solución factible, quedando
la optimización de un problema sin restricciones. No es un método muy óptimo para

resolver el problema de la existencia de solución admisible, pero es la forma más rápida
de tener en cuenta incompatibilidad de restricciones.
La eliminación indiscriminada de restricciones no es adecuada en todas las aplica-
ciones. No debe ser por ejemplo usada en casos en que las restricciones estén directa-
mente relacionadas con l´ımites de seguridad.
Eliminación jerárquica En este caso sólo se eliminan las restricciones que provocan
problemas de incompatibilidad. En este método se asigna en la etapa de diseño una
prioridad a cada restricción, que da un grado de importancia relativa de dicha restric-
ción frente a las otras. Esta prioridad se usará para clasificar las restricciones de una
forma jerárquica (se asigna un número que indica su posición en la jerarqu´ıa). De este
modo, cada vez que haya problemas de factibilidad o existencia de solución el gestor
de restricciones va eliminando por orden las restricciones menos prioritarias hasta que
se restablece la factibilidad de la solución, que se chequea cada periodo de muestreo
para reinsertar restricciones que hubieran sido temporalmente eliminadas.
En este sentido, a la hora de eliminar restricciones se pueden establecer diferentes
tipos de reglas para establecer el número de restricciones que se eliminan, si conviene
eliminar más restricciones a costa de no eliminar una con prioridad superior, etc.
3. Relajación de restricciones
Otro método para tener en cuenta el problema de existencia de solución es la re-
lajación de las restricciones. Se puede hacer una relajación de los l´ımites de forma
temporal o convertir restricciones duras (Ru ≤ c), cambiándolas en restricciones blan-
das (Ru ≤ c + , con ≥ 0) para asegurar la existencia de solución, añadiendo un
término T
T a la función de coste de forma que se penalice la violación de la re-
stricción y obtener un mejor comportamiento del sistema controlado. A largo plazo, el
término de penalización en la función objetivo llevará las variables auxiliares a cero.
4. Otras técnicas
Existen técnicas que se basan en la manipulación del horizonte m´ınimo de las restric-
ciones. Algunos controladores industriales como el qdmc usan el concepto de constraint
window. La constraint window comienza en algún punto en el futuro y continúa hasta
el estado estacionario. Si existe dinámica del tipo de fase no m´ınima, se pueden mejorar
las prestaciones desplazando la ventana hacia el futuro, lo que equivale a ignorar las
restricciones duras en la salida durante la fase inicial de la respuesta.

Apuntes ic4

Más contenido relacionado

La actualidad más candente

Destacado

Similar a Apuntes ic4

Último

Apuntes ic4