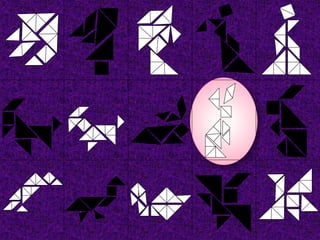
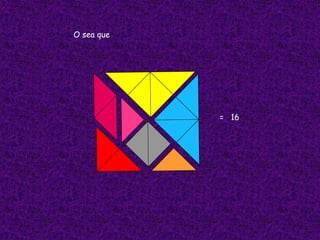
El Tangram es un antiguo rompecabezas chino compuesto por siete piezas de formas geométricas simples. Se desconoce su origen exacto, aunque hay leyendas que lo atribuyen a China en la antigüedad. Fue muy popular en China como juego para mujeres y niños, y hoy en día se usa en diferentes áreas como entretenimiento, psicología y educación, especialmente para enseñar conceptos matemáticos a través de la manipulación lúdica de las piezas.

2. No se sabe con certeza quién inventó el juego ni cuándo, pues las primeras
publicaciones chinas en las que aparece el siglo XVIII, y entonces el juego
era ya muy conocido en varios países.
Cuenta una de las tantas leyendas, que hace mucho tiempo, en china vivía
un hombre llamado Tan que un día dejo caer una baldosa al suelo por
accidente. La baldosa se rompió en siete piezas y Tan trato de
recomponerla pero para su gran sorpresa aquellas piezas no formaban de
nuevo un cuadrado, sino la silueta de un gato, un perro, una casa, un barco y
una persona. Olvidada ya la finalidad original de la baldosa, Tan corrio a
enseñar su descubrimiento a todos sus amigos.
El Tangram posee un insólito poder de comunicación, con tan solo siete
formas geométricas sencillas.
En China, el Tangram era muy popular y se consideraba juego para mujeres
y niños.

3. Se concedía más atención al juego mismo y sus siete componentes, de
forma que el Tangram era producido y vendido como un objeto: tarjetas
con las siluetas, piezas de marfil y envoltorios en forma de caja, etc.
En los libros aparecían unos cuantos cientos de imágenes, en su mayor parte
figurativas, como animales, casas y flores, junto a una escasa
representación de formas muy extrañas.
En 1973, los diseñadores holandeses JOOST ELFFERS Y MICHAEL
SCHUYT produjeron una edición rústica con 750 figuras nuevas, alcanzando
así un total de más de 1.600. La edición de 1973 ha vendido hasta la fecha
más de un millón de ejemplares en todo el mundo.
Hoy en día, el Tangram se usa como entretenimiento, en psicología, en
educación física, en diseño, en filosofía y particularmente en pedagogía. En
el área de enseñanza de las matemáticas el Tangram se emplea para
introducir conceptos de geometría, y para promover el desarrollo de
capacidades psicomotrices e intelectuales de los niños, pues permite ligar
de manera lúdica la manipulación concreta de materiales con la formación
de ideas abstractas.

4. El TANGRAM o juego de formas chino es un juego individual que estimula
la creatividad. Con él se pueden construir infinidad de figuras.
En chino recibe el nombre de tabla de la sabiduría o tabla de los siete
elementos. Como su nombre indica consta de siete figuras:
un cuadrado un paralelogramo
cinco triángulos (dos grandes, dos pequeños y uno mediano).

5. Sus reglas son muy simples; con dichos elementos, ni uno más ni uno
menos, se deben construir figuras.
El tangram se construye en un material didáctico ideal para desarrollar
habilidades mentales, mejorar la ubicación espacial y para enriquecer la
imaginación y la fantasía. Así mismo como ejercicio de concentración.
Por medio de este material se puede conceptualizar sobre las
fracciones y las operaciones entre ellas, comprender y operalizar la
notación geográfica, deducir relaciones, desarrollo de formulas para
área y perímetro de figuras planas.

6. Tangram de ocho piezas Tangram de Fletcher
Tangram de cinco piezas Tangram ruso de 12 piezas

7. Tangram pitagórico Tangram huevo
Cardiograma Tangram de 4 piezas

8. CUENTO
En una bella casa vivía un niño , con su perro
, este niño era muy alegre y le gustaba mucho bailar
, pero cierto día su perro se perdió, y el niño estaba
muy triste
. Hizo dibujos de su perro y se los enseño

9. a todos sus conocidos , alguien le dijo
que había visto a su perro cerca del muelle, el muchacho corrió hasta el
muelle
, el perro al ver a su dueño corrió hacia él
, y los dos felices decidieron realizar un paseo en
bote

10. FIGURAS QUE SE PUEDE REALIZAR

15. PRACTIQUEMOS LAS FRACCIONES CON
EL TANGRAM
Si
= 1
Entonces = 2
y
= 4
= 2
= 2

16. O sea que
= 16

17. Si = 1
Entonces
= 1/2
y
= 2
EL CUADRADO PEQUEÑO COMO LA UNIDAD
= 1
= 1

18. O sea que
= 8

19. EL TRIANGULO GRANDE COMO LA UNIDAD
Si
= 1
Entonces
= 1/2
y
= 1/4
= 1/2
= 1/2

20. O sea que
= 4

21. EL CUADRADO CON TODAS LAS PIEZAS COMO LA UNIDAD
Si
= 1
Entonces
= 1/4
y
= 1/8
= 1/16
= 1/8
= 1/8

22. ACTIVIDADES PARA FRACCIONARIOS
1. Construye una figura con dos triángulos grandes, el triángulo
mediano y dos triángulos pequeños. Si la figura vale 1. ¿Cuál es
el valor de cada pieza?
2. Utiliza las piezas del tangram para ayudarte a encontrar el
cociente de:
1/4 ÷1/16= 2/4 ÷1/8=
1/8 ÷1/8= 3/8 ÷1/16=
1/2 ÷1/4= 3/8 ÷1/4=