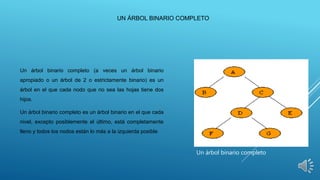
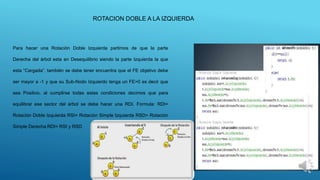
El documento describe diferentes tipos de árboles binarios, incluyendo árboles equilibrados, árboles AVL y sus propiedades. Un árbol AVL es un árbol binario de búsqueda equilibrado donde la altura de los subárboles del nodo no difiere en más de una unidad para cada nodo. Los árboles AVL mantienen esta propiedad de equilibrio mediante rotaciones simples y dobles cuando se insertan o eliminan nodos.

2. Árbol Equilibrado: Es aquel en que la altura de los
dos subárboles de la raíz se diferencian en como
máximo una
Árbol Completo: Es aquel en que todos los nodos
tienen exactamente 0 o dos subárboles unidad.

3. UN ÁRBOL BINARIO COMPLETO
Un árbol binario completo (a veces un árbol binario
apropiado o un árbol de 2 o estrictamente binario) es un
árbol en el que cada nodo que no sea las hojas tiene dos
hijos.
Un árbol binario completo es un árbol binario en el que cada
nivel, excepto posiblemente el último, está completamente
lleno y todos los nodos están lo más a la izquierda posible.
Un árbol binario completo

4. DEFINICIÓN DE UN ÁRBOL AVL
El árbol AVL toma su nombre de las iniciales de los apellidos de sus inventores, Georgii Adelson-Velskii
y Yevgeniy Landis. Lo dieron a conocer en la publicación de un artículo en 1962.
Los árboles AVL están siempre equilibrados de tal modo que para todos los nodos, la altura de la rama
izquierda no difiere en más de una unidad de la altura de la rama derecha o viceversa.
La eficiencia de una búsqueda en un árbol binario ordenado varía entre O(n) y O(log(n)), dependiendo
de la estructura que presente el árbol. Árbol Degenerado Árbol Equilibrado de Búsqueda

5. CARACTERÍSTICA
UN ÁRBOL TOTALMENTE EQUILIBRADO
Un árbol totalmente equilibrado se caracteriza porque la altura de la
rama izquierda es igual que la altura de la rama derecha para cada uno
de los nodos del árbol.
• La estructura de datos de árbol equilibrado que se utiliza es la del
árbol AVL. Son árboles ordenados o de búsqueda que, además,
cumplen la condición de balanceo para cada uno de los nodos.
Árbol Equilibrado
Árbol no Equilibrado

6. ALTURA DE UN ÁRBOL EQUILIBRADO, ÁRBOL AVL
• No resulta fácil determinar la altura promedio de un árbol AVL, por ello se determina la altura en
el peor de los casos, es decir, la altura máxima que puede tener un árbol equilibrado con un
número de nodos n. La altura es un parámetro importante ya que coincide con el número de
iteraciones que se realizan para bajar desde el nodo raíz al nivel mas profundo de las hojas.
• El árbol equilibrado de n nodos menos denso tiene como altura (1.44*log (n)), donde n es el
número de nodos en el peor de los casos del árbol AVL de altura h y se puede afirmar que la
complejidad de una búsqueda es O(Log n).

7. FACTOR DE EQUILIBRIO
Si el factor de equilibrio de cualquier nodo es 1, significa que el
subárbol izquierdo está un nivel más alto que el subárbol
derecho.
Si el factor de equilibrio de cualquier nodo es 0, significa que el
subárbol izquierdo y el subárbol derecho contienen la misma
altura.
Si el factor de equilibrio de cualquier nodo es -1, significa que el
subárbol izquierdo está un nivel más bajo que el subárbol
derecho.
Podemos ver que el factor de equilibrio asociado con cada nodo
está entre -1 y +1. por lo tanto, es un ejemplo de árbol AVL.

8. INSERCIÓN EN AVL
• La Inserción se hace siguiendo el camino de búsqueda
• Puede aumentar la altura de una rama, de manera que cambie el factor
de equilibrio de dicho nodo.
– Implica que se retornará por el camino de búsqueda para actualizar el
FE de c/nodo
– Se puede llegar a Desbalancear (Altura=2) => Rebalanceos.
– O Puede mejorar: Si al Árbol X se le Inserta el 3, resultará en
Perfectamente Balanceado.
• El Proceso termina cuando se llega a la Raíz o cuando termina el
Rebalanceo del mismo.

9. ROTACIÓN DOBLE A LA DERECHA
Para hacer una Rotación Doble Derecha partimos de que la
parte izquierda del árbol esta en desequilibrio siendo la parte
derecha la que esta “Cargada”, también se debe tener encuentra
que el FE objetivo debe ser mayor a 1 y que su Sub-Nodo
Derecho tenga un FE<0, es decir que sea negativo, al cumplirse
todas estas condiciones decimos que para equilibrar ese sector
del árbol se debe hacer una RDD. Formula: RDD= Rotación
Doble Derecha RSD= Rotación Simple Derecha RSI= Rotación
Simple Izquierda RDD= RSD y RSI

10. Para hacer una Rotación Doble Izquierda partimos de que la parte
Derecha del árbol esta en Desequilibrio siendo la parte Izquierda la que
esta “Cargada”, también se debe tener encuentra que el FE objetivo debe
ser mayor a -1 y que su Sub-Nodo Izquierdo tenga un FE>0 es decir que
sea Positivo, al cumplirse todas estas condiciones decimos que para
equilibrar ese sector del árbol se debe hacer una RDI. Formula: RDI=
Rotación Doble Izquierda RSI= Rotación Simple Izquierda RSD= Rotación
Simple Derecha RDI= RSI y RSD
ROTACION DOBLE A LA IZQUIERDA

11. ELIMINACIÓN DE UN NODO AVL
Luego de eliminar un nodo con cierta clave, el árbol resultante debe seguir siendo
AVL
El Algoritmo puede descomponerse en dos parte bien diferenciadas.
1- eliminar el Nodo: según la estrategia que vimos en la Eliminación de Nodo en
Árbol de búsqueda.
2- balancear: se debe seguir el camino de búsqueda en sentido inverso:
2.1. Arreglar el Factor de Equilibrio
2.2.restaurar el equilibrio allí donde se rompe.