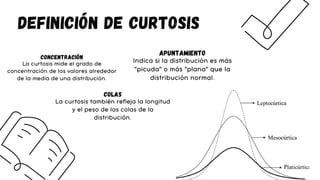
El documento detalla diversas medidas de dispersión y distribución en estadística, como el rango, desviación estándar, varianza y coeficiente de variación, junto con sus fórmulas y aplicaciones para datos agrupados y no agrupados. También se abordan conceptos de simetría y curtosis, que describen la forma y concentración de las distribuciones, así como los coeficientes de correlación que indican la relación entre variables. Se explican procedimientos para calcular la asimetría y curtosis, junto con ejemplos prácticos y recomendaciones para la interpretación de resultados estadísticos.

1. Ing, Sanchez Chavarria Daniel
Writing
ESTADÍSTICA
GENERAL
or
Grupo 7

2. INTEGRANTES:
Arias Huaricancha David
ESPIRITU HUAYNATE, Britzy
GAMARRA ROJAS. Raul
MENDOZA IDELFONSO, Gabriel
ROJAS PALPA, Piero

3. medidas de dispersión para
datos no agrupadas
Rango
Es la diferencia entre el valor máximo y el valor
mínimo de un conjunto de datos. Indica la
extensión total de los datos.
Desviación estándar
Es la raíz cuadrada de la varianza y
proporciona una medida de dispersión
que está en las mismas unidades que los
datos originales. Indica, en promedio,
cuánto se desvían los datos de la media.
Coeficiente de variación
Es la relación entre la desviación estándar y la
media, expresada como un porcentaje. Permite
comparar la dispersión de conjuntos de datos con
diferentes unidades o magnitudes.

4. medidas de dispersión para
datos no agrupadas
Varianza
Mide cuán lejos están los datos de su media. Se
calcula como la media de las diferencias al
cuadrado entre cada dato y la media del
conjunto.
Desviación media
Es la media de las diferencias absolutas
entre cada dato y la media del conjunto.
Es menos sensible a valores extremos que
la varianza y la desviación estándar.

5. medidas de dispersión para
datos agrupadas
Rango
Igual que para datos no agrupados, es la diferencia
entre el valor máximo y el mínimo, pero considerado
dentro de las clases agrupadas. Desviación estándar
Es la raíz cuadrada de la varianza. La
fórmula se ajusta similarmente a la
varianza, usando las frecuencias de las
clases.
Coeficiente de variación
Se calcula como la relación entre la desviación
estándar y la media, multiplicado por 100 para
obtener un porcentaje.

6. medidas de dispersión para
datos no agrupadas
Varianza
La fórmula para la varianza en datos
agrupados toma en cuenta la frecuencia de
cada clase:
Donde fif_i es la frecuencia de la clase ii, xix_i
es el punto medio de la clase, xˉbar{x} es la
media, y NN es el número total de datos.
Desviación media
Se calcula como la media de las
desviaciones absolutas de los valores
respecto a la media, ponderada por las
frecuencias de las clases.

7. medidas de distribucion
Forma de la Distribución
La medida de distribución describe cómo se
distribuyen los valores en una muestra o
población.
Simetría
Evalúa si los datos se agrupan
uniformemente alrededor de la media o si
tienen un sesgo hacia valores más altos o
más bajos.
Apuntamiento
Determina si los datos se concentran
cerca de la media o si tienden a estar
más dispersos.

8. Tipos de distribución: simétrica,
asimétrica positiva y asimétrica
negativa
Simétrica
Los valores se
distribuyen de
manera uniforme a
ambos lados de la
media.
Asimétrica Positiva
La mayoría de los valores se
concentran a la izquierda de
la media, con una larga cola
a la derecha.
Asimétrica Negativa
La mayoría de los valores se
concentran a la derecha de
la media, con una larga cola
a la izquierda.

9. Cálculo de la asimetría
Fórmula de Asimetría
La fórmula utilizada para
calcular la asimetría es:
(media - moda) / desviación
estándar.
Interpretación
Un valor de asimetría positivo
indica una distribución
sesgada hacia la derecha,
mientras que uno negativo
indica sesgo hacia la
izquierda.
Magnitud
La magnitud del
coeficiente de
asimetría refleja el
grado de asimetría
de la distribución.

10. Interpretación de la
asimetría
Escala
La asimetría nos indica la ubicación de
los valores más altos o más bajos en la
distribución.
Forma
Una asimetría positiva produce una
cola larga a la derecha, mientras que
una negativa tiene una cola larga a la
izquierda.
Análisis
La asimetría es un indicador
importante para determinar si los
datos siguen una distribución normal.

11. Definición de curtosis
Concentración
La curtosis mide el grado de
concentración de los valores alrededor
de la media de una distribución.
Apuntamiento
Indica si la distribución es más
"picuda" o más "plana" que la
distribución normal.
Colas
La curtosis también refleja la longitud
y el peso de las colas de la
distribución.

12. Cálculo de la curtosis

13. Interpretación de la curtosis
Leptocúrtica
Una distribución leptocúrtica
indica una mayor concentración
de valores cerca de la media, con
colas más pesadas.
Mesocúrtica
Una distribución mesocúrtica,
como la normal, tiene un
apuntamiento y colas
moderados.
Platicúrtica
Una distribución platicúrtica muestra
una menor concentración de valores
cerca de la media, con colas más
ligeras.

14. ejemplos de ejercicios de
simetria

18. recordar

19. ejemplos de ejercicios de
curtosis

22. recordar

23. En estadística, los coeficientes son valores numéricos que representan la relación entre variables
en un modelo matemático o estadístico. Algunos de los coeficientes más comunes son:
1. Coeficiente de correlación (r): Mide la relación entre dos variables. Va de -1 a 1, donde:
1 indica una correlación positiva perfecta.
-1 indica una correlación negativa perfecta.
0 indica que no hay correlación.
2. Coeficiente de determinación (R²): Indica el porcentaje de variabilidad de la variable
dependiente que es explicado por la variable independiente en un modelo de regresión. Un
valor de 1 indica que el modelo explica toda la variabilidad.
3. Coeficientes de regresión: En un modelo de regresión, estos coeficientes muestran el
cambio esperado en la variable dependiente cuando una variable independiente cambia en
una unidad, manteniendo las demás constantes.
4. Coeficiente de variación (CV): Mide la dispersión relativa de los datos en relación con la media.
Es útil para comparar la variabilidad entre diferentes datasets.
CONOCE LOS COEFICIENTES

28. COEFICIENTES DE REGRESIÓN
LÍNEAL

34. There are many forms of informative or explanatory writing that you may be required
to do throughout your schooling or throughout life so it's important to understand the
style, structure and overall purpose of this text type.
All informative texts seek to accurately convey information to a reader with a
primary purpose to increase knowledge.
You should assume that your audience consists of educated, intelligent, nonspecialists
so try to ensure your writing is accurate, specific and clear to have the best chance
of successfully passing on knowledge of your topic.
Good luck and let's get writing!
recap and final advice

35. CORRELACIÓN.

36. La correlación es una medida
estadística que indica el grado de
relación entre dos variables. En
concreto, la correlación lineal sirve
para determinar cuánto de
correlacionadas linealmente están
dos variables distintas. Dos variables
están relacionadas cuando al variar
los valores de una variable también
cambian los valores de la otra
variable. Por ejemplo, si al aumentar la
variable A también aumenta la
variable B, existe una correlación
entre las variables A y B.
¿Qué es la correlación?

37. tipos de
correlación:
Correlación directa (o correlación
positiva): una variable aumenta cuando
la otra también aumenta.
Correlación inversa (o correlación
negativa): cuando una variable
aumenta la otra disminuye, y al revés, si
una variable disminuye la otra aumenta.
Correlación nula (sin correlación): no
existe ninguna relación entre las dos
variables.

38. INTERPRETACIÓN:

39. CORRELACIÓN
LINEAL DE
PEARSON Y DE
SPEARMAN

40. coeficiente de correlación de Pearson
¿Qué es?
El coeficiente de correlación
de Pearson también llamado
coeficiente de correlación
lineal o simplemente
coeficiente de correlación, es
una medida estadística que
indica la relación entre dos
variables.
¿Cómo calcular?
Para calcular el coeficiente de
correlación de Pearson entre
dos variables se debe dividir la
covarianza de dichas variables
por la raíz cuadrada del
producto de sus varianzas.

41. coeficiente de correlación de
spearman
¿Qué es?
Es una medida no paramétrica
de la correlación de rango. Se
utiliza principalmente para el
análisis de datos.
Mide la fuerza y la dirección de
la asociación entre dos
variables clasificadas.
¿Cómo calcular?
Se calcula con la siguiente
fórmula, donde:
n= número de puntos
di= diferencia de rango
⍴, puede ser +1 y -1