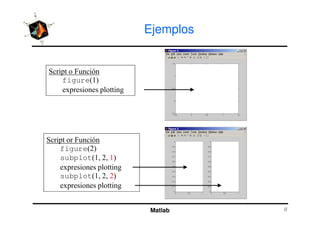
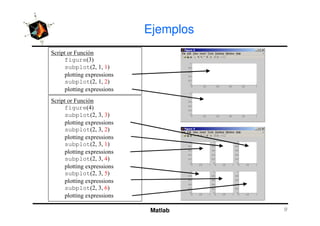
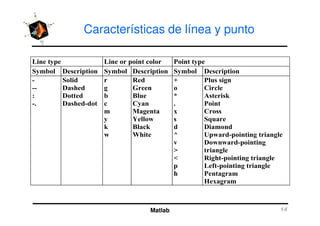
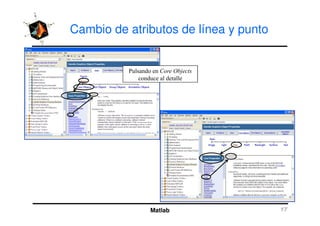
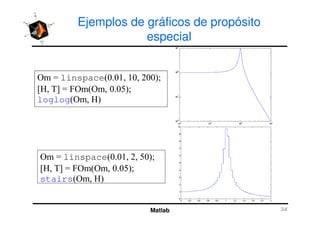
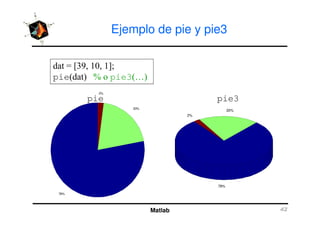
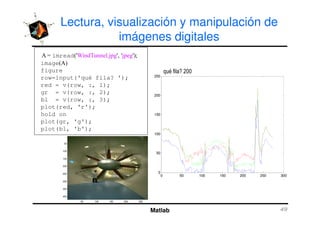
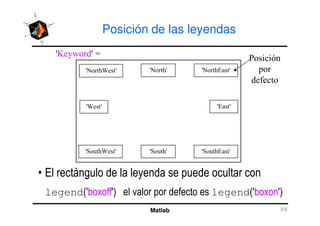
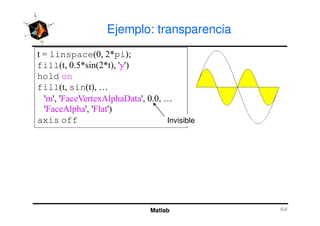
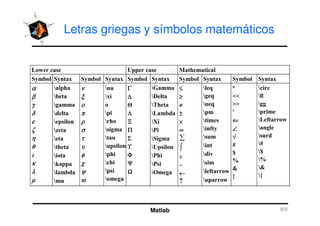
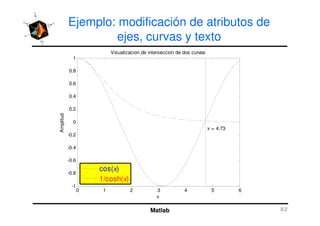
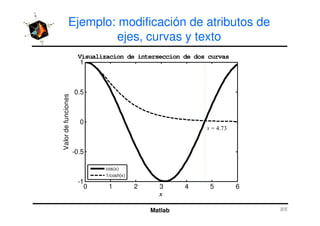
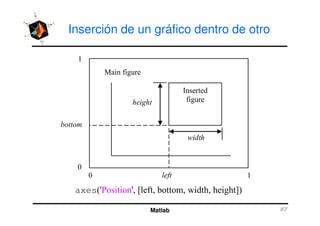
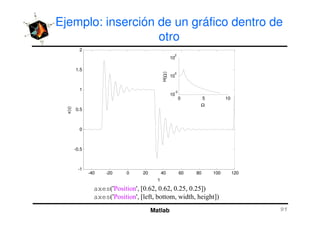
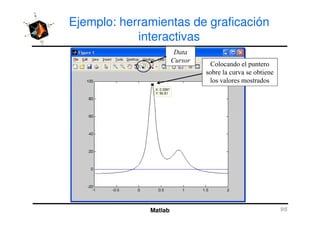
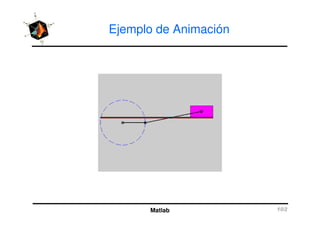
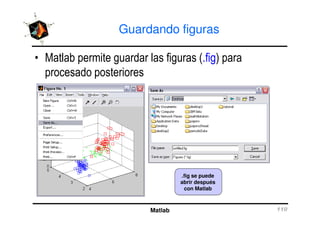
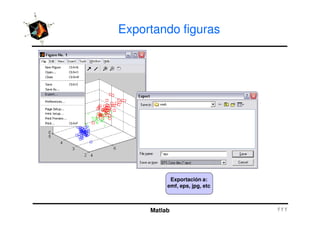
El documento presenta una amplia selección de capacidades para la creación de gráficos en MATLAB, incluyendo comandos básicos de gráficos en 2D y ejemplos prácticos. Además, se detallan mejoras visuales, anotaciones y la visualización de imágenes digitales, así como gráficos de propósito especial como gráficos de pie y gráficos tridimensionales. Se incluye también un índice para facilitar la navegación por los contenidos tratados.