Este documento presenta un resumen de los cambios realizados en la nueva edición de Introducción al Álgebra Lineal. Se realizaron varias modificaciones en la organización de los capítulos y en el contenido para enfatizar las relaciones entre los conceptos clave, suavizar la transición hacia la abstracción, e introducir tempranamente los temas de transformaciones lineales y eigenvalores. También se añadió nuevo material y demostraciones, así como mayor énfasis en la conceptualización y aplicaciones. Se proporcionan dos posibles programas para un























![1.1 Introducción a los sistemas de ecuaciones lineales 1 27
Sumar -1 veces la segunda ecuación a la
primera para obtener
x +yz= 35
y - S z = -17
z = 3
Sumar - 1112 veces la tercera ecuación a la
primera y 7/2 veces la tercera ecuación a la
segunda para obtener
X = 1
y = 2
z ='3
Sumar - 1 veces el segundo renglón al
primero para obtener
0 % ~ 35
Sumar - 1112 veces el tercer rengl6n al
primero y 712 veces el tercer renglón al segundo
para obtener
0 0
La solución
x = l , y = 2 , z = 3
es evidente ahora. A
EJERCICIOS DE LA SECCIóN 1.1
1. De las siguientes ecuaciones, ¿cuáles son lineales en x,, xz y x3?
a) xI + 5x2 - d x 3 = 1 b) xI + 3x2 + x,x3 = 2 C) xi = -7x, + Jx,
d ) xF2 +x+2 8x, = 5 e) x:/' - 2x, + x j = 4 f ) m,- f i x 2 + ;x3 = 7'13
2. Dado que k es una constante, p d e s de las siguientes ecuaciones son lineales?
1
k -
a)x,-xx,+x,=senk b) kxi--x,=9 c) 2kx1+7x2-x3=0
3. Encontrar el conjunto solución de cadau na de las siguientes ecuaciones lineales
a) 7x - 5.v = 3 b) 3x, - 5x2 + 4x3 = 7
C) -8x,+2x2-5x3+6x4=1 d ) 3 ~ - 8 ~ + 2 ~ - ~ + 4 ~ = 0
4. Hallar la matnz aumentada de cada uno de los sigwentes sistemas de ecuaciones lineales.
a) 3x, - 2x, = - 1 b) 2x, + 2x3 = 1 c) X, + 2x2 - x4 + x5 = 1 d) XI = 1
4x, +5x2= 3 3x, - x2 + 4x, = 7 3x2 + x3 -x5=2 x2 =2
7x, +3x2 = 2 6x1 + X, - X, O x3 + 7x4 = 1 xj = 3
a) [: -9 81
5. Determinar un sistema de ecuaciones lineales correspondientae la matriz aumentada.
7 2 1 - 3
1 2 4 0 511 [i i g -:I 0 o 1 4
c, [
[: -: o -2 -;]
5
b) O 0 0
6. a) Encontrar una ecuación lineal en las variables x y y que tenga la solución general x
= 5 + 2 t , y = t .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-24-320.jpg)

![1.2 Eliminación gaussiana / 29
1.2 ELIMINACIÓN GAUSSIANA
En esta sección se dará un procedimiento sistemútico para resolver sistemas de
ecuaciones lineales; el método se basa en la idea de reducir la matriz aumentada
a una forma sujicientemente simple para que el sistema de ecuaciones se pueda
resolver por inspección.
FORMA En el ejemplo 3 de la sección precedente, el sistema lineal se resolvió al reducir la
ESCALONADA matriz aumentada a
REDUCIDA
a partir de lo cual la solución del sistema era evidente. Este es un ejemplo de una
matriz que está en forma escalonada reducida. Para que una matriz sea de esta
forma. debe tener las siguientes propiedades.
1. Si un renglón no consta completamente de ceros, entonces el primer número
diferente de cero en el renglón es un 1. (Que se denomina 1 principal.)
2. Si hay renglones que constan completamente de ceros, se agrupan en la
parte inferior de la matriz.
3. En dos renglones consecutivos cualesquiera que no consten completamente
de ceros, el I principal del renglón inferior aparece más a la derecha que el
1 principal en el renglón superior.
4. Cada columna que contenga un I principal tiene ceros en todas las demás
posiciones.
Se dice que una matriz con las propiedades 1, 2 y 3 (pero no necesariamente con la
propiedad 4) está en forma escalonada.
Ejemplo 1 Las siguientes matrices están en forma escalonada reducida.
[I O O 41 [I O O] [: A -: y I]
o 1 o 7 , 0 1 0 ,
o o 1 - 1
0 0 0 0 0 ’ [: :] O o l o o o o o
Las siguientes matrices están en forma escalonada](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-26-320.jpg)


![317 I/ Sistemas de ecuaciones lineales-v matrices
0 0 - 2 o 7
2 4 - 10 6 12 If] 2 4 -5 6 -5 -1
! Columna de la orilla izquierda diferente de cero
Paso 2. Intercambiar el renglón superior con otro renglón, en caso de ser ne-cesario,
para que en la parte superior de la columna determinada en
el paso 1 haya un elemento diferente de cero.
2 4 -10
o 0 - 2 o 7 1 2 renglones primero y segundo
Paso 3. Si el elemento que está ahora en la parte superior de la columna de-terminada
en el paso l es a, multiplicar el primer renglón por lla a
fin de introducir un 1 principal.
1 2 - 5 3 6
o 0 - 2 o 7 matriz precedente se
2 4 -5 6 -5 - 1
El primer renglón de la
multiplicó por 1/2.
Paso 4. Sumar mdtiplos adecuados del renglón superior a los renglones inferio-res
para queto dos los elementos abajo de1 principal se vuelvan ceros.
1 2 - 5 3
o 0 - 2 o 7 precedente se sumó -2 veces
0 o 5 o -
El primer renglón de la matriz
Paso 5. A continuación, cubrir el renglón superior de la matriz y comenzar
de nuevo con el paso 1 aplicado a la submatriz restante. Continuar de
esta manera hasta que toda la matriz esté en forma escalonada.
1 2 - 5 3
o 0 - 2 0 7
O O 5 O -17 -29
Columna de la orilla izquierda
diferente de cero en la submatriz](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-29-320.jpg)

![34 1 Sistemas de ecuaciones lineales y matrices
OBSERVACI~N. Se puede demostrar que toda matriz tiene una forma esca-lonada
reducida única; es decir, se obtiene la misma forma escalonada reducida
de una matriz dada sin importar cómo se hagan variar las operaciones en los
renglones. (Una demostración de este hecho puede consultarse en el artículo "The
Reduced Row Echelon Form of a Matrix is Unique: A Simple Prooy, de Thomas
Yuster, Mathematics Magazine, Vol. 57, No. 2, 1984, págs. 93 -94.) En contraste,
una forma escalonada de una matriz dada no es única: diferentes secuencias de
operaciones enl os renglones pueden producir formas escalonadasd iferentes.
Ejemplo 3 Resolver por eliminación de Gauss-Jordan
X] + 3x, - 2x, + 2x, = o
2x, + 6x2 - 5x3 - 2x4 + 4x5 - 3x6 = - 1
5x, + lox, + 15x, = 5
2x, + 6x2 + 8x, + 4x, + 18x, = 6
*Karl Friedrich Gauss (1777-1855) fue un matemático y científico alemán. Algunas veces
nombrado "príncipe de los matemáticos", Gauss es considerado junto con Isaac Newton y
Arquimedes como uno de los tres más grandes matemáticos que han existido. En toda la historia de
las matemáticas quizá nunca ha habido un niño tan precoz como Gauss: según cuenta éI mismo, ya
dominaba las bases de las matemáticas aún antes de poder hablar. Un dia, cuando aún no tenia tres
años de edad, su genio se manifestó a sus padres de manera bastante elocuente. Su padre estaba
preparando la nómina semanal de los obreros a su cargo mientras el niño lo observaba en silencio
desde un rincón de la habitación. AI final de los cálculos largos y tediosos, Gauss dijo a su padre
que había un error en el resultado y le dijo la respuesta, a la que había llegado mentalmente. Para
sorpresa de sus padres, jal comprobar los cálculos se dieron cuenta de que Gauss tenía razón!
En su disertación doctoral, Gauss proporcionó la primera demostración completa del teorema
fundamental del álgebra, que establece que toda ecuación polinómica tiene cuando mucho.tantas
soluciones como su grado. A los 19 años de edad resolvió un problema que desconcertó a Euclides:
inscribir un polígono regular de 17 lados en una circunferencia usando sólo regla y transportador; y
en 1801, a los 24 años de edad, publicó su primera obra maestra, Disqursrfrones Anfhrnetrcae,
consrderada por muchos como uno de los logros más brillantes en matemáticas. En este documento,
Gauss sistematizó el estudio de la teoría de números (propiedades de los enteros) y formuló los
conceptos básicos que constituyen los cimientos de ese tema.
Entre la multitud de logros alcanzados, Gauss descubrió la curva "acampanada" o gaussiana que
es fundamental en probabilidad, proporcionó la primera interpretación geométrica de los números
complejos y estableció el papel fundamental de éstos en las matemáticas, desarrolló métodos para
caracterizar superficies intrínsecamentep or medio de las curvas contenidase n aquéllas, desarrolló la
teoría del mapeo conforme (que preserva ángulos) y descubrió la geometría no euclidiana 30 años
antes de que estas ideas fueran publicadas por otros. En fisica realizó contribuciones esenciales a la
teoría de las lentes y a la acción capilar, y junto con Wilhelm Weber realizó trabajo fundamenteanl
electromagnetismo, Gauss inventó el heliotropo, el magnetómetro bifilar y el electrotelegrafo.
Gauss era profundamente religioso y se comportaba como aristócrata. Dominaba fácilmente
otros idiomas, leia bastante y disfrutaba la mineralogia y la botánica como pasatiempos. No le
agradaba dar clases y solía ser frío y poco alentador con otros matemáticos, quizá porque ya había
anticipado el trabajo de éstos. Se hafirmado que si Gauss hubiera publicado todos sus
descubrimientos, el estado actual de las matemáticas habría avanzado 50 años. Sin duda alguna es el
matemático más grande de la epoca moderna.
Wilhelm Jordun (1842-1899) fue un matemático alemán que se especializó en geodesia. Su
contribución a la resolución de sistemas lineales apareció en su libro conocido, Handbuch der
I'errnessungskunde, en 1888.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-31-320.jpg)



![38 ,/ Sistemas de ecuaciones lineales y matrices
a la forma escalonada
[; 1 2 9 -f -y]
El sistema corresponhente eas ta matriz es
x + y + 22= 9
- 2, = -17
2
z = 3
Al despejar las variables principales se obtiene
La sustitución de la ecuacióni nferior en las ecuaciones anteriores da
x = 3 - y
y = 2
z = 3
y la sustitución de la segunda ecuación en la ecuaciósnu perior se obtiene
x= 1
y = 2
z = 3
Esto concuerda con el resultado que se encontró mediante la eliminación de
Gauss-Jordan en el ejemplo 3 de la sección l. l. A
SISTEMAS Se dice que un sistema de ecuaciones lineales es homogéneo si todos los término:
LINEALES constantes son cero; es decir, el sistema es de la forma
HOMOGÉNEOS
a I l x , + ai2x2 + . . . + a,,x, = O
u2,x, + a22x2 + . . . + u2,x, = O
amlxl + am2x2 + . . . + amnx, = O
Todo sistema de ecuaciones lineales homogéneo es consistente, ya que UM
solución de todos estos sistemas es x1 = O, xz = O, . . . , xn = O. Esta solución se
denomina solución trivial; en caso de que haya otras soluciones, se denominan
soluciones no triviales.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-35-320.jpg)



![a ) O l O [: :] b) 1 "1 c) [: 1 y] d) [A 0" f]
42 / Sistemas de ecuaciones lineales y matrices
[" "1 O 0 :] 0 [: O 0 0 '1 [: O 0 0
I :]
f ) l O O g)[: hj i) 0 0 0 O 0 0 O 0 0 O 0 0
2. De las siguientes matnces 3 x 3, ¿cuáles están en forma escalonada? a ) [l O l O
:] "1 [i f b)[i O 0 0 c) O 2 0 d)
1 3 4
0 0 1
-0 o o
3. En cada inciso, determinar si la matriz está en forma escalonada, en forma escalonada
reducida, en ambas formaso en ninguna.
1 2 0 3 0
p '1
a )[O O oO O O OI] b ) [ i c j [ 'o 1o 2 4 0 0 0 0 0
[' '1 [' 1 3 0 2 0
* [i i] dl o -71 3 2 e) o O] f) O 0 0 0 1
0 0 0 0 0
4. En cada inciso, suponer que la matriz aumentada de un sistema de ecuaciones lineales
ha sido reducida mediante operaciones en los renglones a la forma escalonada re-ducida
dada. Resolver el sistema.
1 o 0 - 3 I o 0 - 7 8
,)[O
;] [i -: x 1 - 6 O O 3 - 2
81 O 0 1 0 4 d) O 0 0 1 5
~ 0 0 0 0 0 0
1 O 3 2
o o 1 1 - 5
5. En cada inciso, suponer que la matriz aumentada de un sistema de ecuaciones lineales
ha sido reducida mediante operaciones en los renglones a la forma escalonada dada.
Resolver el sistema.
01 -31 42 q
0 0 1 s 2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-39-320.jpg)


![46 / Sistemas de ecuaciones lineales y matrices
27. Describir las posibles formas escalonadas rqiucidas de
28. Demostrar que si ad - bc f O, entonces la forma escalonada reducida de
29. Usar el ejercicio 28 para demostrar que si ad - bc = O, entonces el sistema
ux + b ~=, k
CY + dv = I
tiene exactamente una solución
30. tlrsolvzr el sistema
para x,, x2 y xj SI
a) k= 1 b) d = 2
31. Considerar el sistema de ecuaciones
ux + bj. = o
C.Y + 41) = o
a) Demostrar que si x = xo, y = y, es cualquier solución del sistema y k es cualquier
constante, entonces x = kr,, y = 4, también es una solución.
b) Demostrar que si x = xo, y = y, y x = x], y = y, son dos soluciones cualesquiera,
entonces x = x. + x,, y =y o +yta,m bién es una solución.
32. Considerar el sistema de ecuaciones
(1) u .+~ b ,, = k (11) ax + by = O
C.Y + dl) = I cx + 4v = o
a) Demostrar que si x = x,, y = y , y x = x*, y = y, son soluciones de I, entonces x = x1
- x2,y =yI - y, es una solución de I I .
de I I , entonces x = x, + x,, y =y , +yeos una solución deI .
b) Demostrar que si x = x], y = y, es una solución de I y x = x,, y = y, es una solución
33. a) En el sistema de ecuaciones numerado con ( 3 ) , explicar por qué sería incorrecto
denotar a las variables principales por xl, x2, , . . , xr en vez de por xk,, xk2, . . . , xk,
como se hizo.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-43-320.jpg)


![1.3 Matrices y operaciones con matrices / 49
Figura 1
Una matriz A con n renglones y n columnas se denomina matriz cuadrada
de orden n,-y se hce que los elementos all, a22, . . . , ann están en la diagonal
principal de A (véanse los elementos en tipo negro en la figura 1).
OPERACIONES Hasta el momento, las matrices se han usado para abreviar el trabajo al resolver
CON MATRICES sistemas de ecuaciones lineales. Para otras aplicaciones, sin embargo, es deseable
desarrollar una "aritmética de matrices" en la que sea posible sumar, restar y mul-tiplicar
matrices de manera útil. El resto de esta sección se dedicará al desarrollo
de esa aritmética.
Definición. Dos matrices son iguales si tienen el mismo tamaño y sus ele-mentos
correspondientes soni guales.
En notación matricial, si A = [a,] y [B = b, ] son del mismo tamaño, entonces A =
B si y sólo si (A), = (B), o, equivalentemente, a, = bo para todo i y j .
Ejemplo 2 Considerar las matrices
Si x = 5, entonces A = B, pero para los demás valores de x las matrices A y B
no son iguales. ya que no todos sus elementos correspondientes son iguales.
No hay ningún valor de x para el que A = C, ya que los tamaños de A y C son
diferentes. A
correspondientes de A, y la diferencia A - B es la matriz obtenida al restar los
elementos de B de los elementos correspondientes de A. No es posible sumar o
restar matrices de tamaños diferentes.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-46-320.jpg)
![7 ' P "*I 6 .,*< r : , : 'i - , ~ . . ,
50 Sistemas de ecuaciones lineales v matrices
En notación matricial, si A = [au] y B = [bJ son del mismo tamaño, entonces
2 1 0 -4 3 5
- 1 O 2 '1 B = [ 2 2 O -:] C = [ ' '1
4 - 2 7 o 3 2 - 4 5 2 2
Ejemplo 3 Considerar las matrices
Entonces
11 -5
Las expresiones A + c', B + C', A - C y B - C no están definidas. A
Definición. Si A es cualquier matriz y c es cualquier escalar, entonces el
producto cA es la matriz obtenidaa l multiplicar cada elemento deA por c.
En notación matricial, si A = [a 1, entonces
r/
cA)ij = c(A),, = cui,
Ejemplo 4 Para las matrices
A = [ 1 3 I ] B = [ - 1 3 - 57 1 c=[ : -r, 2 3 4 o 2
se tiene
Es común denotar (- l)B por -B. A
Si A,, A,, . . . , A,, son matrices del mismo tamaño y cl, c,, . . . , c,, son
escalares. entonces una expresión dlea forma
se denomina combinación lineal de A , , A,, . . . , A,, con coeficientes cl, c2, . . . ,
e,,. Por ejemplo, si A, B y C son las matrices del ejemplo 4, entonces](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-47-320.jpg)

![El elemento en el renglón 1 y eyi In columna 4 de AB (en negro) se calcula como sigue.
l(1.3) + (2.1) + (4.2) = 131
Los cálculos para los demás productos son
(1 '4) + (2.0) + (4.2) = 12
( 1 . 1 ) - ( 2 . 1 ) + ( 4 . 7 ) = 27
( 1 . 4 ) + ( 2 . 3 ) + ( 4 . 5 ) = 30 12 27 30
(2.4) + (6.0) +- (0.2) = 8 8 -4 26 12
(2. 1) - (6.1) + (0.7) = -4
(2.3) + (6.1) + (0.2) = 12 A
131
Para formar el producto AB, la definición de multiplicación de matrices
requiere que el número de columnas del primer factor A sea el mismo que el
número de renglones del segundo factor B. Si no se cumple esta condición.
entonces el producto está indefinido. Una manera conveniente para determinar si
el producto de dos matrices está definido es escribir el tamaño del primer factor y,
a la derecha, escribir el tamaño del segundo factor. Si, como se observa en la
figura 2, los números interiores son iguales, entonces el producto está definido.
Los númcros exteriores proporcionan entonces el tamaño del producto.
A H AB - m x r r x n m x n
b A h S
Medios
Figura 2 Extremos
Ejemplo 6 Suponer que A, B y C son matrices con los siguientes tamaños:
A R C
3 x 4 4x7 7 x 3
Entonces AB está definido y se trata de una matriz 3 x 7; CA está definido y se
trata de una matriz 7 X 4; y BC está definido y se trata de una matriz 4 x 3. Los
productos AC, CB y BA están indefinidos.
Si A = [u,] es una matriz general m x r y B = [b,] es una matriz general Y X
n, entonces como se ilustra con tipo negro de la figura 3, el elemento (AB)v en el
renglón i y la columna j de AB está definido por](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-49-320.jpg)
![1.3 Matrices y operaciones con matrices / 53
PARTICI~ND E
MATRICES
AB =
Figura 3
MULTIPLICA-CIóN
DE
MATRICES
POR COLUMNAS
Y POR
RENGLONES
Una matriz se puede subdividir o partir en matrices más pequeñas insertando
rectas horizontales y verticales entre renglones y columnas selectos. Por ejemplo,
a continuación se muestran tres posibles particiones de una matriz general A 3 X
4: la primera es una partición de A en cuatro submatrices A 1, A 12, A, y A,2; la
segunda es una partición de A en sus matrices renglón rl, r2, r3 y r4; y la tercera
es una partición deA en sus matrices columna cl, c,, c3 y c4:
[ ::: ' I 2 '13 ' 1 4
[ii: A = """""""""_ u22 u23 u24=] 'I2]
A22
1: '31 ' 3 2 ' 3 3 ' 3 4
~ [ill """""""_""
a12 u13 '14
A = u22 a23 = _"""""""""
'31 '32 '33 a34
Algunas veces es necesario encontrar un renglón o una columna particulares de
un producto AB de matrices sin calcular todo el producto. Los siguientes
resultados, cuyas demostraciones se dejan como ejercicios, son útiles para este
propósito:
j-ésima matriz columna dAe B = A b-ésima matriz columna deB ] (3 1
1 i-ésima matriz renglón de AB = (i-ésima matriz renglón de1; 3 B
I.".
Ejemplo 7 Si '4 y B son las matrices del ejemplo 5, entrnces por (3) la segunda
matriz columna de AB se puede obtener al calcular](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-50-320.jpg)

![1.3 Matrices y operaciones con matrices / 55
En palabras, la fórmula (7) establece que el producto Ax de una matriz A y una
matriz columna x es una combinación lineal de las matrices columna de A con los
coejicientes que provienen de la matriz x. En los ejercicios de la sección se pide al
lector demostrar que el producto yA de una matriz y 1 X m y una matriz A m X n
es una combinación lineal de las matrices renglón de A con coejcientes escalares
que provienen de y.
Ejemplo 8 El producto matricial
se puede escribir como la combinación lineal 2[-i]-1
y el producto matricial
[ I -9 -3][-/ -:] = 1 - 1 6 8 351
-2
se puede escribir como la combinación lineal
1[-1 3 2 1 - 9 [ 1 2 - 3 1 - 3 [ 2 1 - 2 ] = [ - 1 6 - 1 8 351 A
Por (5) y (7) se concluye que la j-ésima matriz columna de un producto AB es
una combinación lineal de las matrices columna de A con los coeficientes que
provienen de la j-ésima columna de B.
Ejemplo 9 En el ejemplo 5 se demostró que
AB= 2 411[
4 1 4 3 -
0 - 1 3 1
2 6 0 2 7 5 2-
Las matrices columna de AB se pueden expresar como combinaciones lineales de las
matrices columna de A en la forma siguiente:
['E] = 4 [ ; ] + 0 [ ; ] + 2 [ $](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-52-320.jpg)

![l. 3 Matrices y operaciones con matrices / 5 7
TRANSPUESTA Esta sección termina con la definición de dos operaciones matriciales que carecen
DE UNA MATRIZ de análogo en los números reales.
Definición. Si A es cualquier matriz m X n, entonces la transpuesta de A,
denotada por AT, se define como la matriz n X m que se obtiene al intercambiar
los renglones y las columnas de A; es decir, la primera columna de AT es el
primer renglón de A, la segunda columna de AT del segundo renglón de A, y así
sucesivamente.
Figura 4
Ejemplo 10 A continuación se presentan algunos ejemplos de matrices y sus
transpuestas.
;;; '12 ;;; '13 ;'14 J:] 2 i] 3
A = [ : ! : B = [ t C=[l 3 51 0 = [ 4 1
Observar no sólo que las columnas de AT son los renglones de A, sino que
los renglones de AT son las columnas de A . Así, el elemento en el renglón i y la
columnaj de A es el elemento en el renglónj y la columna i de A, es decir,
Observar la inversión de los subindices.
En el caso especial en que A es una matriz cuadrada, la transpuesta de A se
puede obtener al intercambiar los elementos simétricos con respecto a la diagonal
principal (figura 4). Planteado de otra forma, AT se puede obtener "reflejando" A
con respecto a su diagonal principal.
1 "2 4 - 1 - -2 4 1 3 -5
>.. ,f
simétricos con respecto a la](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-54-320.jpg)
![58 :' Sistemas de ecuaciones lineales y matrices
TRAZA DE UNA
MATRIZ
Definición. Si A es una matriz cuadrada, entonces la truzu de A, denotada por
tr(A), se define como la suma de los elementos de la diagonal principal de A. La
CUADRADA traza de A no está definida si A no es una matriz cuadrada.
Ejemplo 11 A continuación se presentan algunos ejemplos de matrices y sus
trazas.
2 7 0
-2 I tr(A)=a,,+a,,+a,, I Itr(B)= - 1 + 5 + 7 + 0 = 1 1 J A
EJERCICIOS DE LA SECCIÓN 1.3
1. Suponer que A, B, C, D yF son matrices de los tamaiios siguientes:
A B C D E
(4 x 5) (4 x 5 ) (5 x 2) (4 x 2) (5 x 4)
Determinar cuáles de las siguientes expresiones de matnces están definidas. Para las
que estén definidas, proporcionar el tamaño de la matriz resultante.
a) BA bjAC+D c ) . 4 E + B d).4B+B
e) E(A + B) f) E(AC) g) ETA h) (A + E)D
/ 2. Resolver la siguiente ecuación matricial para a, b, c y d.
-[ 3 ad-+b2c a - 4"d c ] = [ ; A] 3. Considerar las matrices.
Calcular lo siguiente (en caso de ser posible)
a) D + E b ) D - E c) 5A d) -7C
e) 2B-C f) 4 E - 2 D g) -3(0 + 2E) h) A - A
i) tr(D) j) tr(D - 3E) k) 4 tr(7B) 1) ' tr(A)
4. Con las matrices del ejercicio3 , calcular lo siguiente (en caso de ser posible)
a) U'+ C b) DT- E' c) (D- E)' d) BT + 5C7
e) $ C ' - ~ A f) B-B' g) 2ET - 30' h) (2ET - 30')'
5. Usar las matrices del ejercicio 3 para calcular lo siguiente (en caso de ser posible).
a) AB b) BA c) (3E)D d) (AWC
e) A W ) f ) cc' g) (DA)' h) (C 'B)A '
i) tr(DD') j) tr(4ET - D) k) tr(CTAT+ 2E')
6 1 3
- 1 1 2
4 1 3](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-55-320.jpg)


![1.4 Inversas; reglas de la aritmética de matrices / 61
18. a) Demostrar que si A contiene un renglón de ceros y B es cualquier matriz para la que
AB está definido, entonces AB también contiene un renglón de ceros.
b) Encontrar un resultado semejante, pero respectoa una columna de ceros.
19. Sea A cualquier matriz m X n y sea O la matriz m X n, cada uno de cuyos elemento es
cero. Demostrar que si kA = O, entonces k = O o A = O.
20. Sea I la matriz n X n cuyo elemento en el renglóni y en la columnaj es
Demostrar que AI = IA = A para toda matriz A n X n
21. En cada inciso, encontrar una matriz [u.] 6 X 6 que cumpla la condición que se
'J
establece. Hacer que las respuestas sean lo más generales posible usando letras en vez
de números específicos para denotarlo s elementos diferentes de cero.
22. Encontrar una matriz A = [ulJ de 4 X 4 cuyos elementos cumplan la condición que se
23. Demostrar lo siguiente: Si A es una matriz m X n, entonces
donde S es la suma de los cuadrados dloes elementos de A
24. Usando el resultado del ejercicio2 3, demostrar lo siguiente.
a) Si A es una matriz m X n tal quemT = O O ATA = O, entonces A = O.
b) Si A es una matriz n X n tal que A = AT y A2 = O, entonces A = O.
I .4 INVERSAS; REGLAS DE LA ARITMÉTICA DE MATRICES
En esta sección se analizarán algunas propiedades de las operaciones aritméticas
sobre matrices. Se verá que muchas de las reglas básicas de la aritmética de los
números reales también se cumplen para matrices, aunque unas cuantnaos.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-58-320.jpg)

![1.4 Inversas; reglas de la aritmética de matrices / 63
patrón general. Como ilustración, se demostrará el inciso 6). La demostración de
la ley asociativa, que es más complicada, se esboza en los ejercicios.
Demostración de d). Es necesario demostrar que A(B + C) y AB + AC son del
mismo tamaño y que los elementos correspondientes son iguales. Para formar A(B
+ C), las matrices B y C deben ser del mismo tamaño, por ejemplo m x n, y
entonces la matriz A debe tener m columnas, de modo que su tamaño debe ser de
la forma r x m. Con lo anterior, se tiene que A(B + C) es una matriz r X n. Se
concluye que AB + A C también es una matriz r X n y, en consecuencia, A(B + C)
y AB + AC son del mismo tamaño.
Suponer que A = [a,], B = [bu] y C = [c,]. Se quiere demostrar que los
elementos correspondientesd e A(B + C) y AB + AC son iguales; es decir, que
[A(B + C ) ] , = [AB + AC I;,
para todos los valores de i y j . Pero por las definiciones de adición y multiplicación
de matrices se tiene
[A(B+ C)];, = a,,(bl,+ cl,) + a,2(b2j+ c2,) + . . . + aim(bm+j cm,)
= (a,,b,, + a,2b2,+ . . . + aimb,,) + (aj l c ,+, U , ~ C+~ ., . . + a,,cmj)
= [AB],, + [AC,,] = [AB + AC I,, u
OBSERVACI~N. Aunque las operaciones de adición y multiplicación de matrices
se definieron para pares de matrices, las leyes asociativas 6) y c) permiten denotar
sumas y productos de tres matrices como A + B + C y ABC sin introducir ningún
paréntesis. Lo anterior se justifica por el hecho de que sin importar cómo se
introducen paréntesis, las leyes asociativas garantizan la obtención del mismo
resultado final. En general, dados cualquier suma o producto de matrices, en las
expresiones se pueden introducir o eliminar pares de paréntesis sin afectar el
resultadojnal.
Ejemplo 2 Como ilustración de la ley asociativa de la multiplicación de matrices,
considerar
Entonces
. . ..](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-60-320.jpg)

![1.4 Inversas; reglas de la aritmética de matrices / 65
Aquí
3 4
AB=,AC= [6 8]
Aunque A # O, es incorrecto cancelar la A en ambos miembros de la ecuación AB
= AC y escribir B = C. Así, la ley de cancelación no se cumple para matrices.
También, AD = O, aunqueA # O y D # O. A
A pesar del ejemplo anterior, existen varias propiedades conocidas de número
real O que se cumplen en las matrices cero. Algunas de las más importantes se
resumen en el siguiente teorema. Las demostraciones e dejan como ejercicio.
Teorema 1.4.2. Si se supone que los tamaAos de las matrices son tales que es
posible efectuar las operaciones que se indican, las siguientes reglas de
aritmética matricial son válidas.
a) A + U = O + A = A
6 ) A - A - O
C) O P A = -A
d) AO= O; OA = O
MATRICES De especial interés son las matrices cuadradas que tienen unos en la diagonal
IDENTIDAD principal y ceros fuera de ésta, como
Una matriz de esta forma se denomina matriz identidady se denota por f. Si es
importante recalcar el tamaño, se escribirá In para denotar la matriz identidad n X n .
Si A es una matriz m X n, entonces, como se ilustra en el siguiente ejemplo,
Así, en aritmética matricial la matriz identidad juega un papel bastante semejante
al que desempeña el número 1 en las relaciones numéricas a ' 1 = 1 . a = a.
Ejemplo 4 Considerar la matriz
Entonces](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-62-320.jpg)


![La inversa de .-1 t i e x cn aritmCtica matricial casi la misma función que cl
recíproco a.-i juega en las relaciones numericas aa-l = 1 y a-"a = 1.
En la siguiente sección se desarrollará m método para determinar inversas de
xnatriccs jnvertibles dc cualquier tamafio; sin embargo, el siguiente teorema
establece condiciones bajo las cuales una matriz 2 X 2 es invertible y proporciona
una fórmula sencilla para cncontrar la inversa.
f O. er? cuyo cuso la Inversa está definida por la
Ud - bc
U
Demostracidn. Se deja para el lector la comprobación de que .M " = I, y A -'A
Teorema 1.4.6. Si A y R son tnatrices invertibles del mismo tamaño, entonces
a) AB es znverlible,
b) (AB)" = 8",4 -1,
Demostración. Si se puede demostrar que (AB)(B"A ") = (N"'A ")(AB) = I,
entonces se habrá demostrado simultáneamente que la matriz AB es invertible y
que (AB) - ] = 5"~". Pero (AR)(B"A-') = A ( B B - ~ ~ "= AIA " =AA" = I.
Con un razonamiento semejante se demuestra que (B"A")(AH) = 1.
Aunque este resultado no se demostrará, se puede extender para incluir tres o
más factores: es decir.
Un producto de cualqurer número de matrices invertibles es invertible, y la
inversa del producto es el producto de las inversas en orden invertido.
Ejemplo 7 Considerar las matnces](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-65-320.jpg)



![I2 ,/ Sistemas de ecuaciones lineales y matrices
Lo anterior, junto con (3), demuestra (2). 0
Aunque no se demostrara este hecho, el inciso 6) del teorema se puede
extender para incluir tres o más factores; es decir,
I La transpuesta de un producto de cualquier número de matrices es igual al
producto de sus transpuestas en orden invertido.
OBSERVACI~N. Nótese la semejanza entre este resultado y el resultado, que está
a continuación del teorema 1.4.6, respecto a la inversa de un producto de matrices.
INVERTIBILIDAD El siguiente teorema establece una relación entre la inversa de una matriz in-
DE UNA vertible y la inversa de su transpuesta.
TRANSPUESTA 1 Teorema 1.4.10. Si A es una matriz invertible, entonces AT también es inver- I
Demostración. Se puede probar la invertibilidad de AT y obtener (4) al
demostrar que
A 7 ' ( . + - l ) T = ( . + - * ) T A T = ]
Pero por el inciso d) del teorema 1.4.9 y el hecho de que IT = Z, se tiene
con lo que se completa la demostración. 11
Ejemplo 10 Considerar las matrices
Al aplicar el teorema 1.4.5 se obtiene](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-69-320.jpg)
![. .
.,a *'
,
1.4 Inversas; reglas de la aritmética de matrices / 73
Como garantiza el teorema 1.4.10, estas matrices satisfacen la fórmula (4). A
EJERClCIOS DE LA SECCIóN 1.4
1. Sean
2 -1 ; i], --; 3 a], - o -2 t], 3
A = [ - ; B = [ : C = [ : u=4, h= -7
Demostrar que
a) A + (B + C) = (A + B) +- C b) (AB)C = A(BC) c) (U + h)C = UC + bC
d) u(B - C) UB - UC
2. Usando las matrices y los escalares del ejercicio I , demostrar que
a) a(BC) = (uB)C= B(uC) b) A(B - C) = AB - AC C) (B + C)A = EA + CA
d) u(bC) = (ub)C
3. Usando las matrices y los escalares del ejercicio 1, demostrar que
a) A b) ( A + B ) 7 = A r + B T c) ( U C ) ~ = U C ~d ) ( A B ) 7 = B 7 A 7
4. Usar el teorema 1.4.5 para calcular las inversas de las sguientes matrices
5. Comprobar que las tres matrices A, B y C del ejercicio 4 satisfacen las relaciones
(AB)" = B"A" y (fit)" = C"B"A"
6. Sean A y B matrices cuadradas del mismo tamaño. = A2B2 es una igualdad ma-tricial
válida? Justificar la respuesta
7. En cada inciso, usar la información dada para encontraAr .
/ 8. SeaA la matriz [: Y]
Calcular A3, A-3 y A' - 2A + I.
1 9 . Sea A la matriz
[: :I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-70-320.jpg)
![224526
74 í Sistemas de ecuaciones lineales y matrices
En cada inciso, determinar p(A).
a) p(x) =x -2 b) p(x) = 2x2 -x + 1 c) p(x) = x3 -2x + 4
10. Seanpl(x) =x2 - 9,p,(x) =x + 3 yp,(x) = x - 3.
a) Demostrar quep , (A)= p,(Alp,(A) para la matrizA del ejercicio9 .
b) Demostrar quep , (A)= p,(A)p,(A) para cualquier matriz cuadradAa
./ 11. Encontrar la inversa de r --ecno s*0 cos 0
12. a) Encontrar matnces A y B 2 X 2 tales que (A + B)' # A2 + 2AB + B2.
b) Demostrar que si '4 y B son matrices cuadradas tales que AB = BA, entonces
('4 + B)2 = A' + 2ilB + B'
c) Encontrar un desarrollo de (A + B)' que sea válido para todas las matrices cuadra-das
.4 = '" "7 y " '
A y B del mismo tamaño.
13. Considerar la matriz
o o " '
o o . ' ' ann
donde a,l a22- . . annf O. Demostrar que' 1 es invertible y encontrar su inversa
14. Demostrar que si una matriz cuadrada A satisface ,43 - 311 + I = O, entonces A" = 31
- A.
15. a) Demostrar que una matnz con un renglón de ceros no puede tener inversa.
b) Demostrar que una matrizc on una columna de cerosn o puede tener inversa.
16. La suma de dos matrices invertibles, ¿necesariamente es invertible?
17. Sean A y B matrices cuadradas tales que AB = O. Demostrar que si A es invertible,
entonces B = O.
18. En el teorema 1.4.2, ¿por qué el inciso d) no se escribió como AO = O = OA?
19. La ecuación real a' = 1 tiene exactamente dos soluciones. Encontrar por lo menos ocho
matrices diferentes 3 X 3 que cumplan la ecuación matricial A2 = I,. [Sugerencia
Buscar soluciones en las que todos los elementos fuera de la diagonal principal sean
iguales a cero.]
20. a) Encontrar una matnz A 3 X 3 diferente de cero tal que A T = A.
b) Encontrar una matriz A 3 X 3 diferente de cero tal que AT = -A.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-71-320.jpg)
![21. Una matriz cuadrada A se denomina simétrica si AT = A y antisimétrica es AT = -A
Demostrar que si B es una matriz cuadrada, entonces
a) B B y~ B + B~ son simétricas.b ) B - BT esa ntisimétrica.
22. Si A es una matriz cuadrada y n es un entero positivo, ¿,es cierto que (A")T = (A')"?
Justificar la respuesta.
23. Sea A la matriz
Determinar si A es invertible y, en caso afirmativo, encontrar su inversa. ISugerencia
Resolver AX = I igualando los elementos correspondientes de ambos miembros.]
24. Demostrar lo siguiente:
a) Inciso b) del teorema 1.4. l . b) Inciso i) del teorema 1.4. l . c) Inciso m) del teore-ma
1.4.1.
25. Aplicar los incisos d) y m) del teorema 1.4.1 a las matrices A, B y (- 1)(' para obtener
el resultado del incison.
26. Demostrar el teorema 1.4.2
27. Considerar las leyes de los exponentesA rAS= A r f S y (A')" = A"".
a) Demostrar que si .4 es cualquier matriz cuadrada, entonces estas leyes son váliGas
b) Demostrar que si A es invertible, entonces estas leyes son válidas para todos los
para todos los valores enteros no negativos dr ey s.
valores enteros negativos der y s.
28. Demostrar que si A es invertible y k es cualquier escalar diferente de cero, entonces
(M)" = PA" para todos los valores enteros de n.
29. a) Demostrar que SI ,4 es invertible y AB = AC, entonces B = C.
b) Explicar por quC el inciso a) y el ejemplo 3 no se contradicen entre sí. I
30. Demostrar el inciso c) del teorema 1.4. l. [Sugerencia Suponer que A es m X n, que B
es n X p y que C es p X q. El 9-ésimo elemento en el miembro izquierdo es 111 = all
BC + u12 BC + . ' ' + alnB C ~y, e,l q -ésimo elemento en el miembro derecho es r
= ~ ~ l ~ , ~ + i l B ~ z c ~ + .~Co.m.pr+obAaBrq~uer1 = r 1 11
P PJ u 11
1.5 MATRICES ELEMENTALES Y UN MÉTODO PARA DETERMINAR A-'
En esta sección se obtendrá un algoritmo para determinar la inversa de una
matriz invertible y se analizarán algunas propiedades básicas de las matrices in-vertibles.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-72-320.jpg)
![76 / Sistemas de ecuaciones lineales y matrices
Definición. Una matriz 11 X n se denomina matriz elemental si se puede obtener
en los renglones.
MATRICES
ELEMENTALES a partir de la matriz identidad In n X n al efectuar una sola operación elemental
con que se obtuvieron. [; O 0 1 0
Ejemplo 1 A continuación se muestran cuatro matrices elementales y las opera-ciones
- 3 el segundo renglones segundo y
renglón de /? ] SumarF 3 veces el tercIeMr ultiplicaEr por ]
Cuando una matriz A se multiplica por la izquierda por una matriz elemental E,
el efecto es efectuar una operación elemental enl os renglones deA . Este es el contenido
del siguiente teorema, cuya demostración se dceojarn o ejercicio para el lector.
Teorema 1.5.1. S i la matriz elemental E resulta de la ejecución de ciertas
operaciones en los renglones de I,,, y si A es una matriz m x n, entonces el
producto EA es la matriz que se obtiene cuando la misma operación en los
renglones se efectúa en .1.
Ejemplo 2 Considerar la matriz
1 0 2
A = [ 2 - 1 3
1 4 4
y considerar la matriz elemental
1 0 0
3 o 1
que resulta al sumar 3 veces el primer renglón de I3 al tercero. El producto E4 es
I 1 0
EA= 2 -1
4 4 1 0 9](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-73-320.jpg)
![1.5 Matrices elementules,v un método pura determinar A” / 77
que es precisamente la misma matriz que se obtiene al sumar 3 veces el primer
renglón de A al tercer renglón. A
Si una operación elemental en los renglones se ejecuta en una matriz ele-mental
I para obtener una matriz elemental E, entonces existe una segunda ope-ración
en los renglones que, al ser efectuada en E, produce nuevamente I. Por
ejemplo, si E se obtiene al multiplicar el i-ésimo renglón de I por una constante c
diferente de cero, entonces I se puede recuperar si el i-ésimo renglón de E se mul-tiplica
por llc. En la tabla l se enumeran las diversas posibilidades.
TABLA 1
Operaciones en los renglones
de Z que producen E de E que reproducen I
Multiplicar el renglón i por c f O
Operaciones en los renglones
Multiplicar el renglón i por 1 /c
Intercambiar los renglones i y J Intercambiar los renglones i y j
Las operaciones en la columna derecha de la tabla se denominan operaciones
inversas de las operaciones correspondientes en la columna izquierda.
Ejemplo 3 En cada una de las siguientes situaciones se efectuó una operación
elemental en un renglón de la matriz identidad 2 X 2 para obtener una matriz ele-mental
E, y luego E se convirtió en la matriz identidad mediante la operación
inversa en el mismo renglón.
[: Y]
[t :]
renglón. I
[Y A]
Multiplicar por 7 el segun- I Multiplicar por 1/7 el se-gundo](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-74-320.jpg)
![78 Sistemas de ecuaciones lineales v matrices
prlmero Y segundo.
[:, :I -+ [: :] " [: P]
I/ Sumar -5 veces el segun-do
renglón al primero.
El siguiente teorema establece una propiedad importante de las matrices ele-mentales.
Teorema 1.5.2. Toda matriz elemental es invertible, y la inversa también es
una matriz elemental.
Demosfración. Si E es una matriz elemental, entonces E se obtiene al efectuar
algunas operaciones en los renglones de I. Sea E, la matriz que se obtiene cuando
la inversa de esta operacion se efectúa en I. Al aplicar el teorema 1.5.1 y usando el
hecho de que las operaciones inversas en los renglones cancelan mutuamente su
efecto, se concluye que
E,E= I y EE,=I
Así. la matriz elemental E, es la inversa de E. 0
El siguiente teorema establece algunas relaciones fundamentales entre in-vertibilidad,
sistemas lineales homogéneos, formas escalonadas reducidas y matri-ces
elementales. Estos resultados son extremadamente importantes y se usarán
muchas veces en secciones ultenores.
Teorema 1.5.3. Si A es una matriz n X n, entonces las siguientes proposiciones
son equivalentes; es decir, todas son verdaderas o todas son falsas.
a) A es Invertible.
b) Ax = O sólo tiene la solución trivial.
c) La.forma escalonada reducida de A es In.
d) A se puede expresar como un producto de matrices elementales.
Demostración. Se demostrará la equivalencia estableciendo la cadena de
implicaciones a * b * c => d * a.
a * b: Suponer que A es invertible y sea x(, cualquier solución de Ax = O; así, Axo
= O. Al multiplicar ambos miembros de esta ecuación por la matriz A" se obtiene](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-75-320.jpg)


![1.5 Matrices elementales y un método para determinar A" / 81
Ejemplo 4 Encontrar la inversa de
Solución. Se desea reducir A a la matriz identidad mediante operaciones en los
renglones y aplicar simultáneamente las operaciones a I para obtener A -l. Para
lograr ésto, la matriz identidad se adjunta a la derecha de A, con lo que se obtiene
una matriz de la forma
y luego se aplican operaciones en los renglones a esta matriz hasta que el lado
izquierdo se reduce a I; estas operaciones convierten el lado derecho en A", de
modo que la matriz final es de la forma
[I A"]
Los cálculos son como sigue:
1 2 3 / 1 0
2 5 3 j 0 1
1 0 8 j O O 1 "1 1 2 3 1 1 0 "1 I Se sumó -2 veces el primer o 1 - 3 1 -2 1 renglón al segundo y e-l v 1e z
0 - 2 5 ; - 1 o 1 primer renglón al tercero.
1 2 3 1 1 0
o 1 - 3 : -2 1
1 2 3 j 1 0
1 2 O j -14
O 1 0 : 1 3 - 5
Se sumó 3 veces el tercer renglón
al segundo y -3 veces el tercer
1 0
o 1 Se sumó -2 veces el segundo](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-78-320.jpg)

![1.5 Matrices elementales y un método para determinar A" / 83
x, + 2x, + 3x, = o
2x, + 5x, + 3x, = o
XI + 8x, = O
sólo tiene la solución trivial. A
EJERCICIOS DE LA SECCIÓN 1.5
1. De las siguientes matrices, ¿cuáles son elementales'?
2. Encontrar una operación en los renglones que convierta la matriz elemental dada en
A = [ & -: -:I, B=[: -: -:I, c=[i 1; -i]
3. Considerar las matrices
3 4 8 1 5 4
Encontrar matrices elementalesE ,, E2,E , y E4 tales que
a) E,A=B b) E$=A c)E#=C d)E4C=A
4. En el ejercicio 3, Les posible encontrar una matriz elemental E tal que EB = C? JUS-tificar
la respuesta.
En los ejercicios 5. 6 y 7, aplicar el método mostrado en los ejemplos 4 y 5 para encontrar
la inversa de la matriz dada si la matnz es invertible, y comprobar la respuesta por
multiplicación.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-80-320.jpg)

![1.6 Otros resultados sobre sistemas e invertibilidad I’ 85
13. Demostrar que r O a O O O
b O c O O
A = O d O e O
O O f O , q
o O o I? o,
no es invertible para cualesquiera valores de los elementos
14. Demostrar que si A es una matriz m X n, entonces existe una matriz invertible C tal
que CA está en forma escalonada reducida.
15. Demostrar que si A es una matriz invertible y B es equivalente por renglones a A,
entonces B también es invertible.
16. a) Demostrar: Si A y B son matrices m X n, entonces A y B son equivalentes por
renglones si y sólo si A y B tienen la misma forma escalonada reducida.
operaciones elementales en los renglones que produzBca a partir de ‘4.
.=II1 ;2 ;3] .-[I O; -;I
b) Demostrar que A y B son equivalente por renglones, y encontrar una sucesión de
17. Demostrar el teorema 1.5.1
1.6 OTROS RESULTADOS SOBRE SISTEMAS DE ECUACIONES E
INVERTIBILIDAD
En esta sección se establecerán más resultados sobre sistemas de ecuaciones
lineales e invertibilidad de matrices. El trabajo dará por resultado un método
totalmente nuevo para resolver sistemas de n ecuaciones con n Incógnitas.
UN TEOREMA Se empezará por demostrar un resultado fundamental sobre sistemas lineales. que
FUNDAMENTAL ya fue anticipado en la primera sección de este libro.
Teorema 1.6.1. Todo sistema de ecuaciones lineales no tiene solución, tiene
exactamente una solucibn o tiene infinidad de soluciones.
~ ~~ ~~~
Demostración. Si Ax = b es un sistema de ecuaciones lineales, entonces exacta-mente
una de las siguientes afirmacicmes es vcrdadcra: a) el sisienla no tiene sch-ción,
b) el sistema tiene exactamentc I ~ I I s;o~l ucltr!. o bien, c) el sistema tiene más
de una solucicin. La demostración cstard conipleri si se puede demostrar que cl
sistema tiene iníínidnd de soluciones en el caso 2).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-82-320.jpg)

![1.6 Otros resultados sobre sistemas e invertibilidad / 87
Por el teorema 1.6.2, la solución del sistema es
o bien, x1 = 1, x2 = -1, x3 = 2. A
OBSERVACI~N. Nótese que el método de ejemplo 1 es aplicable sólo cuando el
sistema tiene tantas ecuaciones como incógnitas y la matriz de coeficientes es in-vertible.
RESOLUCIóN DE Frecuentemente es necesario resolver una sucesión de sistemas
VARIOS
SISTEMAS A x = b , , A x = b 2 , A x = b , . . . , Ax=bk
LINEALES CON
UNAMATRIZ DE COEFICIENTES entonces las soluciones
cada uno de los cuales tiene la misma matriz de coeficientes A. Si A es invertible,
COMÚN
x l = A " b l , x 2 = A " b 2 , x 3 = A P 1 b 3 , . . . , xk=A-lb,
se pueden obtener con una inversión matricial y k multiplicaciones de matrices.
Sin embargo, un método más eficaz es formar la matriz
[.4 I b, I b, . . . bk] (1)
donde la matriz de coeficientes A es "aumentada" por todas las k matrices b,, b,, .
. . , b,. Al expresar (1) en forma escalonada reducida, por eliminación de Gauss-
Jordan se pueden resolver a la vez todos los k sistemas. Este método tiene la
ventaja de que se puede aplicar aun cuando A no sea invertible.
Ejemplo 2 Resolver los sistemas
Solución. Los dos sistemas tienen la misma matriz de Coeficientes. Si esta matriz
de coeficientes se aumenta con las columnas de constantes que están en los
miembros derechos deta les sistemas, se obtiene](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-84-320.jpg)


![90 Sistemas de ecuaciones lineales y matrices
Teorema 1.6.5. Sean A y B matrices cuadradas del mismo tamaño. Si AB es
invertible, entonces A y B también deben ser invertibles.
Más tarde se encontrará que el siguiente problema fundamental aparece en
varios contextos.
Un problema fundamental. Sea A una matriz fija m X n. Encontrar todas las
matrices b m X 1 tales que el sistema de ecuacionesA x = b sea consistente.
Si A es una matriz invertible, el teorema 1.6.2 resuelve por completo este
problema al establecer que para toda matriz b m x 1 el sistema lineal Ax = b tiene
la solución única x = A"b. Si A no es cuadrada, o si A es cuadrada pero no
invertible, entonces el teorema 1.6.2 no es válido. En estos casos la matriz b debe
satisfacer ciertas condiciones a fin de que Ax = b sea consistente. El siguiente
ejemplo ilustra cómo se puede usar la eliminacion gaussiana para determinatra les
condiciones.
Ejemplo 3 ¿Qué*condlciones deben satisfacer b,, 6, y 6, para que el sistema de
ecuaciones
xl + .y2 + 2x, = h,
.xl 3- x3 = b,
2x, + x2 + 3x, = h,
sea consistente?
Solución. La matriz aumentada es
que se puede expresar en forma escalonada reducicdoam o sigue.
1 1 2 bl
Se sumó - 1 veces el primer
o -1 -1 renglón al segundo y se sumó -2
O -1 -1 h,-2h, veces el primer renglón al tercero.
[(!I hl ] T El segundo renglón se
multiplicó por - l .
I b l - b 2 O - I - 1 h3-2bl
1 1 1 b2
o 1 1
O O O b3-bZ-bl
El segundo renglón se
sumó al tercero.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-87-320.jpg)




![1.7 Matrices diagonales, triangulares y simétricas / 95
Ejemplo 1 Si
A = [ : -9 3
entonces
Los productos de matrices en que aparecen factores lagonales son espe-cialmente
o o d3 '31 u32 '33 u34 d3a31 d3a32 d3a33 d3'34 1
fáciles de ][": calcular. Por ejemplo,
::: 1:; "::] [Od l dO2 O = [.a2]
d l a l l dl'13
d2a22 d2a23 d2a24
En palabras, para multiplicar una matriz A por la izquierda por una matriz
diagonal D, es posible multiplicar renglones sucesivos de A por los elementos
diagonales sucesivos de D, y para multiplicar A por la derecha por D es posible
multiplicar columnas sucesivas dAe por los elementos diagonales sucesivosd e D.
MATRICES Una matriz cuadrada en la que todos los elementos arriba de la diagonal principal
TRIANGULARES son cero se denomina triangular inferior, y una matriz cuadrada en la que todos
los elementos abajo de la diagonal principal son cero se denomina triangular
superior. Una matriz que es triangular superior o triangular inferior se denomina
triangular.
Ejemplo 2
Una matriz trian-gular
superior ge- gular inferior gene-](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-92-320.jpg)
![96 i Sistemas de ecuaciones lineales y matrices
OBSERVACI~N. Nótese que las matrices diagonales son tanto triangulares supe-riores
como triangulares inferiores, ya que tienen ceros por abajo y por arriba de la
diagonal principal. Nótese también que una matriz cuadrada en forma escalonada
es triangular superior porque tiene ceros por abajo de la diagonal principal.
A continuación se proporcionan cuatro caracterizaciones útiles de las
matrices triangulares. El lector encontrará instructivo comprobar que las matrices
en el ejemplo 2 tienen las propiedades establecidas.
Una matriz cuadrada A = [aij] es triangular superior si y sólo si el i-ésimo
Una matriz cuadrada A = [aij] es triangular inferior si y sólo si la j-ésima
Una matriz cuadrada A = [aij] es triangular superior si y sólo si [aijJ = O
Una matriz cuadrada A = [aij] es triangular inferior si y sólo si [aij] = O
renglón empieza con por lo menos i - 1 ceros.
columna empieza con por lo menos j - 1 ceros.
para i > j.
para i j.
En el siguiente teorema se enumeran algunas de las propiedades básicas de
las matrices triangulares.
Teorema 1.7.1.
a) La transpuesta de una matriz triangular inferior es triangular superior, y
la transpuesta de una matriz triangular superiore s triangular inferior.
b) El producto de matrices triangulares inferiores es triangular inferior, y el
producto de matrices triangulares superiores es triangular superior.
e> Una matriz triangular es invertible si y sólo si todos sus elementos diago-nales
son diferentes de cero.
d) La inversa de una matriz triangular inferior invertible es triangular infe-rior,
JJ la inversa de una matriz triangular superior invertiblee s triangular
superior.
El inciso a) es evidente a partir del hecho de que la trasposición de una matriz
se puede efectuar reflejando los elementos con respecto a la diagonal principal; se
omite la demostraciónf ormal. Se demostrará b), pero las demostraciones de c) y 6)
se pospondrán para el siguiente capítulo, donde se contará con los medios para
probar los resultados de manera más eficaz.
Demostración de b). Se demostrará el resultado para matrices triangulares infe-riores;
la demostración para matrices triangulares superiores es semejante. Sean A
= lav] y B = [b .] matrices triangulares inferiores n x n, y sea C el
‘- J = [c..] IJ
producto C = AB. Por la observación que precede a este teorema, se puede probar
que C es triangular inferior demostrando que [c..]= O para i < j. Pero por la
definición de multiplicación de matrices,
1J](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-93-320.jpg)
![1.7Matrices diagonales, triangulares y simétricas / 97
si se supone que i < j , entonces los términos de esta expresión se pueden agrupar
como sigue:
cij = ailbl, + aj2b, + . . . +'ai,- ,bi_ , + ajjbj, + . . . + ainbn,
< ,
Términos en los cuales el Términos en los cuales el
número de renglón de b es 'número de renglón de a es
menor que el número de menor que el número de
columna de 6. columna de a.
En el primer agrupamiento, todos los factores 6 son cero, ya que B es triangular
inferior, y en el segundo agrupamiento todos los factores a son cero, ya que A es
triangular inferior. Así, cij = O, que es lo que se queda demostrar. 0
Ejemplo 3 Considerar las matrices triangulares superiores
3 -
11 A = [ : B=
-3 -2
o o "1 O 0 1
La matriz A es invertible, ya que sus elementos diagonales sond iferentes de cero,
pero la matriz B no lo es. Se deja para el lector calcular la inversa de A aplicando
el método de la sección 1.5 y demostrar que
Esta inversa es triangular superior, como garantiza el inciso d) del teorema 1.7. l.
También se deja para el lector comprobar que el producto AB es
-2 -2
:]
A B = [ : Este producto es triangular superior, como garantiza el inciso 6) del teorema 1.7. l. A
MATRICES Una matriz cuadrada A es simétrica si A = A T.
SIMÉTRICAS
Ejemplo 4 Las siguientes matrices son simétricas, ya que cada una es igual a su
propia transpuesta (comprobar).
[-:-: I -4* -3 :]
-5 O 7
4
O
O
O
O
4
O
O
O
O
4
O
O :] *
4](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-94-320.jpg)
![98 ’; Sistemas de ecuaciones Iineales y matrices
Es fácil reconocer las matrices simétricas por inspección: Los elementos de la
&agonal principal pueden ser cualesquierap,e roa sl “imágenes especulares” delo s otros
elementos de la matriz con respecato l a diagonal principal deben seirg uales (figura 1).
Este hecho se concluye porque la transposición de una matriz cuadrada se puede
efectuar al intercambiar los elementos que son simétricos con respecto a la dia-gonal
principal. Expresado en términos de los elementos individuales, una matriz
A = [a’.]e s simétrica si y sólo si [a’.]= [u..]p ara todos los valores de i y j . Como
se ilustra en el ejemplo 4, todas las matrices dlagonales son simétricas. Y Y J’ .
En el siguiente teorema se enumeran las propiedades algebraicas más im-portantes
de las matrices simétricas. Las demostraciones son consecuencias direc-tas
del teorema I .4.9 y se dejan como ejercicios.
Teorema 1.7.2. Si ,4 y B son matrices simétricas del mismo tamaño y si k es
cualquier escalar, entonces:
a) A es simétrica.
h) A f B Y A - B son simétricas.
c) kA essimktrica.
OBSERVACI~N. En general, no es cierto que el producto de matrices simétricas es
simétrico. Para ver esto, sean A y B matrices simétricas del mismo tamaño. Enton-ces
por el inciso 4, del teorema 1.4.9 y por la simetría se tiene
AB)^= B ~ A B~A =
Como AB y BA suelen ser diferentes, se concluye que en términos generales AB no
es simétrico. Sin embargo, en el caso especial en que AB = BA, el producto AB es
simétrico. Si A y B son matrices tales que AB = BA, entonces se dice que A y B
conmutan. En resumen: el producto de dos matrices simétricas es simétrico si y
sólo si las mafrices conmutun.
Ejemplo 5 En la primera de las siguientes ecuaciones se muestra un producto
de matrices simétricas que no es simétrico, y en la segunda se observa un pro-ducto
de matrices simétricas que sí es sinlétrico. Se concluye que los factores de la
primera ecuación no conmutan, pero que los de la segunda sí lo hacen. Se deja
para el lector comprobar ambos hechos. [: :I[ -; ;]=[I: :I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-95-320.jpg)


![1.7 Matrices diagonales, triangulares y simétricas I 10 1
9. Demostrar que A y B conmutan si a - d = 7b
a) A5 = [i -A -:] b) A '=[o 4 o] o o 1
10. Encontrar una matriz diagonal .A que cumpla
o 9 0 0
11. a) Factorizar A en la forma A = BD, donde D es una matriz diagonal
b) La factorización efectuada, Les la única posible? Explicar la respuesta
A = [-i 31, ; ;]
12. Comprobar el teorema 1.7.1b para el producto AB, donde
2 s 2 -8
13. Comprobar el teorema 1.7: 14 para las matricesA y B del ejercicio 12
14. Comprobar el teorema 1.7.3 para la matriz dadaA .
15. Sea A una matriz simétnca.
a) Demostrar que A' es simétnca.
h) lkmostrar que 2 A 2 - 3A + I es simétrica
16. Sea A una matriz simétrica.
a) Demostrar que Ak es simétrica si k es cualquier entero no negativo.
b) Si p(x) es un polinomio, Les necesariamente simétrico p(A)? Explicar la respuesta
17. Sea '4 una matriz triangular superior y sea p(x) un polinomio @(A) es necesariamente
triangular superior? Explicar la respuesta.
18. Demostrar: Si ATA = A, entonces A es simétrica y A = A2
19. ;,Cuál es el número máximo de elementos distintos que puede contener una matriz
simktrica de n X n?](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-98-320.jpg)
![I02 / Sistemas de ecuaciones linealesy matrices
21. Con base en la experiencia adquirida en el ejercicio 20, instrumentar una prueba
gencral que se pueda aplicar a una fórmula para a a fin de determinar si A = u es
simétrica. i/ il
22. Una matriz cuadrada A se denomina untkimdtrica si ,4T = -A. Demostrar lo siguiente:
a) Si A es una matriz antisimétrica invertiblee, ntor-ces A" es antisimétrica.
b] Si A y 4 son antisimétricas, entonces también lo son n T , A + B, A -+ B y kA para
c) roda matriz cuadrada se puede expresar como la suma de una matriz simétrica y
cualquier escalar k.
una matriz antisimétnca.
23. En el texto se demostró que el producto de matrices simétricas es simétrico si y sólo si
las matrices conmutan. El producto de matrices antisimétricas que conmutan, i es
antisimétrico'? Explicar la respuesta.
24. Si la matriz A IZ X n se puede expresar como A = LU, donde L es una matriz triangulm
inferior y li es una matriz triangular superior, entonces el sistema lineal Ax = b se
puede expresar como LUX = b y se puede resolver en dos pasos:
Paso 1. Sea (:x = y, de modo que I,Cix = h se puede expresar como Ly = b. Resolver
este slstc~na
Paso 2. Resolver el sistema Ux = y para x.
En cada inciso, aplicar el método anterior de dos pasos para resolver el sistema dado
1 0 0 2 - 1
2 4 1
EJERCICIOS COMPLEMENTARIOS 1.7 I
1. IJsar eliminación de Gauss-Jordan para resolver parax ' yy' en términos dex y y
x = $y - &'
y = Qx' + g y t
2. lisar climinación de Gauss-Jordan para resolver parax ' y y' en términos de n y y .
3. Encontrar un sistema lineal homogéneo con dos ecuaciones que no sean múltiples entre
sí y tales que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-99-320.jpg)
![1.7 Matrices diagonales, triangulares y simétricas I’ 103
x, = 1, x2 = - 1, xj = 1, xq = 2
Y
x, = 2, x2 = o, xj = 3, x4 = - 1
sean soluciones del sistema.
4. Una caja contiene en total 13 monedas distintas de 1, 5 y 10 centavos, cuyo valor total
es de 83 centavos. ¿Cuántas monedas de cada denominación hay en la caja?
5. Encontrar enteros positivos que cumplan
x+ y+ z= 9
x + 5 y + 1 0 z = 4 4
6. ¿Para qué valor(es) de a el siguiente sistema no tiene solución, tiene exactamente una
solución y tiene una infinidad de soluciones?
x, + x2 + xj = 4
xj = 2
(a2 - 4)x, = a - 2
7. Sea
la matriz aumentada de un sistema lineal. ¿Para qvualéo res de a y b el sistema
a) tiene una solución única? b) tiene una solución de un parámetro?
c) tiene una solución de dos parámetros? d) no tiene solución?
8. Resolver para x, y y z.
XY - 2$ + 3zy = 8
2*y - 3 g y + 2zy = 7
-xy + fi + 2zy = 4
9. Encontrar una matriz K tal que AKB = C dado que
y], 8 6 -6.
- C = [ 6 - 1 1
-4 o o.
10. ¿Cómo se debe elegir los coeficientes a, b y c de modo que el sistema
ax+bL”3z= -3
”x-by+cz= -1
a x + 3 y - c z = -3
tengalasoluciónx= l,y= --I yz=2?
11. En cada inciso, resolver la ecuación matncial paraX](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-100-320.jpg)

![I . 7 Matrices diagonales, triangulares y simétricas I' 105
23. Demostrar: Si A es una matriz m X n y B es la matriz n X 1 integrada completamente
por elementos iguales a Un, entonces
donde 7, es la media de los elementos en el i-ésimo renglón de A.
son funciones diferenciables dxe, entonces se define
Demostrar que si los elementos de A y B son funciones diferenciables de x y los
tattlaiim de las matrices rim tales-fpe. es posible ejecutar 1% óperaciones indi&las,
entonces
a) - (kA) = k - (b) - (A f B) = - + (c) -(AB) = + A- 1 dx dx dx
d dA d dA dB d dB
25. (Para kcfores que ya estudiaron CcflcurO.) Usar el inciso c) del ejercicio 24 para
demostrar que
Escribir todas las hipótesis establecidas para obtener esta fórmula.
26. Encontrar los valores de A, B y C que hacen la ecuación
x2+x-2 A + - +-
Bx+C
" (3x - l)(XZ 1) 3x - 1 x* + 1
una identidad. [Sugerencia Multiplicar todo por (3x - 1)(2 + 1) e igualar los coefi-cientes
correspondientes de los polinomios en cada miembro de la ecuación resultante].
27. Si P es una matriz n X 1 tal que PTP = 1, entonces H = I - 2PPT se denomina matriz
de Householdet correspondiente (en honor del matemático estadunidense A. S.
Householder).
a) Comprobar que PTP = 1 si PT = 3/4 1/6 1/4 5/12 5/12 y calcular la matriz de
Householder correspondiente.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-102-320.jpg)





![2.1 La función determinante / 1 I I
Como indica este ejemplo, una matriz A de n X n tiene n! productos
elementales. Son los productos de la forma aljla2 . . . any, donde olTj 2 , . . ,j ,)
es una permutación del conjunto { 1, 2, 3, . . . , n{ Por un producto elemental con
signo de A se entenderá un producto elemental aljlazj2 ' . ' un? multiplicado por
+1 o por - 1. Si GI, j 2 , . . . ,Jn) es una permutación par se usa el signo +, y si (jl,
j2,. . . ,j ,) es una permutación impar, se usae l signo - .
Ejemplo 6 Enumerar todos los productos elementales con signo dleas matrices
[ 413
a12 a) ['I' "I2] b) a22
a a 2 2 1 2
431 432 u33
Solución.
- a)
Producto
Producto Permutación elemental asociada Par o impar con signo
4, la22 (L2) par a 1 la22
012421 (2, 1) impar -a12421
h)
Ahora ya es posible definir la íünción determinante.
Definición. Sea A una matriz cuadrada. La función determinante se denota
por det, y det(A) se define como la suma de los productos elementales con signo
de A. El número det(A) se denomina determinante de A.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-108-320.jpg)




![verdaderos cuando e11 VCY de "renglón" se escribe la palabra "columna". Para
demostrar una proposiciorl sobre columnas, basta transponer la matriz en cuestión
para convertir la proposicibn sobre columnas en una proposición sobre renglones,
y luego aplicar los resultados conocidos sobre renglones.
DETERMINANTES F1 sigtnicnte teorema facilita la evaluación del determinante de una matriz trian-
DE MATRICES gular, sin imporlar su tamaito.
TRIANGULARES
Teorema 2.2.2. S i -4 es una matriz triangnlar w X n (triangular superior,
triangular inj>rior o diagonalj, pnronces dei(,4) es el producto de los elenlentos
de in diagonal principal; es decir, det(;.l) a, ,a7, . . a,,,,.
A fin de facilitar la notación. se demostrará el resultado para una matriz
triangular inferior 4 X 4
El razonamiento en el caso general n X n es semejante. Para matrices triangulares
superiores se puede obtener una demostración aplicando el teorema 2.2.lh y
observando que la transpuesta de una matriz triangular superior es una matriz
triangular inferior con los mismos elementos en la diagonal.
Dctmstrclc~rcirdl el kmma 2.2.2 (C'nso de una matriz lrianguiar injerior de 4 X 4).
El Único producto elemental de A que puede s a diferente de cero es al la22a33a44.
Para ver que así cs. considerar un producto elemental representativo ~ ~ , , a ~ , ~ n ~ , Corno a,? = o I 3 -
- a14 = O. se debe tenerjl = 1 a fin de tener un productoelemental
diferente de cero. Si ,jl = 1. se debe cumplir que j , = 1, y-¿q ue ninguna pareja de
factores comunes prmienc de la misma columna. Además, como = a = O. se
debe tener], = 2 a fin de que el producto elemental sea d&rente de cero. Proslguicndo
24
de esta manera se obtienejB= 3 y j , = 3. Como n1l c122a33a4s4e multiplica por +I
al formar el producto elemental con signo. se obtiene
Ejemplo 1
2 7 - 3 8 3
0 - 3 7 5 1
O O 6 7 6 = (2)( -3)(6)(9)(4) = - 1296 A
O 0 0 9 8
0 0 0 0 4
EFECTO DE LAS El siguiente teorema muestra cómo una operación elemental en los renglones de
OPERACIONES una matriz afecta el valor de su determinante.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-113-320.jpg)




![2.3 Propiedades de la función determinante I’ 121
En los ejercicios del 4 al 11, evalmr el determinante de la matriz dada refiuciendo la
matriz a forma escalonada.
4. [ -.; y -;] 5. [I 1 21 6. [-: -; 11 7. 3 6 -9 o 3 1 1 - 3 [-3 :- 6 i -!]
3 2 4
3a 36 3c a+g b+h c + i
13. Por medio de la reducción de renglones demostrar que
ik; 1 :2 i2i = (b - u)(c - a)(c - b)
14. Con un razonamiento semejante al de la demostración del teorema 2.2.2, mostrar que
1::; 15. Demostrar los siguientes casos especiales Y:l/ del teorema2 .2.3.
k a t 2 &I3 1:; ‘12 u13 a22 -111: a12
a) all/ = k l : : : a22 b) aI2 = az2
‘31 ‘32 a33 ‘31 ‘32 u33 ‘31 a32 ‘33 a31 ‘32 ‘33
2.3 PROPIEDADES DE LA FUNCIÓN DETERMINANTE
En esta sección se desarrollarán algunas de las propiedades fundamentales de la
función determinante. Con el trabajo aquí realizado se adquirirán mayores cono-cimientos
sobre la relación que hay entre una matriz cuadrada y su determinante.
Una de las consecuencias inmediatas de este material es una importante prueba de
determinante para la invertibilidad de una matriz.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-118-320.jpg)

![2.3 Propiedades de la función determinante / 123
DETERMINANTE
DE UN
PRODUCTODE
MATRICES
Este es un caso especial del siguiente resultado general.
Teorema 2.3.1. Sean A, B y C matrices n X n que sólo difieren en un renglón,
por ejemplo, el r-ésimo, y suponer que el r-ésimo renglón de C se puede
obtener sumando los elementos correspondientes de los r-ésimos renglones de
A y B. Entonces
det(C) = det(4) + det(B).
El mismo resultado es cierto para columnas.
det [ 2 O 3 ] =det[ i i i] +.et[: -:] A
Ejemplo 2 Con la evaluación de los determinantes se puede comprobar que
1 7 5
l + O 4 + 1 7 + ( - 1 )
Cuando se considera la complejidad de las definiciones de la multiplicación de
matrices y determinantes de una matriz, parecería improbable que exista alguna
relación simple entre ellas. Es esto lo que hace tan sorprendente la sencillez del
siguiente resultado. Se demostrará que si A y B son matrices cuadradas del
mismo tamaño, entonces
det (AB) = det (A) det (B) (2)
Como la demostración de este teorema es bastante minuciosa, primero es necesario
desarrollar algunos resultados preliminares. Se empezará con el caso especial de
(2) en que A es una matriz elemental. Debido a que este caso especial es sólo un
preludio a (2), se denomina lema.
Lema 2.3.2. Si B es una matriz n X n y E es una matriz elemental n x n,
entonces
I det@B) = detp) de@)
Demostracidn. Se considerarán tres casos, cada uno dependiendo de la
operación ene l renglón con ques e obtiene E.
Caso 1. Si E se obtiene al multiplicar por k un renglón de Zn, entonces, por el
teorema 1.5.1, EB se obtiene a partir de B al multiplicar por k un renglón; así, por
el teorema 2.2.3a se tiene que
det(EB) = k det(B)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-120-320.jpg)



![2.3 Propiedades de ¡a función determinante / 127
O
A[: ;I[::] - [: :I[::] = [:I
que es de la forma (7) con
AI-.=[ A--4 1 a--32]
El problema de interés esencial en sistemas lineales de la forma (7) es
determinar los valores de para los cuales el sistema tiene una solución no trivial;
ese valor de A se denomina valor característico o eigenvalor' de A. Si les un
eigenvalor de A, entonces las soluciones no triviales de (7) se denominan eigen-vectores
de A correspondientes a A.
De acuerdo con el teorema 2.3.3 se concluye que el sistema ( I - A)x = O
tiene una solución no trivial si y sólo si
Idet(lI-A)=O I
ÉSta se denomina ecuacidn característica de A; los eigenvalores de A se pueden
encontrar resolviendo esta ecuación para l.
Los eigenvalores y los eigenvectores se estudiarán de nuevo en otros
capítulos, donde se analizará su interpretación geométrica y se desarrollarán sus
propiedades con mayor profundidad.
Ejemplo 6 Determinar los eigenvalores y los eigenvectores correspondientes de la
matriz A del ejemplo 5.
Solución. La ecuación característica de A es
*La palabra elgenvalor es una combinación de alemán y espaiiol. El prefijo alemán ergen puede traducirse
como "propio", que resulta de l a s antiguas publicaciones en las que los eigenvalores se conocían como
valores proplos; también se denominan raices latentes.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-124-320.jpg)

![2.3 Propiedades de la función determinante / 129
Teorema 2.3.6. Si A es una matriz n X n, entonces las siguientes proposicio-nes
son equivalentes.
a) A es invertible.
b) Ax = O sólo tiene la solución trivial.
c) La forma escalonada reducida de A es I,,.
d) A se puede expresar como un producto de matrices elementales.
e) Ax = b es consistente para toda matriz b n X 1.
fi Ax = b tiene exactamente una solución para toda matriz b n X 1.
g) det(A) = O.
EJERCICIOS DE LA SECCI~N2.3
1. Comprobar que det(kA) = k" det(A) para
A = [a y .-[i - 1I i]
2. Comprobar que det(AB) = det(A) det(B) para
2 1 0
3. Por inspección, explicar por qué det(A)= O
- 2 8 1 4
4 -6 4 -3
4. Con el teorema 2.3.3, determinar cuáles de las siguientes matrices son invertibles
5. Sea
Suponiendo que det(A) = -7, determinar
a) det(3A) b) det(A") c) det(2A")
6. Sin evaluar directamente demostrar quex = O y x = 2 satisfacen](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-126-320.jpg)

![2.4 Desarrollo por cofactores; regla de Cramer / 13 I
16. Sean A y B matrices n X n. Demostrar que si A es invertible, entonces det(B) =
det(A"BA).
17. a)Expresar
a, + b, c, +dl
a, + b, c, + d,
como una suma de cuatro determinantecsu yos elementos no contengan sumas.
b) Expresar
a1 + bl CI +dl el +fl
a2 + 62 c2 + d2 e2 + f 2
a3 + b3 c3 + d3 e3 + f 3
como una suma de ocho determinantes cuyos elementos no contengan sumas.
18. Demostrar que una matriz cuadrada A es invertible si y sólo si ATA es invertible.
19. Demostrar los casos 2 y 3 del lema 2.3.2.
2.4 DESARROLLO POR COFACTORES; REGLA DE CRAMER
~ ~~
En esta sección se considerará un método para evaluar determinantes que es útil
en la realización de cálculos manuales y reviste importancia teórica. Como
consecuencia del trabajo aquí efectuado, se obtendrá una fórmula para calcular
la inversa de una matriz invertible, así como una fórmula para encontrar la
solución de ciertos sistema de ecuaciones lineales en términos de determinantes.
MENORES Y
COFACTORES denota por M,, y se define como el determinante de la submatriz que queda
Definición. Si A es una matriz cuadrada, entoncese l menor del elementoa i se
después de q6itar el i-ésimo renglón y laj-ésima columna de A. El número
(- l)'+JM,, se denota por C,, y se denomina cofactor del elemento u..
Ejemplo 1 Sea
A = [ : ; 1 -4 i]
El menor del elemento all es](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-128-320.jpg)






![138 Determinantes
APLICACIONES
DE LA
FóRMULA DE
LA ADJUNTA
PARA LA
INVERSA
(véame los renglones sombreados en las dos matrices anteriores).
Si i =j, entonces (7) es el desarrollo por cofactores de det(A) a lo largo del i-ésimo
renglón deA (teorema 2.4.1), y si i = j , entonces las letras a y los cofactores
provienen de renglones diferentes de A. de modo que el valor de (7) es cero. En
consecuencia.
det(A) O . . . O
A adj(,4)=[ " ' . . . o ]=det(A)I (8)
det(A)
Dado que A es invertible, det(A) = O. Por tanto, la ecuación (8) puede volver a
escribirse como
1
det (A)
[A adj(A)] = I
O
.4 [-d etiAj a dj(A) 1 = I
Multiplicando por la izquierda ambos miembros por A -', se obtiene
A- 1 =~ 1
det (A)
adj(A) 0
Ejemplo 7 Por medio de (6), encontrar la inversa de la matriz A del ejemplo 6.
Solución. El lector puede comprobar que det(4 = 64. Así,
i 4 1
r 12 4 12-
A ~ -=1- I
det (A)
adj(A) = - 6 2 - 10
-16 16 16-
Aunque el método del ejemplo precedente es razonable para invertir manualmente
matrices 3 X 3, el algoritmo de inversión que se analizó en la sección 1.5 es más
eficaz para matrices más grandes. Sin embargo,d ebe tenerse en cuenta que el mé-todo
de la sección 1.5 es sólo un procedimiento de cómputo, mientras que la
fórmula (6) es una fórmula real para encontrar la inversa. Como se verá a conti-nuación,
esta fórmula esú til para obtener propiedades de ilna versa.
En la sección 1.7 se establecieron sin demostración dos resultados sobre
inversas.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-135-320.jpg)

![140 /' Determinantes
REGLA DE
CRAMER
basta demostrar que cada menor My con i < j es cero. Para este propósito, sea By la
matriz que se obtiene cuando se quitan el i-ésimo renglón y laj-ésima columna de A, de
modo que
M,, = det@,,) (9)
A partir de la hipótesis que i < j. se concluye que Bq es triangular superior
(ejercicio 32). Como A es triangular superior, su (i + I)-ésimo renglón comienza
con por lo menos i ceros. Pero el i-ésimo renglón de B, es el (i + 1)-ésimo renglón
de A sin el elemento de la j-ésima columna. Ya que i < j, ninguno de los i
primeros ceros se elimina quitando la j-ésima columna; así, el i-ésimo renglón de
B comienza con por lo menos i ceros, lo cual indica que este renglón contiene un
cero i/
en la diagonal principal, Ahora,p or el teorema 2.2.2 se concluye que det(BJ
= O, y por la expresión (9) se concluye que M,] = O. O
El siguiente teorema proporciona una fórmula útil para la solución de ciertos
sistemas lineales de n ecuaciones con n incógnitas. Esta fórmula, denominada
re@ de Cramer , es de interés marginal para efectos de cómputo, aunque es útil
para estudiar las propiedades matemáticas de una soluciónsi n necesidad de resol-ve<
el sistema
*
Teorema 2.4.3. (Regla de Crumer). Si Ax rz b es un sistema de n ecuaciones
lineales con n incdgnitas tal que det(A) = O, entonces la solución del sistema
es única. Esta solucidn es
donde .4 es la matriz que se obtiene al sustituir los elementos de la j-&into
columna de A por los elementos de la matriz J
*Gabriel Cramer (1704-1752), matemático suizo. Aunque Cramer no está considerado al lado de
los grandes matemáticos de su tiempo, sus contribuciones como diseminador de las ideas
matemáticas le ganaron un bien merecido lugar en la historia de las matemáticas. Cramer viaj6
bastante y conoció a muchos de los grandes matemáticos de su época. Estos contactos y amistades
condujeron a una correspondencia abundante a través de la cual se difilndia la informacibn snbrt
nuevos descubrimientos matemáticos.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-137-320.jpg)


![2.4 Desarrollo por cofactores; regla de Cramer / 143
3. Evaluar el determinante de la matriz del ejercicio 1 por desarrollo por cofactores a lo
largo de lo siguiente:
a) El primer renglón. b) La primera columna. c) El segundo renglón.
d) La segunda columna. e)' El tercer renglón. f) La tercera columna.
4. Para la matriz del ejercicio 1, encontrar
a) adj(A). b) A" usando el teorema 2.4.2
En los ejercicios del 5 al 10, evaluar det(A) mediante desarrollo por cofactores a lo largo de
un renglón o una columna que el lector elija.
-3 o 7 -: 3
-!] 5. A = [ 2 5 I] tí. A = [ : -1 o 5
1: 5
i -!
O 10. A = 2
4 0 0 1 0
2 2 4 2
En los ejercicios del 11 al 14, encontrar A" por medio del teorema 2.4.2.
11. A = [ -: -: :] 12. A = [ -: 2 1
13. A = [ : A -:] 14. A = [ -:
2 -3 5 2 0 0
15. Sea
1 : 3 1 1
'8 i]
A = [ ; 1 3 2 2
a) Evaluar A" usando el teorema 2.4.2.
b) Evaluar A" con el método del ejemplo 4 de la sección 1.5.
c) ¿Cuál método requiere menos cálculos?](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-140-320.jpg)
![144 ' Determinantes
En los ejercicios del I6 al 2 l . obtener la solución usando la regla de Cramer cuando sea aplicable.
16. 7 x , - 2 ~=, 3 17. 4x + 5y = 2
3.x, + x? = 5 I l x + y + 2 2 = 3
x + 5y + 2z = 1
18. x - ~ J + Z = 6
4x- y+22= - 1
2x + 2.v - 32 = -20
19. x, - 3.x2 + x, = 4 20. -.x1 - 4x, + 2s, + .xj = -32 21. 3x, - x* + xi = 4
2s, - .x2 = -2 2x, - .x2 + 7x3 + 91, = 14 -x, + 7x, " 2x, = I
41- I - 3x, = o -x, + X2 + 3x, + Xq = 1 I 2x1 + 6x2 - X., = 5
XI - 2s2 + xi - 4x, = -4
22. Ilemostrar que la matriz
cos H sen H O
y]
.-[:O co;H cs invertible para todos los valores de d; luego, encontrar A" usando el teorema 2.4.2
23. Apllcar la regla de Cramer parah allary sin resolver parax , z y MJ
4x+ v + zt u'= 6
3x+7.v- z + M'= 1
71-+3y-5z+8U.= -3
St y + 2 + 2 w = 3
24. Sea Ax = b el sistema del ejercicio 23.
a) Resolver aplicando la regla de Cramer.
b) Obtener la solución por eliminación de Gauss-Jordan.
c) ¿,Cuál mktodo requiere menos cálculos?
25. Demostrar que si d 4 4 ) = 1 y todos los elementos de A son enteros, entonces todos los
elementos de A " son enteros.
26. Sea Ax = b un slsterna de tz ecuaciones lineales con n incógnitas, coeficientes enteros y
constantes enteras. Demostrar que si det(A) = 1, la solución x tiene elementos enteros.
27. Demostrar que si 11 es una matIiz triangular inferior invertible, entonces A -I es trian-gular
mferior.
28. Obtener los desarrollos por cofactores primero y último que se enumeran en la fórmula (3).
29. Demostrar: La ecuación de la recta que pasa por los puntos distintos (a,, b,) y (a2, bz)
se puede escribir como
30. Demostrar: (x,, yl), (x2, y?) v (x3, y,) son puntos colineales si y sólo si](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-141-320.jpg)

![b) Con al rcgla de Crarner obtener fórmulas semejantes para cops y cos y.
6. Por medlo de determinantes, demostrar que para todos los valores reales de jl la única
solución de
x - 2-v = Lx
x - v = A.v
7. Demostrar: Si A es invertible, entonces adj(A) es mvertible y
[ adj ( A ) ] - ' = --A = adj (A - I )
1
det (A)
8. Demostrar- Si A es una matriz n X 11, entonces det [adj(A)] = [det(A)] '-l.
10. a) En la figura 2 que se muestra a contmuacion, el área del triángulo ABC se puede
expresar como
IJsar Csto y el hecho de que el área de un trapezoide es igual a 1/2 de la altura
multiplicada por la suma de los lados paralelos, para demostrar que
[Notu En la obtención de esta fórmula, los vtrtices se identifican de modo que el
triángulo se traza en sentido contrario al movimiento de las manecillas del reloj
procediendo de (x,, y , ) a (x?, y 2 ) a (x3, ,y3). Para una orientación en el sentido del
movimiento de las nmnecillas del reloj, el determinante anterior produce el neguti-vo
del área.]
b) Usar el resultado del inciso a), para determinar el área del triángulo con vkrtices (3,
31, (4, O), ("2, - 1).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-143-320.jpg)
![Ejercicios complementarios / 147
Figura 2 D E F
11. Demostrar: Si la suma de los elementos en cada renglón de m uantari z A n X n es cero,
entonces el determinante de A es cero. [Sugerencia Considerar el producto M, donde
X es la matriz n X 1 cuyos elementos son iguales a 1 .]
12. Sean A una matriz n x n y B la matriz que se obtiene cuando los renglones de A se
escriben en orden invertido. ¿Cómo están relacionados det(Ay) d et(B)?
13. ¿Cómo se afecta A” si
a) se intercambian los renglones i-ésimo yj-ésimo de A?
b) el i-ésimo renglón de A se multiplica por un escalar c diferente de cero?;
c) el i-ésimo renglón de A se suma c veces alfésimo renglón?
14. Sea A una matriz de n X n . Suponer que B, se obtiene al sumar el mismo número t a
cada elemento en el z-ésimo renglón de A, y que B, se obtiene al restar t de cada
elemento en el z-ésimo renglón de A. Demostrar que det(A) = 112 [det(B,) + det(BJ1.
15. Sea .=[a, u12 ;;j u13
a) Expresar det(1Z - A) como un polinomiop(A) = ,I3 + bL2 + d + d.
b) Expresar los coeficientes b y d en términos de determinanteys trazas
16. Sin evaluar directamente el detexminante, demostrar que
sen ct cos a sen (a + 6)
senp cos sen (p + S)
seny cos y sen(?+ 6)
= 0
17. Usar el hecho de que 21 375, 38 798, 34 162, 40 223 y 79 154 son, todos, divisibles
entre 19 para demostrar que
2 1 3 7 5
3 8 7 9 8
3 4 1 6 2
4 0 2 2 3
7 9 1 5 4](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-144-320.jpg)
















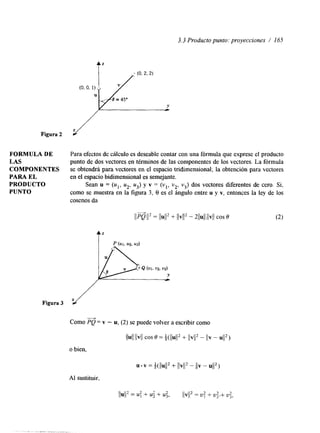









![3.4 Producto cruz / 175
20. Usar el resultado del ejercicio 19 para calcular, hasta el grado más próximo, los án-gulos
que forma una diagonal de una caja de dimensiones 10 cmX 15 cm X 25 cm con
las aristas del a caja. [Nota Se requiere una calculadoroa tablas trigonométncas.]
21. Con referencia al ejercicio 19, demostrar que v1 y v, son vectores perpendiculares en el
espacio tndimensional si y sólo si sus cosenos dlrectores satisfacen
cos 0: cos 4, + cosp, cos p, + cos y, cos y, = o 1
22. Demostrar que si v es ortogonal tanto a w, como a w2, entonces v es ortogonal a k,wl +
k2w2 para todos los escalares k, y k,.
23. Sean u y v vectores diferentes de cero en el espacio bidimensional o en el espacio
tridimensional, y sean k = 1 1 ~ 1 1y I = IIvII. Demostrar que el vectorw = lu + kv biseca el
ángulo entre u y v.
3.4 PRODUCTO CRUZ
En muchas aplicaciones de vectores a problemas de geometría, fisica e ingeniería
es de interés construir en el espacio tridimensional un vector que sea perpen-dicular
a dos vectores dados. En esta sección se introducirá un tipo de multipli-cación
vectorial conq ue se obtiene ese vector.
Definición. Si u = (ul , u*, u3) y v = ( v ~v,2 , v3) son vectores en el espacio
DE VECToRES tridimensional, entonces el producto cruz u X v es el vector definido por
1 o, en notación de determinantes,
oBsERvACIóN. En vez de memorizar (l), las componentes de u x v se pueden
obtener como sigue:
Se forma la matriz 2 X 3
cuyo primer renglón contiene las componentes de u y cuyo segundo ren-glón
contiene las componentes de v.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-172-320.jpg)





![3.4 Producto cruz / 181
por (6), el área A de este paralelogramo está dada por
A = (base)(altura) = llull llvll sen 0 1/11 x VI]
Este resultado es correcto inclusive si u y v son colineales, ya que el paralelogramo
determinado por u y v tiene área cero y por (6) se sabe que u x v = O porque en
este caso 8 = O. Por tanto, se tiene el siguiente teorema.
Teorema 3.4.3. Si u y v son vectores en el espacio tridimensional, entonces u
X v es igual al área del paralelogramo determinado por u y v.
Ejemplo 4 Encontrar el área del triángulo determinado por los puntos PIP, 2, o),
P2(- 1. o, 2) y P,(O, 4, 3).
Solución. El área 4 del tr$ingulo es 4 del área del paralelogramo determinado
por los vectores PIP, y P, P, (figura 5). Usando el método analizado en el ejemplo
2 de la sección 3.1, PIP2 = (-3, -2, 2) y PIP3 = (-2, 2, 3). Se concluye que - b
PIP, x PIP3 = (- 10,5, - 10)
Figura 5 i x I' Pi (2'2. O)
y en consecuencia,
TRIPLE
PRODUCTO
ESCALAR
Definición. Si u, v y w son vectores en el espacio tridimensional, entonces
u (v x w)
se denomina triple producto escalar de u, v y w.
El triple producto escalar de u = (u1, u2, u2), v = (vl, v2, v2) y w = (wl, w2,
wz) se puede calcular a partir de la fórmula
(7)
WI w:! w3,](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-178-320.jpg)







![3.5 Rectas y planos en el espacio tridimensional / 189
26. Demostrar el inciso 6) del teorema 3.4.1. [Sugerencia Demostrar primero el resultado
en el caso en que w = i = (1, O, O), luego cuando w = j = (O, 1, O) y luego cuando w = k
= (O, O, 1). Por Cltimo, hacer la demostración para un vector cualesquiera w = (w,,w z,
w3) escribiendo w = w,i + wzj + w3k.]
27. Demostrar el inciso e) del teorema 3.4.1. [Sugerencia Aplicar el inciso a) del teorema
3.4.2 al resultado del inciso d) del teorema 3.4.1.1
28. Sean u = (1, 3, -l), v = (1, 1,2) y w = (3, -1, 2). Calcular u x (v X W) usando el
ejercicio 26; luego, comprobar el resultado efectuando el cálculo directamente.
29. Demostrar: Si a, b, c y d están el mismo plano, entonces (a X b) x (c X d) = O.
30. En geometría de sólidos existe un teorema que establece que el volumen de un tetrae-dro
es 1/3(área de la base) * (altura). Usar este resultado para demostrar que el volu-men
del tetraedro cuyos lados son los vectores a, b y c es 116 :: . (b X c) (figura 11).
31. Usar el resultado del ejercicio 30 para encontrar el volumen del tetraedro con vértices
P, Q, R Y S.
a) P(- 1, 2, O), Q(2, 1, -31, 4 1 , O, 11, S(3, -2, 3)
b) P(0, O, O), Q(1, 2, - I ) , R(3,4, O), S(- 1, -3, 4)
32. Demostrar los incisos a) y 6) del teorema 3.4.2
33. Demostrar los incisos c) y 6) del teorema 3.4.2.
34. Demostrar los incisos e) yj) del teorema 3.4.2
3.5 RECTAS Y PLANOS EN EL ESPACIO TRIDIMENSIONAL
En esta sección se usarán los vectores para obtener ecuaciones de rectas y planos
en el espacio tridimensional, y estas ecuaciones se utilizarán para resolver
algunos prob lemas de geometría básicos.
PLANOS EN EL En geometría analítica plana, una recta se puede especificar dmdo su pendiente y
ESPACIO uno de sus puntos. De manera semejante, un plano en el espacio tridimensional se
SIONAL tos. Un método conveniente para describir la inclinación es especificar un vector
TRIDIMEN- puede especificar proporcionando su inclinación y especificando uno de sus pun-diferente
de cero (denominado normal) que es perpendicular al plano.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-186-320.jpg)



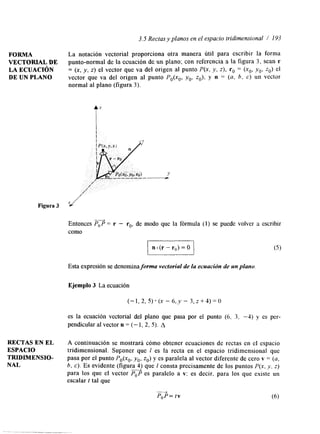


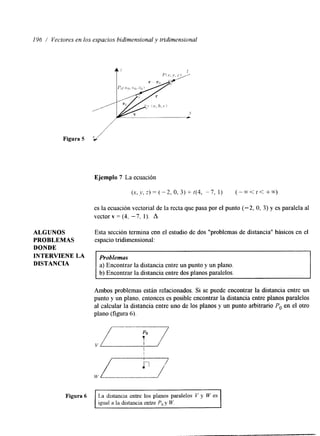


![3.5 Rectas y planos en el espacio tridimensional / 199
3. Encontrar una forma punto-normal
a) - 3 x + 7 y + 2 z = 10 b) ~ - 4 ~ = 0
4. Encontrar la ecuación del plano que pasa por 10s puntos dados
a) P(-4, - 1, - I ) , Q(-2, O, I), R(- 1, -2, -3) b) P(5,4, 31, Q(4, 3, I ) , R(1, 5, 4)
5. Determinar si los planos son paralelos
a) 4 x - y + 2 z = 5 y 7 ~ - 3 y + 4 2 = 8
b ) x - 4 y - 3 ~ - 2 = 0 y 3 ~ - 1 2 ~ - 9 ~ - 7 = 0
c) 2 y = 8 x - 4 z + 5 y x=+z+' 4Y
6. Determinar si la recta y el plano son paralelos.
a ) x = -5-4t, y = l -t, z = 3 + 2 t ; x + 2 y + 3 z - 9 = 0
b ) x = 3 t , y= 1 + 2 t , z = 2 - t ; 4 x - y + 2 ~ = 1
7. Determinar si los planos son perpendiculares.
a) 3 x - y + z - 4 = 0 , x + 2 z = - 1 b) x - 2 y + 3 z = 4 , - 2 x + 5 y + 4 z = - 1
8. Determinar si la recta y el plano son perpendiculares
a) x= - 2 - 4 t , y = 3 - 2 r , z = 1 + 2 t ; 2 x + y - z = 5
b ) x = 2 + t , y = l - t , ~ = 5 + 3 t ; 6 ~ + 6 ~ - 7 = 0
9. Encontrar las ecuaciones paramétncas de la recta que pasa por P y es paralela a n.
a) P(3, - 1, 2), n = (2, 1, 3) b) P(-2, 3, -3); n = (6, -6, -2)
c) P(2, 2, 6); n = (O, 1, O) d) P(0, O, O); n = (1, - 2, 3)
10. Encontrar las ecuaciones paramétricas de la recta que pasa por los puntos dados
a> (5, -2, 4), (7, 2, - 4) b) (O, O, O>, (2, - 1, - 3)
11. Encontrar las ecuaciones paramétricas de la recta de intersección de los planos dados
a) 7 x - 2 ~ + 3 ~ -=2 y - 3 x + y + 2 z + 5 = 0 b) 2 x + 3 y - 5 ~ = 0 y y = O
12. Encontrar la forma vectorial de la ecuación del plano que pasa por Po y cuya nor-mal
es n.
a) P 0 ( - l , 2 , 4 ) ; n = ( - 2 , 4 , 1) b) P0(2,0, -5); n = ( - l , 4 , 3 )
c) P0(5, -2, 1); n = (- I , O, O) d) Po(O, O, O); n = (u, b, c)
13. Determinar si los planos son paralelos
a) ( - l , 2 , 4 ) . ( ~ - 5 , ~ + 3 , ~ - 7 ) = 0 ; (2, -4, - 8 ) - ( ~ + 3 , ~ + 5 , ~ - 9 ) = 0
b ) ( 3 , 0 , - I ) . ( x + I , y - 2 , ~ - 3 ) = 0 ; ( - I , O , ~ ) . ( X + I , ~ - Z , Z - ~ ) = O
14. Determinar si los planos son perpendiculares.
a) ( - 2 , l , 4 ) . ( x - l , y , z + 3 ) = 0 ; ( I , -2, I ) . ( x + ~ , ~ - ~ , z ) = o
b) (3,0, - 2 ) . ( ~ + 4 , ~ - 7 , ~1 )+= O ; (1, I , I) . (x,y,z)=O
15. Encontrar la forma vectorial de la ecuación de la recta que pasa por p, y es pa-ralela
a v.
a) P o ( - l > 2 , 3 ) ; v = ( 7 , - 1 , 5 ) b) Po(2,0, - I ) ; VE(], I , I )
C) Po(L -4, 1); v = (O, O, - 2) d) Po(O, O, O); v = (U, b, C)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-196-320.jpg)


![202 / Vectores en los espacios bidimensional y tridimensional
x=x,+at, y=y,+bt, z = z , + c t (--<<<+-m)
consta de todos los puntos (x, y, z) que satisfacen
x--, - Y - Y o - 2 - %
a h c
Estas expresiones se denominan ecuaciones sim&ricas de la recta
42. Encontrar las ecuaciones simétricas de las rectas de los incisos a) y b) del ejercicio 9.
[Nota Ver el ejercicio 4 1 respecto a la terminología.]
43. En cada inciso, encontrar las ecuaciones de los dos planos cuya intersección es la recta
dada.
a ) x = 7 - 4 t , y = - 5 - 2 t , z = 5 + f (-m<[< +m)
b ) x = 4 t , ,v=2t, z = 7 t (-m<t< +m)
[Sugerencia. Cada igualdad en las ecuaciones simétricas de una recta representa un
plano que contiene a la recta. Ver el ejercicio 4 1 respecto a la terminología.]
44. Dos planos que se cortan en el espacio tridimensional determinan dos ángulos de
intersección: un ángulo agudo (O 5 8 5 90°) y su suplemento 1 SOo - 8 (figura Sa). Si
n1 y n2 son normales diferentes de cero a los planos, entonces el ángulo entre nl y nz
es 8 o 180° - 8 , dependiendo de las direcciones de las normales (figura 8b). En cada
inciso, determinar el ángulo agudo de intersección de los planos, hasta el grado más
próximo.
a)x=O y 2 x - y + z - 4 = 0
b ) x + 2 y - 2 2 = 5 y 6 ~ - 3 . ~ + 2 ~ = 8
[Nota Se requiere calculadora.]
Figura 8
45. Encontrar el ángulo agudo de intersección entre el plano x - y - 32 = 5 y la recta x =
2 - t, y = 2t, z = 3t - 1 hasta el grado más próximo. [Sugerencia Ver el ejercicio 44.1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-199-320.jpg)









![21 2 I Espacios vectoriaIes euclidianos
Figura 4
OTROS TIPOS DE
NOTACIÓN PARA
VECTORES EN R"
U
El siguiente teorema muestra que este resultado se extiende a R".
Teorema 4.1.7. (Teorema de Pitágoras para R"). Si u y v son vectores ortogo-nales
en R" con el producto interior euclidiano, entonces
1111 + VI2 = 11U1l2 + llvll2
U= [;I o u=[., u2 . . . u,]
Un vector u = ul, u2, . . . , U,,) en R" también se puede escribir en notación
matricial como matriz renglón o matriz columna:
u,
Lo anterior se justifica porque con las operaciones matriciales
se obtienen los mismos resultados que con las operaciones vectoriales
u + v = ( U l , u2,. . . , u,) + (u,, u2,. . . , u,) = (u1 + u,, u2 + u,,. . . , un + u,)
ku = k(u,, u2,. . . , u,) = ( k u , , ku,, . . . , ku,)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-209-320.jpg)

![214 / Espacios vectoriales euclidianos
constituyen un vínculo importante entre la multiplicación por una matriz A n X n
y la multiplicación por AT.
Ejemplo 5 Suponer que
1 -2
A = [ 2 4
- 1 o
Entonces
1
a partir de lo cual se obtiene
3 1], .=[-;I, v = [ -p1
1
-: ;][ - ;] = [
..
4 -:I[ -;I= [ -; o 1
I 1 - 1.
AU v = 7( - 2) + lO(0) + 5(5) = I 1
u*ATv=(-1)(--7)+2(4)+4(-1)= 11
Así, Au * v = u A%, como garantiza la fórmula (8). Se deja para el lector la
comprobación de que (9) también se cumple. A
UN PRODUCTO Los productos punto proporcionan otra forma de entender la multiplicación
PUNTO de matrices. Recordar que si A = [a,] es una matriz m X r y B = [b,.] es una
CONSIDERADO matriz Y X n, entonces el ij-ésimo elemento de AB es
COMO
MULTIPLICA-CIÓN
MATRICIAL
que es el producto punto del i-ésimo vector renglón de A
y el j-ésimo vector columna de B](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-211-320.jpg)



![220 1 Espacios vectoriales euclidianos
definen una transformación T:R2 -+ H3. Con esta transformación, la imagen del
punto (xl, xz) es
T(X,, X2) = (11 f X2, 3xlX2, 1: -.X:)
Así, por ejemplo,
T(1, - 2 ) = ( - 1 , -6, -3) A
TRANSFORMA- En el caso especial en que las ecuaciones de (1) son lineales, la trasformación T:Rn
CIONES + K" definida por esas ecuaciones se denomina transformación lineal (u ope-
LINEALES DE rador lineal si m = n). Así, una transformación lineal T:R" -+ Rm está definida por
R " a P ecuaciones de la forma
W] = a,+] + a,2x2 + ' ' . + a,,x,
o bien, en notación matricial,
o, más brevemente,
w =Ax
La matriz A = [a-.1 se denomina matriz estrindar de la transformación lineal T y T
se denomina muhplicación porA .
Ejemplo 2 La transformación lineal T:R4 + R3 definida por las ecuaciones
WI = 2x1 - 3x2 f X3 - 5x4
w 2 = 4x, + x2 - 2x3 + ,x4
w3 = 5x, - x* + 4x3
se puede expresar en forma matricial como
de modo que la matriz estándar para T es](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-215-320.jpg)
![4.2 Transformaciones lineales de R" a Rm / 221
ALGUNOS
COMENTARIOS
SOBRE LA
NOTACI~N
La imagen de un punto (xl, x2, x3, x4) se puede calcular directamente a partir de
las ecuaciones de definición (5) o a partir de (6) por multiplicación de matrices.
Por ejemplo, si (xl, x2, x3, x4) = (1, -3, O, 2), entonces al sustituir en (5) se
obtiene
w I = l , w2=3, w,=8
(comprobar) o, alternativamente, a partir de (6)
Si T:R" + Rm es una multiplicación por A, y si es importante recalcar que A es la
matriz estándar para T, entonces la transformación lineal TR" "* Rm se denota
por TA:R" + Rm. Así,
TA(x) = A x (7)
En esta ecuación se sobrentiende que el vector x en R" se expresa como una matriz
columna.
Algunas veces es tedioso introducir una nueva literal para denotar la matriz
estándar de una transformación lineal T:R" -+ R". En esos casos, la matriz están-dar.
para T se denota por el símbolo [q. Con esta notación, la ecuación (7) asume
la forma
T(x) = [ T ] x (8)
Algunas veces se mezclan las dos notaciones para la matriz estándar, en cuyo caso
se tiene la relación
(9)
OBSERVACI~N. Entre toda esta notación es importante tener en mente que se ha
establecido una correspondencia entre las matrices m X n y las transformaciones
lineales de R" a Rm: a cada matriz A le corresponde una transformación lineal T,:
(multiplicación por A), y a cada transformación lineal T:R" "* Rm le corresponde
una matriz [q m X n (la matriz estándar para 7).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-216-320.jpg)

![4.2 Transfornlaciones lineales de Rn a Rm / 223
w, = --x = "x + oy
u'2 = y = ox + y
4 Y
Figura 2 l
o bien, en forma matricial, [:I = [-:, Y][ :1
Como las ecuaciones en (10) son lineales, T es un operador lineal y por (1 1) se
tiene que la matriz estándar para T es
En general, los operadores sobre R2 y R3 que transforman cada vector en su
imagen simétrica con respecto a alguna recta o algún plano se denominan opera-dores
reflexiidn. Estos operadores son lineales. En las tablas 2 y 3 se enumeran al-gunos
de los operadores reflexih comunes.
'ABLA 2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-218-320.jpg)
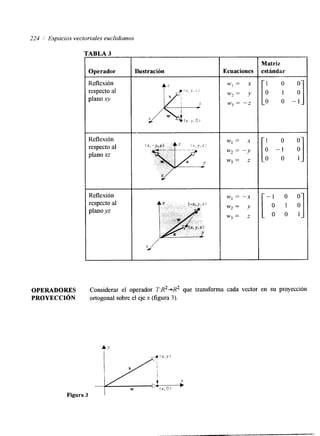
![4.2 Transformaciones lineales de Rn a Rm / 225
Las ecuaciones que relacionan las componentes de x y w = T(x) son
w,=x= x f O y
w* = o = ox + oy
o bien, en forma matricial;
[:I = [:, :][;I
Las ecuaciones en (12) son lineales, de modo que T es un operador lineal y por
(13) se tiene que la matriz estándar para T es
1 0
[T1=[0 o]
En general, un operador proyección (o más precisamente, un operador
proyección ortogonal) sobre R2 o R3 es cualquier operador que transforma
cada vector en su proyección ortogonal sobre una recta o un plano que pasan
por el origen. Es posible demostrar que estos operadores son lineales. En las
tablas 4 y 5 se enumeran algunos de los operadores proyección básicos sobre
R2 y R3.
MBLA 4
I I
Proyección ortogonal
sobre el eje x w, =x
I Proyección ortogonal I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-220-320.jpg)

![4.2 Transformaciones lineales de Rn a Rm / 227
Por medio de las identidades trigonométricas en (1 5) se llega a
w, = r cos O cos 4 - r sen8sen4
w,=rsenOcos ++reos Osen4
y sustituyendo en (14) se obtiene
w, =.xcos O-ysen8
w2=xsen8+ycos8
Las ecuaciones en (16) son lineales, por lo que T es un operador lineal; además;
con base en estas ecuaciones se concluye que lma atriz estándar para í" es
Matriz
Operador
Rotación a través
de un ángulo 8
estándar
St- 8 cos 8 1
(w1,w 2) W, = X C O S 8 - y e cos O -sen O
( & Y )
Ejemplo 5 Si cada vector en R2 se hace girar un ángulo n/6 = (30°), entonces la
imagen w de un vector es
Por ejemplo, la imagen del vector
x= [:]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-222-320.jpg)

![4.2 Transformaciones lineales de R" a Rm / 229
'ABLA 7
Operador
Rotación en
sentido
contrario al
movimiento de
las manecillas
del reloj a través
de un á n a o
respecto al eje x
positivo.
Rotación en
sentido
contrario al
movimiento de
las manecillas
del reloj por un
ángulo
respecto al eje y
positivo.
Rotación en
sentido
Zontrario al
movimiento de
las manecillas
le1 reloj a través
le un ángulo
lespecto al eje z
~ositivo.
Ilustración
tz
t"
Ecuaciones
w, =x
w2 =ycos 0-zsen0
w3 = y sen O + z COS O
w1 = x cos O + z sen0
U'2 = y
= -xsenO+zcosO
w, =xcos 0-ysen0
w2 =xsenO+ycos 0
wj = z
Matriz
estándar
O
cos 8 O sen O .:@I
cos0 - sen0 O
[se; 0 coi O p]
Por completitud, se observa que la matriz estándar para una rotación en
sentido contrario al movimiento de las manecillas del reloj alrededor de un eje en
R3 (detenninado por un vector unitario arbitrario u = (a, b, c) cuyo punto inicial
está en el origen) por un ángulo 8, es
[ a2(I - cos 8) + cos 8 ab(1 - cos 0) - c sen 0 ac(1 - cos 0) + b sen8
ab(l-cos8)+csen8 b2(1-cose)+cos8 b c ( l - c o s ~ ) - u s e n 8
ac(1 - cos 0) - b sen O bc(1 - cos O) + U sen 8 c2(1 - cos 0) + cos O 1 ( 1 7 )
La obtención de este hecho puede consul barse en el libro Yrincipies of Interactive
Computer Graphics, de W. M. Newrnan y R. F. Sproull, 'Nueva York, McGrav-
... . .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-224-320.jpg)



![4.2 Transformaciones lineales de R" a Rm / 233
Figura 8
Ejemplo 7 Sea T,:R2 + R2 el operador reflexión respecto a la recta y = x, y sea
T2:H2 + R2 la proyección ortogonal sobre el eje y. En la figura S se ilustra
grákamente que T, 0 T2 y T2 0 T, tienen efectos distintos sobre un vector x. Esta
misma conclusión se puede obtener mostrando que las matrices estándar para T, y
T, no conmutan:
de modo que [ T, 0 TI ] # [ TI 0 T, 1. A
Ejemplo 8 Sea T,:R2 + R2 la reflexión respecto al eje y, y sea T2:R2 + R2 la
reflexión respecto al eje x. En este caso, T, 0 T2 y Tz 0 T, son iguales; ambas
transforman cada vector x = (x, y ) en su negativo -x = ("x, -y) (figura 9):
t' t'
FTi2g ura 9 T2 T, O O T,](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-228-320.jpg)


![236 / Espacios vectoriales euclidianos
5. Encontrar la matriz estándar para la transformación lineal T definida por la fórmula
a) T(x,, .x2) = (xz, - - S , , xi + 3x,, xI - x2)
b) T(x-, , ,x2, ,uj, x4) = (7x, + 2x2 -x3 + .x4, x2 +x,, -.xi)
c) T(x,, x2. X,) = (O, O, O, O, Oj
d) TCu,, xZr x3, xq) = (x4. x I , xj. x2, .xI -xi)
6. En cada inciso se proporciona la matriz estándar [q de una transformación lineal T.
IJsar la matriz para encontrar í"(x). [Expresar la respuesta en forma matricial.]
7. I?n cada mciso, encontrar í"(x) usando la matriz para T, luego, comprobar el resultado
calculando directamente T(x).
a) T(x,,x,)=(-x,+x,,x,); x = ( - 1 , 4 )
b) 7 ' ( ~ , ,~ 2 X,,) = (2x1 - X > + ~ 3 x,2 + ,uj, O); X = (2, 1, - 3)
8. Por medio de la multiplicación matricial hallar la reflexión de ( - 1,2) respecto a
a) el ejex. b) el ejey. c) la recta y = x.
9. Usar la multipiicación matricial para encontrar la reflexión de (2, -5, 3) respecto al
a) planoxy. b) planoxz. c) plano yz.
10. Mediante multiplicaci6n matricial obtener la proyección ortogonal de (2, -5) sobre
a) el eje x. b) el ejey.
11. Utilizar la multiplicación matricial para encontrar la proyección ortogonal de (-2, 1,
3) sobre el
a) plano x y . b) plano xz. c) plano yz.
12. Usar la multiplicación matricial para encontrar la imagen del vector (3, -4) cuando se
hace girar un ángulo de
a) 0 = 30O b) 8= -60' C) 0 =45O d) 0 = 90°
13. Por medio de la multiplicación matnciai hallar la imagen del vector ( - 2 , 1, 2) si este
se hace girar
a) 30° en sentido contrario al movimiento de las manecillas del reloj con respecto al
eje x.
b) 45O en sentido contrario al movimiento de las manecillas del reloj con respecto al
eje y.
c) 90° en sentido contrario al movimiento de las manecillas del reloj con respecto al
eje z.
14. Encontrax la matrrz estándar para el operador lineal que hace girar un vector en R3 en
sentido del movimiento de las manecillas del reloj hasta describir un ángulo de -60'
con respecto al
a) eje x. b) eje y . c) eje z.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-231-320.jpg)

![,738 Espacios vectoviales euclidianos
20. Determinar si T, U K2 = T, O TI.
a) 7, : R' -+ X' es la proyección ortogonal sobre el eje x y T2X2 += R2 es la proyección
ortogonal sobre el eje y.
b) 7, . R' += R' es la rotación en sentido contrario al movimiento de las manecillas del
reloj hasta describir un ángulo 8, y Tz : R2 -+ R2 es la rotación en sentido contrario
al movimiento de las manecillas del reloj hasta describir un Angulo
c) T I R2 += R2 cs la reflexión respecto al eje x y 7; : R2 += R2 es la reflexión respecto
al eje y.
d) T I : R' + H' es la proyección ortogonal sobre el eje x y T2 : H' -+ R' es la rotación
en sentido contrario ai movimiento de las manecillas del reloj hasta describir un
Lingulo O.
21. Detenninar si T, o 7; = 1- o 7' 1.
a) 7 , : K3 += R 3 cs &a dhatación con factor k y 7, : R 3 + R3 es la rotación en sentido
contrario al movimiento de las manecillas del reloj con respecto al eje z hasta
describir un ángulo
b) T , . R' .+ R3 es la rotación con respecto al eje x hasta describir un ángulo 8, y
T2 : K' -+ R3 es la rotación con respecto al eje z hasta describir un ángulo O,.
22. En R3, las proyecciones ortogonales sobre el eje x, el eje y y el eje z se definen como
respectivamente.
a) Demostrar que las proyecciones ortogonales sobre los ejes de coordenadas son
operadores lineales y encontrar sus matnces estándar.
b) Demostrar que si TR3 + R3 es una proyección ortogonal sobre uno de los ejes de
coordenadas, entonces para todo vector x en R3 los vectores T(x) y x - T(x) son
ortogonales.
c) Hacer una figura mostrando x y x - T(x) en el caso en que T es la proyección
ortogonal sobre el eje x.
23. A partir de la fórmula (1 7), obtener las matnces estándar para las rotaciones en sentido
contrario al movimiento de las manecillas del reloj respecto al eje x, al eje y y al eje z
en R3
24. Usar la fórmula (17) para encontrar la matnz estándar de una rotación de 90° en
sentido contrario al movimiento de las manecillas del reloj respecto al eje determinado
por el vector v = ( 1, 1, 1 ). [Nota La fórmula (1 7) requiere que la longitud del vector
que define el eje de rotación sea 1 .]
25. Comprobar la fórmula (21) para las transformaciones lineales dadas.
a) TI@,, x,) = (si +x,, xI - .y2) y T2(xl, x2) = (3.x,, 2rI + 4*,)
b) T, ( x , ..x 2) = (4u1, -2s, +.Y,, -xI - 3x2) y T,(-~l,xz,x3=(.)Y, + 2.r2 - x 3 , 41, -xj)
c) T,(x,, S ? , .x3) = (-x1 + x2, "Y> + xj, - x 3 + X i ) y T2(.Xl, x2, Xj) =
( - 2.x,, 3x3, - 4x,)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-233-320.jpg)
![4.3 Propiedades de las transformaciones lineales de Rn a Rm / 239
26. Se puede demostrar que si A es una matriz 2 X 2 con det(A) = 1 y tal que los vectores
columna de A son ortogonales y tienen longitud 1, entonces la multiplicación por A es
una rotación en sentido contrario al movimiento de las manecillas del reloj hasta
describir algún ángulo O. Comprobar que
satisface las condiciones planteadas y encontrar el ángulo de rotación.
27. El resultado del ejercicio 26 también es verdadero en R3: se puede demostrar que si A
es una matriz 3 X 3 con det(A) = 1 y tal que los vectores columna de A son ortogonales
por parejas y tienen longitud 1, entonces la multiplicación por A es una rotación en
sentido contrario al movimiento de las manecillas del reloj con respecto a algún eje de rota-ción
hasta describir algún ángulo O. Usar la fórmula (1 7)p ara demostrar que si A satis-face
las condiciones establecidas, entonces el ángulo de rotación satisface la ecuación
tr(A) - 1
cos 0 = ~
2
28. Sea A una matriz 3 X 3 que satisface las condiciones planteadas en el ejercicio 27. Se
puede demostrar que si x es cualquier vector en R3, entonces el vector
u = A x +ATx + [ 1 - t r ( ~ ) ] x
determina un eje de rotación cuando u se coloca con su punto inicial en el origen. [Ver
The Axis of Rotation: Analysis, Algebra, Geomety, de Dan Kalman, Mathematics Ma-gazine,
Vol. 62, No. 4, Oct. 19891.
a) Demostrar que la multiplicación por
es una rotación.
b) Encontrar un vector de longitud 1 que defina un eje de rotación.
c) Usar el resultado del ejercicio 27 para encontrar el ángulo de rotación en sentido
contrario al movimiento de las manecillas del reloj alrededor del eje obtenido en el
inciso b).
4.3 PROPIEDADES DE LAS TRANSFORMACIONES LINEALES DE RnA Rm
En esta sección see studiará la relación entre la invertibilidad deu na matriz y las
propiedades de la transformación matricial correspondiente. También se obten-drá
una representación de las transformaciones lineales de R" a Rm que cons-tituyen
la base paratr ansformaciones lineales más generales que se analizarán en
secciones ulteriores, y se estudiarán algunas propiedades geométricas de los
eigenvectores.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-234-320.jpg)



![4.3 Propiedades de las transformaciones lineales de R" a Rm / 243
Antes de presentar un ejemplo, será de utilidad mencionar algo sobre la
notación. Cuando un operador lineal uno a uno sobre R" se escribe como ZRn "*
R" (en vez de TA:Rn + R"), entonces el inverso del operador T se denota por T " l
(en vez de TA-,). Como la matriz estándar de T" es la inversa de la matriz
estándar para T, se tiene u [ T" ] = [ TI"
Ejemplo 4 Sea TR2 + R2 el operador que hace girar cada vector de R2 hasta des-cribir
el ángulo 0; de modo que por la tabla 6 de la sección 4.2
COS 8 -sen8
1
[ ' 1 = [seno cos 0 Geométricamente es evidente que para deshacer el efecto de T es necesario hacer
girar cada vector de R2 por un ángulo -0. Pero esto es exactamente lo que hace el
operador T- I, ya que la matriz estándar para T- es
[ T " ] = [ T ] " = cos( - 8) -sen( - 8)
sen(- 8) cos( - 8)
(comprobar), que es idéntica a (2), excepto que se sustituye por -0. A
Ejemplo 5 Demostrar que el operador lineal T:R2 + R2 definido por las ecuacio-nes
w, = 2x, + x2
w, = 3x1 + 4x,
es uno a uno, y encontrar T"(W~, w2).
Solución. La forma matricial de estas ecuaciones es
de modo que la matriz estándar para T es
Esta matriz es invertible (de modo que T es uno a uno), y la matriz estándar
para T" es](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-238-320.jpg)

![4.3 Propiedades de las transformaciones lineales de R" a Rm / 245
más términos; por ejemplo, si u, v y w son vectores cualesquiera en R", entonces
agrupando primero v y w y aplicando la propiedad u) se obtiene
T(u + v + w) = T(u + (v + w)) = T(u) + T(v + w) = T(u) + T(v) + T(w)
e, = I] , e2 =
Más generalmente, para vectores cualesquiera Y,, v2, . . . , Vk en R". se tiene
T(v, t v2 + . . ' + V k ) = T(v,) + T(v,) + . . . + T ( V k )
Luego, para encontrar la matriz A , sean e l , e 2., . . , en los vectores
y sea A la matriz cuyos vectores columna consecutivos son T(el), T(e2), . . . ,
T(e,); es decir,
Si
x =
es cualquier vector en R", entonces como se analizó en la sección 1.3, el producto
Ax es una combinación lineal de los vectores columna de A con coeficientes de x,
de modo que
con lo que se completa la demostración. 0
La Expresión (5) es importante por derecho propio, ya que constituye una
fórmula explicita con la cual la matriz esthadar para un operador lineal TR'' -+ Rm
se puede expresar en términos de las imágenes de los vectores e,, e2. . . . , e, bajo
T. Por razones que serán analizadas después, los vectores el, e2' . . . . e, en (4) se](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-240-320.jpg)
![246 ,' Espacios vectoriales euclidianos
denominan vectores estándar brisicos para R". En R2 y R3 se trata de los vectores
de longitud 1 situados a lo largo de'los ejes de coordenadas (figura 4).
Figura 4 I ase normal para P . 1
Debido a su importancia, la expresión (5) se planteará como teorema para
fines de referencias futuras.
Teorema 4.3.3. Si TR" + Rm es una transformación lineal y el, e2, , , . , en
son los vectores estrindar. brisicos para R", entonces la matriz estándar para 7
es
La fórmula (6) es un medio eficaz para encontrar matrices estándar y ana-liza
el efecto geométrico de una transformación lineal. Por ejemplo, suponer que
T:R3 * R3 es la proyección ortogonal sobre el plano xy. Con referencia a la figura
4, geométricamente es evidente que
de modo que por (6)
[ T I = [ : It]
lo que concuerda con el resultado de la tabla 5.
Usando (6) de otra forma, suponer que TA:R3 -+ R2 es la mUltipliCaCiÓn Por
-1 2 1
A = [ 3 o 61](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-241-320.jpg)




![4.3 Propiedades de las transformaciones lineales de R" a Rm / 251
Ejemplo 8 Sea T:R3 -* R3 la proyección ortogonal sobre el plano xy. Los
vectores en el plano xy son transformados en sí mismos bajo T, de modo que
todo vector diferente de cero en el plano xy es un eigenvector correspondiente
al eigenvalor 1 = 1. Todo vector x a lo largo del eje z es transformado en O
bajo T, que está en la misma recta quex , de modo que todo vector diferente de
cero sobre el eje z es un eigenvector correspondiente al eigenvalor A = O. Los
vectores que no están en el plano xy o a lo largo del eje z no son transforma-dos
en múltiplos escalares de ellos mismos, de modo que no existen otros
eigenvectores o eigenvalores.
Para comprobar algebraicamente estas observaciones geométricas, recordar
de la tabla 5 de la sección 4.2 que la matriz estándar para T es
La ecuación característica de A es
det(AZ - A) =
O
A - 1 o o
o a - ] o = o
O O h
cuyas soluciones 1 = O y 1 = 1 ya se anticiparon.
pondientes a un eigenvalor A son las soluciones diferentes de cero de
Como se analizó en la sección 2.3, los eigenvectores de la matriz A corres-
Si A = O, este sistema es [ -; -A O :][:;I =[!I 0 x3
cuyas soluciones son x1 = O, x2 = O, x3 = t (comprobar), o bien, en forma matricial,
Como ya se había anticipado, estos son los vectores a lo largo del eje t. Si ,I =' 1,
entonces el sistema (9) es](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-246-320.jpg)









![5.1 Espacios vectoriales reales 1 261
Figura 1 al hi C l
OBSERVACI~N. En el ejemplo precedente, la atención se centró en el interva-lo
(-m, m). En caso de que la atención se hubiera restringido a algún intervalo
cerrado [a, b] o en algún intervalo abierto (a, b), las funciones definidas en estos
intervalos con las operaciones establecidas en el ejemplo también hubieran produ-cido
espacios vectoriales. Estos espacios vectoriales se denotan por F [a, b] y F(a,
b), respectivamente.
Ejemplo 5 Sea V = R2, con las operaciones de adición y multiplicación escalar de-finidas
como sigue: Si u = (u1, u2) y v = (vl, v2), entonces se define
u + v = ( u , + u , , u , + u , )
y si k es cualquier número real, entonces se define
ku = ( k u , , O)
Por ejemplo, si u = (2, 4) y v = ( - 3 , 5), y k = 7, entonces
u + v = ( 2 + ( - 3 ) , 4 + 5 ) = ( - 1 , 9 )
ku = 7u = (7.2, O) = (14, O)
La operación de adición es la operación de adición estándar sobre R2, pero la
multiplicación escalar no es la multiplicación escalar estándar. En los ejercicios se
pide al lector demostrar que se cumplen los nueve primeros axiomas de espacio
vectorial; sin embargo, existen valores de u para los cuales no se cumple el axioma
10. Por ejemplo, si u = (u,, u2) es tal que u2 # O, entonces
lu = l(u,, u2) = (1 . u , , O) = (u,, O) # u
Por tanto, V no es un espacio vectorial con las operaciones establecidas. A
Ejemplo 6 Sea Vcualquier plano qui: pasa por el ongen en R'. Se demostrara que
los puntos en V constituyen un espacio kectorial bajo las Operaciones estandar de
adxión y multiplicación escalar para veclores en I?'P.o r el ejemplo I, se sabe que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-256-320.jpg)
![262 / Espacios vectoriales genevales
t
R3 mismo es un espacio vectorial bajo estas operaciones. Así, los axiomas 2, 3, 7,
8, 9 y 10 se cumplen para todos los puntos en R3 y en consecuencia, para todos
los puntos en el plano V. Por consiguiente, basta demostrar que se cumplen los
axiomas 1,4, 5 y 6.
Como el plano Vpasa por el origen, tiene una ecuación de la forma
ax + by + cz = O (1)
(Teorema 3.5.1). Por tanto, si u = (ul, u2, u3) y v = (vl, v2, v3s)o n puntos en V,
entonces aul + bu2 + cu3 = O y a v l + bv2 + cv3 = O. Sumando estas ecuaciones se
obtiene
a(u* + U]) + b(u, + u2) + c(u3 + u3) = o
Esta igualdad establece que las coordenadas del punto
u + v = (U] + u1, u2 + u2, u3 + u3)
satisfacen (1); así, u + v está en el plano V. Esto demuestra que se cumple el
axioma 1. Las verificaciones de los axiomas 4 y 6 se dejan como ejercicios; sin
embargo, se demostrará el axioma 5. AI multiplicar aul + bu2 + cu3 = O por - 1 se
obtiene
Así, "u = ( -ul, -u2, -u3) está en I.'. Esto establece el axioma 5. A
Ejemplo 7 Sea V que consta de un solo objeto, el cual se denota por O, y se define
o + o = o
kO = O
para todos los escalares k. Es fácil comprobar que se cumplen todos los axiomas de
espacio vectorial. Este espacio se denomina espacio vectorial cero. A
ALGUNAS A medida que se avance, se agregarán más ejemplos de espacios vectoriales a la
PROPIEDADES lista. Esta sección concluye con un teorema que da una lista útil de propiedades
DE LOS vectoriales.
VECTORES
Teorema 5.1.1. Sean V un espacio vectorial, u un vector en V y k un escalar;
entonces:
a) Ou = O
b) kO = O
c) (-I)u= If "u
d) ku = O, entonces k = O o u = O.
Se demostrarán los incisos a) y c), y las demostraciones de los demás incisos se
dejan como ejercicios. -](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-257-320.jpg)
![5. I Espacios vectoriales reales / 263
Demostración de a). Se puede escribir
ou + ou = (O + O)u [Axioma 81
= ou [ Propiedad del número O 1
Por el axioma 5, el vector Ou tiene un negativo: -0u. Al sumar este negativo a
ambos miembros de la última e>rpresión se obtiene
O
ou + [Ou -t (-Ou)] = ou + (-OU) [Axioma 31
o u + o = o [Axloma 51
ou = o [Axloma 41
Demostración de c). Para probar (- 1)u = “u, es necesario demostrar que u +
(- I)u = O. Para ver esto, obsérvese que
u + ( - l ) u = l u + ( - l ) u [Axloma 101
= (1 + (- 1))u [Axloma 81
= Ou (Propiedad de los números]
= o 0 [ Inciso u)]
EJERCICIOS DE LA SECCIóN 5.1
En los ejercicios del 1 al 13 se da un conjunto de objetos, junto con operaciones de adición
y multiplicación escalar. Determinar cuáles conjuntos son espacios vectoriales bajo las ope-raciones
dadas. Para aquellos que no sean espacios vectoriales, enumerar los axiomas que
no se cumplen.
1. El conjunto de todas las temas de números reales (x, y, z) con las operaciones
(x, y, z) + (x’, y’, z’) = (x + x’, y + y’, i + 2’) y k(x, y, 2) = (kx, ,Y, z)
2. El conjunto de todas las temas de números reales (x, y, z) con las operaciones
(x, y, z) + (x‘, y‘, z‘) = (x + x’, y +y‘, 2 + z‘) y k(x, >, z) = (O, o, O)
3. El conjunto de todas las parejas de números reales (x, y) con las operaciones
(x, Y ) f (x’, Y’) = (x + x‘, y +u‘) y k(x, y) = W x , 2ky)
4. El conjunto de todos los números reales x con las operaciones estándar de adición y
multiplicación.
5. El conjunto de todas las parejas de números reales de la forma (x, O) con las opera-ciones
estándar sobre R2.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-258-320.jpg)




![268 / Espacios vectoriales generales
Estas funciones son de la forma indcada en (l), de modo que p + q y kp están en
W. El espacio vectorial W de este ejemplo se denotará por el símbolo P,. A
Ejemplo 6 (Para quienes ya estudiaron Cálculo). Recuérdese que si f y g son
funciones continuas en el intervalo (- m, m) y k es una constante, entonces f
+ g y kf también son continuas. Así, ías funciones continuas sobre el intervalo
(- m, m) forman un subespacio de F(- m, m), ya que son cerradas bajo la
adición y la multiplicación escalar. Este subespacio se denota por C(- 03, m).
De manera semejante, si f y g son funciones derivables, entonces también f +
g y hf son derivables. Así, las funciones con primeras derivadas continuas
sobre (- m , m ) forman un subespacio de F(- m, m). Este subespacio se
denota por C1(- m, m), donde el supraíndce 1 se usa para recalcar la primera
derivada. Sin embargo, un teorema del Cálculo es que toda función derivable es
continua, de modo que C'( - 03, m) es en realidad un subespacio de C(- m, m).
Continuando con lo anterior, para todo entero positivo m las funciones con
m-ésimas derivadas continuas sobre (- m, m) forman un subespacio de C'( - CQ,
m), así como también las fúnciones que tienen derivadas continuas de todos los
órdenes. El subespacio de las funciones con m-ésimas derivadas continuas
sobre (- m, m) se denota por P(-m , m), y el subespacio de las funciones que
tienen derivadas continuas de todos los órdenes se denota por Cm(- m, m>.
Finalmente, un teorema del Cálculo es que los polinomios tienen derivadas
continuas de todos los órdenes, de modo que P, es un subespacio de Cm (- m. m).
La jerarquía de los subespacios analizados en este ejemplo se representa en la
figura4. A
OBSERVACI~N. En el ejemplo precedente, se atendió al intervalo (- m, m).
En caso de haber atendido al intervalo cerrado [a, 61, entonces los subespacios
correspondientes a los espacios vectoriales definidos en el ejemplo se hubieran de-notado
por C[a, b], Cm [a, b] y C[a, b ] . De manera semejante, sobre un inter-valo
abierto (a, b), esos subespacios se hubieran denotado por C(a, b), ?(u,
b) Y cm(a ,b ).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-263-320.jpg)
![5.2 Subespacios / 269
ESPACIOS Si Ax = b es un sistema de ecuaciones lineales, entonces todo vector x que satis-
SOLUCIóN DE face esta ecuación se denomina vector solucidn del sistema. El siguente teorema
SISTEMAS muestra que los vectores solución de un sistema lineal homogéneo forman un
HOMOGÉNEOS espacio vectorial. que se denomina espacio solución del sistema.
es un sistema lineal homogéneo de m ecuaciones con
n incógnitas, entonces el conjunto de vectores solución es un subespacio de R".
I I
Demostración. Sea W el conjunto de vectores solución. En W existe por 10
menos un vector, a saber, O. Para probar que W es cerrado bajo la adición y la
multiplicación escalar, es necesario demostrar que si x y x' son vectores solución
cualesquiera y k es cualquier escalar, entonces x + x' y b también son vectores
solución. Pero si x y x' son vectores solución, entonces
Ax=O y Ax'=O
a partir de lo cual se deduce que
A(x+x')=Ax+Ax'=O+O=O
Y
A(kx) = kAx = kO = O
lo que demuestra que x + x' y kg son vectores solución. 0
Ejemplo 7 Considerar los sistemas lineales
a) [i -% j[:l-[B1 b) [ -3 1 -2 7
c) [-i -: -:][!]=[d): ][O0 O0 O0]
-2 4
0 0 0
Cada uno de estos sistemas contiene tres incógnitas, de modo que las soluciones
son subespacios de R3. Geométricamente, esto sigmfka que cada espacio solución
debe ser UM recta que pasa por el origen, un plano que pasa por el origen, sólo el
origen o todo R3. A continuación se comprobará que así es (se deja para el lector
la resolución de los sistemas).
Solución.
a) Las soluciones son
x=2s- 34 y=s, z = t
a partir de lo cual se concluye que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-264-320.jpg)



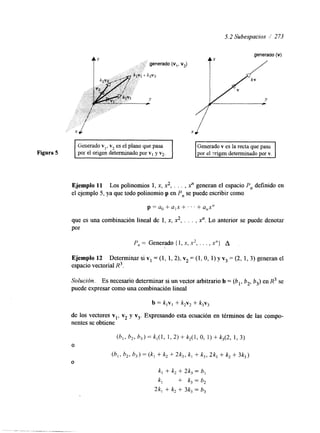

![5.2 Subespacios / 275
a) Todos los polinomios a. + alx + u$ + a+3 para los que a. = O.
b) Los polinomios a0 + alx + a$ + a,$ para los que a. + al + a2 + a3 = o.
c) LOS polinomios a. + alx + U.$ + a3x3 para los que ao, a,, a2 y a3 son enteros.
d) Los polinomios de la forma a,, + a,x, donde a. y a, son números reales.
4. Usar el teorema 5.2.1 para determinar cuáles de los siguientes conjuntos son subespa-cios
del espacioF ( - 03, m).
a) Todas lasftales queflx) O para toda x. b) Todas lasftales quefl0) = O.
c) Todas lasftales quef(0) = 2. d) Todas las funciones constantes.
e) Todas lasfde la forma k, + k, sen x, donde k, y k, son números reales.
5. Usar el teorema 5.2.1 para determinar cuáles de los siguientes conjuntos son subespa-cios
de M,,,,.
k
a) Las matrices A n X n tales que tr A) = O.
b) Las matrices A n X n tales que A = -A.
c) Las matricesA n X n tales que el sistema linealA x = O sólo tiene la solución tnvial.
.)A=[-: -1 1 i] b)A=[-3 1 -2 "1 c ) ,4=[21 52 331
6. Determinar si el espacio solución del sistema Ax = O es una recta que pasa por el
origen, un plano que pasa por el origen o sólo es el origen. Si es un plano, encontrar su
ecuación; si es una recta, encontrar sus ecuaciones paramétricas.
-4 -5 :] -2 -6 1 0 18 8
i]
d)A=[! 2 -6 e ) A = [ i l!] f, A=[: - 3 7. ¿Cuáles de los siguientes vectores son combinaciones lineales de u = (O, -2, 2) y v =
(1,3, -l)?
a) (2,2,2). b) (3, 1,5). c) (O, 4, 5). d) (0, o, O).
8. Expresar cada uno de los siguientes vectores como combinaciones lineales de u = (2, 1,
4), v = (1, -1,3) y w = (3,2, 5).
a) (-9, -7, -15). b) (6, 11,6). c) (0, o, O). d) (7,8, 9).
9. Expresar cada uno de los siguientes polinomios como una combinación lineal de p, = 2
+ x + 4 2 , p 2 = 1 - x + 3 2 y p 3 = 3 + 2 x + 5 2 .
a) -9 - 7x - 152. b)6+11x+62. c) o. d) 7 + 8x+ 92.
10. ¿Cuáles de las siguientes matrices son combinaciones lineales de
11. En cada inciso, determinar si los vectores dados generan R3
a) vl = (2, 2, 21, v2 = (O, O, 31, v3 = (O, 1, 1)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-270-320.jpg)
![13. Ikterminar si los slguientes polinomios generan P,.
p, = I -- x + 3 2 . pz = 3 + x.
p, = 5 ~ - tx 4 *'. ps = - 2 " 2.u Jr 2 2
14. Sean v, = (2, I , O, 3), v, = (3, - 1, 5, 2) y vj = (- 1, O, 2, 1). LCuáIes de los siguientes
vectores están en lin {v,, v2, v3)?
a) (2,3, -7,3). h) (a, O, o. o) C) ( I , I . I. 1). d) -4,6, -13,4).
IS. hcontrar la ecuación del plano generado por los vectores u = (-- 1, 1, I ) y v = (3,4.4).
16. Encontrar las ecuaciones paramétricas de la recta generada por el vector u = ( 3 , -2, 5).
17. Demostrar que los vectores solución de un sistema no homogéneo consistente de m
ccuaciones linealcs con n incógnitas no forma un subespacio de R".
18. Demostrar el teorema 5.2.4
19. Aplicar el teorema 5 2.4 para demostrar que
v , = ( l . h . 4 ) , v , = ( 2 . 4 , -1). v 3 = ( - l , 2 , 5 )
Y
W! = ( I , -2, - 5 ) , WI = (O. 8, 9)
general el msmo subespacio de R'.
20. llna recta L que pasa por el origen en R3 se puede representar por ecuaciones
paramétricas de la forma x = at, y = ht y z = ct. Usar estas ecuaciones para demostrar
que L es un subespacio de R3; es decir, si v, = (x,, y,, z,) y v2 = (x2, y,, z2) son puntos
en L y k es cualquier número real. entonces k v , y v, + v2 también son puntos en L.
21. (Para quienes ya estudiaron Cdkulo). Demostrar que los siguientes conjuntos de
funciones son subespacios de F( - m, m).
a) Las funciones que son continuas en todas partes.
b) Las funciones que son derivables en todas partes.
c) Idas funciones que son derivables en todas partes y que satisfacen f + 2f = O.
22. (Pura quienes ya estudiaron Cúlculo). Demostrar que el conjunto de funciones conti-nuas
f =./(x) sobre [a, bj tales que
f f (x) dx = O
es un subespacio de C [a, h]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-271-320.jpg)











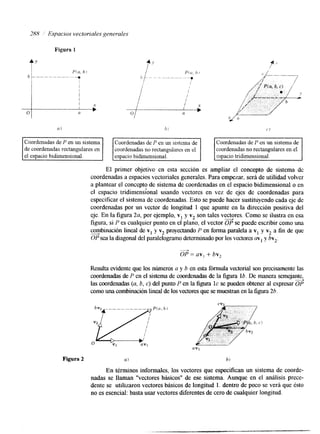





![294 / Espacios vectoriales generales
de modo que S es una base para R3. A
Ejemplo 4 Sea S = {vl, v2. v3] la base de R3 en el ejemplo precedente.
a) Encontrar el vector de coordenadas de v = ( 5, - 1, 9) con respecto a S.
b) Encontrar el vector v en R3 cuyo vector de coordenadas con respecto a la base
Ses ( v ) , ~=(- 1. 3. 2).
Solución de a). Es necesario encontrar escalares cl, c2, c3 tales que
v = c,v, + c2v2 + c3v3
o bien, en términos de las componentes.
(5, - I , 9) = c,(l, 2, 1) + c2(2, 9, O) + c3(3, 3, 2'
Igualando las componentes correspondientes se obtiene
C1 + 2C2 f 3C3 zz 5
2C, + 9C2 + 3C3 = - 1
CI +4c, = 9
Resolviendo este sistema se obtiene c1 = 1, c2 = - 1, c3 = 2 (comprobar). Por
consiguiente,
(v)s = (1, - 1, 2)
Solución de h). Aplicando la definición del vector de coordenadas ( v ) ~ , se
obtiene
v = ( - l ) ~+, 3 ~ +2 2 ~ 3
=(-1)(1,2, 1)+3(2,9,0)+2(3, 3,4)=(11,31,7) A
Ejemplo 5
a) Demostrar que S = { 1, x, x*, . . . . x"} es una base para el espacio vectorial Pn
b) Encontrar el vector de coordenadas del polinomio p a. + alx + a2x2 con
de polinomios de la forma a. + alx + . . . + a&'.
respecto a la base S = { 1, x, x,} para P,.
Solución de a). En el ejemplo 11 de la sección 5.2 se demostró que S genera a
P2, y en el ejemplo 5 de la sección 5.3 se demostró que S es un conjunto
linealmente independiente. Así, S es una base para P,; se denomina base estándar
para P,.
Solución de a). Las coordenadas de p = a. + alx + a2x2 son los coeficientes
escalares de los vectores básicos 1, x y x2, de modo que = (ao, al, a,). A](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-289-320.jpg)
![5.4 Rase y dimensión 1 295
Ejemplo 6 Sean
DIMENSI~N
El conjunto S = {M1, M,, M3, M4) es una base para el espacio vectorial de
matrices 2 x 2. Para constatar que S genera a M,,, obsérvese que un vector
(matriz) cualesquiera
se puede escribir como
Para constatar que S es linealmente independiente, supóngase que
aM, + bM2 + CM, + dA4, = O
Es decir,
a[ 'O O0 ] +b[OO 0 'I+# : ]+d [ oO 0I]=[ : :]
Se concluye que
Así, a = b = c = d = O, de modo que S es linealmente indepenjiente. La base S en
este ejemplo se denomina base estúindar para M2,. De manera más general, la
base estándar para Mnn consta de las mn matrices diferentes que tienen un solo 1
y cuyos elementos restantes son ceros. A
Ejemplo 7 Si S = {vl, v,, . . . , vr} es un conjunto linealmente independiente en
un espacio vectorial V, entonces S es una base para el subespacio lin (S?, ya que
por definicibn de lin (S) e! conjunto S genera a lin (S). A
Definición. Se dice que un espacio vectorial Y diferente de cero es de dimensión
finita si contiene un conjunto finito de vectores vl, v2, . . . , v,, que forma una
base. Si es así, se dice que V es de dimensión infinita. Además, se considera
que el espacio vectorial cero es de dimensión finita. A
Ejemplo 8 Por los ejemplos 2, 5 y 6, los espacios vectoriales R", Pn y M,,,, son de
dimensión finita. Los espacios vectoriales F(- m, m), C(- m, m), Cm( - m, w)
y C" (- m, m) son de dimensión infinita (ejercicio 23). A](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-290-320.jpg)







![5.4 Base y dimensión / 303
Demostración del teorema 5.4.4b Supóngase que S = {vl, v2, . . . , vr} es un
conjunto de vectores en V y, para ser específícos, supóngase que v, es una
combinación lineal de vl, v2, . . . , v,- 1, por ejemplo
Se quiere demostrar que v s,i se quita de S, entonces el conjunto de vectores restante
(vl, v2, . . . , v,.-~} sigue generando a lin (9; es decir, se debe demostrar que todo
vector w en lin (S) se puede expresar como una combinación lineal de {y1, v2, . . . ,
v }. Pero si w está en lin (S), entonces w se puede expresar en la forma r- 1
o bien, sustituyendo en (1 3)
que expresa a w como una combinación lineal de vl, v2, . . . , vr- u
EJERCICIOS DE LA SECCIóN 5.4
1. Explicar por qué los siguientes conjuntos de vectores no son bases de los espacios
vectoriales indicados. (Resolver este problema por inspección.)
a) u, = (1, 2), u2 = (O, 3), uj = (2, 7) para R2
b ) u l = ( - 1 , 3 , 2 ) , u,=(6,1,1)paraR3
C) pI = 1 +x + x2, p2 =x - 1 para P2
2. LCuAles de los siguientes conjuntos de vectores son bases para R2?
a1 (2, 11, (3, 0) b) (4, 11, (-7, -8) C) (0, O), (1, 3) (d) (3,9), (-4, - 12)
3. ¿Cuáles de los siguientes conjuntos de vectores son bases para R3?
a) (1, O, 01, (2,2, O), (3, 3, 3) b) (3, 1, - 4h (2, 5, 6h (1,4, 8)
C) (2. -3, 11, (4, 1, I ) , (0, -7, 1) d) (1, 6, 41, (2, 4, - 11, (- 1, 2, 5)
4. ¿Cuáles de los siguientes conjuntos de vectores son bases para P2?
a) 1 - 3 X + 2 ~ ~ , 1 + ~ + 4 ~ ~ , 1 - 7 ~ b ) 4 + 6 x + x 2 , - 1 + 4 x + 2 x 2 , 5 + 2 x - x 2
c) 1 +x+x2,x+x2,2 d) - 4 + ~ + 3 ~ ~ , 6 + 5 ~ + 2 ~ ~ , 8 + 4 x + x '
5. Demostrar que el siguiente conjunto de vectores es una base paran/iZ2. [: - 0 6 1 1 [-Y - : I 9 [-I: 3 [ -; :]
6. Sea Vel conjunto generado por vl = cos2 x, v2 = sen2 x, v3 = cos 2x
a) Demostrar que S = {y1, v2, v3} no es una base para V.
b) Determinar una base para V.
7. Encontrar el vector de coordenadas de w con respecto a la base S = {u], u2}para R2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-298-320.jpg)

![5.4 Base y dimensión / 305
23. a) Demostrar que para todo entero positivo n, en F( - m, m) se puede hallar n + 1 vec-b)
tores linealmente independientes. [Sugerencia Buscar polinomios.]
Usar el resultado del inciso a) para demostrar que F( -m, m) es de dimensión
c) Demostrar que C( - m, m), Cm( - m, m) y C (- m, m) son espacios vectoriales de
mfihita.
dimensión m f i i t a .
24. Sea S una base de un espacio vectorial V de dimensión n. Demostrar que si vl, v2, . . .
vr forman un conjunto linealmente independiente de vectores en V, entonces los vec-tores
de coordenadas ( v ~(v)JS~, . . . , (v& forman un conjunto linealmente indepen-diente
en R" y recíprocamente.
25. Usando la notación del ejercicio 24, demostrar que si vl, v2, . . . vr generan a V,
entonces los vectores de coordenadas ( v ~ )(~v,&, . . , , ( v ~g)en~er an a R" y recípro-camente.
26.
21.
28.
Encontrar una base para el subespacio de P2 generado por los vectores dados.
a) - 1 + x - 2x2, 3 + 3x + 62, 9 b) 1 +x, x2, -2 +2x2, -3x
C) 1 + X - 3x2, 2 + 2~ - 6x2, 3 + 3~ - 9x2
[Sugerencia Sea S la base estándar para P2 y trabájese con los vectores de
coordenadas relativos a S; consultar los ejercicios 24 y 25.1
En la figura 7 se muestran un sistema de coordenadas rectangularesx y y un sistema de
coordenadas x)' con ejes oblicuos. Suponiendo que en todos los ejes la escala mide 1
unidad, encontrar las coordenadas xy de los puntos cuyas coordenadas xy se propor-cionan.
a> (1, 1). b) (1,O). c) (O, 1). d) (a, b).
X'
Figura 7
En la figura 8 se muestran un sistema de coordenadas rectangulares xy determinado por
los vectores unitarios básicos i y j y un sistema de coordenadas xy determinado por los
vectores unitarios básicos u1 y u2. Encontrar las coordenadas xy de los puntos cuyas
coordenadas xy se proporcionan.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-300-320.jpg)
![5.5 ESPACIO RENGLÓN, ESPACIO COLUMNA Y ESPACIO NULO
Se enipezard con algunas definiciones.
VECTORES
VECTORES
COLUMNA
RENGL ~NY
Definicidn. Para una matriz m X n
r
los vectores
-=: [%! ' ' . U,? 3
:II Rn formados a partir de los renglones de A se denomin
1, y los vectores
ores renglón de
:n Rm fonuados a partir de las columnas de 11 se denominan vedores columna
IcA.
I
Ejemplo I Sea
' "i " I 4
los vectores renglón de A son
r , = [ 2 I O ] y r , = [ 3 -1 41](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-301-320.jpg)


![5.5 Espacio renglón, espacio columna y espacio nulo / 309
lo cual indica que x - x. es una solución del sistema homogéneo Ax = O.
Como vl, v2, . . . , vk es una base para el espacio solución de este sistema,
entonces x - x. se puede expresar como una combinación lineal de estos
vectores, por ejemplo
x - X" = C,V, + c2v2 + ' ' ' + CkVk
Por tanto,
x = xg + CIY] CZVz ' ' ' + CkVk
lo que demuestra la primera parte del teorema. Recíprocamente, para todas las
elecciones de los escalares cl, c2., . . , ck en (3) se tiene
Ax = A(x, + ClVi + c2v2 + ' ' ' t CkVk)
O
Ax = Ax, + c,(Av,) 3- C2(AV2) + . ' . + Ck(AVk)
Pero x. es una solución del sistema no homogéneo y vl, v2, ~ . . , vk son soluciones
del sistema homogéneo, de modo que la idtima ecuación lndlca que
lo cual muestra que x es una solución de Ax = h. 0
OBSERVACI~N. Hay cierta terminología asociada con la fórmula (3). El vector x.
se denomina solución particular de Ax =La expresión x. + clvl + c2v2 f . . . , +
ckvk se llama solución general de Ax = b, y la expresión clvl + c2v2 + . . . , + ckvk
se conoce como solución general de Ax = O. Con esta terminología, la fórmula (3)
establece que la solución general de Ax = b es la suma de cualquier solución
particular de Ax = b y la solución general de As = O.
Para sistemas lineales con dos o tres incógnitas, el teorema 5.5.2 posee una
interpretación geométrica interesante en R2 y en R3. Por ejemplo, considérese el
caso en que Ax = O y Ax = b son sistemas lineales con dos incógnitas. Las
soluciones de Ax = O forman un subespacio de R2 y, por tanto constituyen una
recta que pasa por el origen, sólo el origen o todo R2. Por el teorema 5.5.2, las
soluciones de Ax = b se pueden obtener sumando cualquier solución particular de
Ax = b, por ejemplo xo, a las soluciones de Ax = O. Suponiendo que x. está
colocado con su punto inicial en el origen, esto tiene el efecto geométrico de
trasladar el espacio solución de Ax = O de modo que el punto en el origen se
mueve hacia la punta de x. (figura 1). Esto significa que los vectores solución de
Ax = b forman una recta que pasa por la punta de ~0e.l punto en la punta de x*, o
todo R2. (¿Puede el lector imaginar el Ú h m raso?! De marma semtjante. prrra
sistemas lineales con tres incligl'hits, I;I: so!ucioms de Ax -= b constituyen un
plano que pasa por la punta de cuaicyjier scllnci6rr $. ~.lZicuHsrx *. una recta que pasa
por la punta de x0? o todo R3.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-304-320.jpg)

![5.5 Espacio rengldn, espacio columna y espacio nulo / 31 1
I-
-
x = r
-
- 2 :I O1
- ”
3 r - 4
1
O
O - 2
+ S + t
O 1
O O
O O
- ”-
es la solución general del sistema homogéneo
(comprobar). A
BASES PARA Primero se designaron las operaciones elementales en los renglones para resolver
ESPACIOS sistemas lineales y, por ese trabajo. sabe se que al efectuar una operación
RENGL~N, elemental en los renglones de una matriz aumentada no cambia el conjunto so-
ESPACIOS lución dei sistema lineal correspondiente. Se concluye que realizar una operación
COLUMNA Y elemental en los renglones de una matriz A no modifica el conjunto solución del
ESPACIOS sistema lineal correspondiente Ax = O o, expresado de otra forma, no cambia el
NULOS espacio nulo de A . Así, se tiene el siguiente teorema.
Teorema 5.5.3. Las operaciones elementales en los rengr,:nes no camhrrrn el
espacio nulo de una matriz. 1
Ejemplo 4 Encontrar una base para el espacio nulo de
-iJ 2 2 - -; 1 -p o -:]
1
A = [ Solución. El espacio nulo de A es el espacio solución del sistema homogéneo
2x, + 2x2 - x3 +x, =o
” X] - x2 + 2x, - 3x4 + .xg = 0
x1 + x* - 2x, -xg =o
x3 + x4 + xg = o
En el ejemplo 10 de la sección 5.4 se demostró que los vectores](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-306-320.jpg)

![5.5 Espacio renglón, espacio columna y espacio nulo i 313
Aquí nuevamente la segunda columna es un múltiplo escalar de la primera, de
modo que el espacio columna de B consta de todos los múltiplos escalares del
primer vector columna. Este espacio columna no es el mismo que el espacio
columna de A.
Aunque las operaciones elementales en los renglones pueden cambiar el
espacio columna de una matriz, se demostrará que no importa cuáles sean las
relaciones de independencia o dependencia lineal existentes entre los vectores
columna antes de la ejecución de una operación en los renglones. esas relaciones
también se cumplen para las columnas correspondientes de la matriz que se ob-tiene
al realizar esa operación. Para precisar más este hecho, supóngase que una
matriz B se obtiene al efectuar una operación elemental en los renglones de
una matrizA m x n. Por el teorema 5.5.3, los dos sistemas lineales homogéneos
Ax=O y Bx=O
tienen el mismo conjunto solución. Así, el primer sistema tiene una solución no
trivial si y sólo si lo mismo se cumple para el segundo sistema. Pero si los vectores
columna de A y B, respectivamente, son
C], c2,. . . 9 cn Y c1, c2,. . . , c:, I ,
entonces por (2) ambos sistemas se pueden volver a escribir como
Y
X,Cl + x2c2 + ' . ' +X$, = o
xlc; + x2c; + ' . ' +X$:, = o
Así, (5) tiene una solución no trivial para xl, x*, . . . , x, si y sólo si lo mismo es
cierto para (6). Esto indica que los vectores columna de A son linealmente inde-pendientes
si y sólo si lo mismo es cierto para B. Aunque se omitirá la demostra-ción,
esta conclusión también es d i d a para cualquier subconjunto de los vectores
columna. Así, se tiene el siguiente resultado.
Teorema 5.5.5. Si A y B son matrices equivalentes por renglones, entonces
a) Un conjunto dado de vectores columna de A es linealmente independiente si
y sólo si los vectores columna correspondientes de B son linealmente inde-pendientes.
b) Un conjunto dado de vectores columna de A forma una base para el espacio
columna de A si y sólo si los vectores columna correspondientes de B for-man
una base para el espacio columna de B.
El siguiente teorema hace posible encontrar por inspección bases para lps
espacios renglón y columna de una matriz en forma escalonada.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-308-320.jpg)

![5.5 Espacio renglón, espacio columna y espacio nulo 1 315
de A determinando una base para el espacio renglón de cualquier forma escalona-da
de A. Reduciendo A a forma escalonada se obtiene (comprobar)
Por el teorema 5.5.6, los vectores renglón diferentes de cero de R forman una base
para el espacio renglón de R y, por tanto, forman una base para el espacio renglón
de A. Estos vectores básicos son
' , = [ I - 3 4 -2 5 41
r,=[O O 1 3 -2 -61
r,=[O O O O 1 51
Teniendo en cuenta que A y R pueden tener espacios columna diferentes, no
es posible encontrar una base para el espacio columna de A directamente a partir
de los vectores columna de R. Sin embargo, por el teorema 5.5.56 se concluye que
si se puede hallar un conjunto de vectores columna de R que formen una base para
el espacio columna de R, entonces los vectores columna correspondientes de A
formarán una base para el espacio columna de A.
Las columnas primera, tercera y quinta de R contienen los unos principales
de los vectores renglón, de modo que
forman una base para el espacio columna de R; así, los vectores columna corres-pondientes
c, = [ -1 11, %=[ -4 j], ;[ -5 I]
de A, a saber
forman una base para el espacio columna de A. A
Ejemplo 7 Encontrar una base para el espacio generado por los vectores](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-310-320.jpg)
![316 Espacios vectoriales generales
vI=(1, -2,0,0,3), ~ , = ( 2 , -5, -3, - 2 , 6 ) , v 3 = ( 0 , 5 , 15, lO,O),
v4 = (2, 6, 18, 8, 6)
Solución. Salvo por una variación en la notación, el espacio generado por estos
vectores es el espacio renglón de la matriz
1 - 2 o o 3
2 -5 -3 - 2 6
O 5 15 10 Ó
2 6 1 8 8 6
Reduciendo esta matriz a la I forma escalonada se obtiene 1 -
O
0
O
-2
1
O
O _J O
Los vectores renglón diferentes de cero en esta matriz son
WI =(l, -2,0,0,3), w,=(O, 1,3,2,0), w3=(0,O, 1, 1,O)
Estos vectores forman una base para el espacio renglón y por tanto forman
una base para el subespacio de R5 generado por vl, v2, v3 y v4. A
Obsérvese que en el ejemplo 6 los vectores básicos obtenidos para el espacio
columna de A consistían en los vectores columna de A, pero los vectores básicos
obtenidos para el espacio renglón de A no eran todos los vectores renglón de A. El
siguiente ejemplo ilustra un procedimiento para encontrar una base del espacio
renglón de una matriz A que consta completamente de vectores renglón de A .
Ejemplo 8 Encontrar una base para el espacio renglón de
A = [ --2 ; y;o ;; o ;]
que conste completamente de vectores renglón de A.
Solución. Se transpondrá A, convirtiendo así el espacio renglón de A en el
espacio columna de AT; luego se aplicará el método del ejemplo 6 para encontrar
una base del espacio columna de AT; y luego se transpondrá nuevamente a fin de
convertir los vectores columna de nuevo en vectores renglón. Al transponer A se
obtiene](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-311-320.jpg)
![5.5 Espacio I renglón, espacio columna y espacio nulo / 31 7 1 2 O 2
-2 -5 5 6
AT= O -3 15 18
o -2 10 8
3 6 O 6
Reduciendo esta matriz a forma escalonada se obtiene
O
-5 -
O
O
O
I;] O
O
'-;I O
3
Las columnas primera, segunda y cuarta contienen los unos principales, de modo
que los vectores columna correspondientes en AT forman una base para el espacio
columna de AT; éstos son
c, =
i
Y
c ~ = l2 i ]
Transponiendo de nuevo y ajustando correctamente la notación se obtienen los
vectores básicos
rl =[ 1 -2 O O 31, r 2 = [ 2 -5 -3 -2 61,
Y
r 4 = [ 2 6 18 8 61
para el espacio renglón de A. A
Por el teorema 5.5.5 se sabe que las operaciones elementales en los renglo-nes
no modifican las relaciones de independencia lineal o dependencia lineal entre
los vectores columna; sin embargo, las fórmulas (5) y (6) indican un resultado
incluso más profundo. Debido a que estas fórmulas tienen en realidad los mismos
coeficientes escalares xl, xz, . . . , xn, se concluye que las operaciones elementales
en los renglones no modifícan l a s fórmulas (combinaciones lineales) que relacionan
vectores columna linealmente dependienteSse. omite la demostración formal.
Ejemplo 9
a) Encontrar un subconjunto de los vectores](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-312-320.jpg)



![5.5 Espacio renglón, espacio columna y espacio nulo / 321
7. En cada inciso se proporciona una matriz en forma escalonada. Por inspección, Rallar las
bases de los espacios renglón y columna de A.
[: 1 A 2 4 -:5
I -; [" ' :] c) O 0 0 1 d) O -7 O 0
O 0 0 0
8. Para las matnces del ejercicio 6, encontrar una base para el espacio renglón de A redu-ciendo
la matnz a la forma escalonada.
9. Para las matnces del ejercicio 6, encontrar una base para el espacio columna de A.
10. Para las matrices del ejercicio 6, encontrar una base para el espacio renglón de A que
conste completamente de vectores renglón Ade.
11. Encontrar una base para el subespacio de I? generado por los vectores dados.
a) (1, 1, -4, -31, (2, O, 2, -21, (2, - 1, 3,2) (b) (- 1, 1, -2, O), (3,3, 6, O), (9, 0, 0, 3)
c) (1, 1, o, O), (0, o, 1, 11, (-2, o, 2,2), (O, -3, o, 3)
12. Determinar un subconjunto de los vectores que formen una base para el espacio generado
por los vectores; luego, expresar cada vector que no pertenezca a la base como una com-binación
lineal de los vectores básicos.
a ) v l = ( l , O , l , l ) , v , = ( - 3 , 3 , 7 , 1 ) , v , = ( - 1 , 3 , 9 , 3 ) , v 4 = ( - 5 , 3 , 5 , -1)
b ) v , = ( 1 , - 2 , 0 , 3 ) , ~ , = ( 2 , - 4 , 0 , 6 ) , v 3 = ( - 1 , 1 , 2 , 0 ) , ~ , = ( O , - l , 2 , 3 )
~ ) ~ 1 = ( 1 , - 1 , 5 , 2 )~,, =( -2,3,1,0) ,~,=(4, -5,9,4) ,~,=(0,4,2, -3) ,~,=( -7,18,2, -8)
13. Demostrar que los vectores renglónd e una mabiz invertible A n X n fomm una base para R".
14. a) Sea
A = [ ! i]
y considérese un sistema de coordenadas rectangulares xyz en el espacio tndimensional.
Demostrar que el espacio nulo de A consta de todos los puntos del eje z y que el espacio
columna consta de todos los puntos en el plano v.
t1 ' Espacio nulo de A
Y](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-316-320.jpg)





![5.6 Uav1go y nulidad 1' 327
rango 04) 5 nlín (m, n) ( 5 )
donde mín(m. n) denota el menor de los números m y n si m f n o su valor coniún
si m = 11.
Ejemplo 4 Si A es una matriz 7 x 4, entonces el rango de A es menor o igual que
4 y, en consecuencia, los siete vectores renglón deben ser linealmente
dependientes. Si A es una matriz 4 X 7, entonces nuevamente el rango de A es
menor o igual que 4 y. por tanto, 10s siete vectores columna deben ser linealmente
dependientes. A
SISTEMAS En secciones anteriores se obtuvo unamplia gama de teoremas relacionados con
LINEALES DE m sistemas lineales de n ecuaciones con n incógnitas (véase el teorema 4.3.4). Ahora
ECUACIONES la atención se dirigirá a sistemas lineales de m ecuaciones cn n incógnitas en los
CON n cuales m y n no necesariamente SQII iguales.
LNC~GNITAS El siguiente teorema establece condiciones en las que se garantiza que un sis-tema
lineal de w z ecuaciones con n incógnitas es consistente.
Demostración. Basta demostrar las equivalencias a e h y b 9 c. ya que enton-ces
por lógica se concluye que a e c.
a 9 h. Véase el teorema 5.5.1
h e c. Se demostrar5 que si b atá en el espacio columna de A, entonces los
espacios columna de A y de [..I ' b] son iguales en realidad, a partir de lo cual se
concluir6 que estas dos matrices tienen el mismo rango.
Por definición. el espacio columna de una matriz es el espacio generado por
sus vectores columna, de modo que los espacios columna de A y de 1'4 I bl se
pueden expresar c0m0
Generado { c, , c2, . . . , c, } y generado (c, , c2, . . . , c,, b }
respectivamente. Si b está en el espacio columna de A, entonces cada vector
en el conjunto {cl, c2, , . . , c,, b} es una combinación lineal de los vectores en
{c,, c2, . . . , cn} y recíprocamente (¿por qué?). Así, por, el teorema 5.2.4, el es-pacio
columna de A y el espacio columna de [A ! b] son iguales.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-322-320.jpg)
![328 1 Espacios vectoriales generales
c b Supóngase que A y [A b] tienen el mismo rango Y. Por el teorema 5.4.4,
existe algún subconjunto de los vectores columna de A que forman una base para
el espacio columna de A. Supóngase que estos vectores columna son
I I
C] I c2,. . ’ , c:
Estos Y vectores básicos también pertenecen al espacio columna de dimensión r de
[A I b]; por tanto, según el teorema 5.4.6a, también forman una base para el
espacio columna de [A b]. Esto significa que b se puede expresar como una
combinación lineal de ci,ci, ... ,c; , y, en consecuencia, b está en el espacio
columna de A. 0
No es dificil imaginar por qué este teorema es verdadero si el rango de una
matriz se considera como el número de renglones diferentes de cero que hay en su
forma escalonada reducida. Por ejemplo, la matriz aumentada del sistema
x, - 2x, - 3x, + 2x4 = -4
-3X, +7X2- X,+ X,= -3
2x, - 5x2 + 4x, - 3x, = 7
- 3x, + 6x2 + 9x3 - 6x4 = - 1
es I 1 -
-3
2 -
- 3
- 3
- 1
4 -
9 -
-2 -
7 -
.S
6
2
1
- 3
- 6 I- 1:7 J
que tiene la siguiente forma escalonada reducida (comprobar):
10
O
O O i O
Debido al renglón
0 0 0 0 1
se observa que el sistema es inconsistente. Sin embargo, también es debido a este
renglón que la forma escalonada reducida de la matriz aumentada tiene menos
renglones cero que la forma escalonada reducida de la matriz de coeficientes. Esto
hace que la matriz de coeficientes y la matriz aumentada del sistema tengan ran-gos
distintos.
Ei teorema de consistencia trata sobre las condiciones en las cuales un sis-tema
lineal Ax = b es consistente para un vector espedfico b. El siguiente teore-ma
tiene que ver con las condiciones en que un sistema lineal es consistente para
todas las elecciones posibles de b.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-323-320.jpg)




![5.6 Rango y nulidad / 333
q b. Si la nulidad de A es O, entonces el espacio solución de Ax = O tiene
dimensión O, lo cual significa que sólo contiene al vector cero. Por tanto, Ax = O
sólo tiene la solución trivial. 0
EJERCICIOS DE LA SECCIÓY 5.6
1. Comprobar que rango(A) = rango(AT). 1 2. Encontrar el rango y la nulidad de la matriz; luego, comprobar que los valores
obtenidos satisfacen Id -!la I fórmula (4) del teorema de -a] la dimensión.
o -1
a) A = [ ! b) A = [ : c)A=
1 4 5 6
3 - 2 1 4
-1 o -1 -2
2 3 5 7
d) A =
1 4 5 2
2 1 3 , ]
, - I 3 2 2
6 O -3 '1 1 -3
o 3
-1
-2 9 2 - 4 - 5
3. En cada inciso del ejercicio (2), usar los resultados obtenidos para encontrar el número
de variables principales y el número de parámetros que hay en la solución de Ax = O
sin resolver el sistema.
4. En cada inciso, usar la información que se proporciona en la tabla para encontrar la
dimensión del espacio renglón de A, del espacio columna de A, del espacio nulo de A y
del espacio nulo de AT.
- a) b) C e) d) 0 8)
TamañodeA
Rango de A 3 2 1 2 2 O 2
9 x 5 5 x 9 6 x32x 3 4 x3 4x 3 3 x 3
5. En cada inciso, encontrar el valor máximo posible para el rango de A y el valor mínimo
posible para la nulidad de A.
a) A es 4 X 4. b)Aes3 X 5. c) A es 5 X 3.
6. Si A es una matriz m X n, ¿cuál es el valor máximo posible para su rango y cuál es el
valor mínimo posible para su nulidad? [Sugerencia. Ver el ejercicio 5.1
7. En cada inciso, usar la información que se proporciona en la tabla para determinar si el
sistema lineal Ax = b es consistente. En caso afirmativo, escribir el número de pará-metros
que hay en su solución general.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-328-320.jpg)
![334 Espacios vectoriales generar’es
8. Para cada una de las matrices del ejercicio 7, encontrar la nulidad de A y determinar el
niunero de parámetros que hay en la solución general del sistema lineal homogéneo Ax
=o
9. ¿,Quk condiciones deben satisfacer b,, b,. b,, b, y b, para que el sistema lineal
sobredeterminado
X -- 3 , =~ h ;~
x1 - 21, = h2
S ) i- X? = 11,
.yl - 4x2 = h,
x, + 5 . =~ h~,
sea consistente‘!
10. Sea
A =
“22 “21
Demostrar que el rango de A es 2 si y sólo si uno o más de los siguientes determinantes
“2, 022 “21 ‘23 “22 “23
es diferente de cero.
11. Supóngase que A es una matriz 3 X 3 cuyo espacio nulo es una recta que pasa por el
origen en el espacio tndimensional. ¿Es posible que el espacio renglón o el espacio
columna de A también sea una recta que pasa por el origen? Explicar la respuesta.
a ) A = [ ; l i t ; b ) A = [ - i -: -:] t 3 -
12. Analizar cómo el rango de A varía con t.
13. ¿Existen valores de r y S para los cuales el rango de
[; yO +o ]
sea uno o dos? En caso afirmativo, encontrar los valores](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-329-320.jpg)

![336 i Espacios vectoriales generales
c) Expresar (2a - h + 4c, 3a - c, 4h + c) como una combinación lineal de tres
vectores diferentes de cero.
4. Sea W el espacio generado por f = sen x y g = cos x.
a) Demostrar que para cualquier valor de O, f, = sen (x + O) y g, = cos (x + O) son
vectores en W.
b) Demostrar que f, y g, forman una base para W.
S. a) Expresar v = ( 1, 1) como una combillación lineal de v, = (1, - l), v2 = (3, O), vg =
(2, 1) en dos formas distintas.
b) Demostrar que el resultado del inciso anterior no viola el teorema 5.4.1.
6. Sea A una matriz n X n, y sean v,, v2, . . . , vn vectores linealmente independientes en
12" expresados como matrices n X I . ¿Que debe cumplir A a fin de que Av,, Av,, . . . ,
Avn sean linealmente independientes?
7. ¿Una base para Pn debe cor,tener un polinomio de grado k para todo k = O, 1,2, . . . , n?
Justificar la respuesta.
8. Para efectos de este problema, una "matriz en tablero de ajedrez" se defmirá como una
matriz cuadrada A = [ a ..] tal que
{
II
1 si i +j es par
a,,= O si i + j es impar
Encontrar el rango y la nulidad de las siguientes matrices en tablero de ajedrez:
La matriz 3 X 3. b) La matriz 4 X 4. c) La matriz n X n.
9. Para efectos de este ejercicio, una "matriz en X" se d e f i á como una matriz cuadrada
con un número impar de renglones y de columnas que contiene ceros en todas partes,
excepto en las dos diagonales, donde tiene unos. Encontrar el rango y la nulidad de las
siguientes matrices en X
p O 0 O 11
LO. En cada inciso, demostrar que el conjunto de polinomios es un subespacio de Pn y
encontrar una base para éste.
a) Todos los polinomios en Pn tales que p( -x) = p(x).
b) Todos los polinomios en Pn tales quep(0) = O.
11. (Pata quienes ya esfudiaton Cdculo.) Demostrar que el conjunto de todos los
polinomios en Pn que tienen una tangente horizontal en x = O es un subespacio de Pn.
Encontrar una base para este subespacio.
12. En algebra lineal avanzada se demuestra el siguiente criterio de determinante para el
rango: El rango de una matriz A es r si y sólo si A contiene alguna submatriz r X r
con determinante d$erente de cero y todas las submatrices cuadradas de tamaño su-](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-331-320.jpg)


![6.1 PRODUCTOS INTERIORES
En la sección 4.1 se definió el producto interior euclidiano sobre R” y se usó
para extender los conceptos de longitud y distancia al espacio euclidiano n
dimensional. En esta sección se usarán como axiomas las propiedades más
importantes del producto interior euclidiano para definir el concepto general de
producto interior; luego se demostrará cómo los productos interiores se pueden
utilizar para definir las ideas de longitud y distancia en espacios vectoriales
diferentes a R”.
PRODUCTOS En la sección 4.1, el producto interior euclidiano de dos vectores en R” se denotó
INTERIORES por u v. En esta sección será conveniente introducir la otra notación (u, v) para
GENERALES denotar este producto interior. Con esta notación, las propiedades fundamentales
del producto interior euclidiano enumeradas en el teorema 4.1.2 son precisamente
los axiomas de la siguiente definición
Definición. Un producto interior sobre un espacio vectorial real V es una fun-ción
que asocia un número real {u, v) a cada pareja de vectores u y v en V de
forma que los siguientes axiomas se cumplen para los vectores u, v y w en V y
los escalares k.
(1) (u, v> = (v, u) [Axioma de simetría]
(2) (u + v, w) = (u, w) + { v, w) [Axioma de ahtividad]
339](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-334-320.jpg)
![340 / Espacios con producto interior
(3) (ku, v) = k( u, v) [Axioma de homogeneidad]
(4) (v, v) 2 o [Axloma de positividad]
donde (v, v} = O
si y sólo si v = O
Un espacio vectorial real con un producto interior se denomina espacio real con
producto interior.
OBSERVACI~N. En el capítulo 10 se estudiarán productos interiores complejos;
es decir, productos interiores cuyos valores son números complejos. Hasta ese
momento se usará la expresión "espacio con producto interior" para indmr que se
trata de un "espacio real con producto interior".
Debido a que los axiomas del producto interior se basan en las propiedades
del producto interior eucliciiano, éste satisface de forma automática los axiomas;
este es el contenido del siguiente ejemplo.
Ejemplo 1 Si u = (ul, u2, . . . . un) y v = (vl, vz, . . . , v,J son vectores en R",
entonces la fórmula
( u , v } = U . v = U ~ U , + U 2 U * + ~ ~ ~ + U , u , '
define a (u, v) como el producto interior euclidiano sobre R". Los cuatro axiomas
del producto interior se cumplen debido al teorema 4.1.2. A
El producto interior euclidtmo es el producto interior más importante sobre
R". Sin embargo, existen varias aplicaciones en las que resulta conveniente modi-ficar
el producto interior euclidiano ponderando sus términos de manera Iferente.
En pocas palabras. si
son números reales positivos, que se denominaránpesos, y si u = (u,, u2, . . . , un)
y v = (vl, v2, . . . , vn) son vectores en R", entonces se puede demostrar (ejercicio
26) que la fórmula
define un producto interior sobre R"; se denomina producto interior euclidiano
ponderado con pesos wI, w2, . . . , wn.
Para ver una forma en que puede surgir un producto interior euclidiano
ponderado, supóngase que en algún experimento fisico puede obtenerse cualquiera
de n valores numéricos](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-335-320.jpg)

![342 / Ffspacios con producto interior
Luego,
con lo que se establece el tercer axioma
Finalmente,
Resulta evidente que (v, v} = 3v + 2v 3 O. Además, (v, v} = 3v f + 2v 3 = O si y
sólo si v1 = v2 = O, es decir, si y sólo si v = (vl, v2) = O. Asi, se cumple el cuarto
axioma. A
LONGITVD Y Antes de analizar más ejemplos de productos interiores, se hará una pausa y se
DISTANCIA EN explicará cómo se usan los productos interiores para introducir los conceptos de
ESPACIOS CON longitud y distancia en espacios con producto interior. Recuérdese que en el
PRODUCTO espacio euclidiano n dimensional la longitud euclidiana de un vector u = (u1, u2,
INTERIOR . . , un) se puede expresar en términos del producto interior euclidiano como
l/uil = (u -u)'/?
y la distancia euclidiana entre dos puntos cualesquiera u = (u1, u2, . . . , un) y v =
(vi, v2, . . . . vn) se puede expresar como
d(u, v) = /Iu -vi/ = [(u - V ) . ( r r " v)]':
[Véanse las fórmulas (1) y (2) de la sección 4.1 .] Tomando como motivación estas
fórmulas, se hace la siguiente definición
Definición. Si V es un espacio con producto interior, entonces la norma (o
longitud) de un vector u!e/ n V se denota por u y se define como
!bI! = (u, u)1'2
La distancia entre dos puntos (vectores) u y v se denota por d(u, v) y se define
como
X(u, v) = ¡/u- VI/
Ejemplo 3 Si u = (u,: y2, . . . , U,,) y v = (v,, v2, . . . , vn) son vectores en R3 con el
producto interior euchdlano, entonces
-___
/lul/ = (u, U)I'* = (u. u)1/2 = f l u ; + I ' ' + u;](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-337-320.jpg)
![6.1 Productos interiores / 343
Y
d(u, v) = //u - VI/ = (u - v, u - v)l’2 = [(u - v). (u - v ) y
= V ( U , - U l ) 2 + (u* - u2)2 + ‘ ’ . + (u, - u,)l
Obsérvese que las expresiones anteriores son simplemente las fórmulas estándar
para la norma y la distancia euclidianas que se analizaron en la sección 4.1 [véan-se
las fórmulas (1) y (2) de esa sección.] A
Ejemplo 4 Es importante tener en mente que la norma y la distancia de-penden
del producto interior que se esté usando. Si se cambia el producto in-terior,
entonces también cambian las normas y las distancias entre vectores.
Por ejemplo, para los vectores u = (1, O) y v = (O, 1) en R2 con el producto in-terior
euclidiano se tiene
11u11 = v?TT = 1
d(u, v) = I/u - VI/ = /1(1, - 1)/1 = v,m = v5
Y
Sin embargo, si se cambia al producto interior euclidiano ponderado
(u, v) = 3U,U, + 2u,u,
entonces se obtiene
//u=/ (/u , u)’’’ = [ 3(1)(1) + 2(0)(0)]1’2 = fi
Y
d(u, v) = //-uV I / = ((1, - l ) , ( l , - 1))1’2
= [ 3 ( 1 ) ( 1 ) + 2 ( - 1 ) ( - 1 ) ] ’ ~ 2 = ~A
CIRCUNFEREN- Si Ves un espacio con producto interior, entonces el conjunto de puntos en V que
CIAS Y ESFERAS satisfacen
UNITARIAS EN
ESPACIOS CON I I ~ I I= 1
PRODUCTO
INTERIOR se denomina egera unitaria o algunas veces circunferencia unitaria en I/. En R2
y R3, estos son los puntos cuya distancia al origen es igual a l.
Ejemplo 5
a) Trazar la circunferencia unitaria en un sistema de coordenadas en R2 usan-b)
el producto interior euclidiano (u, v) = ulvl + u2v2.
do el producto interior euclidiano ponderado (u, v) = $ ulvl + $ u2v2.
Trazar la circunferencia unitaria en un sistema de coordenadas xyz en R3 usan-do
Solución de u). Si u = (x, y),e ntonces llull = (u, u ) ~=’ ~,/-, de modo que
la ecuación de la circunferencia unitaria es ,/- = 1 o bien, elevando al cua-drado
ambos miembros,](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-338-320.jpg)



![6. I Productos interiores / 347
Ejemplo 8 Si
p = a. + a,x -1 u2x2 and q = bo + b,x + b2x2
son dos vectores cualesquiera en P,, entonces la siguiente fórmula define un
producto interior sobre P, (comprobar):
(P> S> = aobo + a,b, + 4 9
La norma del polinomio p con respecto a este producto interior es
llPll = (P, P Y = VGF2-G
y la esfera unitaria en este espacio consta de todos los polinomios p en P, cuyos
coeficientes satisfacen la ecuación I I pI I = 1, que elevada al cuadrado queda como
Ejemplo 9 (Para quienes ya estudiaron Cúlculo). Sean f =Ax) y g = g(x) dos
funciones continuas en C [a, b], y se define
Se demostrará que esta fórmula define un producto interior sobre C [a, 61 al
comprobar los cuatro axiomas de producto interior para las funciones f =Ax), g =
g(x) y S = s(x) en C [a, b]:
b
[ (1) i, ( f 9 g) = f ( x M 4 dx = g(x)f@) dx = (g, f )
lo cual demuestra que se cumple el axioma l.
b
(2) ( f + I, g, S) = cf(x> + g(x))s(x) dx
b I, b
= f ( x > W dx + g(x)s(xl dx
= (f, S> + (g, S>](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-342-320.jpg)
![348 / Espacios con producto interior
esto demuestra que el axioma 2 es válido.
(3) ( k t g>= j6 m ) g ( X ) dx = k Jab f(n)g(x)d x = k(f, g)
con lo que queda demostrado que se cumple el axioma 3.
(4) Si f =Ax) es cualquier función en C [a, b], entoncesf(x) 2 O para todo x en
[a, b]; por consiguiente,
Además, debido a que$(x) 2 O y f =Ax> es continua sobre la, 61, se conclu-ye
que 1,” fZ(x)dx = si y sólo si Ax) = O para todo x en [a, 61. Por tanto,
se tiene que (f, f ) = 1,” fZ(x>dx = O si y sólo si f = O. Así se demuestra que se
cumple el axioma 4. A
Ejemplo 10 (Para quienesya esfudiaron Cálculo). Si C [a, b] tiene el producto
interior definido en el ejemplo precedente, entonces la norma de una función f =
Ax) con respecto a este producto interior es
y la esfera unitaria en este espacio consta de todas las funciones f en C [a, b] que
satisfacen la ecuación llfll= 1, que cuando se eleva al cuadrado queda como
lUbf2(x)d x = 1 A
OBSERVACI~N. (Para quienes ya estudiaron Cálculo). Como los polinomios
son funciones continuas sobre (-m, m) entonces son continuas sobre cual-quier
intervalo cerrado [a, 61. Así, para todos estos intervalos el espacio vec-torial
P, es un subespacio de C [a, bj, y la fórmula (6) define un producto in-terior
sobre P,.
OBSERVACI~N. (Para quienes ya estudiaron Cálculo). Recordar que en Cálculo
la longitud de ara de una curva y =Ax) sobre un intervalo [a, b] está definida por la
fórmula
L =
Este concepto de longtud de arco no se debe confundir con Ilfll, que es la longitud
(norma) de f cuando f se considera como un vector en C [a, b]. Las fórmulas (7) y
(8) son bastante diferentes.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-343-320.jpg)
![6.1 Productos interiores / 349
ALGUNAS En el siguiente teorema se enumeran algunas propiedades algebraicas básicas de
PROPIEDADES los productos interiores.
DE LOS
PRODUCTOS
Teorema 6.1.1. Si u, v y w son vectores en un espacio real con producto in-terior
INTERIORES
y k es cualquier escalar, entonces:
a) (O, v) = (v, O) = O
b) (u, v + w) = (u, v) + (u, w)
c) (u, kv) = k( u, v)
d ) (u - v, w) = (u, w) - (v, w)
e) (u, v - w) = (u, v) - (u, w)
I
Demostración. Se demostrará el inciso 6) y la demostración de los demás inci-sos
se deja como ejercicio.
(u, v + w) = (v + w, u) [por simetría]
= (v, u) + (w, u) [por aditividad]
= (u, v) + (u, w) por simetría] 0
El siguiente ejemplo ilustra dmo se pueden usar el teorema 6.1.1 y las propie-dades
que definen los productos interioresp ara efectuar cálculos algebraicos con éstos.
A medida ques e estudie el ejemplos,e rá instructivo que el lector justifiquep laosso s.
Ejemplo 11
(u - ?v, 3u + 4v) = (u, 3u + 4v) - (2v, 3u + 4v)
= (u, 3u) + (u, 4v) - (2v, 3u) - (2v, 4v)
= 3(u, U) + 4( U, V ) - 6 ( ~ , -U 8) ( ~V,)
= 311~11+~ 4(u, V)- 6 ( ~V,) - 8 ( ( ~ / ( ~
3(lu112 - 2(u, V) - 811vI12 A
Como el teorema 6. l. 1 es un resultado general, se tiene la garantía de que se
cumple para fodos los espacios reales con producto interior. Este es el verdadero
poder del desarrollo axiomático de los espacios vectoriales y los productos interio-res:
un sólo teorema demuestra una multitud de resultados de una vez. Por ejem-plo,
sin necesidad de ninguna demostración adicional se tiene la garantía de que
las cinco propiedades dadas en el teorema 6.1.1 son verdaderas para el producto
interior sobre R" generado por cualquier matriz A [fórmula (3)]. Por ejemplo, para
este producto interior se comprobará el inciso b) del teorema 6. l. 1 :
(u, v + w) = (v + w)TATAu
= (VT + wT)ATAu [Propiedad de la transpuesta]
= (V'A~AU+) (w'A 9 ~ )[Prop iedad de la multiplicación de matrices]
= (u, v) + (u, w)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-344-320.jpg)


![352 1' Espacios con producto interior "c">ii Figura 3
20.
21.
22.
23.
24.
25.
26.
27.
Demostrar que la siguiente identidad se cumple para vectores en cualquier espacio con
producto interior.
//u + VI/* + //u - V/IZ = 2//U1l2 + 21jv112
Demostrar que la siguiente identidad se cumple para vectores en cualquier espacio con
producto interior.
(u, v) = +l/u + vil2 - allu - vil2
Demostrar que (U, = ulvl + u2v3 + u3v2 + u4v4 no es un producto interior sobre M2,.
Sean p = p(x) y q = q(x) polinomios en P,. Demostrar que
(P? 9) =p(O)q(O) + P ( M % ) +p(l)q(l)
es un producto interior sobre P,
Demostrar: Si (u, v) es un producto interior euclidiano sobre R" y si A es una matnz n
X n, entonces
(u, .4v) = (ATU,V)
[Sugerencia Usar el hecho de que (u, v) = u . v = vTu.]
Comprobar el resultado del ejercicio 24 para el producto interior euclidiano sobre R3 y
Sean u = (u1, u,, . . . , un) y v = (y1, v2, . . . , v,). Demostrar que
(u,v) = W I U I U , + W2U2U* + ' ' ' + w,u,u,
es un producto interior sobre R" si wl, w2,. . . , w ns on números reales positivos.
calcular (p, q) para los vectores p =p(x) y q = q(x) en P3.
a) p = 1 -x+xxz+5x3 q=x-3x2
b ) p = x - 5 x 3 q = 2 + 8x2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-347-320.jpg)
![6.2 Ángulo y ortogonalidad en espacios con producto interior / 353
28. (Para quienes ya estudiaron C6lculo). En cada inciso, usar el producto interior
(f, g) = Io1 f(x)g(x) dx
para calcular (f, g) de los vectores f =Ax) y g = g(x) en C [O, 11 .
a) f = c o s 2 m , g = s e n 2 m b) f = x , g=e" C) f=tan-x, g= 1
Tr
4
29. Demostrar que el producto interior del ejemplo 7 se puede escribir como (U, =
tr( U%).
30. Demostrar que la fórmula (3) define un producto interior sobre R". [Sugerencia Usar
la otra versión de la fórmula (3), definida por (4).]
31. Demostrar que la matriz (5) genera el producto interior euclidiano ponderado
(u, v) = wlulul + w2u2u2 + ' ' + w,u,u, sobre R".
32. Demostrar los incisos a) y d) del teorema 6. l. l.
33. Demostrar los incisos c) y e) del teorema 6. l. l.
6.2 ÁNGULO Y ORTOGONALIDAD EN ESPACIOS CON
PRODUCTO INTERIOR
En esta sección se definirá el concepto de ángulo entre dos vectores en un espa-cio
con producto interior, y esta idea se usará para obtener algunas relaciones
básicas entre vectores en un espacio con producto interior, incluyendo una rela-cibn
geométrica fundamental entre el espacio nulo y el espacio columna de una
matriz.
DESIGUALDAD Recuérdese por la fórmula (1) de la sección 3.3 que si u y v son dos vectores dife-
DE CAUCHY- rentes de cero en R2 o en R3 y 8 es el ángulo entre estos vectores, entonces
SCHWARZ
u v = llull llvll cos o (1)
o bien, de otra manera,
cos o = - u.v
llull llvll
En el primer objetivo de esta sección es definir el concepto de ángulo entre
dos vectores en un espacio general con producto interior. Para que la definición
sea razonable, sería bueno que fuese consistente con la fórmula (2) cuando se apli-que
al caso especial de R2 y R3 con el producto interior euclidiano. Así, se quiere que
la definición del ángulo 8 entre dos vectores diferentes de cero en un espacio con
producto interior cumpla la relación](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-348-320.jpg)


![356 / Espacios con producto interior
Demostración del teorema 6.2.2d Por definición,
llu + VI12 = (u + v, u + v)
= (u, u) + 2(u, v) + (v, v)
9 (u, u) + 2/(u, v)l + (v, v) [Propiedad del valor absoluto]
5 (u, u >+ ~ l l ~ l l l l ~(lvl ,+v > [ ~ o r ( 4 ) 1
= llU1l2 + 2llull I b ! l + 11vIl2
= (llull + /lv11)2
Extrayendo raíz cuadrada se obtiene
l b + VI1 Ill ull + llvll 0
ÁNGULO ENTRE A continuación se mostrará cómo se puede usar la desigualdad de Cauchy-
VECTORES Schwarz para definir hgulos en espacios generales con producto interior. Supón-gase
que u y v son vectores diferentes de cero en un espacio V con producto inte-rior.
Si ambos miembros de la fórmula (6) se dividen entre llull llvll ', se obtiene
o bien, de manera equivalente,
Luego, si 8 es un ángulo cuya medida en radianes varía de O a x, entonces cos 8
asume todos los valores entre - 1 y 1 (inclusive) exactamente una vez (figura 1).
Así, por (7) existe un h g d o 8 único tal que
Se define a 8 como el ángulo entre u y v. Obsérvese que en R2 o en R3 con el pro-ducto
interior euclidiano, la expresión (8) concuerda con la fórmula usual para el
cosen3 del ángulo entre dos vectores diferentes de cero fórmula (2).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-351-320.jpg)





![362 Espacios con producto interior
2 2 - 1 o 1
1 1 -2 o - 1
O 0 1 1 1
- l -3 '
L
O ]
0
y, por el inciso a) del teorema 6.2.6, el espacio nulo de A es el complemento
ortogonal de W. En el ejemplo 4 de la sección 5.5 se demostró que
forman una base para este espacio nulo. Expresando estos vectores en la misma
notación que wl, w2, w3 y w4 se concluyeq ue los vectores
" I = i1-,1 , o, o, 0) y v 2 = ( - l ,O, -1,o, 1)
forman una base para el complemento ortogonal de W. Como comprobación,
calculando los productos punto necesarios, el lector puede veniicar que v1 y v2 son
ortogonales awl, w2, w3 y w4. A
Teorema 6.2.7. Si A es una matriz n X n, y si TA 1 R" +. R" es la multiplicación
por A, entonces las siguientes proposiciones son equivalentes.
a) A es invertible.
b) Ax = O sólo tiene la solución trivial.
c) La forma escalonada reducida de A es I,,
d) A se puede escribir como un producto de matrices elementales,
e) if x = b es consistente para toda matriz b n X 1.
fi Ax = b tiene exactamente una solución para toda matriz b n X 1.
S> deffJ f o.
h) Id rango de 7> es Rn.
i) TA es uno a uno.
j ) Los vecfores columna de A son linealmente independientes.
k) Los vectores renglón de A son linealmente independientes.
I) Los vectores columna de A generan a R".
m) Los vectores renglón de A generan a Rn.
n) Los vectores columna de A forman una base para R".
o) Los vectores renglón de A forman una base para R".
p) El rango de A es n.
q) La nulidad de A es O.
r) El complemento ortogonal del espacio nulo de A es Rn.
S) El complemento ortogonal del espacio renglón de A es (O) .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-357-320.jpg)

![364 / Espacios con producto interior
¿Cuáles de las siguientes matrices son ortogonales a A con respecto al producto interior
del ejercicio 6?
8. Sea R3 con el producto interior euclidiano. ¿Para qué valores de k son ortogonales u y v?
a) u=(2,1,3), v = ( l , 7 , k ) b) u = ( k , k , l ) , v=(k,5,6)
9. Sea con el producto interior euclidiano. Encontrar dos vectores de norma 1 que sean
ortogonales a los tres vectores u = (2, 1, -4, O), Y = (- 1, - 1,2,2) y w = (3,2,5,4).
10. En cada inciso, con el producto interior euclidiano comprobar que la desigualdad de
Cauchy-Schwarz se cumple para los vectores dados.
a) u = (3, 2), v = (4, - 1) b ) ~ = ( - 3 , 1 , 0 ) , ~ = ( 2 -,1 , 3 )
C) ~ = ( - 4 , 2 ,I) , v = ( 8 , -4, -2) d) u = ( O , - 2 , 2 , I ) , v = ( - l , - 1 , 1, I )
11. En cada inciso, comprobar que la desigualdad de Cauchy-Schwarz se cumple para los
vectores dados.
a) u = (-2, 1) y v = (1, O), usando el producto interior del ejemplo 2 en la sección 6. l.
usando el producto interior del ejemplo 7 en la sección 6.1.
la sección 6.1,
c) p = - 1 + 2x + 2 y q = 2 - 4 2 usando el producto interior dado en el ejemplo 8 de
12. Sea W la recta en R2 cuya ecuación es y = 2x. Encontrar una ecuación para WL
13. a) Sea W el plano en R3 cuya ecuación es x - 2y - 32 = O. Encontrar las ecuaciones
paramétricas para WL
b) Sea Wla recta en R3 con ecuaciones paramétricas
n=2t, J'" -st, z = 4 t ("<<<E)
De t em~ aurn a ecuación para WL
14. Sea
2 - 1 a]
2
A = [ : a) Encontrar bases para el espacio renglón y el espacio nulo de A.
b) Comprobar que todo vector en el espacio renglón es ortogonal a todo vector en el
espacio nulo (como garantiza el teorema 6.2.6~).
15. Sea A la matriz1 ejercicio 14.
a) Encontrar bases para el espacio columna de A y el espacio nulo de AT
b) Comprobar que todo vector en el espacio columna de A es ortogonal a todo vector en
el espacio nulo de AT (como garantiza el teorema 6.2.6b).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-359-320.jpg)
![6.2 Ángulo y ortogonalidad en espacios con producto interior / 365
16. Encontrar una base para el complemento ortogonal del subespacio de R" generado por los
vectores
a) vI = (1, - 1, 3), v2 = (5, -4, -4), v3 = (7. -.6, 21
b) VI = (2, O, - l), vZ = (4, O, -2)
c ) v , = ( l , 4 , 5 , 2 ) , v 2 = ( 2 , 1 , 3 , 0 ) , v 3 = ( - 1 , 3 , 2 , 2 )
d ) ~ , = ( l , 4 , 5 , 6 , 9 ) , ~ ~ = ( 3 , - 2 , 1 ~ 4 , - 1 ) , ~ ~ = ( - I , 0 , - 1 , - 2 , - 1 ) ,
v4 = (2, 3, 5, 7, 8)
17. Sea V un espacio con producto interior. Demostrar que si u y v son vectores ortogonales en
Vtales que llull= llvll= 1, entonces ~lu- VI I = a.
18. Sea V un espacio con producto interior. Demostrar que si w es ortogonal tanto a u, como a
u2, entonces es ortogonal a k,u, + k2u2 para todos los escalares k, y k2. Interpretar
geométricamente este resultado para el caso en que V es R3 con el producto interior
euclidiano.
19. Sea V un espacio con producto interior. Demostrar que si w es ortogonal a cada uno de los
vectores u,, u2, . . . , u,, entonces es ortogonal a todo vector en lin {u,, u2, . . . , u ,} .
20. Sea {v,, v2, . . . , v,} una base para un espacio V con producto interior. Demostrar que el
vector cero es el Úmco vector en V que es ortogonal a todos los vectores básicos.
21. Sea {w,, w2, . . . , w,}una base para un subespacio CV de V. Demostrar que WL consta de
todos los vectores en V que son ortogonales a todos los vectores básicos.
22. Demostrar la siguiente generalización del teorema 6.2.4. Si v,, v2, . . . , Y, son vectores
ortogonales por parejas en un espacio V con producto interior, entonces
23. Demostrar los siguientes incisos del teorema 6.2.2:
a) Inciso a). b) Inciso b). c) Inciso e).
24. Demostrar los siguientes incisos del teorema 6.2.3:
a) Inciso 4). b) Inciso b). c) Inciso c). d) Inciso S,
25. Demostrar el inciso b) del teorema 6.2.5.
26. Demostrar: Si u y v son matrices n X 1 y A es una matriz invertible n X n, entonces
[vTATAu]2 5 (urATAu)(v*A*Av)
27. Por medio de la desigualdad de Cauchy-Schwm, demostrar que para todos los valores
reales de a, b y 8 ,](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-360-320.jpg)
![366 i Espacios con producto interior
29.
30.
31.
32.
Demostrar que la igualdad se cumple en la desigualdad de Cauchy-Schwarz si y sólo si u y
v son linealmente dependientes.
(Para quienes ya estudiaron Ccilculo). Sea C [O, x] con el producto interiol
(f, g) = i h d x ) dx
Y sea f, = cos nx (n = O, 1, 2, . . . ). Demostrar que si k # I, entonces fk y fi son ortogonales
con respecto al producto interior dado.
(Para quienes ya estudiaron Chkulo). Seanfix) y g(x) funciones continuas sobre [O, 11 .
Demostrar:
[Sugerencia Usar la desigualdad de Cauchy-Schwarz.]
Mediante métodos vectoriales, demostrar que el triángulo inscrito en una circunferencia,
de modo que uno de sus lados es el diámetro de la circunferencia, debe ser un triángulo
rectángulo. [Sugerencia Expresar los vectores AB y BC de la figura 3 en términos de u y
v. 1
33. Con respecto al producto interior euclidiano, la norma de los vectores u = (1, a) y
v = (- 1, 3 ) es igual a 2, y el ángulo entre u y v mide 60° (figura 4). Encontrar un pro-ducto
interior euclidiano ponderado con respecto al cual u y v sean vectores unitanos orto-gonales.
Figura 4](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-361-320.jpg)








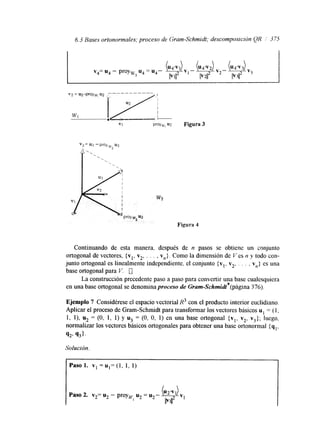

![6.3 Bases ortonormales; proceso de Gram-Schmidt; descomposición QR 1 377
OBSERVACI~N. En el ejemplo precedente se usó el proceso de Gram-Schmidt
para obtener una base ortogonal; luego, una vez que se obtuvo la base ortogonal, se
normalizó para obtener una base ortonormal. De otra manera, es posible nor-malizar
cada vector básico de la base ortogonal en cuanto se obtiene generando,
así, paso a paso la base ortonormal. Sin embargo, este método presenta la ligera
desventaja de producir más raíces cuadradas que manejar.
El proceso de Gram-Schmidt con normalización ulterior no sólo convierte una
base cualesquiera {u1, ~2. ,. . , U,} en una base ortonormal {Sl, q,, . . . , q,}, sino que
también lo hace de modo que para k 2 2 se cumplan las siguientes relaciones:
{ q,, q,, . . . , qk} es una base ortonormal para el espacio generado por {u1,
qk es ortogonal a { u l , u 2 , . . . , Uk-l}.
U p . . . > Uk}.
Se omiten las demostraciones, pero estos hechos debens er evidentes después de un
análisis profundo de la demostración del teorema 6.3.6.
DESCOMPOSI- Se plantea el siguiente problema.
CIÓN QR
Problema. Si A es una matriz m X n con vectores columna linealmente inde-pendientes,
y si Q es la matriz con vectores columna ortonormales que se
obtienen al aplicar el proceso de Gram-Schdt a los vectores columna de A,
¿qué relación, en caso de haber alguna, existe entre A y Q?
Para resolver este problema, supóngase que los vectores columnaA dseo n ul, %,
. . . , u,, y que los vectores columna ortonormales dQe son q,, q2, . . . , 9,; así,
A = [ u l I u2 I ' . . I U,] y Q=[q, 1 9 2 I ' . . I S,]
Por el teorema 6.3.1 se concluye que ul, u,, . . . , u, se pueden expresar en térmi-nos
de q,, q,, . . . , q, como
u1 = (UI> q,)q, + (UI> 9 2 h 2 + ' . . + (u13 q,)q,
u2 = (U2> 91)91 + (u23 9 2 h 2 + ' ' ' + ( u 2 , q,h,
u, = (un, q1)91 + (u,, q 2 h 2 + . . . + ( u , , q,)q,
Recordando de la sección 1.3 que el j-ésimo vector columna de un producto de
matrices es una combinación lineal de los vectores columna del primer factor con
coeficientes provenientes de laj-ésima columna de segundo factor, se concluye que
estas relaciones se pueden expresar en forma matricial como](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-372-320.jpg)

![6.3 Bases ortonormales; proceso de Gram-Schmidt: descomposición QR / 3 79
FUNCIÓN DE LA
DESCOMPOSI-LINEAL
CIÓN QR EN
ÁLGEBRA
y por (9), la matriz R es
A
En años recientes, la descomposición QR ha adquirido una importancia cada vez
mayor como fundamento matemático de una amplia gama de algoritmos numéri-cos
prácticos, incluyendo un algoritmo bastante usado para calcular eigenvalores
de matrices grandes. Los algoritmos se analizan en libros de texto relacionados con
los métodos numéricos del álgebra lineal.
DEMOSTRACI~N ADICIONAL
Demostración del teorema 6.3.4. La demostración se efectúa en dos partes.
Primero es necesario encontrar vectores w1 y w2 con las propiedades enunciadas y
luego demostrar que estos vectores son únicos.
Por el proceso de Gram-Schmidt, existe una base ortonormal { vl, v2, . . . ,
vn} para W. Sean
W] = (u, V I b , + (u, v2)v2 + ' . . + (u, v,)v, (10)
Y
w2=u-w1 (11)
Se concluye que w1 + w2 = w1 + (u - wl) = u, de modo que queda por demostrar
que w1 está en W y que w2 es ortogonal a W. Pero w1 está en W porque es una
combinación lineal de los vectores básicos para W. Para demostrar que w2 es
ortogonal a W es necesario probar que (wz, w) = O para todo vector w en W. Pero
si w es cualquier vector en W, se puede expresar como una combinación lineal
w = k,v, + k2v2 + . . . + knvn](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-374-320.jpg)
![380 ./ Espacios con producto interior
de los vectores básicos v, v2, . . . , v,. Así,
(w2, W)= (U - w,,W )= (U, W) - {w].w j
Pero
(u, w) = (U, k , ~+, k2v2+ . . . f k , ~ , , )
= k!(U, VI> + k2(U, v2) + ‘ . . + k,(U, Vil)
y por el inciso c) del teorema 6.3.2
(w,, = (wu,) v , )k, + (u. v2)k, + ’ ’ ’ + (u, v,)k,
Así, (u, w} y (wl, w) son iguales, de modo que (12) produce (w2, w) = O, que es lo
que quería probarse.
Para ver que (IO) y (1 1) son los únicos vectores con las propiedades enun-ciadas
en el teorema, supóngase que también es posible escribir
donde w i está en W y w i .es ortogonal a W. Si de (13) se resta la ecuación
se obtiene
u = w , + w ,
o = (w; - wl) + (w; - w2)
o bien,
w1 - w; = w; - w? (14)
Como w2 y wi son ortogonales a W, su diferencia también es ortogonal a W, ya
que para cualquier vector w en W se puede escribir
(w, w; - w2> = (w, w;) - (w, w2) = o - 0 =o
Pero w; - w2 es un vector en W. ya que por (14) es la diferencia de los dos
vectores w1 y W; que están en el subespacio W. Así, w; - w2 debe ser ortogonal a
sí mismo; es decir,
(w; - w2, w; - w2) = o
Pero esto significa que wi - w2 = O por el axioma 4 en la definición de producto
interior. Así, w; = w2 y, por (14), w; = wl. O
EJERCICIOS DE LA SECCION 6.3
1. ¿Cuáles de los siguientes conjuntos de vectores son ortogonales con respecto al pro-ducto
interior euclidiano sobre R2?](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-375-320.jpg)
![6.3 Bases ortonormales; proceso de Gram-Schmidt; descomposición QR 1 381
a) (0,I). (2,O) b) (- l/V% I / f i ) , l / d )
C) (- I/‘% - I / f i ) , (l/V‘Z l / d ? ) d) (0,O). (O, 1)
2. ¿Cuáles de los conjuntos del ejercicio 1 son ortonormales con respecto al producto
interior euclidiano sobre R2?
3. ¿Cuáles de los siguientes conjuntos de vectores son ortogonales con respecto al pro-ducto
interior euclidiano sobre R3?
4. ¿Cuáles de los conjuntos del ejercicio 3 son ortononnales con respecto al producto
interior euclidiano sobre R3?
5. ¿Cuáles de los siguientes conjuntos de polinomios son ortononnales con respecto al
producto interior sobre P2 que se analizó en el ejemplo 8 de la sección 6. l?
a) $ - f x + + x 2 , $+Qx-$x’, $ + $ x + $ x 2 b) 1, -x + -x2, x2
I 1
v5v5
6. ¿Cuáles de los siguientes conjuntos de matrices son ortononnales con respecto al pro-ducto
a) [:, 3 [; -4 [-: 3 5 !]> [: 3 5 !]
interior sobre M22 que se analizó en el ejemplo 7 de la sección 6. l?
b, [; [bi [P PI. [Y -;I
7. Comprobar que el conjunto de vectores dado es ortogonal con respecto al producto in-terior
euclidiano; luego, normalizando los vectores convertirlo en un conjunto ortonor-mal.
a) ( - 1, 21, (6, 3) b) -11, (2, 0, 21, (0, 5, 0) C) (i& ,i )(,- f , b O), ($,$, - f )
Demostrar que {x, y}es ortononnal sí R2 tiene el producto interior (u, v) = 3u,vl +
2u2v2, pero que no es ortononnal sí R2 tiene el producto interior euclidiano.
9. Comprobar que los vectores v, = (-+,4,0),v2 =($,$,O ), v2 = (O, O, 1)foman una
base ortonomal para R3 con el producto interior euclidiano; luego, mediante el teo-rema
6.3.1, expresar cada uno de los siguientes vectores como una combinación lineal
de V,’ v2 Y v3.
a) (1, - 1, 2) b) (3, -7, 4) C) (+, -%$I
10. Comprobar que los vectores
VI=(^, -1323 -11, ~ , = ( - 2 , 2 , 3 , 2 ) , v , = ( l , 2 , 0 , - I ) , v,=(I,O,O, 1)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-376-320.jpg)
![3817 1 Espacios con producto interior
11.
12.
13.
14.
IS.
16.
17.
18.
Sea I? con el producto interior euclidiano, y sea S = {M I , w?] la base ortonormal con
w = (++j , w = (5.4) 2 > >
a)l Deternlinar los vectores u y v cuyos vectores de coordenadas son (u), = (1, 1) y (v),
=(-1,4).
b) Calcular Ilull, d(u. v) y {u, v) aplicando e1 teorema 6.3.2 a los vectores de coordenadas
(u), y (v)& luego, comprobar los resultados mediante cálculos directos sobre u y v.
Sea H' con el producto interior euclidimo, y sea S = {w),w, , w3}l a base ortononnal
con w,= (O, - ((),-I,*IV, ),= (1, O, 0 )y w3= (O,y,y).
a) Encontrar los vectores u, v y w cuyos vectores de coordenadas son (u), = (-2, 1, 2),
b) Calcular 11~11, d(u, W) y (w, v} aplicando el teorema 6.3.2 a los vectores de coorde-nadas
(u) , (v).~y (w)& luego, comprobar los resultados mediante cálculos directos
sobre u y v.
4 3
' I F '.
(v), = (3, o, -2) v (w), = ( S , -4, 1).
En cada inciso, S representa alguna base ortotlorma1 de u11 espacio tetradimensional
con producto interior IJsar la información que se proporciona para encontrar IIuII, IIv -
WII, IIv + w11 Y (v, w).
a) (u), = ( - 1. 2, I , 3 ) , (vjS = (0, -3, I , 5), ( w )=~ ( - 2. - 4. 3, 1)
b) (U), = (O. O . - 1. - l), (v),, = (5, 5. - 2, -2). (w),,= (3, O. " 3 . O)
a) Demostrar que los vectoresv, = (1, -2, 3, -4), v2 = (2. I, -4, -3), Y? = (-3, 4, I ,
- 2) y v4 = (4, 3, 2, I foinan una base ortogonal para R;' con el piducto kt&or
cuclidlano.
b) Usando ( 1 ), expresar u = (- 1,2,3, 7 ) como una conlbinaclón lineal de los vectores
cn el inciso a).
Sea R2 con el producto interior euclidiano. Usando el proceso de Gram-Schmidt, trans-fonnar
Is base (u,, u2} en una base ortonormal.
a! u , = ( I . -3L u 2 = ( 2 . 2 ) b) u , = ( l . O ) , u 2 = ( 3 . -5)
Sea H' con el producto interior euclidiano. Con el proceso de Gram-Schmidt, trans-formar
la base { u I. u,, u3} en una base ortononnal.
a) u , = ( 1 , I , I ) , u Z = ( - 1 , 1.0). u,=(1,2. I )
b ) u , = ( I . O , O ) . ~ 2 = ( - 3 , 7 , -2). u ; = ( O . ~ . I )
Sea R4 con el producto interior euclidiano. Usando el proceso de Gram-Schmidt, trans-formar
la base {u1, u,, u3, u4} en una base ortononnal](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-377-320.jpg)








![6.4 Mejor aproximacibn, mínimos cuadrados / 391
Resolviendo este sistema se obtiene que la solución por mínimos cuadrados de Ax
= u es
(comprobarj, de modo que
o bien, en notación horizontal (lo cual es consistente con el planteamiento original
del problema), proy,u = (-2, 3, 4. O). A
OPERADORES En la sección 4.2 se analizaron algunos operadores proyección ortogonal básicos sobre
PROYECCIóN R2 y R3 (tablas 4 y 5 ). El concepto de operador proyección ortogonal se puede extender
ORTOGONAL a espacios generales con producto interior como se muestra enseguida.
Definición. Si W es un subespacio de Rm. entonces la transformación P:Rm +
W que aplica cada vector x en Rm en su proyección ortogonal proy, x en W se
denomina proyección ortogonal de Rm sobre W.
Se deja como ejercicio demostrar que las proyecciones ortogonales son operadores
lineales. Por la fórmula (5) se concluye que la matriz estándar para la proyección
ortogonal de Rm sobre IV es
[ P 1 = A(A 'A) ~ ' 4 ' (6)
donde A se obtiene usando cualquier base para W como sus vectores columna
Ejemplo 3 En la tabla 5 de la sección 4.2 se demostró que la matriz estándar para
la proyección ortogonal de R3 sobre el plano xy es
Para darse cuenta de que lo anterior es consistente con la fórmula (6), considé-rense
los vectores unitarios a lo largo de los ejes x y y positivos como base para el
plano xy, de modo que
A = [i e]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-386-320.jpg)
![392 3 Espacios con producto interior
[ P ] - A A T = [o: :]1[ I O o]=[: "1 0 1 0 o 0 0
Se deja para el lector comprobar que ATA es la matriz identidad 2 x 2; así, (6) se
simplifica a
lo cual concuerda con (7). A
Ejemplo 4 Hallar la matriz estándar para la proyección ortogonal P de R2 sobre la
recta 1 que pasa por el origen y forma un ángulo 8 con el eje x positivo.
Solución. La recta I es un subespacio unidimensional de R2. Como se ilustra en
la figura 3, se puede tomar v = (cos 8 , sen 8 ) como una base para este subespacio,
de modo que
Se deja para el lector comprobar que ATA es la matriz identidad 1 x 1; así, (6) se
simplifica a
[ P I =AAT= [i:: :] e o [ cos e sen 6 1 cos2 sen COS = [ sen e cos e1 .
6 sen2 8
,7';p PIX)
1L +
Figura 3
RESUMEN El teorema 6.4.3 permite agregar un resultado adicional al teorema 6.2.7.
Teorema 6.4.5. Si A es una matriz n X n, y si TA:R" -+ R" es la multiplicación
por A, entonces las siguientes proposiciones son equivalentes.
a) A es invertible.
b) Ax = O sólo tiene la solución trivial.
c) La forma escalonada reducida de A es I,,,
d) A puede escribirse como un producto de matrices elementales,
e) Ax = b es consistente para toda matriz b n X 1,
f,l AH = b tiene exactamente una solución para toda matriz b n X 1.
g) det(A) f O.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-387-320.jpg)


![6.5 Matrices ortogonales; cambio de base 1 395
13. Demostrar: Si A tiene vectores columna linealmente independientes y si b es ortogonal
al espacio columnad e A, entonces la solución pomr ínimos cuadrados deA x = b es x = O.
14. Sea PB" + W la proyección ortogonal de R" sobre un subespacio W.
a) Demostrar que [PI2 = [PI .
b) ¿Qué indica el resultado del inciso a) con respecto a la composición P o P?
c) Demostrar que [PI es simétrica.
d) Comprobar que las matnces en las tablas 4 y 5 de la sección 4.2 tienen las pro-piedades
indicadas en los incisos a) y c).
15. Sea A una matriz m X n con vectores renglol linealmente independientes. Encontrar
una matnz estándar para la proyección ortogonal de Rn sobre el espacio renglón de A.
[Sugerencia Empezar con la fórmula (6).]
6.5 MATRICES ORTOGONALES; CAMBIO DE BASE
Una base que es adecuada para un problema puede no ser para otro, de modo
que en el estudio de los espacios vectoriales un proceso común es cambiar de una
base a otra. Debido a que una base es la generalización a espacios vectoriales
de un sistema de coordenadas, el cambio de base es semejante a cambiar de
ejes de coordenadas en R2 y R3. En esta sección se estudiarán varios problemas
relacionados con el cambio de base. También se obtendrán propiedades de las
matrices cuadradas que tienen vectores columna ortonormales. Estas matrices
surgen en diversos contextos, incluyendo problemas en los que hay un cambio de
una base ortonormal a otra.
MATRICES Las matrices cuyas inversas se pueden obtener por transposiciones son tan im-
ORTOGONALES portantes que existe una terminología asociada con ellas.
Definición. Una matriz cuadrada A con la propiedad
A-l'AT
se denomina matriz ortogonal.
Por la definición anterior se concluye que una matriz cuadrada A es ortogonal si y
sólo si
A A ~ = A ~ A = I (1)
De hecho, por el teorema 1.6.3 se concluye que una matriz cuadrada A es
ortogonal si A A T = I, o bien, A TA = I.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-390-320.jpg)



![6.5 Matrices ortogonales; cambio de base / 399
los operadores que no modifican las longitudes de todos los vectores. Como las
reflexiones y las rotaciones de R2 y R3 tienen esta propiedad, este hecho explica la
observación en el ejemplo 2 de que las matrices estándar para las reflexiones y ro-taciones
básicas de R2 y R3 son ortogonales.
MATRICES DE Recordar por el teorema 5.4.1 que si S = {vl, v,, . . . , vn} es una base para un es-
COORDENADAS pacio vectorial V, entonces todo vector v en V se puede expresar de manera única
como una combinación lineal de los vectores básicos, por ejemplo,
v = k,v, + k2v2 + . . . + k,V,
Los escalares k,, k,, . . . , kn son las coordenadas de v con respecto a S, y el vector
(v)s = (k,, k2, ' ' ' > k,)
es el vector de coordenadas de v con respecto a S. En esta sección será conveniente
enumerar las coordenadas como elementos de una matriz n x l. Así, la matriz
se define como la matriz de coordenadas de v con respecto a S.
CAMBIO DE En las aplicaciones es común trabajar con más de un sistema de coordenadas, y
BASE suele ser necesario conocer la relación entre las coordenadas de un punto o vector
fijo y los diversos sistemas de coordenadas. Como el concepto de base es la gene-ralización
de un sistema de coordenadas a espacios vectoriales, se llega a conside-rar
el siguiente problema.
Problema del cambio de base. Si la base de un espacio vectorial se cambia de
cierta base inicial B a una base nueva B', jdmo está relacionada la matriz de coor-denadas
inicial [vlB de un vector v con la nueva matriz de coordenadas [v]~,?
1
Por sencillez, este problema se resolverá para espacios bidimensionales. La
solución para espacios n dimensionales es semejante y se deja al lector. Sean
B = {U,, U*} y B' = {u;, u;}
las bases inicial y nueva, respectivamente. Serán necesarias las matrices de coor-denadas
para los nuevos vectores básicos con respecto a la base inicial. Supóngase
que las matrices son](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-394-320.jpg)
![400 / Espacios con producto interior
Es decir,
u; = "U1 + bu,
u; = cul + dU2
Ahora, sea v cualquier vector en Vy sea
la nueva matriz de coordenadas, de modo que
Para determinar las coordenadas iniciales de v es necesario expresar v en términos
de la base inicial B. Esto se logra al sustituir (4) en (6). Así se obtiene
O
v = k,(au, + bu, j + k,(CU, + dU2)
v = (k," + k,c)u, + (k,b + k,d)U2
Entonces, la matriz de coordenadas inicial para v es
['IB = i"'" k,b + + k,d k2c1
que se puede escribir como
o bien, por ( 9 ,
Esta ecuación establece que la matriz de coordenadas inicial [VI, se obtiene al
multiplicar la nueva matriz de coordenadas [vIBt por la izquierda por la matriz
Las columnas de esta matriz son las coordenadas de los nuevos vectores básicos
con respecto a la base inicial [véase (3)]. Así, se tiene la siguiente solución para el
problema del cambio de base.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-395-320.jpg)
![6.5 Matrices ortogonales; cambio de base / 401
Sulución delproblema del cambio de base. Si se cambia la base para un
espacio vectorial, V de una base inicial B = {u1, u2, . . . , U,,} a una base nueva
B' = {u;& ,...,un] entonces la matriz de coordenadas inicial [VI, de un vector
[VI está relacionada con la nueva matriz de coordenadas [ V ] ~ ' del mismo vector
v por medio de la ecuación
[VIB = P[VI/?' (7)
donde las columnas de P son las matrices de coordenadas de los nuevos
vectores básicos con respecto a la base inicial; es decir, los vectores columna de
P son
]E, [uilE, ' ' ' > [uAIB
MATRICES DE La matriz P se denomina matriz de transición de B' a B y se puede expresar en
TRANSICI~N términos de sus vectores columna como
Ejemplo 4 Considerar las bases B = {u1, u2} y B' = {u;,ui} paraR2, donde
u1 = (1, O); u2 = (O, 1); U'(1, 1); u' = (2, 1)
a) Encontrar la matriz de transición de B' a B
b) Por medio de (7), hallar [vIB si
Solución de a), Primero es necesario encontrar las matrices de coordenadas de
10s nuevos vectores básicos u1 y u2 con respecto a la base inicial B. Por inspección, I ,
u; = u, + u2
u; = 2u, + u2
de modo que
Así, la matriz de transición de B' a B es](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-396-320.jpg)
![402 / Espacios con producto interior
Solución de b).M dante (7) y la matriz de transición determinada enin ceils o a),
Como comprobación, debe ser posible recuperar el vector v a partir de [vIB o de
[ V ] ~ ' .S e al lector demostrar que - 3 u; + 5 u; = u; + 2 u; = v = (7, 2). A
Ejemplo 5 Considerar los vectores u1 = ( 1 , O), u2 = (O, I), u; = (1, l), u;,=
(2, 1). En el ejemplo 4 se encontró la matriz de transición de la base B' = { ul,
u; } para R2 a la base B = (u1 ~ u*>. Sin embargo, también se podría pedir la
matriz de transición de B a B'. Para obtener esta matriz, simplemente se cam-bia
el punto de vista y se considera a B' como la base inicial y a B como la base
nueva. Como de costumbre, las columnas de la matriz de transición son las coor-denadas
de los nuevos vectores básicos con respecto a la base inicial.
Igualando las componentes correspondientes y resolviendo el sistema lineal
resultante, el lector debe poder demostrar que
u, = -u; + u;
u2 = 2u; - u;
de modo que
Así, la matriz de transición de B a B' es
Si se multiplican entre sí la matriz de transición deB ' a B obtenida en el ejemplo
4 y la matrizd e transición dBe a B' obtenida en el ejemplo5 , se encuentra
lo cual muestra que Q = P- l . El siguiente teorema demuestra que este hecho no es
fortuito.
Teorema 6.5.4. Si P es la matriz de transición de una base B' a una base B,
entonces:
a) P es invertible.
b) P- es la matriz de transición de B a B'.
Demostración. Sea Q la matriz de transición de B a B'. Se probará que PQ = I y
entonces se concluirá que Q = P" para completar la demostración.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-397-320.jpg)
![6.5 Matrices ortogonales; cambio de base / 403
. . Cnn -:I Por (7)
Suponer que B = {ul, u2, . . . , U,} y que
PQ =
Cl I
C2 I
. .
..
rx1B = p[xlB'
Y
[XIB, = Q[xIB
para todo x en V. Multiplicando la ecuación inferior por P por la izquierda y
sustituyendo la ecuación superior se obtiene
1 x 1=~ ~ Q [ X ] B (9)
para todo x en V. Con x = u1 en (9) se obtiene
O
De manera semejante, la sustitución sucesiva de x = u2, . . . , u, en (9) da
. , . . .
'.( O
Por consiguiente, PQ =I.
entonces para todo vector v se cumplen las siguientes relaciones:
En resumen, si P es la matriz de transición de una base B' a una base B,
."I ... . .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-398-320.jpg)

![6.5 Matrices ortogonales; cambio de base / 405
[;:I = p"[ ;]
"
I'
Y
Figura 1
Y
d)
cos H
[u; IR = [sen
De manera semejante, por la figura Id, se observa que las componentes de u; en
la base inicial son cos (O + n12) = -sen O y sen (O + n12) = cos 8, de modo que
[ 4 l S = 1 cos
- sen e
Así, la matriz de transici6rl de H' a E cs
COS 0 -sen 0
sen H cos 8 I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-400-320.jpg)

![6.5 Matrices ortogonales; cambio de base / 407
Figura 2
Y
Ejemplo 7 (Aplicación a la rotación de los ejes de coordenadas en el espa-cio
tridimensional.) Suponer que un sistema de coordenadas rectangulares
xyz se hace girar alrededor de su eje z en sentido contrario a las manecillas
del reloj (mirando sobre el eje z positivo) por un ángulo 9 (figura 2). Si se in-troducen
los vectores unitarios u,, u2 y u3 a lo largo de los ejes x, y y z positi-vos,
y los vectores unitarios ul, D u2 1
y u3 a lo largo de los ejes x!, y' y z' posi-tivos,
la rotación se puede considerar como el cambio de la base anterior B =
{ul, u2: u3} a la base nueva B' = { u;, u;, u; >. En vista del ejemplo 6 debe
ser obvro que
LU;lB = [!]
Además, como u se alarga 1 unidad sobre el eje z' positivo,
Por tanto, la matriz de transición de B' a B es
cos 6 -sen8 y]
O
P = [sei0 co; 8 y la matriz de transición de B a B' es
cos 8 sen 8 O
(comprobar). Así, las nuevas coordenadas ( X I , y', z') de un punto Q se pueden
calcular a partir de sus coordenadas anteriores (x, y, z) por medio de](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-402-320.jpg)

![6.5 Matrices ortogonales; cambio de base /' 409
9. Considerar las matrices de coordenadas
a) Hallar w si S es la base del ejercicio 6(a).
b) Encontrar q si S es la base del ejercicio 7(a)
c) Determinar B si S es la base del ejercicio 8.
10. Considerar las bases B = {U,, u2} y B' = {vl, v2} para R2, donde
a) Hallar la matriz de transición de B' a B.
b) Encontrar la matriz de transición de B a B'.
c) Determinar la matriz de coordenadas [w],, donde
y usando (1 I), calcular W ~ I .
d) Comprobar las respuestas mediante el cálculo directo de [w],~
11. Repetir las instrucciones del ejercicio 10 con
ul=[;a]. u2=[ ;;I, +I, .+], .;=[ 3 vj=
a) Encontrar la matriz de transición de B' a B.
b) Determinar la matnz de coordenadas [w],, donde
12. Considerar las bases B = {u,, u2, u3} y B' = {vI, v2, v3) para R3, donde
w=[;!]
y usando (1 1 ), calcular [wlBt.
c) Comprobar las respuestas mediante el cálculo directo de [w],,.
13. Repetir las instrucciones del ejercicio 12 con el mismo vector w, pero con
"1 l](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-404-320.jpg)
![410 / Espaclos con producto interior
a> Hallar la matriz de transición de B' a B.
b) Encontrar la matriz de transición de B a B'.
c) Calcular la matriz de coordenadas [pIR, donde p = -4 + x, y usando
b1,"
d) Comprobar las respuestas calculando directamente [p],~.
15. Sea Vel espacio generado por f, = sen x y f, = cos x.
a) Demostrar que g, = 2 sen x + cos x y g, = 3 cos x forman una base par
b) Determinar la matriz de transición de B' = {g,, g2) a B = {fl, f,} .
c) Encontrar la matnz de transición de B a B .
1 l), calcular
V.
d) Calcular la matnz de coordenadas [h], , donde h = 2 sen x - 5 cos x, y usando
(1 l), calcular [h],~.
e) Comprobar las respuestas calculando directamente [h],~
16. Sea un sistema de coordenadas rectangulares x)' obtenido al girar un sistema de coor-denadas
rectangulares xy en sentido contrario a las manecillas del reloj por un ángulo 0
= 3~14.
a) Determinar las coordenadas xy del punto cuyas coordenadas xy son (-2,6).
b) Encontrar las coordenadas xy del punto cuyas coordenadas x'y' son (5,2).
17. Repetir el ejercicio 16 con O = x13
18. Sea un sistema de coordenadas rectangulares xyz' obtenido al girar un sistema de
coordenadas rectangulares xyz en sentido contrario a las manecillas del reloj alrededor
del eje z (mirando sobre el eje z) por un ángulo 6 = d 4 .
a) Encontrar las coordenadas x'y!z' del punto cuyas coordenadasx yz son (- 1,2,5).
b) Determinar las coordenadas xyz del punto cuyas coordenadasx yz' son (1,6, - 3).
19. Repetir el ejercicio 18 para una rotación de 0 = z13 en sentido contrario a las maneci-llas
del reloj alrededor del eje y (mirando a lo largo del eje y positivo hacia el origen).
20. Repetir el ejercicio 18 para una rotación de B = 3 ~ 1 4en sentido contrario a las ma-necillas
del reloj alrededor del eje x (mirando a lo largo del eje x positivo hacia el
origen).
21. a) Un sistema de coordenadas rectangulares x'y'z' se obtiene al girar un sistema de
coordenadas xyz en sentido contrario a las manecillas del reloj alrededor del eje y
por un ángulo O (mirando a lo largo del eje y positivo hacia el origen). Encontrar
una matriz A tal que
donde (x, y, z) y ( 2 , y', z') son las coordenadas del mismo punto en los sistemas xyz
y x'y'z', respectivamente.
b) Repetir el inciso a) para una rotación alrededor del eje x.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-405-320.jpg)
![6.5 Matrices ortogonales; cambio de base I' 41 1
22. Un sistema de coordenadas rectangulares x'lyIIz'' se obtiene al girar primero un sistema
de coordenadas xyz en sentido contrario a las manecillas del reloj alrededor del eje z
por un ángulo'de 60° (mirando a lo largo delj e z positivo hacia el origen) para obtener un
sistema de, coordenadas xyz', y luego al girar el sistema de coordenadas xyz' en sentido
contrario a las manecillas del reloj alrededor del eje y por un ángulo de 45O (mirando a
lo largo del eje y positivo hacia el origen). Encontrar una matAri zt al que
donde (x, y, z) y (x", y", z") son las coordenadas q z y x"y"z" y del mismo punto,
respectivamente.
23. ¿Qué condiciones deben cumplir a y b para que la matriz
[ z z ]
sea ortogonal?
24. Demostrar que una matriz ortogonal A tiene una de las dos formas posibles:
cos 0 - sen0 1 o A = [ cos 0 -senO]
A = [sen 0 cos 0 -sen 0 - cos 0
donde O S 8 < h.[S ugerencia. Empezar con una matriz general A = (a..) 2 X 2, y
aplicar el hecho de que los vectores columna formanu n conjunto ortogonal enR '.] I)
25. a) Aplicar el resultado del ejercicio 24 para demostrar que la multiplicación por una
matriz ortogonal2 X 2 es una rotación o una rotación seguida de una reflexióna lre-dedor
del eje x.
b) Demostrar que la multiplicación por A es una rotación si det(A) = 1 y una rotación
seguida de una reflexión si det(A) = - l.
26. Usar el resultado del ejercicio 25 para determinar si la multiplicación por A es una
rotación o una rotación seguida de una reflexión. En cada caso, encontrar el ángulo
de rotación.
27. El resultado del ejercicio 25 tiene un análogo para matrices ortogonales 3 X 3: se
puede demostrar que la multiplicación por una matriz ortogonal A 3 X 3 es una rota-ción
alrededor de algún eje fijo si deyA) = 1 y que es una rotación alrededor de algún
eje fijo seguidad e una reflexión con respecto a algún planod e coordenadas si det(A) =
- l. Determinar si la multiplicación por A es una rotación o es una rotación seguida de
una reflexión.
3 2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-406-320.jpg)





![7. I Eigenvalores y eigenvectores / 41 7
Se puede demostrar (ejercicio 15) que si A es una matriz n X n, enton-ces
el polinomio característico de A es de grado n y el coeficiente de 1" es 1; es
decir, el polinomio característico de una matriz n x n es de laf orma
Por el teorema fundamental del álgebra, la ecuación característica
tiene cuando mucho n soluciones &stintas, por lo que una matriz n X n tiene a lo
sumo n eigenvalores distintos.
Sería conveniente que el lector revise el ejemplo 6 de la sección 2.3, donde
se encontraron los eigenvalores de una matriz 2 X 2 resolviendo la ecuación
característica. En el siguiente ejemplo se usa una matriz 3 X 3.
Ejemplo 2 Encontrar los eigenvalores de
Solución. El polinomio característico de A es
A -1 o
] det(A1-A) = det[ O A - 1 = A3 - 8A2 + 17A- 4
-4 17 A - 8
Por consigwente, los eigenvalores de A deben satisfacer la ecuación cúbica
Para resolver esta ecuación se empezará buscando soluciones enteras. Esta
tarea se puede simplificar bastante aprovechando el hecho de que todas lasso -
luciones enteras (en caso de que haya) de una ecuación polinomial con coefi-cientes
enteros
A* + C,A" +. . ' + c, =o
deben ser divisores del término constante, cn. Así, las únicas soluciones enteras
posibles de (2) son los divisores de -4, es decir, +1, 22, +_4. Sustituyendo
sucesivamente estos valores en (2) se observa que 1 = 4 es una solución entera. En
consecuencia, 1 -4 debe ser un factor del miembro izquierdo de (2). Divi-diendo
1 -4 entre A3 -%I2 + 171 -4 se observa que (2) se puede volver a escri-bir
como](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-412-320.jpg)


![420 Eigenvalores, eigenvectores
Ejemplo 5 Encontrar bases para los elgenespacios de
Solucion. LA ecuación característica de A es A3 - 5A2 + SA - 4 = O o bien, en
forma factorizada, (A - 1)(A - 2)2 = O (comprobar); así los eigenvalores de -4
son A = 1 y I, = 2, de modo que existen dos eigenespacios de A.
Por definición,
es un eigenvector de A correspondiente a A si y sólo si x es una solución no trivial
de (11 - A)x = O; es decir, de
Si A = 2, entonces (3) se convierte en
Resolviendo este sistema se obtiene (comprobar)
x, = "S, x2 = t, x 3 = S
Así, los eigenvectores de A corresponhentes a 1 = 2 son los vectores diferentes de
cero de la forma
x=[-;]=[-!]+[;];.[ -Y 1
Como
son linealmente independientes, estos vectores forman una base para el eigenespa-cio
correspondiente a A = 2.
Si 1 = 1, entonces ( 3 ) se convierte en](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-415-320.jpg)
![7.1 Eigenvalores y eigenvectores / 421
Resolviendo este sistema se obtiene (comprobar)
de modo que
[";I =.y[ -; 1
[ -T]
es una base para el eigenespacio correspondiente a L = l. A
EIGENVALORES Una vez que se han determinado los eigenvalores y los eigenvectores de una
DE LAS matriz A, es fácil encontrar los eigenvalores y los eigenvectores de cualquier
POTENCIAS DE potencia entera positiva de A; por ejemplo, si 1 es un eigenvalor de .4 y x es un
UN MATRIZ eigenvector correspondiente, entonces
A2x = A(Ax) = A(Ax) = A(Ax) = il(dx) = A2x
lo cual demuestra que L2 es un eigenvalor de A2 y que x es un eigenvector corres-pondiente.
En general, se tiene el siguiente resultado
Teorema 7.1.3. Si k es un entero positivo, 1 es un eigenvalor de una matriz A y
x es un eigenvector correspondiente, entonces Lk es un eigenvalor de Ak y x es
un eigenvector correspondiente.
Ejemplo 6 En el ejemplo 5 se demostró que los eigenvalores de
son 1 = 2 y L x 1, de modo que por el teorema 7.1.3 tanto L = 27 =: 128 como 1 =
l7 = 1 SOR eigenvalores deA7. TambiCn se demostró que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-416-320.jpg)


![424 Eigenvalores, eigenvectores
-4 -2
5. Obtener los eigenvalores de las matrices del ejercicio 4.
6. Hallar las bases de los eigenespacios de las matnces del ejercicio 4.
7. Encontrar las ecuaciones características de las siguientes matrices:
8. Determinar los eigenvalores de las matrices del ejercicio 7.
9. Encontrar las bases de los eigenespacios de las matrices del ejercicio 7
10. Por inspección, hallar los eigenvalores de las siguientes matrices:
11. Encontrar los eigenvalores de A' para
3 7 11
O 0 0
O 0 0
12. Encontrar los eigenvalores y bases para los eigenespacios de A25 para
- 1 -2 -2
A = [ - ; -f I]
13. Sea A una matnz 2 X 2. La recta que pasa por el origen de R2 es inwuiante bajo A si
Ax está sobre la recta cuando x también lo está. Encontrar las ecuaciones de las rectas
en R2, en caso de haberlas, que son invariantes bajo la maw dada.
14. Encontrar det(A) dado que A tiene ap@) como su polinomio característico
a) p(a) = a3 - 2a2 + l. + 5 b) p(a) = a4 - l3 + 7
[Sugerencia Véase la demostración del teorema7 .1.4.1
15. Sea A una matriz n X n.
a) Demostrar que el polinomio característico deA es de grado n.
b) Demostrar que el coeficiente de 1'' en el polinomio Característico es 1.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-419-320.jpg)
![7.1 Eigenvalores y eigenvectores / 425
16. Demostrar que la ecuación característica de una matriz A 2 X 2 se puede expresar
como A2 - tr(A)1, + det(A) = O, donde tr(A) es la traza de A.
17. Usando el resultado del ejercicio 16, demostrar que si
entonces las soluciones de la ecuación característica deA son
(u + d) t v ( u - d)' + 4bc I
Usando el resultado anterior, demostrar que A
a) tiene dos eigenvalores reales distintos si (a - d)2 + 4bc > O
b) tiene un eigenvalor real si (a - d)2 + 4bc = O.
c) no tiene eigenvalores reales si (a - q2 + 4bc < O.
18. Sea A la matriz del ejercicio 17. Demostrar que si (a - d)2 + 4bc > O y b f O, entonces
los eigenvectores de A correspondientes a los eigenvalores
Al = $[(u + d ) + v ( u - d)2 + 4bc ] y /I2 = [(u + d ) - d ( u - d)2 + 4bc
son
respectivamente.
19. Demostrar: Si a, b, c y d son enteros tales que a + b = c + d, entonces
tiene eigenvalores enteros, a saber, 1, = a + b y L2 = a - c. [Sugerencia Vease el
ejercicio 17.1
20. Demostrar: Si 1 es un eigenvalor de una matnz invertible A y x es un eigenvector co-rrespondiente,
entonces 111 es un eigenvalor de A" y x es un eigenvector correspon-diente.
21. Demostrar: Si 1 es un eigenvalor de A, x es un eigenvector correspondiente y S es un
escalar, entonces 1 - S es un eigenvalor de A - SZ y x es un eigenvector correspon-diente.
22. Encontrar los eigenvalores y bases para los eigenespaciosd e
Luego, usando 10s ejercicios 20 y 21, encontrar los eigenvalores y bases para 10s
eigenespacios de
a) A-'. b) A - 31. c) A + 21.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-420-320.jpg)
![326 ,/ Eigenvalores, eigenvectores
23. a) Demostrar que si A es una matriz cuadrada, entonces A y AT tienen los mismos
eigenvalores. [Sugerencia Considerar la ecuación característica det(A.1 - A) = O.]
b) Demostrar que A y AT no necesariamente tienen los mismos elgenespacios. [Suge-rencia
IJsando el resultado del ejercicio 18, encontrar una matnz 2 X 2 para la
cual A y AT tengan eigenespaclos diferentes. I
7.2 DIAGONALIZACI~N
En esta sección se vera cómo encontrar un base para R" integrada por eigenvec-tores
de una matpiz dada A n x n. Las bases se pueden usar para estudiar las
propiedades geométricas de A y para simplrficar varios cálculos numéricos donde
aparece A. Estas bases también revisten importanciaJsica en una amplia gama
de aplicaciones, algunas de las cuales serán consideradas después en este texto.
EL PROBLEMA
DE LA
DIAGONALIZA-CIÓN
DE
MATRICES
El objetivo principal de esta sección es mostrar que los dos problemas siguientes,
que a simplc vista parecen muy diferentes, en realidad son equivalentes.
Problema del eigenvector. Dada una matriz A n X n, jexiste una base para
R" integrada por eigcnvectores de A?
Problema de diagonalización (Forma matriciag. Dada una matriz A n X n,
jexiste una matriz invertible P tal que P-IAP sea una matriz diagonal?
El segundo problema sugiere la siguiente terminología.
Definición. Se dice que una matriz cuadrada A es diagonalizable si existe una
matriz invertible P tal que P"AP es una matriz diagonal; se &ce que la matriz
P diagonaliza a A,
El siguiente teorema muestra que el problema del eigenvector y el problema
de diagonalización son equivalentes.
Teorema 7.2.1. Si .-I es una matriz n X n. entonces las siguientes proposiciones
son equivalentcs.
a) A es diagona/izahle.
h) '4 lime n eigenvectores linealrnente independientes.
Demostración de a +- 6): Como se supone que A es diagonalizable, entonces existe
una matriz invertible](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-421-320.jpg)


![7.2 Diagonalización / 429
Ejemplo 1 Encontrar una matriz P que diagonalice a
Solución. En el ejemplo 5 de la sección precedente, se encontró que la ecuación
característica de A es
(A - l)(A - 2)* = o
L=2: p, =[-;I, p2=[;]
y se determinaron las siguientes bases para los eigenespacios:
En total hay tres vectores básicos, de modo que la matriz A es diagonalizable y
diagonaliza a A . Como comprobación, el lector debvee rificar que
1 o - 2 ~ 0 ] [;~ 0 - 2 : I[ - 1 ; 0 - 2 :I=[:: 2 0 ; 0
p - l A p = [ - : ;]A
No existe ningún orden de preferencia para el orden de las columnas de P.
Como el i-ésimo elemento de la diagonal de P-lAP es un eigenvalor para el i-ésimo
vector columna de P, al cambiar el orden de las columnas de P simplemente
se cambia el orden de los eigenvalores sobre la diagonal de P-lAP. Entonces, si
en el ejemplo 1 se hubiera escrito
P = [ - 1 - 2; ;o ]
En el ejemplo 1 se hubiera obtenido](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-424-320.jpg)

![7.2 Diagonalización / 431
Esta matriz de coeficientes también tiene rango 2 y nulidad 1 (comprobar), de
modo que el eigenespacio correspondiente a A = 2 también es unidimensional.
Como los eigenespacios producen un total de dos vectores básicos, la matriz A no
es diagonalizable. A
En el ejemplo 1 se establece la hipótesis de que los vectores columna de P,
que están integrados por vectores básicos de los distintos eigenespacios de A, son
linealmente independientes. En el siguiente teorema se aborda esta cuestión.
Teorema 7.2.2. Si vl, v,, . . , , vk son eigenvectores de A correspondientes a
eigenvalores distintos A,, A,, , . . , A,, entonces { v ~v,,, . , , , vk}e s un conjunto
linealmente independiente.
Demostración. Sean vl, v,, . . . , vk los eigenvectores de A correspondientes a
eigenvalores distintos A,, A,, . . . , A,. Se supondrá que v19 v,, . . . , vk son
linealmente dependientes y se llegará a una contradicción. Entonces la conclusión
será que vl, v,, . . . , vk son linealmente independientes.
Como por definición un eigenvector es diferente de cero, {vl }es linealmente
independiente. Sea r el mayor entero tal que {v,, v,, . . . , vr} sea linealmente in-dependiente.
Como se está suponiendo que {vl, v,, . . . , vk} es linealmente de-pendiente,
r satisface 15 r < k. Además, por la definición de r, {vl, v,, . . . , vr+,}
es linealmente dependiente. Así, existen escalares c,, c, . . . , c,.+~, no todos
iguales a cero, tales que
CIVl + c2v* + ' ' ' + e,.+ ]V,..+ I = o (4)
Multiplicando por A ambos miembros de (4) y usando
se obtiene
C l A 1 V , + c2A,v, + ' ' ' + cy+l Ar+] V,+ 1 = o (5)
Multiplicando por Ar+, ambos miembros de (4) y restando de (5) la ecuación
resultante, se obtiene
Como {vl, v,, . . . , vr} es un conjunto linealmente independiente, esta ecuación
indica que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-426-320.jpg)

![7.2 Diagonalización / 433
4 0
o o 2 - v 3 : I para alguna matriz invertible P. Si se desea, la matriz P puede determinarse
usando el metodo del ejemplo 1 de esta sección. A
Ejemplo 4 Por el teorema 7.1.1, los eigenvalores de una matriz triangular son los
elementos de su diagonal principal. Así, una matriz triangular con elementos
distintos en la diagonal principal es diagonalizable. Por ejemplo,
-
A = [
-2
es una matriz diagonalizable. A
MULTIPLICI- El teorema 7.2.3 no determina completamente el problema de diagonalización, ya
DAD que es posible que una matriz A n X n sea diagonalizable sin tener n eigenvalores
GEOMÉTRICA Y distintos. En el ejemplo 1 se vio esto, donde la matriz dada 3 X 3 tenía sólo dos
MULTIPLICI- eigenvalores distintos, a pesar de lo cual era diagonalizable. Lo que realmente
DAD importa para que una matriz sea diagonalizable son las dimensiones de los
ALGEBRAICA eigenespacios: la suma de estas dimensiones debe ser cuando mucho n a fin de que
una matriz n X n sea diagonalizable. Los ejemplos 1 y 2 ilustran este hecho, las
matrices de estos ejemplos tienen la misma ecuación característica y los mismos
eigenvalores, pero la matriz del ejemplo 1 es diagonalizable porque la suma de las
dimensiones de los eigenespacios es 3, y la matriz del ejemplo 2 no es diago-nalizable
porque la suma de las dimensiones de los eigenespacios sólo es igual a 2.
La profundización en el estudio de las condiciones para diagonalización se
deja para cursos más avanzados, aunque se mencionará un teorema importante que
dará una comprensión más completa de las condiciones. Se puede demostrar que
si A. es un eigenvalor de A, entonces la dimensión del eigenespacio que corres-ponde
a Ao.no puede exceder el número de veces que A - ioapare ce como factor
en el polinomio característico de A. Así, en los ejemplos 1 y 2 el polinomio
característico es
(A - ])(A - 2)2
Por tanto, el eigenespacio correspondiente a A = 1 es cuando mucho (y, por tanto,
exactamente) unidimensional y el eigenespacio correspondiente a A= 2 es a lo
sumo bidimensional. En e! ejemplo 1, el eigenespacio correspondiente a A = 2 en
realidad es de dimensión 2, lo cual da por resultado condiciones para la diagonali-zación,
pero en el ejemplo 2 el eigenespacio sólo es de dimensión 1, lo cual indica
que no hay condiciones para la diagonalización.
Existe una terminología que relaciona las ideas anteriores. Si A. es un
eigenvalor de una matriz A n X n, entonces la dimensión del eigenespacio corres-](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-428-320.jpg)

![7.2 Diagonalización / 435
Ejemplo 5 Usando (lo), encontrar A 13, donde
A = [ ! o -2 i]
Solución. En el ejemplo 1 se mostró que la matriz A es diagonalizada por
: :I -1 o -2
D=P"..=[: 2 0 0 y]
A'3=PD13P" = [ -p A :l[: :3 :'.I-[ : 1 I]
Así, por (lo),
o -2 213 o o 1 0 2
0 -1 (11)
[ - 8190 O -16382
8191 8192
= 8191 O 16383
OBSERVACI~N. Con el método del ejemplo precedente casi todo el trabajo con-siste
en diagonalizar A. Una vez hecho ésto, se puede usar para calcular cualquier
potencia de A. Así, para calcular A loo0 basta cambiar el exponente de 13 a 1000
en la expresión (1 1).
EJERCICIOS DE LA SECCION 7.2
1. Sea A una matriz 6 X 6 con ecuación característica 12(1 - 1 )(A - 2)3 = O. ¿Cuáles son
las dimensiones posibles para los eigenespacios deA ?
2. Sea](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-430-320.jpg)
![a) krlxwnlrar los eigellvalores de 11.
b) Para cada eigenvalor 1, determinar el rango de la matriz111 - <4
c) ¿,Es diagonalizable A? Justificar In respuesta.
En los qercicios del 8 al 1 1. hallar una matriz P que diagonalice a A, y determinar P" AP.
cncontrar una matri7 P que diagonalice a A, y determinar P"AP
18. Con el mktodo del ejercicio 5, calcular A", donde
19. Usar el metodo del ejercicio 5 para calcular A", donde
A = [-A : -"] o 15 -2
20. En cada inciso, calcular la potencia indicada de
21. Encontrar 4" SI II es un entero positlvo y
3
3o'I
3 - 1 4o j](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-431-320.jpg)
![7.3 Diagonalización ortogonal / 43 7
22. Sea
Demostrar las siguientes proposiciones:
a) A es diagonalizable si (a - -+ 4hc > O.
b) A no es diagonalizable si (a - 4' + 4hc < O.
[Sugerencia. Véanse los ejercicios 17 y 18 de la sección 7.1 .]
23. En el caso en que la matnz A del ejercicio 22 es diagonalizable, encontrar una matriz P
24. Demostrar que si A es una matriz diagonalizable, entonces el rango de A es el número
que diagonalice a A.
de eigenvalores diferentes de cero de .4.
25. Demostrar: Si A es invertible y diagonalizable, entonces A" es diagonalizable y una
matriz P que diagonalice a A también diagonaliza a A".
7.3 DIAGONALIZACIÓN ORTOGONAL
En esta sección se abordará el problema de determinar una base ortonormal para
R" con el producto interior euclidiano, integrada por eigenvectores de una matriz
dada A n x n. El trabajo ya realizado sobre matrices simétricas y matrices
ortogonales desempeñará un papel importante aquí.
PROBLEMA DE El primer objetivo de esta sección es demostrar que los dos problemas siguientes
LA DIAGONA- son equivalentes.
ORTOGoNAL DE
UNA MATRIZ
Problema del eigenvector ortonormal Cada una matriz A de n x n, ¿existe
una base ortonormal para R" con el producto interior euclidiano integrada por
eigenvectores de A?
LIZACION
~~~~ ~~
Problema de la diagonalización ortogonal vorma matricial). Dada una matriz
A n X n, ¿existe una matriz ortogonal P tal que la matriz P"AP = PTAP es
diagonal? En caso de que exista la matriz. entonces se dice que A es dia-gonalizable
ortogonalmente, y se dice que P diagonaliza ortogonalmente a A.
Para el segundo problema es necesario considerar dos preguntas'
e ¿Qué matrices son diagonalrmbles ortogonalmente?
o LCómo encontrar una matriz ortogonal a fin de efectuar la diagonaliza-ción?](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-432-320.jpg)

![7.3 Diagonalización ortogonal / 439
D = P “AP
Así,
A = PDP-]
o bien, ya que P es ortogonal,
A = PDPT
Por consiguiente,
A T = (POPT)’= PDTPT= PDPT= A
lo cual demuestra que A es simétrica.
c + a) La demostración de esta parte rebasa el alcance de este texto, por lo que se
omitirá. 0
ALGUNAS El siguiente objetivo es establecer un procedimiento para diagonalizar ortogonal-
PROPIEDADES mente una matriz simétrica, pero antes de hacerlo se requiere un teorema crucial
DE LAS sobre eigenvalores y eigenvectores de matrices simétricas.
MATRICES
SIMÉTRICAS Teorema 7.3.2. Si A es una matriz simétrica, entonces:
a) Todos los eigenvalores de A son números reales.
6) Eigenvectores de eigenespacios diferentes son ortogonales.
Demostración de a). La demostración del inciso a), que requiere resultados sobre
espacios vectoriales complejos, se analizará en la sección 10.6.
Demostración de 6). Sean v1 y v2 eigenvectores correspondientes a eigenvalores
distintos A, y A, de la matriz A. Se quiere demostrar que v, v, = O. La demostra-ción
de este hecho requiere empezar con la expresión Av, * v,. Por la fórmula (8)
de la sección 4.1 y la simetría de A se concluye que
Pero v, es un eigenvector de A correspondiente a Al y v2 es un eigenvector de A
corresponhente a A,, de modo que (3) produce la relación
A , V ] . v2 = V] A*vz
que se puede volver a escribir como](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-434-320.jpg)
![-130 Eigenvalores, eigenvectores
( A - A 2 ) ( V I .v2) =o (4)
Pero Al - 1, f O, ya que se supone que A, y A2 son distintos. Así, por (4) se
concluye que v1 + v2 = O. 0
OBSERVACI~N. El lector debe recordar que hasta el momento se ha supuesto
que todas las matrices tienen elementos reales. De hecho, en el capitulo 10 se
verá que el inciso a) del teorema 7.3.2 es falso para matrices con elementos
complejos.
DIAGONALIZA- Como una consecuencia del teorema precedente se obtiene el siguiente procedi-
CION DE miento para diagonalizar ortogonalmente una matriz simétrica.
MATRICES
SIMÉTRICAS Paso 1. Encontrar una base para cada eigenespacio de A .
Baso 2. Aplicar el proceso de Gram-Schmidt a cada una de estas bases a fin
de obtener una base ortonormal para cada eigenespacio.
Paso 3. Formar la matriz P cuyas columnas son los vectores básicos
obtenidos en el paso 2; esta matriz diagonaliza ortogonalmente a
A .
La justificación de este procedimiento debe ser evidente: El teorema 7.3.2 asegura
que los eigenvectores de eigenespacios drferenfes son ortogonales, mientras que la
aplicación del proceso de Gram-Schmidt asegura que los eigenvectores obtenidos
del murno eigenespacio son ortonormales. Así, todo el conjunto de eigenvectores
obtenidos con este procedimiento es ortonormal.
Ejemplo 1 Encontrar una matriz ortogonal P que diagonalice a
Soluci6n. La ecuación característica de A es
det(A1-A)=det ["--2 : A1-: 4 - 2 =(A-2)2(A-8)=0
Así, los eigenvalores de A son A = 2 y il = S. Por el método usado en el ejemplo S
de la sección 7.1, se puede demostrar que
uF[-;] y %=[ -;]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-435-320.jpg)
![7.3 Diagonalizacidn ortogonal / 441
forman una base para el eigenespacio correspondiente a X = 2. Aplicando el pro-ceso
de Gram-Schmidt a {u1, u2$ se obtienen los siguientes eigenvectores orto-normales
v, = [ l/ofi] y v2=
(comprobar):
- l / v ?
El eigenespacio correspondiente a X = 8 tiene a
como base. Aplicando el proceso de Gram-Schmidt a {u3} se obtiene
Finalmente. usando a vl, v2 y v3 como vectores columna se obtiene
O 2 / d 1/%5 I
- l / u 2 -116 l/V5
p = [ l / v ? - 116 l / v 3
que diagonaliza ortogonalmente a A. (Como comprobación, el lector debe verificar
que PTAP es una matriz diagonal.) A
EJERCICIOS DE LA SECCIÓN 7.3
1. Encontrar la ecuación característica de la matriz simétrica dada, y luego por inspección
determinar las dimensiones de los eigenespaclos
: '1 4 4 0 0
[-2 :- 1; ;o -;I
df e) [4 O o] f ) 2 2 4 0 0 0 0
0 0 0 0 0 0 - I
En los ejercicios del 2 al 9, encontrar una matriz P que diagonalice ortogonalmente a A, y
determinar P"AP.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-436-320.jpg)
![6. A = [ I 1 O] 7 . A = [ : ! :: I!] 8. A = [ ’O 0 o0 0 ‘1 9. A = [ 24O
442 / Eigenvalores, eigenvectores
1 1 0
3 1 0 0 -7 24 O O
O7 - 70 2 O4
O 0 0 0 O O 2 4 7
O 0 0
10. Suponiendo que b f O, encontrar una matriz que diagonalice ortogollalmente a
11. Demostrar que si A es cualquier matnz m X n, entonces ATA tiene un conjunto
ortonormal de n eigenvectores.
12. a) Demostrar que si v es cualquier matnz n X 1 e I es la matriz identidad n X n,
entonces Z - wT es diagonalizable ortogonalmente.
b) Encontrar una matriz P que diagonalice ortogonalmente aI - wTs i
13. Usando el resultado del ejercicio 17 en la sección 7.1, demostrar el teorema 7 . 3 . 2 ~
para matrices simétncas 2 X 2.
EJERCICIOS COMPLEMENTARIOS
1. a) Demostrar que si O < 0 < n, entonces
sen 8 cos 8 1
A = [ cos 0 -sen 0
no tiene eigenvalores y en consecuencia no tiene eigenvectores.
b) Proporcionar una explicación geométrica del resultado del incisao)
2. Encontrar los eigenvalores de
3. a) Demostrar que si D es una matriz diagonal con elementos no negativos en la
diagonal principal, entonces existe una matriz S tal que S’ = D.
b) Demostrar que si A es una matriz diagonalizable con eigenvalores no negativos,
entonces existe una matnz S tal que S’ =A.
c) Encontrar una matriz S tal que S’ = A si](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-437-320.jpg)
![Ejercicios complementarios / 443
4. a) Demostrar: Si A es una matriz cuadrada, entonces A y AT tienen los mismos eigen-valores.
b) Demostrar que A y AT no necesariamente tienen los mismos eigenvectores.
[Sugerencia Usando el ejercicio 18 de la sección 7.1, encontrar una matriz A 2 X 2
tal que A y AT tengan eigenvectores diferentes.]
5. Demostrar: Si A es una matriz cuadrada y p(1) = det(1Z - A) es el polinomio carac-terístico
de A, entonces el coeficiente de 1"" enp(1) es el negativo de la traza de A.
6. Demostrar: Si b # O, entonces
no es diagonalizable.
7. En algebra lineal avanzada se demuestra el teorema de Cayley-Hamilton, que esta-blece
que una matriz cuadradaA satisface su ecuación característica;e s decir, si
c o + c l a + c ~ a ~ + ~ ~ ~ + c ~ ~ , ~ - ~ + a ~ = o
es la ecuación característica de A, entonces
col + c,A + c2A2 + . . . + cn- ,A"-' + A" = O.
Comprobar este resultado para
O 1 0
1 -3 3
En las ejercicios 8, 9 y 10, usar el teorema de Cayley-Hamilton enunciado en el ejercicio7 .
8. Usando el ejercicio 16 de la sección 7.1, demostrar el teorema de Cayley-Hamilton
paramatrices2 X 2.
9. El teorema de Cayley-Hamilton proporciona un método eficiente para calcular poten-cias
de una matnz. Por ejemplo, si A es una matriz 2 X 2 con ecuación característica
co + + a2 = o
entonces cJ + c,A + A2 = O, de modo que
A2 = -cIA -col
Multiplicando todo por A se obtiene A3 = -c,A2 - e&, que expresa A3 en términos de
A2 y A, y multiplicando todo por A2 se obtiene A4 = -c1A3 - c a z , que expresa A4 en
términos de A3 y A2. Continuando de esta manera es posible calcular potencias con-secutivas
de A expresándolas simplemente en términos de potencias inferiores. Usando
este procedimiento, calcular
A2, A3, A4, y As](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-438-320.jpg)





![8. I Transformaciones lineales generales / 449
Ejemplo 5 En la sección 6.4 se definió la proyección ortogonal de R"' sobre un
subespacio W. [Véase la fórmula (6) y la definición precedente a ésta en dicha sec-ción.]
Las proyecciones ortogonales también se pueden definir en espacios
generales con producto interior como sigue: Supóngase que W es un subespacio de
dimensión finita de un espacio V con producto interior; entonces la proyección
ortogonal de Vsobre W es la transformación definida por
(figura 2). Por el teorema 6.3.5 se deduce que si
S = {WI,w2 , . . . , w,)
es cualquier base ortonormal para W, entonces T(v) está definido por la fórmula
T(v) =proyw v = ( v , wI)w,-1 (v, w2)w2+ . . . + (v. w,)~,
La demostración de que T es una transformación lineal es consecuencia de las
propiedades del producto interior. Por ejemplo,
T(u + v) = (u + v, Wl)Wl+ (u + v, w2)w*+ ' ' ' + (u + v, WJW,
= (u, W,)Wl + (u, w2)w2 + . ' ' + (u, WJW,
+ (v, WI)W, + (v, W2)WZ + ' ' ' + (v, WJW,
= T(u) + T(v)
De manera semejante, T ( h ) = kT(u). A
Ejemplo 6 Como un caso especial del ejemplo anterior, sea V = R3 con el
producto interior euclidiano. Los vectores w1 = (1, O, O) y w2 = (O, 1, O) forman
una base ortonormal del plano xy. Por tanto, si v = (x, y, z) es cualquier vector en
R3, entonces la proyección ortogonal de R3 sobre el plano xy está dada por
T(v) = (v, w, )WI + (v, W2)WZ
= x(1, o, 0) + Y a 1, 0)
= (X> Y, 0)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-444-320.jpg)










![460 / Transformacionzs lineales
a) Encontrar (T, 0 TJA), donde A = [: :]
b) ¿Puede el lector obtener (T2 0 T,)(A)? Explicar la respuesta
20. Sean T,:P,+ Pn y T,:P, + Pn los operadores lineales definidos por T , ( p ( x ) )= p ( x
- 1) y T,(p(x)) = p(x + 1). Encontrar (TI 0 T,)(p(x)) y (T2 0 T,)(p(x)).
21. Sea T,:V + V la dilatación T,(v) = 4v. Encontrar un operador lineal T,:V + V tal que
TI 0 T, = I y T, 0 TI = 1.
22. Suponer que las transformaciones heales TI .Pz + P2 y T2F3 + P, están defindas por las
fórmulas T,(p(x))= p(x + 1 ) y T2(p(x))= x&). Encontrar (T, 0 Tl)(ao+ aix+ up’).
23. Sea qo(x) un polinomio fijo de grado m, y la función T con dominio Pn definida por la
fórmula T(p(x)) = p(q,(x)).
a) Demostrar que T es una transformación lineal. b) ¿Cuál es el codominio de T,
24. Con la definición de T3 0 T2 0 TI dada por la fórmula (4), demostrar que
a) T3 0 T2 0 TI es una transformación lineal.
b) T 3 o T 2 o T I =(T30T2)oTl
c) T 3 0 T 2 0 T 1 = T 3 0 ( T 2 0 T I )
25. Sea T:R3 + R3 la proyección ortogonal de H3 sobre el plano q. Demostrar que T 0 T = T
26. a) Sean T: V + W una transformación lineal y k un escalar. La función ( k g : V + W se
define como (k1](v) = k(T(v)). Demostrar que kT es una transformación lineal.
b) Encontrar ( 3 T ) ( x , , x2) si T:R2 + R2 está expresada por la fórmula T(xl, xz) =
@x1 - X,’ x2 +x1>.
27. a) Sean T,:V + W y T2:V + W transformaciones lineales. Las funciones (T, + T2):Y +
W y (TI - TJ: V + W se definen como
(TI + T2)W = + T2W
(T, - T2)W = TI(V) - TAv)
Demostrar que TI + T2 y T, - T2 son transformaciones lineales.
definidas por las fórmulas TI@, y ) = (2y, 3x) y T2(x, y ) = (y, x).
b) Encontrar (TI + T2)(x, y) y (TI - í“,)(x, y) si TI 2’ + R2 y T2:R2 + R2 están
28. a) Demostrar que si al, a2, b, y b, son escalares cualesquiera, entonces la fórmula
m , Y ) = @,x + blY, a2x + b2Y)
defme un operador lineal sobre R2.
Explicar la respuesta.
b) ¿La fórmula F(x,y ) = (up? + b,y ‘2.u,, + b p 2 )d efine un operador lineal sobre R2?
29. (Para quienes ya estudiaron Cálculo). Sean
D(f) = f’(xj y J(f) = j ; i ( t j dt](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-455-320.jpg)






![8.2 Núcleo y recorrido / 467
6. Sea TF, + P, la transformación lineal del ejercicio 5. ¿Cuáles de los siguientes
vectores están en R( o?
a) x+x? b) 1 +x. c) 3 -2.
7. Encontrar una base para el núcleo
a) del operador lineal del ejercicio l.
b) de la transformación lineal del ejercicio 3.
c) de la transformación lineal del ejercicio 5.
8. Encontrar una base para el recorrido
a) del operador lineal el ejercicio 1. b) de la transformación lineal del ejercicio 3.
c) de la transformación lineal del ejercicio 5.
9. Comprobar la fórmula (1) del teorema de la dimensión para
a) el operador lineal del ejercicio 1. b) la transformación lineal del ejercicio 3.
c) la transformación lineal del ejercicio 5.
En los ejercicios del 10 al 13, sea T la multiplicación por la matnz A. Encontrar
10. A = [i -i] 11. A = 1: -a]
a) una base para el recorrido de T. b) una base para el núcleo de T.
c) 1 rango y la nulidad de T. d) el rango y la nulidad de A.
-1 2 0 -
1 4 5 0 9
3 -2 ! o -1
-1 0 -1 o - 1
2 3 5 1 8
14. Describir el recorrido y el espacio nulo de la proyección ortogonal sobre
a) el plano xz.
b) el plano yz.
c) el plano cuya ecuación es y = x.
15. Sea V cualquier espacio vectorial y sea T: V + V definida por T(v) = 3v.
a) ¿Cuál es el núcleo de T? b) ¿Cuál es el recorrido de 77
16. En cada inciso, usando la información proporcionada para obtener la nulidad e T.
a) T A+~ R ? tiene rango 3. b) TP4 + P, tiene rango 1.
c) El recorrido de TR' -D R3 es R3. d) TMZ2 + M,, tiene rango 3.
17. Sea A una matriz 7 X 6 tal que Ax = O sólo tiene la solución trivial, y sea TR' + R7 la
multiplicación por A. Encontrar el rango y la nulidad de A.
18. Sea A una matriz 5 X 7 con rango 4.
a) ¿Cuál es la dimensión del espacio solución de Ax = O?
b) ¿Es consistente Ax = b para todos los vectores b en R'? Explicar la respuesta](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-462-320.jpg)





![8.3 Transformaciones lineales inversas / 473
Ejemplo 7 Sea T:R3 + R3 el operador lineal definido por la fórmula
T(X1, X2, X3) = (3x1 + X2, "2x1 - 4x2 + 3x3, 5x1 + 4x2 - 2x3)
Determinar si T es uno a uno; en caso afirmativo, encontrar T- '(x,, x2, x3).
Solución. Por el teorema 4.3.3, la matriz estándar para T es
3 1 0
[ T I = -2 -4
(comprobar). Esta matriz es invertible y por la fórmula (1) de la sección 4.3, la
matriz estándar para T" es
4 -2 -3
[ T " ] = [ T ] - ' =
-12 7 10
Se concluye que
Expresando este resultado en notación horizontal se obtiene
INVERSAS DE El siguiente teorema muestra que la composición de transformaciones lineales uno
COMPOSICIONES a uno es uno a uno, y relaciona la inversa de la composición con las inversas de
las transformaciones lineales individuales.
Teorema 8.3.3. Si T,: U + V y T2:V + W son transformaciones lineales uno a
uno, entonces:
a) T, 0 TI es uno a uno.
h) (T2 0 Tl)-I = r;' 0 T i - ] .
Demostración de a). Se quiere demostrar que T2 o T, transforma vectores distintos
de U en vectores distintos de W. Pero si u y v son vectores distintos de U, entonces
TI@)y Tl(v)s on vectores distintos de V ya que T, es uno a uno. Lo anterior y el
hecho de que T2 es uno a uno indican que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-468-320.jpg)

![8.3 Transformaciones lineales inversas / 475
o bien, de manera equivalente,
En palabras, esta fórmula establece que la matriz estándar para la inversa de una
composición es el producto de las inversas de las matrices estándar de los opera-dores
individuales en orden invertido.
En los ejercicios se proporcionan algunos problemas en los que se usan las
fórmulas (4) y (S).
EJERCICIOS DE LA SECCIÓN 8.3
1. En cada inciso, encontrar ker(Z') y determinar si la transformación lineal T es uno a
Uno.
a) T : R2+ R2, donde T(x, y) = (y, x)
b) T: R2+R2, donde T(x, y) = (O, 2x + 3y)
c) T: R2+R2, donde T(x, y) = (x +y, X - y )
d) T: R2 + R3, donde T(x, y) = (x, y, x + y)
e) T : R2+ R', donde T(x, y) = (x - y, y - x, 2x - 2y)
f) 2': R3 + R2, donde T(x, y, z) = (x + y + z, x - y - z)
2. En cada inciso, sea T.&2 -* R2 la multiplicación por A. Determinar si T tiene inversa;
en caso afirmativo, hallar
3. En cada inciso, sea TX3 + R3 la multiplicación por A. Determinar si T tiene inversa;
en caso afirmativo, encontrar
a ) A = [ - 1 1 21 ol ] " A = [ - ; ; i] c ) A = [ O1 11 0I] . ) A = [ : -:]
1 5 2 1 0 1
4. En cada inciso, determinar si la multiplicación por A es una transformación lineal uno
a uno.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-470-320.jpg)


![478 ,, Transformaciones lineales
8.4 MATRICES DE TRANSFORMACIONES LINEALES GENERALES
En esta sección se demostrará que si V y W son espacios vectoriales de dimen-siones3nitas
(non ecesariamente R" y Rm),e ntonces con un poco de ingenio cual-quier
transformación lineal T: V -+ W .se puede considerar corno una tran$orma-ción
matricial. La idea básica es trabajar con las matrices de coordenadas de los
vectores, en vez de hacerlo con los vectores mismos.
MATRICES DE
CIONES
LINEALES
TRANSFORMA-Supóngase
que V es un espacio vectorial n dimensional y que W es un espacio
vectorial m dimensional. Si se eligen bases B y B' para V y W, respectivamente,
entonces para todo x en V la matriz coordenadas [xIB es un vector en R" y la
matriz coordenadas [T(x)]p es un vector en Rm (figura 1).
A es un
vector en V
(n-dimensional)
T
X T(x) un es A
I vector en W
I (m-dimensional)
un es A i
vector en R" [x18
Figura 1
A es un
[ Tt4h vector en R~
Si, como se ilustra en la figura 2, se completa el rectángulo sugerido en la figura 1,
se obtiene una aplicación de R" a Rm, que se puede demostrar es una transforma-ción
lineal. Si se deja que A sea la matriz estándar de esta transformación, en-tonces
La matnz A en (1) se denomina matriz para T con respecto a las bases B y B'.
T mapea
Ven W
X T T(x)
I I
t
i
i
Figura 2
La multiplicación
por A mapea
R" en R"](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-473-320.jpg)
![8.4 Matrices de transformaciones lineales generales / 479
Después, en esta sección se darán algunos usos de la matriz A en (l),
pero primero se mostrará cómo se puede calcular. Para este efecto, supóngase
que B = {u1, u2, . . . , U,,} es una base para el espacio n dimensional V, y que
B' = {vl, v2, . . . , vm} es una base para el espacio m dimensional W. Se trata
de encontrar una matriz m X n
A=
tal que (1) se cumpla para todos los vectores x en V. En particular, se quiere que
esta ecuación sea verdadera para los vectores básicos ul, u*, . . . , U,,; es decir,
A [ u I ] B = [ T ( u l ) ] B ' ~ A [ u 2 1 B = [ T ( u 2 ) 1 B r , . . . ) A [ u n l B = [ T ( u n ) l B r (2)
Pero
de modo que
I ' '
O'
1
O
a1 1
a2 1
a12
a12
am2
] =
O](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-474-320.jpg)


![482 ' Transformaciones lineales
Ejemplo 2 Sea T:P, -+ P, la transformación lineal del ejemplo 1. Demostrar que
la matriz
[a o 0
1 y]
TI,.., = (obtenida en el ejemplo 1) satisface (4a) para todo vector x = a + bx en P,
Solución. Como x = p (x) = a + bx, se tiene
T(x) = xp(x) = ax + hx2
Para las bases B y B' del ejemplo I, por inspección se concluyeq ue
[ T(x)],.= [ax + bx2] = [:Ia Por tanto,
de modo que (4a) se cumple. A
Ejemplo 3 Sea T:R2 + R3 la transformación lineal definida por](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-477-320.jpg)

![484 Transformaciones lineales
Por consiguiente,
En consecuencia,
Solución de b). Si
x = [:;I
es cualquier vector en R2, entonces por la fórmula dada para T
[ x1 + x2
= -2x1 + 4x2]
Para encontrar [xIB y [T(x)IB, es necesario expresar (6) y (7) como combinaciones
lineales de u1 y u2. Esto conduce a las ecuaciones vectoriales
Igualando los elementos correspondientes se obtienen los sistemas lineales
k, + k, = x,
k, + 2k, = x2
Y
c1 + c2 = x, + x2
c, + 2c, = -2x, + 4x2
Resolviendo (10) para k, y k, se obtiene
k, =2x1 -x2, k2= -X, +X,
de modo que
[ 2x, - x2
rx1B = -x1 +x2]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-479-320.jpg)
![8.4 Matrices de transformaciones lineales generales i 485
y resolviendo (1 1) para c1 y c2 se obtiene
CI = 4Xl - 2x2, C2 = - 3 X l + 3x2
de modo que
Así,
de modo que (5a) se cumple. A
MATRICES DE Ejemplo 5 B = {u1, u2, . . . , U,,} es cualquier base para un espacio vectorial V de
OPERADORES dimensión finita e I: V * Ves el operador identidad sobre V, entonces
IDENTIDAD
I(U,) = UI, I(u2) = u2, . . . , I(un) = u,
Por consiguiente,
Así,
. . .
. . .
' . .
. . . 1
En consecuencia, la matriz de operador identidad con respecto a cualquier base es
la matriz identidad de n X n. Este resultado se pudo haber anticipado a partir de la
fórmula (5a), ya que la fórmula produce
[zlB[x lE])E'(' [= = ['IR
lo cual es consistente con el hecho de que [Ijs = I. A
Se deja como ejercicio demostrar el siguiente resultado](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-480-320.jpg)
![186 1 Transformaciones lineales
Teorema 8.4.1. Si TR" + Rm es una transformación lineal y si B y 8' son las
bases estándar para R" y R", respectivamente, entonces
[TI,,,. = [ TI (12)
Este teorema, establece que en el caso especial en que T transforma R" en Rm, la
matriz para T con respecto a las bases estándar es la matriz estándar para T. En
este caso especial la fórmula (4a) de esta sección se reduce a
[ T ] x = T(x)
POR QUÉ SON Hay dos razones esenciales para estudiar matrices de transformaciones lineales
IMPORTANTES generales, una teórica y otra bastante práctica:
LAS MATRICES
DE LAS A menudo es posible contestar preguntas teóricas acerca de la estructura de
CIONES finita estudiando simplemente las transformaciones lineales. estas cuestiones
LINEALES se consideran con más detalle en cursos más avanzados de álgebra lineal.
TRANSFORMA- transformaciones lineales generales sobre espacios vectoriales de dimensión
aunque se abordarán en secciones ulteriores de este texto.
o Estas matrices hacen posible calcular imágenes de vectores usando multipli-cación
matricial. Los cálculos se pueden efectuar rápidamente en compu-tadora.
A fin de enfocar la segunda idea, sea T Y + W una transformación lineal.
Como se muestra en la figura 5, la matriz [TIFB se puede usar para calcular T(x)
en tres pasos aplicando el siguiente procedimiento indirecto:
1) Calcular la matriz coordenadas [x]~.
2) Multiplicar xB por la izquierda por [nBBpa ra obtener [T(x)lBl.
3) Reconstruir T(x) a partir de su matriz coordenadas [T(x)]p.
Ejemplo 6 Sea T:P, + P2 el operador lineal definido por
T( p ( x ) )= P(3X - 5)
es decir, T(co + cIx + c2x2) = co + c1(3x - 5) + c2(3x -](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-481-320.jpg)


![8.4 Matrices de transformaciones lineales generales I 489
(T, 0 TI)@, + CIX) = (3x - 5)(c, + CI(3X - 5))
= C0(3X - 5) + Cl(3X - 5)* (16)
En este ejemplo, P, desempeña el papel de U en el teorema 8.4.2 y P, desempeña
los dos papeles de V y W, por tanto, en (13) se puede tomar B' = B", de modo que
la fórmula se simplifica a
[ T, O TI lB',B = [ T2 IB'[ TI IB',B (17)
Se elegirán B = { 1, x} como la base para P, y B' = { 1. x, x,} como la base para P,.
En los ejemplos 1 y 6 se demostró que
Así, por (17) se concluye que
Como comprobación, [T, TilFB se calculará directamente a partir de la fórmula
(4). Como B = { 1, x}, por la fórmula (4) con u1 = 1 y u, = x se concluye que
Aplicando (16) se obtiene
(T, 0 Tl)(l) = 3x - 5 y (T20 T,)(x=) ( 3 -~ 5) , = 9x2 - 3 0 +~ 2 5
Como B' = { 1, x, 2},a p artir de ésto se concluye que
w 2 0 T ~ ) ( =~ N ~ ~ [-a] y w 2 0 ~ ~ ) ( x )=1 ~ , [ -](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-484-320.jpg)
![490 Transformaciones lineales
Sustituyendo en (19) se obtiene
7',1,,,, = [ ; -3;]
-5 25
lo cual concuerda con (18). A
EJERCICIOS DE LA SECCIóN 8.4
1. Sea TP, + P3 la transformación lineal d e f ~ d pao r T(p(x))= xp(x).
a) Encontrar la matriz para T con respecto a las bases estándar
B = {U,, U*, ~ 3 ) y B' = ~ 2 v, i. vql
donde
UI = I , u2 =x, u3 =x>
v, = 1, v2 =x, vj =x2, v4 =x3
b) Comprobar que la matnz [uFBobt enida en el inciso a) satisface la fórmula (4a)
para todo vector x = c o + cIx + e$ en Pz.
2. Sea T:P, + P, la transformación lineal defmida por
T(a, + a,x + U2X2) = (a, + a,) - (2a, + 3 q ) x
a) Encontrar la matriz para T con respecto a las bases estándar B = { 1, x, 2) y B' = 1,
b) Comprobar que la matriz [qF8ob tenida en el inciso a) satisface la fórmula (4a)
x paraP2 y PI.
para todo vector x = co + cIx + cp2 en P2.
3. Sea TPz + P, el operador lineal definido por
T(a, + a,x + a$) = U,) + a,(x - 1) + u2(x - 1)*
a) Encontrar la matnz para T con respecto a la base estándar B = { 1, x, 2) para P,.
b) Cotnprobar que la matriz [7JB obtenida en el inciso a) satisface la fórmula (5a) para
todo vector x = a,, + a,x + up2 en Pz.
4. Sea TX2 .+ R2 el operador lineal definido por
y sea B = ul, u2 la base para la cual
a) Encontrar [qe.
b) Comprobar que la fórmula (5a) se cumple para todo vector x en R2.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-485-320.jpg)

![492 / Transformaciones lineales
c) Encontrar una fórmula para T
d) Aplicar la fórmula obtenida en el inciso c) para calcular T
[-i 3 - 2 5 1 o
:] 10. Sea A = la matnz de of T: R"R3 con respecto a las bases
(c) Encontrar una fórmul
11. Sea A =
~araT[[]). (d)Usarlafórmulaobtenidaen(c)paracalcularT
m ) .
la matnz de of T : Pz -+ P, con respecto a la base
E = {v,, v2, vi), donde vI = 3x + 3x2, v2 = - 1 + 3x + 2x2, vj = 3 + 7x + 2 2 .
a> Encontrar [T(V,)l,, [T(v,)l, y [T(V3)1*. b) Obtener T(v,), T(vJ y T(v3).
c) Hallar una fórmula para T(uo + alx + U$).
d) Aplicar la fórmula obtenida en el inciso c) para calcular T( 1 + 2).
12. Sea T,P I+ P, la transformación lineal d e f ~ d pao r
y sea T2P2 +- P, el operador lineal definido por
T,(p(xj) = p(2x + 1)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-487-320.jpg)
![8.4 Matrices de transformaciones lineales generales / 493
SeanB= {l,x} yB'= {I,x,x?} lasbasesestándarparaP, yP,.
Encontrar T2 O TI lB:B? r21B'> y [ TI lB',B.
b) Escribir una fórmula que relacione las matrices del ixiso a).
c) Comprobar que las matrices del inciso a) satisfacen la fórmula enunciada en el in-a)
ciso b).
13. Sea T,:P, + P, la transformación lineal definda por
T,(co + c,x) = 2c0 - 3c,x
y sea T2F2 + P, la transformación lineal definda por
T,(co+ c,x + c2xZ) = 3c0x + 3 4 + 3 c2x3
S e a n B = { 1 , x } , B " = ( 1 , x , ~ } y B m = { 1 , x , ~ , ~ } .
b) Escribir una fórmula que relacione las matrices del inciso a).
c) Comprobar que las matrices del inciso a) satisfacen la fórmula planteada en el
a) Encontrar [ T2 o TI ]B'.B, [ T21B',B"i Y [ TI 1B':B.
inciso b).
14. Demostrar que si T: V + W es la transformación cero, entonces la matriz T con respecto
a bases cualesquiera para V y W es una matnz cero.
15. Demostrar que si T:V + V es una contracción o una dilatación de V (ejemplo 4 de la
sección 8. l), entonces la matriz para T con respecto a cualquier base para V es una
matriz diagonal.
16. Sea B = {v,, v2, v3, v4) una base para un espacio vectorial V. Encontrar la matriz con
respecto a B del operador lineal TV + V defindo por T(v,)= v2, T(v,)= v,, T(v3)= v4,
T(v4)= VI.
17. (Para quienes ya estudiaron C6lculo). Sea DIP, + P, el operador derivación
D(p)= p'(x). En los incisos a) y b), encontrar la matriz D con respecto a la base B
= {PI, P,. PJ
a) p, = 1, p2 =x, p3 =x2 (b) p, = 2, p2 = 2 - 3x, p3 = 2 - 3x + 8x2
c) Usar la matriz del inciso a) para calcular D(6 - 6x + 242).
d) Repetir las instrucciones del inciso c) para la matriz del inciso b).
18. (Para quienes ya estudiaron CcuCurO). En cada inciso, B = {f,, f2, f,} es una base para
un subespacio V del espacio vectorial de funcionesc on valores reales defindas sobre la
recta real. Encontrar la matriz con respecto a B del operador derivaciónD :V -D V.
a) f, = 1, f2 = senx, f3 = cos x b) f, = 1, f2 = ex, f3 = e2x
c) f, = e2x, f2 =xeZx, f3 =x2eZX
19. Demostrar: Si B y B' son las bases estándar para R" y R"', respectivamente, entonces la
matnz de la transformación lineal T8" + R"' con respecto a las bases B y B' es la
matriz estándar para T.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-488-320.jpg)
![494 Transformaciones lineales
8.5 SEMEJANZA
La matriz de un operador lineal T: V + V depende de la base elegida para V. Uno
de los problemas fundamentaleds el álgebra lineal es elegir una base para V que
simplijque la matriz para T; por ejemplo, diagonal o triangular. En esta sección
se estudiará este problema.
ELECCIÓN DE
BASES A FIN DE
OBTENER
MATRICES
SIMPLES PARA
OPERADORES
LINEALES
Las bases estándar no necesariamente producen las matrices más simples para ope-radores
heales. Por ejemplo, considérense el operadolri neal TR2 += R2 definido por
T ( [ r : l ) = [ - 2'xI ' , + 4x' 2,]
y la base estándar B = {el, e2> para R2, donde
Por el teorema 8.4. I, la matriz para T con respecto a esta base es la matriz están-dar
para T; es decir,
TI, = [ T I = [ V e , ) I T(e2)l
de modo que
En comparación, en el ejemplo 4 de la sección 8.4 se demostró que si
entonces la matriz para T con respecto a la base B' ={ ul, u2} es la matriz diagonal
Esta matriz es más "simple" que (2) en el sentido de que las matrices diagonales
poseen propiedades especiales que no tienen las matrices generales.
Uno de los temas principales en cursos más avanzados de álgebra lineal es
determinar la "forma más simple posible" que se puede obtener para la matriz un
operador lineal al elegir la base correcta. Algunas veces es posible obtener una](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-489-320.jpg)
![8.5 Semejanza / 495
RELACI~N
ENTRE LAS
MATRICES DE
TRANSICI~N
Y LOS
OPERADORES
IDENTIDAD
matriz &agonal (como se acaba de hacer, por ejemplo); otras veces es necesario
establecer una matriz triangular o de alguna otra forma. En este texto sólo será po-sible
mencionar la importancia - de este tema importante.
El problema de determinar una base que produzca la matriz más simple posible
para un operador heal T V V se puede atacar encontrando primerou na matriz para
T con respecto a cualquier base; por ejemplo una base estándar, cuando sea posible, y
luego cambiando la base de manera que se simplifique la matriz. Antes de prosegw
con esta ideas,e rá de utilidad repasar algunos conceptos sobre cambio de base.
Recuérdese por la ftrmula (8) de la sección 6.5 que si B = {ul, u2, . . . , un}
y B' = {u , , u , , . . . , u L} son bases para un espacio vectorial V, entonces la 1 1
matriz de transición de B"a B está definida por la fórmula
p = [[u;], j [u;], j ' ' ' : [ull,]
Esta matriz posee la propiedad de que para todo vector v en
P[VIB' = [VI,
es decir, la multiplicación por P mapea la matriz coordenadas para v con respecto
a B' en la matriz coordenadas para v con respecto a B [véase la fórmula (7)] en la
sección 6.51 . En el teorema 6.5.4 se demostró que P es invertible y P" es la ma-triz
de transición de B a B'.
El siguiente teorema proporciona otro punto de vista útil sobre las matrices de
transición; muestra que la matriz transición de una base B' a una base B se puede
considerar como la matriz operador identidad.
Teorema 8.5.1. Si B y B' son bases para un espacio vectorial V de dimensión
finita y si I:V + V es el operador identidad, entonces [qBp es la matriz de
transición de B' a B.
Demostración. Supóngase que B {u1, u2, . . un} y B' u # u ,
= . , =
{ , , . . . , u }son bases para V. Usando el hecho de que I(v) = v para todo v
en V, por la fórmula (4) de la sección 8.4, con B y B invertidas, se concluye que
Así, por (5), se tiene [IjBg' = P, lo cual demuestra que [JIBB' es la matriz
transición de B' a B. 0
El resultado de este teorema se ilustra en la figura l.
Base = B' Base = B
Figura 1 I [ Z]B,B8 es la matriz de transici6n de B' a B. I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-490-320.jpg)
![496 ' Transformacrones lineales
EFECTO DEL Ahora ya es posible considerar el problema principal de esta sección.
CAMBIO DE
BASES SOBRE
MATRICES DE
Problema. Si B y B' son dos bases para un espacio vectorial V de Imensión
OPERADORES
finita y si T: V + V es un operador lineal, ¿qué relación existe, si la hay, entre
LINEALES
las matrices [goy [ qF?
Esta pregunta se puede contestar considerando la composición de los tres operado-res
lineales sobre V que se ilustra en la figura 2.
I I' I -
Y V
V V V V
Figura 2 Base = B' Base = B Base = B Base = B
En esta figura v primero es mapeado en sí mismo por el operador identidad,
luego v es mapeado en T(v) por T, luego T(v) es mapeado en sí mismo por el
operador identidad. Los cuatro espacios vectoriales de la composición son los
mismos (a saber, 4; sin embargo, las bases para los espacios varían. Como el vector
inicial es v y el vector final es T(v), la composición es la misma que T; es decir,
T= 10 T a l (7)
Si, como se ilustra en la figura 2, a los espacios vectoriales primero y último se
asigna la base B' y a los dos espacios de enmedio se asigna la base B, entonces por
(7) y la fórmula (15) de la sección 8.4 (con un ajuste apropiado en los nombres de
las bases) se concluye que
[ TIB',B' = [Io T o l l B ' , B r = [ I I B ' , R [ T I B , B [ l l E , E ' (8)
o bien, en notación más simple,
Pero por el teorema 8.5.1 se deduce que [dBY,es la matriz transición de B' a B y
que, en consecuencia. I B'B es la matriz transmon de B a B'. Luego, si se hace P =
[ABB" entonces P" = [AEB, de modo que (9) se puede escribir como
[TI,, = P '[ T],P
En resumen. se tiene el siguiente teorema.
Teorema 8.5.2. Sea T:V + V un operador lineal sobre un espacio vectorial V
de dimensión finita, y sean B y B' bases para V. Entonces
I I I donde P es la matriz de transicion de B' a B.
.. .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-491-320.jpg)
![8.5 Semejanza / 497
Advertencia. Cuando se aplica el teorema 8.5.2 es fácil olvidar si P es la matriz
transición de B a B' (incorrecto) o de B' a B (correcto). Puede ser útil escribir (10)
en la forma (9), teniendo en mente que los tres subindices "interiores" son los
mismos, y que los dos subindices exteriores son los mismos:
Una vez que se domina este patrón, basta recordar que P = [ARB' es la matriz
transición de B' a B y que P" = [AFB es su inversa.
Ejemplo 1 Sea TR2 - R2 definido por
T( [::I) = [ -2:: : 4 3
Encontrar la matriz T con respecto a la base estándar B = {el, e,} para R2, y luego
ap!icqr el teorema 8.5.2 para encontrar la matriz T con respecto a la base B' =
{UI.U}~, d onde
u ; = [ ; ] y u;=[;]
Solución. En esta sección ya se demostró ver (2) que
Para encontrar [ a partir de (10) es necesario encontrar la matriz transición
[ver (5)]. Por inspección,
u; = e, + e2
u; = e, + 2e2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-492-320.jpg)


![det(T) -= det([ TIR)
donde B es cualquier base para V.
Ejemplo 2 Sea T:R2 + R2 definido por
T ( [ ~ J )= [ -2:: 14zI]
Encontrar det(7).
Solución. Puede elegirse cualquier base B y calcular det( [ TIB). Si se considera la
base estándar, entonces por el ejemplo 1
de modo que
1 '1 det(T)= = 6
-2 4
Si se hubiese elegido la base B' = {u1, u2} del ejemplo 1, entonces se hubiera
obtenido
Por tanto
1 2 0
1 det(T)= =6
o 3
lo cual concuerda con el cálculo precedente. A
UN EJEMPLO Ejemplo 3 Sea 1 la recta en el plano xy que pasa por el origen y forma un
GEOMÉTRICO ángulo con el eje x positivo, donde O 5 8 < n. Como se ilustra en la figura 3,
sea T:R2 + R2 el operador lineal que mapea cada vector en su reflexión con
respecto a la recta 1.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-495-320.jpg)

![502 1 Transformaciones lineales
Por la fórmula (10) se deducs que
[ T I , = P[ T],,P"
Así, por (12) la matriz estándar para T es
[TI = P[ T],#P" = [cos 8 -senO][l O][ cos 8 sen8
sen8 cos 8 O - 1 -sene cos 0
cos2 8-sen28 2 sen8cos 8
2 sen e cos 8 sen2 8 - cos2 8
cos 28 sen 28
sen28 -cos 28 1
Solución de b). Por el inciso a) se concluye que la fórmula para T en notación
matricial es
EIGENVALORES
DE UN
OPERADOR
LINEAL
Sustituyendo 8 = n/6 en esta fórmula se obtiene
de modo que
Los eigenvectores y los eigenvalores se pueden definir para operadores lineales
también como matrices. Un escalar A se denomina eigenvalor de un operador lineal
T: Y + V si en V existe un vector x diferente de cero tal que Tx = Ax. El vector x se
denomina eigenvector de T correspondiente a A. De manera equivalente, los
eigenvectores de T correspondientes a A son los vectores diferentes de cero en el
núcleo de AI - T (ejercicio 15). Este núcleo se denomina eigenespaciu de T
correspondiente a A.
Se puede demostrar que si V es un espacio vectorial de dmensión finita y B
es cualquier base para Y, entonces
l. Los eigenvalores de T son iguales a los eigenvalores de [ TIB.
2. Un vector x es un eigenvector de T correspondiente a A si y sólo si su matriz
coordenadas [x]B es un eigenvector de [ TIB correspondiente a A.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-497-320.jpg)

![504 / Transformaciones lineales
Encontrar una base para R3 con respecto a la cual la matriz para T sea diagonal.
Solución. Primero se encontrará la matriz estándar para Tr luego se buscarh un
cambio de base que diagonalice la matriz estándar.
Si B = {el, e2, e3> denota la base estándar para R3, entonces
de modo que la matriz estándar para T es
Ahora se quiere cambiar de la base estándar B a una nueva base B' {uI,, u2,( u3}I
= a
fin de obtener una matriz diagonal para T. Si se hace que P sea la matriz
transición de la base desconocida B' a la base estándar B, entonces por el teorema
8.5.2 las matrices T y [qBs'e relacionan mediante
En el ejemplo 1 de la sección 7.2 se encontró que la matriz la expresión (1 3) es
diagonalizada por
- 1 o -2-
P = [ o 1 1
1 o 1-
$ 9 ,
Como P representa la matriz transición de la base B' = (ul,u2,u,>a la base
estándar B = {el, e2, e,},la s columnas de P son [ u;]B, [ &IB, y [ u3IB, de modo
que
Por tanto,
u; = (- l)e, + (O>e, + (l)e3 =](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-499-320.jpg)
![8.5 Semejanza i 505
U; = (O)e, + (I)e, + &Ve3 = [:I1
U; = (-2)e, + (I)e2 + (])e3 =
son vectores básicos que producen una matriz diagonal para [í''IP. Como compro-bación,
en seguida se calculará directamente [í''IB'. Por la fórmula dada para T se
T(u;) = [ -p] = 2u;, T(&) = [i] = 2 4 , T(u;) = [-y] = U;
tiene que
Esto es consistente con (14), ya que
EJERCICIOS DE LA SECCIóN 8.5
En los ejercicios del 1 al 7 encontrar la matnz T con respecto a B, y usando el teorema
8.5.2 para calcular la matriz T con respecto a B'.
1. T.R2 + R2 está definido por
B= {u,, u2} yB'= {vl, v2}, donde](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-500-320.jpg)
![506 í Transformaciones lineales
2.
3.
4.
5.
6,
7.
8.
9.
10.
11.
TR2 + R2 está definido por
TR2 + R2 es la rotación de 45O con respecto al origen; B y B son las bases del
ejercicio 1.
TR3 + R3 está definido por
T( [;;I) ]3x-,:+[ ' X I + 7x3
B es la base estándar para R3 y B = {v,, v2, v3}, donue
TB3+ R3 es la proyección ortogonal sobree l plano q,B y B' son como en el ejercicio
4.
TB2 + R2 está definido por T(x) = 58; B y B son las bases del ejercicio 2
TP, + P, está definido por T(ao + a,x) = a. + a,(x + 1); B = {p,, pz} y B = {q,, q2},
donde p, = 6 + 3x, p2 = 10 + 2x, q, = 2, q2 = 3 + 2x.
Encontrar det(T)
a) T: R2-+R2, donde T(x,, x,) = (3x, - 4x,, -x1 + 7x,)
b) T: R3-+R3, donde T(x,, x,, x3) = (x1 -x,, x, - xj, xj - xI)
c) T: P2+ P,, donde T(p(x)) = p(x - 1)
Demostrar que las siguientes características son invariantes bajo semejanza
a) Rango. b) Nulidad. Invertibilidad.
c) Sea TP4 + P4 el operador lineal definido por la fórmula T@(x)) =p(2x + 1).
a) Encontrar una matnz para T con respecto a alguna base conveniente; luego, usando
el resultado del ejercicio 9, encontrar el rango y la nulidad de T.
b) Con el resultado del inciso a), determinar si T es uno a uno.
En cada inciso, hallar una base para R2 con respecto a la que la matriz para T sea dia-gonal.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-501-320.jpg)
![8.5 Semejarlza i 507
a) T( [::I) = [2 x, -+ 4x2 ”1 b) T( [::I) = [ - 43xx11 + x2
12. En cada inciso, encontrar una base para R3 con respecto a la que la matriz para T sea
diagonal.
13. Sea TP, -* P, defindo por
T(u, + U,X + a2x2)= (5u0 + 6 ~+, 2 u2)- (U, + ~ u , ) x+ (uo- 2u2)x2
a) Encontrar los eigenvalores de T. b) Hallar bases para los eigenespacios de T
14. Sea TMZ2 + Mz2 definido por .([:;I )= [ b -22c c u +d c ]
a) Encontrar los eigenvalores de T.
b) Obtener las bases para los eigenespacios de T.
15. Sea 1 un eigenvalor de un operador lineal T V + V. Demostrar que los eigenvectores de
T correspondientes a I son los vectores diferentes de cero en el núcleo de II - T.
16. Demostrar que si A y B son matrices semejantes, entonces A’ y BZ también son
semejantes. De manera más general, demostrar que Ak y Bk son semejantes, donde k es
un cualquier entero positivo.
17. Sean C y D matrices m X n, y sea B = {v,, v,,. . . , vn} una base para un espacio
vectorial V. Demostrar que si C[x], = D[x], para todo x en V, entonces C = D.
18. Sea I una recta en el plano xy que pasa por el origen y forma un ángulo 8 con el eje x
positivo. Como se ilustra en la figura 5, sea TB2 + R2 la proyección ortogonal de R2
sobre 1. Con el método del ejemplo 3, demostraqr ue [ I]) = [ cos2 e sen O cos e] [ ;]
sene cos e sen2 e
[Nota Ver el ejemplo 5 de la sección 4.3.1
t” y (X.”)
1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-502-320.jpg)
![508 / Transformaciones lineales
EJERCICIOS COMPLEMENTARIOS
L. Sean A una matriz n X n, B una matriz n X 1 diferente de cero y x un vector en R"
expresado en notación matricial. ¿Es T(x) = Ax + B un operador lineal sobre R"?
Justificar la respuesta.
2. Sea
sen8 cos 0 1
A = [ cos 8 -sen0
a) Demostrar que
A'= [c os 28 -sen28 -sen 3c03o 0s
sen20 cos 20
y A 3 = [
sen30 cos 30 1
b) Conjeturar la forma de la maw A" para cualquier entero positivo n.
c) Considerando el efecto geométrico de TB2 + R2, donde T es la multiplicación por
A, obtener geométricamente el resultado del inciso b).
3. Sea vo un vector fijo en un espacio V con producto interior, y sea T:V -D V definido por
T(v) = (v, vo)vo. Demostrar que T es un operador lineal sobre V.
4. Sean Y,, Y,, . . . , vm vectores fijos en R", y sea TR" + Rm la función definda por T(x)
. I
= (x * v,, x . v2, . . . , x * vm), donde x . vi es el producto interior euclidiano sobre R".
a) Demostrar que T es una transformación lineal.
b) Demostrar que la matriz con vectores renglón vl, v2, . . . , vm es la matriz estándar
para T.
5. Sean fe,, e2, e3, e4} la base estándar para @ y T@ + R3 la transformación lineal para
la cual
T(e,) = (1, 2. 11, 7Ye2) =(O, 1, O),
V e , ) = (1, 3, O), T(e,) = (1, 1, 1)
a) Encontrar bases para el recomdo y el núcleo de T. b) Encontrar el rango y la
nulidad de T.
6. Supóngase que los vectores en R3 se denotan por matrices de 1 X 3, y definase TR3 -D
R3 por
-1 2 4-
m x , x2 %I) = [x, x2 %I/ 3 O I]
2 2 5
a) Encontrar una base para el núcleo de T.
b) Encontrar una base para el recomdo de T.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-503-320.jpg)

![51 O _/' lransformaciones lineales
b) Expresar u,, u*, u3 como combinaciones lineales de v,, v2, vj
15. Sean B = {u,, u2, u3} una base para un espacio vectorial V y T:V * Y un operador
lineal tal que
-3 4 7
Encontrar [TIB'd, onde 8 = {vl,v 2, v3] es la base para Y definida POI
16. Demostrar que las matrices
son semejantes, pero que
[-1 -:I [ - I 2
y 1 o]
no lo sox
17. Supóngase que T: V + Ves un operador lineal y que B es una base para V tal que para
cualquier vector x en V
Encontrar [ TI,.
18. Sea T:V + Vun operador lineal, Demostrar que T es uno a uno si y sólo si det(l") f O
19. (Para quienes ya esfudimon Cálculo).
a) Demostrar que la función D:C2(- m, m) + F( - m, QJ) definida por D(f) =f'(x) es
una transformación lineal.
h) Encontrar una base para el núcleo de D.
c) Demostrar que la fimción que satisface la ecuación D(f) =Ax) forma un subespacio
bidimensional de C2( - m, m), y encontrar una base para este subespacio.
T(P(-d) = P(0) r:J a) Encontrar T(x' + 5x + 6).
b) Demostrar que T es una transformación lineal
c) Demostrar que T es uno a uno.
d) Encontrar
20. Sea TP2 + R3 la función d e f ~ d pao r la fórmuia](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-505-320.jpg)









![520 /' Temas complementarios
EJERCICIOS DE LA SECCIóN 9.1
1. a) Resolver el sistema
Y ; = Y1 + 4.h
y; = 2y, + 3y,
b) Encontrar la solución que satisface las condiciones inicialesyl(0) = O,y,(O) = O.
2. a) Resolver el sistema
y; = y , + 3v2
y; = 4.h + 5Y,
b) Encontrar la solución que satisface las condiciones inicialesyl(0) = 2, y2'(0) = l.
3. a) Resolver el sistema
y; = 4y, + y3
y; = -2v, +y,
Y; = -2% + Y3
b) Encontrar la solución que satisface las condiciones iniciales y, (O) = - 1, y2(0) = 1,
Y,(O) = 0.
4. Resolver el sistema
5. Resolver la ecuación diferencial y" - y' - 6y = O. [Sugerencia. Hacer y , =y , y=2 y ' y
luego demostrar que
Y; =Y2 y; = y ' - Y' + 6~ = 6.~1 + y21
7. Demostrar: Toda solución de y' = ay es de la forma y = cP[.S ugerencia. Sea y =AX)
una soluci6n y demostrar quef(x)e-ares constante.]
8. Demostrar: Si A es diagonalizable y](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-515-320.jpg)

![522 / Temas complementarios
‘ABLA 1
Operador
Reflexión con
respecto al eje y
Reflexión con
respecto al eje x
Reflexión con
respecto a la recta
?/=X
Rotación en
sentido contrario a
las manecillas del
reloj por un ángulo
En esta sección, los operadores lineales sobre R2 se considerarán como
transformaciones de puntos en puntos. Una manera de representar el comporta-miento
de un operador lineal es observar su efecto sobre los puntos de figuras
sencillas en el plano. Por ejemplo, en la tabla 1 se muestra el efecto de algunos
operadores lineales básicos sobre un cuadrado unitario que se ha coloreado par-cialmente
Matriz estándar [-A Y]
[A -Y]
COS 0 -sen0
sen0 cos 8 1
Efecto sobre el cuadrado unitario
4 .) 1 . : I , , I . .! I, 1,
En la sección 4.2 se analizaron reflexiones, proyecciones, rotaciones, con-tracciones
y dilataciones de R2. A continuación se considerarán otros operadores
lineales básicos sobre R2.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-517-320.jpg)


![9.2 Geometría de los operadores lineales sobre R2 / 525
de modo que la matriz estándar para T es
De manera semejante, la matriz estándar para un deslizamiento cortante en la
Irección y con factor k es
OBSERVACI~N. La multiplicación por la matriz identidad 2 X 2 es el operador
identidad sobre R2. Este operador se puede considerar como una rotación de Oo,
como un deslizamiento cortante a lo largo de cualquiera de los dos ejes con k = O,
o como una compresión o expansión a lo largo de cualquiera de los dos ejes con
factor k = l.
Ejemplo 2
a) Hallar una matriz de transformación de R2 en R2 que primero efectúe un des-lizamiento
cortante en la dirección x con factor 2 y luego realice una reflexión
con respecto a y = x.
b) Encontrar una matriz de transformación de R2 en R2 que primero efectúe una
reflexión con respecto ay = x y luego un deslizamiento cortante en la dirección
x con factor 2.
Solución de a). La matriz estándar para el deslizamiento cortante es
y para la reflexión es
A , A , = [O1 '0][I 0 1 '1 = [ y :]
Así, la matriz estándar para el deslizamiento cortante seguido de la reflexión es
Solución de b). La reflexión seguida del deslizamiento cortante se representa como](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-520-320.jpg)

![9.2 Geometría de los operadores lineales sobreR 2 / 527
[-b :] = [A -;,I = [A -:][A :,I
Como k, > O, el producto en (3) representa una compresión o expansión a lo largo
del eje x seguida de una reflexión con respecto al eje y, y (4) representa una
compresión o expansión a lo largo del eje y seguida de una reflexión con respecto
al eje x. En el caso en que k = -1, las transformaciones (3) y (4) simplemente son
reflexiones con respecto a los ejes y y x, respectivamente. A
Las reflexiones, rotaciones, expansiones, compresiones y deslizamientos
cortantes son, todas, operadores lineales uno a uno. Este hecho es evidente geomé-tricamente,
ya que todos estos operadores mapean puntos distintos en puntos
distintos. Esto también se puede comprobar de manera algebraica al verificar que
las matrices estándar de los operadores son invertibles.
Ejemplo 4 Intuitivamente resulta evidente que si el plano xy se comprime por un
factor i en la dirección y, entonces el plano xy se debe expandir por un factor 2 en
la drección y a fin de que cada punto regrese a su posición original. En efecto,
esto es asi porque
representa una compresión en la dirección y con factor i, y
es una expansión en la dirección y con factor 2. A
PROPIEDADES Esta sección concluye con dos teoremas que permiten conocer más las propiedades
GEOMÉTRICAS geométricas de los operadores lineales sobre R2.
DE LOS ~~~"
OPERADORES
LINEALES
SOBRE R2
Teorema 9.2.1. Si T:R2 + R2 es la multiplicación por una matriz A invertible,
entonces el efecto geométrico de T es el mismo que el de una sucesión idónea
de deslizamientos cortantes, compresiones, expansiones y reflexiones.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-522-320.jpg)
![528 /' Temas complementarios
Demostración. Como A es invertible, se puede reducir a la identidad mediante
una sucesión finita de operaciones elementales en los renglones. Una operación
elemental en los renglones se puede efectuar multiplicando por la izquierda por
una matriz elemental. Así, existen matriz elementales E,, E*, . . . , Ek tales que
E A .' ' E,EIA = 1
Despejando A se obtiene
o bien, de manera equivalente,
A = E ~]-E - 1 . . . E L1
1 2 (5 1
Esta ecuación expresa a A como un producto de matrices elementales (ya que por
el teorema 1.5.2 la inversa de una matriz elemental también es elemental). El
resultado se concluye ahora por el ejemplo 3. 0
Ejemplo 5 Suponiendo que k, y k, son positivos, expresar la matriz diagonal
como un producto de matrices elementales y describir el efecto geométrico de la
multiplicación por A en términos de expansiones y compresiones.
Solución. Por el ejemplo 1 se tiene que
lo cual demuestra que la multiplicación por A tiene el efecto geométrico de
expandir o comprimir por un factor de k, en la dirección x y luego expandir o
comprimir por un factor de k, en la dirección y. A
Ejemplo 6 Expresar
A = I: :]
como un producto de matrices elementales y luego describir el efecto geométrico
de la multiplicación por A en términos de deslizamientos cortantes, compresiones,
expansiones y reflexiones.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-523-320.jpg)
![9.2 Geometría de los operadores lineales sobre R2 / 529
Solución. A se puede reducir a I como sigue:
I veces al segundo. I I - 4. . .
Las tres operaciones consecutivas en los renglones se pueden efectuar al mul-tiplicar
por la izquierda sucesivamente por
Invirtiendo estas matrices y aplicando (5) se obtiene
Leyendo de derecha a izquierda y observando que
[: -;] = [: -y][: ;]
se concluye que el efecto de multiplicar por A es equivalente a
1) efectuar un deslizamiento cortante por un factor de 2 en la dirección x, luegd
2) expandir por un factor de 2 en la dirección y, luego
3 ) reflejar con respecto al eje x, y finalmente
4) efectuar un deslizamiento cortante por un factor de 3 en la dirección y.
Las demostraciones de algunos incisos del siguiente teorema se analizan en los
ejercicios.
Teorema 9.2.2.S T:R2 + R2 es la multiplicación por una matriz invertible,
entonces:
a) La imagen de una recta es una recta.
b) La imagen de una recta que pasa por el origen es una recta que pasa por
el orrgen.
c) Las imágenes de rectas paralelas son rectas paralelas.
d) La imagen del segmento de recta que une los puntos P y Q es el segmento
de recta que une las imágenes de los puntos P y Q.
e) Las imágenes de tres puntos están sobre una recta si y sólo si los puntos
son colineales.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-524-320.jpg)
![530 Temas complementarios
OBSERVACI~N. Por los incisos c), 6) y e) se concluye que la multiplicación por
una matriz invertible A 2 X 2 transforma triángulos en triángulos y paralelogra-mos
en paralelogramos.
Ejemplo 7 Trazar la imagen del cuadrado con vértices P,(O, O), P2(l, O), P3(0, 1)
y P4( 1, 1) bajo la multiplicación por
Solución. Como [-: --:I[:] =[:I [ -f .-:I[:] = [ -:]
[-i -:][:I = [ -:] I: -:I[ :] = [I]
la imagen del cuadrado es un paralelogramo con vértices (O, O), (- 1, 2), (2, - 1) y
(1, 1) (figura 5). A
Ejemplo 8 Según el teorema 9.2.2, la matriz invertible
transforma la recta y = 2x + 1 en otra recta. Encontrar su ecuación.
Solución. Sea (x, y) un punto sobre la recta y = 2x + 1 y sea (x', Y ' ) su imagen
bajo la multiplicación por A. Entonces](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-525-320.jpg)

![5317 i' 7ema.y contplernentnrros
1.
5.
6.
7.
8.
9.
1 o.
11.
12.
13.
En cada inciso del ejercicio 3, usar la matriz obtenida para calcular T( I , 1, I ) .
Comprobar las respuestas geom6tricamentc. graficando los vectores (1 ~ 1, 1 ) y T( I ,
1, 1)
Encontrar la matriz estándar para el operador lineal 7 X 3 + R3 que
a) hace girar cada vector 90' en sentido contrario a las manecillas del reloj con res-b)
al e ~ ze ( mirando a lo largo del eje z positivo llacia e1 origen).
hace girar cada vector 90' en sentido contrario a las manecillas del reloj con res-c)
hace girar cada vector 90' en sentido contrario a las manecillas del reloj con res-pecto
pecto al eje x (mirando a lo largo del eje x positivo hacia el origen).
pecto al ejev (mirando a lo largo del eje y positivo hacia el origen).
Trazar la iInagen del rectángulo con vértices (O, O), (1, O), (1,2) y (O, 2) bajo
a) una rellexión con respecto al q e x.
b) una reflexión con respecto al eje y.
c) una compresión con factor k = a en la direcclóny.
d) una expansion con factor k = 2 en la dirección x.
e) un deslizamiento cortante con factor k = 3 en la dirección x .
t) un deslizamiento cortante con factor k = 2 en la direccióny.
Trazar la imagen dei cuadrado con vértices (O, O), (1, O), (O, I ) y ( I , 1) bajo la
multiplicación por
A= [ -; y]
Encontrar la matriz que hace girar un punto (x, y) con respecto al origen por un hlgulo
de
a) 45" b) 90" C) 180" d) 270" e) -30"
Encontrar la matriz que produce un deslizamiento cortante con u11 factor de
a) k = 4 en la dirección y. b] k = -2 en la dirección x.
Encontrar la matnz que comprime o expande con un factor de
a) f en la dirección y. b) 6 en la direction x.
En cada inciso, describir el efecto geonlétrico de la multiplicacion por la matriz
dada.
Expresar la matriz como un producto de matrices elementales y luego describir el
efecto de la multiplicaci6n por la matriz dada en términos de compresiones,
expansiones, reflexlones y deslizamientos cortantes.
En cada inciso. encontrar una sola matriz que efectúe la sucesión de operxiones que se
mdica:](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-527-320.jpg)

![534 i Temas complementarios
método del ejempio 8, demostrar que la imagen de esta recta bajo la multiplicación por
la matriz invertible
tiene la ecuación A'x + By + C = O, donde
A' = (dA - c B ) / ( ~-d bc) y B' = ( - bA + u B ) / ( u-~ bc)
Luego, demostrar que ni A' ni B son cero a fin de concluir que la imagen es una recta,]
21. Usando la sugerencia del ejercicio 20, demostrar los incisos b) y c) del teorema 9.2.2.
22. En cada inciso, encontrar la matriz estándar para el operador lineal í?A3 + R3 descrito
por la figura 7.
4 c 4
b) d
23. En R3, el deslizamiento cortanfe en la a'ireccibn xy con factor k es la transformación
lineal que mueve cada punto (x, y, z) paralelo al plano xy a la nueva posición (x + kz, y
+ kz, z). (Véase la figura 8.)
a) Encontrar la matriz estándar del deslizamiento cortantee n la dxecciónx y con factork .
b) ¿Cómo d e f d a el lector el deslizamiento cortante en la dirección xz con factor k y
el deslizamiento cortante en la dirección yz con factor k? Encontrar la matriz
est&dar para cada una de estas transformaciones lineales.
. .. ". ~. ~ ." t; 1 4. . ."
"'ir + kz, y + kz. I)
. .. ,' " .~", ."
Figura 7
Figura 8
24. En cada inciso, encontrar por inspección todos los eigenvectores linealmente inde-pendientes
que sea posible (mediante una representación del efecto geométrico de la
transformación sobre R'). Para cada uno de los eigenvectores, encontrar por inspección
el eigenvalor correspondiente; luego comprobar los resultados calculando los eigen-vaiores
y bases para los eigenespacios partir de la matriz estándar de la transformación.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-529-320.jpg)







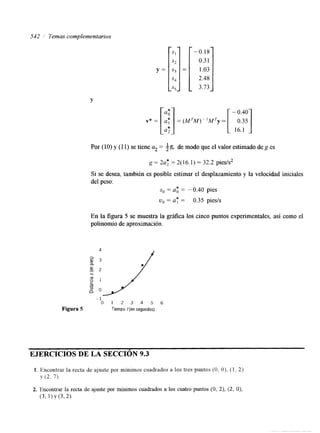
![9.4 Problemas de aproximación: series de Fourier / 543
3. Encontrar el polinomio cuadrático que se ajusta mejor a los puntos (2, O), (3, - 1 lo),
(5, -48) y (6, -76).
4. Encontrar el polinomio cúbico que se ajusta mejor a los puntos (- 1, - 14), (O, -S),
(1 > -4), (2, 1) Y (3,221.
Demostrar que la matriz M en la ecuación (2) tiene columnas linealmente
independientes si y sólo si por lo menos dos de los números xl, x2, . . . , xn son
distintos.
Demostrar que las columnas de la matriz Mn x (m + 1) en la ecuación (9) son
linealmente independientes si n > m y por lo menos m + 1 de los números x,, x2, . . . ,
x,, son distintos.
SeaM la matriz de la ecuación (9). Usando el ejercicio 6, demostrar que una condición
suficiente para que la matriz MM sea invertible es que n > m y por lo menos m + 1 de
los números x], x2, . . . , xn sean distintos.
El propietano de una empresa en rápido crecimiento encuentra que para los cinco
primeros meses del año las ventas (en miles) son $4.0, $4.4, $5.2, $6.4 y $8.0. El
propietario grafica estas cifras y conjetura que para el resto del año la curva de ventas
puede ser aproximada por un polinomio cuadrático. Encontrar el polinomio cuadrático
de ajuste por mínimos cuadrados a la curva de ventas y usarlo para proyectar las ventas
de los doce meses del año.
9.4 PROBLEMAS DE APROXIMACIóN: SERIES DE FOURIER
En esta sección se usarán los resultados de proyecciones ortogonales en espacios
con producto interior para resolver problemas que requieren la aproximación de
una función dada por funciones más simples. Estos problemas surgen en una
variedad de aplicaciones de ingenieria y ciencias.
MEJORES Todos los problemas que se estudiarán en esta sección son casos especiales del
APROXIMA- siguiente problema general.
SIONES
I I
Problema de aproximación. Dada una función f que es continua sobre un
intervalo [a, 61, encontrar la "mejor aproximación posible" a f usando sólo
funciones de un subespacio específico W de C[a, 61.
A continuación se presentan algunos ejemplos dee sos problemas:
a) Encontrar la mejor aproximación posible a eX sobre [O, 11 por un polinomi0 de
la forma a. + alx + ag2.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-538-320.jpg)
![544 / Temas complementarios
b) Encontrar la mejor aproximación posible a sen nx sobre [ - 1, 1 I por una fun-c>
ción de la forma u. + ulc? + + u3e3.‘.
la forma clo + u, sen x + a2 sen 2x + h, cos x + 6, cos 2x.
Encontrar la mejor aproximación posible a x sobre [O, 2x1 por una función de
En el primer ejemplo, W es el subespacio de C[O, 11 generado por 1, x y x,; en el
segundo ejemplo, W es el subespacio de C[ - 1, 11 generado por 1, @, e& y e3x; y
en el tercer ejemplo, U’ es el subespacio de C[O, 2n] generado por 1, sen x, sen 2x,
cos x y cos 2x
MEDICIONES Para resolver problemas de aproximación de los tipos precedentes es necesario
DEL ERROR precisar matemáticamente la expresión “mejor aproximación sobre [u, b]”; para
este efecto se requiere una manera exacta de medir el error que resulta cuando una
función continua es aproximada por otra sobre [a. 61. Si sólo se quisiera la apro-ximación
de,flx) en un simple punto xo, entonces el error en x. por una aproxi-mación
g(x) sería simplemente
error =Axo) - g(xo)
que algunas veces se denomina desviación entre f y g en x. (figura 1). Sin
embargo, se quiere la aproximación sobre todo el intervalo [u, b], no en un solo
punto. En consecuencia, en una parte del intervalo una aproximación g, afpuede
tener desviaciones más pequeñas con respecto a f que una aproximación g, af; y
en otra parte del intervalo bien puede ser al contrario. ¿Cómo decidir cuál es la
mejor aproximación global? Lo que se requiere es alguna forma para medir el
error global en una aproximación g(x). Una posible medida del error global se
obtiene integrando la desviación Axo) - g(xo) sobre todo el intervalo [a, b]; es
decir,
error = l( f(x)- g(x)( dx
Figura 1 Desviación entre f y g en XO.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-539-320.jpg)
![9.4 Problemas de aproximación: series de Fourier i 545
Geométricamente, (1) es al área entre las gráficas def(x) y g(x) sobre el intervalo
[a, b] (figura 2); mientras mayor sea el área, mayor es el error global.
El área entre las gráficas defy g sobre [u, b]
mide el error al aproximarfpor g sobre [a, b].
Si bien la expresión (1) es natural y geométricamente atractiva, casi todos
los matemáticos y científícos suelen inclinarse por la otra medida del error,
denominada error cuadrritico medio.
I I
error cuadrático-medio
I I
El error cuadrático medio recalca el efecto de errores mayores debido a la
elevación al cuadrado y posee la ventaja adicional de permitir aplicar la teoría de
los espacios con producto interior. A fin de ver cómo es posible llevar a cabo lo
anterior, supóngase que f es una función continua sobre [a, b] que se desea
aproximar por una función g de un subespacio Wde C[a, b], y supóngase que en C
[a, b] se define el producto interior
J' h
(f, 8) = f(xlg(x) dx
Se concluye que
Ilf - 81)' = (f - g, f - g) = [ f(x) - g(x)I2 dx = 'error cuadrático medio
de modo que minimizar el error cuadrático medio es lo mismo que minimizar
llf - g1I2. Así, el problema de aproximación planteado informalmente al ihicio de
APROXIMACI~
POR MÍNIMOS
CUADRADOS
esta sección se puede volver a plantear más precisamente como sigue:
IN Problema de aproximación por mínimos cuadrados. Sea f una función que
es continua sobre un intervalo [a, b], sea C[a, b] con el producto interior](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-540-320.jpg)
![y sca Lt' un subespacio de dimensión finita de C[a, b]. Encontrar una función g
em CV que minimice
i
Como Ilf -- gl12 y I(f - gl( son minimizados por la misma función g, el problema
precedente equivale a buscar una función g en W que sea la más próxima a f. Pero
por el teorema 6.4.1 se sabe que g = proywf es la función (figura 3).
Así. se tiene el siguiente resultado.
~ ~ ~~~ ~~~ ~ ~ ~
Solución del problema de aproximación por mínimos cuadrados. Si f es una
función continua sobre [u, b] y W es un subespacio de dimensión finita de C[u,
bl, entonces la función g en W que minimiza el error cuadrático medio
es g = proym: f. donde la proyección ortogonal es con respecto al producto
interior
La función g = proypvf se denomina aproximación por minimos cuadrados a f
desde W.
Una función de la forma
t ( X ) = co t L', cos x + C'2 cos 2x + . ' ' + c, cos nx
+ (2) d , senx + d, sen2x + . . + d, sennx
se denomina polinomio trigonométrico; si c, y u', no son cero, entonces se dice
que [(x) es de orden n. Por ejemplo.
[(x) = 2 + cos x ~ 3 cos 2x + 7sen4s](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-541-320.jpg)
![9.4 Problemas de aproximación: series de Fourier 1 547
es un polinornio trigonométrico con
El orden de t(x) es 4.
o igual que n son las diversas combinaciones lineales posibles de
Por (2) resulta evidente que los polinomios trigonomktricos de orden mcnor
1, cos x, cos 2x, . . . , cos nx, senx, sen2x, . . . , sennx 13)
Se puede demostrar que estas 2n + 1 funciones son linealmente independicnles y
que en consecuencia para cualquier intervalo [a, b] forman una base para
subespacio de dimensión (2n + 1) de C[a, 61.
A continuación se considerará el problema de encontrar la aproximación por
mínimos cuadrados de una función continuaflx) sobre el intervalo [O, 2 z I por u11
polinomio trigonométrico de orden menor o igual que n. Como ya se mencionó, Ea
aproximación por minimos cuadrados a f desde W es la proyección artogonal dc T
sobre W. Para encontrar esta proyección ortogonal es necesario delerminar ma
base ortonormal go, g,, . . . , k,, para W, después de lo cual es posible calculan I n
proyección ortogonal sobre W a partir de la fórmula
[vease el teorema 6.3.5). Es posible obtener una base ortonormal para kt/ medianhe
la aplicación del proceso de Gram-Schmidt a la base (31, usando el producto in-terior
Así se obtiene (ejercicio 6) la base ortonormal
m1 ' g, = - cos x,
1 1
go = -
VG
. . . , g, = __ cos nx, G
1 1
g,, , = senx, . . . , g2, = __ sennx
6
Si se introduce la notación](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-542-320.jpg)
![5411 ,/ lemas complementarios
entonces al sustituir (5) en (4) se obtiene
projcvf = ;a0 +- [ u , c os x + . . . + u,?c os nx] + [ h ,s enx + . . . +- h, sennx]
L.
donde
En resumen.
Los nimeros ao, a19, . , , a,,, b,, . . . , b,, se denominan coeficientes de Fourier*
de f.
Ejemplo 1 Encontrar la aproximación por mínimos cuadrados de Ax) = x sobre
[O, 2 nl por
a) un polinomio trigonométrico de orden menor o igual que 2;
b) un polinomio trigonométrico de orden menor o igual que n.
*Jean Soptiste Joseph Fourier (1768-1830) fue un matemático y fisico francés que descubrió las series
que llevan su nombre e ideas relacionadas cuando trabajaba en problemas de difksión del calor. Este
descubrimiento es uno de los más importantes en la historia de las matemáticas; es la piedra angular de
muchos campos de investigación matemática y una herramienta básica en muchas ramas de la ingeniería.
Fourier, un activista político durante la revolución francesa, fue encarcelado por haber defendido a muchas
victimas durante la Epoca del Terror. Después se convirtió en favorito de Napoleón, quien lo nombró barón
y conde.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-543-320.jpg)
![9.4 Problemas de aproximación: series de Fourier / S49
Solución de a).
Para k = 1,2, . . . al integrar por partes se obtiene (comprobar)
2rr
Así, la aproximación por mínimos cuadrados a x en [O, 23t] por un polinomio
trigonométrico de orden menor o igual que 2 es
a
2
x--"o + a, cos x + a2 cos 2x + b, senx + b2sen 2x
o bien, por (7a), (7b) y (7c),
x= 7r - 2 senx - sen2x
Solución de b). La aproximación por mínimos cuadrados a x en [O. 2n] por un
polinomio trigonométrico de orden menor o igual que n es
x=O + [a, cos x +. . . + a, cos nx] -t [b, sinx + . . . + b, sennx] U
2
o bien, por (7a), (7b) y (7c),
+- +...+"--se- n nx
3 n
n -
T -
2 (sen X
2 (sen X
2 (sen X
2 sen X
"
n -
+
+
4](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-544-320.jpg)
![Es natural esperar que disminuya el error cuadrático medio a medida que
aumenta el número de términos en la aproximación por mínimos cuadrados
fQ + 2 íuk cos kx + b, sen kx)
u
2 k = l
Es posible demostrar que para funciones f en C[O, n] el error cuadrático medio
tiende a cero cuando n -+ + m; este hecho se denota con
7-
f(x) = i- (uk cos kx + bk senkx)
U
2 k - l
El miembro derecho de esta ecuación se denomina serie de Fourier parafsobre el
intervalo C[O, f r ] . Estas series son importantes en ingenieria, ciencias y matemá-ticas.
A
DE LA SlECCIibN 9.4
a . Encontrar la aprcxirnacibn por mínimos cuadrados deAx) = 1 + x sobre el intervalo [O,
Z.X] por
a;) un polinemio trigonomktrico de orden menor o igual que 2.
b) un pclinomio trigonomttrico de orden menor o igual que n.
2. ihconlrar ? a aproximacián por minimos cuadrados deflx) = x2 sobre el intervalo
io, 2x1 por
a) un polinomio trigonomktrico de orden menor o igual que 3.
;:) tm p d i n omi ~tr igonomktrico de orden menor o igual que ?J.
3. 3) Encorttrar la aproximación por mínimos cuadrados de x sobre el intervalo [O, I] por
ma fimcibn de la forma a + b2.
G ;, iincontr-ar cl error cnadrático medio de la aproximación.
4. a) finzontrar la aproximación por mínimos cuadrados de di sobre el intervalo [O, 11
por un polinomio de la forma a. + a,x.
h)Encontrar el error cuadrático medio de la aproximación.
J. :*) I:ncc;nhar la aproximación por mínimos cuadrados de sen zx sobre el intervalo [ - 1,
i I w, un gollllornio da: la forma u. + u,x + u$.
L L
b ) ~ ~ n m ~ t .erl aerrr or cuadrático medio de la aproximación.
:.;., ia/i,cdi¿mtc el proceso de Gram-Schmidt, obtener la base ortonomal(5) a partir de la
¡;;!.;c. (3).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-545-320.jpg)

![S52 1 Temas complementarios
Ejemplo 2
2x2 + ~ X J -J 7v2 = [X y ] [: -:][;I
FORMAS Las formas cuadráticas no se limitan a dos variables. A continuación se define una
CUADRÁTICAS forma cuadratica general.
CON n
VARIABLES Definicibn.Unaforma cuadrritica con las n variables xl, x2, . . . , x,, es una
expresión que se puede escribir como
I donde A es una matriz simétrica den X n.
Si se hace
entonces (3) se puede escribir de manera más abreviada como
x TAx (4)
Además, es posible demostrar que si las matrices en (4) se multiplican, la expre-sión
resultante es dela forma
donde
denota la suma de los términos de la forma a l p . , donde xi y xj son variables &-
ferentes. Los términos a$zc, denotan términos de producto cruzado de la forma
cuadrática.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-547-320.jpg)
![9.5 Formas cuadráticas / 553
Las matrices simétricas son útiles, aunque no esenciales, para representar
formas cuadráticas en notación matricial. Así, para la forma cuadrática 2x2 +
6xy - 7 3 del ejemplo 2, el coeficiente del término de producto cruzado se podría
separar en 5 + 1 o 4 + 2 y escribir
O
Sin embargo, las matrices simétricas producen en general los resultados más
simples, de modo que siempre se usarán. Así, cuando una forma cuadrática se
denote por xTAx se entenderá que A es simétrica, aun cuando no se especifique.
OBSERVACI~N. Si se usa el hecho de que A es simétrica; es decir, A = AT, en-tonces
(4) se puede expresar en términos del producto interior euclilano me-diante
xTAx = xT(Ax) = (Ax, x) = (x, Ax)
Ejemplo 3 La siguiente expresión es una forma cuadrática en xl, x2 y x3:
x: + 7x: - 3x: + 4x,x2 - 2x,x3 + 6x,x, = [x, x2 x3]
Nótese que los principal de producto cruzado t:: coeficientes de los términos al cuadrado aparecen sobre la diagonal
la matriz 3 X 3, y que cada uno de los coeficientes de los términos de
están separados a la mitad y aparecen en las posiciones fuera
de la diagonal como sigue: Coeficiente de A Posiciones en la matriz A
a12 y a21
XlX3 '13 y '31
'23 Y '72
PROBLEMAS EN El estudio de formas cuadráticas es un tema extenso que sólo se puede mencionar
QUE APARECEN en esta sección. A continuación se presentan algunos problemas matemáticos
FORMAS CUA- importantes relacionados con las formas cuadráticas.
DRÁTICAS](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-548-320.jpg)

![I
9.5 Formas cuadráticas 1 555
det( dZ - A) = det [A,, A:21] =d2”d-3=(d-3)(d+ 1)=0
Así, los eigenvalores de A son L = 3 y L = - 1, que son los valores máximo y
mínimo, respectivamente, de la forma cuadrática sujeta a la restricción. Para en-contrar
los valores de x1 y x2 en que ocurren estos valores extremos es necesario
para satisfacer la condición x: t < = 1.
Se deja al lector demostrar que dos bases para los eigenespacios son
encontrar los eigenvectores correspondientes a estos eigenvalores y luego normali-zarlos
Normalizando cada uno de estos eigenvectores se obtiene
Así, sujeto a la restricción x: + < = 1, el valor máximo de la forma cuadrática es A
= 3, que ocurre si x1 = I/ J z , x2 = 1 / J z , y el valor minim0 es = - 1, que ocurre
si x1 = l/&, x2 = - l/&. Además, se puede obtener otras bases para los
eigenespacios al multiplicar por -1 los vectores básicos anteriores. Así, el valor
máximo, A = 3, también ocurre si x1 = - 1/&, xz = - l / f i y el valor mínimo,
L = -1, también ocurre si x1 = - 1/&, x2 = l/&. A
MATRICES
POSITIVAS
Definicih. Una forma cuadrática xTAx se denomina positiva definida si x*Ax >
DEFINIDAS Y O para todo x f O, y una matriz simétrica A se denomina matriz positiva
FORMAS definida si xTAx es una forma cuadrática positiva definida.
CUADRÁTICAS
El siguiente teorema es el resultado principal sobre matrices positivas definidas.
Teorema 9.5.2. Una matriz simétrica A es positiva definida si y sólo si los
eigenvalores de A son positivos.
Demostración. Supóngase que A es positiva definida y sea A cualquier
eigenvalor de A. Si x es un eigenvector de A corresponhente a A, entonces x f O y
Ax =Ax, de modo que
o < X ~ A X = xrax = axrx = a11x112 (6)
donde llxll es la norma euclidiana de x. Como llx112 > O, se deduce que L > O, qui es
lo que se quería demostrar.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-550-320.jpg)




![560 Temas complementarios
IO. Por medio del teorema 9.5.3, determinar cuides de las matrices del ejercicio 9 son posi-
1 tlvas definidas.
11. En cada inciso, clasificar la forma cuadrática como posltiva defmida, positiva semide-finida,
negativa definida, negativa semidefinida o indefinida.
a) .Y; + .Y: b) --X: - 3 ~ : C) (X, - x2)*
dj --(xl - xz)' e) .x: --x: f) x,xz
12. En cada Inciso, clasificar la matnz como positiva definida, positiva semidefinida, nega-tiva
definida, negativa semidefinida o indefinida.
a)
[ -: -: -81 O 0 1
O 0 0 [A y
d) e) [O O O] f j O 0 0 O 0 1
13. Sea X'AX una forma cuadrática en xI, x , x,; definir T:Rn + K por T(x) = x'dx.
F.'
a) Demostrar que T(x + y) = T(x) + 2x Ay + ?"(y). b) Demostrar que T(b) = pT(x).
c) ¿,Es T una transformación lineal? Explicar la respuesta.
14. En cada inciso, encontrar los valores de k con los que la forma cuadrática es positiva
definida.
a) x: + kx: - 4.x1x, b) 5 ~ +: X +: k x: + 4 ~ ~ -x 22 ~ ~ -x 3~ x , x ,
c) 3xi + .x: + 2 4 + 2x1x3 + 2k.rzx3
15. Expresar la forma cuadrática (c,x, + czyz + , . . + C~X,)~ en notación matricial xTAx,
donde A es simétrica.
se denomina media aé la muestra de x,, x2, . . . , xn, y
se denomina variancia de la muestra.
a) Expresar la forma cuadrática S,' en la notación matricial xTAx, donde A es
simétrica.
b) ¿,Es S,' una forma cuadrática positiva definida? Explicar la respuesta.
17. Cnmpletar la demostración del teorema 9.5. I probando que In 5 xTAx si llxll = 1 ya,
= xTAx si x es un eigenvector de A correspondiente a An.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-555-320.jpg)
![9.6 Diagonalización de formas cuadráticas; secciones cónicas 1 561
9.6 DIAGONALIZACIÓN DE FORMAS CUADf3ÁTICAS; SECCIONES
C~NICAS
En esta sección se mostrará cómo eliminar, cambiando las variables, los términos
de producto cruzado que hay en una forma cuadrática, y los resultados se usarán
para estudiar las gráJcas de secciones cónicas.
DIAGONALIZA-CIÓN
DE
FORMAS
CUADRÁTICAS
Sea
xTAx = [xI x2 . . ' x,]
una forma cuadrática, donde A es una matriz simétrica. Por el teorema 7.3.1 se
sabe que existe una matriz ortogonPa lq ue diagonalizaa A; es decir,
donde Al, A2, . . . , A,, son los eigenvalores de A. Si se hace
Y =
:I Y" donde y,, y,, . . . , y, son variables nuevas, y si en (1) se efectúa la sustitución x =
Py, entonces se obtiene
X ~ A =X (PY)~AP=Y yTPTAPy= yTDy
Pero](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-556-320.jpg)






![568 / Temas complementarios
Se quiere girar los ejes de coordenadas xy de modo que la ecuación de la cónica en
el nuevo sistema x’y’ no contenga término de producto cruzado. Esto se puede
lograr como se muestra enseguida.
Paso 1. Encontrar una matriz
que diagonalice ortogonalmente la forma cuadrática xTAx.
Paso 2. Intercambiar las columnas de P, en caso de ser necesario, para
hacer det(P) = 1. Esto asegura que la transformación ortogonal
de coordenadas
x = Px‘, esto es, [;] = p [ ; : ]
es una rotación.
(Px‘)7A(Pxr+) K(Px ’ )+ f = O
o bien,
( x ‘ ) ~ ( P ~ A P+) x(K’ P)x’ + f = O (6)
Como P diagonaliza ortogonalmente a A,
londe A, y A, son eigenvalores de A . Así. (6) se puede volver a escribir como
[donde d ‘ = dp, , + ep21 y e’ = dp,, + ep,,). Esta ecuación no contiene término
je producto cruzado.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-563-320.jpg)

![570 /' Temas complementarios
Asi,
P= [2 l'v'V3 3 - 2/v3 "7
diagonaliza ortogonalmente a aTAx. Además, det(P) = 1, de modo que la
transformación ortogonal de coordenadas
x = Px' (8)
es una rotación. Sustituyendo (S) en (7) se obtiene
( P x ' ) ~ A ( P x-' ) 3 6 = O
o
(X' )~(P'AP)X-' 36 = O
Como
lo 4 0
PTAP= 9]
esta ecuación puede escribirse como
o
4 ~ +" 9 ~ ' '- 36 1 O
O
que es la ecuación de la elipse mostrada en la figura 4. En esa figura. los vectores
v, y v2 son los vectores columna de P. A](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-565-320.jpg)



![574 1 Temas complementarios
9.7 SUPERFICIES CUADRICAS
En esta sección se aplicarán las técnicas de diagonalización obtenidas en la
sección precedente a ecuaciones cuadráticas con tres variables, y los resultados
se usarán para estudiar superficies cuádricas.
SUPERFICIES Una ecuación de la forma
CUÁDRKAS
ax2 + by2 + cz2 + 2dxy + 2exz + 2fyz + gx + hy + iz + j = O (1)
donde no todos los coeficientes a, 6, . . . , f son cero se denomina ecuación
cuadrútica en x, y, y z; la expresión
ax2 + by' + cz' + 2dxy + 2exz + 2 fyz
se denomina forma cuadrútica asociada.
[x y z] d b f y + [ g h i ] y +j=O [: ; :I[:] [:I
La ecuación (1) se puede escribir en forma matricial como
o
donde
x T A x + K x + j = O
Ejemplo 1 La forma cuadrática asociada con la ecuación cuadrática
3x2 + 2y2 - z2 + ~ X , V+ ~ X -Z 8 yz + 7~ + 2 y + 3~ - 7 = O
es
3x2 + 2y2 - z2 + 4xy + 3xz - 8yz A
Las gráfkas de ecuaciones cuadráticas con variables x, y y z se denominan
cuúdricas o superficies cuúdricas. Las ecuaciones más simples de superficies
cuádncas ocurren cuando estas superficies se colocan en ciertas posiciones
normales con respecto a los ejes de coordenadas. En la figura 1 se muestran las
seis superficies cuádricas básicas y las ecuaciones de estas superficies cuando éstas
se colocan en las posiciones normales mostradas en la figura. Si una superficie
cuádrica es cortada por un plano, entonces la curva de intersección se denomina
traza del plano sobre la superficie. Para ayudar a conceptualizar las superficies
cddricas de la figura 1, se muestran y describen las trazas formadas por planos](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-569-320.jpg)



![5 78 1 Temas complementarlos
O 1 donde los dos primeros vectores columna en P son eigenvectores correspondientes
a ,I = 2 y el tercer vector columna es un eigenvector correspondiente a 1 = 8.
Como det(P) = I (comprobar), la transformación ortogonal de coordenadas x
= Px’ es una rotación. Sustituyendo esta expresión en (4) se obtiene
(Px ’ ) 7A(Px ’-) 3 = o
o bien, de manera equivalente,
(x’)7(P?4P)x’- 3 = O
Pero
[: 2 0 :]
0
PTAP= de modo que (5) se convierte en
o bien,
2s’* + 2y’* + 82” = 3
La ecuación anterior se puede volvera escribir como
z!?
- +-+-=I
312 3/2 318
que es la ecuación de un elipsoide. A
EJERCICIOS DE LA SECCION 9.7
1. Encontrar las formas cuadráticas asociadas con las siguientes ecuaciones cuadráticas
a) Y‘ + 2y2 -- zz + 4.ry - 5.v~ + 71 + 22 = 3 b) 31’ + 7z’ + 2.uy - 317 + 4.1.2 - 3x = 4
C) X!’ + Y 2 + )JZ 1 d) .xz +.v‘ - z’ = 7
e ) 3:’ + 3 .~2- 14y + 9 = O f ) 2 2 + 2x2 +y2 + 2x -y + 3z = o
2. Encontrar las matrices de las formas cuadráticas del ejercicio 1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-573-320.jpg)



![582 / Temas complementarios
CONTEO DE Sea Ax = b un sistema de n ecuaciones lineales con n incóptas, y supóngase que
OPERACIONES A es invertible, de modo que el sistema tiene una solución única. También
PARA LA supóngase, para simplificar las cosas, que para escribir la matriz aumentada [A I
ELIMINACIóN b] en forma escalonada reducida no se requiere ningún intercambio de renglones.
DE GAUSS- Esta hipótesis se justifica por el hecho de que los intercambios de renglones se
JORDAN efectúan como regstro de operaciones en una computadora y requieren mucho
menos tiempo que las operaciones aritméticas.
Como no se requiere ningún intercambio de renglones, el primer paso en el
proceso de eliminación de Gauss-Jordan es introducir un 1 principal en el primer
renglón multiplicando los elementos de este renglón por el recíproco del elemento de
la izquierda en el renglón.E ste paso se representa de manera esquemáticcao mo sigue:
1 x x ’ . ‘ x x i x
O O O ” . O 0 ; .
I
1 .
I ‘
I .
X denota una cantidad que se calculará
denota una cantidad que no se calcula
1 Eltamañodelamatrizesn X ( n + 1 ) I
O O O . . ’ O o ; .
. ’ . o ; I
O O O O . Obsérvese que el 1 principal simplemente se registra y que no requiere cálculos:
sólo es necesario calcular los n elementos restantes en el primer renglón.
A continuación se presenta una descripción esquemática de los pasoys el núme-ro
de operaciones necesarias parar educir [A 1 b] a forma escalonada por renglones.
Paso 1
Paso la
Paso 2
Lo x x . . ’ x x
X
8
O
O
O
O
X
X
X
X
1
n multiplicaciones
O adiciones
n multiplicaciones/renglón
n a&ciones/renglón
n - 1 renglones que requieren
cálculos
I n(n - 1) multiplicaciones
n(n - 1) adiciones I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-577-320.jpg)
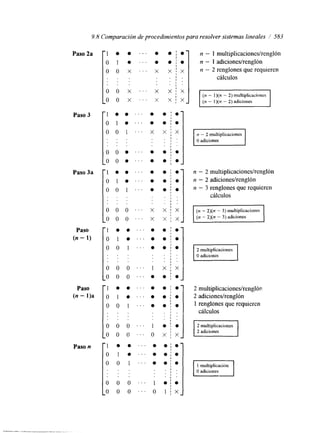
![584 1’ Temas complementarios
Así, el número de operaciones necesarias para completar pasos consecutivos es
como sigue:
Pasos 1 y l a
Multiplicaciones: n + n(n - 1) = n’
Adiciones: n(n - 1) = n2 - n
Pasos 2 y 2a
Multiplicaciones: (n - 1) + (I? - I )(n - 2) = (n - 1 )’
Adiciones (n-I)(n-2)=(n-l)’-(n- 1)
Pasos 3 y 3a
Multiplicaciones: ( n - 2) i(n - 2)(n - 3) = (n - 2)’
Adiciones: (n - 2)(n - 3) = (n - 2)’ - (n - 2)
Pasos (n - 1) y (n - l)a
Multiplicaciones: 4 ( = 2’ )
Adiciones: 2(=2’-2)
Paso n
Multiplicaciones: I ( = I ’ )
Adiciones: O ( = 12- 1)
Por consiguente, el número total de operaciones necesarias para expresar [A
I b] en forma escalonada reducida es
Multiplicaciones: n’ + (n - I)’ + (n - 2)’ + . . . + 1
Adiciones: [n’ + (n - 1)’ + (n - 2)‘ + ’ . ’ + 121
- [ n + ( n - l ) + ( n - 2 > + ” ’ + 1 ]
o bien, aplicando las fórmulas (1) y (2),
Multiplicaciones:
n(n + 1)(2n + 1) n3 n2 n
6
- +-+- 3 2 6
” (5 1
(6)
n(n + 1)(2n + 1) n(n + 1) n3 n Adiciones:
6
-
2 3 3
Así se completa el conteo de operaciones para la fase hacia adelante. Para la fase
hacia atrás es necesario escribir la forma escalonada de [A 1 b] en forma escalo-nada
reducida mediante la introducción de ceros por arriba de los 1 principales. A
continuación se muestran las operaciones:](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-579-320.jpg)

![586 / Temas complementarios
COMPARACI~N
DE METODOS
PARA
RESOLVER
SISTEMAS
LINEALES
En aplicaciones prácticas no es raro encontrar sistemas lineales de miles de
ecuaciones con miles de incógnitas. Así, la tabla 1 reviste especial importancia
para grandes valores de n. Un hecho verdadero para polinomios es que para
grandes valores de la variable, un polinomio puede ser bien aproximado por su
término de grado más alto; es decir, si ak f O, entonces
u. + u,x + . . . + q x k - ukxk parax grande
(ejercicio 12). Así, para grandes valores de n, el conteo de operaciones en la tabla
1 se puede aproximar como se muestra en la tabla 2.
Por la tabla 2 se deduce que cuando n es grande los mejores métodos para
resolver Ax = b son la eliminación gaussiana y la eliminación de Gauss-Jordan. E1
método de multiplicar porA"es bastante peor que los anteriores (requiere el triple
de operaciones), y el método más ineficaz de los cuatro es la regla de Cramer.
TABLA 2 Conteo aproximado de operaciones para una matriz invertible n x n
con n grande
Método I
Número de
adiciones
Resolver Ax = b por eliminación de Gauss-
Jordan
n3
Resolver Ax = b por eliminación gaussiana "
3
EncontrarA-l reduciendo [A I I] a [I /A]" =n3
Resolver Ax = b como x = A"b %n3
Encontrar det(A) por reducción de renglones = - n3
3
Resolver A x = b por la regla de Cramer
n4
3
iT-multiplicaciones
iT-n3
x-
3](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-581-320.jpg)

![588 / Temas complementarios
4. Suponiendo un tiempo de ejecución en computadora de 2.0 microsegundos para las
multiplicaciones y de 0.5 microsegundos para las adiciones, usar los resultados del
ejercicio 3 para escribir los tiempos de ejecución en segundos necesarios para efectuar
los procedimientos de la tabla 4.
Tabla 4
5. Obtener la fórmula
n(n + 1)
1 +2+3+,..+n=-----
2
[Sugerencia Sea Sn = 1 + 2 + 3 + . . . + n. Escribir los términos de S, en orden
invertido y sumar las dos expresiones para S,.]
6. Usando el resultado del ejercicio 5, demostrar que
1 + 2 + 3 + . . . + ( n - l ) = -
(n - 1)n
2
7. Obtener la fórmula
1 2 + 2 2 + 3 2 + . . . + n 2 =
n(n + l)(2n + 1)
6
realizando los pasos siguientes.
a) Demostrarq~e(k+l)~-p=33k2+3k+1.
b) Demostrar que
[2' - 13] + [33 - z3] + [43 - 33] +. . . + [(n + 1)3 - n3] = (n + 1)' - 1
c) Aplicando a) a cada término del miembro izquierdo dbe) , demostrar que
( n + 1 ) 3 - ~ = 3 [ 1 2 + 2 2 + 3 2 + ~ . . + n 2 ] + 3 [ 1 + 2 + 3 + ~ . . + n ] + n
d) Resolver la ecuación del inciso c) para l2 + 22 + 32 + . . . + n', usar el resultado del
ejercicio 5 y luego simplificar.
8. Usando el resultado del ejercicio 7, demostrar que
- (n - l)n(2n - 1)
12+22+32+'"+(n") -
6](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-583-320.jpg)
![9.9 Descomposiciones L U 589
9. Sea R la forma escalonada de una matriz invertible n X n. Demostrar que para resolver
el sistema lineal Rx = b por retrosustitución se requieren
"n2- n
2 2
multiplicaciones
n2 n
2 2
"- adicisnes
10. Demostrar que para reducir una matriz invertible de n X n a I, aplicando el método del
texto se requieren
"n 3- n
3 3
n3 n2 n
3 2 6
multiplicaciones
-" + - adiciones
[Nota Supóngase que no se requiere ningún intercambio de renglones.]
11. Considérese la variante de la eliminación de Gauss-Jordan en que se introducen ceros
arriba y abajo de un 1 principal tan pronto como se obtiene éste, y sea A es una matriz
invertible n X n. Demostrar que para resolver un sistema lineal Ax = b usando esta
versión de la eliminación de Gauss-Jordan se requieren
n3 n2
2 2
-n3 "n
2 2
- + - multiplicaciones
adiciones
[Nota Supóngase que no se requiere ningún intercambio de renglones.]
12. (Paru quienes ya estudiaron C&lculo). Demostrar que si p(x) = u. + a,x + . . . + a,.",
donde ak # O, entonces
[Nota Este resultado justifica la aproximación a. + u,x + . . . + ukx" = u,." para x
grande.]
9.9 DESCOMPOSICIONES LU
Con la eliminación gaussiana y la eliminación de Gauss-Jordan se resuelve un
sistema lineal operando sistemáticamente sobre la matriz aumentada. En esta
sección se analizar& un método difrente basado en la factorización de la matriz
de coejkientes en un producto de dos matrices: una triangular inferior y otra](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-584-320.jpg)


![592 i Temas complementarios
DESCOMPOSI- Ahora que ya se ha visto cómo un sistema lineal de n ecuaciones en n incógnitas
CIONES LU se puede resolver factorizando la matriz de coeficientes, se volverá al problema de
obtener la factorización. Para originar el método, supóngase que una matriz '4 n X
n se ha reducido a una forma escalonada U mediante una sucesión de operaciones
elementales en los renglones. Por el teorema 1.5.1, cada una de estas operaciones
se puede efectuar multiplicando por la izquierda por una matriz elemental
apropiada. Así, es posible encontrar matrices elementales E,, E,, . . . , Ek tales que
E L . ' . E2E,A = U (6)
Por el teorema 1.5.2, E,, E , Ek son invertibles, de modo que es posible
multiplicar sucesivamente por la izquierda ambos miembros de la ecuación (6) por 2' ' '.
para obtener
A =E; 'E, 1 . . . E"
k (7)
En el ejercicio 5 se ayudará al lector a demostrar que la matriz L definida por
L = E" ]E- 1 . . . 1
I 2 (8)
es triangular lnferior en el supuesto de qupea ra reducir A a U no se efectúe ningún in-tercambio
de renglones. Suponiendo que este es el caso, sustituyendo (8) en (7) se
obtiene
A= LU
que es una factorización de A en un producto de una matriz triangular inferior y
una matriz triangular superior.
El siguiente teorema resume el resultado anterior.
Teorema 9.9.1. Si A es una matriz cuadrada que se puede reducir a una forma
escalonada U sin aplicar ningún intercambio de renglones, entonces A se
puede factorizar como A = LU, donde L es una matriz triangular inferior.
Definición. Una factorización de una matriz cuadrada A como A = LU, donde
L es triangular inferior y I/ es triangular superior, se denomina descomposición
LU o descomposición triangular de A:
Ejemplo 2 Encontrar una descomposición LU de
2 -:
6
A = [ - : 2J
Solución. Para obtener una descomposición LU, A = LU, A se reducirá a una
forma escalonada iJ, y luego L se calculará a partir de (8). Los pasos son:](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-587-320.jpg)

![594 / Temas complementarios
Así,
PROCEDIMIEN-TO
PARA
ENCONTRAR
DESCOMPO-Y>
SICIONES LU
por (8):
2 0 0
de modo que
[-2 :- 6: ! I=[ 2 0 -3
4 -3
es una descomposición LU de A. A
o 0 1 0 0
1 oj[o 1
-3 1 O 0 7
:][A ; '1 7 O 0 1
Como se muestra en este ejemplo, casi todo el trabajo para obtener una
descomposición LU se invierte en el cálculo de L. Sin embargo, todo este trabajo
se puede eliminar llevando un registro cuidadoso de las operaciones usadas para
reducir A a U. Como se supone que no se requiere ningún intercambio de ren-glones
para reducir A a U, entonces sólo se realizan dos tipos de operaciones: la
multiplicación de un renglón por una constante diferente de cero y la adición de un
múltiplo de un renglón a otro renglón. La primera operación se usa para introducir
los unos principales y la segunda para introducir ceros abajo de los unos
principales.
En el ejemplo 2 los multiplicadores necesarios para introducir los unos
principales en renglones consecutivos son:
3 para el primer renglón
1 para el segundo renglón
f para el tercer renglón
Obsérvese que los elementos diagonales sucesivos en L eran precisamente los
recíprocos de los multiplicadores (figura 1).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-589-320.jpg)
![9.9 Descomposiciones L U / 595
Luego, obsérvese que para introducir ceros por abajo del 1 principal en el primer
renglón se realizaron las siguientes operaciones:
sumar 3 veces el primer renglón al segundo renglón
sumar -4 veces el primer renglón al tercer renglón
y para introducir el cero por abajo del 1 principal en el segundo renglón se efectuó
la siguiente operación
sumar 3 veces el segundo renglón al tercer renglón
Ahora se observa que en cada posición abajo de la &agonal principal de L (en tipo
negro) el elemento es el negativo del multiplicador en la operación con que se
introdujo el cero en esa posición en U (figura 2).
L=[p-JJ
Figure 2
En resumen, se tiene el siguiente procedimiento para obtener una
descomposición L U de u a matriz cuadrada A, en el supuesto de que A se pueda
reducir a la forma escalonada sin efectuar ningún intercambio de renglones.
Paso 1. Reducir A a una forma escalonada U sin efectuar ningún intercambio
de renglones y sin perder de vists los multiplicadores usados para in-troducir
los unos principales y de los multiplicadores usados para
introducir los ceros abajo de los unos principales.
Paso 2. En cada posición a lo largo de la diagonal principal de L escribir el
recíproco del multiplicador con que se introdujo el uno principal en
esa posición de U.
Paso 3. En cada posición por abajo de la diagonal principal de L escribir el
negativo del multiplicador usado para introducir el cero en esa
posición de U.
Paso 4. Formar la descomposición A = L U.
Ejemplo 3 Encontrar una descomposición LU de
”;[6; --2 ; ;O ]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-590-320.jpg)
![596 / Temas complementarios
Solucidn. Se empezará por reducir A a forma escalonada sin perder de vista a los
multiplicadores.
- multiplicador = 4 /-
" 1
c-- m ultiplicador = - 9 multiplicador = - 3
[ ,1" -1$. i] t-multiplicador = $
t-multiplicador = - 8
t-multiplicador = 1
real, dado que en el tercer renglon ya
Al construir L a partir de los multiplicadores se obtiene la descomposición LU.
6 0 0 j[O 1 -$
A /] [3 8 *
A=LU= 9 2 O O
Esta sección concluye con un breve análisis de dos preguntas fundamentales
sobre las descomposiciones L U:
1. ¿Toda matriz cuadrada tiene una descomposición L I/?
2. ¿Es posible que una matriz cuadrada tenga más de una descomposición L U?
Ya se sabe que si una matriz cuadrada A se puede reducir a la forma
escalonada sin aplicar ningún intercambio de renglones, entonces A tiene una
descomposición L U. En general, si para escribir A en forma escalonada se requiere
intercambiar renglones, entonces no existe ninguna descomposición L U de A. Sin
embargo, en esos casos es posibIe factorizar A en la forma
A = PLU](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-591-320.jpg)
![9.9 Descomposiciones LU 1 597
donde L es triangular inferior, U es triangular superior y P es la matriz que se
obtiene al intercambiar los renglones de I,, de forma idónea (ver el ejercicio 17).
Cuando no hay restricciones adicionales, las descomposiciones LU no son
únicas. Por ejemplo, si
y los elementos diagonales de L son diferentes de cero, entonces es posible
desplazar los elementos diagonales del factor izquierdo al factor derecho
escribiendo
que es otra descomposición triangular de A.
EJERCICIOS DE LA SECCION 9.9
1. Usar el método del ejemplo 1 y la descomposición LU [-: -:I=[-: u][:, -:]
para resolver el sistema
3x, - 6x2 = O
-2x, + 5x, = 1
2. Usar el método del ejemplo 1 y la descomposición LU
para resolver el sistema](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-592-320.jpg)
![598 / Temas complementarios
3x1 - 6x2 - 3x3 = -3
2x1 + 6x3 = -22
-4x1 + 7x2 + 4x, = 3
En los ejercicios del 3 al 10, encontrar una descomposición LU de la matriz de coeficientes;
luego, usar el método del ejemplo 1 para resolver el sistema
=[-;I
11. Sea
2 -; a]
1 -
A = [ - : a) Encontrar una descomposición LU de A
b) Expresar A en la forma A = L,DU,, donde L, es una matriz triangular inferior con
unos en la diagonal principal, U, es una matriz triangular superior y D es una
matnz diagonzl.
c) Expresar A en la forma A = L2U2, donde L, es una matriz tnangular inferior con
unos en la diagonal principal y U2 es una matriz tnangular superior.
12. Demostrar que la matriz
no tiene descomposición LU.
13. Sea
a) Demostrar: Si A f O entonces A tiene una descomposición LU única con unos en la
diagonal principal de I..
b) Encontrar la descomposición LU descrita en el inciso a).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-593-320.jpg)
![9.9 Descomposiciones LU / 599
14. Sea Ax = b un sistema lineal de n ecuaciones con n incógnitas, y supóngase que A es
una matriz invertible que se puede escribir en forma escalonada sin efectuar ningún
intercambio de renglones. ¿Cuántas adiciones y cuántas multiplicaciones son nece-sarias
para resolver el sistema aplicando el método del ejemplo l? [Nota Contar las
sustracciones como adiciones y las divisiones como multiplicaciones.]
15. a) Demostrar: Si L, y L, son matrices triangulares inferiores n X n, entonces también
L,L, es triangular mferior.
b) El resultado del inciso a) es un caso especial de un resultado general que establece
que el producto de un número finito de matrices triangulares mferiores es triangular
inferior. Usando este hecho, demostrar que la matriz L en (8) es triangular inferior.
[Sugerencia Véase el ejercicio 27 de la sección 2.4.1
16. Usando el resultado del ejercicio 15b), demostrar que el producto de un número finito
de matnces triangulares superiores es triangular superior. [Sugerencia Considerar las
transpuestas.]
17. Demostrar: Si A es cualquier matriz n X n, entonces A se puede factorizar como A =
PLU, donde L es triangular inferior, U es triangular superior y P se puede obtener
intercambiando en forma adecuada los renglones de I,. [Sugerencia Sea U la forma
escalonada de A y efectuar primero todos los intercambios de renglones necesarios en
la reducción de A a U. ]
18. Factorizar
como A = PLU, donde P se obtiene a partir de Z3 al intercambiar de manera apropiada
los renglones, L es triangular inferior y U es triangular superior.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-594-320.jpg)



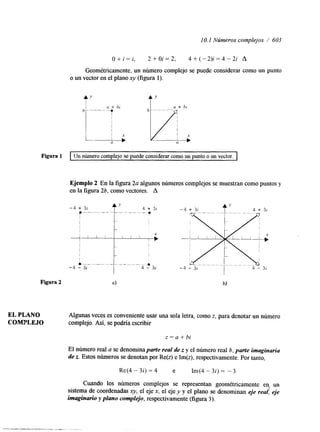

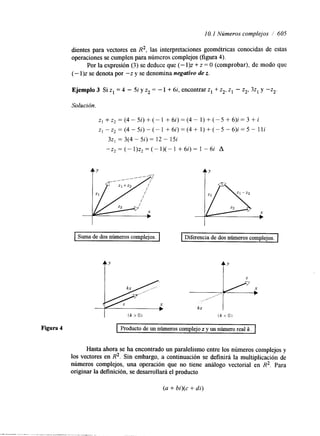
![606 / Espacios vectoriales complejos
siguiendo las reglas algebraicas de costumbre, pero considerando a i2 como - 1.
Así, se obtiene
(a + bi)(c + di) = ac + bdi2 + adi + bci
= (OC - bd) + (ad + b ~ ) i
lo cual sugiere la siguiente definición:
(a + bi)(c + di) = (ac - bd) + (ad + bc)i
Ejemplo 4
(3 + 2i)(4 + Si) = (3 ' 4 - 2 '5) + (3 .5 + 2 '4)i
= 2 + 23i
(4-i)(2-32)=[4.2-(-1)(-3)]+[(4)(-3)+(-1)(2)]i
= 5 - 14i
i 2 = ( O + i j ( O + i j = ( O ~ O - 1 ~ 1 ) + ( O ~ 1 + 1 ~ O ) i =- 1 A
Se deja como ejercicio comprobar las siguentes reglas de aritmética com-pleja:
ZI + z2 = z2 + z,
z1z2 = z 2 z *
ZI + (z2 + z3 j = (z* + z2) + z3
Zl(ZZZ3j = (z1z2)z3
z1(z2 + Zj) = ZlZ2 + z,z3
o + z = z
z + ( - z ) = O
l . z = z
Estas reglas permiten multiplicar números complejos sin necesidad de apli-car
&rectamente la fórmula (4). Siguiendo el procedimiento usado para originar
esta fórmula, basta multiplicar cada término de a + bi por cada término de c + di,
hacer i2 = - 1 y simplificar.
Ejemplo 5
(3 + 2i)(4 + i) = 12 + 3i + 8i + 2i2 = 12 + 1 li - 2 = 10 + 1 li
(5 - 4i)(2 + 32) = 10 + 15i - i - $i2 = 10 + 14i + $ = 9 + 14i
i(I + i)(I - 2i) = i(1 - 2i + i - 2i2) = i(3 - i) = 3i - i2 = 1 + 3i A](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-601-320.jpg)
![1 O. 1 Números complejos / 607
OBSERVACI~N. A diferencia de los números reales, en los números complejos no
existe ordenamiento según el tamaño. Así, los símbolos de orden <, 5, > y no se
usan con números complejos.
Ahora que ya se han definido la ahción, la sustracción y la multiplicación
de números complejos, es posible sumar, restar y multiplicar matrices con elemen-tos
complejos y multiplicar una matriz por un número complejo. Sin entrar en de-talles,
se observa que las operaciones y terminología matriciales analizadas en el
capítulo 1 se cumplen sin ningún cambio para matrices con elementos complejos.
Ejemplo 6 Si
entonces
A B = [ -i][ 'qi]
[ I + i 4 2 - i - 3 i
= ! . i + ( - i ) . ( 2 - 3 i ) 1 .(1 + - i) ( - i ) . 4
( I + i ) . i + ( 4 - i ) . ( 2 - 3 i ) (1 +i).-(i )l+ ( 4 - i ) . 4
- 3 - i 1 -5i =[ 4-13i 18-4i
EJERCICIOS DE LA SECCION 10.1
1. En cada inciso, graficar el punto y trazar el vector que corresponde al número complejo
dado.
a) 2 + 3i. b) 4. c) -3 - 2i. d) -Si.
2. Expresar cada número complejo del ejercicio 1 como un par ordenado de números
reales.
3. En cada inciso, usar la mformación proporcionada para encontrar los números reales x
Y Y.
a) x - i y = - 2 + 3 i b) ( x + y ) + ( x - y ) i = 3 + i
4. Dado que z, = 1 - 2i y z2 = 4 + Si, encontrar
a) z , + z , b) z I - z 2 c) 42, d) -z2 e) 32, +4z, f) 2 1 -9 222
5. En cada inciso, resolver para z.
a) z + ( l - i ) = 3 + 2 i b) -5z=5+10i c) ( i - z ) + ( 2 ~ - 3 i ) = - 2 + 7 i](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-602-320.jpg)




![612 / Espacios vectoriales complejos
o bien
x] + i,vl = (xzx ---v2y+) i(y2x + xzy)
o bien, igualando las partes reales e imaginarias.
o bien,
Como z2 = x2 + zy2 f O, se concluye que x2 y y2 no son cero a la vez, de modo que
Así, por la regla de Cramer (teorema 2.4.3), el sistema (4) tiene la solución ímica
Por tanto,
Así, para z2 f O se define
I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-607-320.jpg)

![61 4 / Espacios vectoriales complejos
1' -'"'I (i)(-1 +3i)-4(1 -2i) -7+7i
- - 1 - i 1; -21
Y = -- -"
i( - i) - 2(4) -7
Así, la solución es x = i, y = 1 - i. A
PROPIEDADES DE Esta sección concluye con la enumeración de algunas propiedades del conjugado
LOS NÚMEROS complejo que serán de utilidad en secciones ulteriores.
COMPLEJOS
Teorema 10.2.3. Para números complejos cualesquiera z, z1 y Z2 1
a) Z] + z, = 2, + z2
" b) m = Z, - z2
Se demostrará el inciso a) y lo demás se deja como ejercicio.
Demostración de a). Sean z1 = al + b,i y z2 = u2 + b2i; entonces
z1 + z2 = (al + az) + (b, + b,)i
= (a, + a2) - (b, + b2)i
= (a, - b,i) + (u2 - b,i)
= z, + z, 0
OBSERVACI~N. Es posible ampliar el inciso a) del teorema 10.2.3 a n términos y
el inciso c) a n factores. En pocas palabras,
z , + z 2 + . ~ ~ + z , = z , + z 2 + ~ ' ~ + ~ ,
" -
Z]Z2. . . z, = z,z*. . .Z"
EJERCICIOS DE LA SECCIÓN 10.2
1. En cada inciso hallar .
a ) z = 2 + 7 i b ) z = - 3 - 5 i c ) z = 5 i d ) z = - i e ) z = -9 f ) z = 0
2. En cada inciso encontrar IzI.
a ) z = i b ) z = - 7 i c ) z = - 3 - 4 i d ) z = l + i e ) z = - 8 f ) z = O](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-609-320.jpg)
![1 O. 2 Módulo; conjugado complejo; división / 615
3. Comprobar que z = kl2 para
a) z = 2 - 4 i b) z = - 3 + 5 i c) z=*-V%
4. Dado que z, = 1 - 5i y zz = 3 + 4i, encontrar
a) zI/zz b) 5,/z2 c) zl/& d) (z1/z2) e) zl/lzzl f) Iz,/z21
5. En cada inciso, encontrar l/z.
a) z = i b) z = 1 -5i c) z=-
-i
7
6. Dado que z, = 1 + i y zz = 1 - 2i, encontrar
En los ejercicios del 7 al 14, realizar los cillculos y expresar el resultado en la forma a + bi.
i 2 7. - I + i
1
8. ___9. ___- (1 - i)(3 + i) (3 + 4)’
10.
2 + i
i( - 3 + 4i)
V3+i
11.
1
12.
(1 - i)(V3 - i) i(3 - 2i)(l + i)
i 1 - 2 i 2 + i
(1 - i)(l - 2i)(l + 2i) 3 + 4i 5i
13.
14.
15. En cada inciso, resolver para z.
a) iz = 2 - i b) (4 - 3i)F =
16. Aplicar el teorema 10.2.3 para demostrar las siguientes identidades:
-
a) z+=z-Si b) z=- iZ c) -i=+Z -1
I-z
17. En cada inciso, trazar el conjunto de puntos en el plano complejo que satisfacen la
ecuación.
a) Iz(=2 b) l z - ( l + i ) / = 1 c) Iz - i ( = ( z + i ( d) Im(Z+i)=3
18. En cada inciso, trazar el conjunto de puntos en el plano complejo que satisfacen la(s)
condición (condiciones) dada(s).
a) Iz + i l s 1 b) 1 < bl < 2 c) (2z - 4il < 1 d) JzI 5 )z + iJ
19. Dado que z = x + Q, encontrar
a) Re(G) b) Im(c) c) Re(i5) d) Im(i5)
20. a) Demostrar que si n es un entero positivo, entonces los únicos valores posibles de
(1li)”son 1, -1,iy -i.
b) Calcular ( l/i)2s09. [Sugerencia. Véase el ejercicio 23(b) de la sección 10.1 ,]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-610-320.jpg)
![616 / Espacios vectoriales complejos
21. Demostrar:
1 I
2 2i
a) -(z + Z ) = Re(z) bj -(z - 5) = Im(zj
22. Demostrar: z = si y sólo si z es un número real
23. Dado que z, = x, + iyl y z2 = x2 + 'y2, encontrar
24. Demostrar: Si (i)2= 2,e ntonces z es real o imaginario puro.
25. Demostrar que Iz; = j 1
26. Demostrar:
" -
a) z, - z, = zI - z2 b) = I,:, c) (zl/z2) = Z,/Z2 d) = z
-
27. a) Demostrar que z2 = (i)2 .
-
b) Demostrar que si n es un entero positivo, entonces Z" = ( 1 j".
c) ¿Es verdadero el resultado del inciso b) si n es un entero negativo? Explicar la
respuesta.
En los ejercicios del 28 al 31, resolver el sistema de ecuaciones lineales aplicando la regla
de Cramer.
28. ix, - ix, = - 2
2x, + x2 = i
30. xI + x, + x3 = 3
x, + x, - xj = 2 + 2i
x, --,+x,= -1
29. x, +x2 = 2
x, - x2 = 2i
31. ix, + 3x, + (1 + i)x3 = - i
x, + ix, + 3x, = -2i
XI + x, + xj = o
En los ejercicios 32 y 33, resolver el sistema de ecuaciones lineales por eliminación de
Gauss-Jordan.
32. [ - l"+ i " --2i ] [ ~ ~ ] = [:] 33. [ "If2 "[;;]=[:I 1
34. Resolver el siguiente sistema de ecuaciones lineales por eliminación de Gauss-Jordan
x, + ix, - ix, = O
-x1 + (1 - i)x, + 2ix3 = O
2x, + (- I + 2i)x, - 3ix3 = O](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-611-320.jpg)
![10.3 Forma polar; teorema de De Moivre / 61 7
35. En cada inciso, aplicar la fórmula del teorema 1.4.5 para calcular la inversa de la
matriz y comprobar el resultado demostrando que AA - ' = A - 'A = I.
36. Sea&) = a. + alx + a,x2 + . . . + anX" un polinomio en el que los coeficientes a,,, a,,
a2, . . . , an son reales. Demostrar que si z es una soluci6n de la ecuación p(x) O,
entonces también lo es.
37. Demostrar: Para cualquier número complejo z, IRe(z)l 5 Izi e IIm(z)l 5 Iz/.
38. Demostrar que
IRe(z)l + IIm(z)l ~ v5
[Sugerenciu Sea z = x + iy y aplicar el hecho de que (bl - b1)2 2 O.]
39. En cada inciso aplicar el método del ejemplo 4 de la sección 1.5 para encontrar A" y
comprobar el resultado demostrando que AA" = A"A = 1.
i O - i
2 - i i
10.3 FORMA POLAR; TEOREMA DE DE MOIVRE
En esta sección se analizará una forma para representar números complejos
usando propiedades trigonométricas. El trabajo efectuado conducirá a una
fórmula fundamental para potencias de números complejos y a un método para
encontrar raíces n-ésimas de números complejos.
FORMA POLAR Si z = x + iy es un número complejo diferente de cero, r = (z( y 8 mide el ángulo
DE UN NúMERO entre el eje real positivo y el vector z, entonces, como se sugiere en la figura 1,
COMPLEJO
Figura 1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-612-320.jpg)

![10.3 Forma polar; teorema de De Moivre / 61 9
así, cos 8 = 112 y sen O = 6 1 2 . El Único valor de O que satisface estas relaciones
y cumple el requisito - n < 8 I n es O = n/3 (= 60") (véase la figura 2a).
Entonces, una forma polar de z es
Solución de h). El valor de r es
1 - i
- 1 = *COS e
-1 = *sene
de modo que cos O = - 1f fi y sen O = - 11 f i . El Único valor de que satisface
estas relaciones y cumple el requisito - n e 8 5 n es O = -3~14 (= - 135')
(figura 26). Por tanto, una forma polar de z es
""1 -+isen- A
4
INTERPRETA- A continuación se mostrará cómo se pueden usar las formas polares para obtener
CIÓN interpretaciones geométricas de la multiplicación y la división de números com-
GEOMÉTRICA plejos. Sean
DE LA
MULTIPLICA-CIÓN
Y LA
z, =?,(cos 0, + i sene,) y z2 = r,(cos 6, + i sen e,)
DMSIÓN Multiplicando, se obtiene
Z,Z, = r,r2[(cos-0C, OS e, -sene, sene,) + i(sen0, cos 0, + COS e, sene,)]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-614-320.jpg)
![620 / Espacios vectoriales complejos
Recordando las identidades trigonométricas
cos(8, + O,) = cos S, cos O, - sen 8, sen S,
sen(0, + 8,) = sen O, cos S, + cos 8, sen 8,
Se obtiene
zlz2 = r,r,[cos(S, + O,) + isen(8, + O,)]
que es una forma polar del número complejo con módulrol rz y argumento
8, +- 8,. Así, se ha demostrado que
l v 2 1 = IZllIZ2l
Y
arg(z,z2) = arg z1 + arg z2
(¿Por qué?)
En palabras, el producto de dos números complejos se obtiene al multiplicar
sus módulos y sumar sus argumentos (figura 3).
Figura 3 Producto de dos números complejos. I
Se deja como ejercicio demostrar que si z2 # O, entonces
~~
a partir de lo cual se concluye que](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-615-320.jpg)
![1 O. 3 Forma polar; teorema de De Moivre / 621
Y
arg k) = arg z1 - arg z2
En palabras, el cociente de dos números complejos se obtiene al dividir sus
módulos y restar sus argumentos (en el orden adecuado).
Ejemplo 2 Sean
Las formas polares de estos números complejos son
(comprobar), de modo que por (3)
zlzz =4[cos(t+:) +isen('+:)]
= 4 [c o s -y+i s e n=- 4 [O+i ]=4 i 2 -1
=cos-T+ isen-=T--+V--i 3 1
6 6 2 2
Como comprobación, zlz2 y z1/z2 se calcularán directamente sin usar las formas
polares de z1 y z2:
.- . .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-616-320.jpg)
![622 / Espacios vectoriales complejos
lo cual concuerda con el resultado previo. A
El número complejo i tiene módulo 1 y argumento n/2 = (90"), por
tanto, el producto iz tiene el mismo módulo que z, pero su argumento es 90" mayor
que el de z. En resumen, al multiplicar z por i gira en sentido contrario a las
manecillas del reloj por un ángulo de 90" (figura 4).
t'
Figura 4 I Al multiplicar por i, z gira 90' en sentido contrario a las manecillas del reloj. I
FÓRMULA DE Si n es un entero positivo y z = r(cos O + i sen e ), entonces por la fórmula (3),
DE M O W
Z " = Z-. Z . t . . .~= r"[cos(8+8+...+8)+isen(8+8+...+8)] n factores n términos n términos
o bien,
z" = r"(cos no + isen ne)
Además, si z f O, se define z-" = l/z".
se convierte en
En el caso especial en que r = 1, se tiene z = cos O + J sen O, de modo que (6)
(cos 8 + i seno)" F cos n8 + i sen no
expresión que se denomina fórmula de De Moivre*. Aunque (7) se obtuvo supo-niendo
que n es un entero positivo, en los ejercicios se demostrará que esta fórmu-la
es válida para todos los enteros n.
*Abraham De Moivre (1667-1754) matemático francés que realizó importantes contribuciones a
probabilidad, estadística y trigonomehia. Desarrolló el concepto de eventos estadísticamente independientes,
escribió un tratado hndamental sobre probabilidad y ayudó a transformar la trigonometría de una rama de
la geometría a una rama del análisis a través del empleo de los números complejos. A pesar de su
importante trabajo, a duras penas se ¡as arreglaba para vivir como tutor y asesor sobre juegos y seguros.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-617-320.jpg)
![1O . 3 Forma polar; teorema de DeM oivre / 623
DETERMINA- A continuación se mostrará cómo usar la fórmula de De Moivre para obtener
C I ~ NDE LAS raíces de números complejos.S i n es un entero positivo y si z es cualquier
RAICES número complejo, entonces la raíz n-ésima de z se define como cualquier nú-n-
ÉSIMAS mero complejo w que cumple la ecuación
Una raíz n-ésima de z se denota por zlln. Si z # O, entonces las fórmulas
para las raíces n-ésimas zd es e pueden obtener como sigue. Sean
w=p(cosa+isena) y z=r(cosO+isen8)
Si se supone quew satisface (8), entonces por( 7) se concluye que
pn(cos n a + i sen na) = r(cos 8 + i sen 8) (9)
Al comparar los módulos delo s dos miembross e observa quep = r o bien, que
donde "6 denota la n-ésima raíz real positiva de r. Además, para que en (9) se
cumplan las igualdades consa = cos 8 y sen n a= sen 8, los ángulos n a y 8 deben
ser iguales o diferir por un múltiplo de 2n. Es decir,
n a=8+2 k r ,k =0 , + 1 , t 2, . . .
O
8 2!cr a=-+-
n n , k=0, kl, 2 2 , .
Así, los valoresd e w = p (cos a + i sen a) que satisfacen( 8) están dados por
w = ( ' h [ c o s ( ! + ~ ) + i s e n ( ~ + ~ ) ] , k=0, k l , k2, ...
Aunque hay muchos valores de k, se puede demostrar (ejercicio 16) que k = O, 1,
2, . . . , n - 1 producen valores distintos de w que satisfacen (8), y que todas las
d e b e lecciones dek producen réplicas de esos valoresE. n consecuencia, existen
exactamente n diferentes raíces n-ésimas de z = r(cos 8 + i sen e), y están dadas
por
= l / n = , [ , , s (8, t ~2k)m+ i S e n ( ! + ~ ) ] , k =O, 1 , 2 , , . . , n - l (IO)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-618-320.jpg)
![624 / Espacios vectoriales complejos
Ejemplo 3 Encontrar las raíces cúbicas de -8.
Solución. Como -8 está sobre el eje real negativo se puede usar 0 = ?t como
argumento. Además, r = bl = 1-81 = 8, de modo que una forma polar de -8 es
-8=8(cos v+isen.rr)
Por (10) con n = 3 se deduce que
[c os (-3+ - 25") +i s en (-3+ - 2 3 ] , k =O, 1,2
Así, las raíces cúbicas de -8 son
2(cos7r+isen7r)=2(-1)= -2
Como se muestra en la figura 5, las tres raíces cúbicas de -8 obtenidas en el
ejemplo 3 son equilstantes, ya que están separadas por una lstancia de n13
radanes (= 120') sobre la circunferencia de radio 2 con centro en el origen. Este
hecho no es fortuito. En general, por la fórmula (10) se concluye que las raíces n-ésimas
de z están sobre la circunferencia de radio "&(=.fi)y son equidstantes,
separadas por una distancia de 2 nln radianes. (¿Puede el lector darse cuenta de
por qué esto es así?) Así, una vez que se ha determinado una raíz n-ésima de z, las
demás n - 1 raíces se pueden generar si esta raíz se hace girar sucesivamente en
incrementos de 2 nln radianes.
4'
Figura 5 Las raíces cúbicas de -8.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-619-320.jpg)






![I O. 4 Espacios vectoriales complejos / 63 I
PRODUCTOS
INTERIORES
EUCLIDIANOS
COMPLEJOS
C(-m, 00) analizado en el ejemplo 7 de la sección 5.2 y se denomina corn-plejo
C(- 00, m). Un ejemplo bastante relacionado es el complejo C[a, b], el
espacio vectorial de todas las funciones con valores complejos que son continuas
sobre el intervalo cerrado [a, b]. A
Recuérdese que en R" el producto interior euclidiano de dos vectores
se definió como
y que la norma (o longitud) euclidiana de u se definió como
llull = (u u)l'2 = vu: + u; + . . ' + u;
Desafortunadamente, estas definiciones no son apropiadas para vectores en C".
Por ejemplo, si (3) se aplicase al vector u = (z, 1) en C2, se obtendría
((u(= VFZ = v% = o
de modo que u sena un vector dverente de cero con longitud cero, situación a
todas luces contradictoria.
Para extender correctamente los conceptos de norma, distancia y ángulo a C" es
necesario modificar un poco el producto interior.
~~ ~ ~ ~ ~ ~ ~~~~
Definicih. Si u = (ul, u2, . . . , un) y v = (vl, v2, . . . , vn) son vectores en Cn,
entonces su producto interior euclidiano complejo u * v se define por
donde i inso n los conjugados de vl,v 2, . . .
1' 2'"" , vn.
OBSERVACI~N. Nótese que el producto interior euclidiano de vectores en C" es
un número complejo, mientras que el producto interior euclidiano de vectores en
Rn es un número red.
Ejemplo 5 El producto interior euclihano complejo de los vectores](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-626-320.jpg)
![632 / Espacios vectoriales complejos
u=(-ii,2, 1 +3i) y v = ( l - i , O , I +3i)
es
u-v = (-i)(l - i) + (2)(0) + (1 + 3i)(l + 32)
= (-i)(l + i) + (2)(0) + (1 + 3i)(l - 3i)
- - i - 22 + 1 - 9I' 2 z I 1 - i A
En el teorema 4.1.2 se mencionaron las cuatro propiedades principales del
producto interior euclidiano sobre Rn. El siguiente teorema es el resultado
correspondiente para el producto interior euclidiano complejo sobre Cn
Teorema 10.4.1. Si u, v y w son vectores en C? y k es cualquier número
complejo, entonces:
a) u.v=v.U
b) (u+v).w=u.w+v.w
c) (ku).v = k(u.v)
d ) v.v?O.Ademas,v.v=O siysófosi v=O.
Obsérvese la diferencia entre el inciso a) de este teorema y el inciso a) del
teorema 4.1.2. Se demostrarán los incisos a) y d) y los demás se dejan como
ejercicio.
Demostración de a). Sean u = (ul, u2, . . . , un) y v = (v,, v2, . . . , v,). Entonces
Y
v. u = U I U I + U2ü2 -t ' . ' + unü,
de modo que
-v.u = U I U l + u2u2 + ' . . + Unün
- - -
+ +- ' ' ' VnUn [Teorema 10.2.3, incisos a) y c)]
= ulul + ü*uz + . . . + Ü,,un [Teorema 10.2.3, inciso e)]
-
= UlÜl + u2ü2 + . . ' + unü,
= u.v](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-627-320.jpg)



![636 / Espacios vectoriales complejos
a) vI = (i, i, i), v2 = (22, 2i, O), v3 = (3i, O, O)
b) V, = (1 + i, 2 - i, 3 + i), vi = (2 + 3i, O, 1 - i)
c) V, = (1, O, -i), v2 = (1 + i, 1, 1 - 24, v3 =(O, i, 2)
d) vI = (1, i, O), v2=(0, -i, I), v3=(1, O, 1)
19. Determinar cuáles de las siguientes fünciones están en el espacio generado por
f = e” y g=e-””
a) cos x b) sen x c) cos x + 3i sen x
20. Explicar por qué los siguientes conjuntos de vectores son linealmente dependientes.
(Resolver este problema por inspección.)
a) u , = ( I - - i , i ) y u 2 = ( 1 + i , -1)enC2
b) u, = (1, - i), u2 = (2 + i, - l), u) = (4, O) en C2
c) A = [ J ’j] y = [ en el complejo
2i O 2 0
21. ¿Cuáles de los siguientes conjuntos de vectores en C3 son linealmente independientes?
a) u, = (1 -i, 1, O), u2 = (2, 1 + i, O), u3 = (1 + i, i, O)
b ) u , = ( I , O , - - i ) , u 2 = ( l + i , l , l - 2 i ) , u 3 = ( 0 , i , 2 )
c ) u , = ( i , O , 2 - i ) , u 2 = ( 0 , 1 , i ) , n , = ( - i , - 1 - 4 i , 3 )
22. Sea V el espacio vectorial de todas las funciones con valores complejos de la variable
real x. Demostrar que los siguientes vectores son linealmente dependientes.
f = 3 + 3i cos 2x, g =sen2 x + i cos2 x, h = cos2 x - isen* x
23. Explicar por qué los siguientes conjuntos de vectores no son bases para los espacios
vectoriales indicados. (Resolver este problema por inspección.)
a) u, = (i, 2i), u2 = (O, 32), u3 = (1, 7i) para C’
b) u, = (- 1 + i, O, 2 - i). u2 = (1, -i, 1 + i) para C3
24. ¿Cuáles de los siguientes conjuntos de vectores son bases para C2?
a) (2i, -i), (4i, O) b) (1 + i, l), (1 + i, i)
c) (O, O), (1 + i, 1 - i) d) (2 - 32, i), (3 + 2i, - I )
25. ¿Cuáles de los siguientes conjuntos de vectores son bases para C3?
a) (1, O, O), (i, i, O), (i, i, i) b) (1, O, -i), (1 - t i , 1, 1 - 2i), (O, i, 2)
c)(i,O,2-i), (O,l,i), ( - i , - 1 - 4 & 3 ) d ) ( I , O , i ) , ( 2 - i , 1 , 2 + i ) , ( O , 3 i , 3 i )
En los ejercicios del 26 al 29, determinar la dimensión y una base para el espacio solución
del sistema.
26. x, + (1 + i)x, = O
(1 - i)x, + 2x2 = O
28. x, + (2 - i)x2 =o
x2 + 3ix, = O
ix, + (2 + 2i)x2 + 3ix3 = O
27. 2x1 - (1 + i)x2 = O
(-1 + i ) x , + x, = o
29. x, + ix, - 2ix3 + x, = O
ix, + 3x, + 4x3 - 2ix, = O](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-631-320.jpg)

![638 / Espacios vectoriales complejos
(i) ( O , v> = (v, O> = O
(ii) (u, v + w) = (u, v) + (u, w)
(iii) (u. kv) = %(u, v)
Como sólo iii) difiere de los resultados correspondientes para productos inte-riores
reales, se demostrará y las otras demostraciones se dejan como ejercicio.
(u, kv) = (kv, u) [Axioma 11
= k(v, U) [ h o m a 31
"
= k( V, u) [Propiedad de los conjugados]
-
k(u, v) [Axioma I]
Ejemplo 1 Sean u = (u1, u2, . . . , un) y v = (vl, v2., . . , vn)v ectores en P.P or el
teorema 10.4.1, el producto interior euclidiano (u, v) = u v =
u1 ulVl +u2V2+...+unVn satisface todos los axiomas de producto interior. A
Ejemplo 2 Si
son matrices cualesquiera 2 X 2 con elementos complejos, entonces la sigwente
fórmula define un producto interior complejo sobre el complejo (comprobar):
Por ejemplo, si
entonces](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-633-320.jpg)
![10.5 Espacios complejos con producto interior / 639
Ejemplo 3 (Para quienes ya estudiaron Cdlculu). Si Ax) = fl(x) + if2@) es una
función con valores complejos de la variable real x y si fl (x) y f2(x) son continuas
sobre [a, b], entonces
IUD b h
J U h f ( 4 dx = [ f l ( 4 + if2(x)ldx = f l ( 4 dx + il, f 2 ( 4 dx
En palabras, la integral de Ax) es la integral de la parte real de f más i veces la
integral de la parte imaginaria de f:
Se deja como ejercicio demostrar que si las funciones f =fl(x) + iJ2(x) y g =
gl(x) + ig2(x) son vectores en el complejo C[a, b], entonces la siguiente fórmula
define un producto interior sobre el complejo C[a, b]:
En espacios con producto interior complejo, así como en espacios con pro-ducto
interior real, la norma (o longitud) de un vector u se define por
y la distancia entre dos vectores u y v se define por
Se puede demostrar que con estas definiciones los teoremas 6.2.2 y 6.2.3 siguen
siendo verdaderos en espacios con producto interior complejo (ejercicio 35).
Ejemplo 4 Si u = (ul, u2, . . . , un) y v = (vl, v2., . . , vn) son vectores en C" con el
producto interior euclidmno, entonces
Y](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-634-320.jpg)
![640 1 Espacios vectoriales complejos
CONJUNTOS
ORTOGONALES
Obsérvese que estas expresiones son justamente las fórmulas para la norma y la
distancia euclidianas analizadas en la sección 10.4. A
Ejemplo 5 (Para quienes ya estudiaron Cálculo). Si el complejo C[O, k]ti ene
el producto interior del ejemplo 3 y si f = elm, donde m es cualquier entero,
entonces con auxilio de la fórmula (15) de la sección 10.3 se obtiene
Las definiciones de conceptos como vectores ortogonales, conjunto ortogonal,
conjunto ortonormal y base ortonormal se aplican sin cambio a espacios unita-rios.
Además, el teorema 6.2.4, los teoremas de la sección 6.3 y el teorema 6.5.4
aún son válidos en espacios con producto interior complejo, y el proceso de
Gram-Schmidt se puede usar para convertir una base cualesquiera de un espacio
con producto interior en una base ortonormal.
Ejemplo 6 Los vectores
u = (i, 1) y v = (1, i)
en 62 son ortogonales con respecto al producto interior euclidiano, ya que
u . v = ( i ) ( i ) + ( 1 ) ( 5 ) = ( i ) ( l ) + ( l ) ( - i ) = o A
Ejemplo 7 Considérese el espacio vectorial C3 con el producto interior euclidiano.
Aplicar el proceso de Gram-Schmidt para transformar los vectores básicos u1 =
( i , i , i ) ,u 2 = (O, i , i), u3 = (O, O, i ) , en una base ortonormal.
Solución.
Paso 1. vI = u, = (i, i, i)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-635-320.jpg)
![1 O. 5 Espacios complejos con producto interior / 641
Así.
forma una base ortogonal para 6 3 . Las normas de estos vectores son
de modo que una base o r t o n o d para C3 es
Ejemplo 8 (Puru quienes ya estudiaron Cúfcufo). Sea el complejo C[O, 2 n ] con
el producto interior del ejemplo 3, y sea W el conjunto de vectores en C[O, 2 n ] de
la forma
elmr = cos mx + i sen mx
donde m es un entero. El conjunto W es ortogonal porque si
son vectores dstintos en W, entonces](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-636-320.jpg)
![642 / Espacios vectoriales complejos
1
- -sen (k - l)x
- [ k - 1 k- 1
= (O) - i(0) = O
Si se normaliza cada vector del conjunto ortogonal W. se obtiene un conjunto
ortonormal. Pero en el ejemplo 5 se demostró que cada vector en W tiene norma
f i , dc modo que los vectores
forman un conjunto ortonormal en el complejo C[O, 2n]. A
EJERCICIOS DE LA SECCIóN 10.5
1. Sean u = ( u , , u 2 ) y v = (v], v2). Demostrar que (u, v) = 3u, 324 i +2u i define un
1 1 2 2
producto interior sobre p.
2. Calcular (u, v) usando el producto interior del ejercicio l.
a) u = (2;. - i), v = ( - i, 3;) b) u =(O, O), v = (1 - i, 7 - 5i)
c) u = (1 + i, I - i), v = (1 - i. 1 + i) d) u = (3i, - 1 + 2i), v = (32, - 1 + 2i)
3. Sean u = ( u , , u 2 )y v = (v,,v 2). Demostrar que
-
(u, v) = u,Ü, + (1 -t- i)u,Ü2 + (1 - i)u,u, + 3u2Ü2
define un producto interior sobre C 2
4. Calcular (u, v) usando el producto interior del ejercicio 3
a) U = (2i, - I ) , v = (- i, 3i) b) u = (O, O), v = (1 - i, 7 - 5i)
C) U = (1 + i, 1 - i), v = (1 - i, 1 + i) d) u = (3i. - 1 + 2i), v = ( 3 , - 1 + 2i)
5. Sean u = ( u , , uz) y v = (vl, v2). Determinar cuáles de las siguientes expresiones son
productos interiores sobre p. Para las que no lo sean, enumerar los axiomas que no se
cumplen.
a) (u, v ) b) (u, v ) u,ü, -
= u,Ü, = + - u p 2 {u, v) (uI/2(u+l (2
d) (u, v) = 2u,U, + iu,ü, + c ) = iu,ü, 2u,ü2 e) (u, v) = 2u,ü, + iu,ü2 - iu,ü, + 2u,ü,](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-637-320.jpg)


![1 O. 5 Espacios complejos con producto interior i 645
25. Sea c3 con el producto interior euclidiano. Usando el proceso de Gram-Schmidt,
transformar la base {ul, u2, ug} en una base ortonormal.
a) uI = (i, i, j), u2 = (-i, i, O), uj = (i, 22, i) b) u1 = (i, O, O), u2 = (3i, 7i, -24, u3 = (0,4i. i)
26. Sea C4 con el producto interior euclidiano. Usando el proceso de Gram-Schmidt,
transformar la base { ul, u2, u3, u4} en una base ortonormal.
u, =(O, 2i, i, O), u2=(i, -i, O, O), u3 =(i, 2i, O, -i), u,=(i, O, i, i)
27. Sea C3 con el producto interior euclidiano. Encontrar una base ortonormal para el
subespacio generado por (O, i, 1 - i) y (-i, O, 1 + 2).
28. Sea C4 con el producto interior euclidiano. Expresar w = (-i, 22,6i, O) en la forma w =
w, + w2, donde el vector w, está en el espacio W generado por u1 = (-i, O, i, 2;) y u2 =
(O, i, O, i), y w2 es ortogonal a W.
29. a) Demostrar: Si k es un número complejo y (u, v) es un producto interior sobre un es-pacio
vectorial complejo, entonces (u - k v , u - kv) = (u, u) - i (u, v) -
k(u,v)+kk(v,v).
b) Usando el resultado del inciso a), demostrar que O I (u, u) - k (U, V) -
k(u,v)+kz(v,v).
30. Demostrar que si u y v son vectorese n un espacio con producto interior complejoe, ntonces
KU. v)l’ 5 (u3 UXV, v)
Este resultado, denominado desigualdad de Cauchy-Schwarz para espacios con
producto interior complejo, difiere de su análogo real (teorema 6.2.1) en que es nece-sario
incluir un signo de valor absoluto en el miembro izquierdo. [Sugerencia Sea k =
(u, v)/(v, v) en la desigualdad del ejercicio 29b).]
31. Demostrar: Si u = (uI, u2, . . . , un> y v = (v,, v2, . . . , v,,) son vectores en c”, entonces
lUlÜI + U’ü2 + ‘ ’ ’ + U,ünl 5 (jU,/’ + /U2/’ + ’ ‘ . + lu,12)1’2(/u,+/2 IU2l2 + ‘ ’ ‘ + JU”J2)”2
Esta es la versión compleja de la desigualdad de Cauchy analizada en el ejemplo 1 de
la sección 6.2. [Sugerencia Usar el ejercicio 30.1
32. Demostrar que en la desigualdad de Cauchy-Schwm para espacios vectoriales
complejos la igualdad se cumple si y sólo si u y v son linealmente independientes.
33. Demostrar que si (u, v) es un producto interior sobre un espacio vectorial complejo,
entonces
(O, v) = (v, O) = o](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-640-320.jpg)
![646 / Espacios vectoriales complejos
35.
36.
37.
38.
39.
40.
(u, v + w) = (u, v) + (u, w)
Los teoremas 6.2.2 y 6.2.3 siguen siendo verdaderos en espacios con producto interior
complejo. En cada inciso, demostrar que así es.
a) Teorema 6 . 2 . 2 ~ .b ) Teorema 6.2.2b.c ) Teorema 6 . 2 . 2 ~d.) Teorema 6.2.2d.
b) Teorema 6 . 2 . 3 ~ .f) Teorema 6.2.36. g) Teorema 6 . 2 . 3 ~h.) Teorema 6.2.3d.
En el ejemplo 7 se demostró que los vectores
forman una base ortonormal para C3. Usando el teorema 6.3.1, expresar u = ( 1 - i, 1 +
i, 1) como una combinación lineal de estos vectores.
Demostrar que si u y v son vectores en un espacio con producto interior complejo, en-tonces
Demostrar: Si {v v , vn} es una base ortonormal para un espacio V con producto
interior complejo y SI u y v son vectores cualesquiera en V, entonces 1’ 2””
[Sugerencia. Aplicando el teorema 6.3.1, expresar u y w como combinaciones lineales
de los vectores básicos.]
(Para quienes ya estudiaron Crflculo).D emostrar que si f =A(.) + If,y( g. =) g , (x)+
ig2(x) son vectores en el complejo C[a, b], entonces la fórmula
define un producto interior complejo sobre C[a, b]
(Para quienes ya estudiaron Ccflculo).
a) Sean f =&(x) + if,(y g. )= g l ( x )+ igz(x) vectores en C[O, 1J , que tiene el producto
interior
-
Demostrar que los vectores
e2 m’mx , m = o, * 1, +2,
forman un conjunto ortogonal.
b) Obtener un conjunto ortonormal normalizandol os vectores del inciso a).](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-641-320.jpg)



![650 .I Espacios vectoriales complejos
Ejemplo 3 Si
i l + i
A = [ L i -5 z;i]
1 - i 2 + i
entonces
1 -i 1 - i
I=[ i -5 2 + i
l + i 2 - i 3
de modo que
lo cual significa que A es hermitiana. A
Es fácil reconocer las matrices hermitianas por inspección: los elementos
de la diagonal principal son números reales (ejercicio 17), y la "imagen especular" de
cada elemento de la diagonal principal es su conjugado complejo (figura 1).
MATRICES Las matrices hermitianas poseen muchas propiedades, aunque no todas, de las
NORMALES matrices simétricas reales. Por ejemplo, así como las matrices simétricas reales
son diagonalizables ortogonalmente, se verá que las matrices hermitianas son dia-gonalizables
unitariamente. Sin embargo, a pesar de que las matrices simétricas
reales son las únicas matrices con elementos reales que se pueden diagonalizar
ortogonalmente (teorema 7.3.1), las matrices hermitianas no constituyen toda la
clase de matrices diagonalizables unitariamente; es decir, existen matrices &ago-nalizables
unitariamente que no son hermitianas. Para explicar por qué es así se
necesita la siguiente definición:
Definición. Una matriz cuadrada A con elementos complejos se denomina
normal si
AA* = A*A](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-645-320.jpg)

![652 / Espacios vectoriales complejos
es diagonalizable unitariamente porque es hermitiana y, por tanto, es normal. En-contrar
una matriz P que diagonalice unitariamente a A.
Solución. El polinomio característico de A es
- l + i 1 - 3 1 = ( a - 2 ) ( a - 3 ) - 2 = a 2 - 5 a + 4
det(AZ-A) = det a - 2 - I - i
de modo que la ecuación característica es
y los eigenvalores son 1 = 1 y 1 = 4.
Por definición,
es un eigenvector de A correspondiente a 1 si y sólo si x es una solución no trivial
de
[ a - 2 -'il[;;]=[;] - l + i A-3
Para encontrar eigenvectores correspondientes a 1 = 1, este valor se sustituye
en (3):
[ - I- +l i -l--i2][ ;:]=[;]
Resolviendo este sistema por eliminación de Gauss-Jordan se obtiene (comprobar)
x, =(-1 "QS, x2=s
Así, los eigenvectores de A correspondientes a ;1 = 1 son los vectores diferentes de
cero en 62 de la forma
x = [ (- 1 - i)s ]+ll-i]](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-647-320.jpg)
![10.6 Matrices unitarias, normales y hermitianas / 653
Por tanto, este eigenespacio es unidimensional con base
u= [ - ' l - i ]
En este caso el proceso de Gram-Schmidt es de un solo paso; la normalización de
este vector. Como
el vector
es una base ortonormal del eigenespacio correspondiente a il = l.
Para encontrar los eigenvectores correspondientes a il = 4, este valor se sustituye
en (3):
[ - l + i -"i][;;] 1 = [o]
Resolviendo este sistema por eliminación de Gauss-Jordan se obtiene (comprobar)
x, = x* = S
de modo que los eigenvectores de A correspondientes a il = 4 son los vectores
diferentes de cero en C? de la forma
X = [(?)S] S = S
Así, el eigenespacio es unidimensional con base](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-648-320.jpg)
![654 1 Espacios vectoriales complejos
EIGENVALORES
DE MATRICES
HERMITIANAS Y
SIMÉTRICAS
Aplicando el proceso de Gram-Schmidt (es decir, normalizando este vector) se
obtiene
Por tanto, r- - 1 - i -l + i
diagonaliza a A y
P”AP= [A y] A
En el teorema 7.3.2 se estableció que los eigenvalores de una matriz simétrica con
elementos reales son números reales. Este importante resultado es un corolario del
siguiente teorema más general.
~~
Teorema 10.6.5. Los eigenvalores de una matriz hermitiana son números
reales.
Demostración. Si A es un eigenvalor y v es un eigenvector correspondiente de
una matriz hermitiana A n X n, entonces
Av = Av
Multiplicando por la izquierda cada miembro de esta ecuación por el conjugado
transpuesto de v se obtiene
Se demostrará que ambas matrices v*Av y v*v 1 x 1 tienen elementos reales, de
modo que por (5) se concluirá que debe ser un número real.
Tanto v*Av como v*v son hermitianas, ya que
(v*Av)* = v*A*(v*)* = V*AV](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-649-320.jpg)
![I O. 6 Matrices unitarias, normales y hermitianas / 655
Y
(v*v)* = v*(v*)* = v*v
Como las matrices *
hermitianas tienen elementos reales sobre la diagonal principal
y como v * ~ vy v v son 1 x 1, se concluye que estas matrices tienen elementos
reales, con lo cual se completa la demostración. 0
Teorema 10.6.6. Los eigenvalores de una matriz simétrica con elementos
reales son números reales.
Demostración. Sea A una matriz simétrica con elementos reales. Debido a que
los elementos de A son reales, se concluye que
A=A
Pero esto indica que A es hermitiana, ya que
Así, por el teorema 10.6.5, A tiene eigenvalores reales. 0
EJERCICIOS DE LA SECCIóN 10.6
1. En cada inciso, encontrar A*.
c) A = [7i O -3i] d) A =
'22 '23
2. ¿Cuáles de las matrices siguientes son hermitianas?
3. Encontrar k, I y m de modo que A sea una matriz hennitiana](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-650-320.jpg)
![656 / Espacios vectoriales complejos
4. Aplicando el teorema 10.6.2.
rias.
, determinar cuáles de las siguientes matrices son unita-r
-v115
c) ["i 1 - 1 -
i] d)
I + + i
L
5. En cada inciso, comprobar que la matriz es unitaria y encontrar su inversa.
i
v5
0 -
"
_i_ v5
-I
v%
i
i 1
d) 3 -v5
3 f i 4 + 3 i
6. Demostrar que la matriz
es unitaria para todo valor real de 8.
En los ejercicios del 7 al 12, encontrar una matriz unitaria P que diagonalice a A y deter-minar
P"AP.
A = [ l ' ; ';;I , . A = [ ; -;] , . A = [ 2 -62 i 2 +42 i 1
r
i i
[3(11 3 : ~ 11. A = [ O - 1 - l + i 12. A = --vZ 5 2 0
-
2 - --
5 0
O 1
v 5 v 5
O -I-i O
i
v5 - 0 2
- -
13. Demostrar que los eigenvalores de la matriz simétrica
no son reales. ¿Este hecho viola el teorema 10.6.6?
14. Encontrar una matnz 2 X 2 que sea hennitiana y unitaria y cuyos elementos no sean
todos números reales.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-651-320.jpg)
![Ejercicios complementarios / 657
"
15. Demostrar: Si A es una matriz n X n con elementos complejos, entonces l b ' . , '! =
__
det(A). [Sugerencia Primero demostrar que los productos cl ": ' . : : :: ;igno
son los conjugados de los productos elementales de A con sign J
16. a) Aplicando el resultado del ejercicio 15, demostrar que si A es una matriz n X n con
elementos complejos, entonces det(A*) = det(A).
b) Demostrar: Si A es hermitiana, entonces det(A) es real.
c) Demostrar: Si A es unitaria, entonces Idet(A)I = l.
17. Demostrar que los elementos sobre la diagonal principal de una matriz hermitiana son
números reales.
18. Sean
matnces con elementos complejos. Demostrar que
a) (A*)* = A b) (A + B)* =A* + B* c) (kA)* = kA* d) (AB)* = B*A*
19. Demostrar: Si A es invertible, entonces también A* lo es, en cuyo caso (A*)" = (A")*.
20. Demostrar que si A es una matriz unitaria, entonces también A* es unitaria
21. Demostrar que una matriz n x n con elementos complejos es unitaria si y sólo si sus
renglones forman un conjunto ortonormal en C" con el producto interior euclidiano.
22. Usando los ejercicios 20 y 21, demostrar que una matriz n X n es unitaria si y sólo si
sus columnas forman un conjunto ortonormal en C" con el producto interior euclidiano.
23. Dzmostrar: Si A = A*, entonces para todo vector x en C", el elemento en la matriz
x Ax de 1 X 1 es real.
24. Sean 1 y p eigenvalores distintos de una matriz hermitiana A.
a) Demostrar que si x es un eigenvector correspondiente a 1 y y 'es un eigenvector
correspondiente a p , entonces x*Ay = 1x y y x Ay = px*y. * *
b) Demostrar el teorema 10.6.4. [Sugerencia Restar las ecuaciones en el inciso a).]
EJERCICIOS COMPLEMENTARIOS
1. Sean u = (uI, u2, . . . , u,) y v = (ul, u2, . . . , u,) vectores en C", y sean - u = (üI,i d 2 , . . . , u,) y v = (U1, ü*, . . . , u,). - -
a) Demostrar: u.V = Ü.V.
b) Demostrar: u y v son ortogonales si y sólo si ii y 7 son ortogonales.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-652-320.jpg)
![658 / Espacios vectoriales complejos
2. Demostrar que si la matriz
es diferente de cero, entonces es invertible.
3. Encontrar una base para el espacio solución del sistema
4. Demostrar: Si a y b son números complejos tales que + lb12 = 1 y si O es un número
real, entonces
es una matriz un~taria
S. Encontrar los eigenvalores de la matriz
donde =
6. a) Demostrar que si z es un número complqo diferente de 1, entonces
Sugerencia Sea S la suma del miembro izquierdo de la ecuación y considérese la
cantidad S - zS.
b) Usando el resultado del inciso a), demostrar que si z" = 1 y z # 1, entonces 1 + z +
=2 + . . . + z"-l = 0
c) Usando el resultado del inciso a), obtener la identidad trigonométrica de Lagrange
1 + c o s O + c o s 2 o + ~ ~ ~ + c o s n O " + 1 sen[ (n + +)O]
2 2sen(O/2)
para O < O < 277. [Sugerencia Sea z = cos O + i sen O.]
7. Seaw=e2n1'3.Demostrarquelosvectoresvl = ( l / f i ) ( l , 1, 1),v2=(1/fi)(1, w,w
2 ) y v3 = ( I / f i ) (1, w2, w4) forman un conjunto ortonormal en ~ 3 [S. u gerencia u s a r
el inciso b) del ejercicio 6.1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-653-320.jpg)


![RESPUESTAS
A LOS
EJERCICIOS
EJERCICIOS DE LA SECCIóN 1.1 (Página 27)
1. a), c), f) 2. 4, b), c)
3. a) x = $ + j t b) xI = {S - 4t + f xI =ir - 0s + i t - u = $q - $r + Qs - QI
y = t x2 = S x2 = r w=q
xj = t X) = S x = r
x, = t y = s
z = t
o 2
[. 1 2 0 - 1 1
i] [: y
c) 3 1 o - 1 d) '1 0 0 1 7 0 1 O 0 1 3 S. a) 2x, =O b) 3x, - 2X) = 5 c) 7x1 + 2x2 + X) - 3x4 = 5
3x, - 4x2 = o 7x, + x, + 4x, = - 3 x1 + 2x2 + 4x, = I
d) XI = 7
x3 = 3
x, = 4
x2 = 1 - 2x2 + x3 = 7
x2 = -2
6. a) x - 2y = 5 b) Sea x = r, entonces t -y = 5. Al despejar y se obtieney = it - 5.
8. k = 6: infinidad de soluciones
k # 6: no hay soluciones
Ningún valor de k produce una solución.
c) Las tres rectas coinciden.
9. a) Las rectas no tienen punto de intersección común. b) Las rectas se intersecan exactamente en un punto
661](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-656-320.jpg)
![1. a) iildeíXd,J b) 4 X 2 e) hdefmda d) Indefinida 2. a = 5, b = - 3, c = 4, d = 1
c) 5 x 5 P) 5 X 2 g) Indefinida h) 5 X 2 ~] d) [ -7 -28 -141
5 -21 -7 -35](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-657-320.jpg)
![Respuestas a los ejercicios / 663
e) [-: :] f) [y -A] g) [ -13 2 I:] h) [ 1 2 9 1 9 - 13 y]
3 9 a a O 1 -6 -1 -4 -6
[ 45
[ [ -: [:n 6
e) 1: -11 l;] f) 2117 3157] g) h) -2: I:]
17 13 24 16
i) 61 (j) 35 (k) 28
7. a) [67 41 411 b) [63 67 571 c) F:] d) [ :] e) [24 56 971 f)
67 63](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-658-320.jpg)
![663 1 Respuestas a los ejercicios
IO. a) [67 41 411 = 3[6 -2 41 - 2 [O 1 31 + 7[7 7 51
[64 21 591 = 6[6 -2 41 + 5 [O 1 31 + 4[7 7 51
[63 67 571 = 0[6 -2 41 + 4[0 1 31 + 9[7 7 51
b) [6 -6 701 = 6[3 -2 71 - 2[6 5 41 +4[0 4 91
[6 17 311 =0[3 -2 71 + 1[6 5 41 + 3[0 4 91
[63 41 1221 = 7[3 -2 71 + 7[6 5 41 + 5[0 4 91
--: r 4 0
13. . ) A = [ ! -3 i],x=[:],b=[-a] b ) A = l 5 1
2 -5
o 3
. .
14. a) 3x, - xz + 2x3 = 2 b) 3w - 2~ + z = O
I S.
4x, + 3x, + 7x3 = - 1 5w + 2 y - 2 z = O
-2x, + x, + 5xs = 4 3 w + x + 4 y + 7 z = O
- - 2 w + 5 ~ + y + 6 ~ = 0
3 1
O -8
9 -1
1 1
16. a) [--; -15 -111 b)
-15 44 35 o 25 5
2 3 23 24
17. a) A,, esunamatrizde2 X 3yB,, esunamatriz 2 X 2. A,,B,, noexiste
21. a)
a,, o o o o o
O a , , O o o o
0 a55
o o ‘66](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-659-320.jpg)
![Respuestas a los ejercicios / 665
a , , o o o
a21 '22 0 0
a31 a32 a33 o
'41 '42 '43 '44
a51 a52 a53 a54
[ '61 '62 a63 a64
2 3 4 5
1 22. a) b)
4 5 6 7
5 6 7 8
'1 1 1 1-
1 2 4 8
1 3 9 2 7
.I 4 16 64-
a , , al2 o o o o
o o o
'21 a22 '23 o o o
u32 a33 '34 0 0 a a 4 a 4 5 4 3 0
o o o a54 '56
o o o o a66
a65 -1 - 1 1 1
[ O
:]
18. OA y A0 no pueden tener el mismo tamaño. 19. ' r 1 o k l
20. a) Un ejemplo es
b) Un ejemplo es [;
o -1
I:].](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-660-320.jpg)
![666 / Respuestas a los ejerciclos
EJERCICIOS DE LA SECCIóN 1.5 (Página 83)
1. c), 4 , f, 2. a) Sumar tres veces el primerenglón al segundo renglón
b) Multiplicar por 3 el tercer renglón.
c) Intercambiar el primer renglón y el cuarto renglón.
d) Sumar + veces el tercer renglón al primer renglón.
3 . a ) ["O o1 O '1 b) [: O 1 1 O :] c) [ y "1 d) [A y
1 0 0 -2 o I 2 0 1
4. No, porque C no se puede obtener efectuando una sola operación en los renglones de B
[ -: -:] [-: z] 5 2
5. a) b) c) Noes invertible
[ -i -1 1 1 "
8 81 b) No es invertible c) - - 2 2 " 2
0 -
I-
1
- 0 0 0
-
kl
o -I o o
8. a) k2
1 o o - o ,
k3
1
k4 -
0 0 0 -
L -1
P
1
0 0 0 -
k'l
1
0 0 - 0
b)
k3
o -1 o o
1
k2
- 0 0 0
kl -
O
O
1
k
-
O
O
O
1
k
-](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-661-320.jpg)
![“lu
Respuestas a los ejercicios 1 667
16. b) Sumar - 1 veces el primer renglón al segundo renglón.
Sumar - 1 veces el primer renglón al tercer renglón.
Sumar - 1 veces el segundo renglón al primer renglón.
Sumar el segundo renglón al tercer renglón.
EJERCICIOS DE LA SECCIóN 1.6 (Página 92)
16. b, = 2b2 17. b, = b2 + b3 18. No hay restricciones 19. 6, = b3 + b,, b2 = 26, + 6,
1 1 12 7 3 27
-6 -8 1 -18 22. a) sólo la solución trivial x1 = x, = x3 = x4 = O; invertible
-15 -21 9 -38 -35 b) Intinidad de soluciones; no es invertible
EJERCICIOS DE LA SECCIóN 1.7 (Página 100)
[’ y] [ -1 o o
F]
1. a) 0 -1 b)No es invertible c) 2. a) [“ 4 -:I b) [ -2; I:: I:]
4 10 60 20 -16
’
b) A z = rl oi, Oo ], A ” - r 9” :], A- . = [ : 3Ok *O0]
o o & O O 16 o o 4k
4. b), c) 5. a) 6. u = 11,b= - 9 , c = -13 [i 7. ~ = 2 , b =- 1
; O $ 0 - 0
8. a) No conmuta b) Conmuta 10. a) - b) [O i 61
- O 0 1
7
/’ +
“__ . -](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-662-320.jpg)
![668 / Respuestas a los ejercicios
[:!: 1 : 3 0 0
11. a) 1::][0 5 O] b) No I Y . -n2 ( I + n )
a32 a33 O O 7
20. a) Es simétrica b) No es simétnca c) Es simétrica d) No es simétrica
24. a) x,=$,x,= ¡,x,= -* b) x , = - + , X , = -$,X,= -3
EJERCICIOS COMPLEMENTARIOS DEL CAPíTULO 1 (Página 102)
I. x'=ix++y,y'= -+x+$ 2. x ' = x c o s ~ + y s e n ~ , y ' = - x s e n ~ - ~ . i v c o s ~
3. Una respuesta posible es 4. 3 monedas de 1 centavo, 4 de 5 centavos y 6 de IO centavos
x, - 2x, - x3 - x, = o
x, + 5x2 + 2x, = o
S. x = 4, y = 2, z = 3 6. Infmidad si a = 2 o a = --% ninguna en caso contrario
7. a) a f O , b # 2 b)a#O,b=2 8. x = $ , y = 9 , 2 = + Y. IC=[: :] C) a=O,b=2 d ) a = O , b # 2
10. a = 2 , b = - I , c = 1 11. a) X =
6 0 1
b) X=
-37 -3i
12. a) Z= [y: -::]X b) z1 = - X , - 7x2+ Ilx, z2 = 1 4 ~+, lox2 - 26x3
EJERCICIOS DE LA SECCIóN 2.1 (Página 114)
I . a) 5 b) Y c) 6 d) 10 e) O f) 2
2. a) Impar b) Impar c) Par d) Par e) Par f) Par
3. 22 4. O S. S2 6. - 3 f i 7. aZ-5a+21 8. O 9. -65 10. -4 11. -123
12. -c4+c3-16c2+8c-2 13. a) a=1,a= -3 b) a= - 2 , ~ = 3 , a = 4
3 t m
16. 275 17. a) = - 120 b) = -120 18. x="--
4
EJERCICIOS DE LA SECCIÓN 2.2 (Pagina 120)
I . a) -30 b) -2 c) O d) O 3. a)-S b) -1 c) 1 4. 30 5. 5 6. -17
7. 33 8. 39 Y. 6 10. -Q I t . -2 12. a) -6 b) 72 c) -6 d) 18](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-663-320.jpg)
![Respuestas a los ejercicios / 669
EJERCICIOS DE LA SECCIóN 2.3 (Página 129j
1. a) det(2A)= -40=2'det(A) b) det(-2A)= -208=(-2),det(A)
2. det AB = - 170 = (det A)(det B) 4. a) Invertible b) No es invertible c) No es invertible d) No es invertible
S. a) - 189 b) - f c) -3 d) - & e) 7 6. Si x = O, los renglones primero y tercero son proporcionales.
Si x = 2, los renglones primero y segundo son proporcionales
5 2 m
12. a)k=-
2 b) k = - 1 14. a) ["-"2 a--21][: :]=[:]
c) ["3 a-tI- 3 I["'] x, = 1 3
EJERCICIOS DE LA SECCIóN 2.4 (Página 142)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-664-320.jpg)
!["
670 Respuestas a los ejercicios
EJERCICIOS COMPLEMENTARIOS DEL CAPíTULO 2 (Página 145)
13. a) Deben intercambiar las columnas i-ésima yj-ésima.
h) La i-ésima columna se debe dividir entre c.
c) I,a~-ksima columna se debe sumar "c veces a la i-ésima colu~nna
1% a) k3 + ( -al l - a22- a33)12+ (alla2,+ u11a33 + u22a33 - a 1 2 ~-2 a1 1 3 ~-3 u1 ~ ~ + u ~ ~ ) ~
18. a) A= - 5 , 1 = 2 , 1 = 4 ; I-:][y,] , [I":] b) A= I ; [ -!]
(alla23a32 + 412u21u33 + a13a22u31 - u11a22a33 - a12u23u31 - u13'21432)
EJERCICIOS DE LA SECCIóN 3.1 (Página 157)
3. a) PIP2 = (- I , - 1)
+ P b) P 1 P 2 = ( - 7 , -2) c) p,p; = (2, 1) d) p,p; = (a, b)
e ) s = ( - 5 , 12, -6) f) PIP2=( l r-1 , -2) g) P,P, =(-a, -b, -c) h) = (a, b, c) - +
4. a) Q(5, IO, - 8) es una respuesta posible. 5. a) P( - 1, 2, - 4) es una respuesta posible.
b) Q( - 7 , - 4, - 2) es una respuesta posible. b) P(7, -2, -6) es una respuesta posible.
6. a) (-2, 1, -4) b) ( - 10, 6 4 ) c) (-7, 1, 10) 7. x = (-9, t, 9)
d) (80, -20, - 80) e) (132, -24, - 72) f) (-77, 8, 94)
8. c , = 2 , c 2 = - l , c , = 2 I O . c, = c, = c3 = o 1 1 . a) (3, -i, -f) 12. a) x' = 5,y' = 8
b) (23 -9 L) 4 , 4 , 4 b)x= - l , y = 3
2 ' 2
EJERCICIOS DE LA SECCIóN 3.2 (Página 162)
1. a) 5 b) fl c) 5 d) 2~ e) 3V% f) 6
2. a) fl b) 2- c) d) 3 f l
3. a) V% b) fi+ac ) 4 f i d ) a e) (- 3 -6 -- m) 4
f) 1
4
1. k *x = 8. Una esfera de radio 1 con centro en (xo, y,, z0)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-665-320.jpg)

![672 1 Respuestas a los ejercicios
4. a) 2y - z + 1 = o b) X + 9V - 5z - 26 = O S. a) No son paralelos b) Son paralelos
c) Son paralelos
h. a) Son paralelos b) No son paralelos 7. a) No son perpendiculares b) Son perpendiculares
X. a) Son perpendiculares b) No son perpendiculares 9. a) x = 3 + 2 t , y = - I + t , z = 2 + 3 t
b ) x = - 2 + 6 t , y = 3 - 6 t , z = - 3 - 2 t
c) x = 2 , v = 2 + t , z = 6
d ) x = t , y = - 2 t , z = 3 t
10. a ) x = 5 + t , y = - 2 + 2 t , z = 4 - 4 t 11. a) X = - 1 2 - 7 t , y = -41 - 2 3 t , z = t
b ) ~ = 2 t , ~- t~,Z== -3t b ) x = $ t , y =O, z = t
12. a) (-2, 4, 1) .(x + I , y - 2, z - 4) = O 13. a) Son paralelos b) No son paralelos
b ) ( - l , 4 , 3 ) . ( X - 2 , ; , ~ + 5 ) = 0
c) (-1,O,O).(.x-5,y+2,z- ])=O
d) (a, h, C) * (x, Y, Z) = 0
14. a) Son perpendiculares
b) No son perpendiculares
15. a) (x,y, z) = (- 1, 2, 3) + t(7, - 1, 5) (-m < t< +m)
b)(x,y,z)=(2,0, - l ) + t ( l , 1, 1) ( - m < t < +m)
c) (x,y,z)=(2, -4, l)+t(O,O, -2) (--co<t< +m)
d) (.x,~vZ,) = (O, O, O) + t ( ~b,, C ) (-m < t < +m)
17. 2 ~ + 3 y - 5 ~ + 3 6 = 0 18. a) z=O b) y=O c) x=O
19. a) z - z o = O b) x-x,=O c) y-y,=O 20. 7 ~ + 4 y - 2 ~ = 0 21. 5 ~ - 2 ~ + ~ - 3 4 = 0
22. (-y-,9 ,y) 2 3 . y + 2 2 - 9 = 0 24. x - y - 4 ~ - 2 = 0 26. x =%t - 2 , y-= % t + 5 , z = t
27. x + ~ v + ~ z1 8- = 0 28. ( ~ - 2 ) + ( y + I ) - 3 ( ~ - 4 ) = O 29. 4 ~ + 1 3 ~ - ~ - 1 7 = 0
30. 3 ~ + 1 0 ~ + 4 ~ - 5 3 = 03 1. 3 ~ - ~ - ~ - 2 = 032 . 5 ~ - 3 , ~ + 2 ~ - 5 = 0
3.3. 2 ~ + 4 v + 8 ~ + 1 3 = 0 36. ~ - 4 ~ + 4 ~ + 9 = 307 . 3) x = g +&t , .Y= - # - $ t , Z = f
b) X = -$t, y = O, z = t
1 4 1 2
39. a) $ b) -qg c) 40. a) - b) O C) -
2 m 6
2 - 2 x + 2 y - 3 z + 3
x - 3
2
42. a) - -
- y + I =- b) -- -
-
3 6 6 2
43. a) X - & - 17=0 y x + 4 z - 2 7 = 0 esunarespuestaposible
b) x - 2y = O y 7.v + 2z = O es una respuesta posible.
44. a) 0 - 35" b) 0 - 79" 45. 0 - 75"
EJERCICIOS DE LA SECCIóN 4.1 (Página 215)
I . a) (-1, 9, - 11, 1) b) (22, 53, - 19, 14) C) (-13, 13, -36, -2)
d) (-90, -114,60, -36) e) (-9, -5, -5, -3) f) (27, 29, -27, 9)
2. (g,d,$,g) 3. ~ , = 1 , c , = I , c , = - I , c , = 1 5. a) b ) 3 c) 13 d ) f i
1 2
h. a) m b) m+ V% c) 4V'% d) m e) - -
di 3 v 5 3 V 5 ' 3 d i](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-667-320.jpg)
![Respuestas a los ejercicios 1 673
8. k = r$ 9. a) 7 b) 14 c) 7 d) 11 10. a)
1 1 . a) b) 2- c) fi d) 10
14. a) Si b) No c) Sí d) No e) No f) Sí 15. a) k = -3 b) k = -2, k = -3
16. S $ ( - 3 4 , 4 4 , - 6 , l l ) 19. x , = ~ , x , = - l , x 3 = 2 20. -6
33. a) Medida euclidiana de la "caja" en R": a, a2 . . . a,
b) Longltud de la diagonal: 'a? + a: + ' ' ' + ai
EJERCICIOS DE LA SECCIóN 4.2 (Página 235)
1. a) Lineal; R3 + R2 b) No lineal; R2 -+ R3
c) Lineal; R3 -+ R' d) No lineal; R4 + R2
[''1 [: -1 111 [-: [I 1 0 y 0 :]
0
2. a) 3 "35 0o - 1 b) c) I:] d) 1 1 1 1
3. [i -1 I : ] ; T ( - 1 , 2 , 4 ) = ( 3 , - 2 , - 3 )
[: -:] [' 1 2 1 [" :]
4. a) b) O] c) [l 5 O] d) o 1
O 0 1 O O -8
S. a) [ -P
1 -
1
[ 7 2 -
o 1
"1 3
- 1 o - O] 1 b, O
d) [OI
O
1
O
O
1
O
-1
[ :] [ [ -2x, + x2 + 4x, [ -x, + x2
6. a) - b) c) 3x, + 5x2 + 7x3] d) 2x, + 4x2]
6x1 - x3 7x, + 8x2
7. a) T(-1,4)=(5,4) (b) T(2,1, -3)=(0, -2,O)
8. a) (-1, -2) (b) (1,2) c) (2, -1) 9. a) (2, -5, -3) b) (2, 5, 3) c) (-2, -5, 3)
IO. a) ( 2,O) (b) (O, -5) 11. a) (-2, 1,O) b) (-2,0,3) c) (O, 1, 3)
12. a) ~ ___ 3fi2 + 4 , 3 -y 3 - 4 v 3 - f i - 4 ?v5 -v5
13. a) ( -2, ",",-_ __ +tfi) b) (O, 1,2v5) c) (-1, -2,2)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-668-320.jpg)

![Respuestas a los ejercicios / 675
S. a) Es uno a uno; [! -!I ; T - ,(MI,,w 2)= (+x, - $x,, +xl + $x2) b) No es uno a uno 3 5
[ o -1
c) Es uno a uno, - o ] ; T P L (w,w, ,) = ( -X,, -xl) d) No es uno a uno
1 -2 4
6. a) Es uno auno, [I I:]; T"(w,, w2, w3) = (x, - 2x, + 4x3, -XI + 2x2 - 3x3, -X1 3% - 5x3)
d) No es uno a uno
7. a) Reflexión con respecto al eje x. b) Rotación por el ánguio - n/4.
e) Contracción por un factor de f . d) Reflexión con respecto al plano yz
e) Dilatación por un factor de 5.
8. a) Lineal b) No lineal c) Lineal d) Lineal
9. a) Lineal b) No lineal e) Lineal d) No lineal
10. a) Lineal b) No lineal 11. a) Lineal b) No lineal
12. a) Para una reflexión con respecto al ejey. T(e,)= [ y T(e,) = [y]. Portanto, T= [-: P]
b) Para una reflexión con respecto al plano xz. T(e,) = [J O T(e2) = [-!) y v e 3 ) = 1 ] .
r1 0 01
Por tanto, T= I O - 1 O I.
Lo 0 11
[A] [:l. [b :].
C) Para una proyección ortogonal sobre el eje x. T(e,) = y í-(e,)= Portanto, T= d) Para una proyección ortogonal sobre el plano z. T(e,)=
e) Para una rotación en un ángulo positivo 0, T(el) =
sen% COS e 1. I
Por tanto, T= [ cost) -sen%](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-670-320.jpg)
![f) Para una dilatación por un factor k 2 1, T( e , )= LO: i , T(e,) = 11k 1 , T(e,) = [OI . Por tanto, T = L :O k: O: I
676 i Respuestas a los ejercicios
[a], [!I, [!l. 1 0 0
b) T(e,) = T(e,) = y T(e,) = Por tanto, T= [O O O]
O 0 0
16. a) Transformación lineal de R2 + R3 b) Transformación lineal de R3 + R2
Ix. a) a= 1; [:I b) a= 1; [:I c) a= 1; [i] d) L = 3; todos los vectores en R2 son eigenvectores
ti). a) L= 1; [!] y [!] b)L= I ; [i] y [!I
a= - 1; [i] L = o;](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-671-320.jpg)


![Respuestas a los ejercicios / 679
13. Base: (4, 1, O, O), (-3, O, 1, O), (1, O, O, 1); dimensión= 3
14. Base: (3, I , O), ( - 1, O, 1); dimensión= 2 15. No es base, dimensión = O
16. Base: (4, -5, l);dimensión= 1 17. a) (g, 1, 0),(-5,0, 1) b) (1, l , O ) , ( O , O , 1)
c) (2, - 1, 4) d) (1, 1, O), (O, 1, 1)
18. a) tndimensional 'b) bidimensional c) unidimensional 19. tndimensional
20. 4 { v l ,v 2, e l ) o { v l , v2, e 2 ) b) {vl, v2, e l l 0 { v I 1v 2, e21 0 { v I ,v 2, e31
21. { v l , v2, eZr e3) o {vl, v2, e2, e41 0. {v,, v2, e3, e4)
26. a) Una respuesta posible es { - 1 + x - 2x2, 3 + 3x + 6x2, 9)
b) Una respuesta posible es { 1 + x, x2, - 2 + 2x2}.
c) Una respuesta posible es { 1 + x - 3x2}.
27. a) (O, f i ) b) (1, O) c) (- 1, f i ) d) (a - b, f i b )
EJERCICIOS DE LA SECCIÓN 5.5 (Pagina 319)
1. r l = ( 2 , - 1 ,O, l ) , r 2 = ( 3 , 5 , 7 , - 1 ) , r 3 = ( 1 , 4 , 2 , 7 ) ; c l = [:3I , c 2 = [-5I , c 3 = [I71 , e 4 = [-!I
3. a) [;:]=[:I-[-:] b) b no es el espacio columna de A](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-674-320.jpg)
![680 / Respuestas a los ejercicios
O
1
b) rl = [l - 3 O O], r,=[O 1 O O], cI = [;]M [ -;]
c) rl =[I 2 4 51, rz= [O 1 -3 O], r3 = [O O 1 -31, r, = [O O O I],
d) rl = [l 2 - 1 51, r2 = [ O 1 4 31, r3 = [O O 1 -7],r4= [O O O I], [ -;Ilc4=[ -,1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-675-320.jpg)


![Respuestas a los ejercicios / 683
EJERCICIOS DE LA SECCIóN 6.2 (Página 363)
1. a) Sí b) No c) Sí d) No e) No f) Sí 2. No
1 3
19
3. a) -- b) m -- c) O 4. a) O b) O 6. a) -
v5 1 o v i b) 0
7. a) Ortogonales b) Ortogonales 8. a) k = - 3 b) k = -2, k = - 3
c) Ortogonales d) No son ortogonales
Y. -t#7(-34,44, -6, 1 1 ) 12.y= -$x 13. a) x = t , y = -2t,z= -3t b) 2x-5y+4z= O
16. a) [ b) [E], [a] c) [I:], [!
1.
-1
-1
1
O
O
33. (u, v) = tu,v, + Qu,v,
EJERCICIOS DE LA SECCIóN 6.3 (Página 380)
1. a), b), d) 2. b) 3. b), d) 4. b), d) S. a) 6.](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-678-320.jpg)

![Respuestas a los ejercicios / 685
2. a) O; los vectores columna no son linealmente independientes.
b) O; los vectores columna no son linealmente independientes.
4. a) (%,E,#) b) (-5, -4, -9) 5. a) (7,2, 9, 5) b) (-y, -j,V,F)
6. (O, - 1, 1, 1)
7. a) [: :] b) [: y] 8. a) [A : "1 b) [: y :] O 0 1 O 0 1
9. a) vI = (1, O, - 5), v2 = (O, 1, 3)
[ 55 10
43 "3% 3%] [ 44x0 + %Yo - &o b) c) %O + %YO + b o ] 4 E15
" -
36 35 - 35x0 + &Yo + %o
IO. a) vI =(2, -1,4) b) [ -; - " $ -i] - C) [-&X, +&Yo-&zo]
-4 2 8 -3i - &x0 - &Yo + #izo
21 21 21 &x0 - &Yo + &o
15. P=AT(AAT)"A
EJERCICIOS DE LA SECCIóN 6.5 (Página 408)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-680-320.jpg)
![686 i Respuestas a los ejercicios
18. a) ( t f i , 3v5, 5) b) ( --$v5, $a, - 3)
19. a) (-&$u5,2, $--$(ba) ( l)-& b , 6 , -$-ifi)
20. a) ( - l , b & $ v 5 ) (b) (1, -ia,:fi)
cos 0 O -sení3 1 O
21. a) A = [ O 1 O , ) A = [ : cos0 se:0] 22.
sen0 O cos O O -sení3 cosí3
23. u' + b2 = 26. a) Rotación b) Rotación
27. a) Rotación seguida de una reflexión b) Rotación
u 5 1
"
- O
2 2
v5fia "-
4 4 2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-681-320.jpg)
![Respuestas a los ejercicios / 687
12. b) Las diagonales de un paralelogramo son perpendiculares si y sólo si los lados del paralelogramo tienen la
misma longitud.
2 1
16. a = O, b = --G, cV = -;5 n o son ímicos
EJERCICIOS DE LA SECCIóN 7.1 (Página 423)
I. a) A2-2A-3=o b ) a 2 - 8 a + 16=0 c) a2- 12=0
d ) A 2 + 3 = 0 e) L2 = O f) a2-2a+ 1 =o
2. a) L = 3 , L = -1 b ) a = 4 C) a = m , a = -VE
d) No hay eigenvalores reales e) 1 = O f) = 1
3. a) Basep arae le igenespacioc orrespondiente a A = 3: [; ];
[PI
[ t ]
base para el eigenespacio correspondiente a A = - 1:
b) Base para el eigenespacio correspondiente a a = 4:
c) Base para el eigenespacio correspondiente a L = a: [+I;
base para el eigenespacio correspondiente a 1 = - a: [-"I
d) No hay eigenespacios. e) Base para el eigenespacio correspondiente a A = O:
f) Base para el eigenespacio correspondiente a a = 1 :
4. a) a3 - 6L2 + 111 - 6 =o b ) a 3 - 2 a = o
c) v + g a 2 + + + 8 = 0 d ) a 3 - a 2 - a - 2 = 0
e) a3 - 6a2 + 12L - 8 = o f) A3 - 2L2 - m + 36 = o
5. a) a = 1 , a = 2 , ; 1 = 3 b) a = o , n = f l , a = -v5 C) a= -8
d ) a = 2 e) a = 2 f) a= - 4 , a = 3
[:I [+(I5 +15fi) 1 [+(I5 -:fi)]
b) A=O: base i ; I = f i : b a s e +(-1 + 2 f i ) ;I-=a : b a s e $(-1 - 2 ~ 5 )](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-682-320.jpg)
![6118 i Respuestas a los ejercicios
c) il = - 8: base [It] d) .=?:base[ )] e) L=2:base [I!]
f) A= -4: base [-!];A=': base[-;j
7 . a) (a - 1)2(n + 2)(il+ I ) = o b) (a - 4)2(i12 + 3) = o
x. a) a=I,a= - 2 , a = -1 b) i l = 4
9. a) A. = I : base [i] y [:];A= -2;base[ -;];A= -l:base[ -:] b) A=."[' O
3'
13. a ) y = x y y=2x b) Nohayrectas c) y=O 14. a)-5 b) 7
c) a, = 3:
EJERCICIOS DE LA SECCIóN 7.2 (Página 435)
1. 1,2 o 3
2. a) 1 = 3,A = 5
b) Parda = 3, el rango de 31 - A es 1 y la nulidad es 2. Para1 = 5, el rango de 51 - A es 2 y la nulidad es 2.
c) .4 es diagonalizable, ya que los eigenespacios producen un total de tres vectores básicos.
3. No es diagonizable 4. No es diagonizable
5. No es diagonizable 6. No es diagonizable
7. No es diagonizable](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-683-320.jpg)
![Respuestas a los ejercicios / 689
10. p = [ O1 01 0l ] ; P - ' A P = [ OO 10 O0] l l . P = [ " i y A] ;P- 'A. - [ . 3 30 o0]
-1 o 1 O 0 2 1 0 0 O 0 2
12. No es diagonizable 13. F = 14. No es diagonizable
20. a) [A y :] b) 1 y :] c) [A 1: :] d) [E
O 0 1 O 0 1 o -1 o -1 "1
21. A" = PD"P" =
EJERCICIOS DE LA SECCIóN 7.3 (Página 441)
1. a) A2 - 5A = O; A= O: unidimensional; A = 5: unidimensional
b) A3 - 27A - 54 = O; A= 6: unidimensional ; A= - 3: bidimensional
c) A3 - 3A2 = O; A = 3: unidimensional ; A = O: bidimensional
d) A3 - 12A2 + 3 6 A - 3 2 = O; A = 2: bidimensional,; A = 8: unidimensional
e) A4 - SA3 = O; A = O: tridimensional; A = 8: unidimensional
f) A4 - SA3 + 22A2 - 24A+ 9 = O; A = 1: bidimensional;
A = 3: bidimensional
[: i] -a y :]; ['H O
:] ; P"AP=
5. P = [ P"AP= - 3 s o 2 O -50](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-684-320.jpg)
![690 Respuestas a los ejercicios
I o -v5
1 o -
o 0
1 0
%
25
EJERCICIOS COMPLEMENTARIOS DEL CAPíTULO 7 (Página 442)
1. b) La transformación rota u11 hgulo 0 los vectores; por consiguiente, si O < 0 < x, entonces ningún vector
diferente de cero es transformado en un vector en la misma dirección o en dirección opuesta.
l i 0
2. L=kconmultiplicidad 3. 3 . c) [O 2 1 1 Y. A * = [ ' : A3 = [ 2 575 15500 ].
0 0 3
375 750 1875 3750
-3 -8
A4 = [ 125 SO], = [ 625 ,:,o] -15 10
IO -24 15
EJERCICIOS DE LA SECCIóN 8.1 (Página 458)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-685-320.jpg)
![Respuestas a los ejercicios / 691
15. T(x~,X ,, X-,) = (-41x1 + 9x2 + 24x3, 14x1 - 3x2 - 8x3); T(7, 13, 7) = (-2, 3)
16. T(2vl - 3v, + 4 ~ 3=) ( - 10, - 7, 6)
17. a) Dominio: R2; espacio imagen: R2; (T2 0 Tl)(x, y) = (2x - 3y, 2x + 3y)
b) Dominio: R2; espacio imagen: la recta y = gx; (T2 0 Tl)(x, y) = (4x - 12y, 3x - 9y)
c) Dominio: R2; espacio imagen: R2; (T2 0 í“,)(x, y) = (2x + 3y, x - 2y)
d) Dominio: R2; espacio imagen: the line x = O; (T, 0 Tl)(x, y) = (O, 2x)
18. a) Dominio: R2; espacio imagen: R2; (T-, 0 T2 0 T,)(x, y) = (3x - 2y, X)
b) Dominio: R2; espacio imagen: la recta y = $x; ( T3 0 T, 0 Tl)(x, y) = (4y, 6y)
19. a) U + d b) (T, 0 T,)(A) no existe porque T,(A) no es una matriz 2 X 2.
20. (Tl O T,)@(X)) = PW; (T2 O TI )@(x)) = P(X)
21. T,(v) = ;V 22. (T, 0 T,)(u, + U,X + a2x2) = (uo -t c1 + uz)x + (ul + 2u2)x2 + u2x3
26. b) (3T)(xI, X*) = (6x1 - 3x2, 3x2 + 3x1)
27. b) (TI + TZ)(X, y) = (3.~3 4x1; (T2 - T~)(x, Y) = (Y, 2x1
28. b) No lineal 29. a) 4 b) 3415 c) 1
EJERCICIOS DE LA SECCIóN 8.2 (Página 466)
l . a), c) 2. a) 3. a), b), c) 4. a) 5. b)
c) No existe base.
10. a) [ i], [ p] b) [ -91 c) Rango (T) = 2; nulidad ( r ) = 1
11. a) [i] ‘b) [:],[!I c) Rango(T)=l;nulidad(T)=2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-686-320.jpg)
![692 / Respuestas a los ejercicios
14. a) Rango: Plano xz, espacio nulo; ejey 15. ker(T) = {O}; R(7') = V
b) Rango: Plano yz; espacio nulo; eje x
c) Rango: Plano y = x, espacio nulo; la recta x = -t, x = t, z = O
16. a) Nulidad (7') = 2 b) Nulidad (T) = 4 17. Nulidad (I") = O; Rango (7') = 6
c) Nulidad (I? = 3 d) Nulidad ( r ) = 1
18. a) Dimensión = Nulidad ( r ) = 3
b) No. Para que Ax = b sea consistente para todo b en R5, se debe tener R(7') = R5. Pero R(r) f R5, ya que
rango (7') = dim R(73 = 4
25. ker(D) consta de todos los polinomios constantes. 26. ker(J) consta de todos los polinomios de la forma h.
27. ker(D o D) consta de todas las funciones de la forma ax + b.
EJERCICIOS DE LA SECCIóN 8.3 (Página 475)
I . a) ker(T)=(O}; 7esunoauno. b) ker(T)={X[-:]]; Tnoesunoauno
c) ker(T)= { O } ; Tesunoauno. d) ker(T)= { O } ; Tesunoauno
d) T" [I.] = [ -::: ::: y:: ] 4. a) No es uno a uno b) No es uno a uno c) Uno a uno
- 4x, - 5x, + 2x,
5. a) ker(T) = { k [ - :I} b) T no es uno a uno porque ker(T) # { O }
6. a) ker(T) = {O} b) T es uno a uno por el teorema 8.3.2.
7. a) Tesunoauno. b) Tnoesunoauno. c) Tnoesunoauno. d) Tnoesunoauno.
8. a) T es uno a uno. t) T es uno a uno. 9. No. A no es invertible.
10. a) Tno es uno a uno. b) T"(x,, x2, xj, . . . , x,,) = (x,,, x,- I , x , - 2 . . . . , xl)
c) T - y x , , x2,x3, . . . ,x,) = (X", XI, X,? , . , >x,- I )](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-687-320.jpg)

![694 / Respuestas a los ejercicios
b, T:~I=) 16 + 5 1+~ 19 x2, T(v,) = - 6 - 5x + SX', T(v,) = 7 + 4 0 +~ 1 5x2
c) T(a, + u,x + u2x2) =
d) T( 1 + x') = 22 + 56x + 14x2
2 3 9 -~ 1~ 6 1+~ 2~8 9 ~ ~ 2-0 1ill^~, ~+ 2 4 7 ~ 2 6 1 ~ 0 - 3 1 + ~1 0~7 ~
24 + 8
X +
12 X2
11 :] 1 1 1
S] 12. a) [T,oT,],,,,= 2 4 , [T2 IB. =[ oO o2 4 , [ Tl BI ' , B = [ i b, ~ T Z a T ~ ~ B ~ , B ~ ~ T ~ ~ EJERCICIOS DE LA SECCIóN 8.5 (Página 505)
1 4 0 4. -; - ~ ] , [ * l B , = [-; -; -%I s. [TI,= [ o 1 o ] ,[TI,,= [ o 1 1 ] 0 0 0 O 0 0](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-689-320.jpg)

![696 /' Respuestas a los ejercicios
1 0 0 0
11. Rango = 3, nulidad = 1 13.
14. a) v, = 2u, + u,, v, = -u1 + u, + u3, v, = 3u, + 4u, + 2u,
15. [ T I E = [ A y -y] 17. [Z']B=[! 1 A]
19. b) x c) e'
b) uI = -2v, - 2v, + v3, u, = 5v, + 4v, - 2v3, u3 = -7v, - 5v, + 3v3
-4 o - 1
o -1
20. a) [ l!] d) - 3 2 + 3
o 1 o o ."
o o 1 o ."
o o o 1 ."
. . . . . . .
.
o o o o ' . '
o o o o " '
e)
~ --12
0-
O
O
o o o " ' o
1 o o " ' o
o 4 o " ' O
25. O O $ ' . . O
.. .. ..
. . .
1
O- -o o o . . ' 1
- n + l
EJERCICIOS DE LA SECCIóN 9.1 (Página 520)
1. a) y, = cle5"- 2c,e-" b) y , = O 2. a) y, = cle7"- 3c,e-" b) y I -- -4L~ e 7 x + s e - x
y, =c ,$x+ c,e-" y, = O y, = 2c,e7"+ 2c,e-" y, = - m27 e - X
3. a) y, = --,eZ' + c3e3x b) y, = eZ' - 2c3" 4. y, = (c, + c2)e2" + cje&
y2 = clex + 2c,e2" - c3e3" y, = ex - 2e2" + 2e3" y, = - c2eh + c3eSx
y, = 2c,eZ" - c3e3" y3 = - 2e2" + 2e3+ y, = - cleZ' + c3e"
5. y = cle3* + c2e-Z' 6. y = c,eX + c2e2' + c3e3"
EJERCICIOS DE LA SECCIóN 9.2 (Página 531)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-691-320.jpg)
![Respuestas a los ejercicios / 697
6. a) Rectángulo con vértices en (O, O), (1, O), (1, -2), (O, -2).
b) Rectángulo con vértices en (O, O), (- 1, O), (- 1,2), (O, 2).
c) Rectángulo con vértices en (O, O), (1, O), (1, ), (O, ).
d) Cuadrado con vértices en (O, O), (2, O), (2,2), (O, 2).
e) Paralelogramo con vértices en (O, O), (1, O), (7,2), (6,2).
r) Paralelogramo con vértices en (O, O), (1, -2), (1, O), (O, 2)
7. Rectángulo con vértices en (O, O), (-3, O), (O, 1). (-3, 1)
1 1
11. a) Expansión por un factor 3 en la dirección x. b) Expansión por un factor - 5 en la dirección y.
c) Deslizamiento cortante por un factor 4 en la dirección x.
12* a) [O '][O '1 factor de2
o o ; expansión en la dirección y por un factor de 3, luego expansión en la dirección x por un
; oblongamiento en la dirección x por un factor de 4, luego oblongamiento en la dirección
; expansión en la dirección y por un factor de -2, luego expansión en la
dirección x por un factor de 4, luego reflexión con respecto ay = x
d) [1 y][ :][A - :] ; oblongamiento en la dirección x por un factor de - 3, luego expansión en la
dirección y por un factor de 18, luego oblongamiento en la dirección y por un
factor de 4
16. 1 6 y - 1 1 x - 3 = 0 17. a)y=fx b) y=x c ) y = i x d) y= -2x
18. [: -:] 19. b) No. A no es invertible. 22. a)
1 0 0
-I . .. . . ~ . .. .](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-692-320.jpg)
![698 1 Respuestas a los ejercicios
1 k O
d) a= 1: [A] e) a= 1 : [ ~ ] f) ( O entero impar múltiplo de T) A= -- 1:
( O entero par múltiplo de x) A. = 1:
(O no múltiplo entero de T) no hay eigenvalores
EJERCICIOS DE LA SECCIóN 9.3 (Página 542)
1. y=++$x 2. ~ = $ + Q x 3. y = 2 + 5 x - 3 x 2 4. y= -5+3x-4x2+2x3
8. y = 4 - .2x +- .2x2; si x = 12, entonces y = 30.4 ($30.4 miles
EJERCICIOS DE LA SECCIóN 9.4 (Página 550)
1. a) ( 1 + ~ ) - 2 s e n x - s e n 2 x b) (1+m)-2 +- 3
4T
3
2. a) 4 ~ +’ 4 cos x + cos 2x + cos 3x - 4 x s enx - 23r sen 2x - - sen 3x
x-- coskx
1 1 1 3 - e
b) $7r2+4 3. a) --+-eX b)
k = l k2 2 e - 1 12 2 e - 2
(3 - e)(7e - 19) 3 6 “ 2
4. a) (4e- 10)+(18 -6e)x b) 5. a) -x b) 1 - - 8. -sen(kx)
2 T T 2 k= I k
EJERCICIOS DE LA SECCIóN 9.5 (Página 558)
3. a) A = [ - : -B b) [-: c ) A = [ $1 O1
9 3 -4 1 -5 5 9 o +
z s
:]
O
4. a) 2x2 + 5y2 - 6xy b) 7x: + 5x,x, c) x2- 3y2 + 5z‘](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-693-320.jpg)


![Respuestas a los ejercicios 1 701
6. a) Elipse b) Elipse c) Bpérbola d) fipérbola e) Circunferencia
f) Parábola g) Parábola h) Parábola i) Parábola j ) Circunferencia
7. a) 9x” + 4 ~= ‘36,~ eli pse b) x” - 16y” = 16, hipérbola
c) yf2 = 8x’, parábola d) x” +y” = 16, circunferencia
e) 18y” - 12x” = 419, hipérbola f) y’ = -+x’2, parábola
8. a) fipérbola, ecuaciones posibles son b) Parábola; ecuaciones posibles son
3x’2 - 2y’2 + 8 = o, - 2x’2 + 3y’2 + 8 = o 2 V w 2 + 9x’ - 7y’ = o, 2V5y12 + 7x’ + 9y’ = o
2v5yQ - 7x’ - 9y’ = o, 2v5Xf2 - 9x’ + 7y’ = o
c) Elipse; ecuaciones posibles son d) Hipérbola; ecuaciones posibles son
7x’2 + 3y‘2 = 9, 3x‘2 + 7y’2 = 9 4-p - y’2 A’=, , 3, - = 3
9. 2xn2+ y”’ = 6, elipse IO. 13~”’- 4 ~= “81,~ hip érbola 11. 2x”’ - 3y”’ = 24, hipérbola
12. 6x”’ + 1 ly”’ = 66, elipse 13. 4y“’ - x”’ = O, hipérbola 14. m x ” - 3y’ = O, parábola
15. a) Dos rectas que se cortan, y = x y y = --x. b) No existe gráfica.
c) La gráfica es el simple punto (O, O). d) La gráfica es la recta y = x.
e ) La gráfica consta de dos rectas paralelas -3 x + -2 y = 2 2. f-) La gráfica es el punto (1,2) ,m m
EJERCICIOS DE LA SECCIóN 9.7 (Página 578)
1. a) x2 + 2y2 - z2 + 4xy - 5yz b) 3x2 + 7z2 + 2xy - 3x2 + 4yz
c) x y + x z + y z d ) X 2 y 2 - z 2
e) 3z2+ 3x2 f-) 2z2 + 2xz + y2
[: -!] [ O ’ L
[i 2. a) o -4 - b) -2 c) P i 0 o -1
d) [i y :]
[: 2
3. a) [x y z] 2 -;]r]+[7 O 21 [:]--3=o
o -4 -1 2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-696-320.jpg)
![4. a) Elipsoide. 5. a) 9x" + 3 6 ~+' 4~zt 2= e 3li 6p,s oide.
b) Hiperboloide de un manto. b) 6 ~+ '3y~t2- 2zI2 = 18, luperboloide de un manto.
c) Kperboloide de dos mantos. 3x12 - 3y0 - z72 = 3, luperboloide de dos mantos.
d) Cono elíptico. d) 4x'* + 9y'2 - z'* = O, cono elíptico.
e) Paraboloide elíptico. e) x" + 16y" - 162' = O, paraboloide elíptico.
f) Paraboloide hiperbólico f, 7xt2 - 3yI2 + z' = O, paraboloide hiperbólico.
g) Esfera. g) x'2 + y'2 + 2'2 = 25, esfera.
6. a) 252' - 3yf2- 5 0 ~-' ~15 0 = O, hiperboloide de dos mantos
bj 2 2 + 2y'' + 82'' - 5 = O, elipsoide.
C) 9 ~+ 4' y''~ - 362' = O, paraboloide elíptico.
d) ,Y'? - y'2 + z' = O, paraboloide hlperbólico.
EJERCICIOS DE LA SECCIóN 9.8 (Página 587)
1. Multiplicaciones: mpn; adiciones: mp(n - 1). 2. Multiplicaciones: (k - l)n3; adiciones: (k - l)(n3 - n2).
3.
Resolver Ax = b por eliminación de Gauss-
Jordan
Resolver Ax = b por eliminación de Gauss
Encontrar A" reduciendo [A I I] a [IIA"]
Resolver Ax = b como x =A" b
Encontrar det(A) por reducción de renglones
Resolver Ax = b aplicando la regla de Cramer
n = 5 I n=lO
+: X: 6550 I
+: X : 433705
t : 810
+: 100 +: 900
X: 150 X: 1100 I
t: 285
n= 100
+: 383,250
X: 343,300
+~: 383,250
X: 343,300
+: 980,100
x : 1,000,000
+: 990,000
x: 1,010,000
+: 328,350
x: 333,399
+: 33,163,350
X: 33,673,399
n = 1000
+: 333,832,500
X: 334,333,000
+ : 333,832,500
X: 334,333,000
+: 998,001,000
x : 1,000,000,000
i : 999,000,000
x : 1,001,000,000
+: 332,833,500
x : 333,333,999
f: 33,316,633 X IO4
X: 33,366,733 X IO4](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-697-320.jpg)
![Respuestas a los ejercicios / 703
4.
Tiempo de
ejecución
Jordan I
Resolver Ax = b por eliminación de Gauss
Encontrar A-’ reduciendo [A 1 I] a [IIA”] 2.84 X 1 0 - ~
I Resolver Ax = b por eliminación de Gauss- x 10-4
1.55 X
3.50 X
Resolver Ax = b como x = A” b
Encontrar det(A) por reducciónd e renglones 1.03 X 1 0 - ~
Resolver Ax = b aplicando la regla de Cramer 6.18 x 1 O-4
EJERCICIOS DE LA SECCIÓN 9.9 (Pagina 597)
n=10 I n=100 I n=1000
I
1.05 X 1 0 - ~ ,878 836
2.41 X 2.49 2499
90.3 x I 83.9 I 834 X IO3
1. x] = 2, x2 = 1 2. XI = -2, x2 = 1, x3 = - 3
3. XI = 3, x2 = - 1 4. XI = 4, x2 = - 1
9. X] = - 3, x2 = 1, x3 = 2, x4 = 1 10. x, = 2, x2 = - 1, x3 = o, x4 = 0
1 0 Ji3 0 3 0 0 1 - 3
!J
[o o J 0 18. A=PLU= o o 1 o 2 o o](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-698-320.jpg)

![Respuestas a los ejercicios / ,705
1 ' . 1
19. a) 3 + 8 i 1 +36 +i 1 72-ii3] + b, [33--25ii 1 3+3 i 6+c5) i ] [ 9 - 5l 1' :
3+3i 2+5i1 f 9 + i 12+2i
;18-2i 13+ i
O 1 b) [ 6 + 2i -11 + 1"-j c) [ -1+6i -9- 5i
13+13i -8+12i -33-22i
7 + 9i -6+ 61 22 - li 2 + 1Oi
SiI -16- 16i
1 v 5
- 5 - 4 i 6 - 22. a) z = - 1 k i b) z=- k - - - i 23. b) i 2 2
9- i - 1 - i_
EJERCICIOS DE LA SECCIóN 10.2 (Página 614)
1. a) 2-7i b) -3 +5i c) -5i 2. a) 1 b) 7 c) 5
d) i e) -9 f ) o d ) f i e ) 8 0 0
4. a) --%-gi b) g+gi c) g-#i d) -u25 +2u5 [' e) 6 - j
a
O s
5. a) -i b) &+Ai c) 7i 6. a) f + f i b) - f + + i c) g+yi d) f + + i 7. i+ij
8. 9 . -1-24' 1 - v 3 1 + v 3 . 625 6 2 5 1 10. - #+&i 11. -+- 4 4 1 12. -&-Ai
13. - & + h i 14. -8 15. a) - 1 -2i b) 25 25l
17. a) $2 , b) 'r) , C) .Y , d) ,
y = -2
X 1;i X X
X](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-700-320.jpg)
![706 / Respuestas a los ejercicios
34. x , = -(I - i)t,x,= - i t , x , = t 35. a) [ -: f] b) [-y ii]
1 + i - i
-7+6i 5 - i 1+4i
I 1 +2i - i 1
EJERCICIOS DE LA SECCIóN 10.3 (Página 627)
I. a) O b) ~ / 2 c) - 7r/2 d) ~ / 4 e) 2 ~ / 3 f) - rr/4 2. a) 5n/3 b) - ~ / 3 c) 5 ~ / 3
3. a) 2[cos (;) + isen(:)] b) COS P+ i m;]
c) 5./I[cos(;) +hen(:)] d) 12[cos(T) +isen($)]
e) 3G[cos(-?) +isen(-?)] f) .[cos(-:) +isen(-:)]
4. a) 6[cos(S) +isen(%)] b) :[cos(;) +isen(;)]
c) ‘2[ cos( -6) +isen( -E)] d) :[cos(%) +isen($)]
1 + v %
5. 1 6. a) -64 b) - i c) - 6 4 f i - 6 4 i d) -- 2048
7. a)
-
_‘2_ + Ll Ty v2](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-701-320.jpg)

![708 i Respuestas a los ejercicios
21. b), c) 22. f - 3g - 3h = O 23. a) Tres vectores en un espacio bidkensional 24. a), b)
b) Dos vectores en un espacio tridimensional
25. a), b), c), d) 26. (- 1 - i, 1); dimensión = 1 27. (1, 1 - i); dimensión = 1
28. (3 t 6i, - 3i, 1); dimensión = 1 29. (jz, -+, 1, O), (-$, 2i, O, 1); dimensión = 2
EJERCICIOS DE LA SECCIóN 10.5 (Página 642)
2. a) - 12 b) O c) 2i d) 37 4. a) -4 + 5i b) O c) 4 - 4i d) 42
S. a) No se cumple el axloma 4. b) No se cumple el.axioma 4. c) No se cumplen los axiomas 2 y 3
d) No se cumplen los axiomas 1 y 4. e) Este es un producto interior.
6. - 9 - 5i 7. No se cumplen los axiomas 1 y 4
9. a) fl b) VÍ6 c) VÍ6 d) O 10. a) VÍ6 b) 2 c) %6 d) O
11. a) ~ b) 2 V 5 c) 5 d) O 12. a) 3 V Í 6 b) 13. a) m b) 2%6
14. a) 2 b) 2 v 3 15. a) 2 G b) 2 v 3 16. a) 7 v 3 b) 2 f l 17. a) -8i b) Paraninguno
18. a), b), c) 20. b) 2 1. b), C)
“ 1. a) [ -2i b) [ T’:i 5 +371 i c) I-:]d ) [TI2 %]
EJERCICIOS DE LA SECCIóN 10.6 (Página 655)
4 -i (111 a21
l f i 3 - i O
- 1 - i i 1 ‘13 ‘23
2. b), d), e) 3. k = 3 + 5 i , Z = i , m = 2 - 4 i 4. a), b)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-703-320.jpg)
![Respuestas a los ejercicios / 709
5. b) A"=
L
-3 - i
2m
-4 - 3i
2v-E
5i
"
2m
7. P =
8. P = ; P"AP= [o4 02]
" v5v5
r 1
i
O
O
71; O
-1
v3
P"AP =
-1
O
-0
O
5
O -2 :I](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-704-320.jpg)
![710 Respuestas a los ejercicios
14. [ -: d] es una posibilidad.
13. a = 2 +- i n ; no, porque A contiene elementos complejos.
3. 1, r] es una posibilidad. 5. A = 1, w, o? (= O) 10. b) Dimensión = 2 o l 1
EJERCICIOS COMPLEMENTARIOS DEL CAPíTULO1 0 (Página 657)](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-705-320.jpg)
![ÍNDICE
Adición de vectores, 150,205, 257-258
627
Adjunta, 135-136
+ngulo de rotación, 228
egulo entre vectores, 114,536
Angulos directores, 174
Anticonmutativa, 609
Aplicaciones, 5 13-579
a formas cuadráticas, 55 1-578
a ecuaciones diferenciales, 5 13-5 19
a problemas de aproximación,
543-549
a series de Fourier, 546-549
Aproximación por mínimos cuadrados,
384-393, 535-543, 545-546
+bol de permutaciones, 108-109
Area de un paralelogramo, 180
Argz, 618
Argumento, 6 18
principal, 6 18
Argumento principal, 6 1 8
Argumento principal, 61 8
Axioma de aditividad, 552,339
Axioma de homogeniedad, 339
Axioma de simetría, 239,638
Axiomas:
para espacios con producto interior,
339,63 1
para un espacio vectorial, 259-260
Base, 290,291
cambio de, 398-400
coordenadas relativas a una, 290,
normal, 246,291,292,294
parahfin, 295
para o", 628
para Pn, 294
parap, 292
parap, 292
399
Base e s t á n d a r :
Base normal de Pn, 294
Base ortogonal, 368
Base ortonormal, 367-377
C(- , + ),268,630
C[a, b], 268,630
Cambio de base, 399-401
Cauchy, Augustin Louis, 208
cero:
matriz, 64
subespacio, 266
transformación, 448
vector, 150,205
Cerrado bajo la adición, 266
Cerrado bajo la multiplicación escalar,
266
Circunferencia unitaria, 343
d: C . 132
628
base normal de, 628
Cociente de números complejo6s, 1 1-
614
Codominio, 2 18
Coeficientes, 50
Coeficientes de Fourier, 548
Columna:
de una matriz, 47
espacio, 307
vector, 306
Combinación lineal, 50,270,627
Complemento ortogonal, 359,360
Componente:
a lo largo de un vector, 169-173
ortogonal a una subespacio, 372-373
ortogonal a un vector, 169-170
deunvector, 152,155,185
Compresión, 523-524
Condición inicial, 5 14
Cónica imaginaria, 573
Cónica no degenerada, 564
Conjugada transpuesta, 547
Conjugado, 77
propiedades del, 614-615,626
Conjunto ortogonal, 367
conjunto ortonormal (de vectores), 367,
Cono elíptico, 575
Contracción (operador), 230, 448
Coordenada (S):
de un punto, 154
de un vector, 399
ejes de, 154-155
independiente de las, 685
matriz de, 399
planos de, 154
Cosenos directores, 174
71 1](https://image.slidesharecdn.com/algebralineal5-140828141652-phpapp02/85/Inroduccion-Algebra-lineal-Howard-Anton-5ta-Edicion-706-320.jpg)




