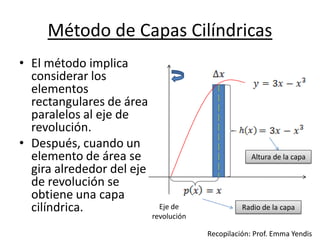
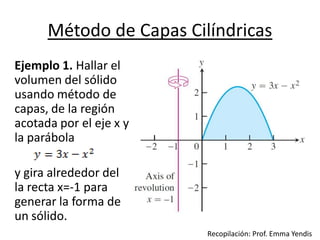
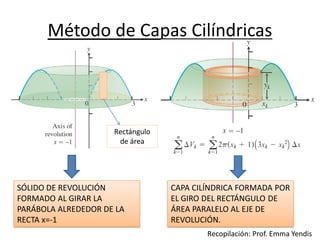
El documento describe el método de capas cilíndricas para calcular el volumen de un sólido de revolución. Explica que cuando un elemento de área rectangular se gira alrededor de un eje, forma una capa cilíndrica cuyo volumen puede calcularse usando una integral definida. Proporciona fórmulas para el cálculo del volumen dependiendo de si el eje de giro es horizontal o vertical y presenta un ejemplo numérico.

1. Cálculo de Volumen
MÉTODO DE CAPAS CILÍNDRICAS O
CASCARONES
Aplicación de Integral Definida
Prof. Emma Yendis
Clase del Lunes 25-04

2. Método de Capas Cilíndricas
Para llevar a cabo el cálculo del volumen de un
sólido de revolución, no siempre es factible el
método de discos o arandelas.
Por Ejemplo: Suponga que desea calcular el
volumen exacto del sólido de revolución
obtenido al girar la región limitada por la gráfica
, el eje y y la recta y=2, alrededor del
eje y
Recopilación: Prof. Emma Yendis

3. Método de Capas Cilíndricas
Si un elemento de área es
perpendicular al eje y
como se muestra en la
Figura 1, el elemento del
volumen es un disco, por
lo que determinar el
volumen del sólido
implica una integral de la
forma
Recopilación: Prof. Emma Yendis

4. Método de Capas Cilíndricas
• Pero para obtener A(y) se necesita resolver la
ecuación cúbica para x en
términos de y, lo cual sería una tarea muy
laboriosa.
• Por lo que se estudiará un procedimiento
alternativo para calcular el volumen de un
sólido de revolución.
Recopilación: Prof. Emma Yendis

5. Método de Capas Cilíndricas
• El método implica
considerar los
elementos
rectangulares de área
paralelos al eje de
revolución.
• Después, cuando un
elemento de área se
gira alrededor del eje
de revolución se
obtiene una capa
cilíndrica. Eje de
revolución
Radio de la capa
Altura de la capa
Recopilación: Prof. Emma Yendis

6. Método de Capas Cilíndricas
Por lo tanto, para hallar el volumen V de un sólido
de revolución por el método de capas cilíndricas ,
debe usarse una de las siguientes fórmulas:
Eje de giro horizontal Eje de giro vertical
Recopilación: Prof. Emma Yendis

7. Método de Capas Cilíndricas
Ejemplo 1. Hallar el
volumen del sólido
usando método de
capas, de la región
acotada por el eje x y
la parábola
y gira alrededor del
la recta x=-1 para
generar la forma de
un sólido.
Recopilación: Prof. Emma Yendis

8. Método de Capas Cilíndricas
SÓLIDO DE REVOLUCIÓN
FORMADO AL GIRAR LA
PARÁBOLA ALREDEDOR DE LA
RECTA x=-1
CAPA CILÍNDRICA FORMADA POR
EL GIRO DEL RECTÁNGULO DE
ÁREA PARALELO AL EJE DE
REVOLUCIÓN.
Rectángulo
de área
Recopilación: Prof. Emma Yendis

9. Método de Capas Cilíndricas
Recopilación: Prof. Emma Yendis

10. Referencias Bibliográficas
• Leithold, L. El Cálculo. 7ma. Edición
– Capítulo 4, pág 391-395
• Larson, R. y otros. Cálculo y Geometría Analítica.
Volumen 1, 6ta. Edición.
– Capítulo 6, pág 483-488
• Thomas, G. Calculus. Part One, Single Variable.
11th Edition.
– Capítulo 6, pág 409-414