Investigación sobre el algoritmo de prim

“AÑO DEL BICENTENARIO, DE LA CONSOLIDACIÓN DE NUESTRA
INDEPENDENCIA, Y DE LA CONMEMORACIÓN DE LAS HEROICAS
BATALLAS DE JUNÍN Y AYACUCHO”
TEMA:
ALGORITMO DE PRIM
CURSO:
ALGORITMOS Y PROGRAMACIÓN II
DOCENTE:
GODOFREDO POCCORI UMERES
ALUMNAS:
➔ HUAMAN BECERRA MARIA DEL PILAR
➔ HUANACUNI CHINO HEIDY YESENIA
➔ CHACNAMA LEON ROY CIPRIAM
CUSCO – PERÚ
2024

1
TABLA DE CONTENIDO
INTRODUCCIÓN..............................................................................................................................................
1. FUNDAMENTO TEÓRICO..........................................................................................................................
1.1 Origen y contexto histórico:......................................................................................................................
1.2 Explicación detallada del algoritmo de Prim:...........................................................................................
1.3 Conceptos Básicos:...................................................................................................................................
1.4 Funcionamiento del Algoritmo:................................................................................................................
Requisitos para su funcionamiento:
➔ ......................................................................................................
¿Cómo funciona?
➔ ..................................................................................................................................
1.5 Complejidad del Algoritmo......................................................................................................................
1.6 Comparación con otros Algoritmos..........................................................................................................
2. EJEMPLO DESARROLLADO.....................................................................................................................
3. ALGORITMO.................................................................................................................................................
4. CODIFICACIÓN Y EJECUCIÓN DEL PROGRAMA.............................................................................
4.1 CÓDIGO (PYTHON)...............................................................................................................................
4.2 EJECUCIÓN.............................................................................................................................................
Estructuras de Datos Utilizadas en el Algoritmo de Prim............................................................................
1. Columna de Prioridad (Min-Heap o Fibonacci Heap):..............................................................................
Aplicaciones Prácticas del Algoritmo de Prim..............................................................................................
1. Redes de Computadoras:.........................................................................................................................
2. Infraestructura de Transporte:..................................................................................................................
3. Diseño de Circuitos:.................................................................................................................................
Ventajas del Algoritmo de Prim......................................................................................................................
Desventajas del Algoritmo de Prim................................................................................................................
CONCLUSIONES..............................................................................................................................................
BIBLIOGRAFÍA.................................................................................................................................................

2
INTRODUCCIÓN
En el ámbito de la informática, la búsqueda de soluciones óptimas es un objetivo constante.
El algoritmo de Prim emerge como una herramienta fundamental para abordar este desafío,
especialmente en el contexto de la construcción de árboles de expansión mínima. Este
algoritmo, simple en su esencia pero poderoso en su aplicación, nos permite conectar un
conjunto de nodos de la forma más eficiente, minimizando el costo total de las conexiones.
Esta monografía explora el algoritmo de Prim, profundizando en su funcionamiento y su
aplicación en diferentes campos. Comenzaremos por analizar su desarrollo histórico,
examinando las ideas y conceptos que lo precedieron y que dieron origen a su formulación.
Posteriormente, profundizaremos en el fundamento teórico que lo sustenta, explorando las
propiedades matemáticas que garantizan su eficiencia y precisión.
Para ilustrar su aplicación práctica, presentaremos un ejemplo desarrollado paso a paso,
mostrando cómo se utiliza para encontrar el árbol de expansión mínima de un grafo dado. A
continuación, analizaremos el algoritmo en detalle, describiendo cada uno de sus pasos y la
lógica que los rige. Para finalizar, nos adentraremos en la implementación del algoritmo en
Python, mostrando el código fuente y su ejecución, lo que permitirá apreciar la eficiencia y la
facilidad de su implementación.
A través de esta monografía busca brindar una comprensión profunda del algoritmo de Prim,
revelando su poder como herramienta para resolver problemas de optimización.
1. FUNDAMENTO TEÓRICO

3
1.1 Origen y contexto histórico:
Su origen se remonta a 1930, cuando el matemático checo Vojtěch Jarník lo
desarrolló por primera vez. Sin embargo, no fue hasta 1957 que el científico
computacional Robert C. Prim lo redescubrió de manera independiente, lo que llevó a
que el algoritmo ganara mayor reconocimiento en la comunidad científica. Más tarde,
en 1959, el renombrado científico Edsger W. Dijkstra también redescubrió el
algoritmo, contribuyendo aún más a su popularidad y uso. Debido a estos múltiples
redescubrimientos, el algoritmo es conocido por varios nombres, incluyendo
Algoritmo de Prim-Jarník, Algoritmo Prim-Dijkstra, y Algoritmo DJP (Dijkstra-
Jarník-Prim).
1.2 Explicación detallada del algoritmo de Prim:
El Algoritmo de Prim es una herramienta esencial en la resolución del problema del
Árbol de Coste Total Mínimo (Minimum Spanning Tree - MST) en grafos conexos y
no dirigidos. Este problema es un clásico en la optimización combinatoria y se centra
en encontrar un subgrafo que conecte todos los vértices del grafo original con el
menor costo total posible.
En otras palabras, el objetivo es construir un árbol recubridor mínimo, que es un
subgrafo que incluye todos los vértices del grafo original y cuya suma de los pesos de
las aristas es la más baja posible. Este algoritmo es fundamental en la teoría de grafos
y tiene numerosas aplicaciones prácticas en áreas como el diseño de redes, la
optimización de rutas y la planificación de circuitos.
1.3 Conceptos Básicos:
● Grafo: Una estructura compuesta por nodos (o vértices) y aristas (o bordes)
que conectan estos nodos.
● Árbol Recubridor: Un subgrafo que incluye todos los vértices del grafo
original y es un árbol (es decir, no tiene ciclos).
● Árbol Recubridor Mínimo (MST): Un árbol recubridor donde la suma de los
pesos de sus aristas es mínima.
1.4 Funcionamiento del Algoritmo:

4
➔ Requisitos para su funcionamiento:
● Ser un grafo conexo: Debe haber un camino entre cualquier par de
nodos.
● Ser un grafo sin ciclos. No debe haber caminos cerrados.
● Tener todos los arcos etiquetados: Todas las aristas del grafo deben
tener un peso asociado.
➔ ¿Cómo funciona?
El Algoritmo de Prim funciona incrementando continuamente el tamaño de un
árbol, comenzando por un vértice inicial y agregando sucesivamente vértices
cuya distancia a los vértices ya incluidos en el árbol es mínima. En cada paso,
se consideran las aristas que inciden en los vértices que ya pertenecen al árbol.
El proceso continúa hasta que todos los vértices del grafo original estén
incluidos en el árbol recubridor mínimo.
El árbol recubridor mínimo está completamente construido cuando no quedan
más vértices por agregar
1.5 Complejidad del Algoritmo
La complejidad temporal del Algoritmo de Prim depende de la implementación.
Usando una cola de prioridad (heap binario), la complejidad es (O(E log V)), donde
(E) es el número de aristas y (V) es el número de vértices. Con un heap de Fibonacci,
la complejidad puede mejorarse a (O(E + V log V)).
1.6 Comparación con otros Algoritmos
El Algoritmo de Prim es uno de los varios algoritmos para encontrar el MST. Otros
algoritmos incluyen el Algoritmo de Kruskal y el Algoritmo de Borůvka.
● Eficiencia en Grafos Densos: El Algoritmo de Prim es generalmente más
eficiente en grafos densos debido a su enfoque de expansión desde un solo
vértice.
● Eficiencia en Grafos Dispersos: El Algoritmo de Kruskal tiende a ser más
eficiente en grafos dispersos, ya que se enfoca en agregar aristas de menor
peso sin preocuparse por la conectividad inicial.

5
● Paralelización: El Algoritmo de Borůvka es adecuado para la paralelización,
ya que puede agregar múltiples aristas en cada fase, lo que lo hace eficiente en
entornos de computación paralela.
● Implementación y complejidad: La elección del algoritmo puede depender de
la estructura del grafo y de los recursos computacionales disponibles. Por
ejemplo, el uso de un heap de Fibonacci puede mejorar la complejidad del
Algoritmo de Prim, pero a costa de una implementación más compleja.
2. EJEMPLO DESARROLLADO
Imagen Descripción No
visto
En el
grafo
En el
árbol
Este es el grafo ponderado de
partida. No es un árbol, ya que
para serlo se requiere que no
haya ciclos, y en este caso sí
hay. Los números cerca de las
aristas indican el peso. Ninguna
de las aristas está marcada, y el
vértice D ha sido elegido
arbitrariamente como el punto
de partida.
C, G A, B, E,
F
D
El segundo vértice es el más
cercano a D: A está a 5 de
distancia, B a 9, E a 15 y F a 6.
De estos, 5 es el valor más
pequeño, así que marcamos la
arista DA.
C, G B, E, F A, D

6
El próximo vértice a elegir es el
más cercano a D o A. B está a 9
de distancia de D y a 7
de A, E está a 15, y F está a 6. 6
es el valor más pequeño, así que
marcamos el vértice F y a la
arista DF.
C B, E, G A, D, F
El algoritmo continúa. El
vértice B, que está a una
distancia de 7 de A, es el
siguiente marcado. En este
punto la arista DB es marcada
en rojo porque sus dos extremos
ya están en el árbol y por lo
tanto no podrá ser utilizado.
null C, E, G A, D,
F, B
Aquí hay que elegir
entre C, E y G. C está a 8 de
distancia de B, E está a 7 de
distancia de B, y G está a 11 de
distancia de F. E está más cerca,
entonces marcamos el
vértice E y la arista EB. Otras
dos aristas fueron marcadas en
rojo porque ambos vértices que
unen fueron agregados al árbol.
null C, G A, D,
F, B, E
Solo quedan
disponibles C y G. C está a 5 de
distancia de E, y G a 9 de
distancia de E. Se elige C, y se
marca con el arco EC. El
arco BC también se marca con
rojo.
null G A, D,
F, B, E,
C

7
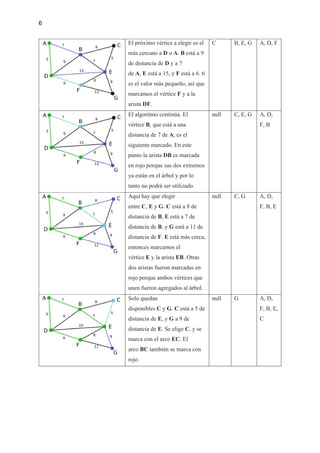
G es el único vértice pendiente,
y está más cerca de E que de F,
así que se agrega EG al árbol.
Todos los vértices están ya
marcados, el árbol de expansión
mínimo se muestra en verde. En
este caso con un peso de 39.
null null A, D,
F, B, E,
C, G
3. ALGORITMO
Prim ( L [1..n , 1..n ]) : #conjunto de arcos
#Inicialización: sólo el nodo 1 se encuentra en B
T =NULL #T contendrá los arcos del árbol de extensión mínima Distmin[1]=-1
para i=2 hasta n hacer
más_próximo [ i ]=1
distmin [ i ]=L [ i , 1]
para i=1 hasta n -1 hacer
min=infinito
para j=2 hasta n hacer
si 0 <= distmin [ j ] < min entonces
min=distmin [ j ]
k=j
T=T union {{mas_próximo [ k ], k }}
distmin [ k ]= -1 'se añade k a B
para j=2 hasta n hacer
si L [ j , k ] < distmin [ j ] entonces
distmin [ j ]=L [ j , k ]
más_próximo [ j ]=k
devolver T

8
4. CODIFICACIÓN Y EJECUCIÓN DEL PROGRAMA
4.1 CÓDIGO (PYTHON)
from heapq import heappop, heappush # Estas funciones permiten
trabajar con una cola de prioridad (min-heap)
from collections import defaultdict # Esta clase permite crear un
diccionario con valores por defecto
class Graph:
def __init__(self):
self.graph = defaultdict(list) # Inicializa un diccionario
vacío para almacenar el grafo
def add_edge(self, u, v, weight):
self.graph[u].append((v, weight)) # Agrega una arista entre
los nodos u y v con peso 'weight'
self.graph[v].append((u, weight)) # Si el grafo es no
dirigido, también se agrega la arista en sentido inverso
def prim(grafo, inicio):
# Algoritmo de Prim para hallar el árbol de expansión mínimo
bosque = [] # Lista para almacenar los nodos del árbol de
expansión mínimo
distancia = 0 # Distancia total del recorrido
visited = set() # Conjunto de nodos visitados
min_heap = [(0, inicio)] # Cola de prioridad (min-heap) con (peso,
nodo)
while min_heap:
peso, u = heappop(min_heap) # Extrae el nodo con menor peso de
la cola de prioridad
if u in visited: # Si el nodo ya ha sido visitado, se ignora
continue

9
visited.add(u) # Marca el nodo como visitado
distancia += peso # Acumula la distancia total
bosque.append(u) # Agrega el nodo al árbol de expansión mínimo
for v, weight in grafo.graph[u]: # Recorre los nodos
adyacentes al nodo actual
if v not in visited: # Si el nodo adyacente no ha sido
visitado
heappush(min_heap, (weight, v)) # Lo agrega a la cola
de prioridad
return bosque, distancia
if __name__ == "__main__":
# Crear el grafo
grafo = Graph()
edges = [
("A", "B", 7),
("A", "D", 5),
("B", "C", 8),
("B", "D", 9),
("B", "E", 7),
("C", "E", 5),
("D", "E", 15),
("D", "F", 6),
("E", "F", 8),
("E", "G", 9),
("F", "G", 11)
]
for u, v, weight in edges:
grafo.add_edge(u, v, weight)
print("n=== Algoritmo Prim ===")
bosque, distancia = prim(grafo, "D")
print("nNodos en el árbol de expansión mínima:", bosque)

10
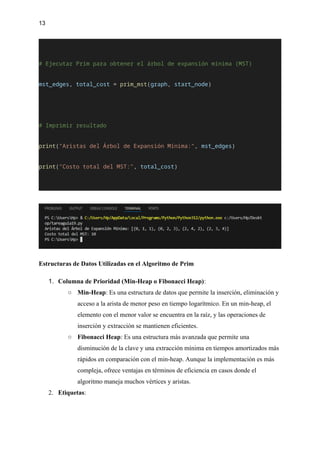
print("Distancia total del recorrido:", distancia)
print("n")
4.2 EJECUCIÓN
ALGORITMO DE PRIM PARA EL ARBOL DE EXPANSION MINIMA
import heapq
def prim_mst(graph, start):
# Inicializar estructuras
visited = set() # Conjunto de nodos visitados
mst_edges = [] # Lista para almacenar las aristas del árbol de
expansión mínima
min_heap = [(0, start, None)] # Cola de prioridad para aristas
(peso, nodo, nodo anterior)
total_cost = 0 # Costo total del MST

11
while min_heap:
# Extraer la arista de menor peso
weight, current_node, previous_node = heapq.heappop(min_heap)
# Si el nodo ya ha sido visitado, lo ignoramos
if current_node in visited:
continue
# Añadir el nodo al conjunto de visitados
visited.add(current_node)
# Si no es el nodo inicial, agregar la arista al MST
if previous_node is not None:
mst_edges.append((previous_node, current_node, weight))
total_cost += weight
# Agregar las aristas adyacentes del nodo actual a la cola de
prioridad

12
for neighbor, edge_weight in graph[current_node]:
if neighbor not in visited:
heapq.heappush(min_heap, (edge_weight, neighbor,
current_node))
return mst_edges, total_cost
# Ejemplo de grafo (listas de adyacencia)
graph = {
0: [(1, 1), (2, 3)], # Nodo 0 conectado a 1 con peso 1, y a 2 con
peso 3
1: [(0, 1), (2, 3), (3, 6)], # Nodo 1
2: [(0, 3), (1, 3), (3, 4), (4, 2)], # Nodo 2
3: [(1, 6), (2, 4), (4, 5)], # Nodo 3
4: [(2, 2), (3, 5)] # Nodo 4
}
# Nodo inicial
start_node = 0

13
# Ejecutar Prim para obtener el árbol de expansión mínima (MST)
mst_edges, total_cost = prim_mst(graph, start_node)
# Imprimir resultado
print("Aristas del Árbol de Expansión Mínima:", mst_edges)
print("Costo total del MST:", total_cost)
Estructuras de Datos Utilizadas en el Algoritmo de Prim
1. Columna de Prioridad (Min-Heap o Fibonacci Heap):
○ Min-Heap: Es una estructura de datos que permite la inserción, eliminación y
acceso a la arista de menor peso en tiempo logarítmico. En un min-heap, el
elemento con el menor valor se encuentra en la raíz, y las operaciones de
inserción y extracción se mantienen eficientes.
○ Fibonacci Heap: Es una estructura más avanzada que permite una
disminución de la clave y una extracción mínima en tiempos amortizados más
rápidos en comparación con el min-heap. Aunque la implementación es más
compleja, ofrece ventajas en términos de eficiencia en casos donde el
algoritmo maneja muchos vértices y aristas.
2. Etiquetas:

14
○ Etiquetas o Distancias: Se utilizan para almacenar el costo mínimo conocido
para conectar cada vértice al MST. Inicialmente, todos los vértices (excepto el
vértice inicial) tienen un costo infinito. A medida que se construye el MST, las
etiquetas se actualizan con los costos de las aristas más cortas encontradas.
Las etiquetas ayudan a determinar la arista de menor peso que debe ser
añadida al MST en cada iteración.
Aplicaciones Prácticas del Algoritmo de Prim
1. Redes de Computadoras:
○ Diseño de Redes de Comunicación: El algoritmo de Prim es útil para
minimizar el costo total de conexión en redes de computadoras. Por ejemplo,
en el diseño de una red de fibra óptica o cableada, el objetivo es conectar todos
los nodos de la red de la manera más económica posible. El MST asegura que
se utilicen las conexiones más baratas entre los puntos de la red, reduciendo
así los costos de instalación y mantenimiento.
2. Infraestructura de Transporte:
○ Planificación de rutas: En la planificación de infraestructura de transporte,
como la construcción de carreteras, ferrocarriles o rutas de transporte público,
el algoritmo de Prim puede ayudar a minimizar el costo de conectar diferentes
localidades. El MST proporciona una manera de construir una red de
transporte que conecta todas las ciudades o estaciones a un costo mínimo, lo
cual es crucial para el diseño eficiente y económico de infraestructura.
3. Diseño de Circuitos:
○ Minimización de Conexiones: En la ingeniería electrónica y el diseño de
circuitos, el algoritmo de Prim se utiliza para minimizar el costo de las
conexiones entre componentes en un circuito impreso. Al asegurar que todas
las conexiones necesarias se realicen con el menor costo total posible, el MST
contribuye a la eficiencia del diseño del circuito y a la reducción de costos de
fabricación.
Ventajas del Algoritmo de Prim
1. Eficiencia en Grafos Densos:

15
○ Optimización en Grafos con Muchas Aristas: El algoritmo de Prim es
particularmente eficiente en grafos densos, donde el número de aristas es alto.
2. Simplicidad Conceptual y Facilidad de Implementación:
○ Facilidad de Entender y Codificar: La idea de Prim de construir el MST
expandiendo desde un vértice inicial es simple y directa. Esto se traduce en
una implementación que es relativamente fácil de entender y codificar,
especialmente cuando se usan estructuras de datos como el min-heap.
3. Aplicaciones Prácticas en Diseño de Redes y Optimización:
○ Relevancia en Problemas del Mundo Real: La capacidad del algoritmo de
Prim para encontrar el MST tiene aplicaciones prácticas significativas en el
diseño de redes, planificación de infraestructura y optimización de recursos,
haciendo que el algoritmo sea valioso en diversos campos industriales y
tecnológicos.
Desventajas del Algoritmo de Prim
1. Requiere un Grafo Conexo:
○ Limitación en Grafos No Conexos: El algoritmo de Prim solo es aplicable a
grafos conexos, donde todos los vértices están conectados entre sí. En un grafo
no conexo, Prim no puede generar un MST que abarque todos los vértices. En
tales casos, se deben encontrar MSTs para cada componente conexo por
separado.
2. Dependencia de la Estructura de Datos Utilizada:
○ Impacto en el Rendimiento: La eficiencia del algoritmo está estrechamente
relacionada con la estructura de datos utilizada para gestionar las aristas. Un
min-heap proporciona una buena eficiencia, pero el uso de un Fibonacci heap
puede mejorar el rendimiento en grafos grandes. La elección de la estructura
de datos puede influir significativamente en el tiempo de ejecución.
3. Menos Eficiente en Grafos Muy Escasos:
○ Comparado con Otros Algoritmos: En grafos muy escasos, donde el número
de aristas es menor, el algoritmo de Kruskal puede ser más eficiente. Kruskal,
que se basa en el ordenamiento de aristas y la unión de conjuntos, puede ser
preferible en estos casos debido a su enfoque directo en la gestión de aristas.
4. No Siempre la Mejor Opción Comparado con Otros Algoritmos:

16
○ Alternativas como Kruskal: Dependiendo de la estructura del grafo y el
contexto del problema, otros algoritmos como Kruskal pueden ofrecer ventajas
adicionales. Kruskal puede ser más simple en algunos escenarios y más
eficiente en grafos con ciertas características.

17
● CONCLUSIONES
● Eficiencia en Grafos Densos: El Algoritmo de Prim es muy eficiente para
grafos densos, donde el número de aristas es alto en comparación con el
número de vértices. Su tiempo de ejecución es favorable para aplicaciones
como redes de comunicación y planificación de transporte.
● Limitaciones en Grafos No Conexos y Escasos: El algoritmo solo funciona
en grafos conexos y es menos eficiente en grafos muy escasos. En grafos no
conexos, se deben encontrar MSTs para cada componente conexo, y para
grafos escasos, el Algoritmo de Kruskal puede ser preferible.
● Aplicaciones y Elección del Algoritmo: Prim es útil en diversas aplicaciones
prácticas, pero la elección del algoritmo (Prim, Kruskal, Borůvka) debe basarse
en la densidad del grafo y el contexto específico del problema.

18
BIBLIOGRAFÍA
AcademiaLab. (2016, mayo 26). ALGORITMO DE PRIM.
https://jcrd0730.wixsite.com/estr/single-post/2016/05/26/algoritmo-de-prim
Castro, A. (2020). ALGORITMO DE PRIM. Studocu.com.
https://www.studocu.com/es-mx/document/itec-universidad/prueba-de-software/pdf-
algoritmo-de-prim-historia/20051438
UNIVERSIDAD INCCA DE COLOMBIA. Algoritmo de Prim. Academia-lab.com.
Recuperado el 11 de septiembre de 2024, de
https://academia-lab.com/enciclopedia/algoritmo-de-prim/
Wikipedia. (s/f). Algoritmo de Prim. Wikipedia, The Free Encyclopedia.
https://es.wikipedia.org/w/index.php?title=Algoritmo_de_Prim&oldid=161321025
Bel, W. (2021). Algoritmos y estructuras de datos en Python. Uader.edu. Recuperado
el 11 de septiembre de 2024, de
https://editorial.uader.edu.ar/wp-content/uploads/2021/04/Algoritmos%20y
%20estructuras%20de%20datos%20en%20Python%20-%20digital.pdf

Investigación sobre el algoritmo de prim

Más contenido relacionado

Similar a Investigación sobre el algoritmo de prim

Último

Investigación sobre el algoritmo de prim