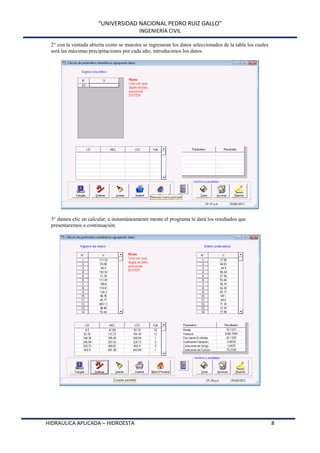
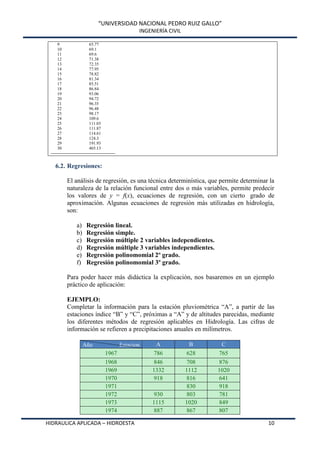
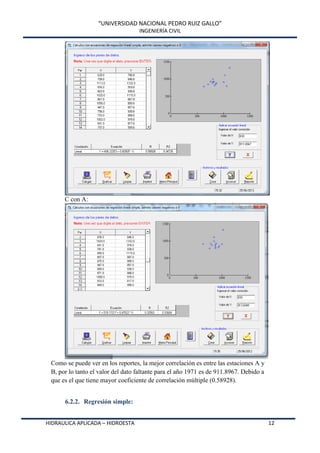
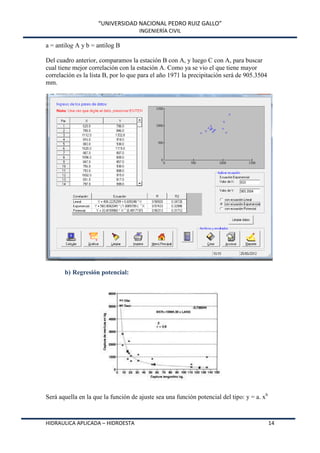
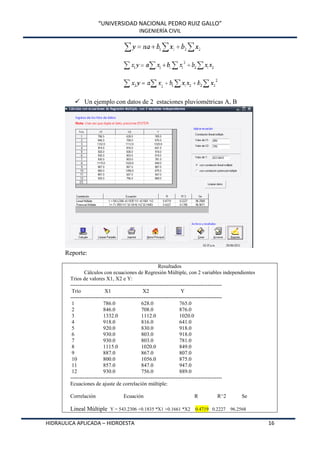
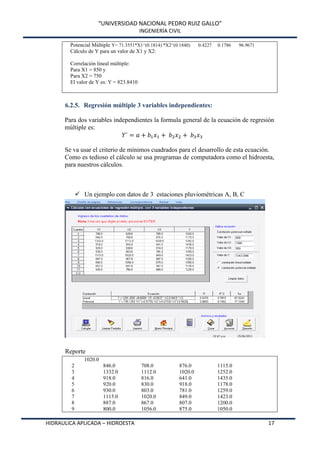
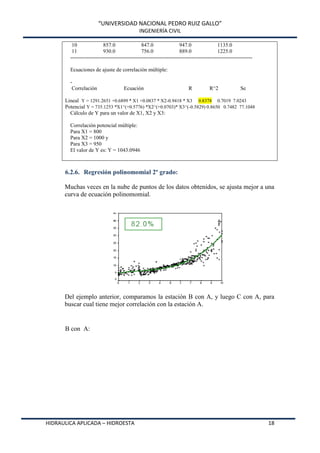
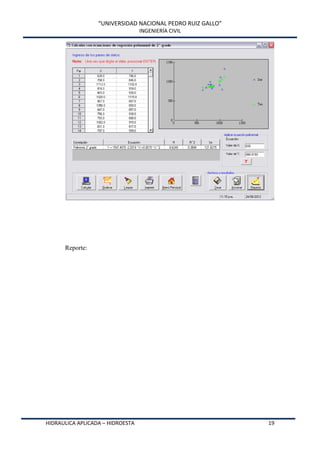
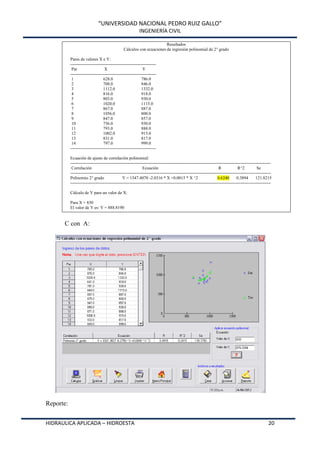
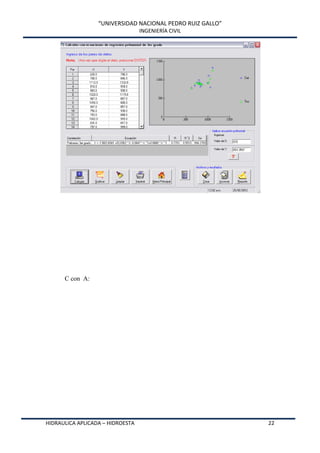
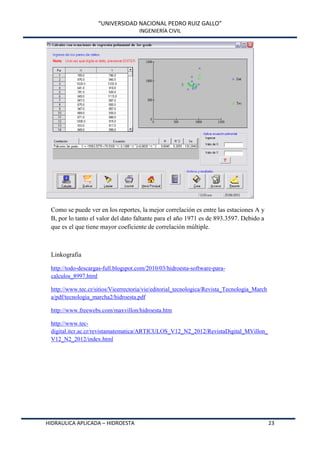
Este documento presenta HidroEsta, un software desarrollado en Visual Basic para realizar cálculos hidrológicos y estadísticos. El software permite calcular parámetros estadísticos, regresiones, ajustes a distribuciones, curvas características, análisis de precipitaciones, aforos, caudales máximos y evapotranspiración. El software agiliza los cálculos hidrológicos comunes y facilita el análisis de grandes volúmenes de datos, lo que permite a los ingenieros optimizar el