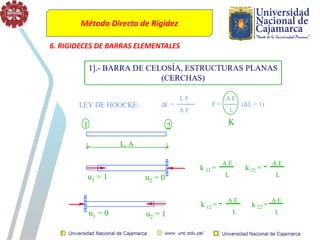
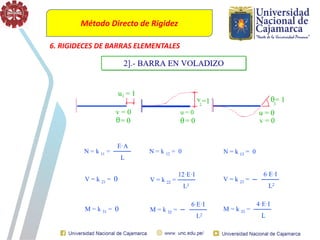
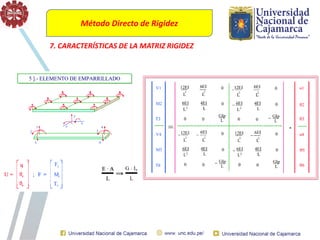
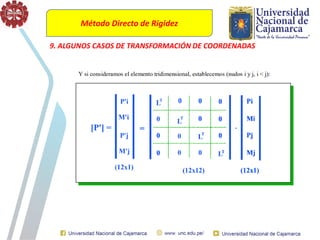
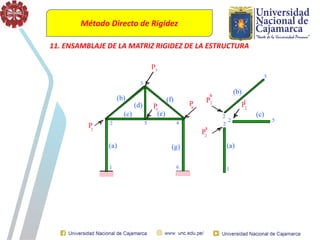
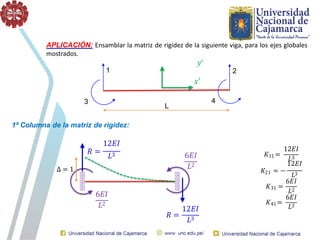
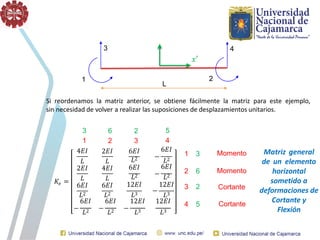
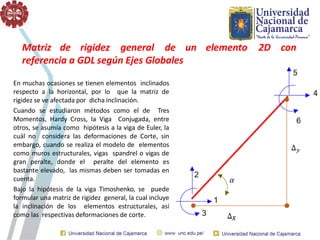
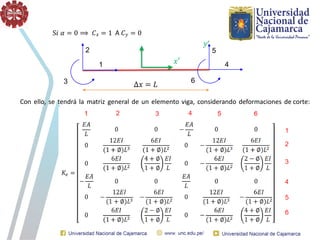
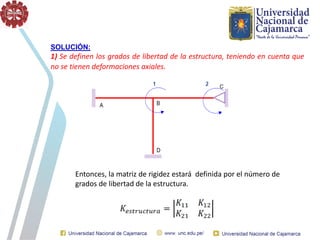
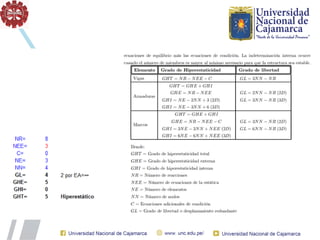
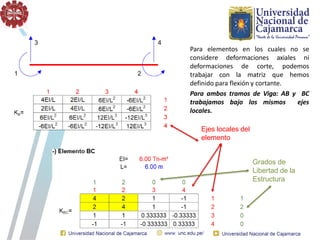
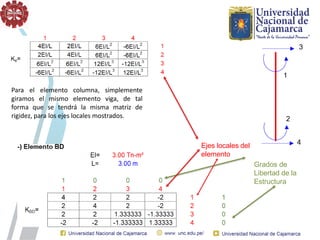
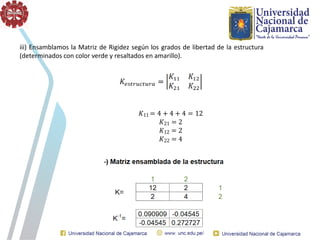
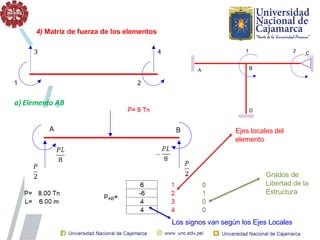
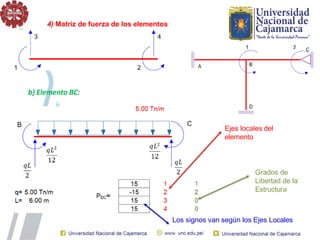
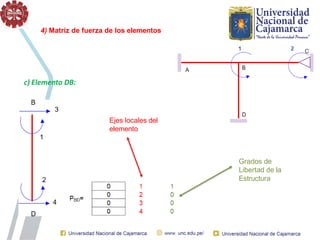
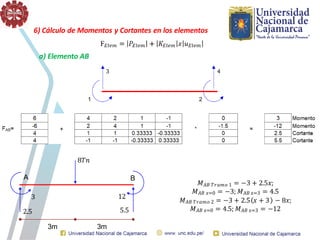
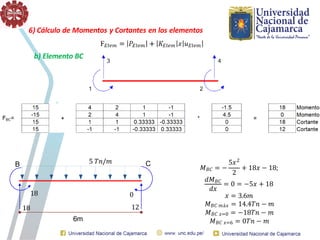
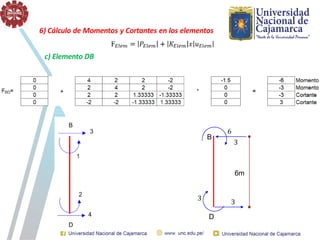
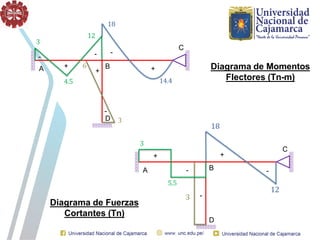
El documento describe el método directo de rigidez, detallando componentes fundamentales como ecuaciones de equilibrio, compatibilidad de movimientos y leyes de comportamiento estructural. Se presentan coeficientes de rigidez, sistemas de coordenadas, ensamblaje de matrices, y aplicaciones prácticas de cálculo de reacciones y esfuerzos en elementos estructurales. También se discuten pasos para calcular momentos y cortantes en estructuras, junto con ejemplos numéricos.

1. • Método Directo de Rigidez.
• Descripción de Método. Problema Primario y
Complementario.
• ANÁLISIS ESTRUCTURAL II (REPASO)
• MG. ING. RONALD J. SALAS BERROSPI
• ASIGNATURA:
• TEMA:
• DOCENTE:

2. Desarrollo del Contenido

3. Método Directo de Rigidez

4. Método Directo de Rigidez
1. RELACIONES FUNDAMENTALES DEL CÁLCULO ESTRUCTURAL
1°) LAS ECUACIONES DE EQUILIBRIO. ( F=0, M=0)
Dentro de la estructura, en cualquier elemento, sección, nudo, barra,
conjunto, y con las cargas exteriores.
2°) LAS ECUACIONES DE COMPATIBILIDAD DE MOVIMIENTOS
Entre los elementos de la estructura y con las condiciones de
contorno; así, por ejemplo; en uniones rígidas tendremos los ángulos
y movimientos solidarios; en uniones articuladas tan solo los
movimientos serán solidarios.
3°) LA LEY DE COMPORTAMIENTO
Que relaciona las tensiones con las deformaciones (leyes de Hooke,
ecuaciones de Lamé,...).

5. Método Directo de Rigidez
2. MÉTODO DE LA RIGIDEZ ≡ MÉTODO DE EQUILIBRIO

6. Método Directo de Rigidez
3. COEFICIENTES DE RIGIDEZ Y DE FLEXIBILIDA

7. Método Directo de Rigidez
3. COEFICIENTES DE RIGIDEZ Y DE FLEXIBILIDA

8. Método Directo de Rigidez
4. COEFICIENTES DE RIGIDEZ Y DE FLEXIBILIDAD

9. Método Directo de Rigidez
4. COEFICIENTES DE RIGIDEZ Y DE FLEXIBILIDAD

10. Método Directo de Rigidez
5. SISTEMAS DE COORDENADAS; DISCRETIZACIÓN

11. Método Directo de Rigidez
5. SISTEMAS DE COORDENADAS; DISCRETIZACIÓN

12. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

13. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

14. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

15. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

16. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

17. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

18. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

19. Método Directo de Rigidez
6. RIGIDECES DE BARRAS ELEMENTALES

20. Método Directo de Rigidez
7. CARACTERÍSTICAS DE LA MATRIZ RIGIDEZ

21. Método Directo de Rigidez
7. CARACTERÍSTICAS DE LA MATRIZ RIGIDEZ

22. Método Directo de Rigidez
7. CARACTERÍSTICAS DE LA MATRIZ RIGIDEZ

23. Método Directo de Rigidez
8. TRANSFORMACIÓN DE COORDENADAS

24. Método Directo de Rigidez
8. TRANSFORMACIÓN DE COORDENADAS

25. Método Directo de Rigidez
9. ALGUNOS CASOS DE TRANSFORMACIÓN DE COORDENADAS

26. Método Directo de Rigidez
9. ALGUNOS CASOS DE TRANSFORMACIÓN DE COORDENADAS

27. Método Directo de Rigidez
9. ALGUNOS CASOS DE TRANSFORMACIÓN DE COORDENADAS

28. Método Directo de Rigidez
9. ALGUNOS CASOS DE TRANSFORMACIÓN DE COORDENADAS

29. Método Directo de Rigidez
9. ALGUNOS CASOS DE TRANSFORMACIÓN DE COORDENADAS

30. Método Directo de Rigidez
10. EL ELEMENTO Y LA ESTRUCTURA; DISCRETIZACIÓN.

31. Método Directo de Rigidez
10. EL ELEMENTO Y LA ESTRUCTURA; DISCRETIZACIÓN.

32. Método Directo de Rigidez
11. ENSAMBLAJE DE LA MATRIZ RIGIDEZ DE LA ESTRUCTURA

33. Método Directo de Rigidez
11. ENSAMBLAJE DE LA MATRIZ RIGIDEZ DE LA ESTRUCTURA

34. Método Directo de Rigidez
12. CONCLUSIONES

35. Método Directo de Rigidez
12. CONCLUSIONES

36. Método Directo de Rigidez
12. CONCLUSIONES

37. Método Directo de Rigidez
13. APLICACIÓN DE LAS CONDICIONES DE CONTORNO: CÁLCULO DE
LAS REACCIONES Y ESFUERZOS EN LOS ELEMENTOS

38. Método Directo de Rigidez
13. APLICACIÓN DE LAS CONDICIONES DE CONTORNO: CÁLCULO DE
LAS REACCIONES Y ESFUERZOS EN LOS ELEMENTOS

39. Método Directo de Rigidez

40. Método Directo de Rigidez

41. Método Directo de Rigidez
14. ACCIONES EXTERIORES SOBRE LOS ELEMENTOS

42. Método Directo de Rigidez
14. ACCIONES EXTERIORES SOBRE LOS ELEMENTOS

43. Método Directo de Rigidez
14. ACCIONES EXTERIORES SOBRE LOS ELEMENTOS

44. Método Directo de Rigidez
14. ACCIONES EXTERIORES SOBRE LOS ELEMENTOS

45. Matriz de Rigidez de Estructuras
Aporticadas, articuladas y mixtas.

46. 1
3
2
4
𝑥′
L
APLICACIÓN: Ensamblar la matriz de rigidez de la siguiente viga, para los ejes globales
mostrados.
𝑦’
1ª Columna de la matriz de rigidez:
𝐾11 =
12𝐸𝐼
𝐿3
21
12𝐸𝐼
𝐾 = −
𝐾31 =
𝐿3
6𝐸𝐼
𝐾41 =
𝐿2
6𝐸𝐼
𝐿2
12𝐸𝐼
𝑅 =
𝐿3
Δ = 1
𝑅 =
12𝐸𝐼
𝐿3
6𝐸𝐼
𝐿2
6𝐸𝐼
𝐿2

47. 2ª Columna de la matriz de rigidez:
12𝐸𝐼
𝐿3
Δ = 1
12𝐸𝐼 6𝐸𝐼
𝐿3 𝐿2
6𝐸𝐼
𝐿2
3ª Columna de la matriz de rigidez:
6𝐸𝐼
𝐿2
𝜃 = 1
6𝐸𝐼
𝐿2
2𝐸𝐼
𝐿
4𝐸𝐼
𝐿

48. 14
6𝐸𝐼
𝐾 =
𝐿2
6𝐸𝐼
𝐾24 = −
𝐿2
𝐾34 =
2𝐸𝐼
𝐿
4𝐸𝐼
𝐾44 =
𝐿
4ª Columna de la matriz de rigidez:
6𝐸𝐼
𝐿2
𝜃 = 1
6𝐸𝐼
4𝐸𝐼
𝐿
2𝐸𝐼
𝐿
La matriz de rigidez ensamblada es la siguiente:
𝑒
𝐾 =
𝐿3 𝐿2 𝐿2
𝐿3
12𝐸𝐼 12𝐸𝐼
−
6𝐸𝐼
−
6𝐸𝐼
−
𝐿3
6𝐸𝐼
𝐿3 𝐿2
6𝐸𝐼 4𝐸𝐼
−
𝐿2
𝐿2
2𝐸𝐼
𝐿2
6𝐸𝐼
𝐿2 𝐿2
𝐿
6𝐸𝐼 2𝐸𝐼
−
𝐿
1
1
12𝐸𝐼
𝐿
4𝐸𝐼
𝐿
4
4
6𝐸𝐼
Matriz general de un
elemento horizontal sometido
a deformaciones de Cortante y
Flexión
3
2
2
3
12𝐸𝐼 6𝐸𝐼
− 1 1
2 3
3 2
4 4
𝐿2

49. 1
2
3
4
𝑥′
L
Si reordenamos la primera matriz con 6 Ejes Globales, se obtiene fácilmente la matriz
para la presente aplicación, sin necesidad de volver a realizar las suposiciones de
desplazamientos unitarios.
𝑒
𝐾 =
12𝐸𝐼
𝐿2
4𝐸𝐼
3
2
6𝐸𝐼
𝐿3
𝐿3
6𝐸𝐼
𝐿2
6𝐸𝐼 2𝐸𝐼
−
−
𝐿2
12𝐸𝐼
𝐿3
𝐿 𝐿2
6𝐸𝐼 12𝐸𝐼
−
𝐿2
𝐿
6𝐸𝐼
−
𝐿2
6𝐸𝐼 2𝐸𝐼
𝐿3
6𝐸𝐼 4𝐸𝐼
−
𝐿2 𝐿2
𝐿 𝐿
5
3
6
4
12𝐸𝐼 6𝐸𝐼
− 1 2
2 3
3 5
4 6
Matriz general de un
elemento horizontal sometido
a deformaciones de Cortante y
Flexión

50. 3
1
4
2
𝑥′
L
Si reordenamos la matriz anterior, se obtiene fácilmente la matriz para este ejemplo,
sin necesidad de volver a realizar las suposiciones de desplazamientos unitarios.
𝑒
𝐾 =
3
1
4𝐸𝐼
𝐿
2𝐸𝐼
6
2
2𝐸𝐼
𝐿
4𝐸𝐼
6𝐸𝐼
−
𝐿2
𝐿2
6𝐸𝐼 6𝐸𝐼
−
𝐿
6𝐸𝐼
𝐿2
𝐿
6𝐸𝐼
𝐿2
𝐿2
12𝐸𝐼
𝐿3
−
𝐿2
12𝐸𝐼
𝐿3
6𝐸𝐼
−
𝐿2
6𝐸𝐼
−
𝐿2 𝐿3
12𝐸𝐼 12𝐸𝐼
−
𝐿3
2
3
6𝐸𝐼
5
4
1 3
2 6
3 2
4 5
Momento
Momento
Cortante
Cortante
Matriz general
de un elemento
horizontal
sometido a
deformaciones de
Cortante y
Flexión

51. Matriz de rigidez general de un elemento 2D con
referencia a GDL según Ejes Globales
En muchas ocasiones se tienen elementos inclinados
respecto a la horizontal, por lo que la matriz de
rigidez se ve afectada por dicha inclinación.
Cuando se estudiaron métodos como el de Tres
Momentos, Hardy Cross, la Viga Conjugada, entre
otros, se asumía como hipótesis a la viga de Euler, la
cuál no considera las deformaciones de Corte, sin
embargo, cuando se realiza el modelo de elementos
como muros estructurales, vigas spandrel o vigas de
gran peralte, donde el peralte del elemento es
bastante elevado, las mismas deben ser tomadas en
cuenta.
Bajo la hipótesis de la viga Timoshenko, se puede
formular una matriz de rigidez general, la cual incluye
la inclinación de los elementos estructurales, así
como las respectivas deformaciones de corte.

52. Matriz de rigidez general de un elemento 2D con referencia a
GDL según Ejes Globales

53. Con ello, se tendrá la matriz general de un elemento viga, considerando deformaciones de corte:
1
2
3
4
5
6
S𝑖 𝛼 = 0 ⟹ 𝐶𝑥 = 1 𝖠 𝐶𝑦 = 0
𝑦’
𝑥′
Δ𝑥 = 𝐿

54. 𝐾𝑒 =
12𝐸𝐼
(1 + ∅)𝐿3
0
3 4
6𝐸𝐼 12𝐸𝐼
− −
(1 + ∅)𝐿2 (1 + ∅)𝐿3
0
0
6𝐸𝐼
𝐸𝐴
𝐿
𝐸𝐴
−
𝐿
0
2 − ∅ 𝐸𝐼
1 + ∅ 𝐿
6𝐸𝐼
−
(1 + ∅)𝐿2
0
0
4 + ∅ 𝐸𝐼
1 + ∅ 𝐿
6𝐸𝐼
0
6𝐸𝐼
(1 + ∅)𝐿2
12𝐸𝐼
0
12𝐸𝐼
−
(1 + ∅)𝐿3
0
(1 + ∅)𝐿2 (1 + ∅)𝐿3
0
(1 + ∅)𝐿2
0
6𝐸𝐼
𝐸𝐴
−
𝐿
0
6𝐸𝐼
𝐸𝐴
𝐿
−
(1 + ∅)𝐿2
0
0
2 − ∅ 𝐸𝐼
1 + ∅ 𝐿 (1 + ∅)𝐿2
0
0
4 + ∅ 𝐸𝐼
1 + ∅ 𝐿
6
6𝐸𝐼
−
(1 + ∅)𝐿2
S𝑖 𝛼 = 90º ⟹ 𝐶𝑥 = 0 𝖠 𝐶𝑦 = 1
Si reemplazamos, se tendrá la matriz de rigidez
general para una columna en 2D.
1 2 5
1
2
3
4
5
6

55. APLICACIÓN: En la estructura mostrada, construya el Diagrama de Momentos Flectores y
Fuerzas Cortantes. Considere EA=∞.
Entonces, la matriz de rigidez estará definida por el número de grados de
libertad de la estructura.

56. SOLUCIÓN:
1) Se definen los grados de libertad de la estructura, teniendo en cuenta que
no se tienen deformaciones axiales.
Entonces, la matriz de rigidez estará definida por el número de
grados de libertad de la estructura.

58. 2) Escribir la matriz de rigidez para cada elemento, según los ejes locales mostrados
(Escribimos la matriz de rigidez de los elementos, según la orientación mostrada - sirve
cuando EA=INFINITA).
Para elementos en los cuales no se
considere deformaciones axiales ni
deformaciones de corte, podemos
trabajar con la matriz que hemos
definido para flexión y cortante.
Para ambos tramos de Viga: AB y BC
trabajamos bajo los mismos ejes
locales.

59. Para elementos en los cuales no se
considere deformaciones axiales ni
deformaciones de corte, podemos
trabajar con la matriz que hemos
definido para flexión y cortante.
Para ambos tramos de Viga: AB y BC
trabajamos bajo los mismos ejes
locales.
Ejes locales del
elemento
Grados de
Libertad de la
Estructura

60. Para el elemento columna, simplemente
giramos el mismo elemento viga, de tal
forma que se tendrá la misma matriz de
rigidez, para los ejes locales mostrados.
Ejes locales del
elemento
Grados de
Libertad de la
Estructura

61. iii) Ensamblamos la Matriz de Rigidez según los grados de libertad de la estructura
(determinados con color verde y resaltados en amarillo).
𝐾11 = 4 + 4 + 4 = 12
𝐾21 = 2
𝐾12 = 2
𝐾22 = 4

62. 4) Matriz de fuerza de los elementos
a) Elemento AB
Ejes locales del
elemento
Grados de
Libertad de la
Estructura
Los signos van según los Ejes Locales

63. b) Elemento BC:
Ejes locales del
elemento
Grados de
Libertad de la
Estructura
Los signos van según los Ejes Locales
4) Matriz de fuerza de los elementos

64. c) Elemento DB:
Ejes locales del
elemento
Grados de
Libertad de la
Estructura
4) Matriz de fuerza de los elementos

65. 5) Ensamblamos la Matriz de Fuerza de toda la estructura
𝑃 = 𝑃𝑛 − Σ𝐹𝐸
𝐷𝑜𝑛𝑑𝑒:
𝑃: 𝑀𝑎𝑡𝑟𝑖𝑧 𝑑𝑒 𝐹𝑢𝑒𝑟𝑧𝑎 𝑑𝑒 𝑡𝑜𝑑𝑎 𝑙𝑎 𝑒𝑠𝑡𝑟𝑢𝑐𝑡𝑢𝑟𝑎
𝑃𝑛:𝑀𝑎𝑡𝑟𝑖𝑧 𝑑𝑒 𝐹𝑢𝑒𝑟𝑧𝑎𝑠 𝑛𝑜𝑚𝑖𝑛𝑎𝑙𝑒𝑠, 𝑓𝑢𝑒𝑟𝑧𝑎𝑠 𝑞𝑢𝑒 𝑠𝑒 𝑎𝑝𝑙𝑖𝑐𝑎𝑛 𝑒𝑛 𝑙𝑜𝑠 𝐺𝑟𝑎𝑑𝑜𝑠 𝑑𝑒
𝐿𝑖𝑏𝑒𝑟𝑡𝑎𝑑 𝑑𝑒 𝑙𝑎 𝑒𝑠𝑡𝑟𝑢𝑐𝑡𝑢𝑟𝑎 𝐹𝑢𝑒𝑟𝑧𝑎𝑠 𝐸𝑥𝑡𝑒𝑟𝑛𝑎𝑠
Σ𝐹𝐸: 𝑀𝑎𝑡𝑟𝑖𝑧 𝑑𝑒 𝑓𝑢𝑒𝑟𝑧𝑎𝑠 𝑑𝑒 𝑙𝑜𝑠 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑜𝑠
𝐸𝑛 𝑒𝑠𝑡𝑒 𝑐𝑎𝑠𝑜: 𝑃𝑛 = 0
𝑃 = −Σ𝐹𝐸
6) Cálculo de Desplazamientos en la estructura
𝑢 = 𝐾 −1𝑥 𝑃
𝑢 =
12
2 4
2 −1
𝑥
−9
15
Grados de
Libertad de la
Estructura

66. 𝑀𝐴𝐵 𝑇𝑟𝑎𝑚𝑜 1 = −3 + 2.5𝑥;
𝑀𝐴𝐵 𝑥=0 = −3; 𝑀𝐴𝐵 𝑥=3 = 4.5
𝑀𝐴𝐵 𝑇𝑟𝑎𝑚𝑜 2 = −3 + 2.5 𝑥 + 3 − 8𝑥;
𝑀𝐴𝐵 𝑥=0 = 4.5; 𝑀𝐴𝐵 𝑥=3 = −12
A B
3 12
2.5 5.5
8𝑇𝑛
3m 3m
6) Cálculo de Momentos y Cortantes en los elementos
a) Elemento AB

67. 𝑀𝐵𝐶 = −
5𝑥2
2
+ 18𝑥 − 18;
𝑑𝑥
𝑑𝑀𝐵𝐶
= 0 = −5𝑥 + 18
𝑥 = 3.6𝑚
𝑀𝐵𝐶 𝑚á𝑥 = 14.4𝑇𝑛 − 𝑚
𝑀𝐵𝐶 𝑥=0 = −18𝑇𝑛 − 𝑚
𝑀𝐵𝐶 𝑥=6 = 0𝑇𝑛 − 𝑚
B C
18
18
0
12
5 𝑇𝑛/𝑚
6m
6) Cálculo de Momentos y Cortantes en los elementos
b) Elemento BC

68. B
D
6
3
3
6m
3
6) Cálculo de Momentos y Cortantes en los elementos
c) Elemento DB

69. Diagrama de Momentos
Flectores (Tn-m)
B
A
C
D
5.5
18
3
3
12
B
A
C
D
4.5
3
3
18
12
14.4
6
- - -
+
+
-
+
+
-
+
-
-
Diagrama de Fuerzas
Cortantes (Tn)

70. BIBLIOGRAFÍA:
MÉTODO DE RIGIDEZ
https://www.uhu.es/javier.pajon/apuntes/matricial.pdf
MATRIZ DE RIGIDEZ EJEMPLOS
https://www.udocz.com/apuntes/128140/rigidez-ejercicios-resueltos-parte-1