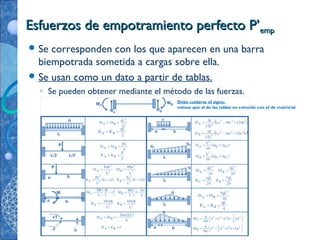
Este documento describe los métodos matriciales para el análisis de estructuras de elementos unidimensionales. Explica los conceptos clave como los grados de libertad, las matrices de rigidez y flexibilidad, y cómo se pueden modelar diferentes tipos de estructuras como pórticos, celosías y emparrillados usando este enfoque. También cubre temas como la discretización, los sistemas de referencia global y local, y cómo se definen y calculan los términos de las matrices de rigidez elementales.

1. Método MatricialMétodo Matricial
El método directo de la rigidez

2. Estructuras de elementos unidimensionalesEstructuras de elementos unidimensionales
 Celosías:
◦ cargas en los nudos
◦ sólo hay tracciones y compresiones en
las barras
 Pórtico plano:
◦ estructura plana (de nudos rígidos
generalmente)
◦ con las cargas en el propio plano
 Emparrillado:
◦ estructura plana (con nudos rígidos
generalmente)
◦ con las cargas en el plano perpendicular
 Pórtico tridimensional:
◦ estructura formada por barras formando
◦ pórticos ortogonales en el espacio
◦ cargas en cualquier dirección

3. Métodos matricialesMétodos matriciales
 Gran simplicidad
 No aportan nuevas ideas conceptuales al análisis de estructuras.
 Son una evolución de las ideas de Maxwell y de Mohr de finales del siglo
XIX.
 Para su comprensión se necesitan
◦ conocimientos de álgebra de matrices
◦ teoremas fundamentales del cálculo clásico de estructuras.
 El éxito de estos métodos radica en su gran adaptación al ordenador.
 Tipos:
◦ Método de la Flexibilidad (método de compatibilidad). Resuelve el problema
planteando la compatibilidad de desplazamientos en primer lugar.
◦ Método de la Rigidez (método de equilibrio). Plantea el equilibrio de fuerzas
primero.

4. Discretzación de estructurasDiscretzación de estructuras
 Elementos unidos por puntos llamados nodos.
 Se obtienen sólo resultados para los nodos de la
estructura.
◦ Los valores entre nodos se interpolarán o se estimarán.
 La discretización más común es aquella en la que
coinciden los nodos con los nudos de unión de barras (a).

5. Grados de libertad g.d.l.Grados de libertad g.d.l.
 Grado de libertad: la posibilidad que tiene cualquier punto de
la estructura para desplazarse o girar
 En los métodos matriciales los grados de libertad se
refieren sólo a los nodos
 Una estructura deformada se define a través de los
desplazamientos y giros en los grados de libertad.

6. Sistema de referencia globalSistema de referencia global
 XYZ permite definir de forma única los desplazamientos y las
fuerzas en los distintos G.D.L. de los nodos.
Pórtico plano:
2 desplazamientos ortogonales y un giro (u, v, θ).
2 fuerzas ortogonales y un momento (Fx, Fy, M) por
cada nodo.
u (A) F (A)
AA
x
A A
y
A A
Fu
v F
Mθ
  
  
= =   
   
   
Celosía plana:
2 desplazamientos ortogonales (u, v) por nodo.
2 fuerzas ortogonales (Fx, Fy) por cada nodo.
u F
x
y
Fu
Fv
  
= =   
   

7. G.D.L. de otros tipos estructuralesG.D.L. de otros tipos estructurales
Emparrillado:
1 desplazamiento en perpendicular al
emparrillado y 2 giros por nodo (w, θx, θy).
1 fuerza perpendicular al emparrillado y 2
momentos por nodo (Fz, Mx, My).
u F
z
x x
y y
w F
M
M
θ
θ
   
   
= =   
   
   
Celosía tridimensional:
3 desplazamientos ortogonales (u, v, w) por
nodo.
3 fuerzas ortogonales (Fx, Fy, Fz) por cada
nodo.
u F
x
y
z
u F
v F
w F
   
   
= =   
   
   

8. G.D.L. de un pórtico tridimensionalG.D.L. de un pórtico tridimensional
Pórtico tridimensional (caso más
general):
3 desplazamientos ortogonales y 3 giros
(u, v, w, θx, θy, θz).
3 fuerzas ortogonales y 3 momentos (Fx,
Fy, Fz, Mx, My, Mz) por cada nodo.
u F
x
y
z
x x
y y
z z
u F
v F
w F
M
M
M
θ
θ
θ
   
   
   
      
= =   
   
   
   
      

9. Sistema de referencia localSistema de referencia local
 Permite definir las relaciones entre los vectores de cargas y
desplazamientos independientemente de la orientación de los
elementos.
 Los sistemas locales van asociados a cada uno de los elementos
 Uno de los ejes seguirá la dirección de la barra y los otros serán
ortogonales.
 Las fuerzas que aparecen en nodos expresadas en sistemas de
referencia locales son los esfuerzos internos (normales, cortantes y
momentos).
Sistema de referencia
global

10. G.D.L. en los elementos (en locales)G.D.L. en los elementos (en locales)
Elemento de pórtico plano:
Los nodos extremos del elemento pueden desplazarse en
la dirección del mismo y la perpendicular, además del giro.
El vector de fuerzas contiene los normales (dirección del
elemento), los cortantes (dirección perpendicular) y los
momentos.
Elemento de celosía plana:
Los nodos extremos del elemento sólo pueden desplazarse
en la dirección del mismo.
El vector de fuerzas contiene normales únicamente.
Elemento de emparrillado:
Los nodos extremos del elemento pueden desplazarse en
la dirección perpendicular al plano, además de girar
alrededor de los dos ejes contenidos en él.
El vector de fuerzas contiene un cortante, un momento
flector y un torsor.
1 1
2 2
3 3
4 4
5 5
6 6
δ P
N
V
M
N
V
M
δ
δ
θ
δ
δ
θ
   
   
   
      
= =   
   
   
   
      
1 1
2 2
δ P
N
N
δ
δ
   
= =   
   
1 1
2 2
3 3
4 4
5 5
6 6
δ F
V
M
T
V
M
T
δ
θ
θ
δ
θ
θ
   
   
   
      
= =   
   
   
   
      

11. S.R. locales y S.R. nodalesS.R. locales y S.R. nodales
3
4
5
6
7
8
9
10
11
12
δ = =
δ
δ
δ
θ
θ
θ
δ
δ
δ
θ
θ
θ
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
  
1 1
2 2
3
4
5
6
7
8
9
10
11
12
N
V
V
T
M
M
N
V
V
T
M
M
P
Ejemplo:
En el nodo A las condiciones de contorno son de
aplicación inmediata, con independencia de la
definición de coordenadas.
El nodo B tiene impedido el desplazamiento según el
eje y’ del sistema nodal representado.
En algunos casos, los nodos tienen condiciones de contorno (apoyos) cuyas restricciones no se
ajustan a los S.R. global o locales. En esos casos deben utilizarse sistemas de referencia nodales.

12. Matrices de rigidez y flexibilidadMatrices de rigidez y flexibilidad
Ley de Hooke para un muelle: P=k·δ
k es la constante de rigidez del muelle y representa la fuerza que
es preciso aplicar para obtener un desplazamiento unidad.
Se puede escribir la ecuación: δ=a·P
a=1/k es el coeficiente de flexibilidad del muelle (inversa de la
rigidez k) y representa el desplazamiento que aparece al aplicar
una fuerza unidad.
Para una estructura de n grados de libertad, el sistema de fuerzas se define por un
vector de fuerzas F y la deformada por un vector de deformaciones u.
F = K u
K = Matriz de rigidez (n x n)
u = A F
A = Matriz de flexibilidad (n x n)
Los vectores F y u están
relacionados por
matrices
K ·A = I ⇒ A = K-1

13. Términos de la matriz de rigidezTérminos de la matriz de rigidez
 Término de la matriz kij término de la fila i columna j
◦ kij=fuerza/momento en el g.d.l. i cuando se aplica un
desplazamiento/giro 1 en el g.d.l. j y 0 en el resto.
 Ejemplo: 3 G.D.L. del extremo de una viga
◦ ¿Qué fuerzas o momentos aparecen en los G.D.L. cuando se aplican
estos desplazamientos o giros?

14. Términos de matriz de rigidezTérminos de matriz de rigidez
g.d.l. (coordenadas) 1 (u=1) 2 (v=1) 3 ( =1)θ
1 (N) N = N = 0 N = 0
2 (V) V = 0 V = V =
3 (M) M = 0 M = M =
3
12EI
L
2
6EI
L
− 4EI
L
2
6EI
L
−
EA
L
 Estos términos pueden obtenerse mediante el PTV

15. Propiedades de todas las matrices de rigidezPropiedades de todas las matrices de rigidez
 kij representa la fuerza/momento en la coordenada i cuando se
impone un desplazamiento/giro unidad en la coordenada j,
siendo cero todos los demás.
 Por la ley de reciprocidad de Maxwell kij = kji, las matrices de rigidez K
son simétricas.
 Los elementos de la diagonal de K no pueden ser negativos pues
representan la fuerza en una coordenada para conseguir un
desplazamiento unidad en ella misma.
 El principio de superposición permite calcular la fuerza en una coordenada
◦ Pi = ki1 δ1 +...+ kii δi +... + kij δj +...+ kin δn
11 1 1 11 1
1
1
1
i j n
i ii ij ini i
j ji jj jnj j
n ni nj nnn n
k k k kP
k k k kP
K K
k k k kP
k k k kP
δ
δ
δ
δ
    
    
    
    
    
= ⇒ =     
    
    
    
    
     
L L L
M M M MM M
L L L
M M M MM M
L K L
M M M MM M
L L L

16. Matrices de rigidez elementalesMatrices de rigidez elementales [k][k] de est. planasde est. planas
ELEMENTO ESQUEMA MATRIZ DE RIGIDEZ COMENTARIOS
ELEMENTO DE
CELOSÍA PLANA
Se obvian los grados de
libertad de giro. Los g.d.l.
perpendiculares a la barra
deben permanecer para
poder hacer posteriores
cambios en la
inclinación del elemento.
ELEMENTO DE
PÓRTICO PLANO
Será una matriz de 6x6 al
considerar 3 g.d.l. por cada
nodo.
ELEMENTO DE VIGA
CONTINUA SIN
CARGA AXIAL
Coincide con la matriz
anterior eliminando las filas y
columnas de los grados de
libertad axiales.
(1ª y 4ª fila y columna)
1 0 1 0
0 0 0 0
k
1 0 1 0
0 0 0 0
EA
L
− 
 
 =
 −
 
 
EA
L
sim0
12EI
L
3
0
6EI
L2
4EI
L
−EA
L
0 0
EA
L
0
−12 EI
L3
−6EI
L2
0
12 EI
L3
0
6EI
L
2
2EI
L
0
−6EI
L
2
4EI
L
K =
K =
12EI
L3
6EI
L2
4EI
L
sim
12EI
L3
−6EI
L2
12EI
L3
6EI
L
2
2EI
L
−6EI
L
2
4EI
L

17. Otras matrices de rigidezOtras matrices de rigidez
ELEMENTO ESQUEMA MATRIZ DE RIGIDEZ COMENTARIOS
ELEMENTO DE
EMPARRILLADO
Incluye términos de
momento torsor y elimina
filas y columnas de axiles
ELEMENTO DE
PÓRTICO
TRIDIMENSIONAL
Es el caso más general, con 6
grados de libertad por nodo.
Considera 2 momentos
flectores diferentes,
cortantes en 2 direcciones y
torsores.
K=
12EI
sim
0
4EI
L
0
GJ t
L
0
0
0
−12 EI
L3
6EI
L2
00
6EI
L2
2EI
L
0
−6EI
L
2
4EI
L
L3
6EI
L
2
GJ t
L
− GJ t
L
12EI
L3
K=
EA
L
0
12EIz
L3
0 0
12 EIy
L3
0 0 0
GJt
L
0 0
- 6EI y
L
2
0
4EI y
L
0
6EI
L2
0 0 0
4EI z
L
EA
L
0
12EI z
L3
0 0
12 EIy
L3
0 0 0
GJt
L
0 0
-
6EIy
L2
0
4EIy
L
0
6EI
0 0 0
4EIz
L
EA
L
0
0
0
0
0
-
L2
12EI z
L3
0
0
0
6EI
L2
12 EIy
L3
0
GJt
L
- 6EIy
L2
0
0 0
-
-
z
0
0
00 0 0
0 0
- 6EI
L2
z
0
6EI y
L
2 0
0
0
0
2EI y
L
2EIz
L
0
sim
z
-
z
x
y
z
2
6
8
12
118
5
2
1
4
6 34 10
5
3
1
9
11
7
9
12 10
7

18. Transformación de coordenadasTransformación de coordenadas
 Es muy común en el cálculo de matricial
◦ Las matrices de rigidez se tienen en coordenadas locales (x’y’)
◦ El problema matricial se plantea en coordenadas globales (xy)
 Cambio de coordenadas de un vector cualquiera P
z
Py'
Px
Px'
x'
x
y
y'
Py
ny'
nx'
α
P
Py sen α
Py cos α
Px sen α
Px cos α
La relación entre las
coordenadas:
Px’= Pxcosα+Pysenα
Py’= -Pxsenα+Pycosα
Matricialmente:
Para pasar de locales a
globales:
'
'
cos
cos
x x
y y
P Psen
senP P
α α
α α
       
=    −       
1
'
'
cos
cos
x x
y y
P Psen
senP P
α α
α α
−
       
=    −       

19. Matriz de cambio de baseMatriz de cambio de base [R][R]
 Así, la matriz para cambiar un vector de coordenadas locales a
globales es:
 Que tiene la propiedad R·RT
=I o R-1
=RT
 Por tanto: P’=RT
·P y P=R·P’ siendo
 Para cambiar de globales a locales vectores correspondientes
a un elemento de un pórtico plano con dos nudos i, j:
cos
cos
sen
R
sen
α α
α α
− 
=  
 
i i
j j
i i
j j
T
T
T
T
R 0P' P
'
P' P0 R
R 0'
'
' 0 R
T
T
P L P
y
L
δ δ
δ δ
δ δ
       
= ⇒ =    
       
       
= ⇒ =    
       

20. Matriz de cambio de baseMatriz de cambio de base [L][L]
 la matriz LT
debe considerar el grado de libertad del giro.
 La transformación de coordenadas de la matriz de rigidez se deduce
de:
Como en coordenadas globales debe cumplirse que P=k· ,δ
entonces: k=Lk’Lk=Lk’LTT
Se cumple que LT
=L-1
T
cos 0 0 0 0
cos 0 0 0 0
0 0 1 0 0 0
L
0 0 0 cos 0
0 0 0 cos 0
0 0 0 0 0 1
sen
sen
sen
sen
α α
α α
α α
α α
 
 − 
 
=  
 
 −
 
 
( )P ' ' ' ' 'T T T
k L P k L P Lk Lδ δ δ= ⇒ = ⇒ =
Ley de Hooke para el elemento en
coordenadas locales
cos 0 0 0 0
cos 0 0 0 0
0 0 1 0 0 0
L
0 0 0 cos 0
0 0 0 cos 0
0 0 0 0 0 1
sen
sen
sen
sen
α α
α α
α α
α α
− 
 
 
 
=  
− 
 
 
 

21. Ensamblaje de la matriz de rigidez [K]Ensamblaje de la matriz de rigidez [K]
 Numerar los grados de libertad de la estructura total.
 Obtener las matrices k en c. globales para cada barra
kI=LkI’LT
kII=LkII’LT
 Ensamblar todas las matrices de rigidez en una sola matriz global. Los nudos
comunes a varias barras tendrán varios términos de rigidez kij en sus g.d.l. que deben sumarse.
Las zonas sin términos se rellenan con ceros.
1
2
3
4
5
6
7
8
9
II
IEjemplo:
9 g.d.l (3 por nodo) al ser estructura plana con nudos rígidos.
cos 0 0 0 0
cos 0 0 0 0
0 0 1 0 0 0
L
0 0 0 cos 0
0 0 0 cos 0
0 0 0 0 0 1
sen
sen
sen
sen
α α
α α
α α
α α
− 
 
 
 
=  
− 
 
 
 
En esta zona
se suman
los términos
1
2
3
4
5
6
7
8
9
1 2 3 4 5 6 7 8 9
KI
KII
0
0
1
2
3
4
5
6
7
8
9
II
I
4
5
6
KII
KI

22. Consideraciones sobre la matriz de rigidezConsideraciones sobre la matriz de rigidez
globalglobal
 Es una matriz cuadrada nxn, siendo n el número de
grados de libertad de los nodos de la estructura.
 Es una matriz simétrica.
 Si los valores distintos de cero se concentran alrededor de la
diagonal principal, sólo será preciso almacenar una banda de
valores a un lado de la diagonal (d = semiancho de banda).
Esto se consigue numerando los nudos y los
grados de libertad de un modo adecuado. Los
ordenadores pueden trabajar de este modo,
reordenando los g.d.l. internamente.

23. Grados de libertad libres L y restringidos RGrados de libertad libres L y restringidos R
 G.D.L. restringidos: en los que se impiden desplazamientos o giros
 Se reordenan los G.D.L. identificando:
◦ L=coordenadas o grados de libertad libres
◦ R=coordenadas o grados de libertad restringidos. En estos grados de libertad aparecerán
reacciones debido a esas restricciones.
Ejemplo:
Los grados de libertad 1, 2, 3, 16 y 17 son grados de
libertad restringidos puesto que los nodos a y f están
impedidos en esas direcciones.
En cada uno de esos grados de libertad aparecerán
reacciones.

24. Resolver: desplazamientos {uResolver: desplazamientos {uLL} y reacciones {F} y reacciones {FRR}}
 Si dividimos los vectores y la matriz según la diferenciación L-R:
 Las incógnitas del problema son:
◦ El vector de los desplazamientos en las coordenadas libres: uL
◦ El vector de las REACCIONES: FR
 Si los G.D.L. restringidos está inmovilizados uR=0, para obtener los
desplazamientos uL el sistema que debe resolverse es:
◦ Por tanto, el sistema de ecuaciones que habrá que resolver es,
simplemente, el que se corresponde con los grados de libertad libres.
 Para obtener las reacciones, conocido uL:
L L
R R
L LLL LR
RL RRR R
F uF u K K
F ,
K KF u F u
u
              
= = ⇒ =         
                
LL L LRF K u K uL R= +
RL L RRF K u K uR R= +
LL LF K uL =
R RL LF K u=

25. Cálculo de esfuerzos {P’}Cálculo de esfuerzos {P’}
 El vector de fuerzas elemental en coordenadas locales P’ es el
que indica los esfuerzos (N, V, M).
 Los esfuerzos se calculan después de resolver los desplazamientos u (a los
desplazamientos para el elemento concreto les llamaremos δ)
◦ EL DESPLAZAMIENTO DE LOS NUDOS CREA ESFUERZOS EN LAS BARRAS
 Para obtener los esfuerzos en un caso con cargas en los nudos
únicamente usamos la matriz elemental en coordenadas globales
sabiendo que P=k·δ:
 Si preferimos utilizar la matriz elemental en locales k’, sabiendo P’=k’· δ’
T T
P' L P L kδ= =
T
' ' ' k' LδP k δ= =

26. Solicitaciones fuera de los nodos: obtener PSolicitaciones fuera de los nodos: obtener Peqeq
 El método está pensado para solicitaciones en los G.D.L. de los nodos.
 Hay que sustituir las cargas sobre barra por cargas aplicadas sobre los
nodos para poder aplicar K·u=F
1. Separar cargas en nudos de cargas sobre el elemento
2. Expresar la carga sobre barra en coordenadas locales (descomponiéndola si es
necesario)
3. Calcular las reacciones de empotramiento perfecto Pemp
4. Las cargas equivalentes son opuestas a las de empotramiento
perfecto:
(3) P’eq=-P’emp ⇒Peq=-Pemp
(a)=(1)+(2)+(3)
(1) Tiene sólo cargas en nudos
(2) Tiene cargas sobre barra pero los nudos están inmóviles
SE DESPRECIA EN MATRICIAL
(3) Tiene las reacciones de empotramiento cambiadas de
signo (Peq)

27. Esfuerzos de empotramiento perfecto P’Esfuerzos de empotramiento perfecto P’empemp
 Se corresponden con los que aparecen en una barra
biempotrada sometida a cargas sobre ella.
 Se usan como un dato a partir de tablas.
◦ Se pueden obtener mediante el método de las fuerzas.
Debe cuidarse el signo:
nótese que el de las tablas no coincide con el de matricial

28. Vector de cargas total y v. de esfuerzos totalVector de cargas total y v. de esfuerzos total
 P’eq= cargas equivalentes para un elemento en coordenadas locales
Debe pasarse a coordenadas globales con la matriz cambio de base L:
◦ Peq=L·P’eq
 El vector de cargas total F será el correspondiente a las cargas
sobre los nudos (INCLUYENDO REACCIONES) más el que
incluya las cargas equivalentes Peq en cada grado de libertad.
 Para el cálculo de esfuerzos en una barra deben sumarse los
esfuerzos que se obtienen a partir de los desplazamientos (matriz
de rigidez elemental en coord. locales x desplazamiento en
coordenadas locales) con los esfuerzos de empotramiento perfecto.
cos 0 0 0 0
cos 0 0 0 0
0 0 1 0 0 0
L
0 0 0 cos 0
0 0 0 cos 0
0 0 0 0 0 1
sen
sen
sen
sen
α α
α α
α α
α α
− 
 
 
 
=  
− 
 
 
 
' ' ' 'empP k Pδ= + Las cargas sobre barra crean
esfuerzos de empotramiento
perfecto
El movimiento de los nudos crea
esfuerzos

29. Caso de desplazamientos impuestos o asientosCaso de desplazamientos impuestos o asientos
 Los desplazamientos o giros impuestos en nudos se corresponden con grados
de libertad restringidos
 MÉTODO DIRECTO
◦ Meterlos en el vector de desplazamientos {u}
◦ Resolver el sistema
 MÉTODO INDIRECTO
◦ Considerar sólo sus cargas equivalentes P0
eq
 Ya vimos que todas las ecuaciones del método matricial de la rigidez tienen la forma F=K·u
⇒Fuerzas=Rigidez· Desplazamientos
 Los desplazamientos impuestos ∆ generan unos esfuerzos de empotramiento perfecto:
P’0
emp=k’·∆’= k’·LT
·∆
 Pasándolo a globales y cambiándolo de signo tendremos P0
eq
P0
eq=L· P’0
eq= -L·P’0
emp
Si tenemos ya la matriz k del elemento en globales lo más sencillo es, directamente:
P0
eq= -k·∆
(a)=(b)+(c)
(b) Los nudos están inmóvilizados y aparecen reacciones de
empotramiento debido al asentamiento ∆
(c) Tiene las reacciones de empotramiento cambiadas de
signo (Peq) y no hay asentamiento ESTE ES EL SISTEMA QUE
REALMENTE SE ESTUDIA POR EL M. INDIRECTO

30. Caso de cargas térmicasCaso de cargas térmicas
 Se trata como el método indirecto de los desplazamientos impuestos.
 Se calculan los esfuerzos de empotramiento perfecto P’#
emp y:
◦ P#
eq=L· P’#
eq= -L·P’#
emp
 Una barra biempotrada como esta no puede ni alargarse ni curvarse, por tanto es
como si le impusiésemos desplazamientos y giros en los empotramientos.
1 2
' #
emp
21 2
1 2
0
00
00
( )0
P k'δ' k' k' 2
( )
2
( )
T T
L
u
T T
v L
h
T T
L
h
α
α
θ
α
 
 
   
   
   
+   −= = =   
   
−   
   
   −
 
 
1 2
1 2
' #
emp
1 2
1 2
( )
2
0
( )
P
( )
2
0
( )
T T
EA
T T
EI
h
T T
EA
T T
EI
h
α
α
α
α
+ 
 
 
 
 −
− 
 =
 +
− 
 
 
 −
 
 
El caso de una barra de celosía no
tendría los valores
correspondientes a las coordenadas
de momentos (3º y 6º).

31. Apoyos elásticosApoyos elásticos
 Cada apoyo elástico o muelle tratados individualmente
sólo afectan a un grado de libertad: ej. 1, 2 y 3
 En los muelles las reacciones se obtienen a partir de los
desplazamientos y siempre son opuestas a ellos:
Rmi=-Sm·ui
1
2
3
0 0
siendo 0 0
0 0
ap
ii
k
K k
k
 
 
=  
 
 
ap ap
i ii iy F = K u
A efectos prácticos, lo único que hay que hacer cuando tengamos
un muelle en el grado de libertad n será sumar la rigidez del
muelle en el término correspondiente de la matriz de rigidez
(término nn).

32. Apoyos no concordantesApoyos no concordantes
 Se usará el subíndice L para el caso de concordancia con las coordenadas globales
y D para los grados de libertad de los nodos con restricciones no concordantes.
 Separando por concordancia habría que resolver
 Si tenemos en cuenta que nos interesa trabajar con los vectores u’D y F’D,
correspondientes a los nodos no concordantes, en el sistema de coordenadas local
del nodo:
uD = L· u’D
FD = L ·F’D
0D
u' u'
u' v'
θ' θ'
   
   
= =   
   
   
En coordenadas nodales x’y’
·
LL LL D L
D DL DD D
F K K u
F K u
F K K u
        
= ⇒ =     
         
' 'T T
L LL LD L
D DL DD D
F K K L u
F L K L K L u
        
=     
         