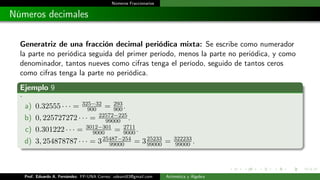
Este documento introduce los conceptos básicos de números fraccionarios y decimales. Explica que una fracción representa el cociente exacto de dos números enteros y clasifica las fracciones en comunes, decimales, propias, impropias y mixtas. También define números decimales exactos, periódicos puros y mixtos, y cómo encontrar la fracción generatriz equivalente para cada tipo de decimal.