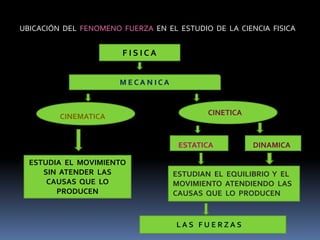
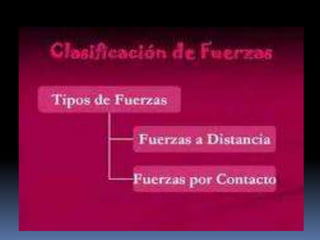
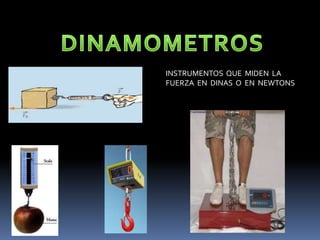
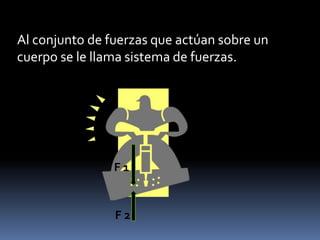
El documento describe las fuerzas físicas, incluyendo su clasificación, propiedades, unidades de medida y conceptos como fuerza resultante, sistemas de fuerzas, equilibrio y composición y descomposición de fuerzas. Explica que una fuerza es una acción capaz de modificar el estado de reposo o movimiento de un cuerpo y que se clasifican en fuerzas de contacto y a distancia, siendo las fundamentales la gravitatoria, eléctrica, nuclear fuerte y nuclear débil.

1. ACCION CAPAZ DE MODIFICAR EL
ESTADO DE REPOSO O
MOVIMIENTO DE UN CUERPO O
TAMBIEN DE CAMBIARLE SU
FORMA

2. UBICACIÓN DEL FENOMENO FUERZA EN EL ESTUDIO DE LA CIENCIA FISICA
F I S I C A
CINEMATICA CINETICA
M E C A N I C A
ESTUDIA EL MOVIMIENTO
SIN ATENDER LAS
CAUSAS QUE LO
PRODUCEN
ESTATICA DINAMICA
ESTUDIAN EL EQUILIBRIO Y EL
MOVIMIENTO ATENDIENDO LAS
CAUSAS QUE LO PRODUCEN
L A S F U E R Z A S

4. FUERZAS DE CONTACTO

5. FUERZAS A DISTANCIA

6. GRAVITATORIAS.
ELECTRICA.
NUCLEAR FUERTE
NUCLEAR DEBIL.
FUERZAS FUNDAMENTALES:

7. Las fuerzas pueden deformar los cuerpos y su
comportamiento ante las deformaciones es
muy distinto. Se clasifican en:
Rigidos.
Elásticos.
Plasticos.

8. LA PLASTICIDAD ES LA PROPIEDAD
POR LA CUAL DETERMINADOS CUERPOS
ADQUIEREN DEFORMACIONES
PERMANENTES CUANDO DEJA DE ACTUAR
SOBRE ESTOS LA FUERZA QUE LOS
DEFORMA.
La elasticidad es una propiedad de la materia
que permite a los cuerpos deformarse cuando
están sometidos a una fuerza y recuperan la
forma inicial cuando la causa de la deformación
desaparece.

9. Medida de las Fuerzas
 PARA MEDIR LA INTESNSIDAD DE LA
FUERZA SE UTILIZA EL DINAMOMETRO
FORMADO POR UN MUELLE QUE DE
ACUERDOCON LA LEY DE HOOKE, SE
ALARGAAL SER SOMETIDO A UNA
FUERZA.

10. INSTRUMENTOS QUE MIDEN LA
FUERZA EN DINAS O EN NEWTONS

11. FUERZA NECESARIA PARA IMPRIMIRLE UNA ACELERACION DE UN CENTIMETRO
SOBRE SEGUNDO CUADRADO A UN GRAMO DE PESO
FUERZA QUE SE REQUIERE PARA IMPRIMIR UNA ACELERACION DE UN METRO
SOBRE SEGUNDO CUADRADO A UN KILOGRAQMO DE PESO
UNIDADES DE MEDICION DE LA FUERZA

12. PUNTO DE APLICACIÓN.— ES EL LUGAR CONCRETO SOBRE EL
CUAL ACTÚA LA FUERZA. EN EL SE COMIENZA A DIBUJAR EL
VECTOR QUE REPRESENTA LA FUERZA.
MAGNITUD O MÓDULO.— INDICA EL VALOR NUMÉRICO DE LA
FUERZA EN NEWTONS. SE CORRESPONDE CON LA LONGITUD DEL
VECTOR.
DIRECCIÓN.— ES LA RECTA A LO LARGO DE LA CUAL SE
APLICA LA FUERZA. LA LÍNEA SOBRE LA QUE SE DIBUJA EL
VECTOR.
SENTIDO.— CON LA MISMA DIRECCIÓN, UNA FUERZA PUEDE
TENER DOS SENTIDOS OPUESTOS. SE INDICA CON LA PUNTA DE
LA FLECHA DEL VECTOR
.
CARACTERISTICAS DE UNA FUERZA

13. C I N ET I C A
ESTATICA Y DINAMICA

14. Al conjunto de fuerzas que actúan sobre un
cuerpo se le llama sistema de fuerzas.
F 1
F 2

15. FUERZA RESULTANTE: ES AQUELLA QUE
PUEDE REEMPLAZAR TODAS LAS
FUERZAS QUE ACTUAN SOBRE UN
CUERPO,Y PRODUCEN EL MISMO
EFECTO.
SISTEMA DE FUERZAS:
Son diversas las fuerzas que actuan al mismo
tiempo sobre un cuerpo.

16. UN CUERPO ESTA EN EQUILIBRIO
CUANDO ESTA EN REPOSO O
CUANDO SE MUEVEN CON UN
MOVIMIENTO RECTILINEOY
UNIFORME.

17. Composición de las Fuerzas: es la operación
que consiste en determinar la fuerza resultante
de la acción de las otras. Se clasifican en:
FUERZAS DE IGUAL DIRECCIÓN Y
SENTIDO.
FUERZAS DE LA MISMA DIRECCIÓN Y
SENTIDO CONTRARIO.
FUERZAS CONCURRENTES.

18. La resultante tiene esa misma dirección y
ese mismo sentido, y su intensidad es la
suma de las intensidades. R = F1 + F2

19. COLINEALES O COPLANARES:
CUANDO ACTUAN EN DIFERENTE PUNTO DE
APLICACIÓN O MODULO, EN LA MISMA DIRECCION Y
EN SENTIDO IGUAL O CONTRARIO .
F2
F1

20. Si las fuerzas tienen el mismo punto de
aplicación se habla de fuerzas
concurrentes también llamadas
angulares.
F 1
F 2
F 3

21. . La fuerza resultante de dos
fuerzas concurrentes se
calcula aplicando la regla
del Paralelogramo.
 Método grafico.

22. Descomposición de las
Fuerzas.
 Cualquier fuerza física podemos
descomponerla en la suma de dos fuerzas o
mas, dirigidas en dos direcciones distintas.
 Según la regla del Paralelogramo
 Fy
 Fr R2 = Fx2 + Fy2
 R = √ Fx2 + Fy2
 Fx

23. Fuerza equilibrante
 Se llama fuerza equilibrante a una fuerza con
mismo modulo y dirección que la resultante
pero de sentido contrario.
 Método Analítico: es aquel donde se utilizan
las proyecciones de un vector a lo largo de los
ejes de un sistema de coordenadas
rectangulares. Estas proyecciones se llaman
componentes.
 Ax = Acos &
 Ay = A sen &

24. La magnitud y dirección de A
están relacionadas por el
teorema de Pitágoras y la
definición de la tangente.
 Magnitud A =√ Ax2 + Ay2
 Ay Dirección: tan & = Ay/ Ax
 A & = tan – 1 = Ay/Ax
 Ax

25. DIBUJE LOS VECTORES A PARTIR DEL PLANO
CARTESIANO.
HALLE LAS COMPONENTES X, Y DE TODOS
LOS VECTORES.
DETERMINE LAS COMPONENTES
PERPENDICULARES DEL VECTOR RESULTANTE.
UTILICE EL TEOREMA DE PITÁGORAS PARA
HALLAR LA MAGNITUD DEL VECTOR
RESULTANTE.
DETERMINE LA DIRECCIÓN DEL VECTOR
RESULTANTE.
Base de Orientación