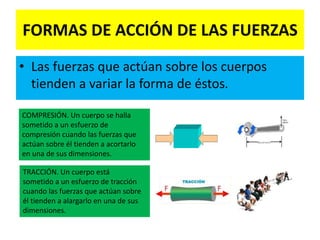
El documento define las fuerzas y sus elementos, incluyendo las unidades de medida como newton y kilopondio, y describe diversos tipos de esfuerzos que las fuerzas pueden generar en los cuerpos, como compresión, tracción y torsión. También se aborda la ley de acción y reacción de Newton, así como métodos para calcular la resultante de fuerzas concurrentes. Finalmente, se mencionan conceptos de descomposición y composición de fuerzas, incluyendo ejemplos de aplicación práctica.

1. FUERZA: APLICACIONES
Jaime Mayhuay Castro
UNIDAD 06

2. DEFINICIÓN.
• FUERZAS Es todo agente capaz de modificar
el estado de reposo o movimiento de un
cuerpo y también produce deformaciones
sobre los cuerpos en los cuales actúa.

3. ELEMENTOS DE UN VECTOR
• A una fuerza lo podemos representar por
vectores. Todos los vectores tienen los
siguientes elementos:
-PUNTO DE APLICACION
-MÓDULO
-DIRECCIÓN
-SENTIDO

4. UNIDADES
• kilopondio. Es la unidad de la
fuerza del sistema técnico. =kg-f
• Newton. Es la unidad de fuerza
del sistema internacional (S.I.)
• Dina. Es la unidad de fuerza del
sistema cegesimal (cgs), está
unidad es sumamente pequeña
y sólo se utiliza en experiencias
de laboratorio.
• Libra fuerza. Es la unidad de
fuerza del sistema inglés.

5. EQUIVALENCIAS
• 1 Kp = 9,8 N = 980 000 dina = 2,2 lb-f
1N = 0,102 Kp 1 lb-f = 0.454 Kp
1 N = 100000 dina

6. FUERZA – PESO.
• El peso, es una fuerza de origen gravitacional
que nos expresa la medida de la interacción
entre la tierra y un cuerpo. Se representa por
un vector vertical y dirigido hacia el centro de
la tierra.
El PESO es el producto de la MASA (m) por la
aceleración de la GRAVEDAD (g).
Gravedad es 9,8 m / s

7. DIAGRAMA DE FUERZA

8. FORMAS DE ACCIÓN DE LAS FUERZAS
• Las fuerzas que actúan sobre los cuerpos
tienden a variar la forma de éstos.
COMPRESIÓN. Un cuerpo se halla
sometido a un esfuerzo de
compresión cuando las fuerzas que
actúan sobre él tienden a acortarlo
en una de sus dimensiones.
TRACCIÓN. Un cuerpo está
sometido a un esfuerzo de tracción
cuando las fuerzas que actúan sobre
él tienden a alargarlo en una de sus
dimensiones.

9. FORMAS DE ACCIÓN DE LAS FUERZAS
FLEXIÓN. Un cuerpo está sometido a
esfuerzos de flexión cuando las fuerzas
actúan perpendicularmente a su eje
longitudinal y tienden a encorvarlo en
dirección de la fuerza.
CIZALLAMIENTO O CORTE. Se produce
esfuerzo de cizallamiento cuando sobre
el cuerpo actúan dos fuerzas con
direcciones superpuestas y sentidos
contrarios. Estas fuerzas tienden a trozar
el cuerpo.
TORSIÓN. Un cuerpo se halla sometido a
esfuerzos de torsión si dos fuerzas actúan
en planos paralelos del cuerpo, de modo
que una de ellas tiende a hacer girar al
cuerpo en un sentido y la otra, en sentido
contrario.

10. FORMAS DE ACCIÓN DE LAS FUERZAS
FLEXION POR FUERZA AXIAL. Se
puede también producir flexión si las
fuerzas actúan en el sentido del eje
del cuerpo, si este tiene cierta
convexidad.

11. ACCIÓN Y REACCIÓN
3ra Ley de Newton
Establece que a toda fuerza de acción le corresponde una fuerza de reacción
simultánea de igual modulo y dirección, pero de sentido opuesto. Esta
presente en nuestra actividad diaria.
Al caminar, se puede constatar que la fuerza se hace para atrás, y sin embargo
nos trasladamos para adelante con una fuerza R.

12. POSICIÓN RELATIVA DE LOS VECTORES
• FUERZAS CONCURRENTES. Son aquellas
cuyas líneas de acción tienen un punto
común.

13. POSICIÓN RELATIVA DE LOS VECTORES
• FUERZAS COLINEALES. Son aquellas que están
ubicadas en una misma recta.

14. OPERACIONES
Con el mismo
sentido: La resultante se
obtiene sumando los
módulos
2.- Sentidos opuestos.
La resultante se obtiene, restan los
módulos

15. VECTORES QUE FORMAN UN ANGULO
3.- Para dos vectores
que forman un ángulo
de 90°
El módulo de éste
vector resultante se
obtiene así:
R =
24 N
7 N

16. VECTORES QUE FORMAN UN ANGULO
3.- Para dos vectores
que forman un ángulo
cualquiera
El módulo de éste
vector resultante se
obtiene así:
R =

17. DESCOMPOSICION DE VECTORES
• Consiste en reemplazar un vector por otros dos,
de tal forma que éstos sean mutuamente
perpendiculares.
Vx = V Cos  Vy = V sen 

18. Ejemplos de Aplicación
Hallar el módulo de la resultante.
* Hallamos “Resultante Horizontal
RH = 120 cos 53º - 90 cos 37º
RH = 120 x - 90 x = 0
Hallamos “Resultante Vertical”
RV = 90 Sen 37º + 120 sen 53º
RV = 90 x + 120 x = 150
La resultante total:
R = = 150

19. HALLAR LA RESULTANTE
A) B)
C) D)

20. 
SUMA DE VECTORES
 la resultante de dos o más fuerzas concurrentes se
puede hallar gráficamente empleando los siguientes
métodos:
MÉTODO DEL PARALELOGRAMO.
Dadas dos fuerzas concurrentes , se trazan
paralelas a las direcciones de cada una de
ellas, de modo que se construye un
paralelogramo, luego se traza la resultante
a partir del origen de las fuerzas.

21. Dadas las dos fuerzas concurrentes se traza una de las
fuerzas a partir del extremo de la otra, manteniendo la
dirección paralela a su línea de acción original; luego se
cierra el triángulo, obteniéndose la resultante.
MÉTODO DEL TRIÁNGULO.

22. Para tres o más fuerzas se aplica éste método.
Se escoge el origen y luego se gráfica una a continuación
de la otra, y la fuerza resultante parte del origen y se
dirige al extremo de la última.
MÉTODO DEL POLÍGONO

23. 
Es proceso por el cual se determina la intensidad,
dirección y sentido de la resultante.
COMPOSICIÓN DE FUERZA

24. 
El procedimiento que determina los componentes de la
fuerza, el cual puede hallarse en forma gráfica y
analíticamente.
DESCOMPOSICIÓN DE FUERZA

25. 
Un jardinero aplica una
fuerza de 50 N sobre la
cortadora de césped,
formando un ángulo de
37° con la horizontal.
Calcular las componentes
de la fuerza que mantiene
pegada a la cortadora con
el césped y la fuerza útil.
PROBLEMA

26. 
El cual establece que la
fuerza resultante de un
sistema de fuerzas que
actúan sobre un cuerpo
debe ser igual a cero.
PRIMERA CONDICIÓN DE
EQUILIBRIO

27. 
Es aquella magnitud vectorial que mide el efecto
rotacional que produce una
fuerza al actuar sobre un cuerpo, respecto de un punto
(A) llamado centro de giros.
MOMENTO DE UNA FUERZA

28. 
Es una
magnitud
vectorial
FORMULA

29. 
 Caso especial
de momento
de fuerzas
Palancas
Inter-apoyante
Inter resistente
Interpotente