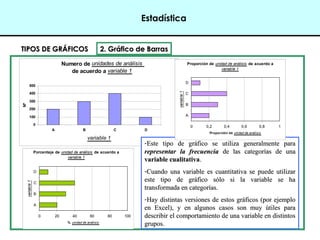
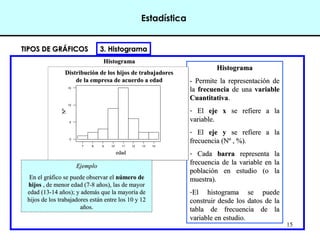
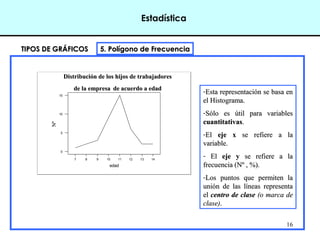
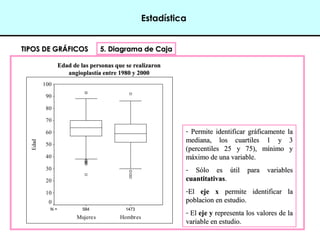
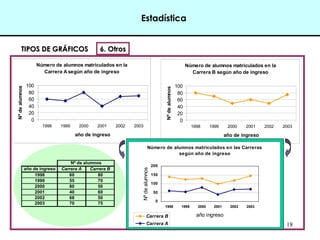
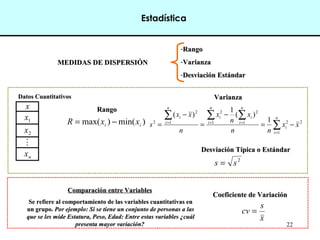
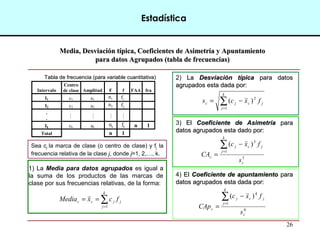
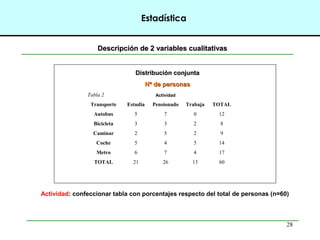
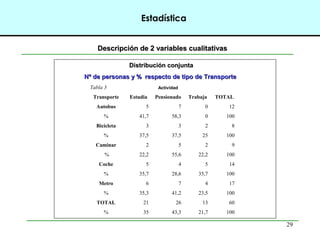
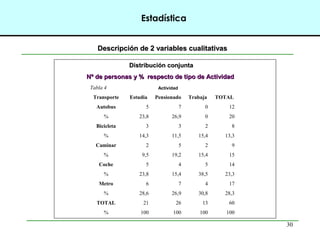
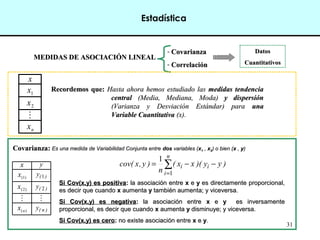
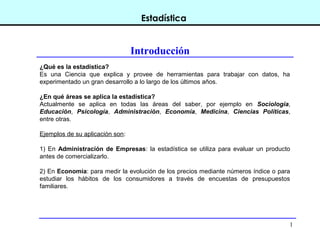
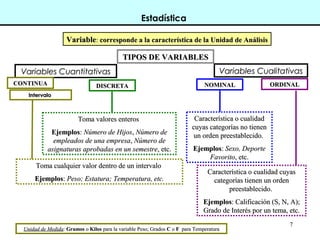
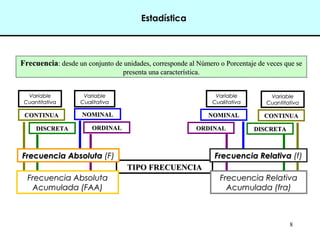
Este documento introduce conceptos básicos de estadística. Explica que la estadística es una ciencia que trabaja con datos para explicarlos y hacer predicciones. Se aplica en diversas áreas como economía, sociología, medicina y administración. Describe las etapas de un estudio estadístico, las variables y sus tipos, y ofrece ejemplos de cómo se podrían plantear problemas de investigación y analizar datos relacionados a la industria de conservas.





![Estadística
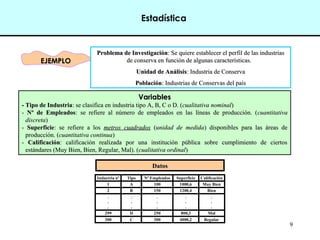
PPrroobblleemmaa ddee IInnvveessttiiggaacciióónn:: SSee qquuiieerree eessttaabblleecceerr eell ppeerrffiill ddee llaass iinndduussttrriiaass ddee ccoonnsseerrvvaa eenn
10
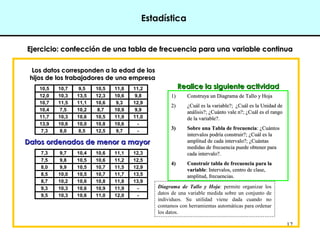
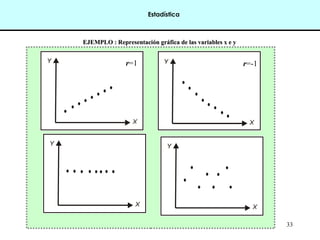
EEJJEEMMPPLLOO
TTAABBLLAASS DDEE
FFRREECCUUEENNCCIIAA
Tipo de
Industria
Frecuencia
Absoluta (Fj)
Frecuencia
Relativa (fj)
Porcentaje
(%)
A
B
C
D
Total 300 1 100
Calificación
Frec.
Absoluta (Fj)
Frec.Relativa
(fj) o %
Frec. Absol.
Acum. (FAAj)
Frec. Relat.
Acum. (fraj) o %
Muy Bien
Bien
Regular
Mal 300 1 (o 100)
Total 300 1 (o 100)
Numero de
Empleados
Frec.
Absoluta (Fj)
Frec.Relativa
(fj) o %
Frec. Absol.
Acum. (FAAj)
Frec. Relat.
Acum. (fraj) o %
<100
[100-150[
..
[950-1000] 300 1 (o 100%)
Total 300 1 (o 100%) Superficie
(mt2)
Frec.
Absoluta (Fj)
Frec.Relativa
(fj) o %
Frec. Absol.
Acum. (FAAj)
Frec. Relat.
Acum. (fraj) o %
<200
[200-400[
..
[50000-5200] 300 1 (o 100%)
Total 300 1 (o 100%)
((11))
((22))
((33))
((44))
ffuunncciióónn ddee aallgguunnaass ccaarraacctteerrííssttiiccaass..
UUnniiddaadd ddee AAnnáálliissiiss:: IInndduussttrriiaa ddee CCoonnsseerrvvaa
PPoobbllaacciióónn:: IInndduussttrriiaass ddee CCoonnsseerrvvaass ddeell ppaaííss](https://image.slidesharecdn.com/presentacinestadstica-140906185310-phpapp01/85/Presentacion-estadistica-10-320.jpg)
![11
Estadística
Elementos de una tabla de frecuencia ccuuaannddoo llaa vvaarriiaabbllee eess ccoonnttiinnuuaa ((xx))
Intervalo
Centro
de clase Amplitud F f FAA fra
I1 c1 a1
I2 c2 a2
.
.
Ik ck ak n 1
Total n 1
[LI1 ; LS1 [
[LI2 ; LS2 [
[LIk ; LSk]
aj = (LSj – LIj)c ) j = (LIj) + LSj )/2](https://image.slidesharecdn.com/presentacinestadstica-140906185310-phpapp01/85/Presentacion-estadistica-11-320.jpg)