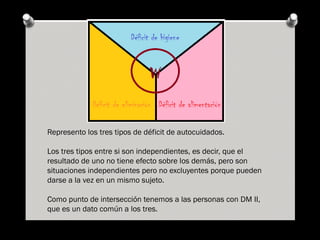
Este documento presenta tres ejercicios sobre probabilidad y estadística relacionados con los déficits de autocuidado en pacientes con diabetes mellitus tipo 2. El primer ejercicio calcula la probabilidad de que un individuo con diabetes tenga déficit en la alimentación. El segundo calcula la probabilidad de déficit en la alimentación y la higiene para personas con diabetes. El tercer ejercicio pide representar gráficamente la situación y explicarla.

1. SEMINARIO 7
PROBABILIDAD Y ESTADÍSTICA

2. Documéntate buscando en la bibliografía
sobre los déficit de autocuidados en
alimentación , higiene y eliminación que tiene
los pacientes con DM II.O
O 1. Calcular la probabilidad de P(AW) que
un individuo elegido al azar.
O 2. Calcular la probabilidad de averiguar:
P(BW) y P(CW).
O 3. Representa la situación en un diagrama y
explícalo.
O 4. Cuélgalo en tu blog portafolio.

3. Ejercicio 1
O Calcular la probabilidad de P(A/W) que un
individuo elegido al azar.
O
O P (W): personas que padecen DM
O P (A): déficit de cuidados en la
alimentación
O

4. DATOS DEL ARTÍCULO
O
O N= 92
O
O P (W) = 22% 0,22
O
O P ( A) = 100% 1
O

5. O
O P (W/A) = probabilidad de encontrar una
persona diabética que tenga déficit de
cuidados en la alimentación.
O Para calcularla tendríamos que utilizar el
teorema de Bayes, pero no se tratan de
datos mutuamente excluyentes por lo
tanto calcularemos su intersección.
O
O P (A∩W) = P(A) . P(W) = 1 . 0,22 = 0,22
22%

6. Ejercicio 2
O Calcular la probabilidad de averiguar:
P(B/W) y P(C/W).
O
O P(B): persona con déficit en la
alimentación
O P(C): persona con déficit en la higiene
O P (corte incorrecto de las uñas)
O P (piel seca)
O

7. DATOS
O P(B) = 80% 0,8
O
O P(C) = P ( uñas) . P ( piel seca) = 0,9 . 0,08 = 0,88
O

8. O Como en el apartado anterior no son datos
excluyentes. Realizamos el mismo
procedimiento.
O
O P(B ∩W) = P(B) . P(W) = 0,8 . 0,22= 0,176
O P(C ∩W) = P(C) . P(W) = 0,88 . 0,22 = 0, 193
O

9. Ejercicio 3
O
O Representa la situación en un diagrama y
explícalo.
O

10. Represento los tres tipos de déficit de autocuidados.
Los tres tipos entre si son independientes, es decir, que el
resultado de uno no tiene efecto sobre los demás, pero son
situaciones independientes pero no excluyentes porque pueden
darse a la vez en un mismo sujeto.
Como punto de intersección tenemos a las personas con DM II,
que es un dato común a los tres.

11. FIN