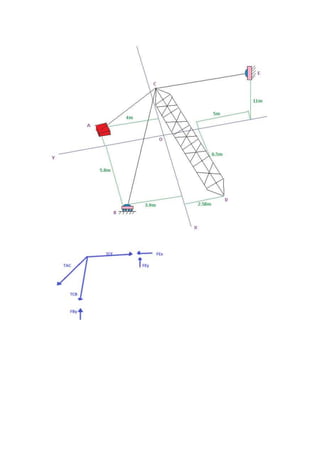
El documento presenta tres problemas relacionados con el cálculo de fuerzas en estructuras. El primer problema involucra determinar la magnitud y ángulos de la fuerza resultante en una torre soportada por tres cables. El segundo problema implica calcular las fuerzas en tres elementos de una armadura abovedada para techo. El tercer problema pide hallar el ángulo b en una figura y luego calcular las fuerzas en tres puntos de una estructura.

1. PROBLEMA ORIGINAL
La torre es sostenida por tres cables. Si las fuerzas en cada cable son las
mostradas, determine la magnitud y los ángulos coordenados de dirección β, ϒ
de la fuerza resultante. Considere x=20 m , y y= 15m
Problemas creados
La torre se encuentra en equilibrio por tres tensiones como se muestra en la
figura determinar la magnitud de la fuerza que se ejerce en la torre de BE, una
vez encontrada hallar la magnitud y los ángulos coordenados de la fuerza
resultante. Considere que AB= 600N ; DB=200N Y CB= 400N.

2. Para la siguiente figura determinar las reacciones que se originan en cada punto
asimismo determinar la magnitud de la fuerza resultante con sus ángulos
directores sabiendo que: AC= 300N, CD= 400N, CB=200N,
CE=500N.(considerar que el punto E conserva la misma altura que la distancia
del punto OC y la tensión CE se ubica en la misma recta del eje “y” tomando la
distancia desde o en “y” )

4. kjikjiTCB
jikjiTCD
kjkjTCE
kjikjiTAC
kji
kjikji
CD
kji
kjikji
CD
kj
kjikji
CE
kji
kjikji
AC
1644090)84.020.045.0(200
6.33780200)84.020.050,0(400
5.411285)823.057.0(500
27910251)93.034.017.0(300
84.030.045.0
033.13
119.39.5
)11()9.3()8.5(
119.38.5
84.020.050.0
035.13
1158.25.6
)11()58.2()5.6(
1158.25.6
823.057.0
359,13
1158.70
)11()58.7()0(
1158.70
93.034.017.0
141
1142
)11()4()2(
1142
222
222
222
222




























En el punto b existe una reacción móvil sin embargo esta no valdría debido a que
las que sostienen la torre solo serian AC y CE pues una torre debe esta sostenida
por un soporte fijo mientras que en el punto E se va a ejercer una reacción igual
que la tensión para mantener un equilibrio.
PROBLEMA ORIGINAL
Una armadura abovedada para techo se carga como indica la figura. Determine
la fuerza presente en los elementes BE, CE, DF










ClbNyFy
ClbAy
AyMN
Ax
Fy
F
3075
2925
)6.33()6.33(150)4.26(1050)2.19(900)8.16(1950)52.11(750)2.7(750)8.4(300
0
?
0

5. )(5026502605550)5.26(cos1175)5.26(cos
)(1175
11750)60.3)(5.26(cos)2.7)(5.26()2.7(1050
)(55500)60.3()2.7(150)2.7(2925
ClbFBDlbFBDFBDFx
ClbFBE
lbFBEFBEsenFBEMA
TlbFCEFCEMB







Problemas creados
La siguiente armadura se carga como se muestra a continuación. Determinar la
fuerza que existe en la reacción de M Y EN LOS PUNTOS GE,DF Y EF.

6. CB= 0 HI=0
lbMylbAY
MyAy
MyAy
MyAy
MyAy
Fy
MyAy
MyAxAy
MF
lbAxAxFx
197)(1397
1200
11080)8()8.6(
1200
100300200300200100
0
011080)8()8.6(
0)8()5(150)5(100)3(200)5(1000)8.1(200)8.3(300)5()8.6(100)8.6(
0
85001501000












Hallar el ángulo b a partir de la figura .Posteriormente determinar las fuerzas que
se encuentran en los puntos de: LI, HG, HB.