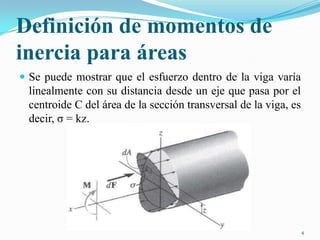
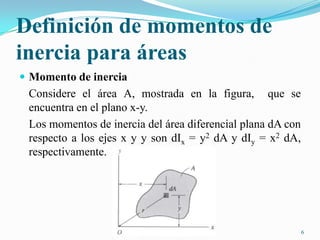
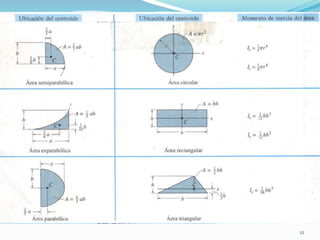
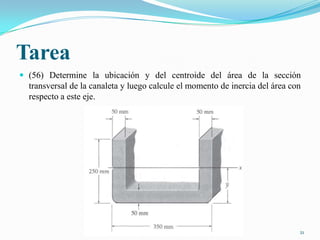
Este documento presenta conceptos sobre momentos de inercia para áreas. Explica cómo calcular los momentos de inercia de un área simple y compuesta con respecto a diferentes ejes utilizando la integración y el teorema de los ejes paralelos. También muestra ejemplos numéricos para practicar el cálculo de momentos de inercia.

1. ESTÁTICA
CAPÍTULO VII
MOMENTOS DE INERCIA
Ing. Andrés Velástegui Montoya, M.Sc.
Facultad de Ingeniería en Ciencias de la Tierra (FICT)
andvelastegui@gmail.com
1

2. Objetivos
 Desarrollar un método para determinar el momento de
inercia de un área
 Presentar el producto de inercia y mostrar cómo
determinar los momentos de inercia máximo y mínimo
de un área
 Analizar el momento de inercia de masa
2

3. Definición de momentos de
inercia para áreas
 En el capítulo anterior determinamos el centroide para un
área considerando el primer momento del área con
respecto a un eje. Para el cálculo tuvimos que evaluar una
integral de la forma ∫xdA.
 A una integral del segundo momento de un área, tal como
∫x2dA, se le llama momento de Inercia para el área.
 El momento de inercia de un área se origina siempre que
relacionamos el esfuerzo normal σ (sigma), o fuerza por
unidad de área, que actúa sobre la sección transversal de
una viga elástica, con el momento M aplicado externo, el
cual causa flexión de la viga.
3

4. Definición de momentos de
inercia para áreas
 Se puede mostrar que el esfuerzo dentro de la viga varía
linealmente con su distancia desde un eje que pasa por el
centroide C del área de la sección transversal de la viga, es
decir, σ = kz.
4

5. Definición de momentos de
inercia para áreas
 La magnitud de la fuerza que actúa sobre el elemento de
área dA, mostrado en la figura, es entonces dF = σ dA =
kz dA.
 Como esta fuerza está localizada a una distancia z del eje
y, el momento de dF con respecto al eje y es dM=dFz =
kz2 dA.
 El momento resultante de la distribución total de esfuerzo
es igual al momento aplicado M; por tanto, M = k ∫z2 dA.
 La integral representa el momento de inercia del área con
respecto al eje y.
5

6. Definición de momentos de
inercia para áreas
 Momento de inercia
Considere el área A, mostrada en la figura, que se
encuentra en el plano x-y.
Los momentos de inercia del área diferencial plana dA con
respecto a los ejes x y y son dIx = y2 dA y dIy = x2 dA,
respectivamente.
6

7. Definición de momentos de
inercia para áreas
 Momento de inercia
Los momentos de inercia son determinados
integración para toda el área; es decir,
por
7

8. Teorema de los ejes paralelos
para un área
 El momento de inercia de un área con respecto a un eje es
igual: al momento de inercia del área con respecto a un eje
paralelo que pase a través el centroide del área, más el producto
del área y el cuadrado de la distancia perpendicular entre los
ejes.
8

9. Radio de giro de un área
 Si se conocen las áreas y los momentos de inercia, los
radios de giro son determinados a partir de las fórmulas.
9

10. Momentos de inercia para
áreas compuestas
 Si el momento de inercia de cada una de esas partes se
conoce o puede ser determinado con respecto a un eje
común, entonces el momento de inercia del área
compuesta es igual a la suma algebraica de los momentos
de inercia de todas sus partes.
10

11. 11

12. 12

13. Momentos de inercia para
áreas compuestas
PROCEDIMIENTO DE ANÁLISIS
 Partes componentes.
Usando un croquis, divida el área en sus partes
componentes e indique la distancia perpendicular desde el
centroide de cada parte hasta el eje de referencia.
13

14. Momentos de inercia para
áreas compuestas
PROCEDIMIENTO DE ANÁLISIS
 Teorema de los ejes paralelos.
El momento de inercia de cada parte debe ser determinado
con respecto a su eje centroidal, que es paralelo al eje de
referencia. Para efectuar el cálculo use la tabla dada.
Si el eje centroidal no coincide con el eje de referencia, el
teorema de los ejes paralelos, I = Ī + Ad2, deberá usarse
para determinar el momento de inercia de la parte con
respecto al eje de referencia.
14

15. Momentos de inercia para
áreas compuestas
PROCEDIMIENTO DE ANÁLISIS
 Sumatoria
El momento de inercia de toda el área con respecto al eje
de referencia es determinado sumando los resultados de
sus partes componentes.
Si una parte componente tiene un "agujero", su momento
de inercia se encuentra "restando" el momento de inercia
del agujero del momento de inercia de toda la parte,
incluido el agujero.
15

16. Ejercicio
 Calcule el momento de inercia del área compuesta mostrada
con respecto al eje x.
16

17. Ejercicio
 Determine los momentos de inercia del área de la sección
transversal de la viga mostrada con respecto a los ejes
centroidales x y y.
17

18. Tarea
 (52) Determine los momentos de inercia del área sombreada con respecto a
los ejes x y y.
18

19. Tarea
 (53) Calcule los momentos de inercia Ix e Iy para el área de la sección
transversal de la viga con respecto a los ejes x y y.
 (54) Determine la distancia Ῡ al centroide C del área de la sección
transversal de la viga y luego calcule el momento de inercia Ī x, con respecto
al eje x'.
19

20. Tarea
 (55) Determine Ῡ, la cual establece el eje centroidal x' del área de la sección
transversal de la viga T, y luego encuentre los momentos de inercia Ī x e Ī y.
20

21. Tarea
 (56) Determine la ubicación y del centroide del área de la sección
transversal de la canaleta y luego calcule el momento de inercia del área con
respecto a este eje.
21