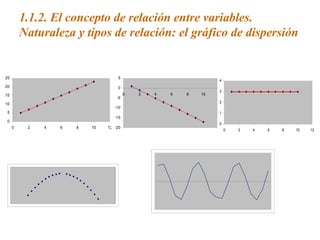
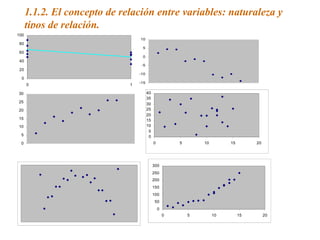
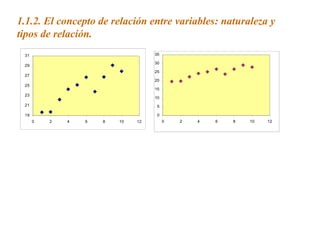
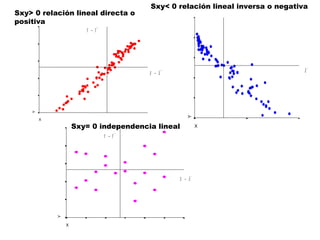
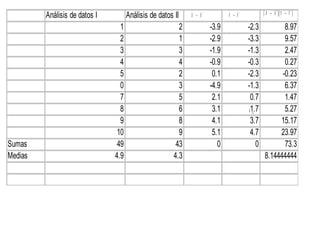
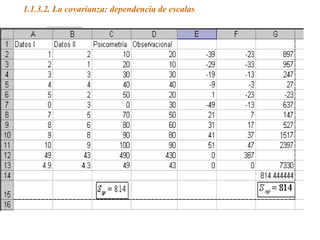
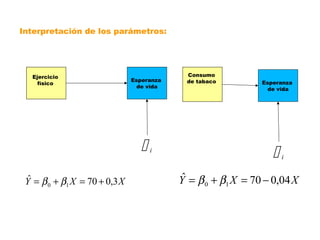
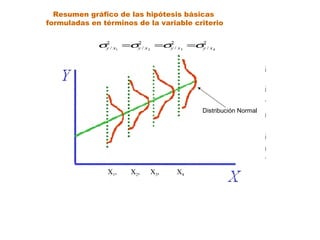
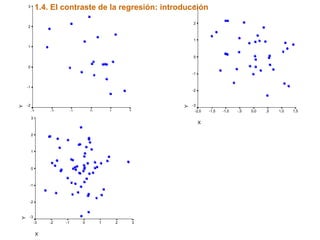
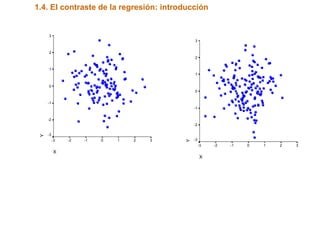
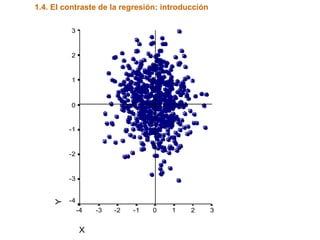
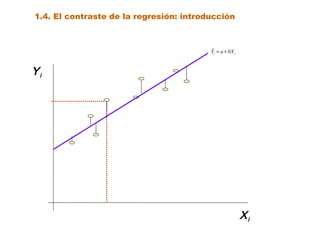
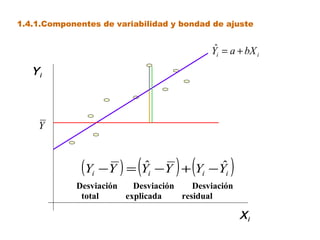
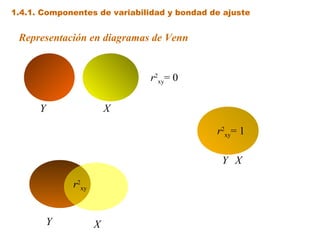
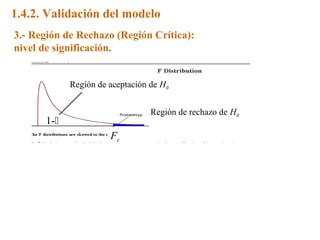
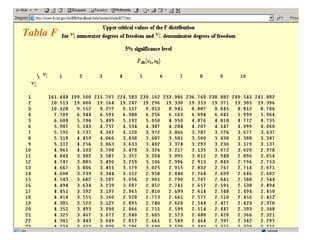
Este documento trata sobre el tema de la regresión lineal simple. Explica el modelo de regresión lineal, incluyendo su estructura, hipótesis y estimación de parámetros. También cubre el contraste del modelo, análisis de residuos, predicción y diagnóstico del modelo. Proporciona ejemplos de cómo se puede utilizar la regresión lineal simple para estudiar diferentes tipos de relaciones entre variables.

1. Tema 1- Regresión lineal simple.
1.1. Introducción
1.2. Especificación del modelo de regresión lineal simple en la población.
1.2.1. Estructura de los modelos de regresión
1.2.2. Hipótesis básicas
1.3. Estimación de los parámetros del modelo de regresión lineal simple
1.3.1. La recta de regresión de mínimos cuadrados en
puntuaciones directas y principales propiedades
1.3.2. La recta de regresión en puntuaciones diferenciales
1.3.3. La recta de regresión en puntuaciones típicas
1.3.4. Relación entre la pendiente de la recta y el coeficiente de
correlación
1.3.5. Interpretación de los coeficientes de la recta de regresión
1.4. El contraste de la regresión
1.4.1.Componentes de variabilidad y bondad de ajuste
1.4.2. Validación del modelo
1.4.3. Significación de parámetros
1.5. Diagnosis del modelo: Análisis de residuos
1.6. Predicción

2. Tema 1- Regresión lineal simple.
1.1. Introducción
1.1.1. Ejemplos de investigaciones en las que puede ser
adecuado utilizar el modelo de regresión simple.
1.1.2. El concepto de relación entre variables: naturaleza y
tipos de relación.
1.1.3. Herramientas para evaluar la relación entre dos
variables
1.1.3.1. El diagrama de dispersión
1.1.3.2. La covarianza
1.1.3.3. El coeficiente de correlación de Pearson

3. 1.1. Introducción
1.1.Ejemplos de investigaciones en las que puede ser adecuado utilizar el
modelo de regresión simple.
Se pretende estudiar si la competencia escolar de niños, medida en
una escala entre 1 y 4, depende del tiempo en meses que llevan
viviendo con un progenitor
Variable dependiente o criterio (endógena) : competencia escolar
Variable independiente o predictora (exógena) : meses de
monoparentalidad
Se pretende estudiar si el ajuste emocional de niños, medido por un
test de ajuste que proporciona puntuaciones en una escala entre 0
y 10, depende del ámbito rural o urbano en el que vive la familia
Variable dependiente o criterio : ajuste emocional
Variable independiente o predictora : ámbito geográfico

4. 1.1. Introducción
1.1.Ejemplos de investigaciones en las que puede ser adecuado utilizar el
modelo de regresión simple.
Se pretende estudiar la relación entre estrés laboral y la variable
trabajo a turno
Variable dependiente o criterio : estrés laboral
Variable independiente o predictora : tipo de turno: fijo o variable
Se pretende estudiar si las notas en Análisis de Datos II dependen
de Análisis de Datos I
Variable dependiente o criterio : Análisis de Datos II
Variable independiente o predictora : Análisis de datos I
Para estudiar empíricamente estas relaciones medimos, en una muestra de sujetos, los valores
de las variables incluidas en la relación. Genéricamente, la información de un sujeto cualquiera de
la muestra Si, vendrá dada por el par (Xi, Yi). El conjunto de pares constituye la matriz de datos
de la investigación y para los ejemplos propuestos tendrá el siguiente formato.

5. Tabla o matriz de datos N=9
Análisis de datos I Análisis de datos II
1 2
Meses comp escolar
2 1 2 4
3 3 18 4
4 4 108 3.66
5 2 24 2.83
0 3 132 2
7 5 60 3.5
8 6 16 2.16
9 8 9 2.66
10 9 84 2.5
N=10
comp escolar ámbito Observar que las variable Turno estrés
ámbito y turno aunque
4 1 0 65
no son métricas las hemos
4 1 codificado como numéricas. 0 76
3.66 1 Hemos elegido el 0 y el 1
para diferenciar entre 0 50
2.83 1 las categorías de las variables. 0 89
2 1 Este tipo de codificación,
muy frecuente en estadística, 0 57
3.5 0 se conoce como codificación 1 45
2.16 0 “dummy” o ficticia
1 34
2.66 0 1 56
2.5 0 1 55
1.83 0 1 61
N=10 N=10

6. 1.1.2. El concepto de relación entre variables.
Naturaleza y tipos de relación: el gráfico de dispersión
25 5
4
20 0
3
15 0 2 4 6 8 10 12
-5
10 2
-10
5 1
-15
0
0
0 2 4 6 8 10 12 -20
0 2 4 6 8 10 12

7. 1.1.2. El concepto de relación entre variables: naturaleza y
tipos de relación.
100
10
80
5
60
0
40
-5
20
-10
0
-15
0 1
30 40
35
25
30
20 25
20
15 15
10 10
5
5 0
0 0 5 10 15 20
300
250
200
150
100
50
0
0 5 10 15 20

8. 1.1.2. El concepto de relación entre variables: naturaleza y
tipos de relación.
31 35
30
29
25
27
20
25
15
23
10
21 5
19 0
0 2 4 6 8 10 12 0 2 4 6 8 10 12

9. 1.1.3.2. La covarianza
N
∑ (X
i =1
i − X )(Y i − Y ) S P C
S = =
x y
N −1 N −1
La covarianza puede tomar valores entre (-∞,+∞) de manera que si:
Sxy= 0 independencia lineal
Sxy> 0 relación lineal directa o positiva
Sxy< 0 relación lineal inversa o negativa
Vamos a ver, utilizando el gráfico de dispersión, porque las relaciones
De orden anteriores están relacionadas con el tipo de relación lineal.

10. Sxy< 0 relación lineal inversa o negativa
Sxy> 0 relación lineal directa o
positiva Y -Y
Y -Y
X - X X - X
Y
Y
X
Sxy= 0 independencia lineal X
Y -Y
X - X
Y
X

11. Análisis de datos I Análisis de datos II X - X Y -Y (X )(
- X Y -Y )
1 2 -3.9 -2.3 8.97
2 1 -2.9 -3.3 9.57
3 3 -1.9 -1.3 2.47
4 4 -0.9 -0.3 0.27
5 2 0.1 -2.3 -0.23
0 3 -4.9 -1.3 6.37
7 5 2.1 0.7 1.47
8 6 3.1 S1.7
xy
5.27
9 8 4.1 3.7 15.17
10 9 5.1 4.7 23.97
Sumas 49 43 0 0 73.3
Medias 4.9 4.3 8.14444444

12. 1.1.3.2. La covarianza: dependencia de escalas

13. 1.1.3.3. El coeficiente de correlación de Pearson
N
S x y
∑ (X
i =1
i − X )(Y i − Y )
r x y = =
S S N N
∑ (X ) ∑ (Y )
x y 2 2
i − X i − Y
i =1 i =1
− 1 ≤ r xy ≤ + 1
rxy = 0
9 12
rxy = 0.88
25
8
10
20 7
6 8
15 5 6
4
10
rxy = 1
4
3
5 2 2
1
0 0
0 0 2 4 6 8 10 12
0 2 4 6 8 10 12 0 2 4 6 8 10
5
0
0 2 4 6 8 10 12
-5
-10
rxy = -1
-15 rxy = -0.88
rxy = 0
-20

14. 1.2. Especificación del modelo de regresión lineal simple en la
población.
1.2.1. Estructura de los modelos de regresión
Xi
predictora
Yi
criterio
 i
independiente dependiente
exógena endógena
explicativa explicada
Expresión matemática del modelo en la población
Y i = f ( X i ) + ε i = β 0 + β 1 X i + ε i = Y i + ε i
Y i = β 0 + β 1 X i Puntuación predicha por la recta de regresión verdadera
ε = Y − Y
i i i Residuo o error de predicción
En el modelo hay dos variables observadas: X e Y y dos parámetros
la ordenada en el origen de la recta de regresión  0 y la pendiente 
1
Interpretación de los parámetros:

15. Interpretación de los parámetros:
Ejercicio Consumo
Esperanza de tabaco Esperanza
físico
de vida de vida
 i
 i
ˆ
Y = β 0 + β1 X = 70 + 0,3 X ˆ
Y = β 0 + β1 X = 70 − 0,04 X

16. 1.2.2. Hipótesis básicas
1. El término de Error es una variable aleatoria con media cero: E (ε i ) = 0
2. Homocedasticidad: la varianza del término de error es constante: Var (ε i ) = σ 2
3. Los errores se distribuyen normalmente: ε i ≈ N (0, σ 2 )
4. Los errores son independientes entre sí.
Las hipótesis anteriores pueden formularse de manera equivalente
en términos de la variable criterio. Así,
YE/( iXα+=) iXβ
E (Y / X i) = α + β X i
1’. La media de Y depende linealmente de E (Y / X i ) = α + β X i
X:
2’. La varianza de Y es constante: Var (Y / X i ) = σ
2
2)
/(XYVar σ=i
3’. La distribución de Y es normal para cada X: Y / X i ≈ N (α + βX i , σ 2 )
4’. Las observaciones Yi son independientes entre sí.

17. Resumen gráfico de las hipótesis básicas
formuladas en términos de la variable criterio
σy / x =σy / x =σy / x =σy / x
2
1
2
2
2 2
3 4
Distribución Normal
X1, X2, X3, X4

18. Resumen gráfico de las hipótesis básicas
formuladas en términos de los residuos

0
X1, X2, X3, X4

19. El objetivo del análisis de regresión será estimar los
parámetros del modelo presentado y contrastar las
hipótesis de partida todo ello a partir de una muestra.

20. 1.3. Estimación de los parámetros del modelo de regresión
lineal simple
1.3.1. La recta de regresión de mínimos cuadrados en
puntuaciones directas y principales propiedades
1.3.2. La recta de regresión en puntuaciones diferenciales
1.3.3. La recta de regresión en puntuaciones típicas
1.3.4. Relación entre la pendiente de la recta y el coeficiente de
correlación
1.3.5. Interpretación de los coeficientes de la recta de regresión

21. 1.3.1. La recta de regresión de mínimos cuadrados en
puntuaciones directas y principales propiedades
Partimos de una muestra de sujetos extraídos de una población
en la que se han tomado valores de las variables X e Y. La situación
más frecuente es que los puntos estén dispersos en el plano definido
por X e Y. La primera pregunta a plantearnos es de las infinitas rectas
que podemos ajustar a la nube de puntos ¿Cuál estimará mejor los
parámetros?. Existen diferentes criterios.

22. 1.3.1. La recta de regresión de mínimos cuadrados en puntuaciones
directas y principales propiedades

8,00

7,00
Y: Análisis de Datos II

6,00
5,00 

4,00
 
3,00
 
2,00

1,00
Y i = a + b X i + e i = Y i + e i
1,00 2,00 3,00 4,00 5,00 6,00 7,00 8,00 9,00 10,00
X: Análisis de datos I
Y i = b 0 + b 1 X i + e i = Y i + e i
Y i = b 0 + b 1 X i
e i = Y i − Y i

23. 1.3.1. La recta de regresión de mínimos cuadrados en
puntuaciones directas y principales propiedades
Criterio de mínimos cuadrados:
∑( ))
N N N
∑ ∑ (Y i − Y i ) Y i − (a + b X
2 2
e i
2
= = i = m in
i =1 i =1 i =1
∂
∑ (Y ))
N
− (a + b X
2
= 0
∂a i =1
i i
∂
∑ (Y ))
N
− (a + b X
2
= 0
∂b i =1
i i

24. 1.4.1. La recta de regresión de mínimos cuadrados en puntuaciones
directas y principales propiedades
Recta de regresión mínimo cuadrática (puntuaciones directas):
a = Y − bX
N
∑ (X
i=1
i − X )( Y i − Y ) S xy Sy
b = 2 = 2 = rxy
N
Sx S xº
∑ (X
i=1
i − X )

Yi = a + b X i = Y + b(X i − X )

25. Ejemplo de cálculo de la recta de regresión de
mínimos cuadrados
x y X X Y Y ( X  X )2 X  X Y  Y 
1 2 -4,5 -2,1 20,25 9,45
2 1 -3,5 -3,1 12,25 10,85
3 3 -2,5 -1,1 6,25 2,75
4 4 -1,5 -0,1 2,25 0,15
5 2 -0,5 -2,1 0,25 1,05
6 3 0,5 -1,1 0,25 -0,55
7 5 1,5 0,9 2,25 1,35
8 4 2,5 2,9 6,25 7,25
9 6 3,5 1,9 12,25 6,65
10 8 4,5 3,9 20,25 17,55
55 41 0 0 82,5 56,5

26. 1.4.1. La recta de regresión de mínimos cuadrados en
puntuaciones directas y principales propiedades
Recta de regresión mínimo cuadrática:
a  Y  bX  4,1  0,743  5,5  0,021
N
 X
i 1
i  X  i  Y 
Y
56,50
b 2   0,743
N
82,50
 X
i 1
i  X

Yi  0,021  0,743 X i
ˆ
Y = 0,021 + 0,742 X i
dependencia de escalas.xls

27. 1.4.1. La recta de regresión de mínimos cuadrados en
puntuaciones directas y principales propiedades
Propiedades de la Recta de regresión mínimo cuadrática:
1) La media de las puntuaciones predichas es igual
a la media de Y
2) Los errores tienen media cero
3) La recta de mínimos cuadrados pasa por el
punto:
4) Los errores no correlacionan ni con la variable predictora
ni con las puntuaciones predichas

28. 1.4.2. La recta de regresión de mínimos cuadrados en
puntuaciones diferenciales
a) Modelo y recta en puntuaciones diferenciales
Y = a + bX + e = (Y − bX ) + bX + e
Y − Y = b( X − X ) + e
y = bx + e
y = bx
ˆ

29. 1.4.2. La recta de regresión de mínimos cuadrados en
puntuaciones estandarizadas
a) Modelo y recta en puntuaciones estandarizadas
y =bx +e
 Sy 
 xy
yi = r
 i +i
x e
 Sx 
yi xi e
= xy
r + i
Sy Sx Sy
Z yi = xy Z xi + ei
r Z
ˆ
Z i = xy Z xi
r

30. Recta de regresión en diferenciales y en tipificadas.
Relación entre b y r. Interpretación de los coeficientes de la
regresión
a) En puntuaciones directas
ˆ
Y = 0,021 + 0,742 X i
b) En puntuaciones diferenciales Sx
rxy = b
y = 0,742 x
ˆ Sy
c) En puntuaciones estandarizadas
ˆ
Z = 0,86 Z x

31. 1.4. El contraste de la regresión: introducción
1,5
1,0
,5
0,0
-,5
-1,0
-1,5
-2,0
Y
-1,0 -,5 0,0 ,5 1,0 1,5
3
X 3
2
2
1 1
0 0
-1
-1
-2
-2
Y -3
-2 -1 0 1 2 3
-3
Y
-3 -2 -1 0 1 2
X
X

32. 3
1.4. El contraste de la regresión: introducción
3
2
2
1
1
0
0
-1
-1
-2
-2 -3
Y
Y
-3 -2 -1 0 1 2 -2,0 -1,5 -1,0 -,5 0,0 ,5 1,0 1,5
3
X X
2
1
0
-1
-2
-3
Y
-3 -2 -1 0 1 2 3
X

33. 1.4. El contraste de la regresión: introducción
3
3
2
2
1
1
0
0
-1
-1
-2
-2
-3
Y
-3 -2 -1 0 1 2 3 -3
Y
-3 -2 -1 0 1 2 3
X
X

34. 1.4. El contraste de la regresión: introducción
3
2
1
0
-1
-2
-3
-4
Y
-4 -3 -2 -1 0 1 2 3
X

35. 1.4. El contraste de la regresión: introducción
ˆ
Yi = a + bX i
Yi
Xi

36. 1.4.1.Componentes de variabilidad y bondad de ajuste
ˆ
Yi = a + bX i
Yi
Y
(Y −Y ) = (Y −Y ) + (Y −Y )
i
ˆ
i
ˆ
i i
Desviación Desviación Desviación
total explicada residual
Xi

37. 1.4.1. Componentes de variabilidad y bondad de ajuste
∑ (Y − Y ) = ∑ (Yˆ − Y ) + ∑ (Y − Yˆ )
N 2 N 2 N 2
i i i
i =1 i =1 i =1
SCt  SCexp  SCres
Variación Variación Variación
Total Explicada Residual
Xi

38. 1.4.1. Componentes de variabilidad y bondad de ajuste
Fórmulas para calcular las sumas de cuadrados en
puntuaciones directas y diferenciales:
2
 N 
N 2 N N
  Yi 
 i1 
SCt   Y
i1
i  Y   
i1
y 2
i  
i1
Yi 2 
N
  N  1S y
2
  N  
2
 ∑ Xi  
( )  
2 2
∑( X − X )
N N N N
SCexp = ∑ Y − Y
ˆ =b 2
= b 2 ∑ xi2 = b 2  ∑ X i2 −  i =1   = b 2 ( N − 1) S x
2
i =1 i =1 i =1  i =1 N 
 
 
( ) = ∑e
N 2 N
SCres = ∑ ˆ
Yi − Yi 2
i = SCt − SCexp
i =1 i =1

39. 1.4.1. Componentes de variabilidad y bondad de ajuste
Fórmulas para calcular las sumas de cuadrados en
tipificadas:
SCt  SCexp  SCres
N
SCt = ∑ Z y = N − 1
2
i =1
N N
SCexp = ∑ Z = r
ˆ
i
2 2
xy ∑ Z x = rxy ( N − 1)
2 2
i =1 i =1
SCres = ( N − 1) 1 − rxy
2
( )

40. 1.4.1. Componentes de variabilidad y bondad de
ajuste SCt SCexp SCres
 
SCt SCt SCt
1  R 2    R2 
1
Bondad de ajuste o Coeficiente de
determinación
∑(Y −Y )
N 2
ˆ
b2 ( X − X )
2
SCexp i
b2Sx2
R =
2
= i=1
= = = rxy
2
∑(Y −Y ) ∑(Y −Y )
N N 2
SCt 2 2 Sy
i i
i=1 i=1

41. 1.4.1. Componentes de variabilidad y bondad de ajuste
Representación en diagramas de Venn
r2xy= 0
Y X
r2xy= 1
Y X
r2xy
Y X

42. 1.4.2. Validación del modelo
Esquema del Contraste de Hipótesis
Contrastar una Hipótesis Estadísticamente es juzgar si cierta
propiedad supuesta para una población es compatible con lo
observado en una muestra de ella.

43. Elementos de una Prueba de Hipótesis
1.- Hipótesis Nula (H0), Hipótesis
Alternativa.
2.- Estadístico de Contraste (Discrepancia).
3.- Región de Rechazo (Región Crítica):
nivel de significación.
4.- Regla de Decisión.

44. 1.4.2. Validación del modelo
1.- Hipótesis Nula (H0), Hipótesis Alternativa.
H 0 : E ( Y / X ) = β 0 = µ ⇒ Yi = µ + ε i
H1 : E ( Y / X ) = β 0 + β 1 X i ⇒ Yi = β 0 + β 1 X i + ε i
2.- Estadístico de Contraste (Discrepancia).
2
SCexp rxy
2
S exp k K
F   
2
Sres SC res 2
1  rxy
N K1 N  K 1

45. 1.4.2. Validación del modelo
3.- Región de Rechazo (Región Crítica):
nivel de significación.
Región de aceptación de H0
Región de rechazo de H0
1-
Fc

46. 1.4.2. Validación del modelo
4.- Regla de Decisión.
Se rechaza la H0 si:
F >Fc
o de manera equivalente si:
p<
Por el contrario, se acepta la H0 si:
F  ≤Fc
o de manera equivalente si:
p ≥

47. Tabla F

48. Tabla F

49. 1.4.3. Significación de parámetros
1.- Hipótesis Nula (H0), Hipótesis Alternativa.
H0 :  1  0 H1 :  1  0
H0 :   0 H1:   0
2.- Estadístico de Contraste (Discrepancia).
b  1 b b rxy  
t    
Sb 2
S res 2
S res 2
1  rxy
N 2
2  N  N  2
 X
i 1
i  X
N
  Xi 
 i 1 
 X i2 
N
i1
Nota: en regresión simple t2 = F

50. 1.4.3. Significación de parámetros
3.- Región de Rechazo (Región Crítica):
nivel de significación.
Región de aceptación de H0
 
2 1  2
∀
Fc
Regiones de rechazo de H0

51. 1.4.3. Significación de parámetros
4.- Regla de Decisión.
Se rechaza la H0 si:
t  >+tc
o de manera equivalente si:
p<
Por el contrario, se acepta la H0 si:
 t  ≤  +tc
o de manera equivalente si:
p≥

52. http://www.stat.ucla.edu/~dinov/courses_students.dir/Applets.dir/T-table.html

53. Tabla t de Student

54. Calculadoras estadísticas en internet
http://faculty.vassar.edu/lowry/VassarStats.htm
http://members.aol.com/johnp71/pdfs.html
http://davidmlane.com/hyperstat/F_table.html
http://davidmlane.com/hyperstat/t_table.html
http://www.psychstat.missouristate.edu/introbook/tdist.htm
http://www.psychstat.missouristate.edu/introbook/fdist.htm
http://calculators.stat.ucla.edu/cdf/

55. 1.6. Predicción
Intervalos de predicción:
 
Y o : Y ± t ( α , N 2 

S res 1 +
1
+
(X − X )
o
2 

− K −1 )  N N

∑ (X − X )
2
 
 i =1
i
