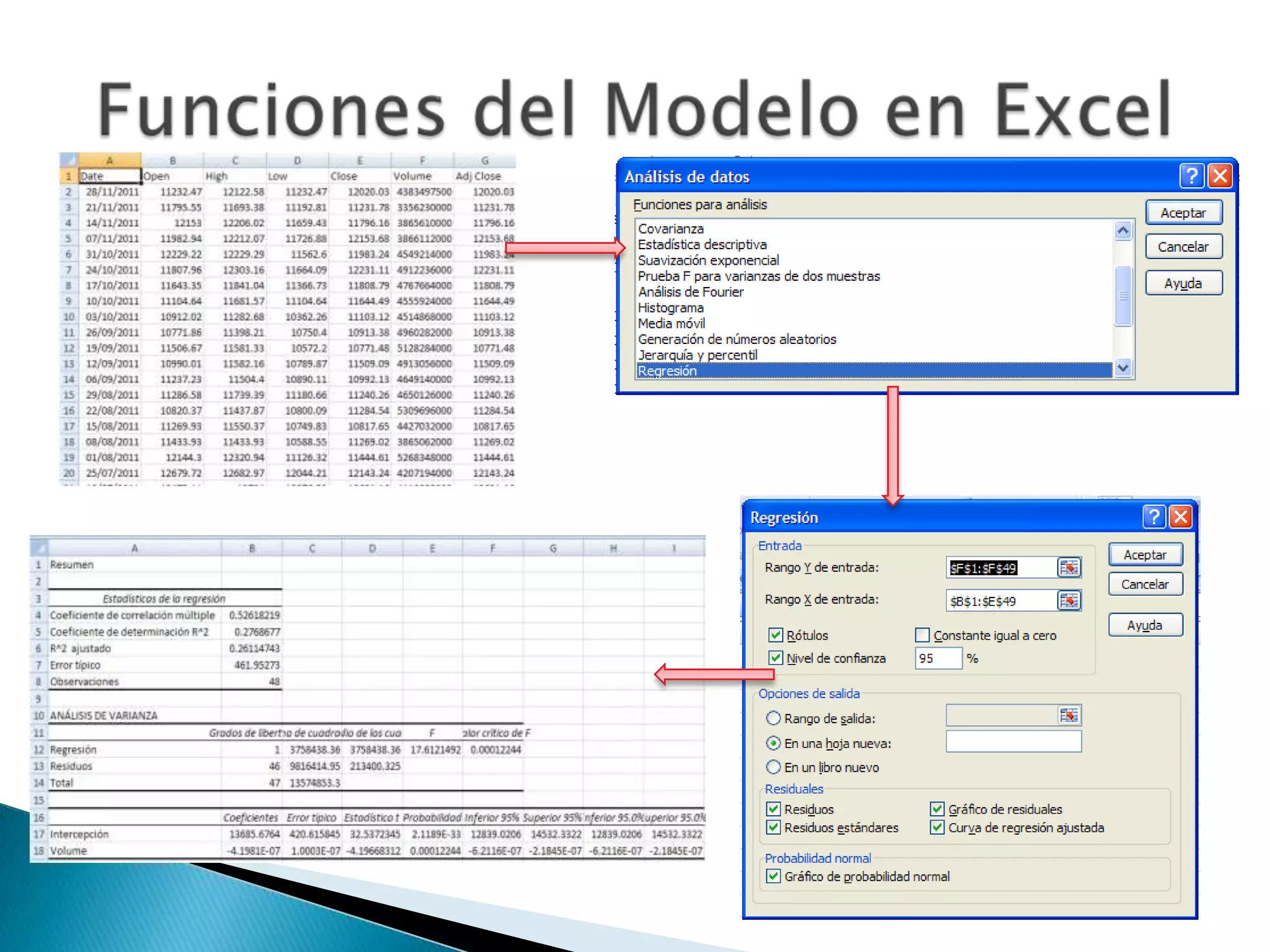
Este documento describe el análisis de regresión múltiple, incluyendo la ecuación de regresión múltiple y el error estándar múltiple de estimación. También cubre el coeficiente múltiple de determinación, las hipótesis de normalidad, homocedasticidad e independencia de errores, y cómo detectar cuando estas hipótesis no se cumplen. Finalmente, explica cómo predecir valores utilizando un modelo de regresión múltiple.

1. LEONARDO LÓPEZ C.
ECONOMIA ESTADISTICA COMPUTARIZADA
PARALELO: 261

2.  Este tipo se presenta cuando dos o más variables independientes
influyen sobre una variable dependiente. Ejemplo: Y = f(x, w, z).
 Objetivo: Se presentara primero el análisis de regresión múltiple al
desarrollar y explicar el uso de la ecuación de regresión múltiple,
así como el error estándar múltiple de estimación. Después se
medirá la fuerza de la relación entre las variables independientes,
utilizando los coeficientes múltiples de determinación.

3. Dispone de una ecuación con dos variables independientes
adicionales:
Se puede ampliar para cualquier número "m" de variables
independientes:

4. Para poder resolver y obtener y en una ecuación de regresión
múltiple el cálculo se presenta muy tediosa porque se tiene atender
3 ecuaciones que se generan por el método de mínimo de
cuadrados:

5. El error estándar
Es una medida de dispersión la estimación se hace más precisa
conforme el grado de dispersión alrededor del plano de regresión
se hace mas pequeño.
Para medirla se utiliza la formula:
Y : Valores observados en la muestra
: Valores estimados a partir a partir de la ecuación de
regresión
n : Número de datos
m : Número de variables independientes

6. El coeficiente de determinación múltiple
Mide la tasa porcentual de los cambios de Y que pueden ser
explicados por X1, X2 y X3 simultáneamente.

7. La hipótesis de normalidad afirma que los errores del
modelo siguen una distribución normal. Esta hipótesis se contrasta
a partir de los residuos estandarizados i = 1n.
 Gráficos para observar la normalidad son: el histograma, estimador
núcleo de la densidad de Rosenblatt-Parzen, gráfico p - p y
gráfico q - q.
 Contrastes de normalidad son: contraste de asimetría y kurtosis,
contraste chi-cuadrado, contraste de Kolmogorov-Smirnov-Liliefors.
La falta de normalidad influye en el modelo en:
 Los estimadores mínimo-cuadráticos no son eficientes (de mínima
varianza).
 Los intervalos de confianza de los parámetros del modelo y los
contrastes de significación son solamente aproximados y no
exactos.

8. Causas que dan origen a la falta de normalidad son:
 Existen observaciones heterogéneas: el modelo especificado no es
correcto porque se han omitido variables regresoras
 Existe asimetría en la distribución: Este problema suele estar
relacionado con otros problemas como falta de linealidad o
heterocedasticidad, la solución de transformar las observaciones
pueden resolverlos conjuntamente.

9. Una hipótesis del modelo de regresión es la homocedasticidad y
todo lo comentado sobre este problema en el modelo de regresión
lineal simple sigue siendo válido en el modelo de regresión
lineal múltiple.
La falta de homocedasticidad influye en el modelo de regresión
lineal, los estimadores mínimo-cuadráticos siguen siendo centrados
pero no son eficientes y las fórmulas de las varianzas de
los estimadores de los parámetros no son correctas. Por tanto no
pueden aplicarse los contrastes de significación.

10. La heterocedasticidad se detecta en los gráficos de residuos:
 De forma general, en el gráfico de residuos frente a las
predicciones .
 En el gráfico de residuos frente a una variable explicativa si se
sospecha que la heterocedasticidad es debida a la variable
explicativa Xj.
 Si los gráficos anteriores son dudosos se pueden hacer grupos de
los residuos ordenados de menor a mayor según las predicciones y
en cada grupo calcular la media de las predicciones y la desviación
típica de los residuos . Si hay homocedasticidad, la nube de
puntos se ajusta a una recta horizontal, en caso contrario, es
necesario transformar los datos.
 Existen contrastes específicos para contrastar la homocedasticidad.

11. La independencia de los errores es una hipótesis básica en el estudio
de un modelo de regresión lineal.
La falta de cumplimiento de la hipótesis de independencia tiene
efectos graves sobre los resultados del estudio. Influye en:
 Los estimadores son centrados pero ineficientes (no son de varianza
mínima).
 El estimador R2 normalmente subestima el parámetro 2, lo que hace
que los contrastes de significación (contrastes individuales de la t) no
sean válidos y tienden a detectar relaciones inexistentes,
denominadas relaciones espúreas, que son relaciones falsas entre
variables independientes que siguen una evolución análoga en el
tiempo y tienen un R2 alto.
 Las predicciones son ineficientes.
 La falta de independencia se suele dar situaciones en que las
observaciones son recogidas secuencialmente en el tiempo. Esto
ocurre en el estudio de muchas variables económicas, sociales y
demográficas. En este caso la variable “tiempo” puede ser una variable
regresora.

12. Se detecta la falta de independencia en:
 Los siguientes gráficos: el gráfico de residuos frente al índice (o
tiempo), ; el gráfico de frente a ; el gráfico de la función de
autocorrelación simple de los residuos (fas).
 Los siguientes contrastes de independencia: el contraste de Durbin-
Watson sobre el primer coeficiente de correlación; el contraste de
Ljung-Box sobre las autocorrelaciones que se consideren significativas.

13. Si existe dependencia entre las observaciones la metodología descrita
para estudiar los modelos de regresión lineal general por mínimos
cuadrados ordinarios no es válida y, en la mayoría de las situaciones,
deben utilizarse técnicas de series de tiempo y regresión dinámica.
En algunas situaciones se pueden estimar los parámetros del modelo
de regresión por el método de mínimos cuadrados generalizados.

14. Se desea predecir el valor de la respuesta, Y , de un individuo del que
se sabe que = t , utilizando el ajuste de un modelo de regresión
lineal de la variable Y respecto al vector de variables regresoras .
El predictor que minimiza el Error Cuadrático Medio de
Predicción, E viene dado por:
Por tanto, la predicción de Y t = Y/ = t es el mismo valor que se
obtiene en la estimación de mt pero su varianza es mayor.